We propose a generic spatial domain control scheme for a class of nonlinear rotary systems of variable speeds and subject to spatially periodic disturbances. The nonlinear model of the rotary system in time domain is transformed into one in spatial domain employing a coordinate transformation with respect to angular displacement. Under the circumstances that measurement of the system states is not available, a nonlinear state observer is established for providing the estimated states. A two-degree-of-freedom spatial domain control configuration is then proposed to stabilize the system and improve the tracking performance. The first control module applies adaptive backstepping with projected parametric update and concentrates on robust stabilization of the closed-loop system. The second control module introduces an internal model of the periodic disturbances cascaded with a loop-shaping filter, which not only further reduces the tracking error but also improves parametric adaptation. The overall spatial domain output feedback adaptive control system is robust to model uncertainties and state estimated error and capable of rejecting spatially periodic disturbances under varying system speeds. Stability proof of the overall system is given. A design example with simulation demonstrates the applicability of the proposed design.

1. Introduction

Rotary systems play important roles in various industry applications, for example, packaging, printing, assembly, fabrication, semiconductor, robotics, and so forth. Design of control algorithm for a motion system often comes up with nonlinearities and uncertainties. Nonlinearities are either inherent to the system or due to the dynamics of actuators and sensors. Uncertainties are mainly caused by unmodeled dynamics, parametric uncertainty, and disturbances. For dealing with nonlinearities, common techniques, for example, feedback linearization and backstepping, are to utilize feedback to cancel all or part of the nonlinear terms. On the other hand, design techniques for conducting disturbance rejection or attenuation in control systems mostly originate from the internal model principle [1], for example, those incorporating or estimating the exosystem of the disturbances [2–6]. Conventional controllers are mostly time-based controllers as they are synthesized and operate in temporal or time domain. Several researches [7–9] have started studying spatial domain controllers ever since a repetitive controller design was initiated by Nakano et al. [10]. In the design of Nakano et al., the repetitive control system has its repetitive kernel (i.e., e^−Ls with positive feedback) synthesized and operated with respect to a spatial coordinate, for example, angular position or displacement. Hence its capability for rejecting or tracking spatially periodic disturbances or references will not degrade when the controlled system operates at varying speed. All existing studies propose design methods starting with a linear time-invariant (LTI) system. After reformulation, a nonlinear open-loop system is obtained in spatial domain. Subsequently, the open-loop system is either linearized around an operating speed or regarded as a quasi-linear parameter varying (quasi-LPV) system and then adjoined with the spatial domain internal model of the tracking or disturbance signal. Design paradigms based on linear (robust) control theory are then applied to the resulting augmented system. However, presuming the open-loop system to be LTI and resorting to design paradigm of linear control will inevitably restrict the applicability and limit the achievable performance of a design method. Chen and Yang [11] introduced a new spatial domain control scheme based on a second-order LTI system with availability of state measurements. To achieve robust stabilization and high-performance tracking, a two-module control configuration is constructed. One of the modules utilizes adaptive backstepping with projected parametric adaptation to robustly stabilize the system. The other module incorporates a spatial domain internal model of the disturbances cascaded with a loop-shaping filter to improve the tracking performance.

This paper extends the work of Chen and Yang [11, 12]. The control scheme has been generalized such that it is applicable to a class of nonlinear systems (instead of just LTI systems). Moreover, the major shortcoming in Chen and Yang’s design [11], that is, which requires full-state feedback, is resolved by incorporation of a nonlinear state observer. Various types of nonlinear state observers have been developed and put into use in the past (e.g., [13, 14]). This paper will study the feasibility of incorporating a K-filter-type state observer [13] into the proposed design. The proposed system incorporating the state observer can be proved to be stable under bounded disturbance and system uncertainties. An illustrative example is given for demonstration and derivation of the control algorithm. Simulation is performed to verify the feasibility and effectiveness of the proposed scheme. Compared to the preliminary work in [12] (which is only applicable to second order systems), the results have been generalized to be suited for nth order systems. Specifically, the design and stability proof are more comprehensive and rigorous than those presented in [12].

Recently, there have been emerging design techniques based on adaptive fuzzy control (AFC), which may cope with nonlinearities and uncertainties with unknown structures [15–17]. The major differences between those techniques and the proposed one are as follows: (1) design being time based (AFC) versus spatial based (the proposed approach); (2) assuming less information about the nonlinearities/uncertainties (AFC) versus more information about the nonlinearities/uncertainties (the proposed approach). Note that the spatial-based design is not just a change of the independent variable from time to angular displacement. A nonlinear coordinate transformation is actually involved. Therefore, the systems under consideration in AFC and the proposed method are different. Next, the capability of the design approaches suggested in AFC for tackling systems subject to a more generic class of nonlinearities/uncertainties lies in the usage of a fuzzy system to approximate those nonlinearities/uncertainties. It is actually not clear regarding the complexity of the fuzzy system (i.e., number of membership functions) that should be used to achieve the required control performance. It is also not clear whether or not the control effort is reasonable. In general, when characteristics of the uncertainties or disturbances are known, such information should be incorporated as much as possible into the design to enhance performance, avoid conservativeness, and result in sensible control input. Hence, instead of assuming the disturbances to be generic (probably just being bounded as by AFC), the proposed design is aiming at a type of disturbances specific to rotary systems and utilizes the spatially periodic nature of the disturbances to establish a well-defined control module integrated into the overall control configuration.

This paper is organized as follows. Reformulation of a generic nonlinear rotary system with respect to angular displacement will be presented in Section 2. Design of the state observer is described in Section 3. Section 4 will cover derivation and stability analysis of the proposed spatial domain output feedback control scheme. Simulation verification for the proposed scheme will be presented in Section 5. Conclusion is given in Section 6.

2. Problem Formulation

In this section, we show how a generic NTI model can be transformed into an NPI model by choosing an alternate independent variable (angular displacement instead of time) and defining a new set of states (or coordinates) with respect to the angular displacement. Note that the transformation described here is equivalent to a nonlinear coordinate transformation or a diffeomorphism. The NPI model will be used for the subsequent design and discussion,

()

where

, Ψ = [1 0 ⋯ 0], and u(t) and y(t) correspond to control input and measured output angular velocity of the system, respectively. d_y(t) represents a class of bounded output disturbances which constitutes (dominant) spatially periodic and band-limited (or nonperiodic) components. Here we refer band-limited disturbances to signals whose Fourier transform or power spectral density is zero above a certain finite frequency. The only available information of the disturbances is the number of distinctive spatial frequencies and the spectrum distribution for band-limited disturbance components. f_t(x(t), ϕ_f) and g_t(x(t), ϕ_g) are known vector-valued functions with unknown but bounded system parameters, that is, ϕ_f = [ϕ_f1 ⋯ ϕ_fk] and ϕ_g = [ϕ_g1 ⋯ ϕ_gl]; Δf_t(x(t), ϕ_f) and Δg_t(x(t), ϕ_g) represent unstructured modeling inaccuracy, which are also assumed to be bounded. Instead of using time t as the independent variable, consider an alternate independent variable θ = λ(t), that is, the angular displacement. Since by definition

()

where ω(t) is the angular velocity, the following condition:

()

will guarantee that λ(t) is strictly monotonic such that t = λ⁻¹(θ) exists. Thus all the variables in the time domain can be transformed into their counterparts in the θ-domain, that is,

()

where we denote

as the θ-domain representation of ∙. Note that, in practice, (2.3) can usually be satisfied for most rotary systems where the rotary component rotates only in one direction. Since

()

Equation (2.1) can be rewritten as

()

Equation (2.6) can be viewed as a nonlinear position-invariant (as opposed to the definition of time-invariant) system with the angular displacement θ as the independent variable. Note that the concept of transfer function is still valid for linear position-invariant systems if we define the Laplace transform of a signal

in the angular displacement domain as

()

This definition will be useful for describing the linear portion of the overall control system.

3. Nonlinear State Observer

Drop the θ notation and note that (2.6) can be expressed as a standard nonlinear system:

()

where terms involving unstructured uncertainty are merged into

with

()

In addition, we have

()

The state variables have been specified such that the angular velocity

is equal to

, that is, the undisturbed output

. It is not difficult to verify that (3.1) has the same relative degree in

as the NTI model in (2.1). If (3.1) has relative degree r, we can define the following nonlinear coordinate transformation:

()

where ψ₁ to ψ_n−r are chosen such that

is a diffeomorphism on D₀ ⊂ D and

()

With respect to the new coordinates, that is,

and

, (3.1) can be transformed into the so-called normal form, that is,

()

where

and

come from

going through the indicated coordinate transformation.

, and (A_c, B_c, C_c) is a canonical form representation of a chain of r integrators. The first equation is called internal dynamics and the second is called external dynamics. Internal dynamics which is not affected by the control u. By setting

in that equation, we obtain

()

which is the zero dynamics of (3.1) or (3.6). The system is called minimum phase if (3.7) has an asymptotically stable equilibrium point in the domain of interest. To allow us to present the proposed algorithm and stability analysis in a simpler context, we will make the following assumptions for the subsequent derivation:

(1)
and are linearly related to those unknown system parameters, that is,
()
(2)
Equation (3.1) is minimum phase, and the internal dynamics in (3.6) is ISS (input-to-state stable).
(3)
The output disturbance is sufficiently smooth, that is, exist.
(4)
exist, that is, the transformed unstructured uncertainty is sufficiently smooth.
(5)
The reference command and its first r derivates are known and bounded. Moreover, the signal is piecewise continuous.

With assumption (2), we focus on designing a nonlinear state observer for external dynamics of (3.6),

()

Since

and

are linearly related to system parameters,

and

can be written as

and

, where

and

are two nonlinear functions, and

, where ℓ is the number of unknown parameters. Next, we adopt the following observer structure:

, where

is the estimate of z₁, and

and

are nonlinear functions with the same structure as W_f(x) and W_g(x) except that each entry of x is replaced by y. Furthermore,

()

By properly choosing

, the matrix A₀ can be made Hurwitz. Define the state estimated error as

. The dynamics of the estimated error can be obtained as

, where

. To proceed, the role of the state observer is replaced by

and the following two K-filters:

()

such that

and Ω^T≜[v₁ ⋯ v_ℓ] ∈ ℝ^r×ℓ. Decompose the second equation of (3.11) into

, where e_r = [0 ⋯ 0 1] ∈ ℝ^r and σ_j = w_1j + w_2ju with w_1j and w_2j are the jth columns of

and

, respectively. With the definition of the state estimated error ε, the state estimate

, and (3.11), we acquire the following set of equations which will be used in the subsequent design:

()

where •_j,i denotes the ith row of •_j.

4. Spatial Domain Output Feedback Adaptive Control System

To apply adaptive backstepping method, we firstly rewrite the derivative of output

()

With the second equation in (3.12), (4.1) can be written as

()

where

In view of designing output feedback backstepping with K-filters, we need to find a set of K-filter parameters, that is, v_ℓ,2, … , v_1,2, separated from

by the same number of integrators between

and

. From (3.11), we can see that v_ℓ,2, …, v_1,2 are all candidates if w_2j are not zero. In the following derivation, we assume that v_ℓ,2 is selected. Hence, the system incorporating the K-filters can be expressed as

()

To apply adaptive backstepping to (4.3), a new set of coordinates will be introduced

()

where

is the prespecified reference command and α_i−1 is the virtual input which will be used to stabilize each state equation. For simplicity, we define

for subsequent derivations.

Step 1 (i = 1). With (4.4), the first state equation of (4.3) can be expressed as

()

Consider a Lyapunov function

and calculate its derivative

()

Define the estimates of ϕ_i as

and

, where

. Note that Θ is the “true” parameter vector while

is the estimated parameter vector. Design the virtual input α₁ as

and specify

()

where c_i, d_i, g_i are variables. Therefore, (4.6) becomes

()

where

Step 2 (i = 2, …, r − 1). With respect to the new set of coordinates (4.4), the second equation of (4.3) can be rewritten as

()

Consider a Lyapunov function

and its derivative

()

Specify

()

The derivative of V_i becomes

()

where

Step 3. With respect to the new set of coordinates (4.4), the third equation of (4.3) can be written as

()

The overall Lyapunov function may now be chosen as

()

where Γ is a symmetric positive definite matrix, that is, Γ = Γ^T > 0. With the definition of state estimated error ε, we can obtain that

()

Specify the control input as

()

where

is an addition input which will be used to target on rejection of uncertainties.

Substituting (4.16) into , we have

()

Write

and we arrive at

()

From (4.18), we may specify the parameter update law in order to cancel the term

. To guarantee the estimated parameters will always lie within allowable region w, a projected parametric update law will be specified as

()

where w is the allowable parameter variation set (compact and convex) with its interior and boundary denoted by w⁰ and ∂w, respectively. If the current estimated parameter vector lies within the allowable parameter variation set, normal update law is employed. If the current estimated parameter vector lies on the boundary of the allowable parameter variation set, projected update law denoted by P_R(·) is employed to prevent the parameter vector from leaving the variation set. With (4.19), (4.18) can be written as

()

Add and subtract terms

; we have

()

Moreover, we obtain

()

As shown in Figure 1, the tracking error

and the control input

are related by

()

where we have chosen

as a low-order and attenuated-type internal model filter, that is,

()

where k is the number of periodic frequencies to be rejected, ω_ni is determined based on the ith disturbance frequency in rad/rev, and ξ_i and ζ_i are two damping ratios that satisfy 0 < ξ_i < ζ_i < 1. We can adjust the gain of

at those periodic frequencies by varying the values of ξ_i and ζ_i.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The control configuration for the proposed spatial domain adaptive control system.

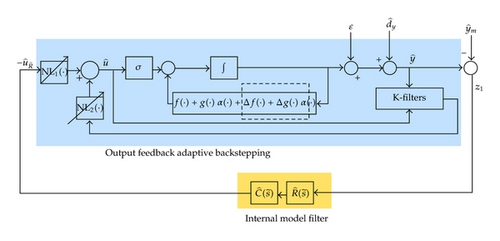
Theorem 4.1. Consider the control law of (4.16) and (4.23) applied to a nonlinear system with unmodeled dynamics, parameter uncertainty and subject to output disturbance as given by (3.1). Assume that (where r is the relative degree) and are known and bounded, are sufficiently smooth, are Lipschitz continuous functions, at least one column of is bounded away from zero. Furthermore, suppose that a loop-shaping filter is designed such that the feedback system is stable. Then the modified parameter update law as given by (4.19) yields the bounded tracking error.

Proof. Step 1 (show that only needs to be considered).

Denote by the component of perpendicular to the tangent plane at so that . Since Θ ∈ w and w is convex, we have . Choose Lyapunov function V(Φ) = Φ^TΦ and use the parameter update law as defined in (4.19). When , we have . When , we have

()

where we use the fact that

()

Thus, we only have to consider the scenario corresponding to

in the sequel.

Step 2. Substituting (4.23) back into (4.22), we have

()

Using the definition of tracking error

, (4.27) can be written as

()

Use the following equality:

()

Equation (4.28) becomes

()

where

. Moreover, the positive designable parameters c_i can be written as

()

where C_j, C_r and h_j, h_r > 0. Thus, (4.30) can be written as

()

Utilizing the fact that

()

we have

()

To design h₁, …, h_r (or c₁, …, c_r ), d_j and g_j such that

()

We arrive at

()

Equation (4.36) implies that

()

where k_v≜min {C₁, …, C_r, λ_min(Γ)}, λ_min (Γ) is the smallest eigenvalue of Γ and

()

is bounded since

are bounded and Φ^TΓ⁻¹Φ is bounded due to the parameter update law specified in (4.19). We conclude that

()

As θ → ∞, we have

()

which implies that the overall system is stable and the bound C/(2k_v) can be decreased by increasing k_v or increasing γ. By (4.14), this implies that

are bounded. Since

is also bounded. From (3.11), we can see that ξ and v₁, …, v_ℓ are bounded since

and

are bounded. Moreover, we conclude that the virtual inputs α are bounded because they consist of bounded terms. Also,

is bounded from (3.12) and also

from the definition of ε. With the ISS assumption and bounded

, we conclude that the internal dynamics

is bounded. Finally,

is bounded by diffeomorphism, that is,

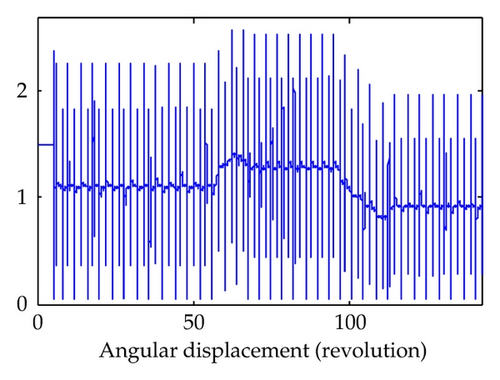
5. Illustrative Example

For realistic simulation, we set up a simulation configuration as shown in Figure 2, in which the controller and parametric adaptation operate in the θ-domain whereas the open-loop system operates in the time domain. The proposed spatial domain output feedback adaptive control scheme is applied to a reformulated system in spatial domain expressed as

()

where

()

with a₀ = 5155, a₁ = 1138, and b₀ = 140368. For verification purpose, the output disturbance is assumed to be a low-pass rectangular periodic signal (with amplitude switching between −0.1 and 0.1) (see Figure 3), that is,

()

where

()

Note that the disturbance has been low-pass filtered so that it is continuously differentiable. Parameters of the internal model filter are specified to target the fundamental frequency and the first three harmonic frequencies of the periodic disturbance, that is,

()

where

()

Furthermore, the stabilizing filter is specified as

()

The parameters of the K-filter are set to k₁ = 1600 and k₂ = 100. The initial values of the estimated parameters are set to

, and

. The allowable parameter variation sets are

()

Note that d_s(t) is set to 0 so that the system performance is not affected by the unstructured uncertainty. Suppose that a variable speed control task demands the system to initially run at 30 rev/s and then speed up to 35 rev/s and finally speed down to 25 rev/s (see Figure 4). To avoid getting infinite value when taking derivative, the reference command is specified to have smooth (instead of instant) change. Figure 5 compares the tracking performance of two scenarios. The figures on the left are for the pure output feedback adaptive backstepping design. The ones on the right are for the proposed output feedback design with internal model control. Without internal model control, the adaptive backstepping design has already shown superb tracking performance. We see that adding the internal model control further reduces the magnitude of the tracking error without noticeable increase in the control input.

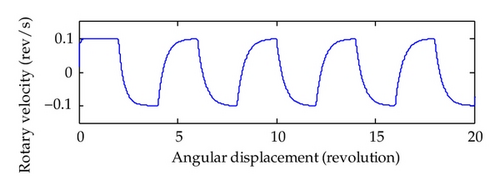
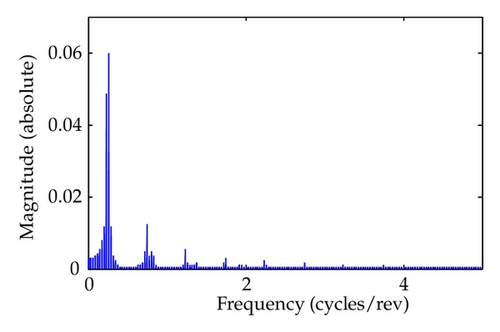
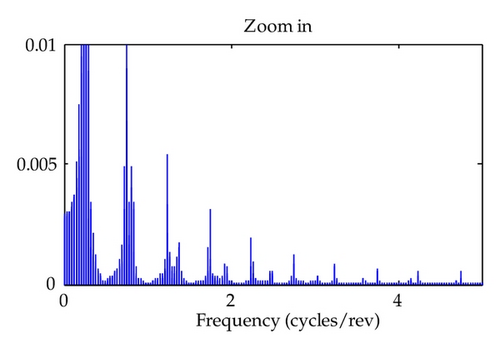
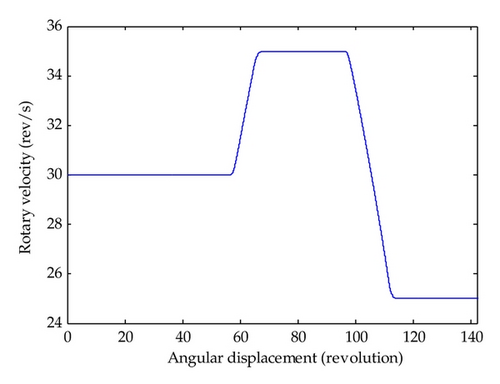
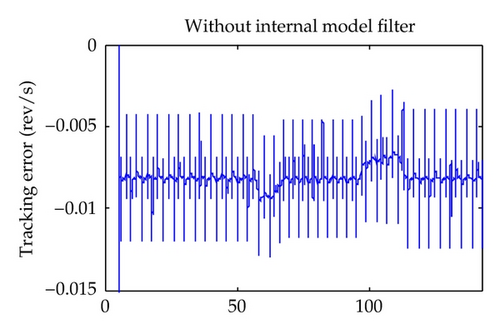
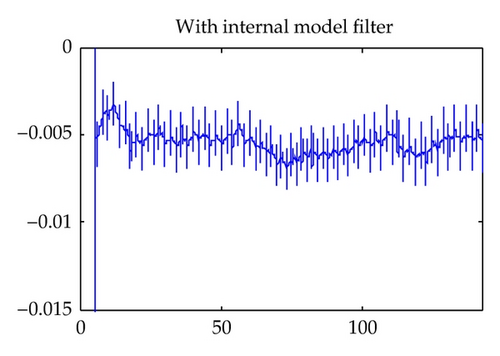
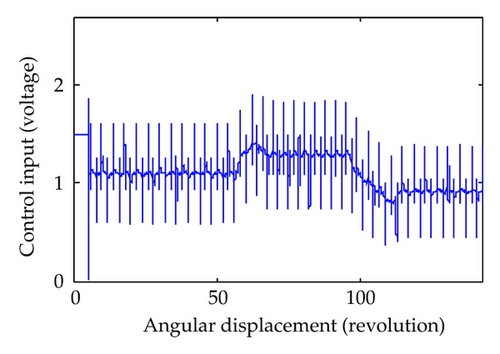
6. Conclusion

This paper presents the design of a new spatial domain adaptive control system, which can be applied to rotary systems operating at varying speeds and subject to spatially periodic and band-limited disturbances and structured/unstructured parametric uncertainties. The proposed design integrates two control paradigms, that is, adaptive backstepping and internal model control. The overall output feedback adaptive control system can be shown to be stable and have bounded state estimated error and output tracking error. Feasibility and effectiveness of the proposed design are further justified by a numerical example. Future effort will be dedicated to implementation and verification of the proposed control design to a practical rotary system, for example, a brushless dc-motor-driven control system.

References

1 Francis B. A. and Wonham W. M., The internal model principle of control theory, Automatica. (1976) 12, no. 5, 457–465, 0429257.
10.1016/0005-1098(76)90006-6
Web of Science® Google Scholar
2 Nikiforov V. O., Adaptive non-linear tracking with complete compensation of unknown disturbances, European Journal of Control. (1998) 4, 132–139.
10.1016/S0947-3580(98)70107-4
Web of Science® Google Scholar
3 Ding Z., Adaptive disturbance rejection of nonlinear systems in an extended output feedback form, IET Control Theory & Applications. (2007) 1, no. 1, 298–303, https://doi.org/10.1049/iet%2Dcta:20050458, 2352164.
10.1049/iet-cta:20050458
Web of Science® Google Scholar
4 Marconi L., Isidori A., and Serrani A., Input disturbance suppression for a class of feedforward uncertain nonlinear systems, Systems & Control Letters. (2002) 45, no. 3, 227–236, https://doi.org/10.1016/S0167%2D6911(01)00180%2D3, 2072238.
10.1016/S0167-6911(01)00180-3
Web of Science® Google Scholar
5 Gentili L. and Marconi L., Robust nonlinear disturbance suppression of a magnetic levitation system, Automatica. (2003) 39, no. 4, 735–742, https://doi.org/10.1016/S0005%2D1098(02)00307%2D2, 2138160.
10.1016/S0005-1098(02)00307-2
Web of Science® Google Scholar
6 Kravaris C., Sotiropoulos V., Georgiou C., Kazantzis N., Xiao M., and Krener A. J., Nonlinear observer design for state and disturbance estimation, Systems & Control Letters. (2007) 56, no. 11-12, 730–735, https://doi.org/10.1016/j.sysconle.2007.05.001, 2356459.
10.1016/j.sysconle.2007.05.001
Web of Science® Google Scholar
7 Mahawan B. and Luo Z.-H., Repetitive control of tracking systems with time-varying periodic references, International Journal of Control. (2000) 73, no. 1, 1–10, https://doi.org/10.1080/002071700219885, 1736051.
10.1080/002071700219885
Web of Science® Google Scholar
8 Chen C. L., Chiu G. T. C., and Allebach J., Robust spatial-sampling controller design for banding reduction in electrophotographic process, Journal of Imaging Science and Technology. (2006) 50, no. 6, 530–536, https://doi.org/10.2352/J.ImagingSci.Technol.(2006)50:6(530).
10.2352/J.ImagingSci.Technol.(2006)50:6(530)
CAS Web of Science® Google Scholar
9 Chen C. L. and Chiu G. T. C., Spatially periodic disturbance rejection with spatially sampled robust repetitive control, Journal of Dynamic Systems, Measurement, and Control. (2008) 130, no. 2, 11–21.
10.1115/1.2837306
Web of Science® Google Scholar
10 Nakano M., She J. H., Mastuo Y., and Hino T., Elimination of position-dependent disturbances in constant-speed-rotation control systems, Control Engineering Practice. (1996) 4, no. 9, 1241–1248, https://doi.org/10.1016/0967%2D0661(96)00130%2DX.
10.1016/0967-0661(96)00130-X
Web of Science® Google Scholar
11 Chen C. L. and Yang Y. H., Spatially periodic disturbance rejection for uncertain rotational motion systems using spatial domain adaptive backstepping repetitive control, Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society, November 2007, Taipei, Taiwan, 638–643.
Google Scholar
12 Yang Y. H. and Chen C. L., Spatially periodic disturbance rejection using spatial-based output feedback adaptive backstepping repetitive control, Proceeding of the American Control Conference, 2008, 4117–4122.
Google Scholar
13 Kreisselmeier G., Adaptive observers with exponential rate of convergence, IEEE Transactions on Automatic Control. (1977) 22, no. 1, 2–8, 0444142, https://doi.org/10.1109/TAC.1977.1101401.
10.1109/TAC.1977.1101401
Web of Science® Google Scholar
14 Marino R., Santosuosso G. L., and Tomei P., Robust adaptive observers for nonlinear systems with bounded disturbances, IEEE Transactions on Automatic Control. (2001) 46, no. 6, 967–972, https://doi.org/10.1109/9.928609, 1836503.
10.1109/9.928609
Web of Science® Google Scholar
15 Tong S. C., He X. L., and Zhang H. G., A combined backstepping and small-gain approach to robust adaptive fuzzy output feedback control, IEEE Transactions on Fuzzy Systems. (2009) 17, no. 5, 1059–1069, https://doi.org/10.1109/TFUZZ.2009.2021648.
10.1109/TFUZZ.2009.2021648
Web of Science® Google Scholar
16 Tong S. and Li Y., Observer-based fuzzy adaptive control for strict-feedback nonlinear systems, Fuzzy Sets and Systems. (2009) 160, no. 12, 1749–1764, https://doi.org/10.1016/j.fss.2008.09.004, 2555717.
10.1016/j.fss.2008.09.004
Web of Science® Google Scholar
17 Tong S., Li C., and Li Y., Fuzzy adaptive observer backstepping control for MIMO nonlinear systems, Fuzzy Sets and Systems. (2009) 160, no. 19, 2755–2775, https://doi.org/10.1016/j.fss.2009.03.008, 2573357.
10.1016/j.fss.2008.09.004
Web of Science® Google Scholar

Citing Literature

All articles

Spatial Domain Adaptive Control of Nonlinear Rotary Systems Subject to Spatially Periodic Disturbances

Abstract

1. Introduction

2. Problem Formulation

3. Nonlinear State Observer

4. Spatial Domain Output Feedback Adaptive Control System

5. Illustrative Example

6. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Spatial Domain Adaptive Control of Nonlinear Rotary Systems Subject to Spatially Periodic Disturbances

Abstract

1. Introduction

2. Problem Formulation

3. Nonlinear State Observer

4. Spatial Domain Output Feedback Adaptive Control System

5. Illustrative Example

6. Conclusion

References

Citing Literature

Figures

References

Related

Information