Volume 2012, Issue 1 546203

Research Article

Open Access

Upscaling of Permeability Field of Fractured Rock System: Numerical Examples

Kai Bao

Computational Transport Phenomena Laboratory, Division of Mathematics and Computer Science and Engineering, King Abdullah University of Science and Technology, Thuwal 23955-6900, Saudi Arabia kaust.edu.sa

Search for more papers by this author

Amgad Salama,

Amgad Salama

Search for more papers by this author

Shuyu Sun,

Corresponding Author

Shuyu Sun

[email protected]

Search for more papers by this author

Kai Bao,

Kai Bao

Search for more papers by this author

Amgad Salama,

Amgad Salama

Search for more papers by this author

Shuyu Sun,

Corresponding Author

Shuyu Sun

[email protected]

Search for more papers by this author

First published: 08 May 2012

https://doi.org/10.1155/2012/546203

Citations: 2

Academic Editor: M. F. El-Amin

Share a link

Email
Wechat
Bluesky

Abstract

When the permeability field of a given porous medium domain is heterogeneous by the existence of randomly distributed fractures such that numerical investigation becomes cumbersome, another level of upscaling may be required. That is such complex permeability field could be relaxed (i.e., smoothed) by constructing an effective permeability field. The effective permeability field is an approximation to the real permeability field that preserves certain quantities and provides an overall acceptable description of the flow field. In this work, the effective permeability for a fractured rock system is obtained for different coarsening scenarios starting from very coarse mesh all the way towards the fine mesh simulation. In all these scenarios, the effective permeability as well as the pressure at each cell is obtained. The total flux at the exit boundary is calculated in all these cases, and very good agreement is obtained.

1. Introduction

The first level of upscaling encountered when studying phenomena occurring in porous media is related to adopting the continuum hypothesis to such complex formations. That is moving from pore scale simulations in which variables are only defined within the fluid region to the continuum description in which macroscopic variables are defined everywhere in the simulation domain. In doing so, certain conditions and length scale constraints need to be fulfilled in order to generate macroscopic quantities that are scale independent [1]. While these length scale constraints may be easily adopted in statistically homogeneous porous media, it may be difficult to satisfy particularly closer to the interface boundaries between media with very different textures [2]. Unfortunately, these sharp interface boundaries are ubiquitous in rock systems which apparently contain several fractures and fissures. These fractures have significant effects on both flow and transport in porous media. They provide fluids and solutes with significantly less resistance paths compared with the surrounding matrix and therefore can lead solutes to reach further distances than what simulations ignoring them would normally predict. There are two approaches to dealing with these fractures depending on their density and distributions in rock systems. For rock systems with few penetrating fractures, it is customary to consider the discrete fracture model (e.g., [3, 4]). In this model, fractures are assumed as two-dimensional surfaces impeded within the given rock matrix domain. These fracture surfaces have their own properties and equations which include interaction terms between the rock matrix and the fractures. When the numbers of the fractures are large and their geometrical distributions are complex such that it becomes exceedingly difficult to consider them in simulation, another alternative is to construct an equivalent porous medium domain by further increasing the averaging representative volume. In this approach, one abandons the fractures and considers another continuum, coarser in nature, but may be acceptable for our engineering application and design.

In terms of simulation, although the discrete fracture model provides an elegant way to deal with fractures when their density is manageable, the drawback of this approach, however, is the fact that the interaction term between the fracture and the surrounding rock matrix is, in most cases, not known and ends up as a fitting parameter. The other approach is to refine the mesh all the way to the fractures level, which apparently poses enormous difficulties in large systems particularly when modeling complex transport problems like multiphase compositional flows. It has been, therefore, proposed that an even higher level of upscaling may be required to generate field properties to reduce the required computing resources and provide certain requirements satisfaction. These requirements are related to the fact that the solution of the upscaled system should produce approximately close results to those obtained from simulating the real system. That is if the permeability field may be relaxed such that the sharp interface boundaries may be smoothed, in a sense, the requirements for denser mesh closer to the sharp interface boundaries may be abandoned, and it may be possible to significantly decrease the number of degrees of freedom of the system. Different approaches have been considered in the literatures based on either deterministic approaches (e.g., [5–13], etc.) or stochastic approaches (e.g., [14–18], etc.). In the next section we introduce a quick review of the previous work emphasizing on two methods which are related to this work closely.

2. Investigation of the Upscaling Techniques

A review on the upscaling of hydraulic conductivities in heterogeneous media may be found in the work of Farmer [11] and in the work of Wen and Gomez-Hernandez [8]. In both reviews the authors pointed out that the need for upscaling stems from the fact that the scales at which measurements are taken and the scale at which reservoirs are discretized are usually different. Therefore, it is suggested that a transformation of hydraulic conductivities from the scale of the measurements into a coarser grid of block conductivity tensors amenable for input to a numerical flow simulator may be needed. Holden and Nielsen [19] pointed out that the scale at which permeability in a reservoir may change is much finer than what is possible to use in a reservoir simulator. They proposed a methodology in which permeability is formulated as a minimization problem. In the method, the upscaled permeability is defined as that which minimizes the difference between the pressure and the velocity fields generated by the fine and coarse scale pressure equations. In this work, however, we apply an averaging over a coarser grid of the porous media domain such that certain quantities are conserved. The problem may be casted as follows: consider a three-dimensional rectangular domain, Ω with boundary ∂Ω, if v represents Darcy’s velocity and p the pressure field of the fluid saturating the porous medium domain, the governing equations describing this system may be written as

(2.1)

(2.2)

From which one obtains an equation only in the pressure given as

(2.3)

The upscaling problem, as described in [11], is to find a corresponding coarse hydraulic conductivity field,

such that the new velocity and pressure fields,

obtained from solving the equivalent system of equations, are close, in some sense, to the fine scale velocity and pressure fields, v, p. The system of equations that need to be solved in this case takes the form

(2.4)

The general methodology is to seek an equivalent (effective) hydraulic conductivity field

, calculated from a set of boundary conditions, and it may be used afterwards to yield accurate results with different boundary conditions. To do so, the rectangular domain is divided into a number of segments in each direction, that is, N_x, N_y, and N_z to form boxes of sizes, H_x, H_y, and H_z. These cells are called the coarse cells. Furthermore, each of the boxes is divided into n_x, n_y, and n_z finer boxes with sizes h_x, h_y, and h_z. The hydraulic conductivity tensor field K, generally, takes a different value in each of the fine cells. There have been two approaches highlighted by Farmer [11], which may be used to construct the coarser hydraulic conductivity field, namely, the global (overall) strategy and the local methods. The first technique is performed in two stages. In the first stage one needs to perform one or more fine grid experiment which may cover the whole domain or at least most of it. Three test cases for each scenario are performed, one in each coordinate direction on the fine grid within each of the coarse cells. In the second stage, the fine grid simulations are used to extract the coarse scale permeability,

. In the second method, which is sometimes called the local-local or the subdomain method, each coarse cell is considered separately, as shown in Figure 1, and the three independent flow experiments in the three directions are performed. In each of these experiments, no flow conditions are assigned to the four surfaces parallel to the flow direction and constant pressure conditions on the two surfaces normal to the flow direction. If the total flux may be computed through one of the faces that were assigned pressure boundary condition, an equivalent permeability for this cell may be computed [20, 21].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Representative coarse and fine mesh.

There are, however, certain requirements for the correct upscaling as defined in [1, 2]. For the case of single phase incompressible fluids, it suffices to require that the flux across any area in the domain should be the same for all levels of upscaled description. This requirement ensures a divergence-free flow field in case there is no source/sink term. This condition can be defined as

(2.5)

where

and v are the velocity vectors at different level of upscaling, and r is the position vector which scans the area A. Applying this requirement on the local-local method mentioned earlier in which each coarse cell is considered separately, the above equation reduces to

(2.6)

where

represents the velocity vector at the center of the coarse cell face, and x is the position vector which defines the center of the cell face. Likewise for volumetric quantities (e.g., the source/sink term, q), Salama and Van Geel [1] pointed out that

(2.7)

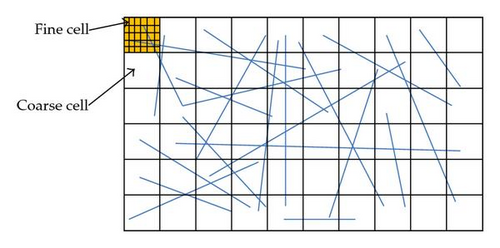
3. The Subdomain Technique

We apply the local-local method to obtain the effective permeability field for a given complex permeability field in fractured rock system. The simulation domain represents a rectangular two-dimensional area with a set of randomly generated fractures. We use the cell-centered finite difference scheme (CCFD) to approximate the governing equations because it satisfies mass conservation law locally. Furthermore, we consider the fractures oriented horizontally and vertically, as shown schematically in Figure 2. The local-local method deals with each macroscopic cell separately. For this purpose, we define two different meshes; the first mesh is the coarse mesh and it is defined globally over the whole simulation domain, and the second mesh is fine according the complexity of the permeability field within each coarse cell. That is we construct the coarse rectangular mesh over the whole simulation domain, {X₀, X₁, X₂, …, X_i, …, X_m} × {Y₀, Y₁, Y₂, …, Y_j, …, Y_n}, and for each coarse mesh we construct a finer mesh given as {x₀, x₁, x₂, …, x_i, …, x_p} × {y₀, y₁, y₂, …, y_j, …, y_q}.

4. Discretization of the Governing Equations

For the generic cell shown in Figure 3, the governing equations for this problem may be approximated using the cell-centered finite difference scheme with the various velocity components at the mid edges of the cell obtained as follows:

(4.1)

(4.2)

(4.3)

(4.4)

Equation (2.2) is discretized, likewise, in the following form:

(4.5)

Now substituting (2.7)–(4.3) into (4.4), one obtains an equation in the pressure only, as explained earlier, which may be solved to obtain the pressure field from which the velocity field may be determined. The permeability at cell edges is obtained based on the harmonic mean relationship which is given as

(4.6)

5. Application of the Local Upscaling Technique to Fractured Rock System

In this work we consider the local-local upscaling technique to generate an effective permeability field which would require less computational load and in the same time would result in reasonable match with the fine scale modeling. As explained earlier the scheme follows the following steps.

(i)
Discretize the whole domain with the appropriate fine mesh based on the complexity of the permeability field and fractures structure.
(ii)
Discretize the whole domain with the required coarse mesh that conforms with the fine mesh (i.e., the mesh coincides with the fine mesh).
(iii)
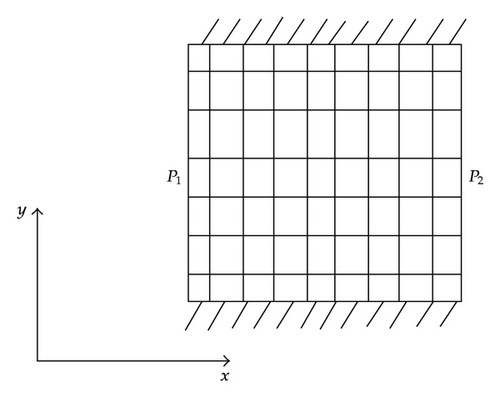
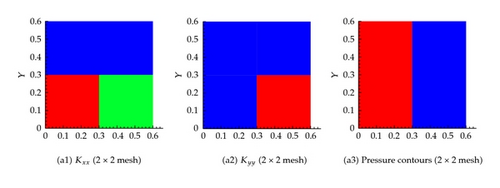
For each coarse cell, solve the boundary value problem given by (2.3) over the finer cells subject to predefined boundary conditions. That is to get the effective permeability in the x and y-directions, K_xx and K_yy, we consider two cases as shown in Figure 4. For example, in Figure 4(a), we consider a no-flow boundary condition at the top and bottom boundaries and prescribed pressure boundary condition (say p₁ = 1 and p₂ = 0) at the other two sides. Similar boundary conditions are suggested in Figure 4(b). The velocity at the finer scale could then be calculated.
(iv)
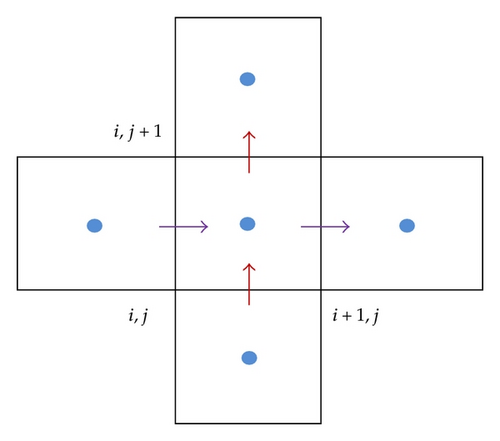
Using (2.6), one may calculate the x and y-velocity at the center of the faces of the coarse cell which encompass the finer mesh.
(v)
These velocities can then be used to calculate the effective permeability components in x and y directions with the Darcy’s equation (2.2).

6. Numerical Examples

Several scenarios with different fractures numbers and distributions have been considered. The simulation domain in all these scenarios is [0, 0.6] × [0, 0.6]. For the sake of simplicity, the width and the length of the fractures in all the simulation scenarios are considered identical as 0.00015 and 0.12, respectively (i.e., 0.2 times the length of the domain). In the 2-fracture scenario, the length of the fractures is chosen 0.3, 0.5 times of the size of the domain. The locations of the fractures are random. The flow rate in the fracture is usually described with the cubic law [22] in which the flux through the fracture is given as a cubic function of the fracture aperture, therefore

(6.1)

where Q is the flux across the fracture section, ρ is the density, μ is the viscosity, g is the gravity, and b is the fracture aperture. Generally, the hydraulic conductivity in the fracture region will be much higher than that in the matrix and plays a dominant role in the flow in the fracture-matrix system. In the paper, the hydraulic conductivity of the fracture region is specified as 3 × 10⁵ times that of the matrix. The mesh size of the fine mesh is 0.0006 for the matrix and 0.00015 for the fractures. Four scenarios with different number of fractures are considered. In the first scenario, only one fracture in the horizontal direction and one fracture in the vertical direction, respectively, are assumed. The other three scenarios consider, respectively, 5, 20 and 400 fractures in both the horizontal and vertical directions. At first, fine meshes are generated with the number of the mesh cells in horizontal and vertical directions are respectively as follows: 1002 × 1002 for the 2-fracture scenario, 1008 × 1008 for the 10-fracture scenario, 1032 × 1035 for the 40-fracture scenario, and 1480 × 1500 for the 800-fracture scenario. The flow equations are solved with the fine mesh, and the pressure distribution is obtained for each scenario. As will be seen later, the flow in the whole domain is very much affected by the fractures. To consider different levels of upscaling, the domain is discretized with a coarse mesh of different resolutions. In this work we consider very coarse resolutions and moderately fine resolutions. In all these levels of resolutions, effective permeability is obtained based on (2.2).

6.1. Example 1: One Fracture in Both the Horizontal and Vertical Directions

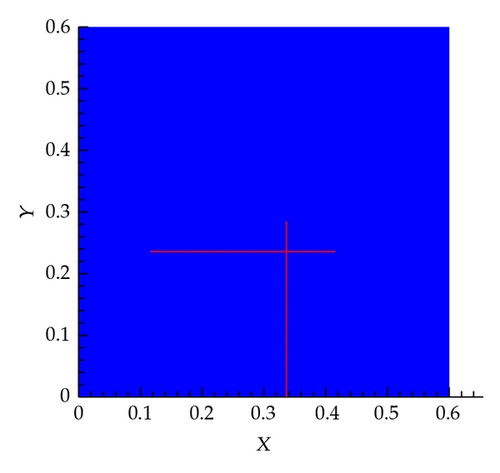
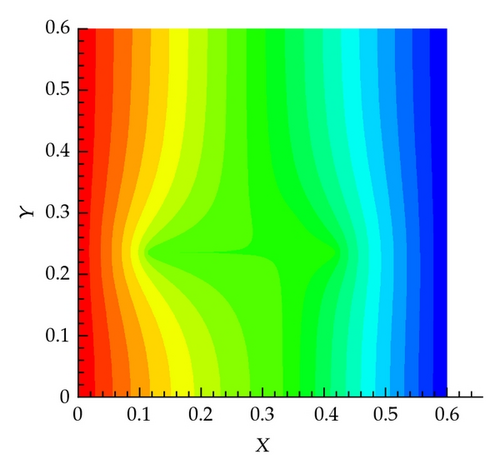
In this scenario, two fractures are generated randomly as shown in Figure 5(a). The pressure field for this system obtained by solving the governing equations using the fine mesh is shown in Figure 5(b), from which we can see the apparent influence of the fractures in distorting the pressure field.

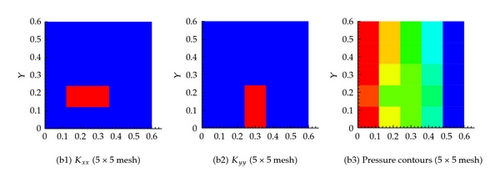
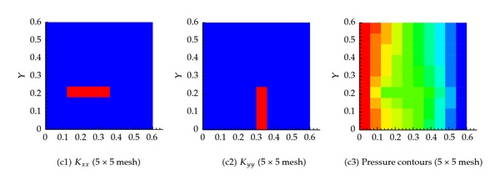
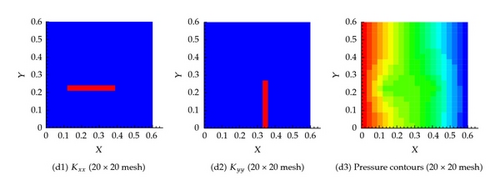
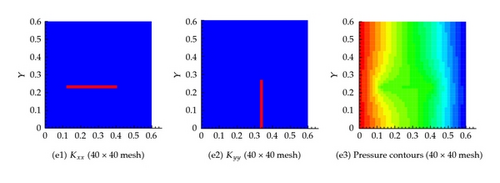
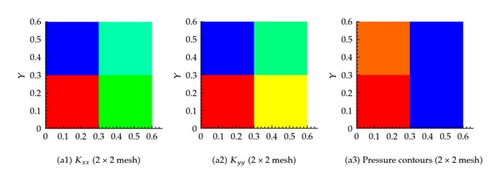
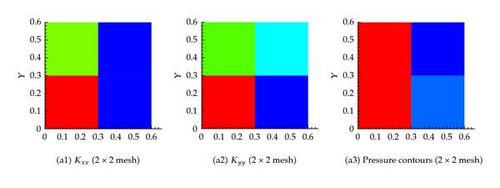
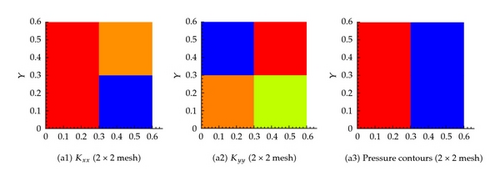
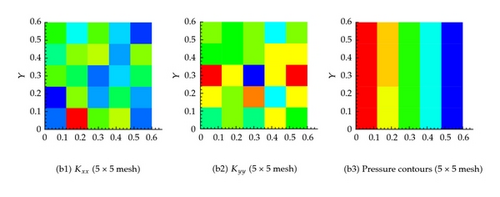
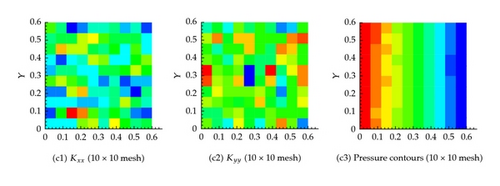
Several coarsening scenarios are considered, namely, 2 × 2, 5 × 5, 20 × 20, 40 × 40, 100 × 100, and 500 × 500. In all these scenarios, the requirement that the flux across any surface calculated using the fine mesh and any other coarse mesh is the same. The generated effective hydraulic conductivity of each cell, and , for different resolution scenarios is shown in Figure 6. Apparently, the permeability of the cells containing fractures is larger. Furthermore, as the resolution of the mesh increases, the permeability contrast sharpens around the fractures. Figure 6 also shows the pressure at the center of each cell for the different resolution scenarios. It is apparent that the pressure field gets closer to the fine scale simulation as the resolution increases. On comparing the flux at the exit boundary (Table 1), it is clear that the flux for different coarsening scenario is close to one another.

Table 1. Flux across the exit boundary for the different fractures and mesh scenarios.

	2 fractures	10 fractures	40 fractures	800 fractures
Reference (fine mesh)	1.238536e − 03	1.140093e − 03	1.784033e − 03	4.037607e + 00
Upscaled (2 × 2)	1.2060398e − 03	1.1671849e − 03	1.7678765e − 03	4.0482439e + 00
Upscaled (5 × 5)	1.2279665e − 03	1.1480335e − 03	1.6639357e − 03	4.0201914e + 00
Upscaled (10 × 10)	1.2305291e − 03	1.1357165e − 03	1.6719508e − 03	4.0624327e + 00
Upscaled (20 × 20)	1.2377141e − 03	1.1567826e − 03	1.7251369e − 03	4.0636998e + 00
Upscaled (40 × 40)	1.2329549e − 03	1.1414539e − 03	1.7356198e − 03	4.0958317e + 00
Upscaled (60 × 60)	1.2330102e − 03	1.1364853e − 03	1.7344252e − 03	3.9842654e + 00
Upscaled (80 × 80)	1.2312922e − 03	1.1368569e − 03	1.7406374e − 03	4.0324003e + 00
Upscaled (100 × 100)	1.2368716e − 03	1.1353105e − 03	1.7651864e − 03	4.0198896e + 00
Upscaled (160 × 160)	1.2354428e − 03	1.1366243e − 03	1.7682102e − 03	3.9614817e + 00
Upscaled (200 × 200)	1.2376183e − 03	1.1376407e − 03	1.7735081e − 03	4.0495773e + 00
Upscaled (240 × 240)	1.2366092e − 03	1.1380291e − 03	1.7735767e − 03	3.9653353e + 00
Upscaled (300 × 300)	1.2393249e − 03	1.1413561e − 03	1.7762217e − 03	3.9176552e + 00
Upscaled (400 × 400)	1.2368358e − 03	1.1370930e − 03	1.7671836e − 03	3.7225614e + 00
Upscaled (500 × 500)	1.2378015e − 03	1.1405213e − 03	1.7877663e − 03	4.0850977e + 00

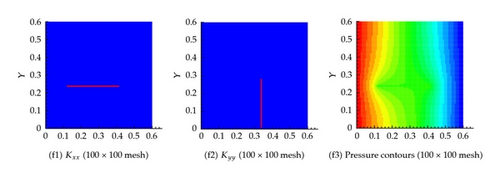
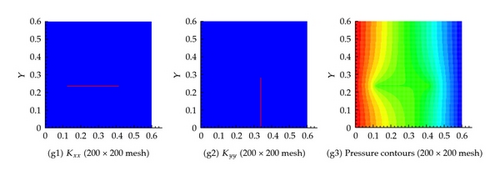
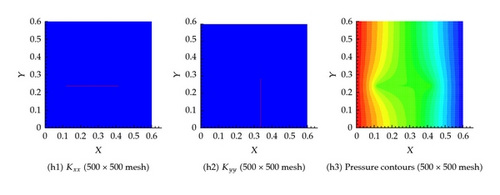
6.2. Example 2: Five Fracture in Both the Horizontal and Vertical Directions

In this scenario, five fractures are generated randomly in both the horizontal and vertical directions (i.e., 10 fractures in total), as shown in Figure 7(a). The pressure field for this system as obtained by solving the governing equations using the very fine mesh is shown in Figure 7(b). Again, the influence of the fractures in distorting the pressure field is significant.

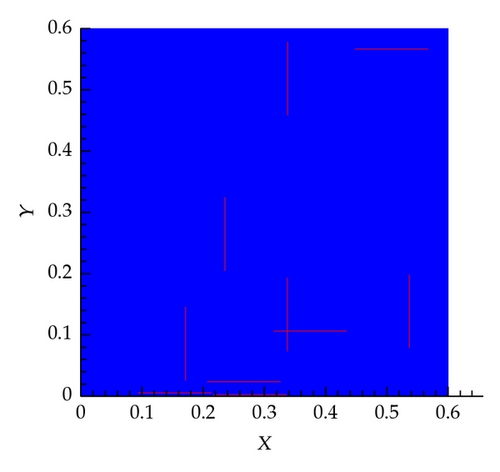
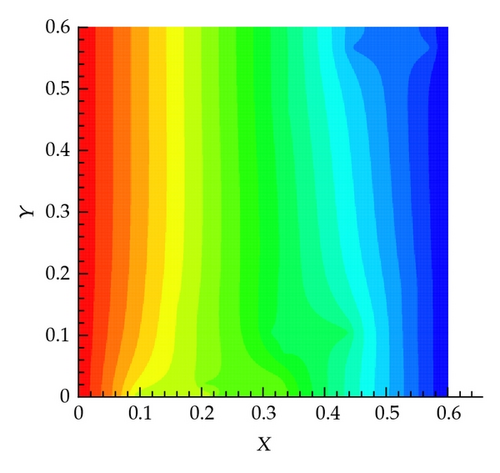
Effective permeability in each cell is shown in Figure 8, which shows that the effective permeability approaches that of the fine mesh simulation as the number of grid cells increase. Again the flux at the exit boundary is very close to the different coarsening scenarios as depicted in Table 1.

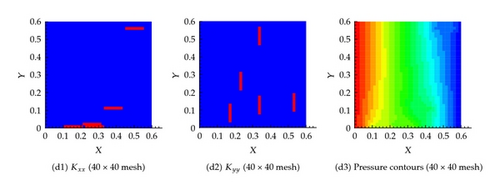
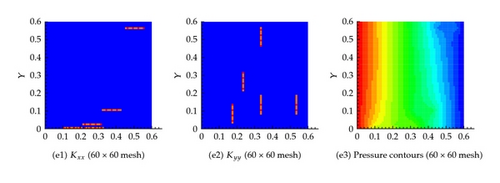
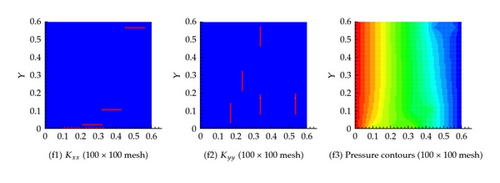
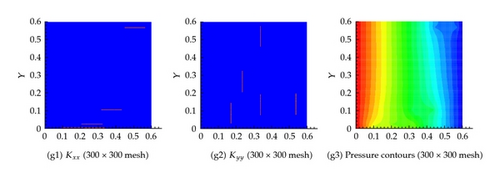
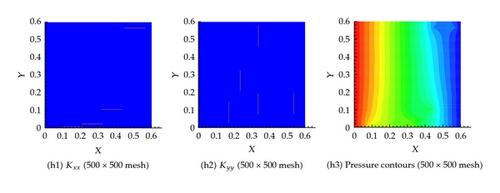
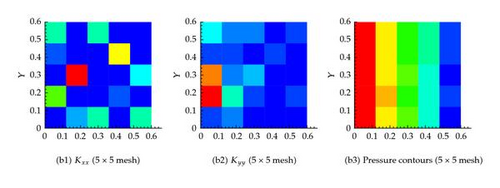
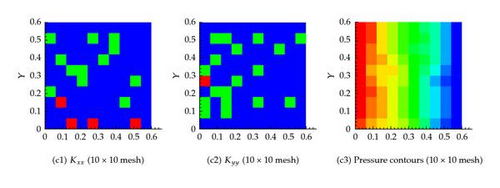
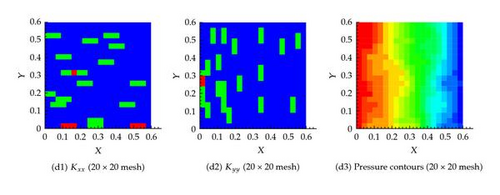
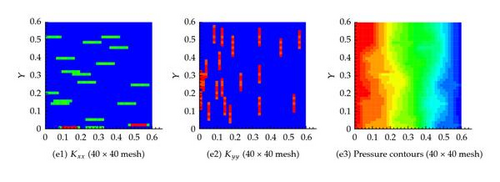
6.3. Example 3: Twenty Fractures in Both the Horizontal and Vertical Directions

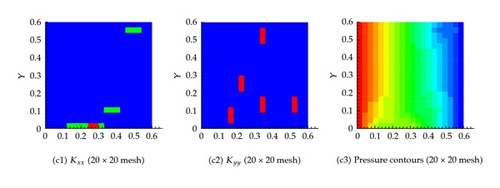
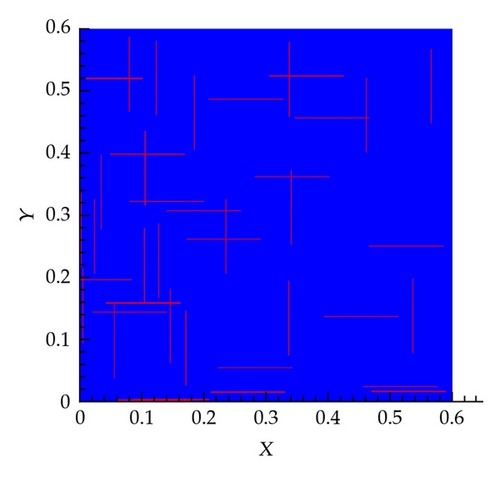
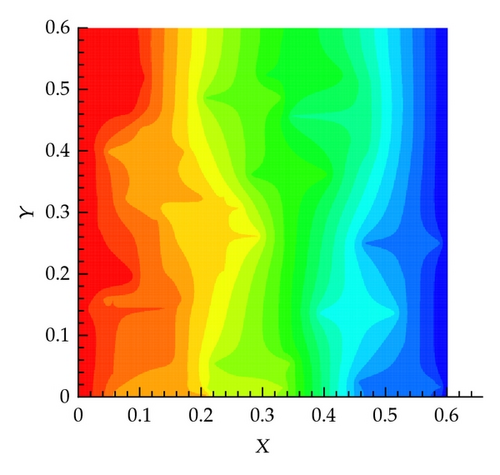
In this scenario, 20 fractures in x and 20 in the y directions are considered, as shown in Figure 9(a). The pressure field obtained by solving the governing equations based on the actual permeability field is shown in Figure 9(b). The effect of the fractures on the pressure field is apparent.

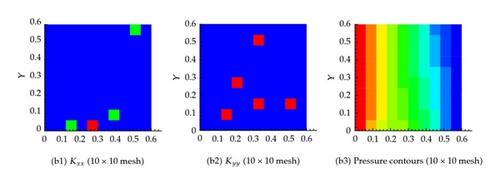
On the other hand, the effective permeability field obtained from solving the equivalent equations as explained earlier is shown in Figure 10. It is clear that as the number of grid cells increases, the system approach that based on the actual permeability field. Table 1 confirms again that the flux at the exit boundary is almost identical for the different coarsening scenarios.

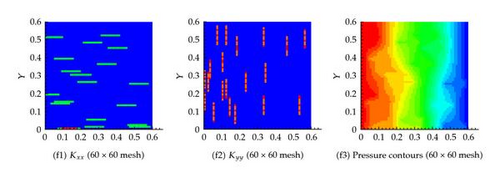
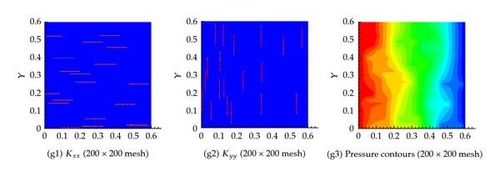
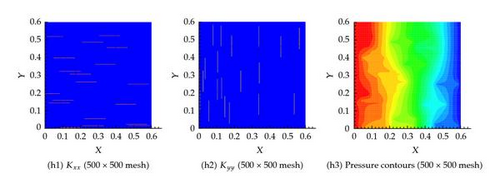
6.4. Example 4: 400 Fractures in Both the Horizontal and Vertical Directions

As shown in Figures 11 and 12, similar behavior is obtained for this scenario which assumes 400 fractures in both the horizontal and vertical directions for both the effective permeability and the pressure fields. In this scenario, we consider several degrees of coarsening including, 2 × 2, 10 × 10, 20 × 20, 40 × 40, 300 × 300, and 500 × 500.

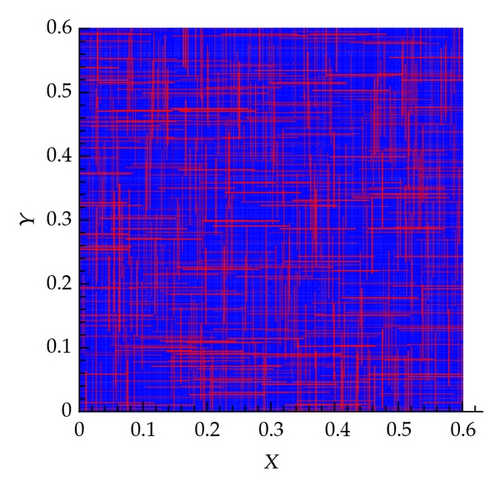
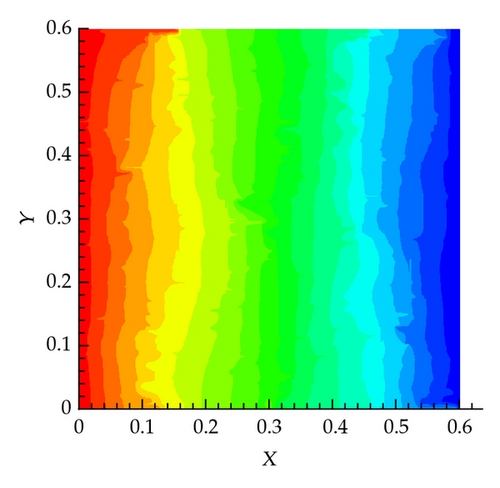
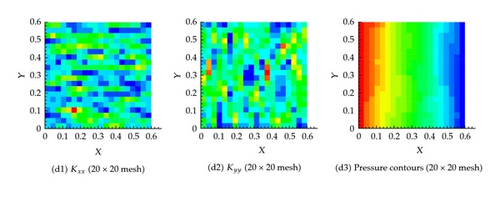
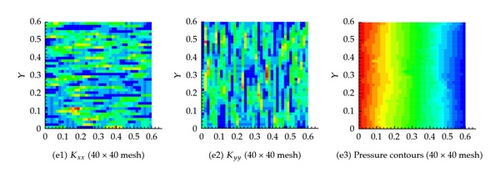
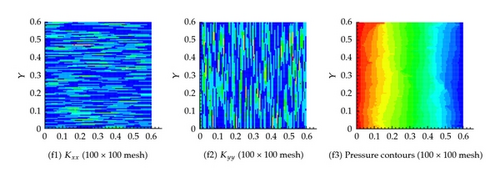
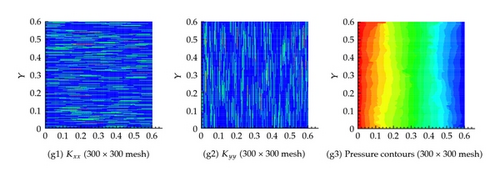
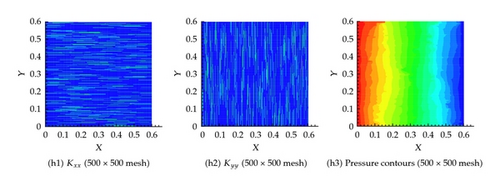
Apparently in this scenario, the large number of fractures will increase the overall effective hydraulic conductivity field which will result in a significantly larger flux compared with the other scenarios. Indeed this is the case as shown in Table 1.

7. Conclusions

In this work several numerical examples have been considered to calculate effective hydraulic properties for a given fractured porous medium domain. Several scenarios of fractured systems have been considered starting with two fractures up to 800 fractures. Cell-centered finite different method has been used, and therefore the fractures orientations are considered only in the horizontal and vertical directions. Different coarsening scenarios have been considered for each fracture scenario starting with very coarse mesh (2 × 2) all the way to the fine mesh. The fine mesh used in this work is that associated with the actual permeability field of both the matrix and the rock. Effective permeability for each cell is obtained for each coarsening scenario based on the requirement that the flux at the face of each cell is the same as that considered with the actual permeability field. It is found that the spatial distribution of effective permeability of the medium changes with the change in the degree of coarsening. That is for coarser mesh the effective permeability spans a larger domain while it reduces to the actual permeability field as the mesh approaches the fine mesh. The usefulness of this approach stems from the significantly less computational effort and memory requirement that would be required when using the upscaled permeability field and in the same time the satisfaction of conservation laws at the new scale.

Acknowledgment

The work is funded by KAUST’s GRP-CF (Global Research Partnership Collaborative Fellows) Program, and KAUST-UTAustin AEA project (7000000058).

References

1 Salama A. and van Geel J., Flow and solute transport in saturated porous media: 1. The continuum hypothesis, Journal of Porous Media. (2008) 11, no. 4, 403–413, 2-s2.0-39049132124, https://doi.org/10.1615/JPorMedia.v11.i4.60.
10.1615/JPorMedia.v11.i4.60
Web of Science® Google Scholar
2 Salama A. and van Geel J., Flow and solute transport in saturated porous media: 2. Violating the continuum hypothesis, Journal of Porous Media. (2008) 11, no. 5, 421–441, 2-s2.0-41849143467, https://doi.org/10.1615/JPorMedia.v11.i5.10.
10.1615/JPorMedia.v11.i5.10
CAS Web of Science® Google Scholar
3 Karimi-Fard M. and Firoozabadi A., Numerical simulation of water injection in fractured media using the discrete-fracture model and the Galerkin method, SPE Reservoir Evaluation and Engineering. (2003) 6, no. 2, 117–126, 2-s2.0-0038692018, https://doi.org/10.2118/83633%2DPA.
10.2118/83633-PA
CAS Web of Science® Google Scholar
4 Kou J., Sun S., and Yu B., Multiscale time splitting strategy for multi-scale multi-physics processes of two-phase flow in fractured media, Journal of Applied Mathematics. (2011) 2011, 24, 861905, https://doi.org/10.1155/2011/861905.
10.1155/2011/861905
Google Scholar
5 Rodriguez A., Klie H., Sun S., Gai X., and Wheeler M., Upscaling of hydraulic properties of fractured porous media: full permeability tensor and continuum scale simulations, Proceedings of the SPE Symposium on Improved Oil Recovery, 2006, Tulsa, Okla, USA.
Google Scholar
6 Noetinger B., Estebenet T., and Quintard M., Up-scaling flow in fractured media: equivalence between the large scale averaging theory and the continuous time random walk method, Transport in Porous Media. (2001) 43, no. 3, 581–596, 2-s2.0-0035358098, https://doi.org/10.1023/A:1010733724498.
10.1023/A:1010733724498
Web of Science® Google Scholar
7 Kfoury M., Ababou R., Noetinger B., and Quintard M., Upscaling fractured heterogeneous media: permeability and mass exchange coefficient, Journal of Applied Mechanics. (2006) 73, no. 1, 41–46, 2-s2.0-33645659199, https://doi.org/10.1115/1.1991864.
10.1115/1.1991864
CAS Web of Science® Google Scholar
8 Wen X. and Gomez-Hernandez J., Upscaling hydraulic conductivities in heterogeneous media: an overview, Journal of Hydrology. (1996) 183, no. 1-2, 9–32, 2-s2.0-0030211952.
10.1016/S0022-1694(96)80030-8
Web of Science® Google Scholar
9 Crotti M. and Cobenas R., Upscaling of relative permeability curves for reservoir simulation: an extension to areal simulations based on realistic average water saturations, Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, 2003, Port-of-Spain, Trinidad & Tobago.
Google Scholar
10 Narsilio G., Buzzi O., Fityus S., Yun T., and Smith D., Upscaling of Navier-Stokes equations in porous media: theoretical, numerical and experimental approach, Computers and Geotechnics. (2009) 36, no. 7, 1200–1206, 2-s2.0-67651004510, https://doi.org/10.1016/j.compgeo.2009.05.006.
10.1016/j.compgeo.2009.05.006
Web of Science® Google Scholar
11 Farmer C., Upscaling: a review, International Journal for Numerical Methods in Fluids. (2002) 40, no. 1-2, 63–78, 2-s2.0-0037056477, https://doi.org/10.1002/fld.267.
10.1002/fld.267
Web of Science® Google Scholar
12 Mayur P. and Edwards M., Effective upscaling using a family of flux-continuous, finite-volume schemes for the pressure equation, Proceedings of the 14th Association of Computational Mechanics in Engineering (ACME ′06), 2006, Belfast, UK, Queen′s University.
Google Scholar
13 Samardzioska T. and Popov V., Numerical comparison of the equivalent continuum, non-homogeneous and dual porosity models for flow and transport in fractured porous media, Advances in Water Resources. (2005) 28, no. 3, 235–255, 2-s2.0-13844297707, https://doi.org/10.1016/j.advwatres.2004.11.002.
10.1016/j.advwatres.2004.11.002
Web of Science® Google Scholar
14 Zhang Y., Gable C. W., and Sheets B., Equivalent hydraulic conductivity of three-dimensional heterogeneous porous media: an upscaling study based on an experimental stratigraphy, Journal of Hydrology. (2010) 388, no. 3-4, 304–320, 2-s2.0-77953693952, https://doi.org/10.1016/j.jhydrol.2010.05.009.
10.1016/j.jhydrol.2010.05.009
Web of Science® Google Scholar
15 Painter S. and Cvetkovic V., Upscaling discrete fracture network simulations: an alternative to continuum transport models, Water Resources Research. (2005) 41, no. 2, 1–10, 2-s2.0-15444372177, https://doi.org/10.1029/2004WR003682.
10.1029/2004WR003682
Web of Science® Google Scholar
16 Öhman J. and Niemi A., Upscaling of fracture hydraulics by means of an oriented correlated stochastic continuum model, Water Resources Research. (2003) 39, no. 10, 2-s2.0-1542752191, https://doi.org/10.1029/2002WR001776.
10.1029/2002WR001776
Web of Science® Google Scholar
17 MacLachlan S. P. and Moulton J. D., Multilevel upscaling through variational coarsening, Water Resources Research. (2006) 42, no. 2, 2-s2.0-33645748300, https://doi.org/10.1029/2005WR003940, W02418.
10.1029/2005WR003940
Web of Science® Google Scholar
18 Sanchez-Vila X., Girardi J. P., and Carrera J., A synthesis of approaches to upscaling of hydraluic conductivities, Water Resources Research. (1995) 31, no. 4, 867–882, 2-s2.0-0029413032, https://doi.org/10.1029/94WR02754.
10.1029/94WR02754
Web of Science® Google Scholar
19 Holden L. and Nielsen B. F., Global upscaling of permeability in heterogeneous reservoirs; the Output Least Squares (OLS) method, Transport in Porous Media. (2000) 40, no. 2, 115–143, 2-s2.0-0033929770, https://doi.org/10.1023/A:1006657515753.
10.1023/A:1006657515753
Web of Science® Google Scholar
20 Warren J. and Price H., Flow in heterogeneous porous media, Society of Petroleum Engineers Journal. (1961) 1, no. 3, 153–169.
10.2118/1579-G
Web of Science® Google Scholar
21 Begg S., Carter R., and Dranfield P., Assigning effective values to simulator gridblock parameters for heterogeneous reservoirs, Society of Petroleum Engineers. (1989) 4, no. 4, 455–463, 2-s2.0-0024770037, https://doi.org/10.2118/16754%2DPA.
10.2118/16754-PA
Google Scholar
22 Witherspoon P. A., Wang J. S. Y., Iwai K., and Gale J. E., Validity of cubic law for fluid flow in a deformable rock fracture, Water Resources Research. (1980) 16, no. 6, 1016–1024, 2-s2.0-0018955124, https://doi.org/10.1029/WR016i006p01016.
10.1029/WR016i006p01016
Web of Science® Google Scholar

Citing Literature

All articles

Upscaling of Permeability Field of Fractured Rock System: Numerical Examples

Abstract

1. Introduction

2. Investigation of the Upscaling Techniques

3. The Subdomain Technique

4. Discretization of the Governing Equations

5. Application of the Local Upscaling Technique to Fractured Rock System

6. Numerical Examples

6.1. Example 1: One Fracture in Both the Horizontal and Vertical Directions

6.2. Example 2: Five Fracture in Both the Horizontal and Vertical Directions

6.3. Example 3: Twenty Fractures in Both the Horizontal and Vertical Directions

6.4. Example 4: 400 Fractures in Both the Horizontal and Vertical Directions

7. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Upscaling of Permeability Field of Fractured Rock System: Numerical Examples

Abstract

1. Introduction

2. Investigation of the Upscaling Techniques

3. The Subdomain Technique

4. Discretization of the Governing Equations

5. Application of the Local Upscaling Technique to Fractured Rock System

6. Numerical Examples

6.1. Example 1: One Fracture in Both the Horizontal and Vertical Directions

6.2. Example 2: Five Fracture in Both the Horizontal and Vertical Directions

6.3. Example 3: Twenty Fractures in Both the Horizontal and Vertical Directions

6.4. Example 4: 400 Fractures in Both the Horizontal and Vertical Directions

7. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information