Journal of Applied Mathematics
Volume 2012, Issue 1 530139
Research Article
Open Access

A Modified NM-PSO Method for Parameter Estimation Problems of Models

An Liu, 

Corresponding Author

An Liu

Department of Computer Science and Information Engineering, St. John’s University, No. 499, Section 4, Tam King Road, Tamsui District, New Taipei City, 25135, Taiwan stjohns.edu

Graduate Institute of Computer and Communication Engineering, National Taipei University of Technology, No. 1, Section 3, Chung-hsiao E. Road, Taipei 10608, Taiwan ntut.edu.tw

Search for more papers by this author
Erwie Zahara, 

Erwie Zahara

Department of Marketing and Logistics Management, St. John’s University, No. 499, Section 4, Tam King Road, Tamsui District, New Taipei City 25135, Taiwan stjohns.edu

Search for more papers by this author
Ming-Ta Yang, 

Ming-Ta Yang

Department of Electrical Engineering, St. John’s University, No. 499, Section 4, Tam King Road, Tamsui District, New Taipei City 25135, Taiwan stjohns.edu

Search for more papers by this author
First published: 23 October 2012
https://doi.org/10.1155/2012/530139
Citations: 8
Academic Editor: Alain Miranville

Abstract

Ordinary differential equations usefully describe the behavior of a wide range of dynamic physical systems. The particle swarm optimization (PSO) method has been considered an effective tool for solving the engineering optimization problems for ordinary differential equations. This paper proposes a modified hybrid Nelder-Mead simplex search and particle swarm optimization (M-NM-PSO) method for solving parameter estimation problems. The M-NM-PSO method improves the efficiency of the PSO method and the conventional NM-PSO method by rapid convergence and better objective function value. Studies are made for three well-known cases, and the solutions of the M-NM-PSO method are compared with those by other methods published in the literature. The results demonstrate that the proposed M-NM-PSO method yields better estimation results than those obtained by the genetic algorithm, the modified genetic algorithm (real-coded GA (RCGA)), the conventional particle swarm optimization (PSO) method, and the conventional NM-PSO method.

1. Introduction

The parameter estimation problems involve estimating the unknown parameters of the mathematical models based on a system of ordinary differential equations by using experiment data that are obtained under well-defined standard conditions. Traditional optimization methods such as the Nelder-Mead (NM) method [1, 2] and the Gauss-Newton method [3] can be applied to find reasonably good estimations of parameters of simple models. However, they are not robust enough for complex problems that involve a huge search space, and they tend to find local optimum points rather than the global optimum points. In addition, quasi-linearization methods and data-smoothing methods are also often used to solve parameter estimation problems [4].

To overcome the problem of finding the global optimum points, several heuristic optimization methods such as the genetic algorithm (GA) [5], the simulated annealing (SA) method, and the particle swarm optimization (PSO) method [6] for solving the parameter estimation problems have been proposed. Some modifications to the heuristic optimization methods have also been proposed in recent years. Khalik et al. proposed the real-coded GA (RCGA) method for parameter estimation to overcome the drawbacks of the binary-coded GA (BCGA) method [7, 8]. Ali et al. proposed the application of a modified differential evolution (MDE) method [9]. Schwaab et al. proved that less computational attempts are needed by the PSO method than the GA method and the SA method for solving parameter estimation problems [10]. Zahara and Liu [6] applied the PSO method and the conventional NM-PSO method to solve parameter estimation problems, demonstrated the advantages of the conventional NM-PSO method, and showed that it is an effective tool in solving unconstrained or constrained optimization problems.

The advantages of the heuristic methods are that they do not require information about the gradient of the objective function [11–13], that they are insensitive to the guessed solutions, and that they can find the global solutions by making extensive calculations of the objective function in the parameter space.

In this research, a modified hybrid Nelder-Mead simplex search and particle swarm optimization (M-NM-PSO) method is proposed to solve the parameter estimation problems. The proposed M-NM-PSO method is applied to three well-known cases, and the results obtained are compared to those obtained by the GA, RCGA, MDE, PSO, and conventional NM-PSO methods to demonstrate its superiority in terms of accuracy, rate of convergence, and feasibility.

The content of this paper is organized as follows. Section 2 describes briefly the parameter estimation problems. Section 3 presents the proposed M-NM-PSO algorithm. Section 4 discusses the numerical simulation cases and compares the results obtained by different methods, and the conclusions are summarized in Section 5.

2. The Parameter Identification Problems

Assume that the mathematical model is defined either by a first-order differential equation
(2.1)
or a second-order differential equation
(2.2)
where p is the parameter vector with n unknown real parameters p1, p2, p3, …, pn.
The experiment data are (ti, yi), i = 1, …, m, where ti are the independent time variables and yi are the experiment data or measured values of the corresponding dependent variables. Typically, we have n ≪ m. The problem considered herein is that of estimating the optimal parameter vector p* as accurately as possible from the given experiment data. This is a problem of minimizing the sum of square errors (SSE), which can be represented as
(2.3)
where y(ti; p) are obtained by the Runga-Kutta method and yi are the experiment data.

Three cases are analyzed in this study to validate the superiority of the proposed M-NM-PSO method. The first two cases are standard minimal SSE problems, and the third case is a more complex seven-dimensional isothermal continuously stirred tank reactor (CSTR) maximal SSE problem.

3. The Proposed M-NM-PSO Method

3.1. The Nelder-Mead (NM) Simplex Search Method

The NM simplex search method is proposed by Nelder and Mead [2], which is a good local search method designed for unconstrained optimization problem without using gradient information. This method rescales the simplex by four basic linear transformations: reflection, expansion, contraction, and shrinkage. Through these transformations, the simplex can successively improve itself towards the optimum point.

Take the problem of finding the simplex 3 solutions in a 2-dimensional search space for example. The basic NM procedures to minimize the two-variable function is illustrated in Figure 1. The NM simplex design begins with a starting point G and initial step sizes to construct points W and B as shown in Figure 1. Suppose that f(W) is the highest (worst) of all function values and the point W is to be replaced by the point R. In this example, R is the reflection of W to the centroid point M between G and B. Suppose f(B) < f(G) < f(W). At this stage, two situations may arise.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Illustration of the NM simplex algorithm.

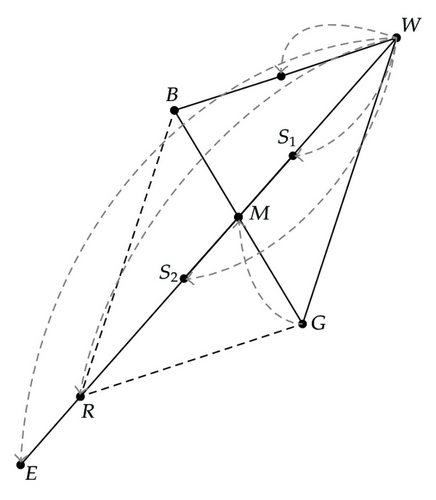
Case 1 (f(R) < f(B)). An extension point, point E, is created. Point W is replaced by point E if f(E) < f(R), otherwise point W is replaced by point R.

Case 2 (f(R) > f(B)). A contraction point, point S, is created. S = S1 if f(W) < f(R), otherwise S = S2.

Point W is replaced by point S if f(S) < f(B), otherwise a shrinkage operation is performed to reduce the size of the simplex by moving point W and point G towards point B.

The advantage of the NM method is that it is intrinsically fast in finding an optimal solution, but the disadvantage is that the solution found may be a local optimal solution rather than a global one. We want to retain its advantages but not its shortcomings in our proposed M-MN-PSO algorithm.

3.2. The Particle Swarm Optimization (PSO) Algorithm

Eberhart and Kennedy [14] were the first to propose the PSO algorithm. As shown in Figure 2, it begins by randomly initializing a flock of birds over the problem space where each bird is called a “particle”.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Position update of particles.
Each particle remembers the best solution which it has found and the best solution found by the entire swarm along the search trajectory. Their velocities and positions are updated by the following equations:
(3.1)
(3.2)
where c1 and c2 are two acceleration constants called the cognitive parameter and the social parameter, respectively, and are typically set to 2.0. The function rand() generates uniformly a random value in the range [0,1]. The parameter w is an inertia weight. Eberhart and Shi [15] suggested that w = 0.5 + (rand()/2).

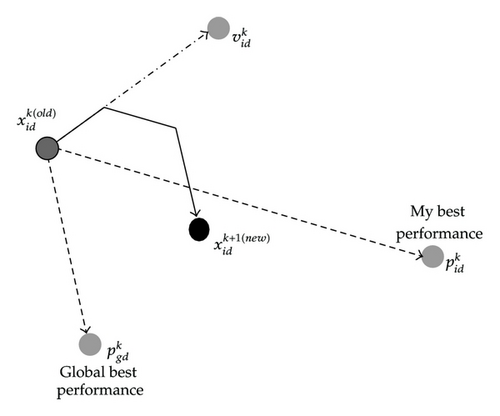
Equation (3.1) yields the new velocity of a particle which is determined by the particle’s previous velocity (Vid), its best position (pid), and the global best position (pgd). It is necessary to impose a maximum limit value Vmax  on the velocity. If the computed new velocity exceeds this threshold, it is set to Vmax  to prevent this particle from flying past the desired solutions in each iteration. Equation (3.2) specifies how each particle’s position is updated in the search space based on their movement over a time interval Δt, which is usually set to 1.

The advantage of the PSO algorithm is that it tends to find the global solution rather than the local one, but improvements on its accuracy and speed of convergence are much desired.

Zahara proposed a hybrid NM-PSO method that combines the NM method and the PSO method, and applied this method to two study cases with excellent results [6]. This paper describes a modified version of the hybrid NM-PSO method, the M-NM-PSO method, with even better results.

3.3. The Proposed M-NM-PSO Method

Two algorithms are integrated in the conventional hybrid NM-PSO optimization method: a conventional algorithm (the NM simplex search algorithm) and an evolutionary algorithm (the PSO algorithm). The efficiency of the NM simplex search algorithm is high because it converges rapidly, but it tends to converge to a local rather than a global optimal solution. On the other hand, the PSO algorithm is capable of finding a global optimal solution, but a large size of particle population and thus great amounts of memory storage and computation time are required during the optimization process.

Based on the above reasoning, the conventional hybrid NM-PSO method was proposed to overcome the shortcomings of the PSO algorithm and the NM algorithm, and to find the global optimal solution accurately and efficiently.

The conventional NM-PSO method was developed by Zahara and Liu [6]. In this method, n optimal particles are reserved, and the NM operator is applied to the first n + 1 particles and to update the (n + 1)th particle. While the conventional NM-PSO method updates only the remaining (N − (n + 1)) particles, the proposed M-NM-PSO method updates all the N particles and thus converges towards the optimal solution more accurately and faster, and increases the possibility of finding a better solution. Figure 3 shows the schematic representation of the proposed M-NM-PSO method.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Schematic representation of the proposed M-NM-PSO method.

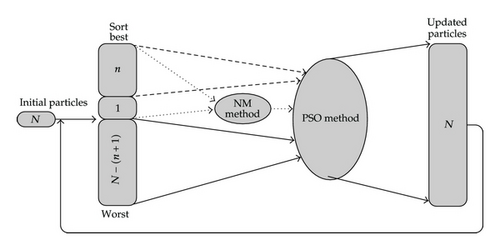
The procedures to implement the proposed M-NM-PSO method are as follows, and the pseudo codes of the proposed M-NM-PSO algorithm are shown in Pseudocode 1. Let the dimension of the problem to be solved is n. First, N particles (N > n + 1) are generated as a swarm. Next, the objective functions are arranged in the order from good to bad, and the N particles are divided accordingly into three groups: the first n particles, the (n + 1)th particle, and the remaining N − (n + 1) particles. Then, the function values of the first n particles and the (n + 1)th particle are calculated using the NM simplex method to find the updated best particle. After the PSO method examines the positions of the (n + 1) best particles and readjusts the N particles, the global optimal particle of the population is determined by the sorted fitness values. The above optimization procedures are repeated until the termination conditions are satisfied.

    Pseudocodes 1: Pseudo Codes of the proposed M-NM-PSO algorithm.

  • (1)  Initialization

  •  Generate particles of population size N (N > (n+1 )).

  • (2)  Solution identification

  •  Arrange the particles in the order from good to bad.

  • (3)  NM Method

  •  Apply NM operator to the first n+1 particles and update the (n+1 )th particle.

  • (4)  PSO Method

  •  Apply PSO operator to update the N particles.

  •  (4.1)  Selection

  •  Select the global best particle and the neighborhood best particle from the population.

  •  (4.2)  Velocity Update

  •  Apply velocity updates to the N particles.

  • (5)  Go to step 2

  •  If the condition is not satisfied. Otherwise stop.

4. Numerical Simulations and Comparisons

In this paper, the proposed M-NM-PSO method is applied to solve three well-known problems [4–9]. The results obtained are compared with those in the cited papers [4–9]. To demonstrate the superiority of the proposed M-NM-PSO method, only a population of 21 particles is used to find the solutions of the three cases. The method is implemented with Matlab, and the programs are run on a PC with a 3.2 GHz dual-core Intel processor and 4 GB memory capacity.

Case 1 (an enzyme effusion problem). The mathematical model of an enzyme effusion problem can be represented as

(4.1)

The experiment data are listed in Table 1, and initial conditions are used by the M-NM-PSO method to solve (4.1) and to estimate the values of the four parameters p1, p2, p3, and p4 in the model.

The results obtained by the M-NM-PSO method using a population of just 21 particles along with those by Scitovski and Jukić [4], GA [5], RGA [7, 8], PSO [6], MDE [9], and conventional NM-PSO [6] are listed in Table 2.

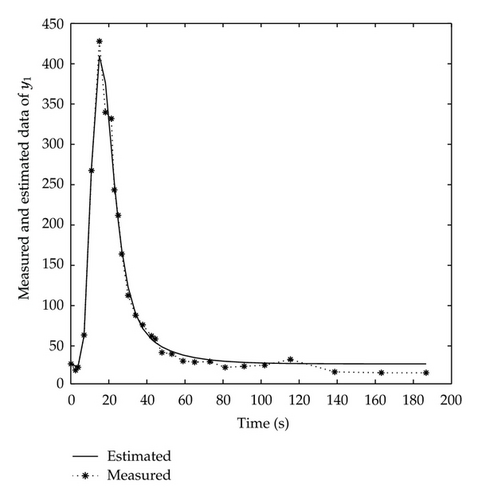
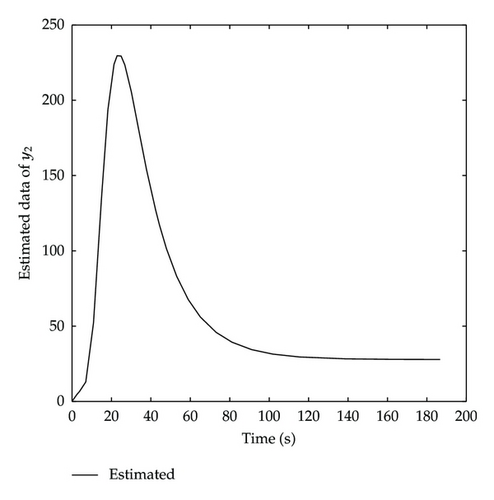
The fact that the results of the M-NM-PSO method are reached after only 150 iterations with an SSE value of 3963.0 validates the superiority of the M-NM-PSO method. The results in Table 2 also show that the M-NM-PSO method yields better estimates and has smaller SSE than those of GA, RGA, PSO, and conventional NM-PSO. Figure 4 shows the plots of the estimated and measured data of y1, which demonstrate the excellent fitness of the estimated data to the measured data. Figure 5 shows the plots of the estimated data of y2.

Table 1. Data of Case 1 (An enzyme effusion problem).
t y1 t y1 t y1 t y1
0.1 27.8 21.3 331.9 42.4 62.3 81.1 23.5
2.5 20.0 22.9 243.5 44.4 58.7 91.1 24.8
3.8 23.5 24.9 212.0 47.9 41.9 101.9 26.1
7.0 63.6 26.8 164.1 53.1 40.2 115.4 33.3
10.9 267.5 30.1 112.7 59.0 31.3 138.7 17.8
15.0 427.8 34.1 88.1 65.1 30.0 163.2 16.8
18.2 339.7 37.8 76.2 73.1 30.6 186.7 16.8
Table 2. Results of Case 1 (An enzyme effusion problem).
Method P 1 P 2 P 3 P 4 y 1 at 0.1 y 2 at 0.1 Population size Iterations SSE
Ref. [4] 0.3180 2.6900 0.4188 0.1035 22 38 28 — 5301.2
Ref. [4] 0.3793 2.7211 0.4199 0.1030 22.9 40 68 — 5250.3
Ref. [4] 0.3190 2.7010 0.4190 0.1031 22 39 128 — 5076.6
GA [5] 0.3194 2.7010 0.3892 0.0782 21.00 38.75 — 100 5229.7
GA [5] 0.3050 2.6987 0.4005 0.1166 22.02 39.44 — 200 4547.3
GA [5] 0.2845 2.6717 0.3927 0.1614 23.99 40.14 — 500 4068.4
RGA [7] 0.2454 2.6092 0.3326 0.3217 22.005 38.608 60 100 4431.5
RGA [7] 0.2561 2.6269 0.3449 0.2696 22.043 38.403 60 200 4193.9
RGA [7] 0.2619 2.6336 0.3524 0.2575 21.986 38.704 60 300 4136.7
RCGA [8] 0.2624 2.6378 0.3599 0.2212 28.5443 0.2339   100 3068
RCGA [8] 0.2710 2.6442 0.3676 0.2429 28.5203 0.2566   500 3120
PSO [6] 0.2667 2.6437 0.3636 0.2282 28.5443 0.2339 20 100 3982.0
PSO [6] 0.2668 2.6440 0.3635 0.2280 28.5443 0.2339 20 200 3981.9
PSO [6] 0.2713 2.6513 0.3690 0.2079 28.5443 0.2339 20 300 3971.2
DE [9] 23.4543 37.3712 0.2726 2.6527 0.3643 0.2064   100 4048.7
DE [9] 23.2648 37.0019 0.2728 2.6535 0.3648 0.2095   300 4044.5
DE [9] 23.2548 37.0000 0.2728 2.6536 0.3649 0.2093   500 4044.5
MDE [9] 23.2437 37.0013 0.2729 2.6537 0.3650 0.2091   100 4044.5
MDE [9] 23.2543 37.0000 0.2728 2.6536 0.3649 0.2093   300 4044.5
MDE [9] 23.2543 37.0000 0.2728 2.6536 0.3649 0.2093   500 4044.5
NM-PSO [6] 0.2711 2.6504 0.3686 0.2098 28.5443 0.2339 21 149 3968.9
  
M-NM-PSO 0.2729 2.6539 0.3710 0.2004 27.8000 0.2339 21 150 3963.0
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The plots of the estimated and measured data of y1 in Case 1 (149 iterations).
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The plots of the estimated data of y2 in Case 1 (149 iterations).

Case 2. A mathematical model may be represented by a second-order ordinary differential equation (ODE)

(4.2)

The values of the parameters p1, p2, p3, and p4 in (4.2) are to be estimated from the data in Table 3, and the results are listed in Table 4. Note that given the estimated values of the parameters p1, p2, p3, and p4, the SSE values of the RGA [7] should be 0.4315 rather than 0.3204, and 0.3969 rather than 0.2827, as listed in Table 4.

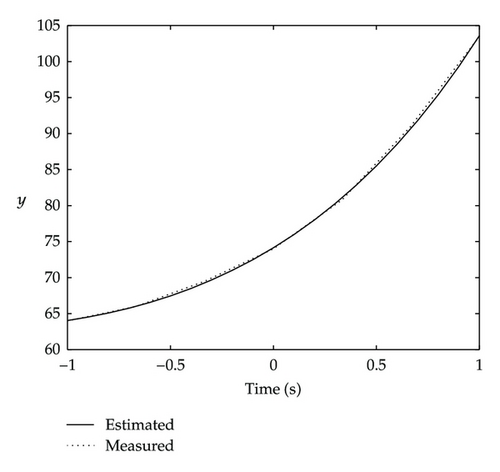
As expected, the M-NM-PSO method yields better estimated results and lower SSE values than those of the GA, RGA, PSO, and conventional NM-PSO methods. It yields the same results as the NM-PSO method but with less iteration. Figure 6 shows the plots of the estimated and measured data of y in the given range, which demonstrates the excellent fitness of the estimated data to the measured data.

Table 3. Data of Case 2 (A second-order system).
t −1 −2/3 −1/3 0 1/3 2/3 1
y 64.0 66.0 69.5 74.0 80.8 91.0 103.5
Table 4. Results of Case 2 (A second-order system).
Method P1 P2 P3 P4 Population size Iterations SSE
GA [5] 43.2233 30.8774 0.6170 −0.2812 — 100 0.4396
GA [5] 40.8112 33.3234 0.6400 −0.2464 — 200 0.3859
GA [5] 37.7414 36.3533 0.6753 −0.2123 — 500 0.3347
RGA [7] 42.5032 31.5469 0.6265 −0.2749 80 100
  • 0.4315
  • (0.3204)*
RGA [7] 41.4371 32.6713 0.6346 −0.2563 80 200
  • 0.3969
  • (0.2827)*
DE [9] 36.0250 38.1356 0.6933 −0.1895 — 100 0.3260
DE [9] 34.1450 39.9841 0.7155 −0.1702 — 300 0.2963
DE [9] 34.1266 40.0000 0.7157 −0.1699 — 500 0.2960
MDE [9] 35.4350 38.6848 0.6987 −0.1823 — 100 0.3142
MDE [9] 34.1266 40.0000 0.7157 −0.1699 — 300 0.2960
MDE [9] 34.1266 40.0000 0.7157 −0.1699 — 500 0.2960
PSO [6] 30.0761 44.0683 0.7680 −0.1279 20 100 0.2851
PSO [6] 30.7589 43.3814 0.7587 −0.1348 20 200 0.2847
NM-PSO [6] 30.5386 43.6025 0.7617 −0.1326 21 60 0.2847
  
M-NM-PSO 30.8616 43.2783 0.7573 −0.1358 21 53 0.2847
  • *Given the estimated values of  P1,  P2,  P3, and P4, the SSE values of the RGA [7] should be 0.4315 and 0.3969, rather than 0.3204 and 0.2827, respectively.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The plots of the estimated and measured data of y in Case 2 (53 iterations).

Case 3 (an isothermal continuously stirred tank reactor (CSTR) problem). A seven-dimensional isothermal CSTR problem [7, 16] is represented by the equations

(4.3)
where
(4.4)

This case is different from the previous two cases. The problem is to find the optimal parameter values u1, u2, u3, and u4 that maximize the performance index (PI) or x8(t):

(4.5)

A first-order differential equation is used to find the optimal parameter vector U = [u1, u2, u3, u4].

The initial starting point x(0) is given by the vector [0.1883,  0.2507,  0.0467, 0.0899,  0.1804,  0.1394,  0.1046], and the bounds of the unknown parameter u1, u2, u3,u4 are

(4.6)

This seven-dimensional system has a PI function with four control parameters and appears to be a difficult task for the proposed M-NM-PSO method. The results with u4 fixed at 6.0 are shown in Table 5 for comparison. Compared with the RGA [7] method, the M-NM-PSO method uses a smaller particle population and yields better estimates and a larger PI. Compared with the conventional NM-PSO method, M-NM-PSO yields the same results in less iteration.

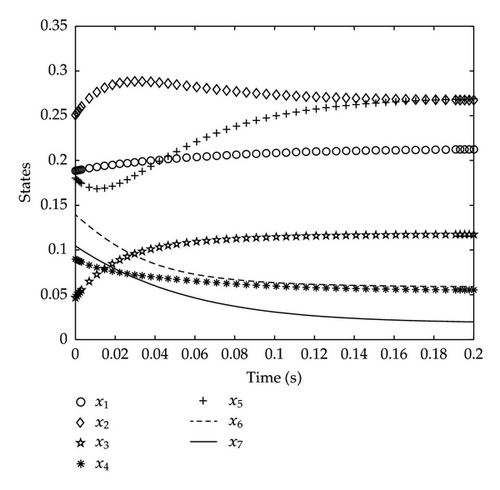
The M-NM-PSO method can still be applied using 21 particles even if the value of u4 is not fixed, and the results are reached in 53 iterations: PI = 19.9404, U = [11.7618,  3.4781,  0.8401,  12.0752], which are also shown in Table 5. As expected, the M-NM-PSO method not only yields better results but also requires less iteration than the other methods. The plots of the seven states (x1 ~ x7) are shown in Figure 7.

Table 5. Results of Case 3 (An isothermal CSTR problem).
Method u 1 u 2 u 3 u 4 Population size Iterations PI (the larger the better)
RGA [7] 11.455 4.5222 0.6865 set u4 = 6.0 50 100 19.0437
NM-PSO 11.5891 4.9420 0.7118 set u4 = 6.0 21 52 19.0597
M-NM-PSO 11.5891 4.9420 0.7118 set u4 = 6.0 21 45 19.0597
M-NM-PSO 11.7618 3.4781 0.8401 12.0752 21 53 19.9404
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
The plots of the seven states in Case 3 (An isothermal CSTR problem).

5. Conclusion

All of the results of the three cases indicate that the proposed M-NM-PSO method can be applied efficiently to solve the estimation problems of unknown parameters in mathematical models. The application of the proposed M-NM-PSO method is demonstrated by three study cases. The results indicate that the proposed M-NM-PSO method is indeed more accurate, reliable, and efficient in finding global optimal solutions than the other alternative algorithms or methods. Furthermore, the proposed M-NM-PSO method converges accurately as well as quickly, thus greatly improves the efficiency of solving the parameter estimation problems.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.