Journal of Applied Mathematics
Volume 2012, Issue 1 529176
Research Article
Open Access

System Identification Using Multilayer Differential Neural Networks: A New Result

J. Humberto Pérez-Cruz, 

Corresponding Author

J. Humberto Pérez-Cruz

Centro Universitario de Ciencias Exactas e Ingenierías, Universidad de Guadalajara, Boulevard Marcelino García Barragán No. 1421, 44430 Guadalajara, JAL, Mexico udg.mx

Search for more papers by this author
A. Y. Alanis, 

A. Y. Alanis

Centro Universitario de Ciencias Exactas e Ingenierías, Universidad de Guadalajara, Boulevard Marcelino García Barragán No. 1421, 44430 Guadalajara, JAL, Mexico udg.mx

Search for more papers by this author
José de Jesús Rubio, 

José de Jesús Rubio

Sección de Estudios de Posgrado e Investigación, ESIME-UA, IPN, Avenida de las Granjas No. 682, 02250 Santa Catarina, NL, Mexico

Search for more papers by this author
Jaime Pacheco, 

Jaime Pacheco

Sección de Estudios de Posgrado e Investigación, ESIME-UA, IPN, Avenida de las Granjas No. 682, 02250 Santa Catarina, NL, Mexico

Search for more papers by this author
First published: 12 April 2012
https://doi.org/10.1155/2012/529176
Citations: 10
Academic Editor: Hector Pomares

Abstract

In previous works, a learning law with a dead zone function was developed for multilayer differential neural networks. This scheme requires strictly a priori knowledge of an upper bound for the unmodeled dynamics. In this paper, the learning law is modified in such a way that this condition is relaxed. By this modification, the tuning process is simpler and the dead-zone function is not required anymore. On the basis of this modification and by using a Lyapunov-like analysis, a stronger result is here demonstrated: the exponential convergence of the identification error to a bounded zone. Besides, a value for upper bound of such zone is provided. The workability of this approach is tested by a simulation example.

1. Introduction

During the last four decades system identification has emerged as a powerful and effective alternative to the first principles modeling [1–4]. By using the first approach, a satisfactory mathematical model of a system can be obtained directly from an input and output experimental data set [5]. Ideally no a priori knowledge of the system is necessary since this is considered as a black box. Thus, the time employed to develop such model is reduced significantly with respect to a first principles approach. For the linear case, system identification is a problem well understood and enjoys well-established solutions [6]. However, the nonlinear case is much more challenging. Although some proposals have been presented [7], the class of considered nonlinear systems can result very limited. Due to their capability of handling a more general class of systems and due to advantages such as the fact of not requiring linear in parameters and persistence of excitation assumptions [8], artificial neural networks (ANNs) have been extensively used in identification of nonlinear systems [9–12]. Their success is based on their capability of providing arbitrarily good approximations to any smooth function [13–15] as well as their massive parallelism and very fast adaptability [16, 17].

An artificial neural network can be simply considered as a nonlinear generic mathematical formula whose parameters are adjusted in order to represent the behavior of a static or dynamic system [18]. These parameters are called weights. Generally speaking, ANN can be classified as feedforward (static) ones, based on the back propagation technique [19] or as recurrent (dynamic) ones [17]. In the first network type, system dynamics is approximated by a static mapping. These networks have two major disadvantages: a slow learning rate and a high sensitivity to training data. The second approach (recurrent ANN) incorporates feedback into its structure. Due to this feature, recurrent neural networks can overcome many problems associated with static ANN, such as global extrema search, and consequently have better approximation properties. Depending on their structure, recurrent neural networks can be classified as discrete-time ones or differential ones.

The first deep insight about the identification of dynamic systems based on neural networks was provided by Narendra and Parthasarathy [20]. However, none-stability analyses of their neuroidentifier were presented. Hunt et al. [21] called attention to determine the convergence, stability and robustness of the algorithms based on neural networks for identification and control. This issue was addressed by Polycarpou and Ioannou [16], Rovithakis and Christodoulou [17], Kosmatopoulos et al. [22], and Yu and Poznyak [23]. Given different structures of continuous-time neural networks, the stability of their algorithms could be proven by using Lyapunov-like analysis. All aforementioned works considered only the case of single-layer networks. However, as it is known, this kind of networks does not necessarily satisfy the property of universal function approximation [24]. And although the activation functions of single-layer neural networks are selected as a basis set in such a way that this property can be guaranteed, the approximation error can never be made smaller than a lower bound [24]. This drawback can be overcome by using multilayer neural networks. Due to this better capability of function approximation, the case multilayer was considered in [25] for feedforward networks and for continuous time recurrent neural networks for first time in [26] and subsequently in [27]. By using Lyapunov-like analysis and a dead-zone function, boundedness for the identification error could be guaranteed in [26]. The following upper bound for the “average” identification error was reported,
(1.1)
where Δt is the identification error, Q0 is a positive definite matrix, is a upper bound for the modeling error, Υ is an upper bound for a deterministic disturbance, and [·]+ is a dead-zone function defined as
(1.2)
Although, in [28], open-loop analysis based on the passivity method for a multilayer neural network was carried out and certain simplifications were accomplished, the main result about the aforementioned identification error could not be modified. In [29], the application of the multilayer scheme for control was explored. Since previous works [26–29] are based on this “average” identification error, one could wonder about the real utility of this result. Certainly, boundedness for this kind of error does not guarantee that Δt belongs to L2 or L∞. Besides, none value for upper bound of identification error norm is provided. Likewise, none information about the speed of the convergence process is presented. Another disadvantage of this approach is that the upper bound for the modeling error must be strictly known a priori in order to implement the learning laws for the weight matrices. In order to avoid these drawbacks, in this paper, we propose to modify the learning laws employed in [26] in such a way that their implementation does not require anymore the knowledge of an upper bound for the modeling error. Besides, on the basis of these new learning laws, a stronger result is here guaranteed: the exponential convergence of the identification error norm to a bounded zone. The workability of the scheme developed in this paper is tested by simulation.

2. Multilayer Neural Identifier

Consider that the nonlinear system to be identified can be represented by
(2.1)
where xt ∈ ℜn is the measurable state vector for t ∈ ℜ+ : = {t : t ≥ 0},   ut ∈ ℜq is the control input, f : ℜn × ℜq × ℜ+ → ℜn is an unknown nonlinear vector function which represents the nominal dynamics of the system, and ξt ∈ ℜn represents a deterministic disturbance. f(xt, ut, t) represents a very ample class of systems including affine and nonaffine-in-control nonlinear systems. However, when the control input appears in a nonlinear fashion in the system state equation (2.1), throughout this paper, such nonlinearity with respect to the input is assumed known and represented by γ(·) : ℜq → ℜs.
Consider the following parallel structure of multilayer neural network
(2.2)
where is the state of the neural network, ut ∈ ℜq is the control input, A ∈ ℜn×n is a Hurwitz matrix which can be specified by the designer, the matrices W1,t ∈ ℜn×m and W2,t ∈ ℜn×r are the weights of output layers, the matrices V1,t ∈ ℜm×n and V2,t ∈ ℜr×n are the weights of hidden layers, σ(·) is the activation vector-function with sigmoidal components, that is, σ(·) : = ,
(2.3)
where aσj, cσj,i, and dσj are positive constants which can be specified by the designer, ϕ(·) : ℜr → ℜr×s is also a sigmoidal function, that is,
(2.4)
where aϕij, cϕij,l, and dϕij are positive constants which can be specified by the designer, γ(·) : ℜq → ℜs represents the nonlinearity with respect to the input—if it exists—which is assumed a priori known for the system (2.1). It is important to mention that m and r, that is, the number of neurons for σ(·) and the number of rows for ϕ(·), respectively, can be selected by the designer.

The problem of identifying system (2.1) based on the multilayer differential neural network (2.2) consists of, given the measurable state xt and the input ut, adjusting on line the weights W1,t, W2,t, V1,t, and V2,t by proper learning laws such that the identification error can be reduced.

Hereafter, it is considered that the following assumptions are valid;
  • (A1)

    System (2.1) satisfies the (uniform on t) Lipschitz condition, that is,

(2.5)
  • (A2)

    The differences of functions σ(·) and ϕ(·) fulfil the generalized Lipschitz conditions

    (2.6)
    where
    (2.7)
    Λ1 ∈ ℜm×m, Λ2 ∈ ℜr×r, Λσ ∈ ℜn×n, Λϕ ∈ ℜn×n are known positive definite matrices, and are constant matrices which can be selected by the designer.

    As σ(·) and ϕ(·) fulfil the Lipschitz conditions and from Lemma A.1 proven in [26] the following is true:

    (2.8)
    (2.9)
    where
    (2.10)
    νσ ∈ ℜm and νiϕ ∈ ℜn are unknown vectors but bounded by , , respectively; , , l1 and l2 are positive constants which can be defined as , , where Lg,1 and Lg,2 are global Lipschitz constants for σ(·) and ϕi(·), respectively.

  • (A3)

    The nonlinear function γ(·) is such that where is a known positive constant.

  • (A4)

    Unmodeled dynamics is bounded by

    (2.11)
    where and are known positive constants and Λ3 ∈ ℜn×n is a known positive definite matrix and can be defined as and are constant matrices which can be selected by the designer.

  • (A5)

    The deterministic disturbance is bounded, that is, , Λ4 is a known positive definite matrix.

  • (A6)

    The following matrix Riccati equation has a unique, positive definite solution P:

    (2.12)
    where
    (2.13)
    Q0 is a positive definite matrix which can be selected by the designer.

Remark 2.1. Based on [30, 31], it can be established that the matrix Riccati equation (2.12) has a unique positive definite solution P if the following conditions are satisfied;

  • (a)

    The pair (A, R1/2) is controllable, and the pair (Q1/2, A) is observable.

  • (b)

    The following matrix inequality is fulfilled:

    (2.14)
    Both conditions can relatively easily be fulfilled if A is selected as a stable diagonal matrix.

  • (A7)

    It exists a bounded control ut, such that the closed-loop system is quadratic stable, that is, it exists a Lyapunov function V0 > 0 and a positive constant λ such that

    (2.15)
    Additionally, the inequality must be satisfied.

Now, consider the learning law:
(2.16)
where s is the number of columns corresponding to ϕ(·),   K1 ∈ ℜn×n,   K2 ∈ ℜn×n,   K3 ∈ ℜm×m, and K4 ∈ ℜr×r are positive definite matrices which are selected by the designer. st is a dead-zone function which is defined as
(2.17)
Based on this learning law, the following result was demonstrated in [26].

Theorem 2.2. If the assumptions (A1)–(A7) are satisfied and the weight matrices W1,t, W2,tV1,t, and V2,t of the neural network (2.2) are adjusted by the learning law (2.16), then

  • (a)

    the identification error and the weights are bounded:

    (2.18)

  • (b)

    the identification error Δt satisfies the following tracking performance:

(2.19)

In order to prove this result, the following nonnegative function was utilized:
(2.20)
where ; .

3. Exponential Convergence of the Identification Process

Consider that the assumptions (A1)–(A3) and (A5)-(A6) are still valid but the assumption (A4) is slightly modified as follows.
  • (B4)

    In a compact set Ω ∈ ℜn, unmodeled dynamics is bounded by where is a constant not necessarily a priori known.

Remark 3.1. (B4) is a common assumption in the neural network literature [17, 22]. As mentioned in Section 2, is given by . Note that and are bounded functions because σ(·) and ϕ(·) are sigmoidal functions. As xt belongs to Ω, clearly xt is also bounded. Therefore, assumption B4 implies implicitly that f(xt, ut, t) is a bounded function in a compact set Ω ∈ ℜn.

Although certainly assumption (B4) is more restrictive than assumption (A4), from now on, assumption (A7) is not needed anymore.

In this paper, the following modification to the learning law (2.16) is proposed:
(3.1)
where k1, k2, k3, and k4 are positive constants which are selected by the designer; P is the solution of the Riccati equation given by (2.12); α : = λmin (P−1/2Q0P−1/2); s is the number of columns corresponding to ϕ(·). By using the constants k1, k2, k3, and k4 in (3.1) instead of the matrices K1, K2, K3, and K4 in (2.16), the tuning process of the neural network (2.2) is simplified. Besides, none dead-zone function is now required. Based on the learning law (3.1), the following result is here established.

Theorem 3.2. If the assumptions (A1)–(A3), (B4), (A5)-(A6) are satisfied and the weight matrices W1,t, W2,t, V1,t, and V2,t of the neural network (2.2) are adjusted by the learning law (3.1), then

  • (a)

    the identification error and the weights are bounded:

    (3.2)

  • (b)

    the norm of identification error converges exponentially to a region bounded given by

(3.3)

Proof of Theorem 3.2. Before beginning analysis, the dynamics of the identification error Δt must be determined. The first derivative of Δt is

(3.4)
Note that an alternative representation for (2.1) could be calculated as follows:
(3.5)
Substituting (2.2) and (3.5) into (3.4) yields
(3.6)
Subtracting and adding the terms , , , and and considering that , , , , , , (3.6) can be expressed as
(3.7)
In order to begin analysis, the following nonnegative function is selected:
(3.8)
where P is a positive solution for the Riccati matrix equation given by (2.12). The first derivative of Vt is
(3.9)
Each term of (3.9) will be calculated separately. For ,
(3.10)
substituting (3.7) into (3.10) yields
(3.11)
The terms , , , and in (3.11) can be bounded using the following matrix inequality proven in [26]:
(3.12)
which is valid for any X, Y ∈ ℜn×k and for any positive definite matrix 0 < Γ = ΓT ∈ ℜn×n. Thus, for and considering assumption (A2),
(3.13)
For and considering assumptions (A2) and (A3)
(3.14)
By using (3.12) and given assumptions (B4) and (A5), and can be bounded, respectively, by
(3.15)
Considering (2.8), can be developed as
(3.16)
By simultaneously adding and subtracting the term into the right-hand side of (3.16),
(3.17)
By using (3.12) and considering assumption (A2), the term can be bounded as
(3.18)
And consequently, is bounded by
(3.19)
For and considering (2.9),
(3.20)
Adding and subtracting the term into the right-hand side of (3.20),
(3.21)
By using (3.12), can be bounded by
(3.22)
but considering that
(3.23)
and from assumptions (A2) and (A3), the following can be concluded:
(3.24)
Thus, is bounded by
(3.25)
Consequently, given (3.13), (3.14), (3.15), (3.19), and (3.25), can be bounded as
(3.26)
With respect to , using several properties of the trace of a matrix,
(3.27)
As , the derivative of W1,t is clearly . However, is given by the learning law (3.1). Therefore, by substituting (3.1) into and the corresponding expression into the right-hand side of (3.27), it is possible to obtain
(3.28)
Proceeding in a similar way for
(3.29)
it is possible to obtain
(3.30)
By substituting (3.26), (3.28), and (3.30) into (3.9), the following bound for can be determined:
(3.31)
Simplifying like terms
(3.32)
Adding and subtracting into the right-hand side of the last inequality yields the expression ATP + PA + PRP + Q. That is
(3.33)
However, the expression ATP + PA + PRP + Q is, in accordance with the assumption (A6), equal to zero. Therefore,
(3.34)
Now, considering that and using Rayleigh’s inequality, the following can be obtained:
(3.35)
or alternatively
(3.36)
In view of (3.36), it is possible to establish that
(3.37)
As α : = λmin (P−1/2Q0P−1/2), finally the following bound for can be concluded:
(3.38)
Equation (3.38) can be rewritten in the following form
(3.39)
Multiplying both sides of the last inequality by exp (αt), it is possible to obtain
(3.40)
The left-hand side of (3.40) can be rewritten as
(3.41)
or equivalently as
(3.42)
Integrating both sides of the last inequality yields
(3.43)
Adding V0 to both sides of the inequality,
(3.44)
Multiplying both sides of the inequality (3.44) by exp (−αt), the following can be obtained:
(3.45)
and, consequently,
(3.46)
As P and Q0 are positive definite matrices, then α is always a positive scalar and therefore Vt is an upperly bounded function. However, in reference to (3.8), Vt is also a nonnegative function. Consequently, Δt, W1,t, W2,t, V1,t, V2,t ∈ L∞, and, thus, the first part of the Theorem 3.2 has been proven. With respect to the final part of this theorem, from (3.8), it is evident that . Besides, from Rayleigh’s inequality, . Consequently, . Nonetheless, in accordance with (3.46), Vt is bounded by . This means that
(3.47)
Finally, taking the limit as t → ∞ of the last inequality, the last part of Theorem 3.2 has been proven.

Remark 3.3. Based on the results presented in [32, 33], and, from the inequality (3.38), uniform stability for the identification error can be guaranteed.

Remark 3.4. Although, in [34], the asymptotic convergence of the identification error to zero is proven for multilayer neural networks, the considered class of nonlinear systems is much more restrictive than in this work.

Remark 3.5. In [35], the main idea behind Theorem 3.2 was utilized but only for the single layer case. In this paper, the generalization for the multilayer case is presented for first time.

4. Tuning of the Multilayer Identifier

In this section, some details about the selection of the parameters for the neural identifier are presented. In first place, it is important to mention that the positive definite matrices Λ1 ∈ ℜm×m, Λ2 ∈ ℜr×r, Λσ ∈ ℜn×n, Λϕ ∈ ℜn×n, Λ3 ∈ ℜn×n, and Λ4 ∈ ℜn×n presented throughout assumptions (A2)–(A5) are known a priori. In fact, their selection can be very free. Although, in many cases, identity matrices can be enough, the corresponding freedom of selection can be used to satisfy the conditions specified in Remark 2.1.

Other important design decision is related to the proper number of elements m or neurons for σ(·). A good point of departure is to select m = n where n is the dimension of the state vector xt. Normally, this selection is enough in order to produce adequate results. In other case, m should be selected such as m > n. With respect to ϕ(·), for simplicity, a first attempt could be to set the elements of this matrix as zeroes except for the main diagonal.

Another very important question which must be taken into account is the following: how should the weights be selected? Ideally, these weights should be chosen in such a way that the modelling error or unmodeled dynamics can be minimized. Likewise, the design process must consider the solution of the Riccati equation (2.12). In order to guarantee the existence of a unique positive definite solution P for (2.12), the conditions specified in Remark 2.1 must be satisfied. However, these conditions could not be fulfilled for the optimal weights. Consequently, different values for and could be tested until a solution for (2.12) can be found. At the same time, the designer should be aware of that as take values increasingly different from the optimal ones, the upper bound for unmodeled dynamics in assumption B4 becomes greater. With respect to the initial values for W1,t, W2,t, V1,t, and V2,t, some authors, for example [26], simply select , and .

Finally, a last recommendation, in order to achieve a proper performance of the neural network, the variables in the identification process should be normalized. In this context, normalization means to divide each variable by its corresponding maximum value.

5. Numerical Example

In this section, a very simple but illustrative example is presented in order to clarify the tuning process of the neural identifier and compare the advantages of the scheme developed in this paper with respect to the results of previous works [26–29].

Consider the following first-order nonlinear system:
(5.1)
with the initial condition x0 = 0.7 and the input given by ut = sin (t).

For simplicity, ξt is assumed equal to zero. It is very important to note that (5.1) is only used as a data generator since apart from the assumptions (A1)–(A3), (B4), (A5)-(A6), none previous knowledge about the unknown system (5.1) is required to satisfactorily carry out the identification process.

The parameters of the neural network (2.2) and the learning laws (3.1) are selected as
(5.2)
(5.3)
Note that Riccati equation (2.12) becomes a simple second-order algebraic equation for this case:
(5.4)
As , and given the previous values for these parameters, (5.4) has the following solution: P = 1. The rest of the parameters for the neural identifier are selected as α = 2,   l1 = 4,   l2 = 0.0625,   k1 = 500,   k2 = 400,   k3 = 600,   k4 = 800. The initial condition for the neural identifier is selected as .

The results of the identification process are displayed in Figures 1 and 2. In Figure 1, the state xt of the nonlinear system (5.1) is represented by solid line whereas the state is represented by dashed line. Both states were obtained by using Simulink with the numerical method ode23s. In order to appreciate better the quality of the identification process, the absolute value of the identification error is showed in Figure 2. Clearly, the new learning laws proposed in this paper exhibit a satisfactory behavior.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Identification process.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Identification error evolution.

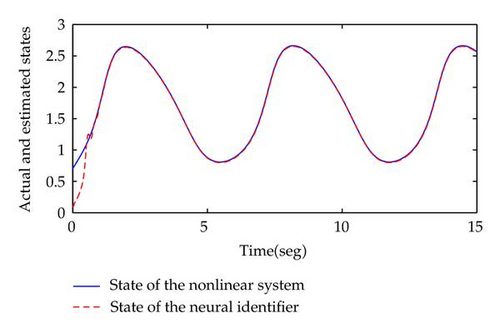
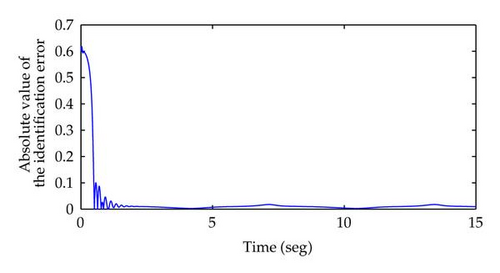
Now, which is the practical advantage of this method with respect to previous works [26–29]? The determination of and more still (parameters associated with assumption A.4) can result difficult. Besides, assuming that is equal to zero, can result excessively large inclusive for simple systems. For example, for system (5.1) and the values selected for the parameters of the identifier, can approximately be estimated as 140. This implies that the learning laws (2.16) are activated only when |Δt| ≥ 70 due to the dead-zone function st. Thus, although the results presented in works [26–29] are technically right, on these conditions, that is, , the performance of the identifier results completely unsatisfactory from a practical point of view since the corresponding identification error is very high. To avoid this situation, it is necessary to be very careful with the selection of weights , and in order to minimize the unmodeled dynamics . However, with these optimal weights, the matrix Riccati equation could have no solution. This dilemma is overcome by means of the learning laws (3.1) developed in this paper. In fact, as can be appreciated, a priory knowledge of is not required anymore for the proper implementation of (3.1).

6. Conclusions

In this paper, a modification of a learning law for multilayer differential neural networks is proposed. By this modification, the dead-zone function is not required anymore and a stronger result is here guaranteed: the exponential convergence of the identification error norm to a bounded zone. This result is thoroughly proven. First, the dynamics of the identification error is determined. Next, a proper nonnegative function is proposed. A bound for the first derivative of such function is established. This bound is formed by the negative of the original nonnegative function multiplied by a constant parameter α plus a constant term. Thus, the convergence of the identification error to a bounded zone can be guaranteed. Apart from the theoretical importance of this result, from a practical point of view, the learning law here proposed is easier to implement and tune. A numerical example confirms the efficiency of this approach.

Acknowledgments

The authors would like to thank the anonymous reviewers for their helpful comments and advice which contributed to improve this paper. First author would like to thank the financial support through a postdoctoral fellowship from Mexican National Council for Science and Technology (CONACYT).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.