General Computational Model for Human Musculoskeletal System of Spine

1. Introduction

The human lumbar spine can support large loads during daily activities such as standing, walking, running, and lifting, where the loads are up to several thousand Newtons [1, 2]. However, it has been reported in experimental studies [3, 4] that an intact ligamentous lumbar spine buckled at the load less than 100 N when a load was applied at the superior end in the vertical direction. Although the trunk muscles have been known to play an important role to withstand external loads [5–7], the principle of trunk muscle activation to obtain such load-carrying capacity of the spine has not been elucidated. Recent experimental studies [4, 8] have demonstrated that the load-carrying capacity of the human spine significantly increased as the load applied to the spine was transferred along a path that approximates its curvature, which is called a follower load path originated from the field of mechanical engineering to solve the problems associated with the stability of columns [9, 10] since the 1950s. In the follower load case, a nearly compressive force was produced in the spine with a small shear force. The follower load concept is a possible principle of muscle activation pattern.

It is not easy to directly investigate trunk muscle activations because there have been difficulties in the in vivo measurements of the activated muscle forces, and the responses of the lumbar spine, such as the intradiscal pressure, resultant joint forces and moments at each vertebral joint. Thus, the computational modeling of the human musculoskeletal system is indispensable to predict the forces of the muscles and the responses of the lumbar spine. Several computational models of the lumbar spine and trunk muscles have been developed to estimate the trunk muscle forces [5, 11–21]. Although the follower load concept was considered in [14, 16–21], it is necessary to improve the generality of model to reflect the physiological conditions of the human spine. In this study, a general computational model of the human lumbar spine and trunk muscles including optimization formulations was provided to predict muscle forces based on the follower load. A three-dimensional numerical example was tested to validate the given model.

2. Preliminaries

2.3. Resultant Joint Force and Resultant Joint Moment

The resultant joint force at each vertebra is the sum of all the muscle forces, the applied external forces, and the force transmitted from the upper vertebra. Hence, the resultant joint force, $$, at ith vertebra is calculated iteratively: for i = 1,2, …, N,

$$ ()

with $$.

The follower load path direction at each node was defined in order to decompose the resultant joint force into the compressive force and the shear force. Let the compressive force direction vector c_i at ith node be

$$ ()

under the assumption that p₀ = 0, which indicates the direction of ith beam element.

Then, $$ can be decomposed into two perpendicular compressive forces $$ and shear force $$ at ith node for i = 1,2, …, N (Figure 1) as

$$ ()

The resultant joint moment $$ at ith node for i = 1,2, …, N is the same to the motion segment moment $$.

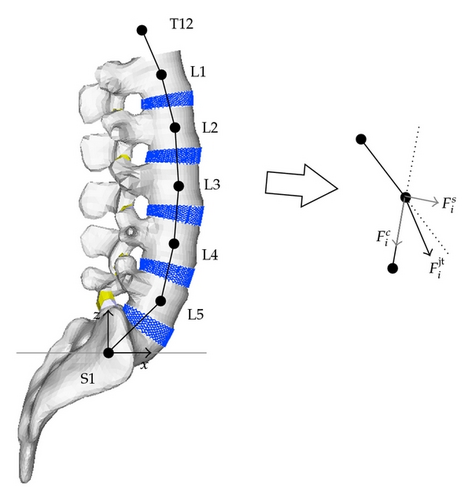
3. Formulation of Optimization Scheme

4. Numerical Tests

A three-dimensional problem of the spine from T12 to S1 is tested to confirm the developed computational model and the formulation of the optimization scheme predicting the muscle forces (N = 7). Here, 117 pairs of trunk muscles were considered (M = 234): 5 longissimus pars lumborum, 4 iliocostalis pars lumborum, 12 longissimus pars thoracis, 8 iliocostalis pars thoracis, 11 psoas, 5 quadratus lumborum, 6 external oblique, 6 internal oblique, 1 rectus abdominus, 12 thoracic multifidus, 20 lumbar multifidus, 6 interspinales, 10 intertransversarii, and 11 rotatores. The anatomical data at the initial position of the vertebrae, muscle attachments, and physiological cross-sectional areas were obtained from the literature and medical images [11, 19–22]. The stiffness matrix K was obtained from previous experimental studies [23, 24].

In this test, (3.2) was used for the objective function. The weight factors w₁,w₂, and w₃ are supposed to be 3, 3, and 1, respectively, since 3 N of force and 1 Nmm of moment are considered equally based on the presumed safe limits of intervertebral loads being approximately 3000 N for forces and 9000 Nmm for moments as shown in [12]. The restriction coefficient α was selected to be 0.25 based on [20] and the maximum muscle stress σ was assumed to be 0.46 MPa based on [26]. The upperbounds of all translation component and rotation component were 20.0 mm and 10.0°, respectively. An upright standing posture was considered for the external loading as 300 N of the upper body weight, 3 Nm of the resulting flexion moment applied to T12, and a vertebral weight of 10 N was added to each lumbar vertebra from L1–L5.

The muscle force distribution satisfying the formulated optimization problem was obtained using MATLAB (MathWorks Inc., USA). The number of activated muscles according to the ratio of muscle force to maximum muscle force was summarized in Table 1. The maximum compressive force and the maximum shear force were 691.1 N and 172.8 N while the maximum joint moment was 2271 Nmm. The previous in vivo studies reported that the maximum compressive force, shear force, and joint moment were about 650 N, 190 N, and 8400 Nmm, respectively, in the upright standing posture [1, 14, 15, 27]. The validity of our results seems to be indirectly achieved since the models in [1, 14, 15, 27] were not exactly same to our model.

5. Conclusion

In this study, a general computational model of the human lumbar spine and trunk muscles including optimization formulations was provided. For a given condition, the trunk muscle forces could be predicted. The feasibility of the solution could be indirectly validated by comparing the compressive force, the shear force, and the joint moment. The presented general computational model and optimization technology can be fundamental tools to understand the control principle of human trunk muscles.