Journal of Applied Mathematics
Volume 2012, Issue 1 458701
Research Article
Open Access

Cubic B-Spline Collocation Method for One-Dimensional Heat and Advection-Diffusion Equations

Joan Goh, 

Corresponding Author

Joan Goh

Pusat Pengajian Sains Matematik, Universiti Sains Malaysia, 11800 Pulau Pinang, Malaysia usm.my

Search for more papers by this author
Ahmad Abd. Majid, 

Ahmad Abd. Majid

Pusat Pengajian Sains Matematik, Universiti Sains Malaysia, 11800 Pulau Pinang, Malaysia usm.my

Search for more papers by this author
Ahmad Izani Md. Ismail, 

Ahmad Izani Md. Ismail

Pusat Pengajian Sains Matematik, Universiti Sains Malaysia, 11800 Pulau Pinang, Malaysia usm.my

Search for more papers by this author
First published: 13 May 2012
https://doi.org/10.1155/2012/458701
Citations: 20
Academic Editor: Ram N. Mohapatra

Abstract

Numerical solutions of one-dimensional heat and advection-diffusion equations are obtained by collocation method based on cubic B-spline. Usual finite difference scheme is used for time and space integrations. Cubic B-spline is applied as interpolation function. The stability analysis of the scheme is examined by the Von Neumann approach. The efficiency of the method is illustrated by some test problems. The numerical results are found to be in good agreement with the exact solution.

1. Introduction

The combination of advection and diffusion is important for mass transport in fluids. It is well known that the volumetric concentration of a pollutant, u(x, t), at a point x  (a ≤ x ≤ b) in a one-dimensional moving fluid with a constant speed β and diffusion coefficient α in x direction at time t  (t ≥ 0) is given by the one-dimensional advection-diffusion equation, which is in the form
(1.1)
subject to the initial condition
(1.2)
and the boundary conditions
(1.3a)
(1.3b)
where g0 and g1 are assumed to be smooth functions. It should be noted that, when β = 0, the advection-diffusion equation will be reduced to the one-dimensional heat equation in the case of thermal diffusion.

Advection-diffusion equation arises very frequently in transferring mass, heat, energy, and vorticity in chemistry and engineering. Thus, it has been of interest to many authors. A third-degree B-spline function has been used by Caglar et al. for solving one-dimensional heat equation with a nonlocal initial condition [1]. Mohebbi and Dehghan [2] have presented a fourth-order compact finite difference approximation and cubic C1-spline collocation method for the solution with fourth-order accuracy in both space and time variables, O(h4, k4). In [3], Dag and Saka concluded that collocation scheme is easy to implement compared to other numerical methods with giving a better result.

In this paper, a combination of finite difference approach and cubic B-spline method would be considered to solve the one-dimensional heat and advection-diffusion equation. Forward finite difference approach would be used for discretizing the derivative of time, while cubic B-spline would be applied to interpolate the solutions at time t. Von Neumann approach would be used to prove the unconditionally stable property of the method. Finally, the approximated solutions and the numerical errors would be presented to demonstrate the efficiency of the method.

2. Collocation Method

In this paper, cubic B-splines are used to construct the numerical solutions to solve the problems. Consider a partition of [a, b] that is equally divided by knots xi into n subinterval [xi, xi+1], where i = 0,1, …, n − 1 such that a = x0 < x1 < ⋯<xn = b. Hence, an approximation U(x, t) to the exact solution u(x, t) based on collocation approach can be expressed as [4]
(2.1)
where Ci(t) are time-dependent quantities to be determined and B3,i(x) are third-degree B-spline functions which are defined by the relationship [5]
(2.2)
where h = (b − a)/n. The approximation at the point (xi, tk) over the subinterval [xi, xi+1] can be simplified into
(2.3)
where i = 0,1, …, n. To obtain the approximations of the solutions, the values of B3,i(x) and its derivatives at the knots are needed. Since the values vanish at all other knots, they are omitted from Table 1.
Table 1. Values of Bi, , and .
xi xi+1 xi+2 xi+3 xi+4
Bi 0 0
0 0 0
0 0
The approximations of the solutions of (1.1) at tj+1th time level can be considered by [6]:
(2.4)
where and the superscripts k and k + 1 are successive time levels, k = 0,1, 2, …. Now, discretizing the time derivative by a first-order accurate forward difference scheme and rearranging the equation, we obtain
(2.5)
where Δt is the time step. Note that the system becomes an explicit scheme when θ = 0, a fully implicit scheme when θ = 1, and a mixed scheme of Crank-Nicolson when θ = 0.5 [6]. Here, Crank-Nicolson approach is used. Hence, (2.5) takes the form
(2.6)
for i = 0,1, …, n at each level of time. Therefore, a linear system of order (n + 1) is obtained with (n + 3) unknowns at the level time t = tk+1. To solve the system, two additional linear equations are needed. Thus, (2.3) is applied to the boundary conditions (1.3a)-(1.3b) to obtain
(2.7a)
(2.7b)
Equations (2.6), (2.7a)-(2.7b) lead to a (n + 3) × (n + 3) tridiagonal matrix system, which can be solved by the Thomas algorithm. Once the initial vector C0 has been calculated from the initial conditions [7], the approximation solution at each level of time tk+1 can be determined by the vector Ck+1 which is found by solving the recurrence relation repeatedly.
The initial vector C0 can be obtained from the initial condition and boundary values of the derivatives of the initial condition as the following expressions [6]:
  • (1)

    , i = 0,

  • (2)

    , i = 0,1, …, n,

  • (3)

    , i = n.

This yields a (n + 3) × (n + 3) matrix system where the solution can be found by Thomas algorithms.

3. Stability Analysis

Von Neumann stability method is applied for analyzing the stability of the proposed scheme. This type of stability analysis had been used by many researchers [3, 8–10]. Consider the trial solution (one Fourier mode out of the full solution) at a given point xm
(3.1)
where and η is the mode number. By substituting (2.3) into (2.5) and rearranging the equation, it leads to
(3.2)
where
(3.3)
Inserting the trial solution (3.1) into (3.2) and simplifying the equation give
(3.4)
where
(3.5)
If the amplification factor |δ| ≤ 1, then the proposed scheme is stable, or else the approximations grow in amplitude and become unstable. As θ = 0.5 is used in the proposed scheme, thus substitute the θ value into (3.4) and after some algebraic manipulation, it can be noticed that
(3.6)
Thus, this had been proved that the presented numerical scheme for the advection-diffusion equation is unconditionally stable.

4. Numerical Results

4.1. Problem 1

Suppose the heat equation is as follows [11]:
(4.1)
with initial and boundary conditions
(4.2)
The exact solution is known to be u(x, t) = exp (−π2t)sin (πx). This problem is tested by different values of h and Δt to show the capability of the presented method for solving one-dimensional heat equation. The final time is chosen as T = 1. The maximum absolute errors of the method are compared with those obtained by Crank-Nicolson (CN) scheme and compact boundary value method (CBVM) in [11]. The numerical errors are presented in Table 2. Although the fourth-order compact boundary value method gives a much more better solution, the present method is still well compared with the Crank-Nicolson scheme.
Table 2. Maximum absolute error obtained for problem 1.
h = Δt CN [11] CBVM [11] Present method
1/5 1.1   ×   10−1 2.8   ×   10−2 1.4145   ×   10−1
1/10 3.0   ×   10−2 3.8   ×   10−3 3.7195   ×   10−2
1/20 6.9   ×   10−3 2.7   ×   10−4 8.4588   ×   10−3
1/40 1.7   ×   10−3 1.3   ×   10−5 2.0698   ×   10−3
1/80 4.2   ×   10−4 5.1   ×   10−7 5.1473   ×   10−4

4.2. Problem 2

Consider the advection-diffusion equation in (1.1) with β = 1, α = 0.1, as follows [2]:
(4.3)
where the initial condition is given by
(4.4)
and the exact solution
(4.5)
The boundary conditions at x = 0 and x = 1 can be obtained from the exact solution. Table 3 shows the absolute errors of the approximations at the grid points when T = 2. It can be noticed that the present method is comparable with cubic C1-spline collocation method. The approximations of the solutions over a time period t ∈ [0,2] along x is depicted in Figure 1.
Table 3. Absolute error obtained with Δt = 2h at T = 2 for problem 2.
Grid point h = 0.02 h = 0.01
C1-spline [2] Present method C1-spline [2] Present method
0.1 7.1744   ×   10−6 8.2212   ×   10−6 1.8035   ×   10−6 2.0556   ×   10−6
0.2 1.1019   ×   10−5 2.2566   ×   10−5 2.7685   ×   10−6 5.6432   ×   10−6
0.3 1.6596   ×   10−5 4.5188   ×   10−5 4.1679   ×   10−6 1.1298   ×   10−5
0.4 2.4579   ×   10−5 7.7748   ×   10−5 6.1705   ×   10−6 1.9435   ×   10−5
0.5 3.5871   ×   10−5 1.2011   ×   10−4 9.0026   ×   10−6 3.0020   ×   10−5
0.6 5.1637   ×   10−5 1.6809   ×   10−4 1.2955   ×   10−5 4.2001   ×   10−5
0.7 7.3208   ×   10−5 2.1002   ×   10−4 1.8360   ×   10−5 5.2464   ×   10−5
0.8 1.0163   ×   10−4 2.2264   ×   10−4 2.5476   ×   10−5 5.5602   ×   10−5
0.9 1.3624   ×   10−4 1.6833   ×   10−4 3.4134   ×   10−5 4.2039   ×   10−5
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Spatial-time approximations for problem 2 with h = 0.05 and Δt = 0.5h.

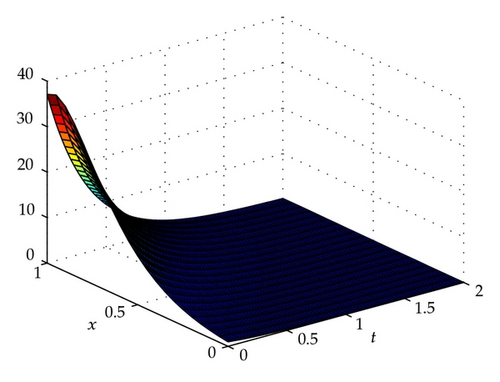
5. Conclusions

A numerical method based on collocation of cubic B-spline had been described in the previous section for solving one-dimensional heat and advection-diffusion equations. A finite difference scheme had been used for discretizing time derivatives and cubic B-spline for interpolating the solutions at each time level. From the test problems, the obtained results show that the presented method is capable for solving one-dimensional heat and advection-diffusion equations accurately with a promised stability.

Acknowledgment

The authors would like to acknowledge with thanks the financial support from Malaysian Government in the form of Fundamental Research Grant Scheme (FRGS) of number 203/PMATHS/6711150.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.