The interactions between signal setting and traffic assignment can directly affect the urban road network efficiency. In order to improve the coordination of signal setting with traffic assignment, this paper created a traffic control algorithm considering traffic assignment; meanwhile, the link impedance function and the route choice function were introduced into this paper to study the user′s route choice and the road network flow distribution. Then based on the above research, we created a system utility value model. Finally through the VISSIM software to simulate the test network, we verified the superiority of the coordination algorithm and the model and gave the optimal flow of the road network.

1. Introduction

In urban transportation systems, the equilibrium of the road network supply and demand is an important problem, which can directly impact the road network efficiency. For a fixed road structure and traffic flow, signal setting is the primary influencing factor to traffic supply, and traffic assignment is the primary influencing factor to traffic demand [1, 2]. In order to balance the traffic demand and supply of urban road network and maximize the efficiency of transportation resources, experts and scholars from allover the world have done a lot of research and made great progress in the coordination of signal setting with traffic assignment aspects.

Firstly, Allsop [3] and Gartner [4] researched the relationship between signal setting and traffic assignment, and held that signal setting strategy can directly affect user’s route choice and traffic flow distribution. Then they proposed a solution program to traffic equilibrium problem by alternately updating green split signal settings for fixed flows. On these bases, in order to achieve the global optimization, Tan et al. [5] and Smith [6, 7] converted the signal setting and traffic assignment into a hybrid optimization problem. Their research showed that in some actual situation traffic setting even had deteriorated travel time by 30%; thus, they proposed a new signal setting policy under the constraint of stable traffic supply and traffic demand. Subsequently, Gartner et al. [8] and Fisk [9] proposed that we may take the signal setting and traffic assignment as a game problem of Stackberg, which regards traffic managers as superior decision-makers and travelers as subordinate decision-makers. Then, Yang and Yagar [10] proposed a bilevel programming model based on the above method; the model indicated that we can get queuing delay of saturated sections by the network equilibrium parameters instead of conventional delay calculation formula.

Since some traffic control systems and algorithms often require the real-time traffic flow distributed information to make traffic management strategy, Gartner et al. [11, 12] presented a combined framework about the real-time signal setting and traffic assignment, which can make appropriate dynamic control strategies and avoid traffic congestion according to dynamic traffic assignment model. With the research continued, Lee and Machemehl [13] studied the stochastic heuristic algorithms in coordination with signal setting and traffic assignment and applied the genetic algorithms in it. Chen and Ben-Akiva [14] regarded dynamic traffic control and traffic assignment as a noncooperation game problem; we could get the optimal signal setting and traffic assignment by iteration.

In recent years, many new methods emerged on the study of signal setting and traffic assignment relationship, for example, Chiou [15] introduced derivative information of the signal control variables into the TRANSYT system and then estimated the average vehicle delay in the road network based on sensitivity algorithm. Cipriani and Fusco [16] discussed the global optimization problem of signal setting and traffic assignment based on gradient projection method. Cascetta et al. [17] studied the optimization models and algorithms for urban signal settings with a small-scale real network based on stochastic traffic assignments. In the study of Gao et al. [18] and Chiou [19], the problem of signal setting and traffic assignment relationship was formulated as a nonlinear mathematical program with equilibrium constraints, in which the optimal signal settings were determined while trip rates and network flow are in equilibrium.

By summarizing the above research experience, this paper proposed a synergetic algorithm of dynamic signal setting and traffic assignment. In the algorithm, traffic control parameters can be updated in real time with the change of traffic demand. The basic idea of the algorithm is to change the road impedance by adjusting the split of the signal setting scheme and then cause the traffic volume transfer to realize the aim of the road network flow redistribution and the systems’ efficiency optimization. Therefore, in order to further clarify the mechanism of signal setting and traffic assignment, this paper creates a simple and practical integrated model by introducing the link impedance function and the route choice function. Finally, a system utility value calculation method is given, by which we can get the optimal flow and optimal path impedance and then compare the real flow and path impedance with the optimal flow and optimal path impedance to determine whether the road network is in equilibrium. We use the above discrimination method to optimize the efficiency of the road network.

2. Problem Formulation

The coordination of signal setting and traffic assignment problem can be formulated as the problem of finding out the relationship between traffic demand and traffic supply, which is the problem of finding out the relationship between signal control parameters and user’s route choice. Firstly, we consider a traffic network G(P, L) consisting of a set of nodes P and connected by a set of directed arcs L. Since traffic supply mainly includes traffic control and basic road information, the initial traffic control program setup is based on historical flows from road network, which adjusts the traffic flow of road network by signal parameters, such as signal cycle and green time. Thus, we can describe the relationship between the above items in the following equation:

(2.1)

where U is traffic signal control program; C_j is signal cycle of junction j; g_j is green time of junction j; q_k0 is the initial traffic flow of link k; c_k0 is traffic capacity of link k; i is the signal phase of junction.

Meanwhile, the user’s route choice is usually affected by the signal control program, which is an important factor in restricting the road network flow distribution; another important restrictive factor is the origin-destination (O-D) Thus, we can describe the relationship between signal control program, user’s route choice, and O-D in the following equation:

(2.2)

where F_k is the actual traffic flow of link k;

is the probability of path k being selected from origin (r) to destination (s);

are the origin location and the destination location of traffic flow.

Since the effects of signal control program and traffic flow are reflected in traffic participant’s travel time, we can analyze the traffic supply and traffic demand to determine the optimal flow of road network and then compare the difference between the actual travel time and the optimal travel time to discriminate whether the road network is in equilibrium.

On the basis of the above statement, two questions can be summed up from the above representations. First, a coordination algorithm of traffic demand and traffic supply should be established if you want to achieve the mutual feedback traffic control and flow distribution. Second, we should create some appropriate model about traffic control and traffic assignment to implement the algorithm.

3. Algorithm Establishments

The algorithm establishment consists of two parts in this paper: the first part of the algorithm mainly analyzes the relationship between signal setting and flow distribution. Before we establish the algorithm, a stable state of the road network flow is needed to realize the objective of traffic flow equilibrium, which means that the difference between road network inflow (q_ui) and road network outflow (q_vi) should be less than a fixed value (ε), q_ui − q_vi < ε, where, q_ui is the total vehicles enter the fixed road network; q_vi is the total vehicles leave the fixed road network. Meanwhile, the similarity degree of the path impedance needs to be known; we can describe it as follows: , where is the impedance of path (k) from origin (r) to destination (s). The relationship between signal setting and flow distribution is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The relationship between signal setting and flow distribution.

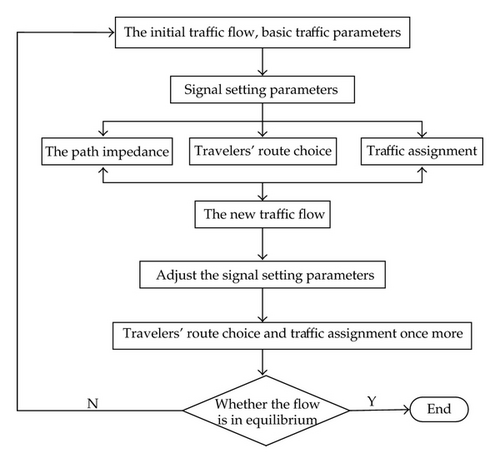
The process of algorithm analysis is showed in Figure 1, which is summarized as follows.

Step 1. Obtain the initial traffic flow information based on real-time detection.

Step 2. Determine a set of signal setting parameters based on the initial traffic flow.

Step 3. Adjust the impedance of each path in the road network by traffic control, thereby affecting travelers’ route choice.

Step 4. Calculate the flow after superimposed according to the travelers’ route choice and the initial traffic flow.

Step 5. Adjust the signal setting parameters and traffic assignment again.

Step 6. Through the system utility value, determine the equilibrium situation.

The second part of the algorithm is to decide the signal setting parameters in order to balance the traffic flow under the influence of travelers’ route rechoice. The main idea of this part is to determine the maximum green (g_max) time or the minimum green time (g_min) of each signal phase and then to extend or shorten the signal cycle (C) and green time (g) to ensure that the flow ratio (y_i) and the split (λ_i) are approximately equal. The signal control method under the impact of changing flow is shown in Figure 2.

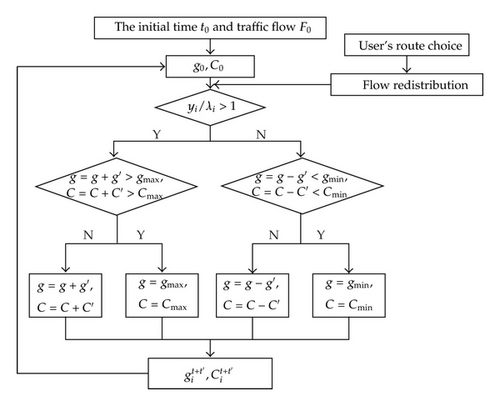
The process of algorithm analysis is shown in Figure 2, which is summarized as follows.

Step 1. Obtain the initial traffic flow information based on real-time detection.

Step 2. Calculate the initial signal cycle C₀ and the initial green time g₀ according to the following equation:

(3.1)

where t_L is the total lost time of intersection; Y is the flow ratio of intersection.

Step 3. Combined with the redistribution flow of road network to judge whether y_i/λ_i is approximate to 1, we can calculate the y_i/λ_i according to the following equation [20]:

(3.2)

where V_i is the average flow of phase i in critical lane; t_ri is the time interval of phase i from green time end to green time start; V_Si is the saturation flow of phase i in critical lane.

Step 4. Determine the C_max, C_min, g_max, and g_min for Step 5 to determine the suitable C and g. Generally, the cycle and the green time should not increase too much or too little; for this part we determine the C_max and C_min based on the following equation:

(3.3)

Then we determine the g_max, g_min under the constraints of C_max, C_min; the specific calculation method can be expressed as follows:

(3.4)

where g_ir is the real green time of phase i; g_ymax is the maximum green time of phase i which can be increased:

(3.5)

where g_ic is the compression time of phase i; y_ir is the real green time of phase i.

Step 5. Increase or reduce the signal cycle and green time according to traffic demand under the constrains of C_max, C_min.

Step 6. Feed back the determined signal cycle and green time to Step 2.

4. Algorithm Implementation

4.1. Supply and Demand Balance Analysis

The supply of the road network mainly refers to the maximum capacity that can be provide under fixed road conditions, and the demand of road network refers to the number of users in traffic network. The traffic supply and demand can be expressed as follows:

(4.1)

where Q_s, Q_d are traffic supply and traffic demand;

is the intersection correlation coefficient of path k from r to s; Q₀ is the initial traffic flow of road network; r_uk(t), r_vk(t) are inflow and outflow rate of road network:

(4.2)

where dd(t) is equalization index.

When the relationship between supply and demand meets dd(t) < 0.95, traffic managers should shorten part of the signal cycle length in order to reduce the delay time. When the relationship between supply and demand meets 0.95 ≤ dd(t) < 1.05, we think that it is equilibrium of supply and demand. When the relationship between supply and demand meets dd(t) ≥ 1.05, traffic managers should adjust the signal setting parameters in order to change the relationship between supply and demand [21].

4.2. User’s Route Choice Model

For most users prefer the small impedance path to travel, based on this, we use user’s route choice model. The conventional path impedance mainly includes link travel time and intersection delay. This paper uses an empirical formula considering the mixed traffic running characteristic based on BPR road impedance function to calculate link travel time and uses a simplified formula, Webster’s delay function, to calculate intersection delay. The specific calculation model can be expressed as follows:

(4.3)

where t_l is travel time between adjacent intersections; t_j is the delay of intersection; t₀ is travel time under free speed between adjacent intersection; V₁, V₂ are the volumes of vehicle and nonmotorized vehicle; C₁, C₂ are the capacities of vehicle and nonmotorized vehicle; c, λ are the signal cycle and split of the intersection; X is intersection saturation.

Combined with (3.3), we can get path impedance as follows:

(4.4)

After determining the calculation method of path impedance, we need to research the relationship between the path impedance and the user’s route choice. Dial (1971) proposed a route choice model which assumed that path impedance and route choice are independent of each other and obey the Gumbel probability distribution, but other path impedances are usually affected when one of path impedances changes. Thus, Wang Wei did some research and proved the model. This paper calculates the user’s route choice based on the proved model, which is expressed as follows:

(4.5)

where

is the probability of path k is chosen between origin (r) and destination (s);

is the impedance of path k from origin (r) to destination (s);

is the average impedance of path k from origin (r) to destination (s).

4.3. Utility Functions Establishment

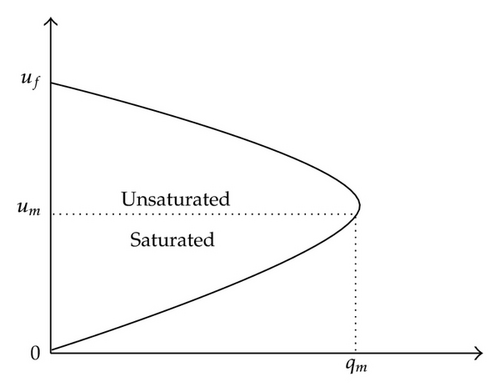
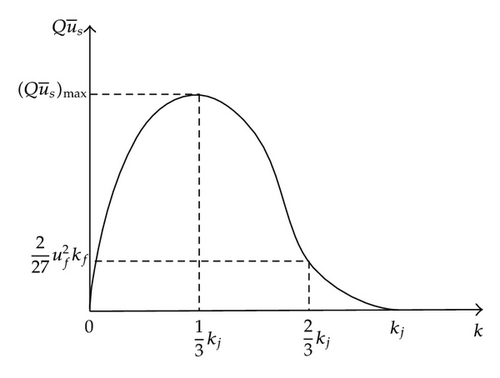
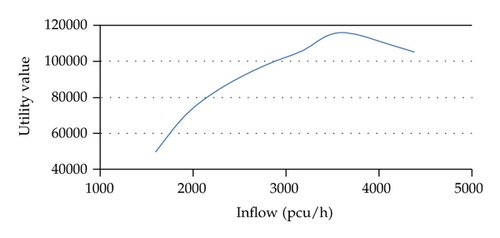
We can find that speed decreases with increasing flow in unsaturated and flow and speed decrease in saturated from speed-volume graph (Figure 3(a)); meanwhile, we also can find the maximum product of flow and speed from speed-volume graph (Figure 3(b)).

By analyzing Figure 3, for the realization of the maximum number of vehicles passing per unit of time, we consider the product of the flow and speed as the system utility value function, which can be expressed as follows:

(4.6)

where J^rs is the system utility value from origin (r) to destination (s); q_u is the inflow volume of road network;

is the difference between inflow and outflow;

is the initial traffic flow of path k; l_k is the length of path k from origin (r) to destination (s);

is the optimal flow of path k;

is the optimal impedance of path k.

4.4. User’s Equilibrium Traffic Assignment Discriminant Model

Since we have already known the path impedance and the user’s route choice and have established a utility function, we can summarize the above analysis results to discriminate the user’s equilibrium degree of road network based on the following formulas:

(4.7)

where dd(k) is the equilibrium degree of path k; dd(v) is the equilibrium degree between path k and (k + i); τ is a fixed value where 0 ≤ τ ≤ 1.

5. Numerical Example

The test network is a simplified region of road network from Changchun city which consists of 12 links and 5 intersections. All links of the road network are bidirectional and of four lanes, and the initial data is obtained by manual collection. The number of links in the road network is shown in Figure 4(a), and the road link’ traffic flow is shown in Figure 4(b). The links length is shown in Table 1.

Table 1. The links length.

Number	1	2	3	4	5	6	7	8	9	10	11	12
Length	532	1118	1244	478	593	616	1494	1566	1609	1428	336	314

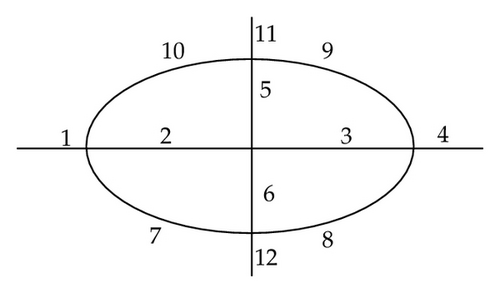
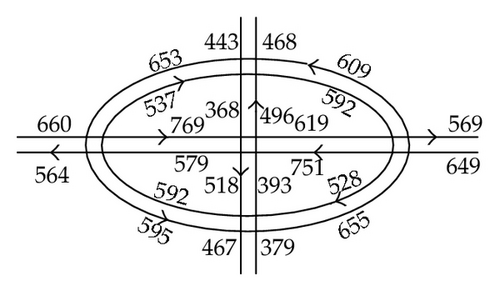
We can find four pairs of O-D which, respectively, belong to link 1, link 4, link 11, and link 12. This paper simulated a pair of O-D (from link 1 to link 4) to determine the equilibrium degree of road network and to verify the superiority of the coordination algorithm. There are seven paths from link 1 to link 4, that is, path A (1-2-3-4), path B (1-7-8-4), path C (1-7-6-3-4), path D (1-10-9-4), path E (1-10-5-3-4), path F (1-2-5-9-4), and path G (1-2-6-8-4). We can find that the shortest distance is the path 1-2-3-4, but there is a heavy traffic flow on link 2 and link 3.

In the simulation test process, we set the traffic signal based on Synchro Studio 7 which is a traffic signal design software; we also have embedded the above algorithms into the traffic signal design software. During the inflow increase from 1600 pcu/h to 4400 pcu/h, we first get the path impedance based on VISSIM traffic simulation software which is shown in Table 2.

Table 2. The path impedance based on simulation data.

Volume (pcu/h)	Number
	Path impedance after application of algorithm(s)
	A	B	C	D	E	F	G
1600	315	311	340	334	387	352	368
2000	324	333	368	359	422	378	401
2400	356	359	391	385	451	405	425
2800	395	402	436	425	489	443	461
3200	431	426	473	447	536	479	508
3600	488	458	525	486	593	562	547
4000	609	551	646	588	704	625	652
4400	637	654	716	654	729	724	718

Then we can get the optimal impedance, the optimal flow, and the optimal utility value based on formula (4.2) as follows (the specific data is shown in Table 3 and the relationship between utility value and flow is shown in Figure 5):

(5.1)

Table 3. The optimal flow and speed.

	A	B	C	D	E	F	G
(pcu/h)	581	538	493	526	507	497	486
(km/h)	26	31	35	29	37	35	33
(s)	467	472	449	503	416	446	470

We next verify the superiority of the algorithm by inputting the initial data into the test network. During the simulation, we should mark all vehicles in order to record the different paths’ impedance and then obtain the average impedance of each path. The average impedance and the equilibrium degree are shown as follows.

As seen in Tables 4 and 5, the new algorithm achieved the equilibrium of road network and that could save 21 seconds for each vehicle from point 1 to point 4 in the test network. Although this test network demonstrates a better performance of the coordination algorithm, more extensive tests need to be performed to validate the algorithm, for the above test only simulated a pair of O-D and did not consider the impact of distance on the users’ route choice.

Table 4. Before application of algorithms.

	A	B	C	D	E	F	G
Paths impedance	494	423	518	466	502	487	496
Equilibrium degree(s)	0.945126	1.117364	0.866541	1.07808	0.828577	0.914520	0.947947
Average impedance(s)	484

Table 5. After application of algorithms.

	A	B	C	D	E	F	G
Paths impedance	483	474	438	506	433	454	456
Equilibrium degree(s)	0.966650	0.997141	1.024814	0.992858	0.960614	0.980994	1.031100
Average impedance(s)	463

6. Conclusions

In this paper, we presented a traffic control algorithm considering traffic assignment of road network, which has been implemented successfully by introducing the link impedance function and the route choice function. In the process of optimizing the coordination algorithms, we also get the optimal flow of path, the optimal impedance, the maximum system utility value, and so forth. Finally, we verified the superiority of the coordination algorithm and the model through a numerical example based on the VISSIM software.

For further issues, we should introduce traffic guidance information into the coordination algorithm of traffic control and traffic assignment and then verify it by the road network with multiorigin and multidestination to be closer to the actual situation.

Acknowledgments

This work is partly supported by the National Science Foundation of China (Grant nos. 50908100, 51108208), China Postdoctoral Science Foundation funded Project (no. 20110491307), and the Fundamental Research Funds for the Central Universities (no. 201103146). The authors thank the anonymous reviewers for their valuable input and suggestions.

References

1 Qi H., Research on the Modelling of Network Traffic Flow Considering Signal Control, 2011, Jilin University, Jilin, China.
Google Scholar
2 Hu S., Study on the Equilibrium Theory between Traffic Supply and Traffic Demand, 2004, Changan University, Shanxi, China.
Google Scholar
3 Allsop R. E., Some possibilities for using traffic control to influence trip distribution and route choice, Transportation and Traffic Theory, 1974, Elsevier, New York, NY, USA, 345–373.
Google Scholar
4 Gartner N. H., Area traffic control and network equilibrium, Proceedings of the International Symposium on Traffic Equilibrium Methods, 1976, Berlin, Germany, 274–297.
Google Scholar
5 Tan H. N., Gershwin S. B., and Athans M., Hybrid optimization in urban traffic networks, LIDS Technical Report, 1979, MIT Press, Cambridge, Mass, USA.
Google Scholar
6 Smith M. J., The existence, uniqueness and stability of traffic equilibria, Transportation Research Part B. (1979) 13, no. 4, 295–304, https://doi.org/10.1016/0191-2615(79)90022-5, 551841.
10.1016/0191-2615(79)90022-5
Web of Science® Google Scholar
7 Smith M. J., A local traffic control policy which automatically maximises the overall travel capacity of an urban road network, Traffic Engineering and Control. (1980) 21, no. 6, 298–302, 2-s2.0-0019022549.
Web of Science® Google Scholar
8 Gartner N. H., Gershwin S. B., Little J. D. C., and Ross P., Pilot study of computer-based urban traffic management, Transportation Research B. (1980) 14, no. 1-2, 203–217, 2-s2.0-0018922567.
10.1016/0191-2615(80)90045-4
Web of Science® Google Scholar
9 Fisk C. S., Game theory and transportation systems modelling, Transportation Research Part B. (1984) 18, no. 4-5, 301–313, https://doi.org/10.1016/0191-2615(84)90013-4, 770379.
10.1016/0191-2615(84)90013-4
Web of Science® Google Scholar
10 Yang H. and Yagar S., Traffic assignment and signal control in saturated road networks, Transportation Research A. (1995) 29, no. 2, 125–139, 2-s2.0-0029271191.
CAS Web of Science® Google Scholar
11 Gartner N. H. and Stamatiadis C., Framework for the integration of dynamic traffic assignment with real-time control, Proceedings of the 3rd Annual World Congress on Intelligent Transportation Systems, 1996, Orlando, Fla, USA, 125–137.
Google Scholar
12 Gartner N. H. and Al-Malik M., Combined model for signal control and route choice in urban traffic networks, Transportation Research Record. (1996) 1554, 27–35, 2-s2.0-0030232022.
10.1177/0361198196155400104
Google Scholar
13 Lee C. and Machemehl R. B., Genetic algorithm, local and iterative searches for combining traffic assignment and signal control, Proceedings of the Conference on Traffic and Transportation Studies (ICTTS ′98), July 1998, Beijing, China, 27–29.
Google Scholar
14 Chen O. J. and Ben-Akiva M. E., Game-theoretic formulations of interaction between dynamic traffic control and dynamic traffic assignment, Transportation Research Record. (1998) no. 1617, 179–188, 2-s2.0-0032154417.
10.3141/1617-25
Web of Science® Google Scholar
15 Chiou S. W., TRANSYT derivatives for area traffic control optimisation with network equilibrium flows, Transportation Research B. (2003) 37, no. 3, 263–290, 2-s2.0-0037353489, https://doi.org/10.1016/S0191-2615(02)00013-9.
10.1016/S0191-2615(02)00013-9
Web of Science® Google Scholar
16 Cipriani E. and Fusco G., Combined signal setting design and traffic assignment problem, European Journal of Operational Research. (2004) 155, no. 3, 569–583, https://doi.org/10.1016/j.ejor.2003.08.006, 2054680, ZBL1049.90014.
10.1016/j.ejor.2003.08.006
Web of Science® Google Scholar
17 Cascetta E., Gallo M., and Montella B., Models and algorithms for the optimization of signal settings on urban networks with stochastic assignment models, Annals of Operations Research. (2006) 144, 301–328, https://doi.org/10.1007/s10479-006-0008-9, 2257914, ZBL1159.90308.
10.1007/s10479-006-0008-9
Web of Science® Google Scholar
18 Gao H., Chen T., and Lam J., A new delay system approach to network-based control, Automatica. (2008) 44, no. 1, 39–52, https://doi.org/10.1016/j.automatica.2007.04.020, 2530467, ZBL1138.93375.
10.1016/j.automatica.2007.04.020
CAS Web of Science® Google Scholar
19 Chiou S.-W., Optimization of a nonlinear area traffic control system with elastic demand, Automatica. (2010) 46, no. 10, 1626–1635, https://doi.org/10.1016/j.automatica.2010.06.029, 2877318, ZBL1205.90074.
10.1016/j.automatica.2010.06.029
Web of Science® Google Scholar
20 Bie Y., Wang D., Song X., and Xing Y., Conditional bus signal priority strategies considering saturation degree restriction at isolated junction, Journal of Southwest Jiaotong University. (2011) 46, no. 4, 657–663, 2-s2.0-79961192894, https://doi.org/10.3969/j.issn.0258-2724.2011.04.021.
10.3969/j.issn.0258?2724.2011.04.021
Google Scholar
21 Binglin L. and Aiwu K., Nonequilibrium study on the supply and demand of urban road networks, Shanxi Science and Technology. (2008) 58–60.
Google Scholar

Citing Literature

All articles

A Study on the Coordination of Urban Traffic Control and Traffic Assignment

Abstract

1. Introduction

2. Problem Formulation

3. Algorithm Establishments