Exponential Stability of Impulsive Stochastic Delay Differential Systems
Abstract
This paper investigates the stability of stochastic delay differential systems with two kinds of impulses, that is, destabilizing impulses and stabilizing impulses. Both the pth moment and almost sure exponential stability criteria are established by using the average impulsive interval. When the impulses are regarded as disturbances, a lower bound of average impulsive interval is obtained; it means that the impulses should not happen too frequently. On the other hand, when the impulses are used to stabilize the system, an upper bound of average impulsive interval is derived; namely, enough impulses are needed to stabilize the system. The effectiveness of the proposed results is illustrated by two examples.
1. Introduction
Impulsive dynamical systems have attracted considerable interest in science and engineering in recent years because they provide a natural framework for mathematical modeling of many real-world problems where the reactions undergo abrupt changes [1–3]. These systems have been found to have important applications in various fields, such as control systems with communication constraints [4], network system [5, 6], sampled-data systems [7, 8], and mechanical systems [9]. On the other hand, impulsive control based on impulsive systems can provide an efficient way to deal with plants that cannot endure continuous control inputs [3]. In recent years, the impulsive control theory has been generalized from deterministic systems to stochastic systems and has been shown to have extensive applications [10, 11].
Stability is one of the most important issues in the study of impulsive stochastic differential systems (see, e.g., [12–20]). When the continuous dynamical system is unstable, there is some literature that is concerned with the pth moment exponential stability with stabilizing impulses. For example, several criteria on the global exponential stability and instability are obtained in [17]. The pth moment exponential stability is discussed in [18] by using the vector Lyapunov functions. The authors in [19] investigated impulsive stabilization of stochastic delay differential systems, and both pth moment and almost sure exponential stability criteria are established by using the Lyapunov-Razumikhin method. Recently, both continuous dynamical stable system and continuous dynamical unstable system are studied in [20].
The average impulsive interval was proposed in [21], and it is useful to study the synchronization problem of dynamical networks with destabilizing impulses (see, e.g., [21–23]). The average impulsive interval can be used to control frequency of the impulsive occurrence. When the continuous dynamical system is stable and the impulsive effects are destabilizing, in order to maintain the stability of the system, the impulses should not happen too frequently. Therefore, there should exist a lower bound; if the average impulsive interval is not less than the bound, the stability can be maintained. On the other hand, when the continuous dynamical system is unstable, and the impulses are used to stabilize the unstable system, there should exist enough impulses to stabilize the system, that is, the frequency of impulsive occurrence should exceed a lower bound. Thus there exists an upper bound of the average impulsive interval; if the average interval is less than the upper bound, the system is stabilized by the impulses.
In this paper, by using the average impulsive interval, we investigate the pth moment and almost sure exponential stability for stochastic delay differential systems with two kinds of impulses, that is, destabilizing impulses and stabilizing impulses. When the continuous dynamical system is stable, the lower bound of the average impulsive interval is obtained, by which we can estimate how intensive impulsive disturbance the stable system can endure. On the other hand, when the continuous dynamical system is unstable, the upper bound of the average impulsive interval is derived. From this bound, we can estimate the minimum impulsive frequency needed to stabilize the system. The effectiveness of the proposed results is illustrated by two examples.
The rest of this paper is organized as follows. In Section 2, we introduce some notations and definitions. We establish several stability criteria for impulsive stochastic delay differential systems in Section 3. In Section 4, two examples are given to illustrate the effectiveness of our results.
2. Preliminaries
Throughout this paper, let (Ω, ℱ, P) be a complete probability space with some filtration {ℱt} t⩾0 satisfying the usual conditions (i.e., the filtration is increasing and right continuous while ℱ0 contains all P-null sets). Let B = (B(t), t ≥ 0) be an m-dimensional ℱt-adapted Brownian motion.
For x ∈ ℝd, |x| denotes the Euclidean norm of x. For −∞ < a < b < ∞, we say that a function from [a, b] to ℝd is piecewise continuous if the function has at most a finite number of jumps discontinuous on (a, b] and continuous from the right for all points in [a, b). Given τ > 0, PC([−τ, 0]; ℝd) denotes the family of piecewise continuous functions from [−τ, 0] to ℝd with norm ∥φ∥ = sup −τ≤θ≤0φ(θ). For p > 0 and t ≥ t0, let be the family of ℱt-adapted and PC([−τ, 0]; ℝd)-valued random variables φ such that E∥φ∥p < ∞. Let ℕ = 1,2, … and ℝ+ = [0, +∞).
As a standing hypothesis, f, g, and I are assumed to satisfy necessary assumptions so that, for any , system (2.1) has a unique global solution . In addition, we suppose that f(t, 0) ≡ 0, g(t, 0) ≡ 0, and I(t, 0) ≡ 0 for all t ≥ t0. Then system (2.1) admits a trivial solution x(t) ≡ 0.
The purpose of this paper is to discuss the stability of system (2.1). Let us begin with the following definitions.
Definition 2.1. The trivial solution of system (2.1) is said to be
- (1)
pth moment exponentially stable if for any initial data , the solution x(t) satisfies
(2.4)where λ and C are positive constants independent of t0, - (2)
almost exponentially stable if the solution x(t) satisfies
(2.5)for any initial data and λ > 0.
Definition 2.2. The average impulsive interval of the impulsive sequence {tk} k∈ℕ is equal to a positive number Ta if there exists a positive integer N0 such that
3. Main Results
In this section, we will establish some stability criteria of stochastic delay differential system with destabilizing impulses or stabilizing impulses. The first theorem addresses the case where the continuous dynamics in the system (2.1) is stable. It is shown that under some conditions the impulsive disturbance do not destroy the stability of system (2.1).
Theorem 3.1. Assume that there exist positive constants c1, c2, p, γ1 such that
-
(H1) c1 | x|p ≤ V(t, x) ≤ c2 | x|p,
-
(H2) for t ∈ [tk−1, tk), k ∈ ℕ,
(3.1)provided satisfying that EV(t + θ, φ(θ)) ≤ qEV(t, φ(0)), θ ∈ [−τ, 0], -
(H3) there exists a positive constant μ > 1 such that
(3.2) -
(H4) , Ta > ln μ/γ1.
Proof. According to (H1), we see that
Remark 3.2. Theorem 3.1 gives the conditions under which the impulsive disturbances do not destroy the stability of system (2.1). When the impulsive effects are destabilizing, the impulses should not happen too frequently. Therefore, in order to maintain the stability of continuous dynamical system, the average impulsive interval is used to control the impulsive frequency.
Remark 3.3. In Theorem 3.1, the impulses are regarded as disturbance; therefore, the condition μ > 1 is reasonable. It is worth pointing out that in Theorem 3.1, for arbitrary small ɛ and any Ta > 0, the impulsive interval can be less than ɛ and simultaneously the average impulsive intervals are not less than Ta. That is, high-density impulses are allowed to happen in a certain interval, but we need low-density impulses to follow as a compensation.
In the following theorem, when the continuous dynamics in the system (2.1) is unstable, it is shown that the system (2.1) can be stabilized by impulses.
Theorem 3.4. Let β = inf k∈ℕ{tk − tk−1} and there is a positive integer l such that (l − 1)β < τ ≤ lβ. Assume that there exist positive constants c1, c2, p, γ2 such that
-
(H1) c1 | x|p ≤ V(t, x) ≤ c2 | x|p,
-
(H2) for t ∈ [tk−1, tk), k ∈ ℕ,
(3.18)provided satisfying that EV(t, φ(θ)) ≤ qEV(t, φ(0)), θ ∈ [−τ, 0], -
(H3) there exists a positive constant μ < 1 such that
(3.19) -
(H4) qμl ≥ 1, Ta < −ln μ/γ2.
Proof. In view of (H1), we obtain
According to (3.16), we obtain
Remark 3.5. Theorem 3.4 shows that an unstable stochastic delay differential system can be successfully stabilized by impulses. The average impulsive interval is used to estimate the impulsive frequency; namely, the impulsive frequency should exceed a lower bound so that there exist enough impulses to stabilize the unstable continuous dynamical system.
In Theorem 3.4, we need to assume that qμl ≥ 1 and μ < 1, which means the impulsive interval cannot be small enough. However, if system (2.1) is an impulsive stochastic differential system without delay, then the system can still be exponential stability when inf k∈ℕ{tk − tk−1} is extremely small.
Corollary 3.6. Let θ ≡ 0 and τ = 0 in system (2.1). Assume that there exist positive constants c1, c2, p, γ2 such that
-
(H1) c1|x|p ≤ V(t, x) ≤ c2|x|p,
-
(H2) for t ∈ [tk−1, tk), k ∈ ℕ,
(3.34) -
(H3) there exists a positive constant μ < 1 such that
(3.35) -
(H4) ln μ/Ta + γ2 < 0.
Proof. The proof is similar to the proof given in Theorem 3.4, so we omit the detailed proof.
The following theorem shows that the trivial solution of system (2.1) is almost surely exponentially stable, under some additional conditions.
Theorem 3.7. Assume that p ≥ 1, β = inf k∈ℕ{tk − tk−1} and there exists a positive integer l such that (l − 1)β < τ ≤ lβ. Suppose that the conditions in Theorem 3.1 or Theorem 3.4 hold. Moreover, there exists a constant L > 0, such that
Proof. By Theorem 3.1 or Theorem 3.4, we derive that the trivial solution of system (2.1) is pth moment exponentially stable. Therefore, there exists a positive constant M1 such that
4. Numerical Examples
In this section, two numerical examples are given to show the effectiveness of the main results derived in the preceding section.
Example 4.1. Consider an impulsive stochastic delay differential system as follows:
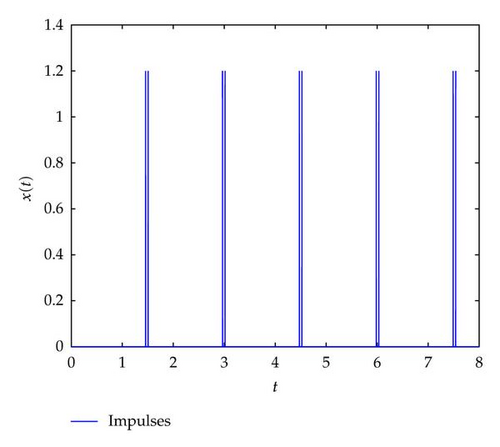
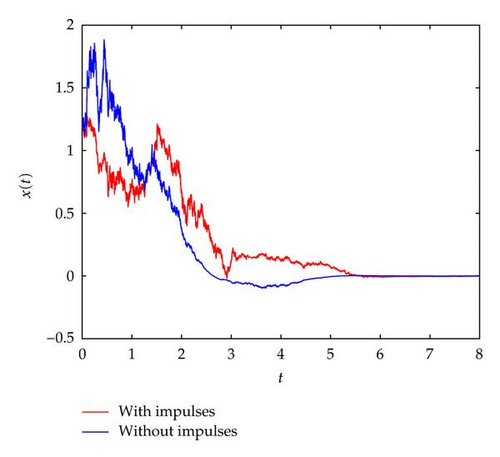
Figure 1 describes the destabilizing impulsive sequence in the system (4.1) when ɛ = 0.05. It can be seen from Figure 2 that the destabilizing impulses do not destroy the stability of system (4.1).
Example 4.2. Consider an impulsive stochastic delay differential system as follows:
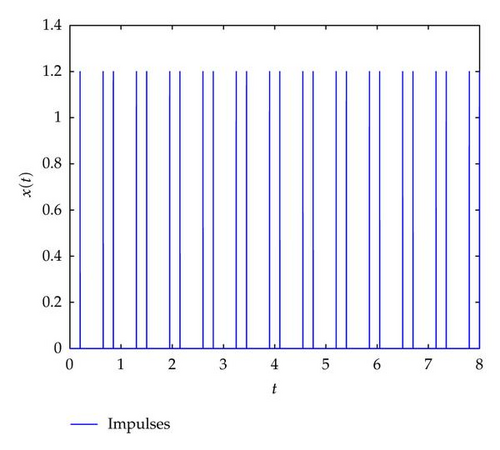
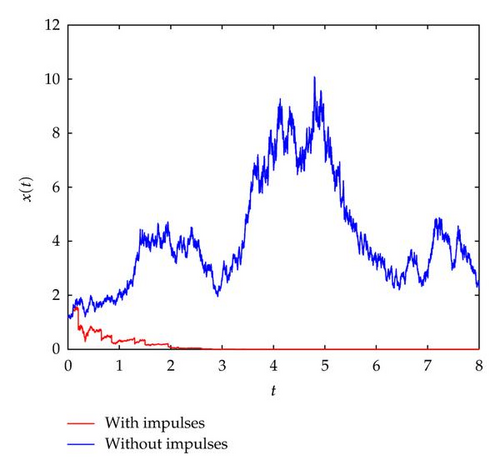
The stabilizing impulsive sequence in the system (4.3) is described in Figure 3. It can be seen from Figure 4 that unstable continuous dynamics in the system (4.3) can be successfully stabilized by the impulses.
5. Conclusion
The pth moment and almost sure exponential stability are investigated in this paper. By using the average impulsive interval, several sufficient conditions are established for stability of stochastic delay differential systems with destabilizing impulses or stabilizing impulses. Finally, two numerical simulation examples are offered to verify the effectiveness of the main results.
Acknowledgments
The authors would like to thank the Associate Editor and anonymous referee for their helpful comments and suggestions which greatly improved this paper. This work was supported by the National Natural Science Foundation of China (no. 10871041 and no. 71171003). Also, this work was partially supported by the Natural Science Foundation of Anhui Province (no. 10040606Q03).




