Primitive Zero-Symmetric Sign Pattern Matrices with Zero Diagonal Attaining the Maximum Base

Definition 1.1. A  square generalized sign pattern matrix A is called powerful if each power of A contains no # entry.

In [1], Li et al. introduced the concepts of base and period for (powerful) sign pattern matrices which are the generalizations of the concepts of “index of convergence” and period for square nonnegative matrices. These concepts are extended from (powerful) sign pattern matrices to (square) generalized sign pattern matrices by You et al. in [12] as follows.

Definition 1.2 (see [12].)Let A be a square generalized sign pattern matrix of order n and A, A², A³, … the sequence of powers of A. (Since there are only $$ different generalized sign patterns of order n, there must be repetitions in the sequence.) Suppose A^l is the first power that is repeated in the sequence, that is, l is the least positive integer such that A^l = A^l+p holds for some positive integer p. Then l is called the generalized base (or simply base) of A, and is denoted by l(A). The least positive integer p such that A^l = A^l+p holds for l = l(A) is called the generalized period (or simply period) of A and is denoted by p(A).

For a sign pattern matrix A, we use |A| to denote the (0,1) matrix obtained from A by replacing each nonzero entry by 1.

A nonnegative square matrix A is primitive if some power A^k > 0. The least such as k is called the primitive exponent (or simply exponent) of A, denoted by exp (A). For convenience, a square sign pattern matrix A is called primitive if |A| is primitive, and in this case we define exp (A) = exp (|A|).

Definition 1.3 (see [3].)A square sign pattern matrix A = (a_ij) _n×n is called zero-pattern symmetric (abbreviated zero-symmetric, or simply ZS) if |A| is symmetric.

It is well known that graph-theoretical methods are often useful in the study of the powers of square matrices, so we now introduce some graph-theoretical concepts.

Let D be a digraph with vertex set V and arc set E (which permits loops but no multiple arcs). By assigning a sign of 1 or −1 to each arc of the digraph D, we obtain a signed digraph S. By a walk W in the digraph D (or the signed digraph S), we mean a sequence of vertices (v₀, v₁, v₂, …, v_k) such that e_i = (v_i−1, v_i) is an arc of D for i = 1, …, k. The number k is called the length of the walk W, denoted by l(W). If the vertices v₀, v₁, …, v_k−1 are distinct, the walk W is called a path, if v_k = v₀, the path W is called a cycle in D (and in S). The sign of the walk W in  S, denoted by sgn (W), is defined to be $$ where sgn (e_i) is the sign of the arc e_i.

Definition 1.4 (see [10].)Let D be a digraph (permitting loops but no multiple arcs). Digraph D is called primitive if there is a positive integer k such that for all ordered pairs of vertices v_i and v_j (not necessarily distinct) in D, there exists a walk of length k from v_i to v_j. The least such k is called the primitive exponent of D, denoted by exp (D).

It is well known that a digraph D is primitive if and only if D is strongly connected and the greatest common divisor (gcd for short) of the lengths of all the cycles of D is 1 (see [13]).

Definition 1.5 (see [3].)Let S be a signed digraph of order n. Then there is a sign pattern matrix A of order n whose associated signed digraph S(A) is S. We say that S is powerful if A is powerful. Also we define l(S) = l(A).

We say that a sign pattern matrix A = (a_ij) has zero diagonal if a_ii = 0 for all i. A digraph D with vertex set {v₁, …, v_n} and arc set E is called symmetric provided that (v_i, v_j) ∈ E iff (v_j, v_i) ∈ E for all i, j. It is clear that a sign pattern matrix A is ZS iff its associated digraph D(A) is symmetric. For simplicity, we represent a symmetric (signed) digraph by its underlying graph.

The base set of primitive ZS sign pattern matrices and the base set of primitive ZS sign pattern matrices with zero diagonal are given, respectively, in [3, 10]. In [2], Cheng and Liu characterized the primitive ZS sign pattern matrices with the maximum base.

In this paper, we characterize the primitive sign pattern matrices with zero diagonal attaining the maximum base. Our main result is given in the following theorem.

Theorem 1.6. Let A = (a_ij) be an n × n primitive zero-symmetric sign pattern matrix with zero diagonal. Then

and the equality holds if and only if A is nonpowerful and skew symmetric, namely, a_ij = −a_ji for all 1 ≤ i ≤ j ≤ n, and the associated digraph D(A) is isomorphic to G (see Figure 1).

Theorem 2.1 (see [8].)Let A be an n × n primitive symmetric (0,1) matrix with zero diagonal. Then exp (A) ≤ 2n − 4 and the primitive exponent set of n × n primitive symmetric (0,1) matrix with zero diagonal is {2,3, …, 2n − 4}∖D, where D is the set of odd numbers in {n − 2, n − 1, …, 2n − 5}.

Theorem 2.2 (see [10].)Let A be an n × n primitive ZS sign pattern matrix with zero diagonal. Then l(A) ≤ 2n − 1.

Definition 2.3. Two walks W₁ and W₂ in a signed digraph are called a pair of SSSD walks, if they have the same initial vertex, same terminal vertex, and same length, but they have different signs.

Lemma 2.4 (see [8].)Let D be a symmetric digraph. Then D is primitive if and only if D is strongly connected and there exists an odd cycle in D.

Lemma 2.5 (see [1], [12].)If S is a primitive signed digraph, then  S  is nonpowerful if and only if S contains a pair of cycles C₁ and C₂, with lengths p₁ and p₂, respectively, satisfying one of the following conditions:

•  

  A₁ p₁ is odd and p₂ is even and sgn (C₂) = −1;

•  

  A₂ both p₁ and p₂ are odd and sgn (C₁) = −sgn (C₂).

Lemma 2.6 (see [12].)Let S be a primitive, nonpowerful signed digraph. Then we have the following.

• (1)

  There is an integer k such that there exists a pair of SSSD walks of length k from each vertex x to each vertex y in S.

• (2)

  If there exists a pair of SSSD walks of length k from each vertex x to each vertex y, then there also exists a pair of SSSD walks of length k + 1 from each vertex u to each vertex v in S.

• (3)

  The minimal such k (as in (1)) is just l(S), the base of S.

Lemma 2.7 (see [7].)Suppose that an n × n sign pattern matrix A = (a_ij) is skew symmetric. Let S(A) be the associated signed digraph of A. Let r be an odd integer with 3 ≤ r ≤ n (n ≥ 3). Then l(S(A)) = 2n − 1 if and only if S(A) is isomorphic to G (see Figure 1).

Lemma 3.1. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. If all the 2 cycles in S(A) are positive, then l(A) ≤ 2n − 2.

Proof. Since A is primitive, it follows from Lemma 2.4 that S(A) is strongly connected and there is an odd cycle C^′ in S(A) such that l(C^′) = l^′. Since A has zero diagonal, there are no loops in S(A) and so l^′ ≥ 3. Without loss of generality, we assume that C^′ is an odd cycle with the least length in S(A).

Case  1. There exists at least one negative even cycle in S(A).

Let C be a negative even cycle in S(A). Without loss of generality, we assume that C is a negative even cycle with the least length in S(A). Since all 2 cycles in S(A) are positive, l(C) = l ≥ 4.

Subcase  1.1. C and C^′ have no common vertices.

Let P be the shortest path from C to C^′. Suppose P intersects C at vertex u and intersects C^′ at vertex v and there are k vertices on P where k ≥ 2. Let G₀ = C ∪ P ∪ C^′. Let x and y be any two (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₀ and intersects G₀ at vertex x^′ and P₂ is the shortest path from y to G₀ and intersects G₀ at vertex y^′. Then 0 ≤ l(P₁),  l(P₂) ≤ n − l − l^′ − k + 2, where l ≥ 4 and l^′ ≥ 3. By the proof of Case  1 of Lemma  4.5 in [3], there exists a pair of SSSD walks from x to y of length 2n − 2. Therefore, by Lemma 2.6, l(A) ≤ 2n − 2.

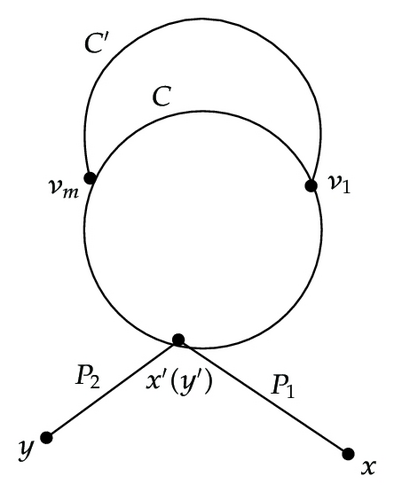
Subcase  1.2. C and C^′ have at least one common vertex.

Let G₁ = C ∪ C^′. Let x and y be any two (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₁ and intersects G₁ at vertex x^′ and P₂ is the shortest path from y to G₁ and intersects G₁ at vertex y^′. Denote C∩C^′ by R. Assume R has m vertices, where 1 ≤ m ≤ min (l, l^′), then

If m ≥ 2, then R is a path with vertex set V(R) = {v₁, v₂, …, v_m} and edge set E(R) = {(v₁, v₂), (v₂, v₃), …, (v_m−1, v_m)}. In this case, if m = min (l, l^′) = l, then there exists another odd cycle with length l^′ − l + 2 < l^′, which contradicts our assumption that C^′ is an odd cycle with the least length in S(A). Therefore, m < l and if m = min (l, l^′), then m = l^′.

Subcase  1.2.1. x^′ = y^′ and 1 ≤ m ≤ min (l, l^′).

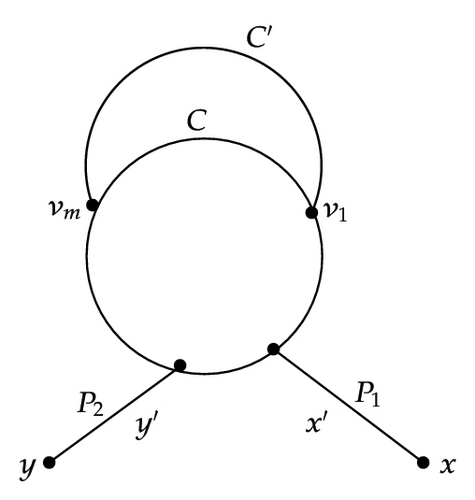
Subcase  1.2.1.1. x^′ = y^′ ∈ C∖R. See Figure 2(a).

We consider two subcases: the subcase 1 ≤ m < min (l, l^′) and the subcase m = min (l, l^′) = l^′.

First, we consider the subcase 1 ≤ m < min (l, l^′). Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(x^′ → v_m)). Let w = l(P₁) + l(C) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, $$ and l(Q_R(v₁ → v_m)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is even, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Then, we consider the subcase m = min (l, l^′) = l^′. Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(x^′ → v_m)). Let

If w is even, set Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since $$ is an odd cycle, l(Q_C∖R(x^′ → v₁)) and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is even, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.2.1.2. x^′ = y^′ ∈ C^′∖R. See Figure 2(b).

The proof for this subcase is similar to that of the Subcase 1.2.1.1 and is omitted.

Subcase  1.2.1.3. x^′ = y^′ ∈ R. See Figure 2(c).

Let w = l(P₁) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since l^′ is odd, we see that both l(W₁) and l(W₂) are even. Then, if w is even, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

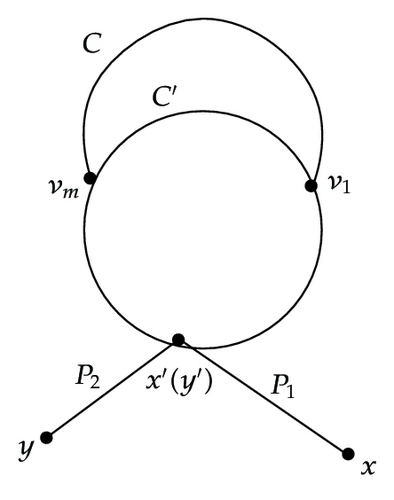
Subcase  1.2.2. x^′ ≠ y^′ and 2 ≤ m ≤ min (l, l^′).

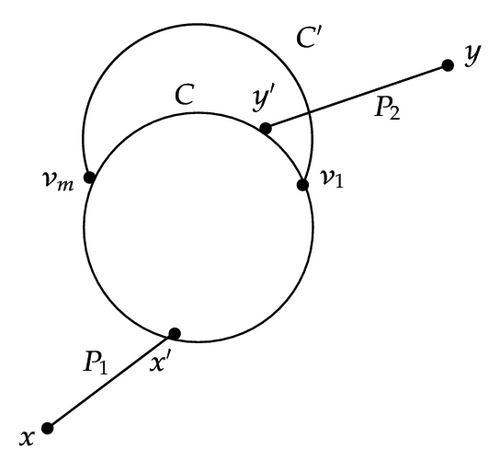
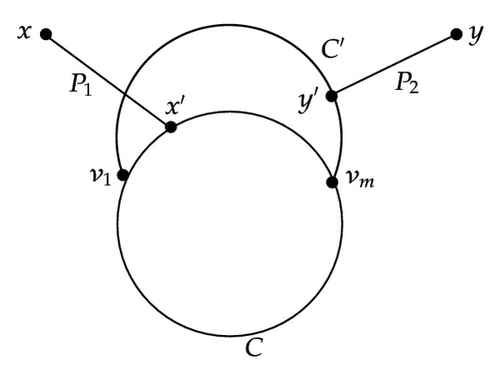
Subcase  1.2.2.1. x^′ ∈ C∖R and y^′ ∈ C∖R. See Figure 3(a).

Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(y^′ → v₁)). Let w = l(P₁) + l(Q_C∖R(x^′ → v₁)) + l(Q_R(v₁ → v_m)) + l(Q_C∖R(v_m → y^′)) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, $$ and l(Q_R(v₁ → v_m)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that W₃ = P₁ + Q_C∖R(x^′ → v₁) + Q_R(v₁ → v_m) + Q_C∖R(v_m → y^′) and $$ are paths of S(A), we have l(W₃),  l(W₄) ≤ n − 1. Then Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

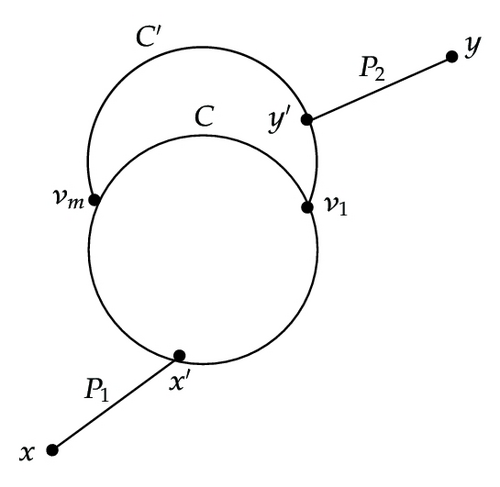
Subcase  1.2.2.2. x^′ ∈ C∖R and y^′ ∈ R. See Figure 3(b).

Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(x^′ → v_m)). Then we consider two subcases: the subcase x^′ ∈ C∖R, y^′ ∈ R and y^′ ≠ v₁ and the subcase x^′ ∈ C∖R and y^′ = v₁.

First, we consider the subcase x^′ ∈ C∖R, y^′ ∈ R and y^′ ≠ v₁. Let w = l(P₁) + l(Q_C∖R(x^′ → v₁)) + l(Q_R(v₁ → y^′)) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, l(Q_R(v₁ → y^′)) and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that W₃ = P₁ + Q_C∖R(x^′ → v₁) + Q_R(v₁ → y^′) and $$ are two paths of S(A), then we have l(W₃),  l(W₄) ≤ n − 1. Then Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Then, we consider the subcase x^′ ∈ C∖R and y^′ = v₁. Let w = l(P₁) + l(Q_C∖R(x^′ → v_m)) + l(Q_R(v_m → v₁(y^′))) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, l(Q_R(v_m → v₁(y^′))) and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that W₃ = P₁ + Q_C∖R(x^′ → v_m) + Q_R(v_m → v₁(y^′)) and $$ are two paths of S(A), we have l(W₃),  l(W₄) ≤ n − 1. Then Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

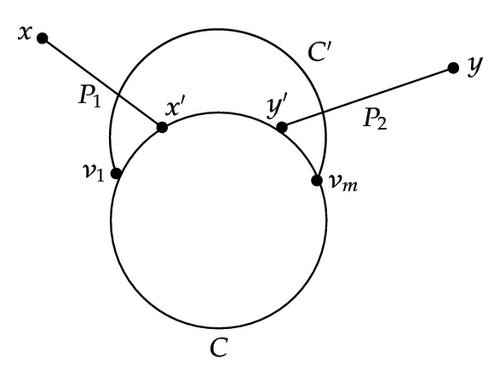
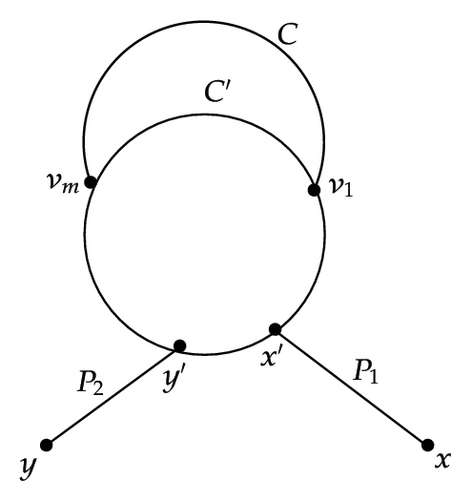
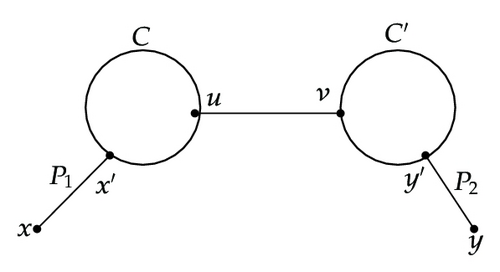
Subcase  1.2.2.3. x^′ ∈ C∖R and y^′ ∈ C^′∖R. See Figure 3(c).

The proof for this subcase is similar to that of the Subcase 1.2.2.1 and is omitted.

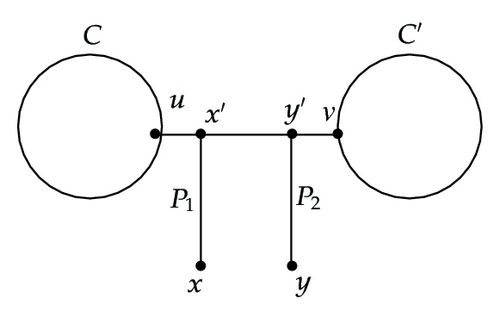
Subcase  1.2.2.4. x^′ ∈ R and y^′ ∈ R. See Figure 3(d).

Let $$. If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, $$ and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Then if w is even, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.2.2.5. x^′ ∈ R and y^′ ∈ C^′∖R. See Figure 3(e).

The proof for this subcase is similar to that of Subcase 1.2.2.4, so we omit it.

Subcase  1.2.2.6. x^′ ∈ C^′∖R and y^′ ∈ C^′∖R. See Figure 3(f).

Without loss of generality, we assume that $$. Let $$. If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, $$ and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that $$ and $$ are two paths of S(A), then we have l(W₃) ≤ n − 1 and l(W₄) ≤ n − m. Then, if w is even, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

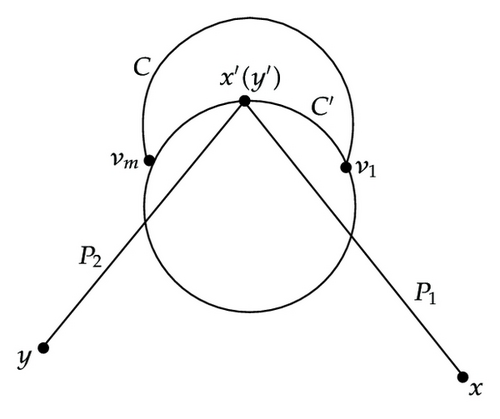
Subcase  1.2.3. m = 1 and x^′ ≠ y^′. We assume that V(C)∩V(C^′) = {u}.

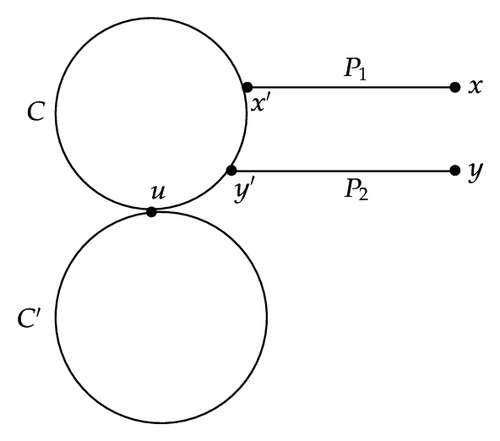
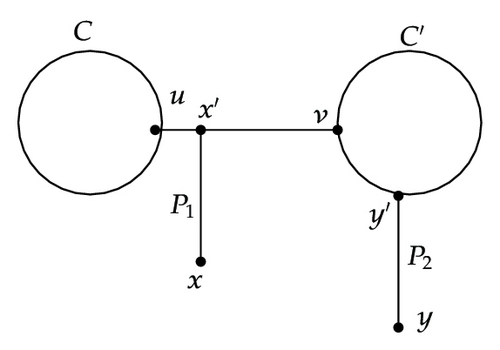
Subcase  1.2.3.1. x^′ ∈ C and y^′ ∈ C. See Figure 4(a).

Let w = l(P₁) + l(Q_C(x^′ → u)) + l(Q_C(u → y^′)) + l(P₂). If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since l^′ is odd, both l(W₁) and l(W₂) are even. Then, if w is even, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

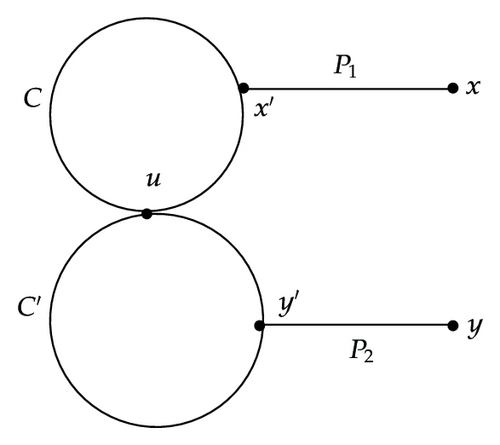
Subcase  1.2.3.2. x^′ ∈ C, y^′ ∈ C^′, and x^′ ≠ y^′ ≠ u. See Figure 4(b).

Let $$. If w is even, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains vertex x. Since C^′ is odd, $$ and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that $$ and $$ are two paths of S(A), we have l(W₃),  l(W₄) ≤ n − 1. Then,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.2.3.3. x^′ ∈ C^′ and y^′ ∈ C^′. See Figure 4(c).

The proof for this subcase is similar to that of the Subcase 1.2.3.1 and is omitted.

Thus in each of the above subcases, there exists a pair of SSSD walks from x to y with length 2n − 2. Therefore, we get l(A) ≤ 2n − 2 by Lemma 2.6.

Case  2. There exists no negative even cycle in S(A).

Since A is primitive, nonpowerful and there exist no negative even cycles in S(A), it follows from Lemma 2.5 that there exist two odd cycles C and C^′ with different signs in S(A). We assume that l(C) = l and l(C^′) = l^′. Since the trace of A is zero, there are no loops in S(A) and so l,  l^′ ≥ 3. Without loss of generality, we assume l ≥ l^′ ≥ 3.

Subcase  2.1. C and C^′ have no common vertices.

Let P be the shortest path from C to C^′. Suppose P intersects C at vertex u and intersects C^′ at vertex v and there are k vertices on P where k ≥ 2. Let G₂ = C ∪ P ∪ C^′. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₂ and intersects G₂ at vertex x^′ and P₂ is the shortest path from y to G₂ and intersects G₂ at vertex y^′. Then

Since C and C^′ have diffident signs, if there exists an even walk W with length l(W) ≤ 2n − 2 − l, then W₁ = W + C and W₂ = W + ((l − l^′)/2)C₂ + C^′ have the same length l(W₁) = l(W₂) ≤ 2n − 2 and different signs. As the proof of Subcase  1.1, we can construct an even walk W with length l(W) ≤ 2n − 2 − l. So there exists a pair of SSSD walks from x to y of length 2n − 2. It remains to consider the following subcase.

Subcase  2.2. C and C^′ have at least one common vertex.

Let G₃ = C ∪ C^′. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₃ and intersects G₃ at vertex x^′ and P₂ is the shortest path from y to G₃ and intersects G₃ at vertex y^′. Denote C∩C^′ by R. Assume R has m vertices, where 1 ≤ m ≤ min (l₁, l₂), then

If m > 1, then R is a path with vertex set V(R) = {v₁, v₂, …, v_m} and edge set E(R) = {(v₁, v₂), (v₂, v₃), …, (v_m−1, v_m)}. If m = l^′, since there exists no negative even cycles in S(A), then C and C^′ have the same sign, a contradiction. Therefore, 1 ≤ m < l^′.

Subcase  2.2.1. x^′ ∈ C∖R and y^′ ∈ C∖R. See Figure 3(a).

Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(y^′ → v₁)). Let w = l(P₁) + l(Q_C∖R(x^′ → v₁)) + l(Q_R(v₁ → v_m)) + l(Q_C∖R(v_m → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains x. Since C^′ is odd, l(Q_R(v₁ → v_m)) and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  2.2.2. x^′ ∈ C∖R and y^′ ∈ R. See Figure 3(b).

Let w = l(P₁) + l(Q_C(x^′ → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains x. Since C is odd, C∖Q_C(x^′ → y^′) and Q_C(x^′ → y^′) have different parity, Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  2.2.3. x^′ ∈ C∖R and y^′ ∈ C^′∖R. See Figure 3(c).

Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(x^′ → v_m)). Let $$. If w is odd, set

Otherwise, set Let where C₂ is a positive 2-cycle that contains x. Since C^′ is odd, $$ and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Noting that $$ and $$ are paths of S(A), then we have l(W₃),  l(W₄) ≤ n − 1. Therefore, Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  2.2.4. x^′ ∈ R and y^′ ∈ R. See Figure 3(d).

The proof for this subcase is similar to that of Subcase 2.2.2, so we omit it.

Subcase  2.2.5. x^′ ∈ R and y^′ ∈ C^′∖R. See Figure 3(e).

The proof for this subcase is similar to that of Subcase 2.2.2, so we omit it.

Subcase  2.2.6. x^′ ∈ C^′∖R and y^′ ∈ C^′∖R. See Figure 3(f).

The proof for this subcase is similar to that of Subcase 2.2.1, so we omit it.

From all the above subcases, there exists a pair of SSSD walks from x to y with length 2n − 2. Therefore, we get l(A) ≤ 2n − 2 by Lemma 2.6.

Lemma 3.2. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. If there exist a negative 2-cycle and a positive 2-cycle in S(A), then l(A) ≤ 2n − 2.

Proof. Since A is primitive, it follows from Lemma 2.4 that S(A) is strongly connected and there is an odd cycle C in S(A) with length l(C) = l. Since A has zero diagonal, there are no loops in S(A) and so l ≥ 3. Without loss of generality, we assume that C is an odd cycle with the least length in S(A). Since A is ZS and S(A) contain a positive 2-cycle and a negative 2-cycle, there exists a positive 2-cycle $$ and a negative 2-cycle $$ such that $$. Let $$.

Let P be the shortest path from u to C. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose there are k vertices on P and P intersects C at v, where k ≥ 1. Suppose P₁ is the shortest path from x to P ∪ C and P₁ intersects P ∪ C at x^′ and P₂ is the shortest path from y to P ∪ C and P₂ intersects P ∪ C at y^′ where 0 ≤ l(P₁),  l(P₂) ≤ n − l − k + 1. We consider the following three cases.

Case  1. x^′ ∈ P and y^′ ∈ P.

By the Subcase 2.1 of Lemma  4.2 in [3], there exists a pair of SSSD walks from x to y of length 2n − 2.

Case  2. Only one of x^′ and y^′ belongs to P.

By the Subcase  2.2 of Lemma  4.2 in [3], there exists a pair of SSSD walks from x to y of length 2n − 2.

It remains to consider the following case.

Case  3. x^′ ∉ P and y^′ ∉ P. See Figure 5.

Subcase  3.1. x^′ = y^′.

Let w = l(P₁) + l(Q_C(x^′ → v)) + 2l(P) + l(Q_C(v → y^′)) + l(P₂). If w is even, set

Otherwise, set Let Since C is odd, l(Q_C(v → x^′)) and l(C∖Q_C(v → x^′)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  3.2. x^′ ≠ y^′.

Without loss of generality, we assume that l(Q_C(x^′ → v)) ≤ l(Q_C(y^′ → v)). Let P₃ = Q_C(x^′ → v) and $$. Let w = l(P₁) + l(P₃) + l(P₄) + 2l(P) + l(P₂), If w is odd, set

Otherwise, set Let Since C is odd, l(P₃) + l(P₄) and $$ have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Therefore, l(A) ≤ 2n − 2 by Lemma 2.6.

Lemma 3.3. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. If l(A) = 2n − 1, then all 2-cycles in S(A) are negative.

Proof. Assume that l(A) = 2n − 1. By Lemma 3.1, S(A) has at least one negative 2-cycle. It then follows from Lemma 3.2 that all 2-cycles in S(A) are negative.

Lemma 3.4. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. Suppose that l(A) = 2n − 1. Then there exists an odd cycle C in S(A) and C is the only cycle of length at least 3 in S(A).

Proof. Since A is primitive, it follows from Lemma 2.4 that S(A) is strongly connected and there is an odd cycle C = (v₁, v₂, …, v_l) in S(A) with length l(C) = l. Since A has zero diagonal, there is no loop in S(A) and so l ≥ 3. Consider the following two directed cycles:

Since there exists no positive 2-cycle in S(A) by Lemma 3.3, the arcs (v_i, v_i+1) and (v_i+1, v_i) have different signs. Thus sgn (C¹) = −sgn (C²) by the fact that l is odd. Without loss of generality, we assume that C is an odd cycle with the least length in S(A).

If l(A) = 2n − 1, suppose there exists another cycle C^′ with length l(C^′) = l^′ ≥ 3, we consider the following two cases.

Case  1. C and C^′ have no common vertices.

Let P be the shortest path from C to C^′. Suppose P intersects C at vertex u and intersects C^′ at vertex v and there are k vertices on P where k ≥ 2. Let G₄ = C ∪ P ∪ C^′. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₄ and intersects G₄ at vertex x^′ and P₂ is the shortest path from y to G₄ and intersects G₄ at vertex y^′. Then

We consider the following six subcases.

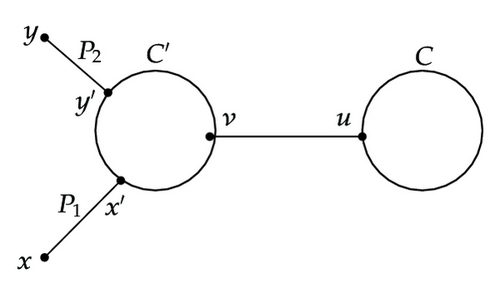
Subcase  1.1. x^′ ∈ C and y^′ ∈ C. See Figure 6(a).

Let w = l(P₁) + l(Q_C(x^′ → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let Since C is odd, l(Q_C(x^′ → y^′)) and l(C∖Q_C(x^′ → y^′)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.2. x^′ ∈ C and y^′ ∈ P. See Figure 6(b).

Let W = l(P₁) + l(Q_C(x^′ → u)) + l(Q_P(u → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let Since C is odd, l(Q_C(x^′ → u)) and l(C∖Q_C(x^′ → u)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.3. x^′ ∈ C and y^′ ∈ C^′. See Figure 6(c).

Let $$. If w is odd, set

Otherwise, set Let Since C is odd, l(Q_C(x^′ → u)) and l(C∖Q_C(x^′ → u)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.4. x^′ ∈ P and y^′ ∈ P. See Figure 6(d).

Without loss of generality, we assume that l(Q_P(x^′ → u)) ≤ l(Q_P(y^′ → u)). Let w = l(P₁) + l(Q_P(x^′ → u)) + l(P) + l(Q_P(v → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.5. x^′ ∈ P and y^′ ∈ C^′. See Figure 6(e).

Let $$, if w is odd, set

Otherwise, set Let Since C is odd, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  1.6. x^′ ∈ C^′ and y^′ ∈ C^′. See Figure 6(f).

Let $$. If w is odd, set

Otherwise, set Let Since C is odd, both l(W₁) and l(W₂) are even. Then if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Therefore, l(A) ≤ 2n − 2 by Lemma 2.6, a contradiction.

Case  2. C and C^′ have at least one common vertex.

Let G₅ = C ∪ C^′. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to G₅ and intersects G₅ at vertex x^′ and P₂ is the shortest path from y to G₅ and intersects G₅ at vertex y^′. Denote C∩C^′ by R. Assume R has m vertices, where 1 ≤ m ≤ min (l₁, l₂), then

If m > 1, then R is a path with vertex set V(R) = {v₁, v₂, …, v_m} and edge set E(R) = {(v₁, v₂), (v₂, v₃), …, (v_m−1, v_m)}. If l^′ is odd, m = min (l, l^′) = l by the minimality of C. If l^′ is even, suppose min (l, l^′) = l^′, then there exists an odd cycle C^′ with l(C^′) < l which contradicts our assumption that C is an odd cycle with the least length in S(A). Therefore, if m = min (l, l^′), then m = l < l^′. We consider the following three subcases.

Subcase  2.1. x^′ ∈ C and y^′ ∈ C.

Let w = l(P₁) + l(Q_C(x^′ → y^′)) + l(P₂). If w is odd, set

Otherwise, set Let Since C is odd, l(Q_C(x^′ → y^′)) and l(C∖Q_C(x^′ → y^′)) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  2.2. x^′ ∈ C∖R and y^′ ∈ C^′∖R.

Without loss of generality, we assume that l(Q_C∖R(x^′ → v₁)) ≤ l(Q_C∖R(x^′ → v_m)). Let $$. If w odd, set

Otherwise, set Let Since C is odd, l(Q_C∖R(x^′ → v₁)) and l(Q_C∖R(x^′ → v_m)) + l(Q_R(v_m → v₁)) have different parity. Therefore, both l(W₁) and l(W₂) are even.

Then, if w is odd,

Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Subcase  2.3. x^′ ∈ C^′∖R and y^′ ∈ C^′∖R.

The verification for this subcase is similar to that of the Subcase 2.2 and is omitted.

Therefore, l(A) ≤ 2n − 2 by Lemma 2.6, a contradiction.

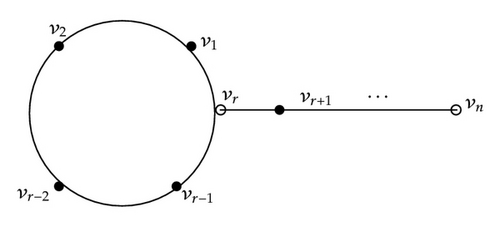
Lemma 3.5. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. If l(A) = 2n − 1, then S(A) is isomorphic to G (see Figure 1).

Proof. Let A be an n × n primitive nonpowerful ZS sign pattern matrix with zero diagonal. Since A is primitive, it follows from Lemma 2.4 that S(A) is strongly connected and there is an odd cycle C = (v₁, v₂, …, v_l) in S(A) with length l(C) = l. Since A has zero diagonal, there is no loop in S(A) and so 3 ≤ l ≤ n. Without loss of generality, we assume that C is an odd cycle with the least length in S(A). If l(A) = 2n − 1, then by Lemma 3.3, there exists no positive 2-cycle in S(A). Then S(A) is isomorphic to G by Lemma 2.7. We will give anther proof of the theorem.

Denote the vertex set of S(A) by V and the vertex set of C by V^′. By Lemmas 3.4 and 3.3, the cycle C is the only cycle of length at least 3 in S(A) and there exists no positive 2-cycle in S(A). Consider the two directed cycles C¹ = (v₁, v₂, …, v_l, v₁) and C² = (v₁, v_l, …, v₂, v₁). Since there exists no positive 2-cycle in S(A), the arcs (v_i, v_i+1) and (v_i+1, v_i) have different signs. Thus sgn (C¹) = −sgn (C²) by the fact that l is odd. Let x and y be two arbitrary (not necessarily distinct) vertices in S(A). Suppose that P₁ is the shortest path from x to C and intersects C at vertex x^′ and P₂ is the shortest path from y to C and intersects C at vertex y^′. If l = n, S(A) is isomorphic to an odd cycle of length n. If l < n, it is enough to show that there exists a vertex u ∉ V^′ in S(A) such that l(P) = n − l where P is the shortest path from u to C and P intersects C at v. Suppose not, then

Now we consider the following three cases.

Case  1. x ∈ V∖V^′ and y ∈ V∖V^′.

Let w = l(P₁) + l(Q_C(x^′ → y^′)) + l(P₂)). If w is odd, set

Otherwise, set Let Since C is odd, Q_C(x^′ → y^′) and C∖Q_C(x^′ → y^′) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Case  2. x ∈ V∖V^′ and y ∈ V.

In this case, y^′ = y. Let w = l(P₁) + l(Q_C(x^′ → y)). If w is odd, set

Otherwise, set Let Since C is odd, Q_C(x^′ → y) and C∖Q_C(x^′ → y) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

Case  3. x ∈ V and y ∈ V.

In this case, x^′ = x and y^′ = y. Let w = Q_C(x → y). If w is odd, set

Otherwise, set Let Since C is odd, Q_C(x → y) and C∖Q_C(x → y) have different parity. Therefore, both l(W₁) and l(W₂) are even. Then, if w is odd, Otherwise,

Since both l(W₁) and l(W₂) are even, it follows that l(W₁) = l(W₂) ≤ 2n − 2. We see that the pair W₁, W₂ is a pair of SSSD walks with even length. Therefore, there exists a pair of SSSD walks from x to y with length 2n − 2.

From all the above cases, there exists a pair of SSSD walks from x to y with length 2n − 2, therefore, l(A) ≤ 2n − 2 by Lemma 2.6, a contradiction.

Proof of Theorem 1.6. We get l(A) ≤ 2n − 1 from Theorem 2.2. Suppose that A is nonpowerful and skew symmetric and S(A) is isomorphic to G. Then l(A) = 2n − 1 by Lemma 2.7.

Conversely, suppose that l(A) = 2n − 1. We need to prove that A is nonpowerful and skew symmetric and S(A) is isomorphic to G. In [1], Li et al. showed that if an irreducible sign pattern matrix A is powerful, then l(A) = l(|A|). Therefore, if A is powerful, then l(A) ≤ 2n − 4 by Theorem 2.1, which contradicts l(A) = 2n − 1. Hence A is nonpowerful. Consequently, A is skew symmetric by Lemma 3.3 and S(A) is isomorphic to G by Lemma 3.5.