Computer virus spread model concerning impulsive control strategy is proposed and analyzed. We prove that there exists a globally attractive infection-free periodic solution when the vaccination rate is larger than θ₀. Moreover, we show that the system is uniformly persistent if the vaccination rate is less than θ₁. Some numerical simulations are finally given to illustrate the main results.

1. Introduction

Computer virus is a kind of computer program that can replicate itself and spread from one computer to others. Viruses mainly attack the file system and worms use system vulnerability to search and attack computers. As hardware and software technology develop and computer networks become an essential tool for daily life, the computer virus starts to be a major threat. Consequently, the trial on better understanding of the computer virus propagation dynamics is an important matter for improving the safety and reliability in computer systems and networks. Similar to the biological virus, there are two ways to study this problem: microscopic and macroscopic models. Following a macroscopic approach, since [1, 2] took the first step towards modeling the spread behavior of computer virus, much effort has been done in the area of developing a mathematical model for the computer virus propagation [3–13]. These models provide a reasonable qualitative understanding of the conditions under which viruses spread much faster than others.

In [4], the authors investigated a differential SIRS model by making the following assumptions.

(H1)
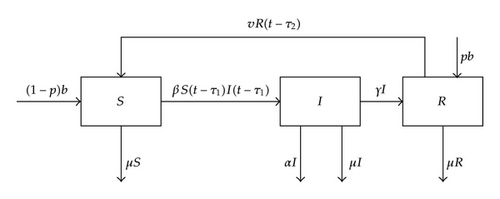
The total population of computers is divided into three groups: susceptible, infected, and recovered computers. Let S, I, and R denote the numbers of susceptible, infected and recovered computers, respectively.
(H2)
New computers are attached to the computer network with constant rate b. For the sake of antivirus software, some new nodes have temporary immunity with probability p, some have not with probability 1 − p. Hence, new nodes are added into the susceptible class with rate (1 − p)b and into the recovered class with rate pb.
(H3)
Computers are disconnected to the computer network with the constant rate μ and are disconnected from the attack of malicious object with probability α.
(H4)
S computers become I with constant rate β and with constant time delay τ₁; R computers become S with constant rate γ and with constant time delay τ₁; I computers become R with constant rate γ.

According to the above assumptions, the following model (see Figure 1) is derived:

(1.1)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Original model.

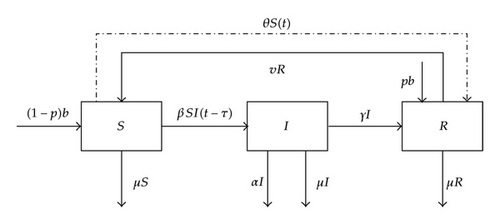
As we know, antivirus software is a kind of computer program which can detect and eliminate known viruses. There are two common methods that an antivirus software application uses to detect viruses: using a list of virus signature definitions and using a heuristic algorithm to find viruses based on common behaviors. It has been observed that it does not always work in detecting a novel computer virus by using the heuristic algorithm. On the other hand, obviously, it is impossible for antivirus software to find new computer viruss signature definitions on the dated list. So, to keep the antivirus soft in high efficiency, it is important to ensure that it is updated. Based on the above facts, we propose an impulsive system to model the process of periodic installing or updating antivirus software on susceptible computers at fixed time for controlling the spread of computer virus.

Based on above facts, we propose the following assumptions.

(H5)
The antivirus software is installed or updated at time t = kT (k ∈ N), where T is the period of the impulsive effect.
(H6)
S computers are successfully vaccinated from S class to R class with rate θ (0 < θ < 1).

According to the above assumptions (H1)–(H6), and for the reason of simplicity we propose the following model with one time delay (see Figure 2):

(1.2)

The total population size N(t) can be determined by N(t) = S(t) + I(t) + R(t) to form the differential equation

(1.3)

which is derived by adding the equations in system (1.1). Thus the total population size N may vary in time. From (1.2), we have

(1.4)

It follows that b/(μ + α) ≤ inf lim _x→∞N(t) ≤ lim _x→∞sup N(t) ≤ b/μ.

Before going into any details, we simplify model (1.1) and restrict our attention to the following model:

(1.5)

The initial conditions for (1.5) are

(1.6)

From physical considerations, we discuss system (1.5) in the closed set

(1.7)

where

denotes the nonnegative cone of R³ including its lower-dimensional faces. Note that it is positively invariant with respect to (1.7).

The organization of this paper is as follows. In Section 2, we first state three lemmas which are essential to our proofs and establish sufficient condition for the global attractivity of infection-free periodic solution. The sufficient condition for the permanence of the model is obtained in Section 3. Some numerical simulations are performed in Section 4. In the final section, a brief conclusion is given and some future research directions are also pointed out.

2. Global Attractivity of Infection-Free Periodic Solution

In this section, we prove that the infection-free periodic solution is globally attractive under some conditions. To prove the main results, two lemmas (given in [14]) which are essential to the proofs are stated here.

Lemma 2.1 (see [14], Lemma 1.)Consider the following impulsive system:

(2.1)

where a > 0, b > 0, 0 < θ < 1. Then there exists a unique positive periodic solution of system (2.1)

(2.2)

which is globally asymptotically stable, where u^* = a(1 − θ)(1 − e^−bτ)/(b(1 − (1 − θ)e^−bτ)).

Lemma 2.2 (see [14], Lemma 2.)Consider the following linear neutral delay equation:

(2.3)

or −a₁ = a₂ ≠ 0, then increasing τ does not change the stability of (2.3).

When λ = 0, (2.3) becomes

(2.4)

Corollary 2.3. Consider system (2.4) and assume that a₁, a₂, ω > 0; x(t) > 0 for −ω ≤ t ≤ 0. Then we have the following statements:

(i)
assume that a₁ < a₂, then lim _x→∞x(t) = 0;
(ii)
assume that a₁ > a₂, then lim _x→∞x(t) = +∞.

From the third and sixth equations of system (1.5), we have lim _t→∞N(t) = b/μ. Further, if I(t) ≡ 0, we have the following limit system

(2.5)

From the second and fourth equations of system (3.5), we have lim _t→∞N(t) = b/μ and have the following limit systems of (3.5):

(2.6)

According to Lemma 2.1, we know that the periodic solution of system (3.10) is of the form

(2.7)

and it is globally asymptotically stable, where S^* = (((1 − p)b + νb/μ)(1 − θ)(e^(μ+ν)τ − 1)/((μ + ν)(e^(μ+ν)τ − 1 + θ))).

Theorem 2.4. The infection-free periodic solution of system (1.5) is globally attractive provided that R₀ < 1, where

(2.8)

Proof. Since R₀ < 1, we can choose ε₁ > 0 sufficiently small such that

(2.9)

It follows from the third equation of system (1.5) that

(2.10)

There exists an integer k₁ > 0 such that N(t) ≤ b/μ, t > k₁τ.

From the first equation of system (1.5), we have

(2.11)

For t > k₁τ, k > k₁, we consider the following comparison differential system:

(2.12)

In view of Lemma 2.1, we know that the unique periodic solution of system (2.12) is of the form

(2.13)

and it is globally asymptotically stable. From (1.5), we have

(2.14)

From (2.9), we have that βδ < μ + γ + α. According to Corollary 2.3 we have

(2.15)

Therefore, for any ε₁ > 0 (sufficiently small), there exists an integer k₃ > k₂ such that I(t) < ε for all t > k₃τ. From the third equation of system (1.5), we have

(2.16)

Consider the comparison equation

(2.17)

It is easy to see that lim _t→∞z(t) = (b − αε₁)/μ. It follows by the comparison theorem that there exists an integer k₄ > k₃ such that

(2.18)

Since ε₁ is arbitrarily small, from lim _t→∞sup N(t) ≤ b/μ and (2.18) we have

(2.19)

It follows from (2.15) and (2.19) that there exists k₅ > k₄ such that

(2.20)

Hence, from the first equation of system (1.5) we have that

(2.21)

Consider the following comparison impulsive differential equations for t > k₅τ and k > k₅,

(2.22)

In view of Lemma 2.1, we periodic solution of system

(2.23)

which is globally asymptotically stable, where

(2.24)

According to the comparison theorem for impulsive differential equation, there exists an integer k₆ > k₅ such that

(2.25)

Because ε₁ is arbitrarily small, it follows from (2.25) that

(2.26)

is globally attractive, that is,

(2.27)

It follows from (2.15), (2.19), (2.27), and the restriction N(t) = S(t) + I(t) + R(t) that

. Hence, the infection-free periodic solution

of system (1.5) is globally attractive. The proof is completed.

Corollary 2.5. The infection-free periodic solution of system (1.5) is globally attractive, if θ > θ₀ where θ₀ = (e^(μ+ν)τ − 1)(((1 − p + ν/μ)/((μ + γ)(μ + γ + α))) − 1).

Theorem 2.4 determines the global attractivity of (1.5) in Ω for the case R₀ < 1. Its realistic implication is that the infected computers vanish so the computer virus removed from the network. Corollary 2.5 implies that the computer virus will disappear if the vaccination rate is larger than θ₀.

3. Permanence

In this section, we say the computer virus is local if the infectious population persists above a certain positive level for sufficiently large time. The locality viruses can be well captured and studied through the notion of permanence.

Definition 3.1. System (1.5) is said to be uniformly persistent if there is an φ > 0 (independent of the initial data) such that every solution (S(t), I(t), R(t), N(t)) with initial conditions (1.7) of system (1.5) satisfies

(3.1)

Definition 3.2. System (1.5) is said to be permanent if there exists a compact region Ω₀ ∈ int Ω such that every solution of system (1.5) with initial data (1.7) will eventually enter and remain in region Ω₀. Denote

(3.2)

Theorem 3.3. Suppose that R₁ > 1. Then there is a positive constant m_I such that each positive solution (S(t), I(t), R(t)) of system (1.5) satisfies I(t) ≥ m_I, for t large enough.

Proof. Now, we will prove there exist m_I > 0 and a sufficiently large t_p such that I(t) ≥ m_I holds for all t > t_p. Suppose that for all t > t₀. From the first equation of (1.5), we have

(3.3)

Consider the following comparison system:

(3.4)

By Lemma 2.1, we know that, there exists t₁ such that

(3.5)

It follows from the second equation of (1.5) that

. Consider the comparison system

. Noting that R₁ > 1 and ε is sufficiently small, we have

Corollary 2.3 implies that t → ∞, I(t) > z₃(t) → ∞. This contradicts I(t) ≤ b. Hence, we can claim that, for any t₀ > 0, it is impossible that

(3.6)

By the claim, we are left to consider two cases. First,

for t large enough. Second, I(t) oscillates about

for t large enough. Obviously, there is nothing to prove for the first case. For the second case, we can choose t₂ > t₁ and ξ > 0 satisfy

(3.7)

I(t) is uniformly continuous since the positive solutions to (1.5) are ultimately bounded and I(t) is not effected by impulses.

Therefore, it is certain that there exists η (0 < η < τ, and η is independent of the choice of t₂) such that

(3.8)

In this case, we shall consider the following three possible cases in term of the sizes of η, ξ and τ.

Case 1. If ξ ≤ η < τ, then it is obvious that , for t ∈ [t₂, t₂ + ξ].
Case 2. If η < ξ ≤ τ, then from the second equation of system (1.5), we obtain . Since , it is obvious that , for t ∈ [t₂, t₂ + ξ].
Case 3. If η < τ ≤ ξ, it is easy to obtain that for t ∈ [t₂, t₂ + τ]. Then, proceeding exactly the proof for above claim, we have that for t ∈ [t₂ + τ, t₂ + ξ].

Owing to the randomicity of t₂, we obtain that there exists , such that I(t) > m_I holds for all t > t_p. The proof of Theorem 3.3 is completed.

Theorem 3.4. Suppose R₁ > 1. Then system (1.5) is permanent.

Proof. Let (S(t), I(t), N(t)) be any solution to system (1.5). First, from the first equation of system (1.5), we have . Consider the following comparison system:

(3.9)

By Lemmas 2.1 and 2.2, we know that for any sufficiently small ε > 0, there exists t₁ (t₁ is sufficiently large) such that

(3.10)

From the third equation of (1.5), we have

. It is easy to see that

. Let

. By Theorem 3.3 and above discussions, we know that the set Ω₀ is a global attractor in Ω, and of course, every solution of system (1.5) with initial conditions (1.7) will eventually enter and remain in region Ω₀. Therefore, system (1.5) is permanent. The proof is completed.

Corollary 3.5. It follows from Theorem 3.4 that the system (1.5) is uniformly persistent provided that θ < θ₁, where θ₁ = (e^μτ − 1)((β(1 − p)b/((μ + α)(μ + α + γ))) − 1).

4. Numerical Simulations

In this section, we perform some numerical simulations to show the geometric impression of our results. To demonstrate the global attractivity of infection-free periodic solution to system (1.5), we take the following parameter values: b = 1, μ = 0.5, γ = 0.3, α = 0.02, β = 0.3, ν = 0.7, θ = 0.4, and τ = 1. In this case, we have R₀ = 0.5894 < 1. In Figures 3(a), 3(b), and 3(c) display respectively the susceptible, infected and recovered population of system (1.5) with initial conditions: S(0) = 3, I(0) = 4 and R(0) = 5. Figure 3(d) shows their corresponding phase-portrait.

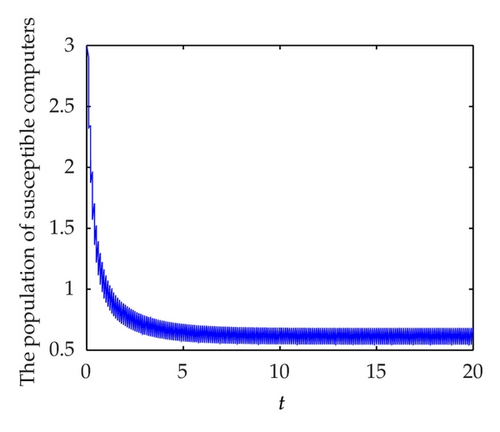
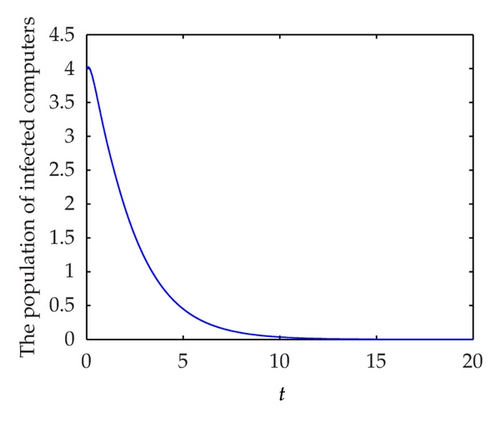
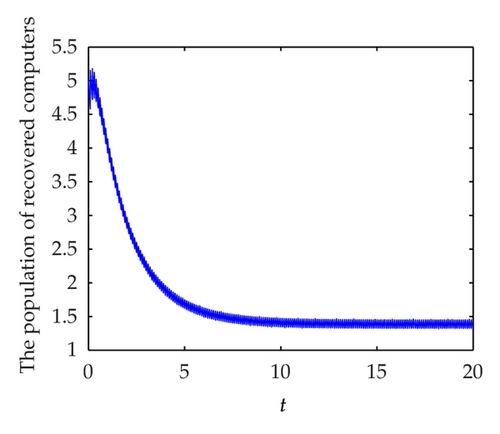
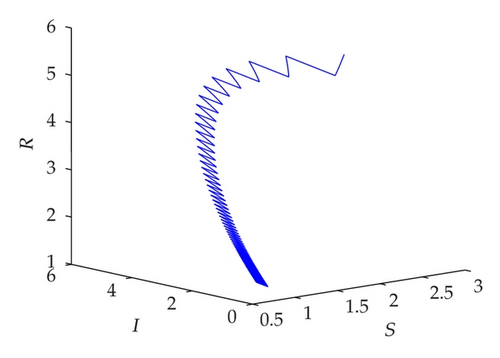
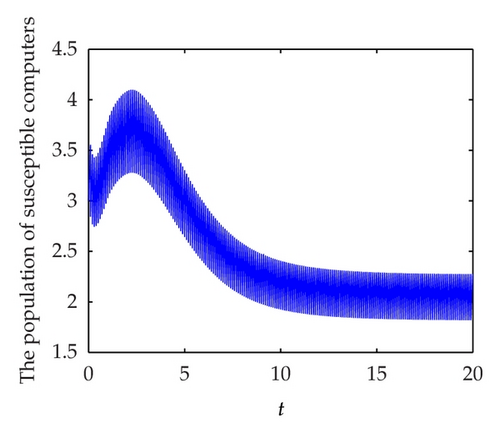
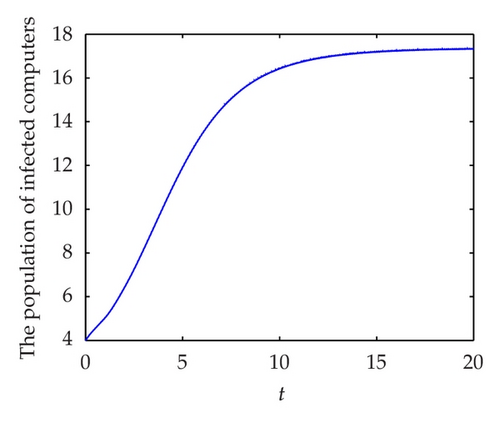
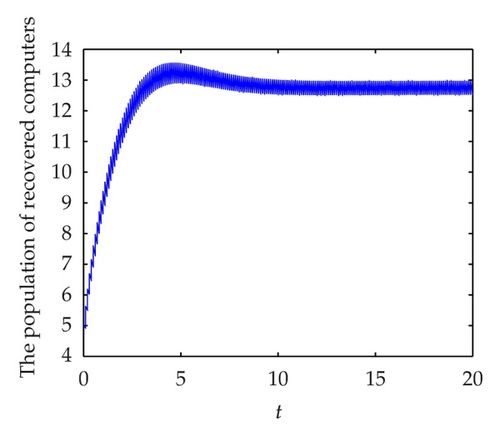
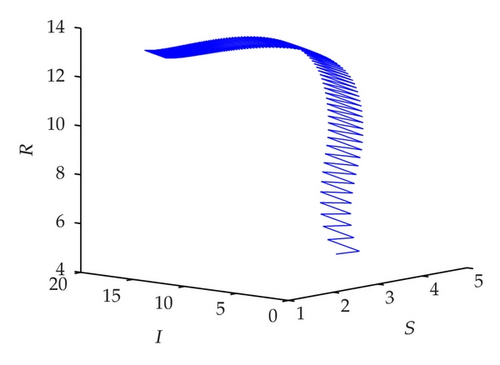
To demonstrate the permanence of system (1.5) we take following set parameter values: b = 10, μ = 0.3, γ = 0.3, α = 0.02, β = 0.3, θ = 0.2, ν = 0.7, and τ = 1. In this case, we have R₁ = 2.2195 > 1. In Figures 4(a), 4(b), and 4(c) display, respectively, the susceptible, infected and recovered population of system (1.5) with initial conditions: S(0) = 3, I(0) = 4, and R(0) = 5. Figure 4(d) shows their corresponding phase portrait.

5. Conclusion

We have analyzed the delayed SIRS model with pulse vaccination and varying total population size. We have shown that R₁ > 1 or θ < θ₁ implies that the disease will be endemic, whereas R₀ < 1 or θ > θ₀ implies that the disease will fade out. We have also established sufficient condition for the permanence of the model. Our results indicate that a short interpulse time or a large pulse vaccination rate will lead to eradication of the computer virus.

In this paper, we have only discussed two cases: (i) R₀ < 1 (or θ > θ₀) and (ii) R₁ > 1 (or θ < θ₁). But for closed interval [R₀, R₁] (or [θ₁,θ₀]), the dynamical behavior of model (3) have not been studied, and the threshold parameter for the reproducing number (or the pulse vaccination rate) between the extinction of the computer viruses and the uniform persistence of the viruses have not been obtained. These issues would be left to our future consideration.

Acknowledgment

This paper is supported by the National Natural Science Foundation of China (no. 61170320), the Natural Science Foundation of Guangdong Province (no. S2011040002981) and the Scientific research Foundation of Guangdong Medical College (no. KY1048).

References

1 Kephart J. O. and White S. R., Directed-graph epidemiological models of computer viruses, Proceedings of the IEEE Symposium on Security and Privacy, 1991, 343–359, 2-s2.0-0027150413.
Google Scholar
2 Kephart J. O., White S. R., and Chess D. M., Computers and epidemiology, IEEE Spectrum. (1993) 30, no. 5, 20–26.
10.1109/6.275061
Web of Science® Google Scholar
3 Billings L., Spears W. M., and Schwartz I. B., A unified prediction of computer virus spread in connected networks, Physics Letters A. (2002) 297, no. 3-4, 261–266, https://doi.org/10.1016/S0375-9601(02)00152-4, 1912464, ZBL0995.68007.
10.1016/S0375-9601(02)00152-4
CAS Web of Science® Google Scholar
4 Han X. and Tan Q., Dynamical behavior of computer virus on Internet, Applied Mathematics and Computation. (2010) 217, no. 6, 2520–2526, https://doi.org/10.1016/j.amc.2010.07.064, 2733695, ZBL1209.68139.
10.1016/j.amc.2010.07.064
Web of Science® Google Scholar
5 Mishra B. K. and Jha N., Fixed period of temporary immunity after run of anti-malicious software on computer nodes, Applied Mathematics and Computation. (2007) 190, no. 2, 1207–1212, 2-s2.0-34250656571, https://doi.org/10.1016/j.amc.2007.02.004.
10.1016/j.amc.2007.02.004
Web of Science® Google Scholar
6 Mishra B. K. and Saini D., Mathematical models on computer viruses, Applied Mathematics and Computation. (2007) 187, no. 2, 929–936, https://doi.org/10.1016/j.amc.2006.09.062, 2323098, ZBL1120.68041.
10.1016/j.amc.2006.09.062
Web of Science® Google Scholar
7 Mishra B. K. and Pandey S. K., Dynamic model of worms with vertical transmission in computer network, Applied Mathematics and Computation. (2011) 217, no. 21, 8438–8446, https://doi.org/10.1016/j.amc.2011.03.041, 2802253, ZBL1219.68080.
10.1016/j.amc.2011.03.041
Web of Science® Google Scholar
8 Piqueira J. R. C. and Araujo V. O., A modified epidemiological model for computer viruses, Applied Mathematics and Computation. (2009) 213, no. 2, 355–360, https://doi.org/10.1016/j.amc.2009.03.023, 2536658, ZBL1185.68133.
10.1016/j.amc.2009.03.023
Web of Science® Google Scholar
9 Piqueira J. R. C., Dynamic models for computer viruses, Computers and Security. (2008) 27, no. 7-8, 355–359, 2-s2.0-55649121612.
10.1016/j.cose.2008.07.006
Web of Science® Google Scholar
10 Ren J., Yang X., Yang L.-X., Xu Y., and Yang F., A delayed computer virus propagation model and its dynamics, Chaos, Solitons & Fractals. (2012) 45, no. 1, 74–79, https://doi.org/10.1016/j.chaos.2011.10.003, 2863589.
10.1016/j.chaos.2011.10.003
Web of Science® Google Scholar
11 Ren J., Yang X., Zhu Q., Yang L.-X., and Zhang C., A novel computer virus model and its dynamics, Nonlinear Analysis. (2012) 13, no. 1, 376–384, https://doi.org/10.1016/j.nonrwa.2011.07.048, 2846848.
10.1016/j.nonrwa.2011.07.048
Google Scholar
12 Wierman J. C. and Marchette D. J., Modeling computer virus prevalence with a susceptible-infected-susceptible model with reintroduction, Computational Statistics & Data Analysis. (2004) 45, no. 1, 3–23, https://doi.org/10.1016/S0167-9473(03)00113-0, 2041255.
10.1016/S0167-9473(03)00113-0
Web of Science® Google Scholar
13 Yuan H. and Chen G., Network virus-epidemic model with the point-to-group information propagation, Applied Mathematics and Computation. (2008) 206, no. 1, 357–367, https://doi.org/10.1016/j.amc.2008.09.025, 2474981, ZBL1162.68404.
10.1016/j.amc.2008.09.025
Web of Science® Google Scholar
14 Ren J., Yang X., Zhu Q., Yang L.-X., and Zhang C., A novel computer virus model and its dynamics, Nonlinear Analysis. (2012) 13, no. 1, 376–384, 2-s2.0-80052789013, https://doi.org/10.1016/j.nonrwa.2011.07.048.
10.1016/j.nonrwa.2011.07.048
Google Scholar

Citing Literature

All articles

An Impulse Model for Computer Viruses

Abstract

1. Introduction

2. Global Attractivity of Infection-Free Periodic Solution

3. Permanence

4. Numerical Simulations

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Impulse Model for Computer Viruses

Abstract

1. Introduction

2. Global Attractivity of Infection-Free Periodic Solution

3. Permanence

4. Numerical Simulations

5. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information