The current research attempts to offer a new method for solving fuzzy linear Volterra integral equations system. This method converts the given fuzzy system into a linear system in crisp case by using the Taylor expansion method. Now the solution of this system yields the unknown Taylor coefficients of the solution functions. The proposed method is illustrated by an example and also results are compared with the exact solution by using computer simulations.

1. Introduction

Many mathematical formulations of physical phenomena contain integral equations. These equations appear in physics, biological models, and engineering. Since these equations are usually difficult to solve explicitly, so it is required to obtain approximate solutions. In recent years, numerous methods have been proposed for solving integral equations. For example, Tricomi, in his book [1], introduced the classical method of successive approximations for nonlinear integral equations. Variational iteration method [2] and Adomian decomposition method [3] were effective and convenient for solving integral equations. Also the Homotopy analysis method (HAM) was proposed by Liao [4] and then has been applied in [5]. Moreover, some different valid methods for solving this kind of equations have been developed. First time, Taylor’s expansion approach was presented for solution of integral equations by Kanwal and Liu in [6] and then has been extended in [7–9]. In addition, Babolian et al. [10] by using the orthogonal triangular basis functions solved some integral equation systems. Jafari et al. [11] applied Legendre’s wavelets method to find numerical solution system of linear integral equations. Also Sorkun and Yalçinbaş [12] approximated a solution of linear Volterra integral equations system with the help of Taylor’s series.

In this paper, we want to propose a new numerical approach to approximate the solution of a fuzzy linear Volterra integral equations system. This method converts the given fuzzy system that supposedly has a unique fuzzy solution, into crisp linear system. For this scope, first, the Taylor expansions of unknown functions are substituted in parametric form of the given fuzzy system. Then we differentiate both sides of the resulting integral equations of the system N times and also approximate the Taylor expansion by a suitable truncation limit. This work yields a linear system in crisp case, so the solution of the linear system yields the unknown Taylor coefficients of the solution functions. An interesting feature of this method is that we can get an approximate of the Taylor expansion in arbitrary point to any desired degree of accuracy. Here is an outline of the paper. In Section 2, the basic notations and definitions of the integral equation and the Taylor polynomial method are briefly presented. Section 3 describes how to find an approximate solution of the given fuzzy Volterra integral equations system with using proposed approach. Finally in Section 4, we apply the proposed method by an example to show the simplicity and efficiency of the method.

2. Preliminaries

In this section, the most basic used notations in fuzzy calculus and integral equations are briefly introduced. We started by defining the fuzzy number.

Definition 2.1. A fuzzy number is a fuzzy set u : ℝ¹ → I = [0,1] such that

(i)
u is upper semicontinuous,
(ii)
u(x) = 0 outside some interval [a, d],
(iii)
there are real numbers b, c : a ≤ b ≤ c ≤ d, for which:
- (1)
  u(x) is monotonically increasing on [a, b],
- (2)
  u(x) is monotonically decreasing on [c, d],
- (3)
  u(x) = 1, b ≤ x ≤ c.

The set of all fuzzy numbers (as given by Definition 2.1) is denoted by E¹ [13, 14]. An alternative definition which yields the same E¹ is given by Kaleva [15] and Ma et al. [16].

Definition 2.2. A fuzzy number v is a pair of functions and , which satisfy the following requirements:

(i)
is a bounded monotonically increasing left continuous function on (0,1] and right continuous at 0,
(ii)
is a bounded monotonically decreasing left continuous function on (0,1] and right continuous at 0,
(iii)
.

A popular fuzzy number is the triangular fuzzy number v = (v_m, v_l, v_u) where v_m denotes the modal value and the real values v_l ≥ 0 and v_u ≥ 0 represent the left and right fuzziness, respectively. The membership function of a triangular fuzzy number is defined as follows:

(2.1)

Its parametric form is

(2.2)

Triangular fuzzy numbers are fuzzy numbers in LR representation where the reference functions L and R are linear.

2.1. Operation on Fuzzy Numbers

We briefly mentioned fuzzy number operations that have had been defined by the extension principle [17, 18].

(2.3)

where A and B are fuzzy numbers, μ_*(·) denotes the membership function of each fuzzy number, ∧ is the minimum operator, and f is a continuous function.

The above operations on fuzzy numbers are numerically performed on level sets (i.e., α-cuts). For 0 < α ≤ 1, a α-level set of a fuzzy number A is defined as

(2.4)

and

. Since level sets of fuzzy numbers become closed intervals, we denote [A] ^α by

(2.5)

where

and

are the lower and the upper limits of the α-level set [A] ^α, respectively. From interval arithmetic [19], the above operations on fuzzy numbers are written for the α-level sets as follows:

(2.6)

For arbitrary

and

, we define addition (u + v) and multiplication by k as [13, 14]:

(2.7)

Definition 2.3. For arbitrary fuzzy numbers u, vϵE¹ the quantity

(2.8)

is the distance between u and v. It is shown that (E¹, D) is a complete metric space [20].

Definition 2.4. Let f : [a, b] → E¹. For each partition P = {t₀, t₁, …, t_n} of [a, b] and for arbitrary ξ_iϵ[t_i−1, t_i] (1 ≤ i ≤ n), suppose

(2.9)

The definite integral of f(t) over [a, b] is

(2.10)

provided that this limit exists in the metric D. If the fuzzy function f(t) is continuous in the metric D, its definite integral exists [13]. Also,

(2.11)

More details about properties of the fuzzy integral are given in [13, 15].

2.2. System of Integral Equations

The basic definition of integral equation is given in [21].

Definition 2.5. The Fredholm integral equation of the second kind is

(2.12)

where

(2.13)

In (2.12), k(s, t) is an arbitrary kernel function over the square a ≤ s, t ≤ b and f(t) is a function of t : a ≤ t ≤ b. If the kernel function satisfies k(s, t) = 0, s > t, we obtain the Volterra integral equation

(2.14)

In addition, if f(t) be a crisp function, then the solution of the above equation is crisp as well. Also if f(t) be a fuzzy function, we have Fredholm’s fuzzy integral equation of the second kind which may only process fuzzy solutions. Sufficient conditions for the existence and uniqueness of the solution of the second kind equation, where f(t) is a fuzzy function, are given in [22, 23].

Definition 2.6. The second kind fuzzy linear Volterra integral equations system is in the form

(2.15)

where a ≤ s ≤ t ≤ b and λ_ij ≠ 0 (for i, j = 1, …, m) are real constants. Moreover, in system (2.15), the fuzzy function f_i(t) and kernel k_i,j(s, t) are given and assumed to be sufficiently differentiable with respect to all their arguments on the interval a ≤ t, s ≤ b. Also we assume that the kernel function k_i,j(s, t)ϵL²([a, b]×[a, b]) and F(t) = [F₁(t), …, F_m(t)] ^T is the solution to be determined.

Now let and (0 ≤ r ≤ 1; a ≤ t ≤ b) be parametric form of f_i(t) and F_i(t), respectively. To simplify, we assume that λ_ij > 0 (for i, j = 1, …, m). In order to design a numerical scheme for solving (2.15), we write the parametric form of the given fuzzy integral equations system as follows:

(2.16)

where

(2.17)

2.3. Taylor’s Series

Let us first recall the basic principles of the Taylor polynomial method for solving Fredholm’s fuzzy integral equations system (2.15). Because these results are the key for our problems, therefore, we explain them. Without loss of generality, we assume that

(2.18)

With above supposition, the system (2.16) is transformed to the following form:

(2.19)

Now we want to obtain the solution of the above system in the form of

(2.20)

(for j = 1, …, m) which are the Taylor expansions of degree N at t = z for the unknown functions

and

, respectively. For this scope, we calculate pth (for p = 0, …, N) derivative of each equation in the system (2.19) with respect to t and get

(2.21)

For brevity, we define symbols as below:

(2.22)

The aim of this study is to determine the coefficients

and

, (for p = 0, …, N; j = 1, …, m) in system (2.21). For this intent, we expanded

and

in Taylor’s series at arbitrary point z : a ≤ z ≤ b and substituted its Nth truncation in (2.21). Now we can write

(2.23)

where

(2.24)

Consequently, the matrix form of expression (2.23) can be written as follows:

(2.25)

where

(2.26)

Parochial matrices W^(i,j) (for i, j = 1, …, m) are defined with the following elements:

(2.27)

where

(2.28)

3. Convergence Analysis

In this section, we proved that the above numerical method converges to the exact solution of fuzzy system (2.15).

Theorem 3.1. Let the kernel be bounded and belong to L² and and for j = 1, …, m) be Taylor polynomials of degree N that their coefficients are produced by solving the linear system (2.25). Then these polynomials converge to the exact solution of the fuzzy Volterra integral equations system (2.15), when N → +∞.

Proof. Consider the system (2.15). Since, the series (2.20) converge to and , respectively, then we conclude that

(3.1)

(for i = 1, …, m) and it holds that

(3.2)

We defined the error function e_N(t, r) by subtracting (2.19) and (3.1) as follows:

(3.3)

where

(3.4)

We must prove when N → +∞, the error function e_N(t) becomes zero. Hence, we proceed as follows:

(3.5)

Since ∥k_i,j∥ is bounded, therefore,

and

imply that ∥e_N∥→0 and proof is completed.

4. An Example

In this section, we present an example of fuzzy linear Volterra integral equations system and results will be compared with the exact solution.

Example 4.1. Consider the system of fuzzy linear Volterra integral equations with

(4.1)

kernel functions

(4.2)

and a = 0, b = 2, N = 1, λ_i,j = 1 (for i, j = 1,2). The exact solution in this case is given by

(4.3)

In this example, we assume that z = 0. Using (2.23)–(2.25), the coefficients matrix W + V is calculated as follows:

(4.4)

where

(4.5)

With using above matrices, we can rewrite the linear system (2.25) as follows:

(4.6)

The vector solution of the above linear system is

(4.7)

After propagating this vector solution in (2.20), we have

(4.8)

As shown in Figures 1 and 2, the present method gives the analytical solution for this kind of fuzzy equations system, if the exact solution be polynomial.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

and for Example 4.1.

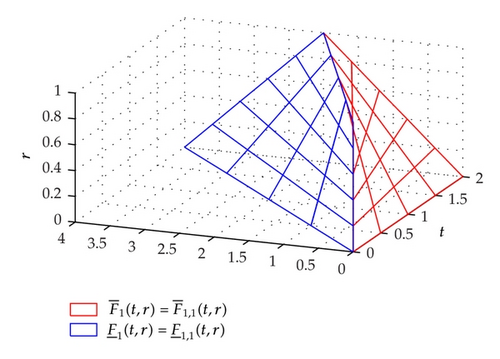
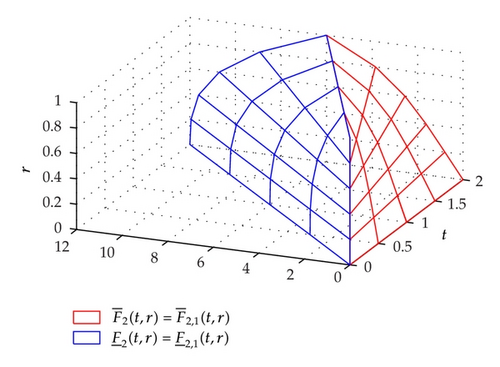
5. Conclusions

Fuzzy integral equations systems, which have a very important place in physics and engineering, are usually difficult to solve analytically. Therefore, it is required to obtain approximate solutions. In this study, mechanization of solving fuzzy linear Volterra integral equations system of the second kind by using the Taylor expansion method have proposed. This Taylor method transforms the given problem to a linear algebraic system in crisp case. The solution of the resulting system is used to compute unknown Taylor coefficients of the solution functions. Consider that to get the best approximating solutions of the given fuzzy equations, the truncation limit N must be chosen large enough. An interesting feature of this method is finding the analytical solution for given fuzzy system, if the exact solution be polynomials of degree N or less than N. The results of the example indicate the ability and reliability of the present method.

References

1 Tricomi F. G., Integral Equations, 1982, Dover Publications, New York, NY, USA, 809184.
Google Scholar
2 Xu L., Variational iteration method for solving integral equations, Computers & Mathematics with Applications. (2007) 54, no. 7-8, 1071–1078, https://doi.org/10.1016/j.camwa.2006.12.053, 2398128.
10.1016/j.camwa.2006.12.053
Web of Science® Google Scholar
3 Babolian E., Sadeghi Goghary H., and Abbasbandy S., Numerical solution of linear Fredholm fuzzy integral equations of the second kind by Adomian method, Applied Mathematics and Computation. (2005) 161, no. 3, 733–744, https://doi.org/10.1016/j.amc.2003.12.071, 2113514.
10.1016/j.amc.2003.12.071
Web of Science® Google Scholar
4 Liao S. J., Beyond Perturbation: Introduction to the HomoTopy Analysis Method, 2003, Chapman Hall/CRC Press, Boca Raton, Fla, USA.
10.1201/9780203491164
Google Scholar
5 Abbasbandy S., Numerical solutions of the integral equations: homotopy perturbation method and Adomian′s decomposition method, Applied Mathematics and Computation. (2006) 173, no. 1, 493–500, https://doi.org/10.1016/j.amc.2005.04.077, 2203403.
10.1016/j.amc.2005.04.077
Web of Science® Google Scholar
6 Kanwal R. P. and Liu K. C., A Taylor expansion approach for solving integral equations, International Journal of Mathematical Education in Science and Technology. (1989) 20, 411–414, https://doi.org/10.1080/0020739890200310.
10.1080/0020739890200310
Google Scholar
7 Maleknejad K. and Aghazadeh N., Numerical solution of Volterra integral equations of the second kind with convolution kernel by using Taylor-series expansion method, Applied Mathematics and Computation. (2005) 161, no. 3, 915–922, https://doi.org/10.1016/j.amc.2003.12.075, 2113528.
10.1016/j.amc.2003.12.075
Web of Science® Google Scholar
8 Nas S., Yalçınbaş S., and Sezer M., A Taylor polynomial approach for solving high-order linear Fredholm integro-differential equations, International Journal of Mathematical Education in Science and Technology. (2000) 31, no. 2, 213–225, https://doi.org/10.1080/002073900287273, 1751379.
10.1080/0020739X.2022.12131593
Google Scholar
9 Nas S., Yalçınbaş S., and Sezer M., A Taylor polynomial approach for solving high-order linear Fredholm integro-differential equations, International Journal of Mathematical Education in Science and Technology. (2000) 31, no. 2, 213–225, https://doi.org/10.1080/002073900287273, 1751379.
10.1080/0020739X.2022.12131593
Google Scholar
10 Babolian E., Masouri Z., and Hatamzadeh-Varmazyar S., A direct method for numerically solving integral equations system using orthogonal triangular functions, International Journal of Industrial Mathematics. (2009) 2, 135–145.
Google Scholar
11 Jafari H., Hosseinzadeh H., and Mohamadzadeh S., Numerical solution of system of linear integral equations by using Legendre wavelets, International Journal of Open Problems in Computer Science and Mathematics. (2010) 5, 63–71.
Google Scholar
12 Sorkun H. H. and Yalçinbaş S., Approximate solutions of linear Volterra integral equation systems with variable coefficients, Applied Mathematical Modelling. (2010) 34, no. 11, 3451–3464, https://doi.org/10.1016/j.apm.2010.02.034, 2651780.
10.1016/j.apm.2010.02.034
Web of Science® Google Scholar
13 Goetschel R. and Voxman W., Elementary fuzzy calculus, Fuzzy Sets and Systems. (1986) 18, no. 1, 31–43, https://doi.org/10.1016/0165%2D0114(86)90026%2D6, 825618.
10.1016/0165-0114(86)90026-6
Web of Science® Google Scholar
14 Nguyen H. T., A note on the extension principle for fuzzy sets, Journal of Mathematical Analysis and Applications. (1978) 64, no. 2, 369–380, 0480044.
10.1016/0022-247X(78)90045-8
Web of Science® Google Scholar
15 Kaleva O., Fuzzy differential equations, Fuzzy Sets and Systems. (1987) 24, no. 3, 301–317, https://doi.org/10.1016/0165%2D0114(87)90029%2D7, 919058.
10.1016/0165-0114(87)90029-7
Web of Science® Google Scholar
16 Ma M., Friedman M., and Kandel A., A new fuzzy arithmetic, Fuzzy Sets and Systems. (1999) 108, no. 1, 83–90, https://doi.org/10.1016/S0165%2D0114(97)00310%2D2, 1714662.
10.1016/S0165-0114(97)00310-2
Web of Science® Google Scholar
17 Zadeh L. A., The concept of a linguistic variable and its application to approximate reasoning. III, Information Sciences. (1975) 9, no. 1, 43–80, 0386371.
10.1016/0020-0255(75)90017-1
Web of Science® Google Scholar
18 Zadeh L. A., Toward a generalized theory of uncertainty (GTU) an outline, Information Sciences. (2005) 172, no. 1-2, 1–40, https://doi.org/10.1016/j.ins.2005.01.017, 2153009.
10.1016/j.ins.2005.01.017
Web of Science® Google Scholar
19 Alefeld G. and Herzberger J., Introduction to Interval Computations, 1983, Academic Press, New York, NY, USA, 733988.
Web of Science® Google Scholar
20 Puri M. L. and Ralescu D. A., Fuzzy random variables, Journal of Mathematical Analysis and Applications. (1986) 114, no. 2, 409–422, https://doi.org/10.1016/0022%2D247X(86)90093%2D4, 833596.
10.1016/0022-247X(86)90093-4
Web of Science® Google Scholar
21 Hochstadt H., Integral Equations, 1973, John Wiley & Sons, New York, NY, USA, 0390680.
Google Scholar
22 Congxin W. and Ming M., On the integrals, series and integral equations of fuzzy set-valued functions, Journal of Harbin Institute of Technology. (1990) 21, 9–11.
Google Scholar
23 Friedman M., Ma M., and Kandel A., Numerical solutions of fuzzy differential and integral equations, Fuzzy Sets and Systems. (1999) 106, no. 1, 35–48, https://doi.org/10.1016/S0165%2D0114(98)00355%2D8, 1689568.
10.1016/S0165-0114(98)00355-8
Web of Science® Google Scholar

Citing Literature

All articles

A Numerical Scheme to Solve Fuzzy Linear Volterra Integral Equations System

Abstract

1. Introduction