Volume 2012, Issue 1 163821

Research Article

Open Access

A Coupled Method of Laplace Transform and Legendre Wavelets for Lane-Emden-Type Differential Equations

Fukang Yin,

Corresponding Author

Fukang Yin

[email protected]

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

Junqiang Song,

Junqiang Song

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

Fengshun Lu,

Fengshun Lu

China Aerodynamics Research and Development Center, Sichuan, Mianyang 621000, China

Search for more papers by this author

Hongze Leng,

Hongze Leng

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

Fukang Yin,

Corresponding Author

Fukang Yin

[email protected]

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

Junqiang Song,

Junqiang Song

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

Fengshun Lu,

Fengshun Lu

China Aerodynamics Research and Development Center, Sichuan, Mianyang 621000, China

Search for more papers by this author

Hongze Leng,

Hongze Leng

College of Computer, National University of Defense Technology, Changsha 410073, China nudt.edu.cn

Search for more papers by this author

First published: 19 November 2012

https://doi.org/10.1155/2012/163821

Citations: 14

Academic Editor: Sazzad H. Chowdhury

Share a link

Email
Wechat
Bluesky

Abstract

A coupled method of Laplace transform and Legendre wavelets is presented to obtain exact solutions of Lane-Emden-type equations. By employing properties of Laplace transform, a new operator is first introduced and then its Legendre wavelets operational matrix is derived to convert the Lane-Emden equations into a system of algebraic equations. Block pulse functions are used to calculate the Legendre wavelets coefficient matrices of the nonlinear terms. The results show that the proposed method is very effective and easy to implement.

1. Introduction

The Lane-Emden-type equation has attracted much attention from mathematicians and physicists, since it is widely used to investigate the theory of stellar structure, the thermal behavior of spherical cloud gas, and theory of thermionic currents [1–3]. One of the general forms of Lane-Emden type equations is

()

subject to conditions

()

where a and b are constants and f(x, y) is a nonlinear function of x and y.

The solution of the Lane-Emden equations is numerically challenging due to the singularity behavior at the origin and nonlinearities. Therefore, much attention has been paid to searching for the better and more efficient methods for determining a solution, approximate or exact, analytical or numerical, to the Lane-Emden equations. The existing methods fall into two groups: the analytical methods and the numerical ones. The analytical methods express the exact solution of the equation in the form of elementary functions and convergent function series, such as the Adomian decomposition method (ADM) [4–7], homotopy perturbation method (HPM) [8–10], variational iteration method (VIM) [11–13], homotopy analysis method (HAM) [14, 15], power series solution [16], and differential transformation method [17, 18]. Unlike the analytical methods, the numerical ones approximate the exact solution on a finite set of distinct points, such as the Legendre Tau method [19] and sinc-collocation method [20], Lagrangian approach [21], successive linearization method [22], wavelets and collocation method [23–26], and spectral method [27].

The Laplace transform is a wonderful tool for solving linear differential equations and has enjoyed much success in this realm. However, it is totally incapable of handling nonlinear equations because of the difficulties caused by nonlinear terms. Since Laplace Adomian decomposition method (LADM) was proposed by Khuri [28] and then developed by Khan [29] and Khan and Gondal [30], the couple methods that based on Laplace transform and other methods have received considerable attention in the literature. What is more, the homotopy perturbation method [31] and the variational iteration method [32] are combined with the well-known Laplace transform to develop a highly effective technique for handling many nonlinear problems. For example, the coupled methods [33–38] based on the homotopy perturbation method and Laplace transform have been proved to be very effective for the solution of nonlinear problems.

Wavelets theory, as a relatively new and emerging area in mathematical research, has received considerable attention in dealing with various problems of dynamic systems. The fundamental idea of this technique is that it reduces these problems to those of solving a system of algebraic equations, thus greatly simplifies the problem and reduces the computation cost [6]. Moreover, wavelets establish a connection with fast numerical algorithms. Yousefi [25] has obtained the numerical solutions of the Lane-Emden equations (1.1) by converting it into an integral equation and then using Legendre wavelets and Gaussian integration method. Furthermore, Pandey et al. [26] obtained the numerical solutions of Lane-Emden equations by using the operational matrix of derivative of the Legendre polynomials.

Motivated and inspired by the ongoing research in these areas, we propose a coupled method of Laplace transform and Legendre wavelets to establish exact solutions of (1.1). The advantage of our method is its capability of combining the two powerful methods to obtain exact solutions of nonlinear equations. The remainder of the paper is organized as follows. In Section 2, we describe some preliminaries about Legendre wavelets and Block function pulses. The proposed method is detailed in Section 3. Four examples are given in Section 4 to demonstrate the validity and applicability of the proposed method. Finally the concluding remarks are given in Section 5.

2. Preliminaries

2.1. Legendre Wavelets

Legendre wavelets

have four arguments:

, n = 1,2, 3, …, 2^k−1, k is any positive integer, m is the order for Legendre polynomials, and t is the normalized time. They are defined on the interval [0, 1) as follows:

()

where m = 0,1, 2, …M − 1, n = 1,2, …, 2^k−1. The coefficient

is for orthonormality, the dilation parameter a = 2^−k, and the translation parameter

. Here, L_m(t) are Legendre polynomials of order m defined on the interval [−1,1].

A function f(t) defined over [0,1), may be expanded by Legendre wavelet series as

()

with

()

and <·, ·> denoting the inner product.

If the infinite series in (2.2) is truncated, then it can be written as

()

where C and Ψ(t) are 2^k−1M × 1 matrices defined as

()

2.2. Block Pulse Functions

Block pulse functions (BPFs) form a complete set of orthogonal functions that are defined on the interval [0, b) as

()

for i = 1,2 , …, m. It is also known that for arbitrary absolutely integrable function f(t) on [0, b) can be expanded in block pulse functions:

()

in which

()

where f_i are the coefficients of the block-pulse function, given by

()

The elementary properties of BPFs are as follows.

(1)
Disjointness: the BPFs are disjoined with each other in the interval t ∈ [0, T):
()
for i, j = 1,2, …, m.
(2)
Orthogonality: the BPFs are orthogonal with each other in the interval t ∈ [0, T):
()
for i, j = 1,2, …, m.
(3)
Completeness: the BPFs set is complete when m approaches infinity. This means that for every f ∈ L²([0, T)), when m approaches to the infinity, Parseval’s identity holds:
()
where
()

Definition 2.1. Let A and B are two vectors of m; then .

Lemma 2.2. Assuming f(t) and g(t) are two absolutely integrable functions, which can be expanded in block pulse function as f(t) = FB(t) and g(t) = GB(t) respectively, then one has

()

where H = F ⊗ G.

Proof. By using the property of BPFs in (2.11), we have

()

and this completes the proof.

2.3. Nonlinear Term Approximately

The Legendre wavelets can be expanded into m-set of block-pulse functions as

()

Taking the collocation points as in the following,

()

The m-square Legendre matrix Φ_m×m is defined as

()

The operational matrix of product of Legendre wavelets can be obtained by using the properties of BPFs. Let f(t) and g(t) be two absolutely integrable functions, which can be expanded in Legendre wavelets as f(t) = F^TΨ(t) and g(t) = G^TΨ(t), respectively.

From (2.17), we have

()

By employing Lemma 2.2 and (2.17), we get

()

3. Laplace Legendre Wavelets Method (LLWM)

In this section, we will briefly demonstrate the utilization of the LLWM for solving the Lane-Emden equations given in (1.1).

By multiplying x and then applying the Laplace transform to both sides of (1.1), we obtain

()

where L is operator of Laplace transform and L^′{y} = dL{y}/ds.

Equation (3.1) can be rewritten as

()

By integrating both sides of (3.2) from 0 to s with respect to s, we have

()

Taking the inverse Laplace transform to (3.3), we get

()

By using the initial conditions from (1.2), we have

()

For convenience, we define an operator

. Therefore, (3.5) can be represented as

()

Now, we will show how to derive the Legendre wavelets operational matrix of operator Π. First of all, three corollaries are given.

Corollary 3.1. Let Ψ(x) be the one-dimensional Legendre wavelets vector defined in (2.6), then one has

()

where B is M × M matrix

()

Proof. Let ; then by expanding Ψ(x) by Φ(x), we obtain

()

where A is M × M matrix. For example, when M = 5, we have

()

From (3.9), we obtain

()

and this completes the proof.

Corollary 3.2. Let Ψ(x) be the one-dimensional Legendre wavelets vector defined in (2.6), then one has

()

Proof. From the definition of operator Π, we can know

()

By further analysis, we obtain

()

where matrix B is give in (3.8) and matrix D is defined as

()

So we finally have

()

Let H = ADBA⁻¹, we get (3.12), and this completes the proof.

Corollary 3.3. Let Ψ(x) be the one dimension Legendre wavelets vector defined in (2.6); then one has

()

where H_x = ABDBA⁻¹:

()

In order to use Legendre wavelets method, we approximate y(x), f(x, y), and xg(x) as

()

Substituting (3.19) into (3.6) and then using the Corollary 3.3, we have

()

Finally, we can get

()

Equation (3.21) is a nonlinear equation which can be solved for the elements of C in (3.19) by the Newton iterative method.

4. Numerical Examples

In this section, four different examples are examined to demonstrate the effectiveness and high accuracy of the LLWM.

Example 4.1. Consider the lane-Emden equation given in [6]

()

subject to the initial conditions

()

with the exact solution y = x² + x³.

Applying the method proposed in Section 3, we have

()

When k = 1 and M = 5, the numerical solution and the absolute error of Example 4.1 are plotted in Figure 1. We see that a good approximation is obtained by using a few terms of Legendre wavelets.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Numerical solution and absolute error of Example 4.1.

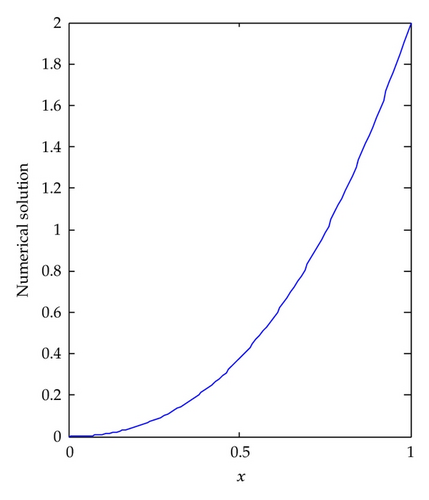
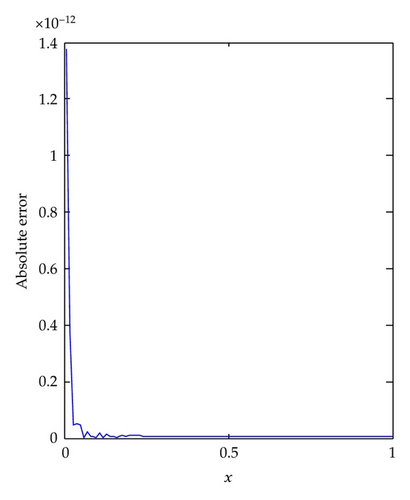
Example 4.2. Consider the lane-Emden equation of index n:

()

subject to the initial conditions

()

When n = 1 and n = 5, the exact solutions are y = sin x/x and

, respectively.

Applying the method developed in Section 3, we have

()

From [18], we can get the four terms approximate solution of (4.4) as follows:

()

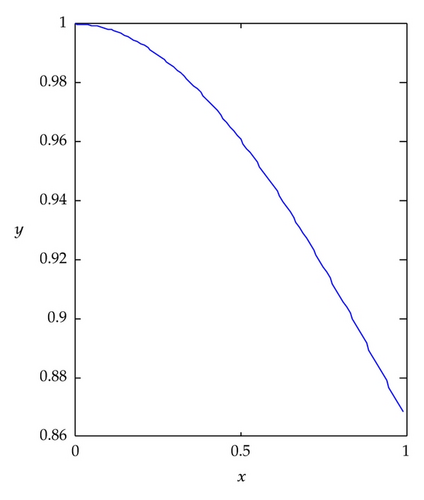
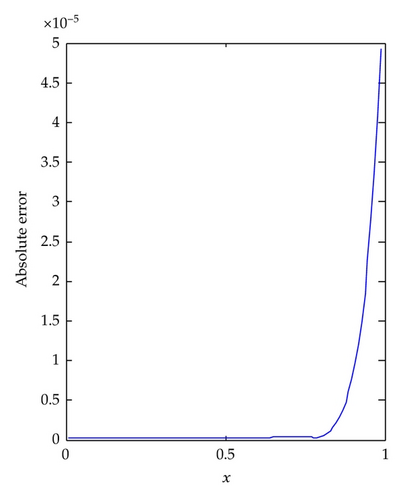
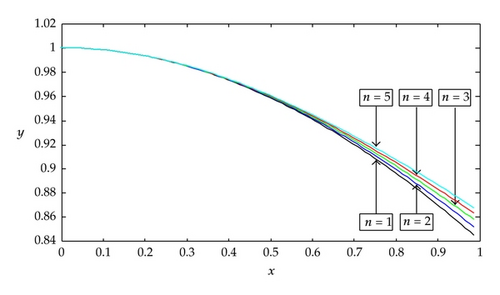
In the case of n = 1, when k = 1 and M = 11, the results of Example 4.2 are plotted in Figure 2. We observe that the accuracy of LLWM solution is very high. For the case of n = 5, which has strong nonlinearity, we plot the results when k = 1 and M = 16 in Figure 3. It can be noted that the LLWM solution is very close to the exact solution. In addition, we give the numerical solutions of difference n in Figure 4.

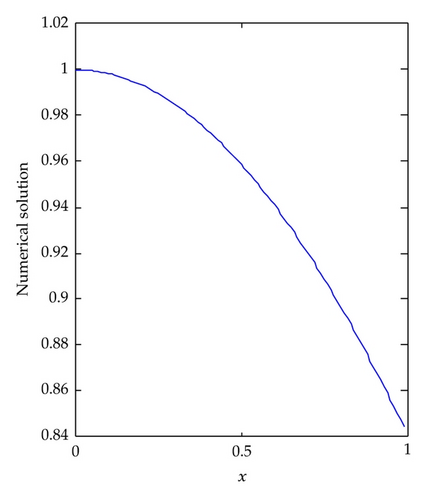
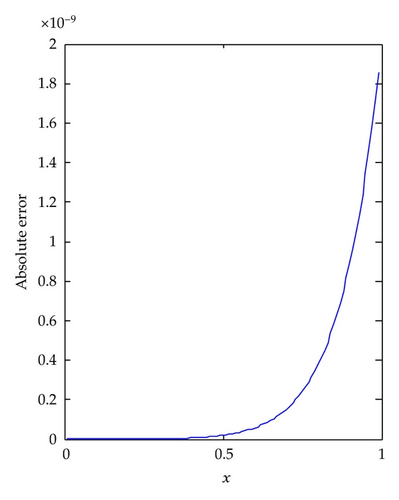
Example 4.3. Consider the Lane-Emden equation given in [7] by

()

subject to the initial conditions

()

with the exact solution y = x².

Applying the method developed in Section 3, we have

()

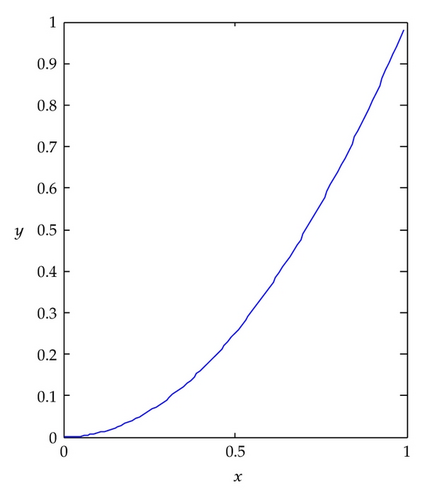
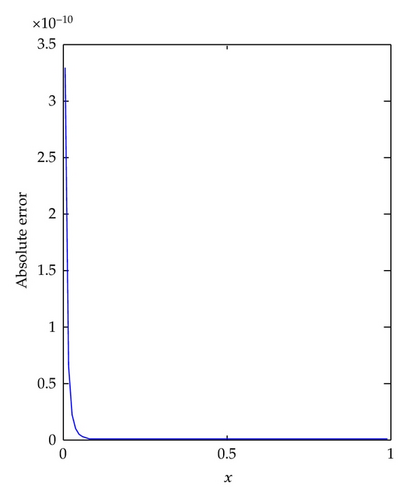
When k = 1 and M = 9, the numerical solution and the absolute error of Example 4.3 are plotted in Figure 5. We observe that the accuracy of LLWM is very high and only needs a few terms of Legendre wavelets.

Example 4.4. Consider the following nonlinear Lane-Emden differential equation [7, 8, 13]:

()

subject to initial conditions

()

The exact solution is y(x) = −2ln (1 + x²).

Here, we first expand f(x, y) = 4(2e^y + e^y/2) by Taylor series and then have

()

Considering only the first five terms we can write

()

We let g(x) = 12x and then approximate g(x) and f(x, y) − g(x) by the Legendre wavelets as

()

By applying the LLWM, we have

()

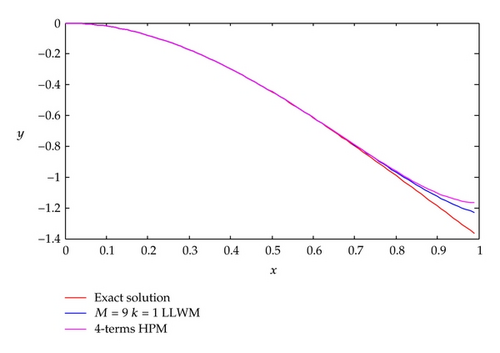
The analytical methods, such as the ADM [7], HPM [8], and VIM [13], can get the exact solution of Example 4.4. From [7, 8, 13], we can know that the four-term solution of the above methods is y(x) = −2(x² − (1/2)x⁴ + (1/3)x⁶ − (1/4)x⁸).

When k = 1 and M = 9, the numerical solutions of Example 4.4 are plotted in Figure 6. We observe that the LLWM solution is more accurate than the four-term solution of HPM or ADM or VIM. The LLWM can only get the approximate solution because of the error caused by expanding the nonlinear term. However, the LLWM can avoid the symbolic computation and only needs a few terms of Legendre wavelets. Since the exact solution is an analytic function, the higher accuracy can be obtained by taking M > 9.

5. Conclusion

In this paper, we have successfully developed a coupled method of Laplace transform and Legendre wavelets (LLWM) for solution of Lane-Emden equations. The advantage of our method is that only small size operational matrix is required to provide the solution at high accuracy. It can be clearly seen in the paper that the proposed method works well even in the case of high nonlinearity. Compared to the analytical methods, such as the ADM, VIM, and HPM, the LLWM can only get the approximate solution because of the error caused by expanding highly nonlinear terms. However, the developed vector-matrix form makes LLWM a promising tool for Lane-Emden-type equations, because LLWM is computer-oriented and can use many existing fast algorithms to reduce the computational cost.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Grant no. 41105063). The authors are very grateful to reviewers for carefully reading the paper and for his (her) comments and suggestions which have improved the paper.

References

1 Chandrasekhar S., An Introduction to the Study of Stellar Structure, 1967, Dover, New York, NY, USA, 0092663, ZBL0123.23604.
Google Scholar
2 Davis H. T., Introduction to Nonlinear Differential and Integral Equations, 1962, Dover, New York, NY, USA, 0181773, ZBL0217.54002.
Google Scholar
3 Richardson O. U., The Emission of Electricity From Hot Bodies, 1921, Zongmans Green and Company, London, UK.
Google Scholar
4 Shawagfeh N. T., Nonperturbative approximate solution for Lane-Emden equation, Journal of Mathematical Physics. (1993) 34, no. 9, 4364–4369, https://doi.org/10.1063/1.530005, 1233277, ZBL0780.34007.
10.1063/1.530005
Web of Science® Google Scholar
5 Wazwaz A.-M., A new algorithm for solving differential equations of Lane-Emden type, Applied Mathematics and Computation. (2001) 118, no. 2-3, 287–310, https://doi.org/10.1016/S0096%2D3003(99)00223%2D4, 1812960, ZBL1023.65067.
10.1016/S0096-3003(99)00223-4
Web of Science® Google Scholar
6 Wazwaz A.-M., A new method for solving singular initial value problems in the second-order ordinary differential equations, Applied Mathematics and Computation. (2002) 128, no. 1, 45–57, https://doi.org/10.1016/S0096%2D3003(01)00021%2D2, 1891179, ZBL1030.34004.
10.1016/S0096-3003(01)00021-2
Web of Science® Google Scholar
7 Olga F. and Zdeněk Š., A domian decomposition method for certain singular initial value problems, Journal of Applied Mathematics. (2010) 3, no. 2, 91–98.
Google Scholar
8 Ramos J. I., Series approach to the Lane-Emden equation and comparison with the homotopy perturbation method, Chaos, Solitons and Fractals. (2008) 38, no. 2, 400–408, https://doi.org/10.1016/j.chaos.2006.11.018, 2415942, ZBL1146.34300.
10.1016/j.chaos.2006.11.018
Web of Science® Google Scholar
9 Yildirim A. and Öziş T., Solutions of singular IVP′s of Lane-Emden type by homotopy pertutbation method, Physics Letters A. (2007) 369, 70–76.
10.1016/j.physleta.2007.04.072
CAS Web of Science® Google Scholar
10 Chowdhury M. S. H. and Hashim I., Solutions of a class of singular second-order IVPs by homotopy-perturbation method, Physics Letters A. (2007) 365, no. 5-6, 439–447, https://doi.org/10.1016/j.physleta.2007.02.002, 2308783, ZBL1203.65124.
10.1016/j.physleta.2007.02.002
CAS Web of Science® Google Scholar
11 He J.-H., Variational approach to the Lane-Emden equation, Applied Mathematics and Computation. (2003) 143, no. 2-3, 539–541, https://doi.org/10.1016/S0096%2D3003(02)00382%2DX, 1981715, ZBL1022.65076.
10.1016/S0096-3003(02)00382-X
Web of Science® Google Scholar
12 Dehghan M. and Shakeri F., Approximate solution of a differential equation arising in astrophysics using the variational iteration method, New Astronomy. (2008) 13, no. 1, 53–59, 2-s2.0-34548509029, https://doi.org/10.1016/j.newast.2007.06.012.
10.1016/j.newast.2007.06.012
Web of Science® Google Scholar
13 Yildirım A. and Öziş T., Solutions of singular IVPs of Lane-Emden type by the variational iteration method, Nonlinear Analysis. (2009) 70, no. 6, 2480–2484, https://doi.org/10.1016/j.na.2008.03.012, 2498349, ZBL1162.34005.
10.1016/j.na.2008.03.012
Web of Science® Google Scholar
14 Liao S., A new analytic algorithm of Lane-Emden type equations, Applied Mathematics and Computation. (2003) 142, no. 1, 1–16, https://doi.org/10.1016/S0096%2D3003(02)00943%2D8, 1978243, ZBL1022.65078.
10.1016/S0096-3003(02)00943-8
Web of Science® Google Scholar
15 Bataineh A. S., Noorani M. S. M., and Hashim I., Homotopy analysis method for singular IVPs of Emden-Fowler type, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 4, 1121–1131, https://doi.org/10.1016/j.cnsns.2008.02.004, 2468944, ZBL1221.65197.
10.1016/j.cnsns.2008.02.004
Web of Science® Google Scholar
16 Mohan C. and Al-Bayaty A. R., Power-series solutions of the Lane-Emden equation, Astrophysics and Space Science. (1980) 73, no. 1, 227–239, https://doi.org/10.1007/BF00642378, 596868, ZBL0457.76039.
10.1007/BF00642378
Web of Science® Google Scholar
17 Ertürk V. S., Differential transformation method for solving differential equations of Lane-Emden type, Mathematical & Computational Applications. (2007) 12, no. 3, 135–139, 2396843, ZBL1175.34007.
10.3390/mca12030135
Google Scholar
18 Mukherjee S., Roy B., and Chaterjee P. K., Solution of Lane-Emden equation by differential transform method, International Journal of Nonlinear Science. (2011) 12, no. 4, 478–484, 2875902.
Google Scholar
19 Parand K. and Razzaghi M., Rational legendre approximation for solving some physical problems on semi-infinite intervals, Physica Scripta. (2004) 69, no. 5, 353–357, 2-s2.0-2442639373, https://doi.org/10.1238/Physica.Regular.069a00353.
10.1238/Physica.Regular.069a00353
CAS Web of Science® Google Scholar
20 Parand K. and Pirkhedri A., Sinc-Collocation method for solving astrophysics equations, New Astronomy. (2010) 15, no. 6, 533–537, 2-s2.0-77950338358, https://doi.org/10.1016/j.newast.2010.01.001.
10.1016/j.newast.2010.01.001
CAS Web of Science® Google Scholar
21 Parand K., Rezaei A. R., and Taghavi A., Lagrangian method for solving Lane-Emden type equation arising in astrophysics on semi-infinite domains, Acta Astronautica. (2010) 67, no. 7-8, 673–680, 2-s2.0-78049432455, https://doi.org/10.1016/j.actaastro.2010.05.015.
10.1016/j.actaastro.2010.05.015
Web of Science® Google Scholar
22 Motsa S. S. and Sibanda P., A new algorithm for solving singular IVPs of Lane-Emden type, Proceedings of the 4th International Conference on Applied Mathematics, Simulation, Modelling (ASM ′10), July 2010, Corfu Island, Greece, NAUN International Conferences, 176–180.
Google Scholar
23 Karimi Vanani S. and Aminataei A., On the numerical solution of differential equations of Lane-Emden type, Computers & Mathematics with Applications. (2010) 59, no. 8, 2815–2820, https://doi.org/10.1016/j.camwa.2010.01.052, 2607987, ZBL1193.65151.
10.1016/j.camwa.2010.01.052
Web of Science® Google Scholar
24 Yang C. and Hou J., A numerical method for Lane-Emden equations using hybrid functions and the collocation method, Journal of Applied Mathematics. (2012) 2012, 9, 316534, https://doi.org/10.1155/2012/316534, 2880829, ZBL1235.65107.
10.1155/2012/316534
Google Scholar
25 Yousefi S. A., Legendre wavelets method for solving differential equations of Lane-Emden type, Applied Mathematics and Computation. (2006) 181, no. 2, 1417–1422, https://doi.org/10.1016/j.amc.2006.02.031, 2270772, ZBL1105.65080.
10.1016/j.amc.2006.02.031
Web of Science® Google Scholar
26 Pandey R. K., Kumar N., Bhardwaj A., and Dutta G., Solution of Lane-Emden type equations using legendre operational matrix of differentiation, Applied Mathematics and Computation. (2012) 218, no. 14, 7629–7637, https://doi.org/10.1016/j.amc.2012.01.032, 2892729, ZBL1246.65115.
10.1016/j.amc.2012.01.032
Web of Science® Google Scholar
27 Boyd J. P., Chebyshev spectral methods and the Lane-Emden problem, Numerical Mathematics. (2011) 4, no. 2, 142–157, 2862664.
Google Scholar
28 Khuri S. A., A Laplace decomposition algorithm applied to a class of nonlinear differential equations, Journal of Applied Mathematics. (2001) 1, no. 4, 141–155, https://doi.org/10.1155/S1110757X01000183, 1884973, ZBL0996.65068.
10.1155/S1110757X01000183
Google Scholar
29 Khan Y., An effective modification of the laplace decomposition method for nonlinear equations, International Journal of Nonlinear Sciences and Numerical Simulation. (2009) 10, no. 11-12, 1373–1376.
10.1515/IJNSNS.2009.10.11-12.1373
Web of Science® Google Scholar
30 Khan M. and Gondal M. A., A new analytical solution of foam drainage equation by laplace decomposition method, Journal of Advanced Research in Scientific Computing. (2010) 2, no. 2, 53–64, 2792623.
Google Scholar
31 Abbasbandy S., Application of He′s homotopy perturbation method for Laplace transform, Chaos, Solitons and Fractals. (2006) 30, no. 5, 1206–1212, 2-s2.0-33745835072, https://doi.org/10.1016/j.chaos.2005.08.178.
10.1016/j.chaos.2005.08.178
Web of Science® Google Scholar
32 Khuri S. A. and Sayfy A., A laplace variational iteration strategy for the solution of differential equations, Applied Mathematics Letters. (2012) 25, no. 12, 2298–2305, 2-s2.0-84865482047, https://doi.org/10.1016/j.aml.2012.06.020.
10.1016/j.aml.2012.06.020
Web of Science® Google Scholar
33 Madani M. and Fathizadeh M., Homotopy perturbation algorithm using laplace transformation, Nonlinear Science Letters A. (2010) 1, 263–267.
Google Scholar
34 Khan M., Gondal M. A., and Karimi Vanani S., On the coupling of homotopy perturbation and laplace transformation for system of partial differential equations, Applied Mathematical Sciences. (2012) 6, no. 9–12, 467–478, 2879393, ZBL1247.65136.
Google Scholar
35 Madani M., Fathizadeh M., Khan Y., and Yildirim A., On the coupling of the homotopy perturbation method and laplace transformation, Mathematical and Computer Modelling. (2011) 53, no. 9-10, 1937–1945, https://doi.org/10.1016/j.mcm.2011.01.023, 2782897, ZBL1219.65121.
10.1016/j.mcm.2011.01.023
Google Scholar
36 Khan Y. and Wu Q., Homotopy perturbation transform method for nonlinear equations using He′s polynomials, Computers & Mathematics with Applications. (2011) 61, no. 8, 1963–1967, https://doi.org/10.1016/j.camwa.2010.08.022, 2785523, ZBL1219.65119.
10.1016/j.camwa.2010.08.022
Web of Science® Google Scholar
37 Gupta V. G. and Gupta S., Homotopy perturbation transform method for solving initial boundary value problems of variable coefficients, International Journal of Nonlinear Science. (2011) 12, no. 3, 270–277, 2862359.
Web of Science® Google Scholar
38 Singh J., Kumar D., and Rathore S., Application of homotopy perturbation transform method for solving linear and nonlinear Klein-Gordon equations, Journal of Information and Computing Science. (2012) 7, 131–139.
Google Scholar

Citing Literature

All articles

A Coupled Method of Laplace Transform and Legendre Wavelets for Lane-Emden-Type Differential Equations

Abstract

1. Introduction