Volume 2012, Issue 1 161484

Research Article

Open Access

Simulation of Thermal Flow Problems via a Hybrid Immersed Boundary-Lattice Boltzmann Method

Corresponding Author

J. Wu

[email protected]

Department of Aerodynamics, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Yudao Street, Nanjing 210016 Jiangsu, China nuaa.edu.cn

Search for more papers by this author

C. Shu,

C. Shu

Department of Mechanical Engineering, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, nus.edu.sg

Search for more papers by this author

N. Zhao,

N. Zhao

Department of Aerodynamics, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Yudao Street, Nanjing 210016 Jiangsu, China nuaa.edu.cn

Search for more papers by this author

J. Wu,

Corresponding Author

J. Wu

[email protected]

Department of Aerodynamics, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Yudao Street, Nanjing 210016 Jiangsu, China nuaa.edu.cn

Search for more papers by this author

C. Shu,

C. Shu

Department of Mechanical Engineering, National University of Singapore, 10 Kent Ridge Crescent, Singapore 119260, nus.edu.sg

Search for more papers by this author

N. Zhao,

N. Zhao

Department of Aerodynamics, College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Yudao Street, Nanjing 210016 Jiangsu, China nuaa.edu.cn

Search for more papers by this author

First published: 15 March 2012

https://doi.org/10.1155/2012/161484

Citations: 3

Academic Editor: Fu-Yun Zhao

Share a link

Email
Wechat
Bluesky

Abstract

A hybrid immersed boundary-lattice Boltzmann method (IB-LBM) is presented in this work to simulate the thermal flow problems. In current approach, the flow field is resolved by using our recently developed boundary condition-enforced IB-LBM (Wu and Shu, (2009)). The nonslip boundary condition on the solid boundary is enforced in simulation. At the same time, to capture the temperature development, the conventional energy equation is resolved. To model the effect of immersed boundary on temperature field, the heat source term is introduced. Different from previous studies, the heat source term is set as unknown rather than predetermined. Inspired by the idea in (Wu and Shu, (2009)), the unknown is calculated in such a way that the temperature at the boundary interpolated from the corrected temperature field accurately satisfies the thermal boundary condition. In addition, based on the resolved temperature correction, an efficient way to compute the local and average Nusselt numbers is also proposed in this work. As compared with traditional implementation, no approximation for temperature gradients is required. To validate the present method, the numerical simulations of forced convection are carried out. The obtained results show good agreement with data in the literature.

1. Introduction

As a long-standing challenge in the computational fluid mechanics, the flow problems with complex geometry have been widely studied. In terms of grid applied, the numerical methods can be generally classified into two categories. In the traditional approach, the body-fitted mesh is employed to discretize the governing equation [1]. Thereafter, the boundary condition could be implemented directly. As a result, the solution of problems strongly depends on the quality of generated mesh. Moreover, the mesh regeneration procedure is usually unavoidable when the object is not fixed. To relieve this cumbersome requirement, the alternative choice is to decouple the governing equation from the computational mesh. In this category, the most famous algorithm is the immersed boundary method (IBM) proposed by Peskin [2].

In IBM, the discretization of governing equation is performed on the Cartesian (Eulerian) mesh, and the boundary of object is represented through a set of Lagrangian points. Different from the body-fitted solver, the boundary condition in this method is depicted by introducing a body force (restoring force) into the governing equation, which replaces the effect of boundary on the surrounding flow field. Since the governing equation is independent of the boundary, IBM is extremely suitable for handling various flow problems with complex geometry.

To acquire accurate solution via IBM, the appropriate calculation of force density is of great importance. Up till now, there are several ways to fulfill this task. By treating the boundary as deformable with high stiffness, Peskin [2] firstly applied the Hook’s law, associated with the use of free parameter, to compute the restoring force (named penalty method). Fadlun et al. [3] viewed the momentum equations as to be satisfied at boundary points and hence the force density could be subsequently computed (named direct forcing method). This approach has been widely used in current IBM application. Different from two methods introduced above, which are based on the Navier-Stokes (N-S) solver, another force calculation technique was proposed by Niu et al. [4] in the framework of lattice Boltzmann method (LBM) [5]. The concept of momentum exchange at the boundary is utilized in this approach (named momentum exchange method). Nonetheless, it should be stressed that the force density is calculated explicitly in the conventional methods. Consequently, the nonslip boundary condition cannot be guaranteed. Recently, we presented a boundary condition-enforced IB-LBM [6], in which the force density is raised from the velocity correction and is computed implicitly by enforcing the boundary condition. As compared to the conventional IBM, the nonslip boundary condition can be guaranteed in this method.

The idea of IBM has been extensively introduced into numerous isothermal flow problems. On the other hand, its application in thermal flow problems is limited and is still in progress. A few attempts have been made in this aspect [7–9]. Similar to the use of force density in isothermal flow problems, a heat source term is employed to meet the influence of boundary in thermal flow problems. However, same as the force calculation in conventional methods, the heat source term is computed explicitly in recent studies [7–9]. In this way, the thermal boundary condition cannot be accurately satisfied, which may affect the accuracy of solution. To address this problem, in this work, we develop a hybrid IB-LBM for simulation of thermal flow problems following the idea of velocity correction in [6]. In this method, the flow field is solved based on the IB-LBM in [6]. In the meanwhile, the temperature field is obtained by solving the conventional energy equation with additional heat source term, which is equivalent to temperature correction. With the temperature correction evaluated implicitly, the thermal boundary condition can be satisfied strictly. In addition, the Nusselt number is a crucial parameter in thermal flow problems. Based on the established temperature correction, in this paper, both the local and average Nusselt numbers can be efficiently computed. In this manner, the troublesome temperature gradient calculation at the boundary points could be eliminated. To validate the proposed algorithm, the forced convection from a stationary isothermal circular cylinder is simulated. The numerical results show good agreement with available data in the literature.

2. Methodology

2.1. Boundary Condition-Enforced Immersed Boundary-Lattice Boltzmann Method

For viscous incompressible flow problems with an immersed boundary, the governing equations in the framework of lattice Boltzmann equation (LBE) can be written as

(2.1)

(2.2)

(2.3)

where f_α is the distribution function,

is its corresponding equilibrium state, τ is the single relaxation parameter, e_α is the lattice velocity, w_α are coefficients which depend on the selected lattice velocity model, and f is the force density which is distributed from the boundary force density. Here, the D2Q9 lattice velocity model is used, which is

(2.4)

and the corresponding equilibrium distribution function is

(2.5)

with w₀ = 4/9, w_α = 1/9, (α = 1 ~ 4), and w_α = 1/36, (α = 5 ~ 8).

is the sound speed of this model. The relationship between the relaxation time and the kinematic viscosity of fluid is

In order to satisfy the nonslip boundary condition, the force density f in (2.2) and (2.3) should be set as unknown [6]. It can be calculated from the fluid velocity correction δu. Furthermore, δu can be obtained from the boundary velocity correction δu_B. The final expression for δu_B is

(2.6)

where

(2.7)

(2.8)

Here, m is the number of Lagrangian (boundary) points, and n is the number of surrounding Eulerian points.

is the unknown velocity correction vector at the boundary points.

and

is the delta function, which is expressed as

(2.9)

and Δs_l is the arc length of boundary element.

is the boundary velocity. The intermediate fluid velocity u^* is calculated by

(2.10)

By solving equation system (2.6), the unknown variables

can be obtained. After that, the fluid velocity correction δu can be calculated by

(2.11)

As shown in (2.3), the relationship between the force density f and the fluid velocity correction δu can be written as

(2.12)

In the LBM, the macroscopic variables such as density and pressure are calculated by

(2.13)

2.2. Implicit Temperature Correction for Energy Equation

After the flow field is accurately solved through the boundary condition-enforced IB-LBM [6], the temperature field can be obtained by using the conventional energy equation with additional heat source term, which can be written as

(2.14)

where T is the temperature, c_p is the specific heat of the fluid, k is the thermal conductivity of the fluid, and q is the heat source density distributed from the boundary heat flux.

To solve (2.14), the fractional step technique is used. First, the energy equation without heat source density is solved, which is called Predictor step:

(2.15)

The solution of (2.15) is regarded as intermediate temperature T^*. In the second step, or named Corrector step, the following equation is solved:

(2.16)

Here, (2.16) means the effect of heat source on temperature field. Using the Euler explicit scheme, ∂T/∂t can be rewritten as Tⁿ⁺¹ − T^*/δt = δT/δt, where Tⁿ⁺¹ is the required temperature at next time step. Therefore, (2.16) becomes

(2.17)

where δT is the temperature correction which determines the unknown variable q. It means that to calculate heat source term is equivalent to correcting the temperature field near the boundary. Similar to the implementation of velocity correction in IB-LBM [6], δT can further be calculated from the boundary temperature correction δT_B. By enforcing the constant temperature boundary condition, δT_B can computed from the following equation system:

(2.18)

where

(2.19)

(2.20)

Here,

is the specified boundary temperature. The parameters m, n, δ_ij, and

have the same meaning as those in equation system (2.6). After δT_B is obtained from equation system (2.18), the temperature correction δT can be calculated through

(2.21)

Consequently, the corrected temperature can be computed by

(2.22)

2.3. Local and Average Nusselt Number Evaluation

In thermal flow problems, the Nusselt number is an important measurement parameter. The local Nusselt number Nu on the surface of boundary is defined as

(2.23)

where h is the local convective heat transfer coefficient and L_c is the characteristic length. According to Newton’s cooling law and Fourier’s law, the heat conducted away from the boundary should be equal to the heat convection from the boundary, that is,

(2.24)

where T_∞ is the free stream temperature. Substituting (2.24) into (2.23) gives

(2.25)

Further averaging over the entire boundary, we can have the surface overall mean Nusselt number

(2.26)

where L is the total length of boundary. Usually, the average Nusselt number can be used to estimate the rate of heat transfer from the heated surface.

As shown in (2.25) and (2.26), to evaluate the local and average Nusselt numbers, the calculation of temperature gradient at the boundary point is required. Since the temperature is located at the Eulerian mesh which is not coincided with boundary, we cannot calculate the boundary temperature derivatives directly. On the other hand, according to the Fourier’s law, we can have the following expression for heat flux on the boundary Q:

(2.27)

At the same time, similar to (2.17), the boundary heat flux can be calculated using the boundary temperature correction

(2.28)

Substituting (2.27) and (2.28) into (2.25) and (2.26), the expressions for the local and average Nusselt numbers can be rewritten as

(2.29)

(2.30)

As can be seen from (2.29) and (2.30), the local and average Nusselt numbers can be easily calculated by using the solved boundary temperature correction, which avoids the temperature gradient computation on the boundary.

3. Results and Discussion

As a benchmark case, the forced convection from a stationary circular cylinder has been extensively simulated to validate the numerical methods. Both the experimental and numerical results are available in the literature [10–12]. To characterize this thermal flow problem, two nondimensional parameters are used: the Reynolds number Re = ρU_∞D/μ and Prandtl number Pr = μc_p/k. Here, U_∞ is the free stream velocity, D is the cylinder diameter, and μ is the dynamic viscosity. In current simulation, the Prandtl number is fixed at Pr = 0.7. Meanwhile, several low Reynolds numbers are selected: Re = 20, 40 (steady flow), and 80, 150 (unsteady flow). Since this is a one-way interaction problem, the velocity field can influence the temperature field while cannot be affected by the temperature field. As the developed IB-LBM can accurately simulate velocity field [6], we only focus on the temperature field in this case.

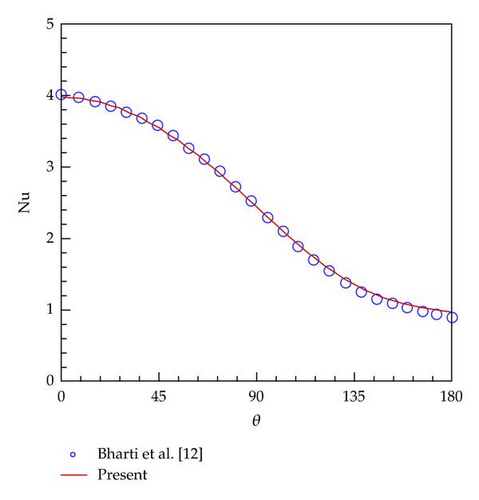
For the steady flow simulation, the computational domain is 60D × 40D with the nonuniform mesh size of 321 × 241. The cylinder is located at (20D, 20D). The region around the cylinder is 1.2D × 1.2D with a finest and uniform mesh size of 49 × 49. To apply the IB-LBM on nonuniform mesh, the Taylor series expansion and least-squares-based LBM [13] are utilized. Figure 1 shows the temperature contours at Re = 20 and 40. It can be seen from the figure that the isotherms cluster heavily in the front part of cylinder. When the Reynolds number is increased, the behavior of isotherm clustering is strengthened. The clustering of isotherm indicates that the temperature gradient is large there. As a result, the heat transfer rate near the front of cylinder is much larger than other regions. This phenomenon can be further verified via the local Nusselt number distribution on the surface of cylinder, as shown in Figure 2 for the case of Re = 20. Without evaluation of temperature gradient on the boundary point, the local Nusselt number can be easily computed from the solved boundary temperature correction, as shown in (2.29). To make comparison, the result of Bharti et al. [12] is also involved. In this figure, θ = 0^∘ means the front stagnation point of cylinder. From Figure 2, it can be found that the value of local Nusselt number located at θ = 0^∘ is maximum and it decreases monotonously with respect to θ. Also can be seen from the figure is that the result of current simulation shows good agreement with that of Bharti et al. [12].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Temperature contours for steady forced convection from a stationary circular cylinder.

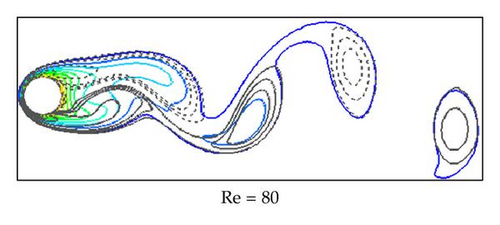
For the unsteady flow simulation, the computational domain is 50D × 40D with the mesh size of 401 × 301. The region around the cylinder keeps 1.2D × 1.2D with a uniform mesh size of 97 × 97. The cylinder is still located at (20D, 20D). Figure 3 plots the isotherms as well as vorticity contours at Re = 80 and 150. The regular vortex shedding occurs at these two Reynolds numbers. Concurrently, the isotherms lose symmetry and start to display shedding behavior, which synchronously moves downstream with vortex.

To illustrate the performance of average Nusselt number calculation by using (2.30), the obtained numerical results for all Reynolds numbers considered here are shown in Table 1. To compare with available results in the literature, the numerical results of Lange et al. [11] and Bharti et al. [12] are also listed in the table. It is clear that the results from current method basically agree well with the reference data. Besides, the value of average Nusselt number increases with Reynolds number as expected.

Table 1. Nusselt number comparison at different Reynolds numbers.

References	Cases	Nu
Lange et al. [11]	Re = 20	2.409
	Re = 40	3.281
	Re = 80	4.571
	Re = 150	6.396

Bharti et al. [12]	Re = 20	2.465
	Re = 40	3.283
	Re = 80	—
	Re = 150	—

Present	Re = 20	2.472
	Re = 40	3.281
	Re = 80	4.611
	Re = 150	6.432

4. Conclusion

In this paper, a hybrid immersed boundary-lattice Boltzmann method is developed to simulate the heat transfer problems. Employing the newly proposed IB-LBM [6], the nonslip boundary condition is enforced in simulation, and thus the velocity field can be accurately simulated. In the meanwhile, the temperature field is resolved by using the conventional energy equation with additional heat source term which mimics the influence of boundary on temperature field. Similar to the idea of velocity correction in [6], the heat source term is equivalent to the temperature correction and is set as unknown. By enforcing the thermal boundary condition, this unknown variable can be determined. Furthermore, utilizing the relationship between the temperature correction and heat flux, a simple approach for local and average Nusselt number evaluation is proposed. Different from the conventional way, there is no requirement for temperature gradient calculation.

The efficiency and capability of developed method as well as way to calculate the local and average Nusselt numbers are illustrated by the simulation of forced convection problems. The obtained numerical results show good agreement with available data in the literature. It is demonstrated that the present method has a promising potential for solving thermal flow problems with complex geometry.

References

1 Hirt C. W., Amsden A. A., and Cook J. L., An arbitrary Lagrangian-Eulerian computing method for all flow speeds, Journal of Computational Physics. (1974) 14, no. 3, 227–253, 2-s2.0-49549150963.
10.1016/0021-9991(74)90051-5
Web of Science® Google Scholar
2 Peskin C. S., Numerical analysis of blood flow in the heart, Journal of Computational Physics. (1977) 25, no. 3, 220–252, 0490027, https://doi.org/10.1016/0021%2D9991(77)90100%2D0, ZBL0403.76100.
10.1016/0021-9991(77)90100-0
Web of Science® Google Scholar
3 Fadlun E. A., Verzicco R., Orlandi P., and Mohd-Yusof J., Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations, Journal of Computational Physics. (2000) 161, no. 1, 35–60, https://doi.org/10.1006/jcph.2000.6484, 1762073, ZBL0972.76073.
10.1006/jcph.2000.6484
Web of Science® Google Scholar
4 Niu X. D., Shu C., Chew Y. T., and Peng Y., A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating incompressible viscous flows, Physics Letters A. (2006) 354, no. 3, 173–182, 2-s2.0-33646098168, https://doi.org/10.1016/j.physleta.2006.01.060.
10.1016/j.physleta.2006.01.060
CAS Web of Science® Google Scholar
5 Succi S., The Lattice Boltzmann Equation, For Fluid Dynamics and Beyond, 2001, Oxford University Press, 1857912.
10.1093/oso/9780198503989.001.0001
Google Scholar
6 Wu J. and Shu C., Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications, Journal of Computational Physics. (2009) 228, no. 6, 1963–1979, 2-s2.0-59149088844, https://doi.org/10.1016/j.jcp.2008.11.019.
10.1016/j.jcp.2008.11.019
CAS Web of Science® Google Scholar
7 Kim B. S., Lee D. S., Ha M. Y., and Yoon H. S., A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations, International Journal of Heat and Mass Transfer. (2008) 51, no. 7-8, 1888–1906, 2-s2.0-39749193516, https://doi.org/10.1016/j.ijheatmasstransfer.2007.06.033.
10.1016/j.ijheatmasstransfer.2007.06.033
CAS Web of Science® Google Scholar
8 Young D. L., Jan Y. J., and Chiu C. L., A novel immersed boundary procedure for flow and heat simulations with moving boundary, Computers & Fluids. (2009) 38, no. 6, 1145–1159, https://doi.org/10.1016/j.compfluid.2008.11.010, 2645716.
10.1016/j.compfluid.2008.11.010
Web of Science® Google Scholar
9 Wang Z., Fan J., Luo K., and Cen K., Immersed boundary method for the simulation of flows with heat transfer, International Journal of Heat and Mass Transfer. (2009) 52, no. 19-20, 4510–4518, 2-s2.0-67650093871, https://doi.org/10.1016/j.ijheatmasstransfer.2009.03.048.
10.1016/j.ijheatmasstransfer.2009.03.048
Web of Science® Google Scholar
10 Hatton A. P., James D. D., and Swire H. W., Combined forced and natural convection with low-speed air flow over horizontal cylinders, Journal of Fluid Mechanics. (1970) 42, 14–31.
10.1017/S0022112070001040
Web of Science® Google Scholar
11 Lange C. F., Durst F., and Breuer M., Momentum and heat transfer from cylinders in laminar crossflow at 10⁻⁴ ≤ Re≤200, International Journal of Heat and Mass Transfer. (1998) 41, no. 22, 3409–3430, 2-s2.0-0032214495.
10.1016/S0017-9310(98)00077-5
CAS Web of Science® Google Scholar
12 Bharti R. P., Chhabra R. P., and Eswaran V., A numerical study of the steady forced convection heat transfer from an unconfined circular cylinder, Heat and Mass Transfer. (2007) 43, no. 7, 639–648, 2-s2.0-34248163951, https://doi.org/10.1007/s00231%2D006%2D0155%2D1.
10.1007/s00231-006-0155-1
Web of Science® Google Scholar
13 Shu C., Niu X. D., and Chew Y. T., Taylor-series expansion and least-squares-based lattice Boltzmann method: two-dimensional formulation and its applications, Physical Review E. (2002) 65, no. 3, 1–13, 2-s2.0-33646976817, https://doi.org/10.1103/PhysRevE.65.036708, 036708.
10.1103/PhysRevE.65.036708
Web of Science® Google Scholar

Citing Literature

All articles

Simulation of Thermal Flow Problems via a Hybrid Immersed Boundary-Lattice Boltzmann Method

Abstract

1. Introduction

2. Methodology

2.1. Boundary Condition-Enforced Immersed Boundary-Lattice Boltzmann Method

2.2. Implicit Temperature Correction for Energy Equation

2.3. Local and Average Nusselt Number Evaluation

3. Results and Discussion

4. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Simulation of Thermal Flow Problems via a Hybrid Immersed Boundary-Lattice Boltzmann Method

Abstract

1. Introduction

2. Methodology

2.1. Boundary Condition-Enforced Immersed Boundary-Lattice Boltzmann Method

2.2. Implicit Temperature Correction for Energy Equation

2.3. Local and Average Nusselt Number Evaluation

3. Results and Discussion

4. Conclusion

References

Citing Literature

Figures

References

Related

Information