Volume 2012, Issue 1 158720

Research Article

Open Access

The Hybrid Adaptive Control of T-S Fuzzy System Based on Niche

Tong Zhao,

Corresponding Author

Tong Zhao

[email protected]

Department of Mathematics, East China Normal University, Shanghai 200241, China ecnu.edu.cn

Department of Mathematics, Nantong Shipping College, Jiangsu, Nantong 226010, China

Search for more papers by this author

Guo-ping Lu,

Guo-ping Lu

Department of Mathematics, Jiangsu College of Information Technology, Jiangsu, Wuxi 214400, China

Search for more papers by this author

Yun-li Hao,

Yun-li Hao

Faculty of Science, Jiangsu University, Jiangsu, Zhenjiang 212013, China ujs.edu.cn

Search for more papers by this author

Yi-min Li,

Yi-min Li

Faculty of Science, Jiangsu University, Jiangsu, Zhenjiang 212013, China ujs.edu.cn

Search for more papers by this author

Tong Zhao,

Corresponding Author

Tong Zhao

[email protected]

Department of Mathematics, East China Normal University, Shanghai 200241, China ecnu.edu.cn

Department of Mathematics, Nantong Shipping College, Jiangsu, Nantong 226010, China

Search for more papers by this author

Guo-ping Lu,

Guo-ping Lu

Department of Mathematics, Jiangsu College of Information Technology, Jiangsu, Wuxi 214400, China

Search for more papers by this author

Yun-li Hao,

Yun-li Hao

Faculty of Science, Jiangsu University, Jiangsu, Zhenjiang 212013, China ujs.edu.cn

Search for more papers by this author

Yi-min Li,

Yi-min Li

Faculty of Science, Jiangsu University, Jiangsu, Zhenjiang 212013, China ujs.edu.cn

Search for more papers by this author

First published: 02 July 2012

https://doi.org/10.1155/2012/158720

Citations: 1

Academic Editor: Zhiwei Gao

Share a link

Email
Wechat
Bluesky

Abstract

Based on the niche characteristics, a hybrid adaptive fuzzy control method with the function of continuous supervisory control is proposed in this paper. Considering the close degree of Niche as the consequent of adaptive T-S fuzzy control system, the hybrid control law is designed by tracking, continuous supervisory, and adaptive compensation. Adaptive compensator is used in the controller to compensate the approximation error of fuzzy logic system and the effect of the external disturbance. The adaptive law of consequent parameters, which is achieved in this paper, embodies system adaptability as biological individual. It is proved that all signals in the closed-loop system are bounded and tracking error converges to zero by Lyapunov stability theory. The effectiveness of the approach is demonstrated by the simulation results.

1. Introduction

In recent years, fuzzy technique has gained rapid development in complex nonlinear plants [1]. Fuzzy logic offers human reasoning capabilities to capture nonlinearities and uncertainties, which cannot be described by precise mathematical models. Theoretical proofs of fuzzy models as universal approximators have been presented in the last decade [2, 3]. Fuzzy adaptive control methodologies have emerged in recent years as promising ways to approach nonlinear control problems. Fuzzy control, in particular, has had an impact in the control community because of the simple approach it provides to use heuristic control knowledge for nonlinear control problems. Recently, fuzzy systems have aroused a great resurgence of interest from part of the control community on the ground that they may be applied to model ill-defined complex systems. Direct and indirect schemes are two staple configurations for adaptive fuzzy controls. It has been established that indirect and direct controls (DAFC and IAFC) are able to incorporate plant knowledge and control knowledge, respectively, to yield stable and robust control systems [4]. The last two decades or so have witnessed a large quantity of results on indirect [5, 6] or direct [7–11] adaptive control (IAC/DAC) using fuzzy systems. However, the fuzzy adaptive controller proposed in [6, 7] ensure that the tracking error asymptotically convergence to zero (or a neighborhood of the origin) if the minimum approximation error is squared integrable along the state trajectory. And those algorithms are just confined to the linear and nonlinear systems whose state variables are assumed to be available for measurement. In many complicated cases, all state variables are not measurable such that output feedback or observer-based adaptive control techniques have to be applied. In [12–15], observer-based IAC and DAC algorithms are proposed for nonlinear systems, respectively. But [6, 12, 13] proposed adaptive control gain is only applicable to nonlinear systems with unknown constant gain. So a hybrid adaptive fuzzy control is needed.

In order to exploit the relative advantages of indirect and direct adaptive configurations at the same time, some researchers have developed several hybrid IAC and DAC algorithms [16–18] where a weighting factor, which can be adjusted by the tradeoff between knowledge of the plant and knowledge of the control, is adopted to sum together the control efforts from both the IAC and DAC. However, those schemes have their limitations. Above all, they take full-state feedback, which can be unsuitable for nonlinear systems without state variables available. Moreover, the conventional adaptive controller proposed in [19] combines indirect, direct, and variable structure methods; nonetheless its plants are assumed to be linear systems only. The author of [6] has developed a hybrid adaptive fuzzy control (HAFC) for nonlinear systems. However, input gains are required to be a constant 1 and control gain is an unknown constant. The HAFC algorithm of [20] can just be applied to robot manipulators with bounds estimation whereas that of [21] derives an unsupported HAFC scheme from a faulty Lyapunov derivative. On the other hand, a certain observer-based combined direct and indirect adaptive fuzzy neural controller is developed in [22]. Sensor fault may be in any form, even unbounded, which will make the system failure unavoidably. Paper [23] proposed a reliable observer-based controller, which makes the system work well no matter whether sensor faults occur or not.

Among various kinds of fuzzy models, there is a very important class of Takagi-Sugeno (T-S) fuzzy models [24] which have recently gained much popularity because of their special rule consequent structure and success in a functional approximation [6, 25]. In the recent two years, with the stability theory of T-S fuzzy system drawing lots of researchers attention, Yeh et al. [25] proposed stability analysis of interconnected and robustness design of time-delay fuzzy systems using fuzzy Lyapunov method. Moreover, T-S fuzzy model plays an important role in dealing with practical problems, such as oceanic structure [26], Vehicle occupant classification [27], and engineering systems [28], in which T-S fuzzy systems are applied to sensor fault estimation.

Upon all the fuzzy control method mentioned above, the consequent rules only contain the mathematical expressions without the practical significances. In this paper, the self-adaptability of the ecosystem is introduced into the fuzzy control method. Ecosystem is a complex large system, the interaction between individuals within the system, the interaction between the system and the outside world, made the internal dynamics of ecological system extremely complex. Biological evolution in complex ecosystems displays a strong nonlinearity [29], and increasing complexity is an indication of biological evolution, which makes it easier for organisms to adapt to environmental changes, and higher adaptability is the performance of a higher degree of evolution, that is, the so-called “survival of the fittest” [30]. Because of the redundancy and stability of ecological system, individuals acquire their own living ability and evolve to the advantage direction. This is why the ecological system could keep balance. The stability of the system is closely related with individuals’ ecological niche. Through such feature, Wang and Yi-min [31] discussed a method of fuzzy control based on niche model. The basic concept and methods of niche are introduced. Using the similarity measures, the capabilities of the living’s self-learning and self-organization are joined in fuzzy system, gaining the fuzzy system which has the meaning of niche. Considering the high-order nonlinearity, complexity, and biological individuals’ adaptability of ecological systems, we combine biological characteristics with adaptive fuzzy control method and raise a new hybrid T-S fuzzy adaptive control way, which contains great biological significance itself. The consequent of fuzzy system is parameter’s ecological niche close degree functions for T-S model. In condition of immeasurable biological individuals’ ecological factors, in [18, 30], the author designs controller and obtains adaptive law with consequent parameter which takes good tracking effect to changing error target function. Fuzzy T-S system of ecological niche reflects the degree of biological exploiting and usage and develops to its favorable way. During this course, the system moves forward by mutual changes, coordination with environment and themselves. This fuzzy adaptive control of niche reflects that the biology of individual organisms in the new environment has a strong adaptability, strong in the biological and practical significance, but also provided a reference value for the artificial cultivation of rare species. Therefore, fuzzy control background gets its biological meaning in this way.

2. Problem Formulation

Consider the nth-order nonlinear system of the following form:

()

where f and g are unknown but bounded functions, u, y ∈ R are the input, output of the system, respectively, and y and d(t) is the external bounded disturbance.

is the state vector where not all x_i are assumed to be available for measurement. In order for the system (2.1) to be controllable, it is required that g(X) ≠ 0 for X in a certain controllability region U_c ⊂ Rⁿ. Since g(X) is continuous, we assume 0 < g(X) ≤ ∞ for X ∈ U_c. The control objective is to design a combined controller, tune the correlation parameters of adaptive law, and force the system output y to follow a bounded reference signal y_m(t) under the constraint that all signals involved must be bounded. To begin with, the signal vector

, the tracking error vector e, and estimation error vector

are defined as

, where

and

denote the estimates of X and e, respectively. If the functions f(X) and g(X) are known and the system is free of external disturbance d(t), then we can choose the controller u^* to cancel the nonlinearity and design controller. Let

be chosen such that all roots of the polynomial sⁿ + k_0nsⁿ⁻¹ + ⋯+k₀₁ are in the open left half-plane and control law of the certainty equivalent controller is obtained as

()

Substituting (2.2) to (2.1), we get the main objective of the control is lim _t→∞e(t) = 0. However f(X) and g(X) are unknown, the ideal controller (2.2) cannot be implemented, and not all system states X can be measured. So we have to design an observer to estimate the state vector X in the following.

3. T-S Fuzzy System Based on Niche

3.1. Description of T-S Fuzzy System Based on Niche

Because f(X) and g(X) are unknown, T-S fuzzy systems are used to approximate them. The basic configuration of T-S [24] system is expressed as

()

Here,

are fuzzy sets, λ^l = (x₁, x₂, …, x_n) represents the real ecological factor of ecologic niche, and

is the ideal ecological factor. Consequent indicates the difference between real state of ecologic niche and ideal one. we choose Gaussian membership function, which satisfies

, where

are the centers and σ is the variance of the functions. Then difference could be showed by approach functions as

, where

. From approach functions above, we could know consequent is a zero-order T-S mode. Here, we use

for convenience. Let m be the number of systems with central average defuzzifier, and product inference and singleton fuzzifier can be expressed as

()

where

;

and u_D(X∣θ_D) = η(X)^Tθ_D can be expressed similarly.

3.2. Niche T-S Model Parameter Optimization Method

Niche fuzzy T-S model based on parameter optimization of backpropagation algorithm known input and output data , the task is to determine the form (3.2) Niche T-S model parameters, To fitting error the minimum. Assume M is known, by adjusting , and let e^p be the minimum. To facilitate the discussion, use to represent , and . , .

Using gradient descent to determines the parameters [6]

()

determines the steps.

Then

()

Then,

()

Equally,

()

adjustable parameters

with the same way:

()

where

and

can be optimized directly.

4. Hybrid Controller with Supervisory and Compensation Control Scheme

The overall control law is constructed as

()

where u_I is an indirect controller, u_D is the output of the T-S controller, u_s is the supervisory control to force the state within the constraint set, α ∈ [0,1] is a weighting factor, and u_c is the compensate controller of adaptive control. Since X cannot be available and f(X) and g(X) are unknown, we replace the functions f(X), g(X), and error vector e by estimation functions

, and

. The certainty equivalent controller can be rewritten as

()

The indirect control law is written as

. Applying (4.2), (4.1) to (2.1), the error dynamic equation is

()

defining k_c = (k_cn, …, k_c1) as the observer vector, the observation errors are defined as

from (4.2) and [24] and we get

()

where

()

Let

be strictly Hurwitz matrix; so there exists a positive definite symmetric n × n matrix P,

which satisfies the Lyapunov equation Λ^TP + PΛ = −Q,

, where

and Q are arbitrary n × n definite symmetric matrix. Let

. Since

and k_c are designer by the designer, we can choose

and k_c, such that

. Hence,

is a bounded function and there exists a constant value

, such that

5. Hybrid Adaptive Control of Niche

We will develop the hybrid adaptive control such that the closed-loop output y(t) follows y_m(t). Let us replace

, and

, respectively. Therefore, the error dynamics (4.3) can be rewritten as

()

Let

then using (5.1), we have

()

In order to design u_s so that , we need the following assumption.

Assumption 5.1. We could find three functions as f^u(X), g^u(X), g_l(X) and get and , in which X ∈ U_c and . This is due to the fact that we can choose k_c to let . Also external disturbance is bounded. We design |d(t)| ≤ d_m.

From Assumption 5.1, we choose the supervisory control u_s as

()

And we choose

, and c_o is a nonnegative constant. Considering the case

and substitute (5.3) into (5.2), we obtain

. Therefore, if the closed-loop system with the fuzzy controller u as

()

works well in the sense that the error is not too large, if

, then the supervisory control u_s is zero. If the system tends to diverge, that is,

, then be u_s gins to force

6. Design of Adaptive Law

In order to adjust the parameters in the fuzzy logic system, we have to derive adaptive laws. Hence, the optimal parameters estimates

, and

are defined as

()

where Ω_f, Ω_g, Ω_D, Ω_X, and

, are compact sets of suitable bounds on

, and X, respectively, and they are defined as

()

where

and M_X, are positive constants. Define the minimum approximation errors as

()

Now consider the Lyapunov function

()

where

and

is expressed similarly. We get the adaptive law as

()

Furthermore, the adaptive law of niche factors is derived as follows. We derived the adaptive law of real ecologic factors, see Formula (6.7), (6.8), which represented the real niche always develop towards the ideal one. It reflected the compensation of the control system to the external disturbance:

()

The same way we have

()

Applying u_s we have .

Design parameters of, vector adaptive law of θ_f, θ_g, θ_D, stability, and performance analysis are similar to those of [18]; here we omit it.

7. Simulation

Form combined fuzzy adaptive control of two-dimensional predation system [32] as

()

where x₁(t) means total number of food at the time of t and x₂(t) denotes the total number of predators; a, b, c, q, k, α, β are the regular numbering ecology, and k is transforming factor, q represents death ratio of predators. h(x) is the function of Holling’s functional responses, and

is the third kind of Holling’s functional responses. The demonstration of the two-dimensional predator system without the controller is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Two-dimension predator system without the controller.

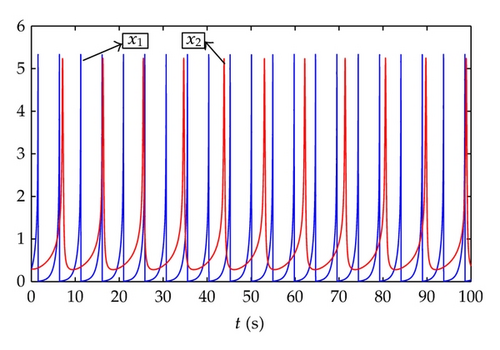
In order to reach an ideal ecologic balance in this two-dimension predators system, we get a way to control it, where .

Then

()

In order to establish the direct relation between output y and controller u, we need the derivation of y. After derivating twice, we get

()

Here, we command

()

Then (7.2) and (7.3) could be shown as

()

If hoping to apply adaptive fuzzy controlling system here, we have to firstly confirm the boundary of f^u, g^u, and g_l. From [29], we know that 0.2 < |x₁| < 5.5,1.5 < |x₂| < 5, then

()

According to the above, we find out that the scope of f(x₁, x₂) is larger than g(x₁, x₂). Therefore, we choose

. Then we select M_f = 7.7, M_g = 31, M_D = 31, ε = 0.5, |u| ≤ 5. The proposal method of this paper does not need to predefine the reference signal, but to reach the balance of each individual self-adaptively. Conveniently, we suppose k_c = [89 184] (in this way, s² + k₁s + k₂ could be stable) and k₀ = [4 4], we select

, from

, then we solve

, and

so we have

; when letting λ_min = 2.93, we could get

. In this way, we get the ideal = 0, σ = 1. The adaptive law comes out as follows:

()

We choose x₁(0) = 0.3, x₂(0) = 1.0, then the trend of the prey and predator numbers with T-S controller show as in Figures 2 and 3. The trend of the T-S controller is shown in Figure 4.

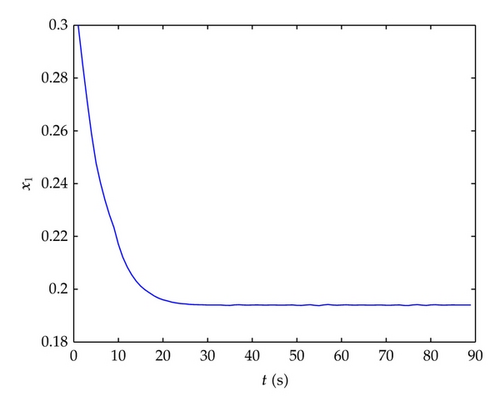
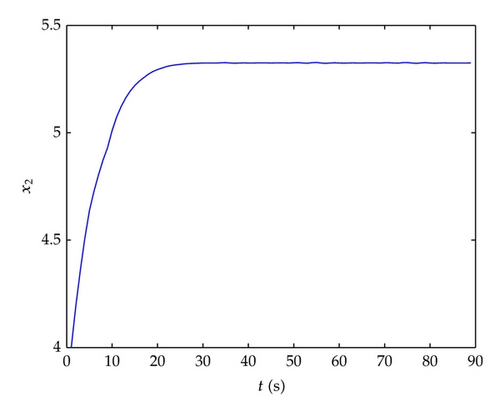
From the simulation figures, we can see that the prey and predator numbers reach a stable status in a short period of time under the control of the proposed method in this paper. The creature individuals show a characteristic of self-adaptation according to outside changes.

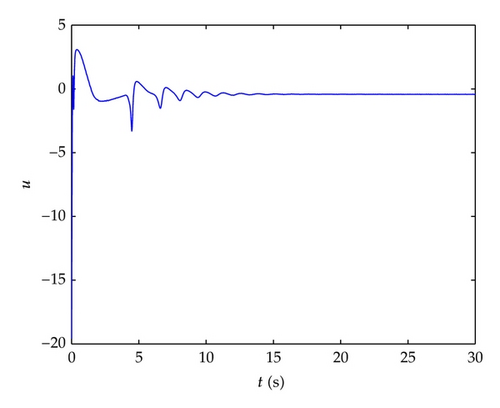
From the figure of the trend of the T-S controller, it also reaches an ideal status to maintain the overall balance of the two-dimension predator system. The ecological system is optimized with the use of this control method.

8. Conclusion

For the ecological niche, a hybrid adaptive fuzzy control method with the function of continuous supervisory control is proposed in this paper. Let the close degree of Niche which contains parameters as the consequent of adaptive T-S fuzzy control system, then designs the hybrid control law by tracking, continuous supervisory and adaptive compensation. Using gradient descent to optimize the parameters, we get the adaptive law of consequent parameters, embodying biological individual’s ability of adaptability. Based on Lyapunov stability theory, it is proved that all signals in the closed-loop system are bounded and tracking error converges to zero. This paper shows that the fuzzy methods provide good results in practical engineering problems. The performance of the developed approach is illustrated by simulation, on two-dimension predation system model.

Acknowledgment

Work supported by national science foundation (11072090).

References

1 Chen C. W., Yeh K., and Liu K. F. R., Adaptive fuzzy sliding mode control for seismically excited bridges with lead rubber bearing isolation, International Journal of Uncertainty, Fuzziness and Knowlege-Based Systems. (2009) 17, no. 5, 705–727, 2-s2.0-70349904299, https://doi.org/10.1142/S0218488509006224.
10.1142/S0218488509006224
Web of Science® Google Scholar
2 Kosko B., Fuzzy systems as universal approximators, IEEE Transactions on Computers. (1994) 43, no. 11, 1329–1333, 2-s2.0-0028532753, https://doi.org/10.1109/12.324566.
10.1109/12.324566
Web of Science® Google Scholar
3 Rovatti R., Fuzzy piecewise multilinear and piecewise linear systems as universal approximators in sobolev norms, IEEE Transactions on Fuzzy Systems. (1998) 6, no. 2, 235–249, 2-s2.0-0032074869.
10.1109/91.669022
Web of Science® Google Scholar
4 Wang L. X., A Course in Fuzzy Systems and Control, 1997, Prentice Hall, Englewood Cliffs, NJ, USA.
Google Scholar
5 Shahnazi R. and Akbarzadeh-T M. R., PI adaptive fuzzy control with large and fast disturbance rejection for a class of uncertain nonlinear systems, IEEE Transactions on Fuzzy Systems. (2008) 16, no. 1, 187–197, 2-s2.0-40549142442, https://doi.org/10.1109/TFUZZ.2007.903320.
10.1109/TFUZZ.2007.903320
Web of Science® Google Scholar
6 Wang L. X., Stable adaptive fuzzy control of nonlinear systems, IEEE Transactions on Fuzzy Systems. (1993) 1, no. 2, 146–155, 2-s2.0-0027591320, https://doi.org/10.1109/91.227383.
10.1109/91.227383
Google Scholar
7 Phan P. A. and Gale T. J., Direct adaptive fuzzy control with a self-structuring algorithm, Fuzzy Sets and Systems. (2008) 159, no. 8, 871–899, https://doi.org/10.1016/j.fss.2007.09.012, 2401936, ZBL1170.93345.
10.1016/j.fss.2007.09.012
Web of Science® Google Scholar
8 Labiod S. and Guerra T. M., Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems, Fuzzy Sets and Systems. (2007) 158, no. 10, 1126–1137, https://doi.org/10.1016/j.fss.2006.11.013, 2311820, ZBL1113.93070.
10.1016/j.fss.2006.11.013
Web of Science® Google Scholar
9 Park J. H., Huh S. H., Kim S. H., Seo S. J., and Park G. T., Direct adaptive controller for nonaffine nonlinear systems using self-structuring neural networks, IEEE Transactions on Neural Networks. (2005) 16, no. 2, 414–422, 2-s2.0-15344350446, https://doi.org/10.1109/TNN.2004.841786.
10.1109/TNN.2004.841786
PubMed Web of Science® Google Scholar
10 Wang M., Chen B., and Dai S.-L., Direct adaptive fuzzy tracking control for a class of perturbed strict-feedback nonlinear systems, Fuzzy Sets and Systems. (2007) 158, no. 24, 2655–2670, https://doi.org/10.1016/j.fss.2007.06.001, 2374212, ZBL1133.93350.
10.1016/j.fss.2007.06.001
Web of Science® Google Scholar
11 Ge S. S. and Han T. T., Semiglobal ISpS disturbance attenuation with output tracking via direct adaptive design, IEEE Transactions on Neural Networks. (2007) 18, no. 4, 1129–1148, 2-s2.0-34547101708, https://doi.org/10.1109/TNN.2007.899159.
10.1109/TNN.2007.899159
PubMed Google Scholar
12 Qi R. and Brdys M. A., Stable indirect adaptive control based on discrete-time T-S fuzzy model, Fuzzy Sets and Systems. (2008) 159, no. 8, 900–925, https://doi.org/10.1016/j.fss.2007.08.009, 2401937, ZBL1170.93347.
10.1016/j.fss.2007.08.009
Web of Science® Google Scholar
13 Hyun C.-H., Park C.-W., and Kim S., Takagi-Sugeno fuzzy model based indirect adaptive fuzzy observer and controller design, Information Sciences. (2010) 180, no. 11, 2314–2327, https://doi.org/10.1016/j.ins.2010.02.002, 2602958, ZBL1214.93063.
10.1016/j.ins.2010.02.002
Web of Science® Google Scholar
14 Tong S., Li H.-X., and Wang W., Observer-based adaptive fuzzy control for SISO nonlinear systems, Fuzzy Sets and Systems. (2004) 148, no. 3, 355–376, https://doi.org/10.1016/j.fss.2003.11.017, 2101197, ZBL1057.93029.
10.1016/j.fss.2003.11.017
Web of Science® Google Scholar
15 Leu Y. G., Wang W. Y., and Lee T. T., Observer-based direct adaptive fuzzy-neural control for nonaffine nonlinear systems, IEEE Transactions on Neural Networks. (2005) 16, no. 4, 853–861, 2-s2.0-23044495263, https://doi.org/10.1109/TNN.2005.849824.
10.1109/TNN.2005.849824
PubMed Web of Science® Google Scholar
16 Ciliz M. K., Combined direct and indirect adaptive control for a class of nonlinear systems, IET Control Theory & Applications. (2009) 3, no. 1, 151–159, https://doi.org/10.1049/iet%2Dcta:20070236, 2488051.
10.1049/iet-cta:20070236
Web of Science® Google Scholar
17 Zheng Y. Q., Liu Y. J., Tong S. C., and Li T. S., Combined adaptive fuzzy control for uncertain MIMO nonlinear systems, Proceedings of the American Control Conference (ACC ′09), June 2009, St. Louis, Mo, USA, 4266–4271, 2-s2.0-70449629332, https://doi.org/10.1109/ACC.2009.5160221.
10.1109/ACC.2009.5160221
Google Scholar
18 Ding Q., Chen H., Jiang C., and Chen Z., Combined indirect and direct method for adaptive fuzzy output feedback control of nonlinear system, Journal of Systems Engineering and Electronics. (2007) 18, no. 1, 120–124, 2-s2.0-34347338673, https://doi.org/10.1016/S1004%2D4132(07)60061%2D9.
10.1016/S1004-4132(07)60061-9
Web of Science® Google Scholar
19 Ye X. and Huang J., Decentralized adaptive output regulation for a class of large-scale nonlinear systems, IEEE Transactions on Automatic Control. (2003) 48, no. 2, 276–281, https://doi.org/10.1109/TAC.2002.808480, 1957326.
10.1109/TAC.2002.808480
Web of Science® Google Scholar
20 Hovakimyan N., Lavretsky E., Yang B. J., and Calise A. J., Coordinated decentralized adaptive output feedback control of interconnected systems, IEEE Transactions on Neural Networks. (2005) 16, no. 1, 185–194, 2-s2.0-13844296860, https://doi.org/10.1109/TNN.2004.836198.
10.1109/TNN.2004.836198
PubMed Web of Science® Google Scholar
21 Tong S., Li H. X., and Chen G., Adaptive fuzzy decentralized control for a class of large-scale nonlinear systems, IEEE Transactions on Systems, Man, and Cybernetics, Part B. (2004) 34, no. 1, 770–775, 2-s2.0-0742272544, https://doi.org/10.1109/TSMCB.2003.817039.
10.1109/TSMCB.2003.817039
PubMed Web of Science® Google Scholar
22 Stanković S. S., Stipanović D. M., and Šiljak D. D., Decentralized dynamic output feedback for robust stabilization of a class of nonlinear interconnected systems, Automatica. (2007) 43, no. 5, 861–867, https://doi.org/10.1016/j.automatica.2006.11.010, 2306733, ZBL1117.93057.
10.1016/j.automatica.2006.11.010
Web of Science® Google Scholar
23 Gao Z., Breikin T., and Wang H., Reliable observer-based control against sensor failures for systems with time delays in both state and input, IEEE Transactions on Systems, Man, and Cybernetics Part A. (2008) 38, no. 5, 1018–1029, 2-s2.0-51449095198, https://doi.org/10.1109/TSMCA.2008.923050.
10.1109/TSMCA.2008.923050
Web of Science® Google Scholar
24 Takagi T. and Sugeno M., Fuzzy identification of systems and its applications to modeling and control, IEEE Transactions on Systems, Man and Cybernetics. (1985) 15, no. 1, 116–132, 2-s2.0-0021892282.
10.1109/TSMC.1985.6313399
Web of Science® Google Scholar
25 Yeh K., Chen C.-Y., and Chen C.-W., Robustness design of time-delay fuzzy systems using fuzzy Lyapunov method, Applied Mathematics and Computation. (2008) 205, no. 2, 568–577, https://doi.org/10.1016/j.amc.2008.05.104, 2464000, ZBL1152.93040.
10.1016/j.amc.2008.05.104
Web of Science® Google Scholar
26 Chen C.-W., The stability of an oceanic structure with T-S fuzzy models, Mathematics and Computers in Simulation. (2009) 80, no. 2, 402–426, https://doi.org/10.1016/j.matcom.2009.08.001, 2582122, ZBL1174.86002.
10.1016/j.matcom.2009.08.001
Web of Science® Google Scholar
27 Gao Z. and Zhao Y., Vehicle occupant classification algorithm based on T-S fuzzy model, Procedia Engineering. (2011) 24, 500–504, https://doi.org/10.1016/j.proeng.2011.11.2684.
10.1016/j.proeng.2011.11.2684
Google Scholar
28 Gao Z., Shi X., and Ding S. X., Fuzzy state/disturbance observer design for T-S fuzzy systems with application to sensor fault estimation, IEEE Transactions on Systems, Man, and Cybernetics, Part B. (2008) 38, no. 3, 875–880, 2-s2.0-44849144684, https://doi.org/10.1109/TSMCB.2008.917185.
10.1109/TSMCB.2008.917185
PubMed Web of Science® Google Scholar
29 Goldberger A. L., Fractal mechanisms in the electrophysiology of the heart, IEEE Engineering in Medicine and Biology. (1992) 11, no. 2, 47–52, https://doi.org/10.1109/51.139036.
10.1109/51.139036
CAS PubMed Web of Science® Google Scholar
30 Babloyantz A. and Destexhe A., Is the normal heart a periodic oscillator?, Biological Cybernetics. (1988) 58, no. 3, 203–211, https://doi.org/10.1007/BF00364139, 930347.
10.1007/BF00364139
CAS PubMed Web of Science® Google Scholar
31 Wang X.-M. and Yi-min L. I., Kind of new niche fuzzy control method, Science Technology and Engineering. (2007) 24, 6318–6321.
Google Scholar
32 Li S. P., Dynamical behavior analysis and control of two functional ecosystem, Jiang Su University. (2005) 33–43.
Google Scholar

Citing Literature

All articles

The Hybrid Adaptive Control of T-S Fuzzy System Based on Niche

Abstract

1. Introduction

2. Problem Formulation

3. T-S Fuzzy System Based on Niche

3.1. Description of T-S Fuzzy System Based on Niche

3.2. Niche T-S Model Parameter Optimization Method

4. Hybrid Controller with Supervisory and Compensation Control Scheme

5. Hybrid Adaptive Control of Niche

6. Design of Adaptive Law

7. Simulation

8. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Hybrid Adaptive Control of T-S Fuzzy System Based on Niche

Abstract

1. Introduction

2. Problem Formulation

3. T-S Fuzzy System Based on Niche

3.1. Description of T-S Fuzzy System Based on Niche

3.2. Niche T-S Model Parameter Optimization Method

4. Hybrid Controller with Supervisory and Compensation Control Scheme

5. Hybrid Adaptive Control of Niche

6. Design of Adaptive Law

7. Simulation

8. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information