Fundamental Domains of Gamma and Zeta Functions
Abstract
Branched covering Riemann surfaces (ℂ, f) are studied, where f is the Euler Gamma function and the Riemann Zeta function. For both of them fundamental domains are found and the group of cover transformations is revealed. In order to find fundamental domains, preimages of the real axis are taken and a thorough study of their geometry is performed. The technique of simultaneous continuation, introduced by the authors in previous papers, is used for this purpose. Color visualization of the conformal mapping of the complex plane by these functions is used for a better understanding of the theory. A version of this paper containing colored images can be found in arXiv at Andrian Cazacu and Ghisa.
1. Introduction
Following [1, page 98] we call fundamental region, or fundamental domain of an analytic function f, a domain which is mapped conformally by f onto the whole plane, except for one or more cuts (or slits). It has been proved in [2] that every neighborhood of an isolated essential singularity of an analytic function f contains infinitely many nonoverlapping fundamental domains of f. In fact this is true as well for essential singularities which are limits of poles or of isolated essential singularities [2–5]. The Euler Gamma function and the Riemann Zeta function have ∞ as their unique essential singularity. For the function Gamma, ∞ is a limit of poles, while for the function Zeta it is an isolated essential singularity. It follows that for each one of these functions, the complex plane can be written as a disjoint union of sets whose interiors are fundamental domains, that is, domains which are mapped conformally by the respective function onto the complex plane with a slit. By analogy with the well-known case of elementary functions we use the preimage of the real axis in order to find such a disjoint union of sets. As we will see next, for the function Gamma there is a great similarity with that case, while for the function Zeta a supplementary construction is needed. However, in both cases there is a noticeable difference, namely, while for the elementary functions the slit is the same for every fundamental domain, for the functions Gamma and Zeta it can vary from one fundamental domain to the other. This fact implies some complications when trying to define the cover transformations of the respective branched covering Riemann surfaces. However, the method of fundamental domains allows one to extract a lot of information about the function, in particular about its zeros, as well as the zeros of its derivative and to reveal global mapping properties of the function. Since the fundamental domains are leafs of the corresponding branched covering Riemann surface, the study of the group of cover transformations of the respective surface must start from them. This has been done in [3–5] for some classes of Blaschke products, in [6] for arbitrary rational functions, and in [2] for functions obtained composing the exponential function with a Möbius transformation and we deal here with this topic in Section 3 for the function Gamma and in Section 7 for the function Zeta. Sometimes we need to use a rather descriptive language. This is because we fully adopted Ahlfors opinion [1, page 99]: whatever the advantage of such a representation may be, the clearest picture of the Riemann surface is obtained by direct consideration of the fundamental regions in the z-plane. We apply repeatedly the general method of simultaneous continuations in order to construct the fundamental domains and then color visualization perfected in the previous papers [2–6] in order to illustrate the facts, but never as logical proofs. Expressions indicating motion should be taken only as figures of speech. One can always replace them by static pictures.
Before starting the study of the two functions, let us illustrate the method of fundamental domains on the elementary function w = f(z) = cos z presented in [1, page 98-99], with the interpretation of the facts proper to this method. The function f has the branch points zk = kπ, k ∈ ℤ, where f′(z) = −sinz cancels. The points kπ are simple zeros of f′(z), and therefore the preimage of a small interval of the real axis centered at w = 0 produces at every zk a configuration similar to that of [1, page 133], obtained for n = 2. In the following we will call such a configuration star configuration. Since cos z ∈ ℝ for z ∈ ℝ, one of the arcs of this configuration is an interval of the real axis containing zk and the other one a Jordan arc orthogonal to it at zk. Since cos (kπ + it) = (−1) kcosh t ∈ ℝ, such an arc is necessarily a vertical segment of line. When performing simultaneous continuations over the real axis of these intervals, we obtain the net of [1, Figures 3–11]. Indeed, the continuation of every vertical interval is unlimited, since there is no critical point of cos z in its way, while the continuation of horizontal intervals join two by two at (2k + 1)(π/2), as w reaches 1 and respectively −1. If we denote by Ωj, j ∈ ℤ the vertical strips between x = jπ and x = (j + 1)π, then by the conformal mapping correspondence theorem, every Ωj is mapped conformally by f onto the complex plane with a slit alongside the part of the real axis complementary to the interval (−1,1). The domains Ωj are fundamental domains of the function f. It is obvious that the functions Uk : Ωj − >Ωj+2k, k, j ∈ ℤ defined by Uk(z) = z + 2kπ, are such that f∘Uk(z) = f(z), that is, they are cover transformations of (ℂ, f).
We can obtain Uk by the method we used in [2–6], which will be used also for the functions Gamma and Zeta in Section 3, respectively, Section 7. Let us denote for every z ∈ Ωj and notice that f∘Uk(z) = f(z), . Since for x ∈ (jπ, jπ + π), f(x + 2kπ) = f(x), we have that Uk(x) = x + 2kπ, that is, the functions z − >z + 2kπ and Uk(z) coincide on ℝ∖{jπ}, j ∈ ℤ. Being analytic functions, they must coincide on Ω. We can extend by continuity to every ∂Ωj the functions Uk so defined and they become the analytic functions z − >z + 2kπ with the domain ℂ. They form an infinite cyclic group G1. Every couple of fundamental domains Ωj and Ωj+2k determines a unique cover transformation Uk ∈ G1 which maps conformally Ωj onto Ωj+2k. Indeed, suppose that U is an arbitrary cover transformation of (ℂ, f), that is, U is analytic in ℂ, f∘U(z) = f(z) for every z ∈ ℂ and suppose as well that U maps conformally Ωj onto Ωj+2k. Then . The involution H(z) = −z is also a cover transformation of (ℂ, f) due to the fact that cos (−z) = cos z. We have that H(Ωj) = Ω−j−1 and then Uk∘H(Ωj) = Ω−j−1+2k, thus the cover transformation which maps conformally Ωj onto Ωj+k with arbitrary j, k ∈ ℤ is Up if k = 2p and Um∘H, where m = j + p + 1 if k = 2p + 1. The involution H does not belong to G1. It is an elementary exercise to show that the group G generated by U1 and H is the group of cover transformations of (ℂ, f).
2. Global Mapping Properties of the Euler Gamma Function
It is obvious from this representation that Γ has the set of simple poles A = {0, −1, −2, …} and has no zero. The product converges uniformly on compact subsets of ℂ∖A and therefore w = Γ(z) is a meromorphic function in the complex plane ℂ.
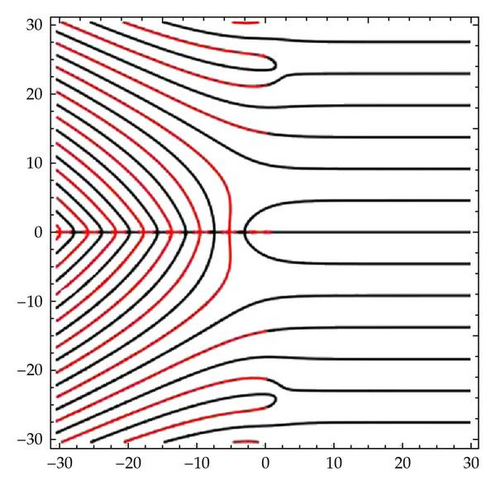
Theorem 2.1. The preimage by Γ of the real axis is formed with infinitely many unbounded curves (components). The components corresponding to the positive and to the negative real half axis alternate and do not cross each other. Some of them start however from the same poles of Γ.
Proof. The number Γ(x) is real for every real x and the graph of the function x → Γ(x) has the lines x = 0, x = −1, x = −2, … as vertical asymptotes [7].
Figure 1 can be found in most of the books of complex analysis serving as texts for graduate studies. We used the online document [7]. It shows the graph of the real function x → Γ(x), which can be used to draw some information about the complex function Γ.
The respective graph has local minima and maxima, which correspond to the points where Γ′(z) = 0. All these points are on the real axis, namely, x0 ∈ (1,2), and for every positive integer n, there is a unique xn ∈ (−n, −n + 1) such that Γ′(xn) = 0. Indeed, let us denote
The sequence (Γn) converges uniformly on compact sets of ℂ∖A to Γ. It can be easily checked that for every n ∈ ℕ, the equation is equivalent to an algebraic equation of degree n + 1 and has exactly n + 1 real solutions situated one in every interval (−k, −k + 1), k = 1,2, …, n and one in the interval (0, ∞). Therefore cannot have nonreal solutions. Since converges in turn uniformly on compact subsets of ℂ∖A to Γ′, we infer that every interval (−n, −n + 1), n ∈ ℕ, contains exactly one solution xn of the equation Γ′(z) = 0, and there is one more solution x0 ∈ (1,2). There are no other solutions of this equation. It is also obvious that
Based on this information, we can reveal the preimage by Γ of the real axis, denoted Γ−1(ℝ). Since all xn, n ≥ 0 are simple roots of Γ′(z) = 0, in a neighborhood Vn of every xn, Γ(z) has the form [1, page 133]
By the Big Picard Theorem, the preimage by Γ of Γ(xn) is for every n a countable set of points. The formula (2.1) shows that , thus this set is of the form {zn,k}∪, k = 0,1, 2, … having the unique accumulation point ∞. Suppose that zn,0 is xn. Then by (2.5), the preimage of a small interval (an, bn) of the real axis centered at Γ(xn) is the union of an interval (αn, βn)∋xn of the real axis and another Jordan arc γ−n orthogonal to the real axis at xn (let n = 2 in [1, Figure 4.8]) and symmetric with respect to the real axis, as well as infinitely many other Jordan arcs passing each one through a zn,k, respectively, , k ∈ ℕ. Simultaneous continuations [6] over the real axis of these preimages have as result the interval (−n, −n + 1) for (αn, βn). Indeed, −n and −n + 1 being poles for Γ, we have that for x ∈ (xn, xn+1), x − >−n and x − >−n + 1 if and only if Γ(x)−>±∞. The continuations have as result an unbounded curve crossing the real axis at xn for γ−n and infinitely many other unbounded curves passing each one through zn,k, or through for k ∈ ℕ. The unboundedness is guaranteed by the fact that the continuation is unlimited, since there are no poles of Γ off the real axis. We use the same notation γ−n for the curves passing through xn and γn,k, respectively, for the others. We notice that these curves cannot intersect each other, since in such a point of intersection z0 we would have Γ′(z0) = 0, which is excluded. Also, the curves γn,k, and , k ≠ 0 cannot intersect the real axis, for a similar reason. We call these curves components of Γ−1(ℝ).
Since 0 is a lacunary value for Γ, there can be no continuity (except at the poles) between the preimage of the real positive half axis and negative half axis, which means that each one of these components is unbounded. Moreover, if we use two different colors, say black and red for the preimage of the negative, respectively, positive real half axis, then these colors must alternate, since minima and maxima for the real function Γ(x) are alternating. Hence the intervals (αn, βn) have alternating colors, which imply alternating colors for γ−n. Indeed, due to the continuity of Γ, except at the poles, change of color can happen only there, which means that the color of γ−n and that of (αn, βn) must agree. Thus, the colors of γ−n are alternating. On the other hand, if a point travels on a small circle centered at origin in the w-plane (w = Γ(z)), it will meet alternatively the positive and the negative half axis, which implies alternation into the colors of γn,k. If xn were multiple zeros of Γ′ then more than one curve γ−n of the same color would start from xn violating this rule of color alternation. Thus, as previously stated, Γ′ has only simple zeros.
We notice that, by Formula (2.1), if z = x + iy ∈ γn,k, or then lim x→−∞ Γ(z) = 0 and lim x→+∞ Γ(z) = ∞. Therefore, when z describes any γn,k or its image Γ(z) describes the positive or the negative real half axis, the correspondence z − >Γ(z) being bijective there. Also, if z ∈ γ−n, then lim x→−∞ Γ(z) = 0.

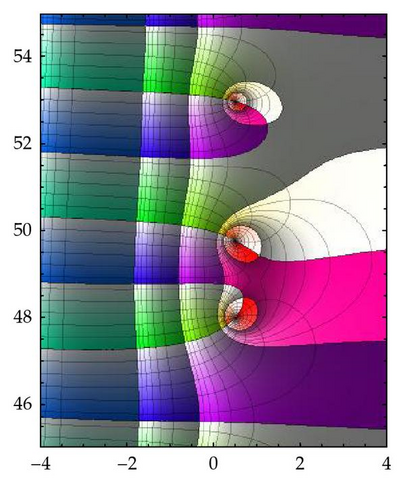
The preimage of the real axis seen in the computer generated picture in Figure 2 illustrates these affirmations. These limits will help next to prove the following theorem.

Figure 2 shows the computer generated preimage by Γ of the real axis. Since zero is a lacunary value, red curves meet black curves only at the poles.
Theorem 2.2. The complex plane ℂ can be written as a disjoint union of sets bounded by the components of Γ−1(ℝ) such that the interior of each one of them is a fundamental domain of Γ. These domains accumulate to infinity and only there. The function Γ extended to the boundary of each one of them maps them surjectively onto .
Proof. Let us introduce first some notations. We denote by Ω−n the domain bounded by γ−n−1 and γ−n, n = 0,1, 2, …. Let Ω1 be the domain from the upper half plane bounded by γ0, the interval [x0, +∞) and the second component of Γ−1(ℝ) situated in the upper half plane and which does not intersect the real axis, Ω2 be the domain bounded by this component and the fourth one and so forth. We denote by , n ∈ ℤ the domain symmetric to Ωn with respect to the real axis. Obviously, for n ≤ 0, we have .
Let us notice that, by the conformal correspondence theorem, the image by Γ of every Ω−n, n = 0,1, 2, … is the complex plane with a slit L−n alongside the real axis, from Γ(xn−1) to Γ(xn), while the image of every Ωn and of every , n ∈ ℕ is the complex plane with a slit Ln = [0, +∞) (the same for every n ∈ ℕ). It is obvious that the union of the closures of the domains Ωn and , n ∈ ℤ, is the complex plane and if the common boundary of every adjacent couple of them is counted just once, we obtain a disjoint union. As proven in [2], for an arbitrary analytic function having the unique essential singularity at ∞, these domains accumulate to ∞ and only there in the sense that every neighborhood V of ∞ contains infinitely many domains Ωn and and any compact set in ℂ intersects only a finite number of these domains. Finally, since for every Ωn and every w ≠ 0 there is such that w = Γ(z) (z ∈ Ωn if w is not on the corresponding slit and z ∈ ∂Ωn if w is on the slit) we have that is surjective. The same is true for every .
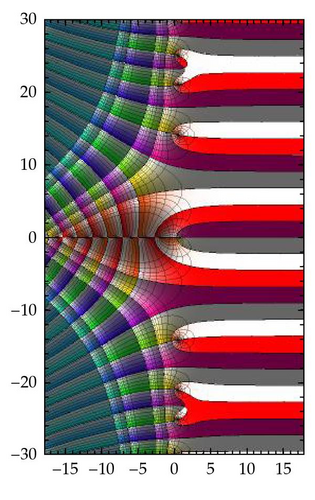
Figure 3 represents a visualization of the way the fundamental domains are mapped conformally by Γ onto the complex plane with a slit. Figure 3(a) is obtained by taking preimages of colored annuli centered at the origin of the w-plane Figures 3(b)–3(d) and imposing the same color, saturation, and brightness on the preimage of every point. The very big annuli Figure 3(d) have preimages around the poles, and this is obvious when looking at the colored pictures on the web project. However, the same colors appear for z = x + iy with big positive values of x characterizing the fact that lim x→+∞ Γ(x + iy) = ∞. Coupled with the preimage of orthogonal rays to these annuli, the picture in Figure 3(a) gives a pretty accurate graphic of the function.
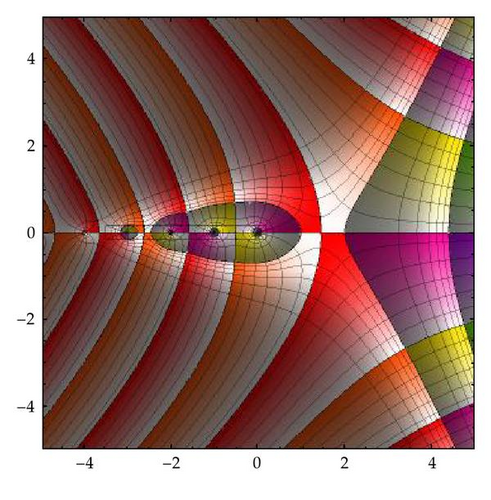
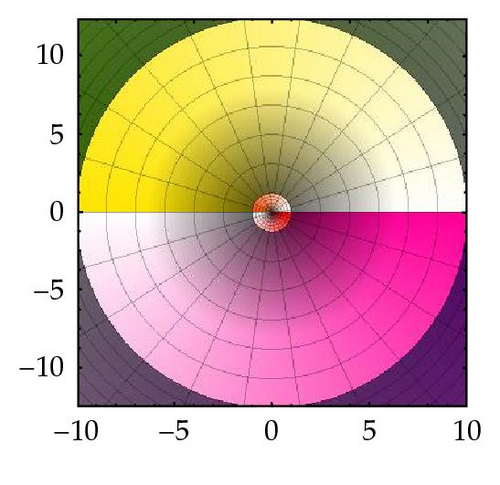
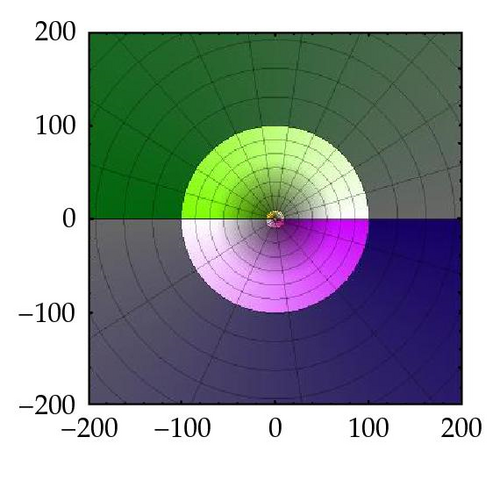
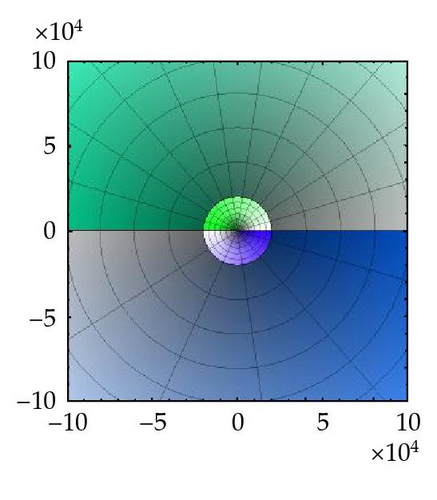
3. The Group of Cover Transformations of (ℂ, Γ)
The results from the previous section allow one to treat (ℂ, Γ) as a branched covering Riemann surface of whose leafs are the fundamental domains Ωn. We call cover transformation of (ℂ, Γ) an analytic function U : ℂ∖E − >C∖E such that Γ∘U(z) = Γ(z), where E is a countable set of slits. The cover transformations of (ℂ, Γ) form a group.
Theorem 3.1. The group G of cover transformations of (ℂ, Γ) has two generators: an involution and a transformation generating an infinite cyclic subgroup of G.
Proof. We notice that Uk are conformal mappings in ℂ∖E since the branch points xn belong to E. For every k ∈ ℤ we have Γ∘Uk(z) = Γ(z), z ∈ ℂ∖E. Moreover, Uk(Ωj∖E) = Ωk+j∖E, .
Finally we define , j ∈ ℤ by
It can be easily seen that H is an involution and Γ∘H(z) = Γ(z), , , , and so forth. We notice also that
This shows in particular that U1 generates an infinite cyclic subgroup. It is an elementary exercise to show that the group generated by U1 and H is the group of covering transformations of (ℂ, Γ).
4. The Riemann Zeta Function
The Riemann Zeta function is one of the most studied transcendental functions, in view of its many applications in number theory, algebra, complex analysis, and statistics as well as in physics. Another reason why this function has drawn so much attention is the celebrated Riemann conjecture regarding its nontrivial zeros, which resisted proof or disproof until now.
We are mainly concerned with the global mapping properties of Zeta function. The Riemann conjecture prompted the study of at least local mapping properties in the neighborhood of nontrivial zeros. There are known color visualizations of the module, the real part and the imaginary part of Zeta function at some of those points, however they do not offer an easy way to visualize the global behavior of this function.
5. The Preimage by ζ of the Real Axis
We will make use of the preimage by ζ of the real axis in order to find fundamental domains for the branched covering Riemann surface (ℂ, ζ) of . By the Big Picard Theorem, every value z0 from the z-plane (z = ζ(s)), if it is not a lacunary value, is taken by the function ζ in infinitely many points sn accumulating to ∞ and only there. This is true, in particular, for z0 = 0.
A small interval I of the real axis containing 0 will have as preimage by ζ the union of infinitely many Jordan arcs γn,j passing each one through a zero sn of ζ, and vice versa, every zero sn belongs to some arcs γn,j. Since ζ(σ) ∈ ℝ, for σ ∈ ℝ, and by the formula (4.5), the trivial zeros of ζ are simple zeros and the arcs corresponding to these zeros are intervals of the real axis, if I is small enough. For such an arc γn,j the subscript j is superfluous. Due to the fact that ζ is analytic (except at s = 1), between two consecutive trivial zeros of ζ, there is at least one zero of the derivative ζ′, that is, at least one branch point of (ℂ, ζ). Since we have also ζ′(σ) ∈ ℝ for σ ∈ ℝ, if we perform simultaneous continuations over the real axis of the components included in ℝ of the preimage of I, we encounter at some moments these branch points and, as in the case of Γ, the continuations follow on unbounded curves crossing the real axis at these points.
The argument for the unboundedness of these curves and of the fact that they have no common points is the same as in the case of Γ. Only the continuation of the interval containing the zero s = −2 stops at the unique pole s = 1, since lim σ↗1ζ(σ) = ∞. Similarly, if instead of z0 = 0 we take another real z0 greater than 1 and perform the same operations, since lim σ↘1ζ(σ) = ∞, the continuation over the interval (1, ∞) stops again at s = 1. In particular, the preimage by ζ of this interval can contain no zero of the Zeta function. Thus, if we color red the preimage by ζ of the negative real half axis and let black the preimage of the positive real half axis, then all the components of the preimage of the interval (1, +∞) will be black, while those of the interval (−∞, 1) will have a part red and another black, the junction of the two colors corresponding to a zero (trivial or not) of the function Zeta.
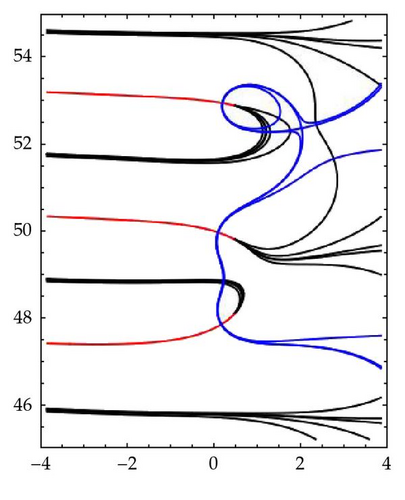
Figure 4 represents the preimage of the real axis in which the components previously described are visible. We notice the existence of branch points on the negative real half axis and their color alternation, as well as the trivial zeros between them. Since these zeros are those of sinπs/2, they are simple zeros and consequently there is no branching at them. Some nontrivial zeros are also visible.
The red and the black unbounded curves passing through the branch points on the real axis cannot meet elsewhere (except at ∞). Indeed, such an intersection point would be a zero of ζ and the two curves would bound a domain which is mapped conformally by ζ onto the complex plane with a slit alongside the real axis from the image of one branch point to the image of the next one. Yet such a domain should contain a pole of the function, which is impossible.
The components of the preimage of the real axis passing through nontrivial zeros form a more complex configuration. This configuration has something to do with the special status of the value z = 1. Let us introduce notations which will help making some order here and justifying the configurations shown on the computer generated picture, Figure 4. Due to the symmetry with respect to the real axis, it is enough to deal only with the upper half plane. Let x0 ∈ (1, +∞) and let sk∈ζ−1({x0})∖ℝ. Continuation over (1, +∞) from sk is either an unbounded curve such that lim σ→+∞ ζ(σ + it) = 1, by (4.2), and lim σ→−∞ζ(σ + it) = +∞, where s = σ + it∈, or there are points u such that ζ(u) = 1, thus the continuation can take place over the whole real axis. We notice that it is legitimate to let σ tend to −∞ on , since if supremum of |s| were reached for a finite s0, then that s0 would be a pole of ζ, which is impossible.
The existence of and that of u with ζ(u) = 1 is attested by computation. The graphs just illustrate this computational fact. However, they hint to something more, namely, that the number of these entities is infinite. This can be proved rigorously. Indeed, suppose that for a no other unbounded curve situated above it is mapped by ζ onto the interval (1, +∞). For a point s0 above let z0 = ζ(s0) and let z ∉ (1, ∞) be arbitrary. We can connect z0 and z by a Jordan arc γ not intersecting the interval (1, ∞). If we perform continuation by ζ over γ starting from s0 we arrive at a point s above such that ζ(s) = z. Then the closed domain above would be mapped by ζ onto the whole complex plane, which is absurd.
Theorem 5.1. Consecutive curves and form strips Sk which are infinite in both directions. The function ζ maps these strips (not necessarily bijectively) onto the complex plane with a slit alongside the interval [1, +∞) of the real axis.
Proof. Indeed, if two such curves met at a point s, one of the domains bounded by them would be mapped by ζ onto the complex plane with a slit alongside the real axis from 1 to ζ(s). Such a domain must contain a pole of ζ, which cannot happen.When a point s travels on and leaving the strip at left, ζ(s) moves on the real axis from 1 to ∞ and back.
When the continuation can take place over the whole real axis, we obtain unbounded curves each one containing a nontrivial zero of ζ and a point u with ζ(u) = 1. Such a point u is necessarily interior to a strip Sk since the borders of every Sk and ζ−1({1}) are disjoint.
Theorem 5.2. There are infinitely many points u with ζ(u) = 1.
Proof. Let us denote by uk,j the points of Sk for which ζ(uk,j) = 1, by Γk,j the components of ζ−1(ℝ) containing uk,j and by sk,j the nontrivial zero of ζ situated on Γk,j. When lim σ−>+∞ ζ(σ + it) = 1, σ + it ∈ Γk,j, we assign (by abuse!) the value ∞ to the respective uk,j. We will see later that every Sk contains a unique Γk,j with this property. The monodromy theorem assures that there is a one to one correspondence between sk,j (counted with multiplicities if they exist), uk,j, and Γk,j. If sk,j is a zero of order m, then m curves Γk,j cross at that zero making a star configuration. The color alternation rule is still respected. Since there are infinitely many nontrivial zeros of ζ, it follows that there are infinitely many points uk,j.
Let us notice that every strip Sk can contain only a finite number jk of nontrivial zeros, since they belong also to the critical strip and then infinitely many of them would have an accumulation point in ℂ, which is not allowed (see [1, page 127]).
Consequently, the given Sk contains also exactly jk points uk,j with ζ(uk,j) = 1 (including ∞) and exactly jk components Γk,j. This analysis suggests that the value z = 1 behaves simultaneously like a lacunary value since lim σ→+∞ζ(σ + it) = 1, and like an ordinary value, since ζ(uk,j) = 1. We can call it quasilacunary.
Theorem 5.3. When the continuation takes place over the whole real axis, the components Γk,j are such that the branches corresponding to both the positive and the negative real half axis contain only points σ + it with σ < 0 for |σ| big enough.
Proof. Indeed, a point traveling in the same direction on a circle γ centered at the origin of the z-plane meets consecutively the positive and the negative real half axis. Thus the preimage of γ should meet consecutively the branches corresponding to the preimage of the positive and the negative real half axis. It can be easily seen that two components Γk,j can meet only at multiple nontrivial zeros of ζ (if they exist!) and no Γk,j can intersect any . Thus, those components of preimages of circles centered at the origin which cross a , will continue to cross alternatively red and black components of the preimage of the real axis. These last components are mapped by ζ either on the interval (−∞, 1), or on the whole real axis.
On the other hand, due to the continuity of ζ on , if a component of ζ−1(γ) meets a , it should cross it and all , l ≥ 1 meeting consecutively the branches corresponding to the preimage of the positive and of the negative real half axis. Such an alternation is possible only if the previously stated condition on σ is fulfilled.
Theorem 5.4. For every k there is a unique component of ζ−1(ℝ) situated in the strip Sk, say Γk,0, which is mapped bijectively by ζ onto (−∞, 1), that is, such that lim σ−>+∞ζ(σ + it) = 1, and lim σ−>−∞ζ(σ + it) = −∞, σ + it ∈ Γk,0.
Proof. The strip Sk is mapped by ζ onto the complex plane with a slit alongside the real axis from 1 to +∞. The mapping is not necessarily bijective. For every x0 ∈ (1, +∞), there is and such that ζ(sk) = ζ(sk+1) = x0. Let us connect sk and sk+1 by a Jordan arc η interior to Sk (except for its ends). Then ζ(η) is a closed curve Cη bounding a domain D or a Jordan arc travelled twice in opposite directions, in which case D = ∅. We need to show that Cη intersects again the real axis, in other words η intersects the preimage of (−∞, 1). Indeed, otherwise Cη would be contained either in the upper or in the lower half plane. Then ζ would map half of the strip Sk bounded by η and the branches of and corresponding to σ → +∞ onto with a slit alongside the real axis from x0 to 1. We can take x0 big enough such that this half strip contains no zero of ζ, which makes impossible such a mapping.
Let us show that Sk cannot contain more than one component of the preimage of (−∞, 1). Indeed, if there were more, we could repeat the previous construction with two consecutive such components, taking sk and sk+1 with ζ(sk) = ζ(sk+1) > 0 and arrive again to a contradiction.
Figure 5 represents dynamically the birth of a strip. We picked up the strip S5 with t in the range of 45 to 55 on the imaginary axis. It shows consecutively domains which are mapped conformally by ζ onto the sectors centered at the origin with angles from α to 2π−α, where α takes, respectively, the values of π/30, π/100, and π/1000. It is visible how the border of such a domain splits into , and Γ5,0 previously defined as α → 0. Between them can be seen the curves Γ5,−1 and Γ5,1.
Theorem 5.5. Every strip Sk contains a unique unbounded component of the preimage of the unit disc.
Proof. Indeed, to see this it is enough to take the preimage of a ray making an angle α with the real half axis and let α → 0. A point s ∈ ζ−1({z}) with |z| = 1, argz = α, tends to ∞ as α → 0 if and only if the corresponding component of the preimage of that ray tends to Γk,0 as α → 0, which happens if and only if the component of the preimage of the closed unit disc containing the point s is unbounded. The uniqueness of Γk,0 implies the uniqueness of such a component. Obviously, the respective unbounded component can contain besides sk,0 some other nontrivial zeros of ζ, as it appears on the pictures in Figures 6 and 7. We notice that some of Sk contain bounded components of the preimage of the unit disc and some others do not contain such components, and this is another experimental fact. For example S5, S7, S10 do contain one bounded component, while the others in this range do not. However, it looks like the existence of bounded components becomes a rule for k big enough, when there can be several bounded components of the preimage of the unit disc in every strip Sk (see Figure 7). We have found (see [8]) that the strip corresponding to t ∈ (10,008; 10,016) has three bounded components of the preimage of the unit circle, one of which contains two nontrivial zeros and the strip corresponding to t ∈ (1,000,002; 1,000,012) has six of them, one containing three nontrivial zeros.
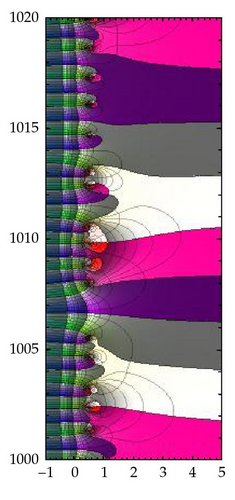
We do not try to answer the question “why is it so?". On the other hand it is obvious that, as ρ increases past 1, all the unbounded components of the preimage of γρ fuse into a unique one intersecting every . Since lim σ−>−∞ ζ(σ + it) = +∞ as , the points of intersection of this component with every move to the left as ρ increases, such that the bounded components of the preimage of γρ will touch the unbounded one for some values of ρ fusing with it. It might be interesting to know what is the greatest value of ρ (if any!) for which such a fusion takes place.
Theorem 5.4 does not exclude the possibility of Sk containing several other components Γk,j, j ∈ Jk ⊂ ℤ, which are mapped bijectively by ζ onto the whole real axis. Every one of the components Γk,j, contains a nontrivial zero of ζ and, for j ≠ 0, intersects the preimage of the unit circle in two points corresponding to z = −1 and z = 1. There is no point corresponding to z = 1 on Γk,0. Using the approximation of ζ by the partial sums from (4.3), it can be easily shown that for s = σ + it ∈ Γk,j, j ≠ 0, we have σ → −∞ as ζ(s) → ∞. If Sk contains jk components Γk,j we will call it jk-strip. Every jk-strip contains jk nontrivial zeros of ζ (counted with multiplicities, if they exist). Let us denote them by sk,j = σk,j + itk,j. The computer generated data suggest that the height of every strip Sk is approximately 10. A rigorous proof of this fact and an estimation of jk could bring us to an alternative formula for the estimate of the number N(T) of nontrivial zeros of ζ for t ∈ (0, T).
6. Fundamental Domains of the Riemann Zeta Function
The preimage of circles centered at the origin of the z-plane are useful in the study of the configuration of the components Γk,j. A circle with radius less than 1 has bounded components of its preimage containing one or several zeros. All the components of the preimage of the respective circle must meet alternatively components of the preimage of the positive and negative real half axis. Indeed, a point moving in the same direction on a circle centered at the origin will cross alternatively the positive and the negative real half axis. A corollary of this fact is as follows
Theorem 6.1. All the real zeros of ζ′ are simple zeros and they alternate with the trivial zeros of ζ.
Proof. Indeed, since the color change can happen only at a zero of ζ (and at s = 1) and the trivial zeros of ζ are simple, if several branches of the preimage of the positive or of the negative half axis crossed the real axis at the same point or in different points between consecutive trivial zeros of ζ, the color alternation for those branches would be violated.
A way to envision this violation is to keep in mind that the function ζ is locally conformal, except at the branch points, hence the orthogonal net formed with the real axis and a family of circles centered at the origin of the z-plane is the image by ζ of an orthogonal net in which the components of the preimages of the negative and of the positive half axis must alternate when travelling in the same direction on each one of the components of the preimage of those circles.
The preimages of circles centered at the origin of radius less than or equal to 1 cannot meet the curves (which belong to the preimage of (1, +∞)). We will see later that there are bounded components of the preimage of circles of radius greater than 1, but close to 1 with the same property. However, the unbounded components of the preimages of these circles must intersect every , which are then counted in the alternation of the branches of the preimage of the positive and negative half axis.
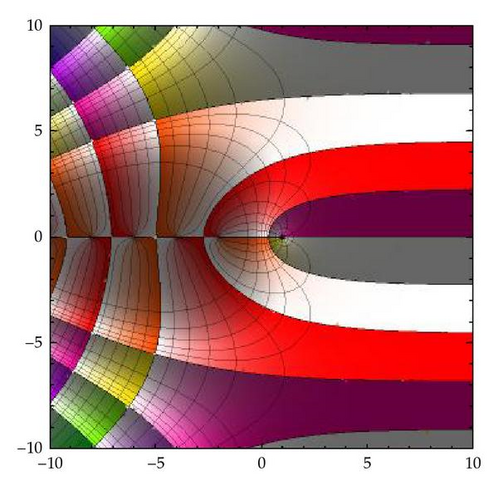
The mesh they give rise of is formed with quadrilaterals of different conformal modules, which are the images by ζ of quadrilaterals from the s-plane having the same conformal modules and colors with the same saturation and brightness for the corresponding points. The preimage of the unit disc in the next pictures is formed with domains colored red and white (which is in fact degraded red). Several unbounded components of it are visible in Figures 6 and 7, one containing trivial zeros and the others containing nontrivial zeros. For the fundamental domains containing nontrivial zeros, the parts mapped onto the unit disc and onto different annuli interior or exterior to the unit disc are obvious. The same is true for the fundamental domains containing nontrivial zeros, except for those unbounded parts which are mapped onto a small quadrilateral around the point z = 1. More exactly, in the respective pictures, this quadrilateral is that bounded by rays of angle ±π/6 and by the circles of radius 0.8 and, respectively, 2.5 in Mathematica′s grid. We will make next more precise statements about this mapping.
Figure 6 shows the preimages by ζ of the colored annuli from Figure 3 intersecting the preimage of the real axis in the box [−15,15]×[−30,30] in Figure 6(a) with a zoom on the origin in Figure 6(b). The curves on the left side in Figure 6(a) crossing alternatively components of the preimage of the negative and positive real half axis are preimages of circles centered at the origin with radius greater than 1. The preimage of annuli coupled with the preimage of some orthogonal rays give a pretty accurate description of the mapping.
Figure 7 displays a 7-strip situated in the area corresponding to t ∈ (1005,1016). There are clearly visible two components of the preimage of the unit circle: one bounded situated in the upper part of the strip containing a unique nontrivial zero, and one unbounded containing the other 6 nontrivial zeros. We notice in the strip above this 7-strip two bounded components of the preimage of the unit circle. It appears that the number of these bounded components in consecutive strips also increases (on the average) with t.
Theorem 6.2. If Sk is a jk-strip with jk ≥ 2, then it contains at least one and at most jk − 1 zeros (counted with multiplicities, if any) of the derivative ζ′.
Proof. Let us notice first that S1 is a 1 strip, thus the derivative ζ′ cannot have any zero in S1. This is attested by the fact that ζ maps conformally S1 onto the complex plane with a slit alongside the interval (1, +∞) of the real axis; therefore there cannot be branch points of ζ in S1. The strips S2 and S3 are 2 strips, S4, S5, and S6 are 3 strips, and so forth. Let γρ be a circle |z| = ρ for a small enough value of ρ, such that the preimage of γρ consists of disjoint closed curves. If such a curve ηk,j is in the critical strip, then we can suppose that it contains a unique nontrivial zero sk,j of ζ. Suppose first that sk,j belongs to the unbounded component of the preimage of the unit disc. As ρ increases the corresponding curves ηk,j expand such that for some value of ρ,ηk,j will meet another curve of the same type at point vk,h(j). Indeed, starting with S2 there are at least two such curves and each one will cover, as ρ varies from 0 to 1, the whole component of the preimage of the unit disc. It is obvious that vk,h(j) must be a branch point of ζ, due to the fact that ζ takes the same value in points situated on different curves ηk,j in every neighborhood of vk,h(j). Since vk,h(j) cannot be a multiple pole, we have necessarily that ζ′(vk,h(j)) = 0. All the zeros of ζ′ we could visit were simple zeros. However, up to now, nothing allows us to say that this should always be the case. If more than two curves ηk,j touch at the same point vk,h(j) for a ρ = ρ0, then that point must be a multiple zero of ζ′. Let us see what global mapping properties of ζ can be described in such a case. At a multiple zero vk,h(j) of order m of ζ′ the preimage of the segment of line γ from 1 to ζ(vk,h(j)) produces a star configuration with m + 1 arcs converging to vk,h(j). The simultaneous continuation of those arcs over γ must end up in points uk,j with ζ(uk,j) = 1, or at ∞, as lim σ−>+∞ ζ(σ + it) = 1. The theorem of domain preservation (which says that an analytic function in an open and connected set maps that set onto another one of the same type) assures that the respective uk,j are different. Thus, if m > 1, at least two of these arcs must turn to different points uk,j with ζ(uk,j) = 1. It is obvious that those uk,j are consecutive on the preimage of the unit circle. Then the domains bounded by those arcs and the preimage of the unit circle is mapped conformally by ζ onto the unit disc with a slit alongside γ. Consequently, the domains bounded by the preimage of the interval [1, +∞) and those arcs are mapped conformally by ζ onto the complex plane with a slit alongside this interval followed by a slit alongside γ.
When ρ increases past ρ0 the respective ηk,j fuse into a unique closed curve. This last curve can meet for a ρ > ρ0 another ηk,j or another curve obtained by fusion and so on until we obtain a curve turning around all the zeros of ζ contained in the respective unbounded component of the preimage of the unit disc. The fact that these curves must fuse and not simply intersect each other is obvious. Indeed, due to the continuity of ζ if ηk,j crossed each other, this would have happen at points as close as we wanted of vk,h(j), which is impossible, since the zeros of ζ′ are isolated points. Finally, since for a v in the preimage of the unit disc with ζ′(v) = 0, the preimage of γρ passing through v must contain at least two different components ηk,j, we conclude that the points vk,h(j) are the only zeros of ζ′ having images by ζ situated in the unit disc.
The preimage of any circle γρ with ρ > 1 contains a unique unbounded component obtained by the fusion of all unbounded components when increasing ρ past 1. This component intersects every since γρ intersects the interval (1, +∞). As ρ increases, the respective component moves to the left covering unbounded domains in every Sk which are mapped by ζ onto a small quadrilateral situated in the neighborhood of the point z = 1 and exterior to the unit circle. The real axis divides this quadrilateral into two quadrilaterals, the preimages of which have unbounded components. The respective components are curvilinear 4n-gones with two unbounded sides, one corresponding to a segment of the real axis and the other one to an arc of the unit circle having both one end in z = 1. For bigger values of ρ (ρ = 2.5 is big enough!) these domains are the quadrilaterals which can be seen in Figures 6 and 7 on the left of the critical strip. The unbounded component of the preimage of γρ touches bounded components of the preimage of γρ for some values of ρ in zeros of ζ′ which project by ζ outside the unit disc. Figures 6 and 7 do not give us an accurate description of the intermediate positions of this component at the right of critical strip, since the increment of ρ is too rough and the range of t is too small. Such a position can be seen in the supplementary pictures of [8] for t = 1,000,025. There the preimage of γρ has a bounded component for ρ ≈ 3.5 and the unbounded component of γ2.5 is on its right side.
A zero of ζ′ in some strip Sk with image by ζ outside the unit disc cannot belong to components of preimages of γρ with different values of ρ, due to the fact that ζ is a single valued function. The only way for a branch point of ζ to have the image on a with ρ0 > 1 is for it to be the touching point of two bounded components of the preimage of or of a bounded and unbounded component of the preimage of . When increasing ρ past ρ0 the two components fuse into a unique one, which is unbounded if the two components were not both bounded. To facilitate the counting of the zeros of ζ′ in Sk, we form a full binary tree in which the leafs are the zeros of ζ and the internal vertices are the zeros of ζ′,corresponding to the points where the curves ηk,j come into contact. If a zero of ζ′ is multiple of order m, we can build the tree such that it generates m internal vertices. It follows easily by recursion that if the number of leafs is jk, then the number of internal vertices is jk − 1 and the conclusion of the theorem is obvious.
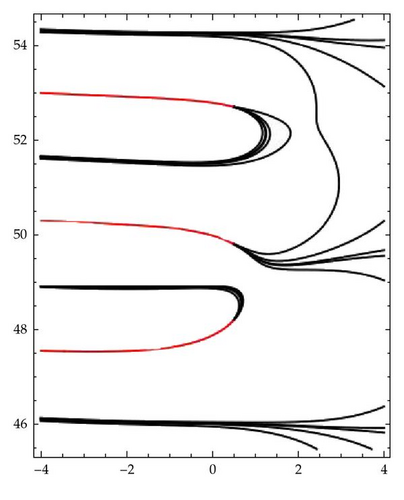
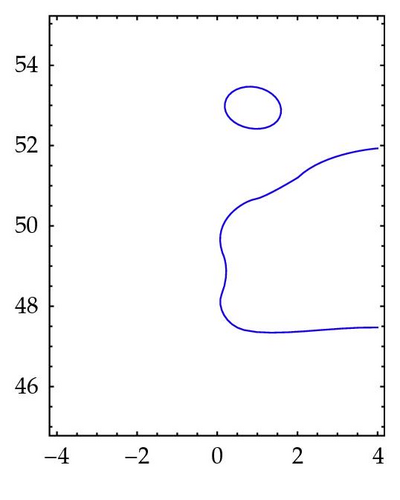
Figure 8 illustrates the situation where a component of the preimage of γρ has a self-intersection point. In the box [−4,4]×[45,55], Figure 8(a), two components of the preimage of the circle γρ with ρ = 1 are visible: a bounded one on the upper part of the box, containing a unique nontrivial zero of ζ and an unbounded one covering the right lower corner of the box and containing two nontrivial zeros. As the radius ρ takes values greater than 1, the two components expand, Figures 8(b), 8(c), touching each other for ρ = ρ0 ≈ 1.042 in Figure 8(b). We can interpret the preimage of as having a unique unbounded component with a self-intersection point v5,2. It borders three domains, one bounded and two unbounded. As ρ takes values greater than ρ0, the bounded component opens, Figure 8(c), and we get a unique unbounded component separating the plane into two unbounded domains. It is obvious that v5,2 is a branch point of ζ. Indeed, the arcs of the preimage of situated in a small neighborhood of v5,2 are mapped by ζ onto an arc of containing ζ(v5,2). Thus ζ′(v5,2) = 0 and v5,2 is a simple zero of ζ′. Figure 8(e) is a superposition of Figures 5 and 8(a)–8(c) showing the domains mapped by ζ outside the circles γρ and the sectors in Figure 5. It helps to locate v5,2 on Figure 8(d).
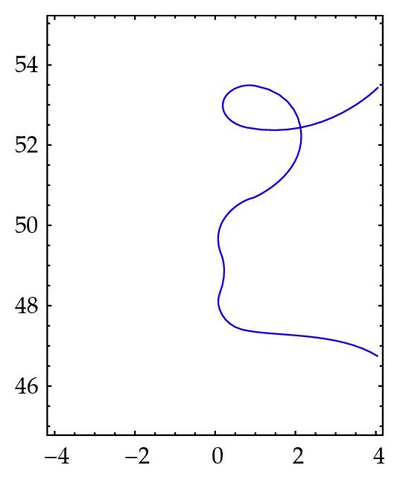
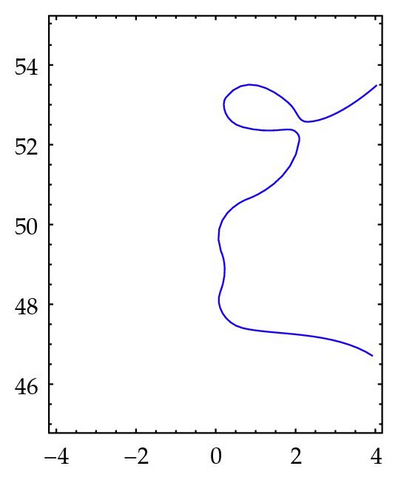
It is obvious that the scenario described in Figure 8 repeats itself in every strip Sk which contains bounded components of the preimage of γρ with ρ ≥ 1. Some of the vk,h(j) can be obtained as the touching points of these components as ρ increases. In other words, to every uk,j, except for uk,0( = ∞), corresponds a branch point vk,h(j) of ζ situated in the strip Sk. We notice that components of the preimage of γρ with different values of ρ cannot intersect, since this would contradict the single value nature of ζ. Thus, ζ cannot have branch points other than vk,h(j). The way vk,h(j) have been obtained suggests that they are all situated in the right half plane. We have no knowledge of a proof of this affirmation, nor could we provide a proof of it, hence we make the following.
Conjecture 6. All the nonreal zeros of ζ′ are situated in the right half plane.
In order to build fundamental domains for ζ it is enough to deal with an arbitrary strip Sk. Since every simple nontrivial zero of ζ from Sk belongs to one and only one fundamental domain, and every multiple zero of order m, if it exists, must be a common boundary point of exactly m fundamental domains, it is important to know as much as possible about the branch points of ζ and the existence of multiple zeros. In our knowledge, there are just statistical estimations of the proportion of such zeros [9], and this happens only if the Riemann hypothesis were true. This topic transcends the scope of the present paper and a separate study will be devoted to it.
Theorem 6.3. If Sk is a jk-strip, then Sk is the disjoint union of exactly jk substrips, whose interiors are fundamental domains of ζ.
Proof. The only 1 strip in the upper half plane is S1 and it has no branch point of ζ. It is by itself a fundamental domain of ζ and it is mapped conformally by ζ onto the complex plane with a slit alongside [1, +∞). As we have seen in Theorem 5.2, a jk-strip Sk contains exactly jk components Γk,j of ζ−1(ℝ) and exactly jk points uk,j with ζ(uk,j) = 1, and one of these points being considered (by abuse!) as ∞ (which is the only one for S1). For k ≥ 2, there is a number hk,1≤hk ≤ jk − 1 of branch points vk,h(j) of ζ in Sk. If we connect all the points ζ(vk,h(j)) to the point z = 1 by a segment of line γk,h(j) (which is the interval [0,1] when sk,j is a multiple zero of ζ) and follow the protocol of Theorem 6.2, we obtain jk − 1 arcs or unbounded curves Lk,j belonging to Sk which are projected by ζ onto different γk,h(j). The arcs Lk,j connect consecutive points uk,j via a point vk,h(j), while the unbounded curves go from uk,j to ∞ via a point vk,h(j). For every vk,h(j) at most one of the arcs Lk,j containing vk,h(j) can be unbounded. There cannot be unbounded Lk,j containing a vk,h(j) when this point is between two embraced curves Γk,j, as in the case where t ∈ (1,000,001; 1,000,002) appearing in supplementary pictures of [8]. By the conformal correspondence theorem, the sub-strips formed by consecutive arcs or unbounded curves Lk,j and consecutive components of ζ−1{[1, +∞)} are mapped conformally by ζ onto the complex plane with a slit alongside [1, +∞) followed by at most three slits alongside intervals starting at z = 1 and ending in some ζ(vk,h(j)). Every such sub-strip contains a unique sk,j, if it is a simple zero of ζ, and if sk,j is a multiple zero of order m then exactly m sub-strips meet at sk,j. Thus the number of sub-strips of Sk is exactly jk. If the joint boundary of every couple of adjacent sub-strips is counted just once, Sk is the disjoint union of these sub-strips, which proves completely the theorem.
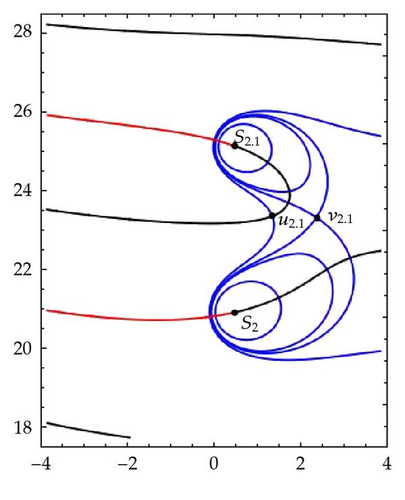
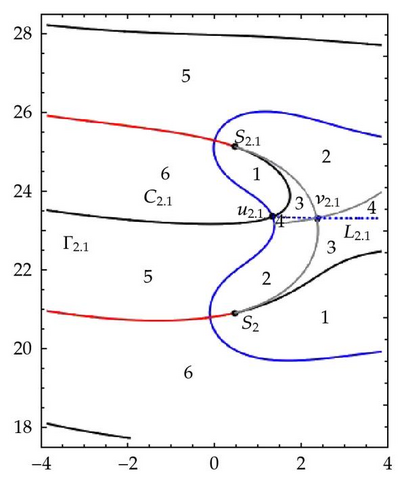
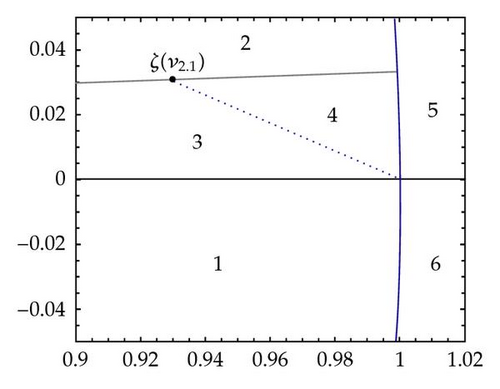
Figure 9 describes the conformal mapping by ζ in the strip S2. Figure 9(a) shows the way in which v2,1 is obtained as the point where the components of the preimage of the circle γρ meet each other for ρ = ρ0 ≈ 0.9296. In Figure 9(b) a curve L2,1 is shown such that C2,1 obtained by adding to L2,1 the part of Γ2,1 corresponding to [1, +∞) divides the strip S2 into two fundamental domains. Details of the conformal mapping by ζ of these domains onto the complex plane with a slit are visible when one compares Figures 9(b) and 9(c).
7. The Group of Cover Transformations of (ℂ, ζ)
Theorem 7.1. The group G of cover transformations of (ℂ, ζ) has two generators: an involution and a transformation generating an infinite cyclic subgroup of G.
Proof. In order to find the group of cover transformations of (ℂ, ζ) we need to rename the fundamental domains. We proceed in a way similar to what we did in the case of the function Gamma. Let us denote by σn the branch points of ζ situated on the negative real half axis counted in an increasing order of their module. Let Ω0 be the domain bounded by the branches of the components of the preimage of the positive real half axis crossing the real axis at σ1 (see Figure 4). It is mapped conformally by ζ onto the complex plane with a slit alongside the real axis from ζ(σ1) to 1. Let Ω−1 be the domain bounded by the component of the preimage of the negative real half axis crossing the real axis in the s-plane at σ2, by the boundary of Ω0, by and its symmetric with respect to the real axis. We notice that Ω−1 is mapped conformally by ζ onto the complex plane with a slit alongside the real axis complementary to the interval (ζ(σ2), ζ(σ1)), The domains Ω−n, n ≥ 2 are those bounded by the branches of the preimage of the real axis crossing the real axis at σn, respectively σn+1. They are mapped conformally by ζ onto the complex plane with a slit alongside the complementary with respect to the real axis of the interval between ζ(σn) and ζ(σn+1). Finally the domains Ωn, n ∈ ℕ are the former domains Ωk,j counted starting from the positive real half axis and going up. In order to have consecutive subscripts for all adjacent domains, we take Ω−1 = Ω1. All the domains Ωn, n ∈ ℤ are fundamental domains of ζ. So are the domains symmetric to them with respect to the real axis. For n ≤ 1, we have .
We define, as in the case of the function Gamma mappings Uk and H by the formulas similar to (3.1) and (3.3), where Γ is replaced by ζ. As in that case we need to perform slits into every Ωj such that for every j and k, ∂Ωj, and ∂Ωj+k are mapped by ζ onto the same slits into the z-plane in order for these formulas to be applicable. We notice that the group generated by U1 and H is the group G of covering transformations of (C, ζ). The group generated by U1 is an infinite cyclic subgroup of G.
Acknowledgment
The authors are grateful to Cristina Ballantine for providing computer generated graphics.




