We construct a stability cone, which allows us to analyze the stability of the matrix delay difference equation x_n = Ax_n−1 + Bx_n−k. We assume that A and B are m × m simultaneously triangularizable matrices. We construct m points in ℝ³ which are functions of eigenvalues of matrices A, B such that the equation is asymptotically stable if and only if all the points lie inside the stability cone.

1. Introduction

Parameters of linear systems are subject to time changes. That is why in order to construct such systems it is desirable to know if they are not only stable but also able to estimate the distance of the system from the boundary of the stability region in the parameter space. Therefore, it makes sense to investigate the geometry of the subset of stable polynomials in the space of characteristic polynomials of linear systems (in the canonical space [1]). This idea has already been applied to the investigation of geometry of the subset of stable polynomials in a two-dimensional subspace of the canonical space [2, 3], the stability simplex for general difference equations [4], connections of the convexity of the coefficients sequence with stability of difference equations [5], and stability ovals for matrix difference equations of the form x_n = x_n−1 + Bx_n−k with the delay k [6].

Consider the matrix equation

(1.1)

where k ∈ ℤ₊ is the delay. Equations of the form (1.1) have been used for investigations of a delayed discrete-time Hopfield neural network [7, 8]. The suitable representation of the solution of (1.1) with commutative matrices A, B and nonsingular A is given in [9]. But [9] does not solve the stability problems of (1.1). The stability of (1.1) was investigated in [7, 8, 10, 11] with special 2 × 2 matrices A, B. In [12], the stability of (1.1) was investigated without any restriction on the dimension but with the special matrix A = αI, α ∈ ℝ, 0 ⩽ α ⩽ 1, where I is the identity matrix.

In this paper we give a geometric solution to the problem of asymptotic stability of (1.1) in any dimension with simultaneously triangularizable matrices A, B. It is known that commuting matrices are simultaneously triangularizable [13]. As usual, we say that (1.1) is stable if its zero solution is stable. Our solution is based on constructing the stability ovals which, in turn, form a stability cone. At the same time we give an algorithm for checking the stability of the scalar equation

(1.2)

with complex coefficients a, b.

The paper is organized as follows. In the second section, we recall the results on the stability of the scalar equation (1.2) with real nonnegative a and any real b [14, 15]. Further in that section we construct the stability oval for (1.2) with real nonnegative coefficient a and complex coefficient b. In Section 3, we consider a wider class of equations of the form (1.2) with a, b being complex numbers. In Section 4, we state a system of inequalities allowing us to check the stability of the scalar equation (1.2) with two complex coefficients. In Section 5, we give a geometrical criterion for the asymptotic stability of matrix equation (1.1) with simultaneously triangularizable matrices. Besides, we establish nongeometric necessary and sufficient conditions for the stability of matrix equation (1.1) in terms of inequalities. In Section 6, we use the stability ovals and cones for analysis of some numerical examples.

2. The Stability Oval for (1.2) with Real Nonnegative a and Complex b

We start by stating the results from [14, 15] in the form which is suitable for us. Since the case k = 1 is obvious, we consider only the case k > 1.

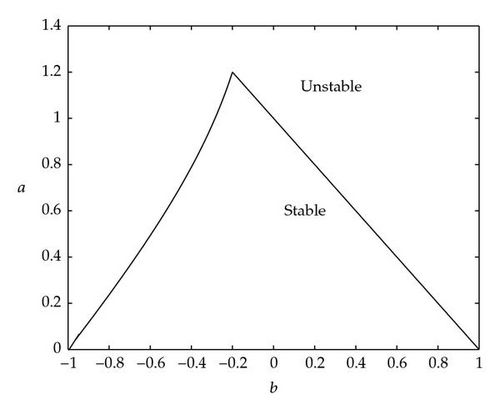
Theorem 2.1 (see [14], [15].)In (1.2) let a and b be real, a⩾0, k > 1.

(1)
If a⩾k/(k − 1), then (1.2) is unstable.
(2)
If 0 ⩽ a < k/(k − 1), then (1.2) is asymptotically stable if and only if
(2.1)
where ω₁ ∈ [0, π/k] is the root of the equation

(2.2)

Stability region of (1.2) is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The domain of asymptotic stability of (1.2), a⩾0, k = 6.

Our first new result about the case of nonnegative real a and complex b in (1.2) is the following.

Theorem 2.2. Let a⩾0 be a real number and b a complex number, k > 1.

(1)
If a⩾k/(k − 1), then (1.2) is unstable.
(2)
If 0 ⩽ a < k/(k − 1), then (1.2) is asymptotically stable if and only if b lies inside the oval bounded by
(2.3)
where ω₁ ∈ [0, π/k] is the root of (2.2).
(3)
If 0 ⩽ a < k/(k − 1) and b is outside of the stability oval (2.3), then (1.2) is unstable.
(4)
If 0 ⩽ a < k/(k − 1) and b lies on the boundary (2.3) of the stability oval, then (1.2) is stable (nonasymptotically).

Proof. We will use the D-decomposition method (parameter plane method) [16, 17]. A characteristic polynomial for (1.2) is the following:

(2.4)

For any fixed value of a, the complex plane of the parameter b is divided into some regions by a curve f(exp (iω)) = 0, that is,

(2.5)

Hence, D-decomposition occurs in the plane of the complex parameter b by means of a curve

(2.6)

The example of the D-decomposition for k = 6, a = 0.7 is shown in Figure 2. From (2.6) we obtain

(2.7)

Therefore, |b| increases monotonically when ω runs from 0 to π. Similarly, |b| increases monotonically when ω runs from 0 to (−π). Let us construct an increasing sequence

of all values ω ∈ [0, π], such that Im (b(ω_i)) = Im (b(−ω_i)) = 0. Here 1 ⩽ r ⩽ k, ω₀ = 0, ω_r = π. Each pair of the curves (2.6) formed by motion ω on intervals [ω_i, ω_i+1], [−ω_i+1, −ω_i] creates a new region of D-decomposition of the complex plane of parameter b. This region necessarily contains some real values of b as the function |b(ω)| is monotone on [0, π] and on [−π, 0]. Due to the properties of the regions, if some inner point of this region is an asymptotically stable point, then the whole region consists of asymptotically stable points. If a⩾k/(k − 1), then according to Theorem 2.1 there are no stable points on the axis Im (b) = 0. Hence, there are no stable points on the complex plane of parameter b. Let now a < k/(k − 1). Let ω₁ ∈ [0, π/k] be the root of (2.2). Then the unique D-decomposition region containing the real straight line segment (2.1) is the oval with the boundary (2.3). Parts 1–3 of Theorem 2.2 are proved. Direct checking shows that the derivative of a characteristic polynomial (2.4) is not equal to zero on the boundary of the stability oval. Therefore, when the parameter b runs along the boundary of the stability oval, all the corresponding roots z of the characteristic equation, satisfying |z | = 1, are simple. Hence, (1.2) is stable (nonasymptotically). Theorem 2.2 is proved.

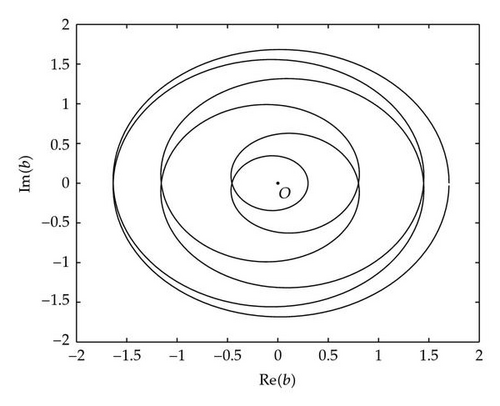
Example 2.3. Let k = 6 and, also, (1) a = 0.2, (2) a = 0.75, and (3) a = 1.1. Let b = 0.33 exp (iα), 0 ⩽ α < 2π. Let us analyze the asymptotic behavior of the solutions of (1.2) for all values of α. We construct three stability ovals for three values of a and also the circle b = 0.33exp (iα) (Figure 3). Theorem 2.2 and Figure 3 give the following result. (1) For a = 0.2, the equation is asymptotically stable for any value of α. (2) For a = 0.75, the equation is asymptotically stable for 2.0918≅α₀ < α < 2π − α₀≅4.1914, it is unstable for α ∉ [α₀, 2π − α₀], and it is stable (nonasymptotically) for α = α₀ and α = 2π − α₀. (3) Finally, for a = 1.1, the equation is unstable for any value of α.

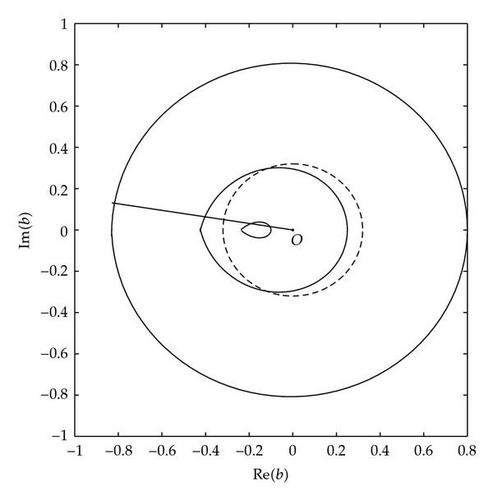
Example 2.4. Let k = 6 and, also, (1) a = 0.2, (2) a = 0.75, and (3) a = 1.1. Let b = rexp (i 19π/20), r⩾0. Let us find the asymptotic behavior of (1.2) for all values of r. We construct the beam b = rexp (i 19π/20) together with three stability ovals (Figure 3). Theorem 2.2 and Figure 3 give the following result.

(1)
For a = 0.2, the equation is asymptotically stable for 0 ⩽ r < r₁≅0.8276, it is unstable for r > r₁, and it is stable (nonasymptotically) for r = r₁.
(2)
For a = 0.75, the equation is asymptotically stable for 0 ⩽ r < r₂≅0.4080, it is unstable for r > r₂, and it is stable (nonasymptotically) for r = r₂.
(3)
Finally, for a = 1.1, the equation is stable for 0.1063≅r₃₁ < r < r₃₂≅0.1944, it is unstable for r ∉ [r₃₁, r₃₂], and it is stable (nonasymptotically) for r = r₃₁, r = r₃₂.

3. The Stability Cone for (1.2) with Complex Coefficients

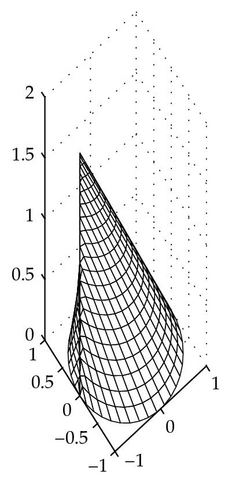
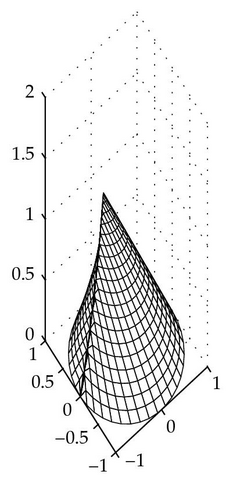
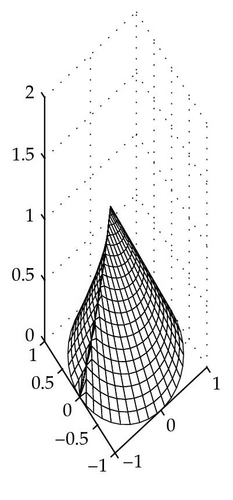
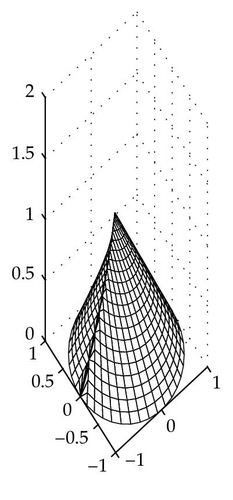
The family of stability ovals depending on a ∈ k/(k − 1) forms a surface which we call the stability cone.

Definition 3.1. The stability cone for delay k is a surface in a three-dimensional space (Re(b), Im (b), z) with 0 ⩽ z ⩽ k/(k − 1), such that its intersection with any plane z = a (0 ⩽ a ⩽ k/(k − 1)) is the stability oval (2.3).

The stability cone is the image of the two-dimensional domain in the space (ω, a)

(3.1)

under the mapping into ℝ³ by the functions

(3.2)

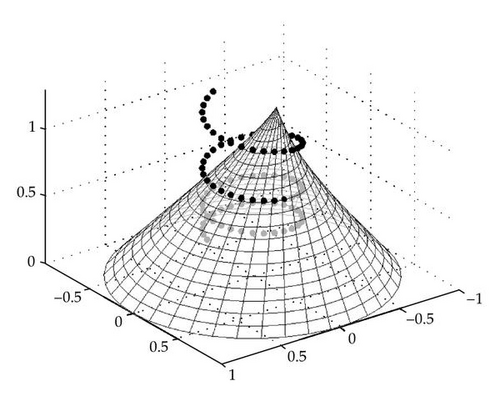
The stability cone for k = 6 is presented in Figure 4.

Let us now study the problem of the stability of scalar equation (1.2) with complex coefficients a, b. We consider the equation

(3.3)

with real nonnegative ρ₁, ρ₂ and real α₁, α₂. We set x_n = y_nexp (inα₁). Then (3.3) becomes

(3.4)

Obviously, (3.4) is stable (asymptotically stable) if and only if (3.3) is stable (asymptotically stable). The stability problem of (3.4) can be solved due to Theorem 2.2. Thus, we obtain the following theorem.

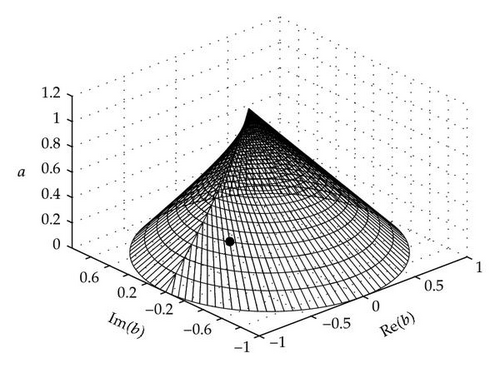
Theorem 3.2. Consider (3.3). Put

(3.5)

Construct the point M = (Re(b), Im (b), a) in ℝ³.

(1)
Equation (3.3) is asymptotically stable if and only if the point M lies inside the cone (3.2) (if a = 0 and (Re(b)) ² + (Im (b)) ² < 1, then the point M is assumed to be the inner point of the cone).
(2)
If the point M lies outside the cone (3.2) or on its top Re(b) = −1/(k − 1), Im (b) = 0, a = k/(k − 1), then (3.3) is unstable.
(3)
If the point M lies on the boundary of a cone (3.2), but not on its top, then (3.3) is stable (nonasymptotically).

Example 3.3. Let us test the stability of the equation with complex coefficients

(3.6)

with a real parameter σ and a delay k = 6. Put first σ⩾0. By Theorem 3.2, according to (3.5) we calculate

(3.7)

The vertical line (Re(b), Im (b), σ), (0 ⩽ σ < ∞) in ℝ³ intersects the boundary of the stability cone at z = σ₀≅0.3442 (Figure 4). To study the negative values of σ we rewrite (3.6):

(3.8)

By Theorem 3.2, according to (3.5) we calculate

(3.9)

As the results (3.9), (3.7) coincide, we obtain the following answer: (3.6) is asymptotically stable for (−σ₀) < σ < σ₀≅0.3442, and it is unstable for σ ∉ [−σ₀, σ₀]. According to part 2 of Theorem 3.2 for σ = σ₀ or σ = −σ₀, (3.6) is stable (nonasymptotically).

Example 3.4. We test (3.6) with a real parameter σ for stability. Unlike the previous example let now the delay be odd: k = 7. For positive σ by Theorem 3.2, according to (3.5) we obtain

(3.10)

The vertical line (Re(b), Im (b), σ) in ℝ³ intersects the boundary of the stability cone at z = σ₀≅0.3377. To study the negative values of σ similarly to the previous example, we obtain

(3.11)

The results (3.10), (3.11) do not coincide. For (3.11) the vertical line (Re(b), Im (b), σ), (0 ⩽ σ < ∞) intersects the boundary of the stability cone at z = σ₁≅0.3002. We obtain the following answer: (3.6) with k = 7 is asymptotically stable if (−0.3002)≅−σ₁ < σ < σ₀≅0.3377, it is unstable if σ ∉ [−σ₁, σ₀], and it is stable (nonasymptotically) for σ = σ₀ or σ = −σ₁.

Comparison of Examples 3.3 and 3.4 reveals the difference in the behavior of (3.3) for even and odd values of the delay k. Let us compare the stability of (1.1) and the following equations:

(3.12)

(3.13)

Substituting x_n = (−1) ⁿy_n reduces (1.1) to

(3.14)

Equations (1.1) and (3.14) are simultaneously stable or unstable. Therefore, we have the following symmetry property of the stability region for (1.1).

Theorem 3.5. For even delays k the (asymptotic) stability of (1.1) implies the (asymptotic) stability of (3.12) and vice versa. For odd k the (asymptotic) stability of (1.1) implies the (asymptotic) stability of (3.13) and vice versa.

Similar properties of symmetry have been specified in [11, 15] for the scalar equation (1.2) with real a, b.

4. A System of Inequalities for Checking the Stability of (3.3)

In the previous sections we used some geometric procedures. In this section we construct a system of inequalities in order to check the stability of (3.3). Henceforth we assume 0 ⩽ arg(z) < 2π for a complex variable z.

Theorem 4.1.

(1)
If ρ₁ < 1 − ρ₂, then (3.3) is asymptotically stable.
(2)
If 1 − ρ₂ ⩽ ρ₁ < min(1 + ρ₂, k/(k − 1)), then for the asymptotic stability of (3.3) it is necessary and sufficient to fulfill simultaneously the following conditions ((H1)), ((H2)):
( ( H 1 ) )
where ω₁ ∈ [0, π/k] is the root of the equation
( ( H 2 ) )
(3)
If ρ₁⩾min (1 + ρ₂, k/(k − 1)), then (3.3) is not asymptotically stable.

Proof. The stability of (3.3) is equivalent to the stability of (3.4), so we will work with (3.4).

(1)
For ρ₁ < 1 − ρ₂ by Theorem 2.2 the stability oval exists and the circle of radius ρ₂ lies completely inside the oval. Therefore, Theorem 2.2 implies the asymptotic stability of (3.4). Part 1 of Theorem is proved.
(2)
Let 1 − ρ₂ ⩽ ρ₁ < min (1 + ρ₂, k/(k − 1)). Let us consider two cases.

Case 1 ((1 − ρ2) ⩽ ρ1 < 1). In this case, the stability oval exists by Theorem 2.2, and the origin of the coordinates lies inside the oval. For (3.4) to be asymptotically stable, it is necessary and sufficient to satisfy the two following conditions. The first one is that the circle of radius ρ₂ should intersect the stability oval. It is equivalent to ((H1)). The second condition is that the argument of a point exp (i(α₂ − kα₁)) should be between the arguments of the two crosspoints M₁, M₂ of a circle of radius ρ₂ with the stability oval (2.3). Let us assume that Im (M₁) > 0, and let the parameter ω correspond to the point M₁. We obtain

(4.1)

from (2.3). But we also obtain

(4.2)

from (2.7). Equalities (4.1), (4.2) give

(4.3)

It follows from (4.3) that the second requirement is equivalent to ((H2)). Part 2 of Theorem 4.1 is proved in Case 1.

Case 2 (1 ⩽ ρ1 < min(1 + ρ2, k/(k − 1))). By virtue of the inequality ρ₁ < k/(k − 1), the stability oval exists, and, since ρ₁⩾1, the origin does not lie inside the oval. The same requirements as in the previous case lead to the same conditions ((H1)), ((H2)). Part 2 of the Theorem is proved.

(3)
Let ρ₁⩾min (1 + ρ₂, k/(k − 1)). We consider two cases.

Case 1 (1 + ρ2 ⩽ ρ1 < k/(k − 1)). In this case the stability oval exists by Theorem 2.2, and, by virtue of the inequality ρ₁⩾1, the origin does not lie inside the oval. Due to the inequality ρ₂ ⩽ ρ₁ − 1, no point of the circle of radius ρ₂ lies inside the oval and so (3.4) is not asymptotically stable by Theorem 2.2.

Case 2 (ρ1⩾k/(k − 1)). In this case, (3.4) is unstable by Theorem 2.2.

Theorem 4.1 is proved.

As we see, the text of Theorem 4.1 does not contain any geometric terms. However, Theorem 3.2 has a considerable advantage over Theorem 4.1 because of its simplicity and geometric visualization. That is why in the future examples we prefer describing the stability of matrix equation (1.1) in geometric terms.

5. The Stability Cone for the Matrix Equation with Simultaneously Triangularizable Matrices

In this section we consider (1.1) with simultaneously triangularizable matrices A, B.

Theorem 5.1. Let A, B, S ∈ ℝ^m×m and S⁻¹AS = A_T and S⁻¹BS = B_T, where A_T, B_T are the lower triangular matrices with elements, respectively, λ_js, μ_js(1 ⩽ j, s ⩽ m). Let

(5.1)

and let the points M_j in ℝ³ be constructed by

(5.2)

Then (1.1) is asymptotically stable if and only if for any j(1 ⩽ j ⩽ m) the point M_j lies inside cone (3.2).

If for some j (1 ⩽ j ⩽ m) the point M_j lies outside cone (3.2), then (1.1) is unstable.

Proof. In (1.1) we substitute x_n = Sy_n and multiply the equation by S⁻¹. We obtain

(5.3)

with lower triangular matrices A_T, B_T. By virtue of the nondegeneracy of matrix S, the stability of (5.3) is equivalent to the stability of (1.1). Let us assume that

. The system (5.3) consists of m scalar equations

(5.4)

As usual,

. Equation (5.4) is called exponentially stable if there are real C > 0, q ∈ (0,1), such that for any solution

the estimate

(5.5)

holds. The exponential stability is equivalent to the asymptotic stability for the equations under consideration. It is more convenient to prove the exponential stability. Let the points (5.2) (1 ⩽ j ⩽ m) lie inside the cone (3.2). Due to Theorem 3.2, all equations of the form

(5.6)

are exponentially stable. Let us prove by induction on j that (5.4) are exponentially stable. For j = 1, (5.4) coincides with (5.6), so it is exponentially stable. Let, for any r < j, (5.4) with r instead of j be exponentially stable. Then (5.4) is represented in the form

(5.7)

where

has an estimate of the form (5.5) by the induction assumption. Assuming

, we represent (5.7) in the form

(5.8)

where G ∈ ℝ^k×k, G is a stable matrix, and |h_n| has an estimate of the form (5.5). From (5.8) we obtain

, which implies the exponential stability of (5.4). The induction is finished, and asymptotic stability of (1.1) is proved.

Let us assume that some point (5.2) does not lie strictly inside the cone. Then, for the initial data in (5.4), we assume that for any s, n, such that 1 ⩽ s ⩽ j, 1 ⩽ n ⩽ k. Thus, (5.4) becomes (5.6). If the point (5.2) lies on the cone boundary, then (5.6) has a trajectory which does not tend to zero because the characteristic polynomial of (5.6) has a root z such that |z | = 1. If some point (5.2) lies outside the cone, then by Theorem 3.2 the equation has unlimited trajectories. Theorem 5.1 is proved.

Remark 5.2. If no points (5.2) lie outside the stability cone, but some of them lie on the cone boundary, then (1.1) can be stable (nonasymptotically) or unstable.

Remark 5.3. The stability cones (Figure 5) are constructed for each delay k independently of the dimension m in (1.1). If k → ∞, then the intersection of all stability cones is the right circular cone with the base radius 1 and the height 1. The interior of this cone is the “absolute stability domain,” that is, the stability domain for any delay.

The next theorem, which is the evident consequence of Theorems 4.1 and 5.1, will establish the asymptotic stability criterion in the form of inequalities for matrix equation (1.1).

Theorem 5.4. Let A, B, S ∈ ℝ^m×m and S⁻¹AS = A_T and S⁻¹BS = B_T, where A_T, B_T are the lower triangular matrices with elements λ_js, μ_js (1 ⩽ j, s ⩽ m), respectively. Let

(5.9)

Construct a set AS⊆P = {j ∈ ℤ₊ : 1 ⩽ j ⩽ m} by the following rules (cf. Theorem 4.1).

(1)
If ρ_1j < 1 − ρ_2j, then j ∈ AS.
(2)
If 1 − ρ_2j ⩽ ρ_1j < min(1 + ρ_2j, k/(k − 1)), then for j ∈ AS it is necessary and sufficient to fulfill simultaneously the following conditions ((H1j)), ((H2j)):
( ( H 1 j ) )
where ω_1j ∈ [0, π/k] is the root of the equation
( ( H 2 j ) )
(3)
If ρ_1j⩾min (1 + ρ_2j, k/(k − 1)), then j ∉ AS.

Equation (1.1) is asymptotically stable if and only if AS = P.

6. Examples of the Stability Oval and the Cone for Matrix Equations

Example 6.1. Consider the equation

(6.1)

where

(6.2)

with α = 0.0314, β = 0.1745. Let us find out for what values of s ∈ ℤ₊ (6.1) is stable. Matrices A, B are commuting; therefore, they are simultaneously triangularizable. The eigenvalues of matrices A, B are λ_1,2 = exp (±0.0314i) and μ_1,2 = exp (±0.1745i) correspondingly. In Figure 6 the stability oval is shown, which is the section of the stability cone (3.2) on the level z = 1.0309. By Theorem 5.1 we have to know whether the points

(6.3)

lie inside the cone. Figure 6 illustrates that points M^(s) enter the oval of stability twice (s = 53, s = 87) and leave it twice (s = 58, s = 94). The conclusion is that the system (6.1), (6.2) is stable for 53 ⩽ s ⩽ 58 and for 87 ⩽ s ⩽ 94 and is unstable for all the other values of s.

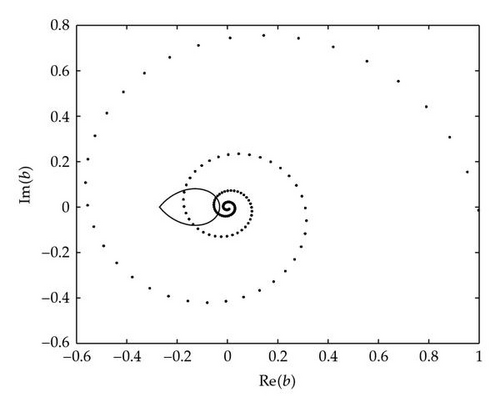
Example 6.2. Consider the equation

(6.4)

where

(6.5)

Let us find out for what values of s ∈ ℤ₊ (6.4) is stable. The eigenvalues of A are λ_1,2 = 1.0150exp (±0.0374i). Stability ovals are symmetric about the real axis. Therefore, by Theorem 5.1, only points

(6.6)

(see Figure 7) should be checked. Figure 7 displays that points M^(s) for 1 ⩽ s ⩽ 49 are inside the stability cone (3.2) and for s⩾50 points are outside of the stability cone. The conclusion is that (6.4) is stable for 1 ⩽ s ⩽ 49 and it is unstable for s⩾50.

7. Conclusion

The stability analysis for (1.1) in ℝ^m can be reduced to the pole placement problem for a polynomial of degree km. Our geometric approach allows us to reduce the dimension. To use the approach, we need to know the eigenvalues of A, B. This is the problem of finding the roots of a polynomial of degree m. Using these eigenvalues, we get a finite sequence of points in ℝ³ such that their position with respect to the stability cone allows us to make a conclusion about the stability of (1.1).

In our future work we intend to analyze the stability of equation x_n = Ax_n−m + Bx_n−k with two delays m, k with simultaneously triangularizable matrices A, B. The scalar version of this equation was examined in [2, 3, 18]. The stability cone for the matrix differential equation was introduced in [19].

Acknowledgment

The authors are indebted to K. Chudinov, I. Goldsheid, and D. Sheglov for very useful comments.

References

1 Fam A. T. and Meditch J. S., A canonical parameter space for linear systems design, IEEE Transactions on Automatic Control. (1978) 23, no. 3, 454–458, 0528928, https://doi.org/10.1109/TAC.1978.1101744, ZBL0377.93021.
10.1109/TAC.1978.1101744
Web of Science® Google Scholar
2 Nikolaev Y. P., The geometry of D-decomposition of a two-dimensional plane of arbitrary coefficients of the characteristic polynomial of a discrete system, Automation and Remote Control. (2004) 65, no. 12, 1904–1914, https://doi.org/10.1023/B:AURC.0000049876.54417.e6.
10.1023/B:AURC.0000049876.54417.e6
Web of Science® Google Scholar
3 Kipnis M. M. and Nigmatulin R. M., Stability of trinomial linear difference equations with two delays, Automation and Remote Control. (2004) 65, 1710–1723.
10.1023/B:AURC.0000047886.46498.79
Web of Science® Google Scholar
4 Kipnis M. M. and Komissarova D. A., A note on explicit stability conditions for autonomous higher order difference equations, Journal of Difference Equations and Applications. (2007) 13, no. 5, 457–461, https://doi.org/10.1080/10236190601132933, 2314583, ZBL1119.39007.
10.1080/10236190601132933
Web of Science® Google Scholar
5 Gilyazev V. M. and Kipnis M. M., Convexity of a sequence of coefficients and the stability of discrete systems, Automation and Remote Control. (2009) 70, 1856–1861.
10.1134/S0005117909110095
Web of Science® Google Scholar
6 Levitskaya I. S., A note on the stability oval for x_n+1 = x_n + Ax_n−k, Journal of Difference Equations and Applications. (2005) 11, no. 8, 701–705, https://doi.org/10.1080/10236190512331333851, 2156648, ZBL1080.39014.
10.1080/10236190512331333851
Web of Science® Google Scholar
7 Guo S., Tang X., and Huang L., Stability and bifurcation in a discrete system of two neurons with delays, Nonlinear Analysis: Real World Applications. (2008) 9, no. 4, 1323–1335, https://doi.org/10.1016/j.nonrwa.2007.03.002, 2422546, ZBL1154.37381.
10.1016/j.nonrwa.2007.03.002
Web of Science® Google Scholar
8 Kaslik E. and Balint S., Bifurcation analysis for a two-dimensional delayed discrete-time Hopfield neural network, Chaos, Solitons & Fractals. (2007) 34, no. 4, 1245–1253, 2331279, https://doi.org/10.1016/j.chaos.2006.03.107, ZBL1142.39300.
10.1016/j.chaos.2006.03.107
Web of Science® Google Scholar
9 Diblík J. and Khusainov D. Y., Representation of solutions of discrete delayed system x(k + 1) = Ax(k) + Bx(k − m) + f(k) with commutative matrices, Journal of Mathematical Analysis and Applications. (2006) 318, no. 1, 63–76, 2210872, https://doi.org/10.1016/j.jmaa.2005.05.021, ZBL1094.39002.
10.1016/j.jmaa.2005.05.021
Web of Science® Google Scholar
10 Matsunaga H., Stability regions for a class of delay difference systems, Differences and Differential Equations, 2004, 42, American Mathematical Society, Providence, RI, USA, 273–283, Fields Institute Communications, 2089617, ZBL1067.39012.
Google Scholar
11 Matsunaga H. and Hajiri C., Exact stability sets for a linear difference system with diagonal delay, Journal of Mathematical Analysis and Applications. (2010) 369, no. 2, 616–622, 2651707, https://doi.org/10.1016/j.jmaa.2010.03.062, ZBL1198.39027.
10.1016/j.jmaa.2010.03.062
Web of Science® Google Scholar
12 Kaslik E., Stability results for a class of difference systems with delay, Advances in Difference Equations. (2009) 2009, 13, 938492, 2588199, ZBL1187.39025.
10.1155/2009/938492
Google Scholar
13 Horn R. and Johnson C., Matrix Theory, 1986, Cambridge University Press, Cambrige, UK.
Google Scholar
14 Kuruklis S. A., The asymptotic stability of x(n + 1) − ax(n) + bx(n − k) = 0, Journal of Mathematical Analysis and Applications. (1994) 188, no. 3, 719–731, https://doi.org/10.1006/jmaa.1994.1457, 1305480, ZBL0842.39004.
10.1006/jmaa.1994.1457
Web of Science® Google Scholar
15 Papanicolaou V. G., On the asymptotic stability of a class of linear difference equations, Mathematics Magazine. (1996) 69, no. 1, 34–43, https://doi.org/10.2307/2691392, 1381584, ZBL0866.39001.
10.1080/0025570X.1996.11996377
Google Scholar
16 Gryazina E. N. and Polyak B. T., Stability regions in the parameter space: D-decomposition revisited, Automatica. (2006) 42, no. 1, 13–26, https://doi.org/10.1016/j.automatica.2005.08.010, 2183067, ZBL1121.93028.
10.1016/j.automatica.2005.08.010
Web of Science® Google Scholar
17 Šiljak D. D., Parameter space methods for robust control design: a guided tour, IEEE Transactions on Automatic Control. (1989) 34, no. 7, 674–688, https://doi.org/10.1109/9.29394, 1000661, ZBL0687.93033.
10.1109/9.29394
Web of Science® Google Scholar
18 Dannan F. M., The asymptotic stability of x(n + K) + ax(n) + bx(n − 1) = 0, Journal of Difference Equations and Applications. (2004) 10, no. 6, 589–599, https://doi.org/10.1080/10236190410001685058, 2060414, ZBL1054.39003.
10.1080/10236190410001685058
Web of Science® Google Scholar
19 Khokhlova T., [email protected], Kipnis M., and [email protected], Malygina V., [email protected], The stability cone for a delay differential matrix equation, Applied Mathematics Letters. (2011) 24, no. 5, 742–745, https://doi.org/10.1016/j.aml.2010.12.020.
10.1016/j.aml.2010.12.020
Web of Science® Google Scholar

Citing Literature

All articles

The Stability Cone for a Matrix Delay Difference Equation

Abstract

1. Introduction

2. The Stability Oval for (1.2) with Real Nonnegative a and Complex b

3. The Stability Cone for (1.2) with Complex Coefficients

4. A System of Inequalities for Checking the Stability of (3.3)

5. The Stability Cone for the Matrix Equation with Simultaneously Triangularizable Matrices

6. Examples of the Stability Oval and the Cone for Matrix Equations

7. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Stability Cone for a Matrix Delay Difference Equation

Abstract

1. Introduction

2. The Stability Oval for (1.2) with Real Nonnegative a and Complex b

3. The Stability Cone for (1.2) with Complex Coefficients

4. A System of Inequalities for Checking the Stability of (3.3)

5. The Stability Cone for the Matrix Equation with Simultaneously Triangularizable Matrices

6. Examples of the Stability Oval and the Cone for Matrix Equations

7. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information