The stress induced in a loaded beam will not exceed some threshold, but also its maximum deflection, as for all the elastic systems, will be controlled. Nevertheless, the linear beam theory fails to describe the large deflections; highly flexible linear elements, namely, rods, typically found in aerospace or oil applications, may experience large displacements—but small strains, for not leaving the field of linear elasticity—so that geometric nonlinearities become significant. In this article, we provide analytical solutions to large deflections problem of a straight, cantilevered rod under different coplanar loadings. Our researches are led by means of the elliptic integrals, but the main achievement concerns the Lauricella hypergeometric functions use for solving elasticity problems. Each of our analytic solutions has been individually validated by comparison with other tools, so that it can be used in turn as a benchmark, that is, for testing other methods based on the finite elements approximation.

1. Introduction

1.1. A Literature′s Overview

As early as 1691, Jakob Bernoulli proposed to find out the deformed centerline (planar “elastica”) of a thin, homogeneous, straight, and flexible rod under a force applied at its end, and ignoring its weight. Studying the geometry of its deflection, he established, Curvatura laminae elasticae (1694), the differential equation of the centerline, say y = y(x), of the rod ab appenso pondere curvata to be

(1.1)

Not succeeding in solving it, he was led to look for its arclength, arriving at the same elliptic integral

(1.2)

of lemniscate rectification. Daniel Bernoulli, Johann′s son and Jakob′s nephew, obtained in 1738 subspecie integralis the potential energy stored in a bent rod; in October 1742 he wrote to Leonard Euler the rod should attain such a shape as to minimize the function of squared curvature. Accordingly, Euler dealt elastica as an isoperimetric problem of calculus of variations, De curvis elasticis (1744), arriving at elastica′s differential equation and identifying nine shapes of the curve, all equilibrium states of minimal energy. Anyway, Colin Maclaurin had realized the elastica′s connection to elliptic integrals, see A treatise on fluxions (1742), § 927 entitled “The construction of the elastic curve, and of other Figures, by the rectification of the conic sections”. In 1757, Euler authored a paper, Sur la force des colonnes, concerning the buckling of columns again, where the critical load is approached through a simplified expression to the elastica′s curvature, coming again over the problem again in 1770 and 1775; for all this historical concern, see [1, 2]. Some analytic solutions to elastic planar curves through elliptic integrals of I and II kind can be read at [3–5]. Almost half a century ago, the analytic treatment of flexible rods inspired a nice book, [6], which collects many problems ordered according to the constraint type, and all solved by the elliptic integrals of I and II kind, while the III kind and Theta functions appear there marginally in the 6th Chapter concerning the three dimensional deformations. In order to fix just right from the start, the true concept of rod will be recalled from [7] as follows:

A rod is something of a hybrid, that is, a mathematical curve made up of material points. It has no cross section, yet it has stiffness. It can weigh nothing or it can be heavy. We can twist it, bend it, stretch it and shake it, but we cannot break it, it is completely elastic. Of course, it is a mathematical object, and does not exist in the physical world; yet it finds wide application in structural (and biological) mechanics: columns, struts, cables, thread, and DNA have all been modeled with rod theory.
A rod which offers no resistance to bending is called a string: it is completely flexible. The string model finds applications in the study of long slender structural members such as cables, where an external load dominates the mechanics and the rods flexural stiffness is negligible.

The link between elliptic functions and elastica was always understood so close, to induce the elliptic functions to be plotted through suitable curved rubber rods (G. Greenhill: Graphical representation of the elliptic functions by means of a bent elastic beam, 1876), while the paper [8] is founded on the use of the Weierstrass ℘ function. For recent developments, see: [8–15]. Inextensibility and circular shape of undeformed rod are (numerically) analyzed in [16, 17] where the load is a uniform centrally directed force.

Our object is the analytical solutions to large-deflection problems of a planar slender cantilever under coplanar loads. The slender structures are those much longer in one direction than in the other two, and their deflection will be described by elastic rod theory if one is interested in phenomena on length scales much larger than the lateral dimensions of the structure. For Dirichlet problems relevant to large deformations, see [18, 19]. A simplified version of this theory, beam theory, suffices if only small deflections need to be considered; the majority of structural engineering applications are adequately modelled by a beam; bridges and buildings are not designed to suffer large deformations. But in other applications of structural mechanics, deflections may be large, meaning that nonlinear geometric effects must be taken into account; the full (geometrically nonlinear) rod theory is then necessary. Mathematically, a rod is modelled as a curve with effective mechanical properties such as bending and torsional stiffnesses, see [20]. Although such problems belong to statics, they have a strong relation with dynamics; arclength along the rod plays a role similar to time in a dynamical system. In its simplest form, this analogy (Kirchhoff′s Dynamic Analogy: Über das Gleichgewicht und die Bewegung eines unendlich dűnnen elastischen Stabes, 1859, see [21]) is seen between the deformations of an elastic strut and the motions of a swinging pendulum. A less known analogy links a twisted rod and a spinning top, and the precession of a top does correspond to a rod helical deformation. Engineering problems where rod theory is applied include the looping of ocean cables [22] and the buckling of oil well drilling strings, which nowadays can be over 5 km long. Furthermore, there is a deep reason for a great interest in applying the elastic rod theory to the supercoiling and packing of DNA molecules and proteins (such as collagen): as a matter of fact, due to its double helical nature, DNA is unusually stiff (in both, bending and torsion) for a polymer and, hence, well described by a rod. Finally, the study of strings and rods is of interest to electrodynamic space tethers¹, generally credited of great potential for future space missions in order to bring down space debris (derelict spacecraft, etc.). Unlike the majority of tethers, which can be treated as cables, Space European Tether (SET, see [23]) is a prototype designed to withstand torsional and bending forces so that it needs to be modelled as a spinning rod (and not a cable), namely, a 3D-elastica². All above provide enough motivations to implement exact solutions within the rod theory, see [10].

The exact governing equations for the finite displacement rod theory become highly nonlinear, and, hence, it is very difficult to solve these equations analytically. Thus, for practical purposes, problems of this kind are usually solved by the methods based on the finite elements approximations. However, the closed form solutions for these problems are still important to the practical point that the accuracy of the approximate methods can be precisely evaluated by these solutions, to say nothing of the mathematical importance.

1.2. Aim of the Paper

It is well known why the elastic curve of a rod is essential, in fact not only the stresses, but also its maximum deflection will not exceed a fixed amount. Furthermore, (see Mattiasson [24]).

When developing finite element methods, there is also a need for checking the results against an exact solution. In the case of finite element methods for geometrically nonlinear beam, frame and shell structures, elliptic integral solutions of large deflection beam and frame problems offer such exact solution.

Nevertheless, his approach is a bit obsolete nowadays because he computes the elliptic integrals numerically through the arithmetic-geometrical means.

We are going to analyze an elastic, thin, flexible rod, clamped at one end (cantilever) bent under different loadings whose plane coincides with that of the strained centerline. Equating the exact curvature in cartesian coordinates to the bending moment divided into the flexural rigidity, one is led to a second-order nonlinear and nonautonomous differential equation. Boundary conditions are given both on the clamped end (Cauchy problem), so that, for example, if the constraint is perfect, displacement and rotation have to be zero there. We discarded the illusion of a general system of loads and rods and restricted ourselves to only one configuration, charged by a single load and treating each single problem by means of the special functions of mathematical physics. The chosen loads are constant couple, evenly distributed load, shear at the tip, hydrostatic load, and sinusoidal load. All our force loads have to be understood as “dead load”, namely, always equal to itself and then not “follower” as are currently named the loads keeping a fixed inclination to the rod before and after the strain.

For one of the above loads, based on the rod′s unextensibility, we computed in closed form the Ω free tip coordinates, parametrized to the load itself. We use everywhere nondimensional quantities; the reader will see how advantageous is such a choice in producing “universal” relationships which (in elliptical and/or hypergeometric cloth) keep their formal validity in several situations.

1.3. Special Functions Tools

We assume that the reader knows the elliptic functions (see [25] for details), but let us recall hereinafter the less known Lauricella hypergeometric ones.

The hypergeometric series first appeared in the Wallis′s Arithmetica infinitorum (1656)

(1.3)

for |x| < 1 and real parameters a, b, c. The product of n factors

(1.4)

called Pochhammer symbol (or truncated factorial) allows to write ₂F₁ as

(1.5)

The first meaningful contributions about various ₂F₁ representations are due to Euler³; nevertheless, he does not seem to have known the integral representation

(1.6)

traditionally ascribed to him, but really due to A. M. Legendre⁴. For all this and for the Stirling contributions, see [26]. The above integral relationship is true if c > a > 0 and for |x| < 1, even if this bound can be discarded due to analytic continuation.

Several functions have been introduced in the 19th century for generalizing the hypergeometric functions to multiple variables, but we will mention only those introduced and investigated by Lauricella (1893) and Saran (1954). Among them our interest is focused on the hypergeometric function

of n ∈ ℕ⁺ variables (and n + 2 parameters), see [27, 28], defined as

(1.7)

with the hypergeometric series usual convergence requirements |x₁| < 1, …, |x_n| < 1. If Re c > Re a > 0, the relevant integral representation theorem (IRT) provides

(1.8)

allowing the analytic continuation to ℂⁿ deprived of the cartesian n-dimensional product of the interval ]1, ∞[ with itself.

2. Bent Slender Rod: A Large Deflections 2D-Model

Let us tackle a L-long, thin, and weightless rod whose end A is clamped and B free. We put at B the origin O of a (x, y) cartesian reference frame with x along the undeformed rod, from B to A; and y downwards, normal at B to x. Our basic assumptions are

(A₁)
the rod is thin, initially straight, homogeneous, with uniform cross-section and uniform flexural stiffness EJ, where E is the Young modulus, and J the cross-section moment of inertia about a “neutral” axis normal to the plane of bending and passing through the central line;
(A₂)
the slender rod is charged by coplanar dead loads;
(A₃)
linear constitutive load: the induced curvature is proportional via 1/(EJ) to the bending moment. The rod undergoes large deflections but small strains;
(A₄)
the shear transverse deformation is ignored, and the rod is assumed to keep constant its previous length (inextensibility);
(A₅)
a stationary strain field, by isostatic equilibrium of active loads and reactive forces, takes place, and, due to rest of static equilibrium, no rod element undergoes acceleration.

The key Bernoulli-Euler linear constitutive law connects flexural stiffness EJ and bending moment M to the consequent curvature ϰ of the deflected centerline ±EJϰ = M(x). With our (traditional) reference frame (x, y), the curvature has always opposite sign to the bending moment

(2.1)

where y = y(x) is the unknown elastica′s cartesian equation and

(2.2)

To (2.1) a useful dress can be given

(2.3)

to be solved together to the perfect clamping boundary conditions

(2.4)

Throughout all the paper, it will be minded that the Cauchy problem

(2.5)

can be solved in such a way. Putting

(2.6)

the solution of (2.5) is

(2.7)

In the sequel, we are going to use dimensionless variables ξ = x/L, η = y/L, so that the previous relationship becomes

(2.8)

whose solution is

(2.9)

2.1. Rod Inflected by a Constant Bending Couple at Its Tip

The clamped section is at x = L, see Figure 1. In such a case, the equation to be integrated is (2.5), with M(x) = −ℳ₀, and (2.9) provides, in nondimensional form,

(2.10)

where χ = ℳ₀L/EJ > 0. The elastica is more readable reverting at a dimensional form

(2.11)

half circle of centre C(L, Lχ) and radius Lχ, see Figure 1, as it is well known.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

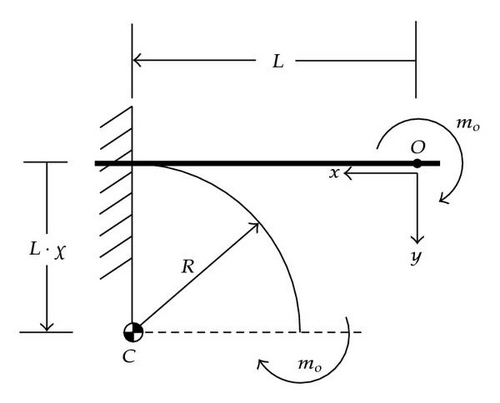
Horizontal cantilever rod inflected by a constant bending couple at its tip.

2.2. The Horizontal Heavy Rod

The classic elastica theory started by the “lamina”, namely, a thin rod without weight but capable to withstand the flexure and loaded at its free end only. Chapter 5 of [6] on the specific problem of the horizontal cantilever under uniform load gives (page 173):

This problem… has shown considerable resistance to a closed form solution and all investigations dealing with it have employed approximate methods only.

Accordingly, he obtains elastica coordinates as parametric functions of the arclength s, stopping their Maclaurin expansions to s¹⁰.

Let us consider at Figure 2 a horizontal, flexible, homogeneous, heavy and cantilever; it will be inflected by the uniform evenly continuous load q (weight for unity span length). Its elastica, according to the approximate beam theory, would consist of a fourth-order rational function of x. Being

(2.12)

we obtain, in nondimensional coordinates, using (2.9)

(2.13)

and finally, passing to the variable λ = σ/(ξ³ − 1):

(2.14)

By identification, we obtain the solution to our elastica through a Lauricella function of 3 variables x₁ = 1 − ξ³, x₂ = ν(ξ³ − 1), x₃ = ν(1 − ξ³), so that

(2.15)

For being compliant with the IRT requirements, it shall be

, and then ν < 1. Otherwise, it will be necessary another method.

We got there three ν-ranges. The first is the very narrow one, where the small deflections assumption is true, first-order theory. By |η^′(ξ)| < h², h ∈ (0,1), we get

(2.16)

which at ξ = 0, gives

. For instance, if h = 1/10, then

(i)
if 0 < ν < 0.0099, the first-order approximation can be accepted;
(ii)
if 0.0099 < ν < 1 by (IRT), the hypergeometric function is capable of describing our solution (2.14);
(iii)
if ν ≥ 1, the solution (2.14) will be numerically computed.

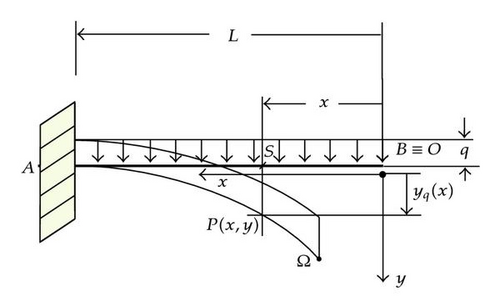
Formula (2.15), founded on the Lauricella hypergeometric functions, provides a very compact explicit solution to the elastica of a thin clamped heavy rod. We cannot give now the due importance to (2.15) due to the lack of software packages whose quickness and precision of computing are comparable to those available on Mathematica for the Gauss or Appell hypergeometric functions. We did invite Wolfram to consider such a necessity, but no forecasting is possible. As far as we are concerned, the integral (2.14) cannot be led to any other known special functions or to any combination of them.

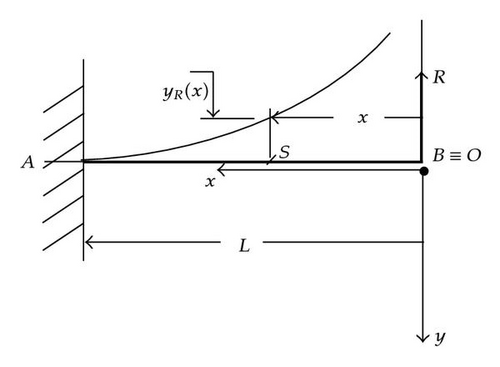
2.3. A Tip-Sheared Horizontal Rod

We refer to Figure 3, where the force R is transversal (in [29] is studied the inclined end load) but not a follower one; we have M(x) = Rx, so that, after defining the nondimensional μ = RL²/2EJ, we obtain

(2.17)

being the bending moment always greater than zero, so will be H(x), and then it will be η_ξ > 0. For this load too, the hypergeometric treatment is possible. Passing from ζ to λ, with λ = (1 − ζ²)/(1 − ξ²), we obtain

(2.18)

We can see that, recognizing the Lauricella parameters a = 2, b_i = 1/2, c = 3

(2.19)

compliant to the IRT requirements if μ < 1. For this load, we have to the Lauricella′s alternative of the elliptic integrals (not applicable to the heavy nor to the submerged rod), so that we will cover with much more details this approach. Investigating the elastica of a thin cantilever, the majority of authors (Landau and Lifchitz [30], Love [21], Mathieu [31], Burgatti [4], Panayotounakos and Theocaris [11, 12, 14], Chucheepsakul and Phungpaigram [9], Basoco [8], Frisch-Fay [6]) use the slope-arclength formulation (ϑ, s) they integrate a first time for getting ϑ as a function of s. But dx = ds cos ϑ(s) and dy = ds sin ϑ(s), so that they get, through a second integration, the elastica′s x and y coordinates parametrized on s. Only few develop a different (x, y) parametric equations, for example, Saalschütz, in [32]. Anyway a treatment leading to explicit sole cartesian coordinates does not seem to be ever established, and it is exactly what we are doing. An old reference, rather fit to Jakob Bernoulli (1694) and Euler (1744) formulae, is that of Kiepert (1912), who⁵ stops without reducing his elliptic integral to the Legendre standard form. It will be just the elliptic integral (2.17) our startup. First let us change variables in (2.17) passing from ζ to t = 1 − ζ², obtaining

(2.20)

For the reader convenience, let us fix some notation. Let a > b > x > y > c. Consider the definite elliptic integral

(2.21)

Combining formulae given in [25]: integral 234.16 page 76 and integral 340.01 page 205, introducing

(2.22)

we obtain:

(2.23)

where F(φ, k) and Π(φ, k², k) are the I and III kind elliptic integrals. Now assuming that μ < 1 we have the identification

(2.24)

which allows to give (2.17) via (2.20) by means of the integration formula

(2.25)

where:

(2.26)

being

(2.27)

Formula (2.25) provides the dimensionless deflection η to the position ξ and to the load μ: its 3D-plot, via Mathematica, as shown in Figure 4.

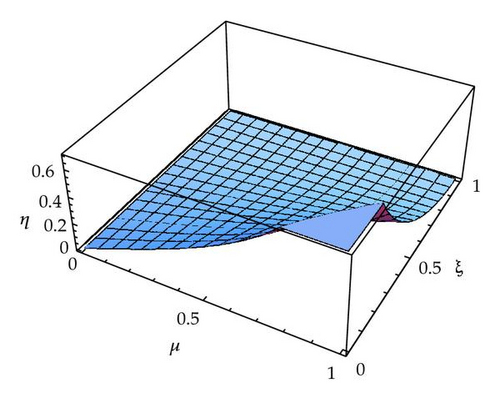
From it, one could obtain the relevant contour plots cutting by planes of μ = constant. The thing is shown in Figure 5, where the clamped end is on the left. The deflection curves are given for some values of μ : 0.2; 0.4; 0.6; 0.8. Each of them is compared with the dot curve coming from the approximate theory⁶. Mind that ξ is ranged as ξ_Ω < ξ < 1, and ξ_Ω has to be found from (3.12). Accordingly, each single μ-curve has been plotted between ξ = 1 and ξ_Ω(μ). From the physical viewpoint, the lines′⁷ comparison shows at the low loads an agreement which is becoming worst for increasing loads when the approximate theory is progressively failing.

It is worth noting that the power series expansion of (2.25) drives back to the approximate expression for η(ξ) used in literature. Of course, we deeply exploited the computer algebra power for this task. First we compute the Maclaurin third-order expansion of (2.25) with respect to ξ obtaining

(2.28)

where (φ(μ) is the quantity introduced in (2.27))

(2.29)

Now we expand the elliptic integrals of I and III kind with respect to μ, with initial point μ₀ = 0

(2.30)

arriving at

(2.31)

Moreover recalling the Maclaurin first-order expansion with respect to μ

(2.32)

adding (2.31) and (2.32), we obtain eventually

(2.33)

that is, the usual approximation.

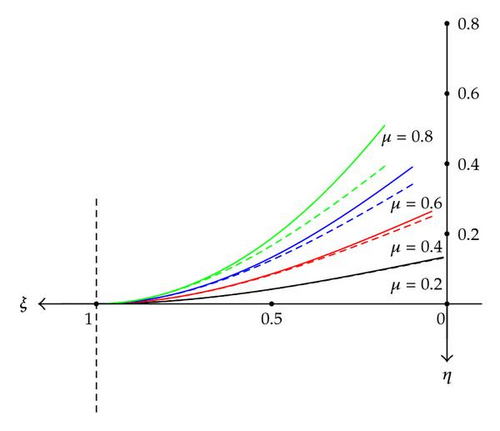
Going again to formula (2.25), his peculiarities are: it is nondimensional; it is new, in closed form, exact, and explicit. Moreover, for being implemented, no previous transcendental equation has to be solved; it requires only to compute the dimensionless parameter μ = (RL²)/(2EJ) holding all the rod physical data.

On the purpose, it will be observed that in [33], an eigenvalue problem is solved through a double boundary condition of no rotation at the ends of the rod. The authors get the coordinates of elastica parametrized to the external load and marked by the mode number. For our same load, they show four elastica each relevant to a given load, but referring to the static mode n = 1. Other curves are provided referring to the first dynamic mode, n = 2. Furthermore, the module k of the Jacobi elliptic functions involved there, is on its own depending on the tip load P via an equation to be solved previously. Nevertheless the (essential!) relationship k⇆P keeps unrevealed, because the authors at page 740 write:

The modulus of elliptic functions k and the parameter F₁ play the role of integration constants and they are related to the force P and the angle φ₀ by boundary conditions for each case of rod bending.

In fact, they do not provide the k computation at all, marking their plot solutions not in terms of P (as it should be done), but of a sequence of k values 0.5; 0.6; 0.85; 1 − 10⁻⁵ see Figure 2, page 742 of [33], so that their (x, y) solution seems to be not easily accessible from P.

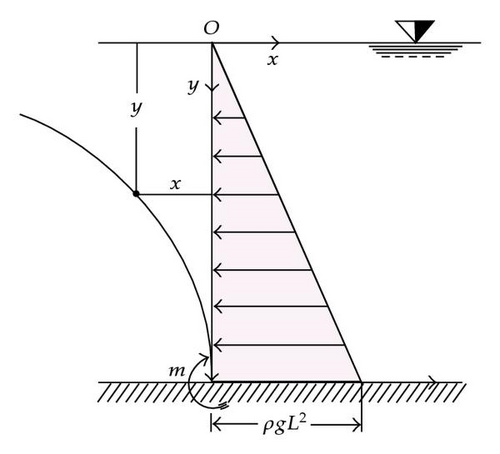
2.4. The Rod Inflected by Hydrostatic Pressure

We are looking for the shape of a (L, EJ) slender and thin cantilever clamped at the bottom of a pool of calm water. The rod weight has been deliberately ignored, being partially balanced by the Archimedes buoyancy. The rod is at full length submerged, being obvious the adjustments for a rod leaning out the water or whose tip is under the sheet of water. We assume, as in Figure 6, a reference with the y axis downwards and x over the water surface. The hydrostatic head, being ρ the liquid mass density and g the gravity, will have a linearly deep-growing profile (Stevin), so that, integrating twice such a head, one arrives at the bending moment

(2.34)

By the usual identification, we obtain the solution to our elastica through the Lauricella function of three variables

(2.35)

where σ = ρgL⁵/24EJ, so that

(2.36)

For being compliant with the IRT requirements, it will be |x_k| < 1, and then σ < 1.

2.5. The Rod Loaded by a Sinusoidal Bending Moment

Assumption A3 implies that our systems are ruled by differential equations affected by a geometrical nonlinearity due to the nonlinear link between the curvature ϰ and y_x. But ϰ, which is the consequence on the rod, is linked to its cause, namely, the bending moment M, by a Linear Constitutive Law ϰ = ±M/EJ, being EJ the flexural stiffness. Such a linearity implies that, by superposition, whenever some moment distribution is repeated periodically, we can make its Fourier expansion, so that the rod bending moment is broken out into the addition of an infinitely many harmonics sine/cosine. In such a way, one will get the elastica by superposition, of course retaining those harmonics deemed useful or necessary.

What above provides enough motivation for analyzing once for all, the effect of the sinusoidal load, whose a half wave only is taken, omitting all the possible variants or subcases. Seeing Figure 7, let q(x) be the continuous transverse load (whose highest value is Q) over the unit of an L-length flexible cantilever

(2.37)

Integrating twice such a load, one arrives at the bending moment affecting the x-section

(2.38)

In such a way, introducing ε = L³Q/(π³EJ) > 0, with⁸ ε ≪ 1, following (2.9), we find

(2.39)

If 1 + cos (πζ) = u/ε, so that

(2.40)

By the integration Tables [25], entries 254.12 page 113 and 337.01 page 201, we can establish an integration formula, embedding (2.40) as a particular case: let a > b ≥ y > c > d and define

(2.41)

then

(2.42)

where Π(φ, α², k) is again the elliptic integral of third kind and F(φ, k) of first kind. Being 2ε < 1, in (2.40), we do the identification

(2.43)

so that our elastica is

(2.44)

where

(2.45)

Figure 8, performed through Mathematica, provides the overlapping of the integral (2.39) numerically computed and the plot consequent to our compact smart formula (2.44).

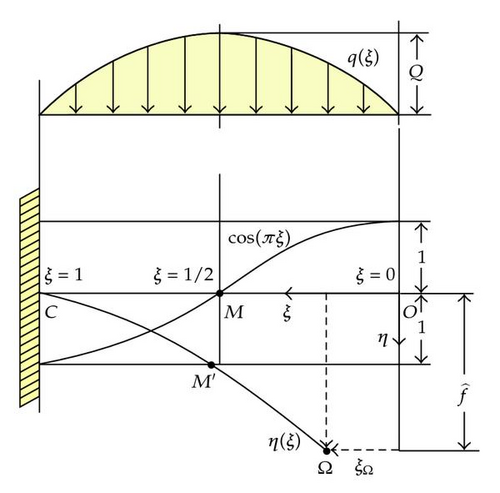
3. How to Compute the Tip Position after the Strain

Considering the small deflections, the deformed centerline′s curvature is approximately equated to the deflection′s second derivative, assuming the rod deformation field to proceed along purely vertical displacements. If it is so, the free end O(ξ = 0, η = 0) will be mapped to ξ = 0, with η(0) ≠ 0, but having the elastica as horizontal projection, its full unstrained length, then the rod will undergo extension.

With large displacements all, this is not true any more, and a further unknown will appear, namely, the abscissa ξ_Ω of the new position Ω, where O has been mapped to. Rod′s behavior under strain can be modeled in several ways. For instance in [9] after integrating the elastica, the authors write five congruence relationships involving geometric quantities before and after the strain and then leave the rod free of extension.

Following a completely different method, in [34] some possible alternatives like rotational load, load always perpendicular to the tangent at the tip and so on, are taken into account.

Anyway, the simplest criterion is the inextensibility assumption A4; the rod keeps its originary length⁹. For the horizontal weightless cantilever inflected by a tip shear (see Figure 3), the elastica η(ξ) has been provided by means of the elliptic integrals, see formula (2.25). Wishing to compute the tip deflection f, the approximate beam theory would answer f = η(0), but with large deflection, we have first to detect ξ_Ω what is done assuming the unextensibility

(3.1)

We see that ξ_Ω is the sole unknown, having been previously found η_ξ, so that, after ξ_Ω, we will compute f = η(ξ_Ω). let us provide the full treatment for such a case. By plugging

(3.2)

in (3.1), after the change 1 − ξ² = t, we get

(3.3)

Our unknown appears in the upper integration limit; in order to solve (3.3), we need to establish an existence-uniqueness Lemma.

Lemma 3.1. Consider the transcendental x-equation where a > b ≥ x > y ≥ c

(3.4)

Defining

(3.5)

then the equation (3.4) has a unique real root x if and only if

(3.6)

and such a root is given by

(3.7)

where sn(u, k) is the Jacobi sine amplitude of module k.

Proof. Let a > b ≥ x > y ≥ c. Observe that the function

(3.8)

is strictly increasing, and that (3.6) ensures existence of solution of equation (3.4). In order to prove the Lemma, we will refer to [25], formula 234.00, page 74, to establish that

(3.9)

with the φ and k meanings previously introduced. The very last step follows from the inversion:

(3.10)

which delivers x from (3.9), after equating the right hand side to 2μ.

We can then use the Lemma to solve (3.3) via the identification

(3.11)

where it has been assumed¹⁰ μ < 1. Minding that a = 1/μ and c = −1/μ, it should be seen that (3.6) provides an upper limit to the dimensionless load μ solving numerically a transcendental inequality. To such a limit, a physical meaning can be found as the highest allowable load beyond which the linear constitutive law (curvature versus bending couple) is not true any more.

Solving to ξ_Ω, we find out that

(3.12)

Therefore, increasing R intensities¹¹, and then μ, the successive positions of the free tip, that is, the components of the displacement

will be described as functions of μ at Figures 9 and 10.

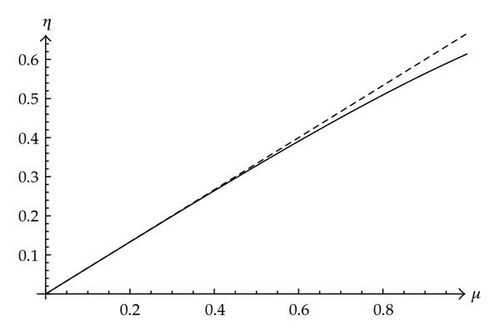
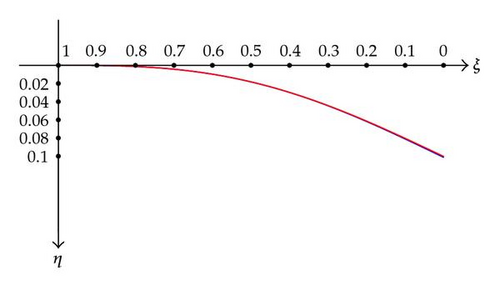
First, the (3.12) relationship is plotted as shown in Figure 9.

Plugging (3.12) in (2.25), we obtain for the tip η as a function of μ alone. But such a formula is too long, and then we will omit here, providing its relevant plot.

4. Conclusions

Five elasticae have been analytically solved of a thin cantilever rod bent by different coplanar “dead” loadings¹², namely, whose direction remains unchanged during the deformation of the rod. They are concentrated couple, tip shear, evenly continuous load, hydrostatic load, and sinusoidal load. Each of them describes a single physical situation for which we obtain the large deflections in closed form through elliptic and/or hypergeometric functions. Some care has been put (tip sheared rod) in providing analytically, via the isometric assumption, the free end position after the strain, parametrizing its coordinates as a function of the load. Some of our solutions, specially that to the heavy rod by the Lauricella functions, have enriched the literature on the elastica.

Acknowledgments

The authors are indebted to their friend Aldo Scimone who drew some Figures of this paper; they hereby take opportunity for thanking him warmly. They wish also to thank the anonymous referee whose valuable criticism improved their article.

Endnotes

1.
A space tether is a long cable used to connect spacecraft to other orbiting bodies such as space stations, boosters, payload, and so forth in order to transfer energy and momentum.
2.
The problem of 3D-elastica is very old, but out of our purpose. We will say only that it first appeared in Lagrange′s Mécanique Analytique 2nd edition (1811). J. Binet (Mémoire sur l′intégration des équations de la courbe élastique à double courbure, 1844) and M. Wantzel (Note sur l′intégration des équations de la courbe élastique à double courbure, 1844) arrived at the same differential system, vaguely formulated, and not affronted. A modern treatment of a particular case can be read in [35], with its specific bibliography.
3.
We quote three works: (a) De progressionibus transcendentibus, Op. omnia, S.1, vol. 28; (b) De curva hypergeometrica Op. omnia, S.1, vol. 16; (c) Institutiones Calculi integralis, 1769, vol. II.
4.
A.M. Legendre, Exercices de calcul intégral, II, quatriéme part, sect. 2, Paris 1811.
5.
In [36] putting R = 2/a, he gets the elastica y(x) through the integral
(4.1)
“Die Kurve welche diese Gleichung entspricht, heißt die elastische Linie weil ein elastischer Stab der an dem Ende befestigt und an dem andern Ende belastet ist, diese Form annimmt.”
6.
Under transversal load at the cantilever tip, this problem in strength of materials is solved in cartesian coordinates following the linear approximation; the solution is found (e.g., see [37, page 305]) to be
(4.2)
in dimensionless form.
7.
Notice that the plots are coming after Mathematica′s computation of our explicit solution (2.25), but adding the map ξ → 1 − ξ in order to provide the geometrical true configuration of the stressed rod.
8.
Inserting in ε some numerical values, for example, L = 5 m, q = 6 N × m⁻¹, EJ = 100 N × m², g = 9,81 m × s⁻², one gets: ε ≈ 3 × 10⁻², so that, unless of assuming unrealistic lengths, ε is essentially much less than unity.
9.
Only in some special cases such a tip path description is quick. For instance for a rod loaded by a fixed couple (Section 2.1), one gets ξ_Ω = 1 − χ, f = χ.
10.
Having for instance L = 1 m, R = 10 N, EJ = 100 N × m², we get μ = RL²/2EJ = 0.05.
11.
Nothing to say, apart from the more strict link imposed by the transcendental inequality (linearity range), (3.12) requires μ ≤ 1.
12.
The contrary case is that of the follower load which is being unchanged in its relationship with the rod, for example, keeping its direction perpendicular—or inclined—to it during and after the strain.

References

1 Fraser C. G., Mathematical technique and physical conception in Euler′s investigation of the elastica, Centaurus. (1991) 34, no. 3, 211–246, https://doi.org/10.1111/j.1600-0498.1991.tb00695.x, 1166072, ZBL0752.01005.
10.1111/j.1600-0498.1991.tb00695.x
Web of Science® Google Scholar
2 Benvenuto E., La Scienza delle Costruzioni e il Suo Sviluppo Storico, 1981, Sansoni, Firenze, Italy.
Google Scholar
3 Schell W., Theorie der Bewegung und der Kräfte, 1880, 2, B.G. Teubner, Leipzig, Germany.
Google Scholar
4 Burgatti P., Teoria Matematica dell′Elasticità, 1931, Zanichelli, Bologna, Italy.
Google Scholar
5 Tricomi F. G., Funzioni Ellittiche, 1951, Zanichelli, Bologna, Italy, 0051362.
Google Scholar
6 Frisch-Fay R., Flexible Bars, 1962, Butterworths, London, UK.
Google Scholar
7 Goss V. G. A., The history of the planar elastica: insights into mechanics and scientific method, Science and Education. (2009) 18, no. 8, 1057–1082, 2-s2.0-71449117434, https://doi.org/10.1007/s11191-008-9166-2.
10.1007/s11191-008-9166-2
Google Scholar
8 Basoco M. A., On the inflexional elastica, The American Mathematical Monthly. (1941) 48, 303–309, 0004315.
10.1080/00029890.1941.11991117
Google Scholar
9 Chucheepsakul S. and Phungpaigram B., Elliptic integral solutions of variable-arc-length elastica under an inclined follower force, Zeitschrift für Angewandte Mathematik und Mechanik. (2004) 84, no. 1, 29–38, https://doi.org/10.1002/zamm.200410076, 2031243, ZBL1047.74036.
10.1002/zamm.200410076
Web of Science® Google Scholar
10 Goto Y., Yoshimitsu T., and Obata M., Elliptic integral solutions of plane elastica with axial and shear deformations, International Journal of Solids and Structures. (1990) 26, no. 4, 375–390, https://doi.org/10.1016/0020-7683(90)90063-2, 1040389, ZBL0706.73039.
10.1016/0020-7683(90)90063-2
Web of Science® Google Scholar
11 Panayotounakos D. E. and Theocaris P. S., Exact solution of the non-linear differential equation concerning the elastic line of a straight rod due to terminal loading, International Journal of Non-Linear Mechanics. (1982) 17, no. 5-6, 395–402, 687305, https://doi.org/10.1016/0020-7462(82)90009-9, ZBL0498.73042.
10.1016/0020-7462(82)90009-9
Web of Science® Google Scholar
12 Panayotounakos D. E. and Theocaris P. S., Exact solution for an approximate differential equation of a straight bar under conditions of a non-linear equilibrium, International Journal of Non-Linear Mechanics. (1986) 21, no. 5, 421–429, https://doi.org/10.1016/0020-7462(86)90024-7, 870067, ZBL0601.73049.
10.1016/0020-7462(86)90024-7
Web of Science® Google Scholar
13 Panayotounakos D. E. and Sotiropoulos A. B., Exact parametric analytic solutions of the elastica ODEs for bars including effects of the transverse deformation, International Journal of Non-Linear Mechanics. (2004) 39, no. 10, 1555–1570, https://doi.org/10.1016/j.ijnonlinmec.2003.09.004, 2085730.
10.1016/j.ijnonlinmec.2003.09.004
Web of Science® Google Scholar
14 Panayotounakos D. E. and Theocaris P. S., Analytic solutions for nonlinear differential equations describing the elastica of straight bars: theory, Journal of the Franklin Institute. (1988) 325, no. 5, 621–633, https://doi.org/10.1016/0016-0032(88)90037-3, 952306, ZBL0655.73028.
10.1016/0016-0032(88)90037-3
Web of Science® Google Scholar
15 Lardner T. J., A note on the elastica with large loads, International Journal of Solids and Structures. (1985) 21, no. 1, 21–26, https://doi.org/10.1016/0020-7683(85)90102-7, 867167.
10.1016/0020-7683(85)90102-7
Web of Science® Google Scholar
16 Jung J. H., Kang T. J., and Lee K. W., Elliptic integral solutions of the large deflection of a fiber cantilever with circular wavy crimp, Textile Research Journal. (2003) 73, no. 1, 47–54, 2-s2.0-0037281290, https://doi.org/10.1177/004051750307300109.
10.1177/004051750307300109
CAS Web of Science® Google Scholar
17 Dickey R. W. and Roseman J. J., Equilibria of the circular elastica under a uniform central force field, Quarterly of Applied Mathematics. (1993) 51, no. 2, 201–216, 1218364, ZBL0774.73033.
10.1090/qam/1218364
Web of Science® Google Scholar
18 Mingari Scarpello G. and Ritelli D., Elliptic integrals solution to elastica′s boundary value problem of a rod bent by axial compression, Journal of Analysis and Applications. (2007) 5, no. 1, 53–69, 2297083, ZBL1141.74313.
Google Scholar
19 Mingari Scarpello G. and Ritelli D., Elliptic functions solution to exact curvature elastica of a thin cantilever under terminal loads, Journal of Geometry and Symmetry in Physics. (2008) 12, 75–92, 2498781, ZBL1157.74024.
Google Scholar
20 Antman S. S., Nonlinear Problems of Elasticity, 1995, Springer, New York, NY, USA, 1323857.
10.1007/978-1-4757-4147-6
Google Scholar
21 Love A. E. H., A Treatise on the Mathematical Theory of Elasticity, 1944, 4th edition, Dover, New York, NY, USA, 0010851.
Google Scholar
22 Coyne J., Analysis of the formation and elimination of loops in twisted cable, IEEE Journal of Oceanic Engineering. (1990) 15, no. 2, 72–83, 2-s2.0-0025418925, https://doi.org/10.1109/48.50692.
10.1109/48.50692
Web of Science® Google Scholar
23 Beletsky V. V. and Levin E. M., Dynamics of Space Tether Systems, 1993, American Astronautical Society, Advances in the Astronautical Sciences Volume 83.
Google Scholar
24 Mattiasson K., Numerical results from large deflection beam and frame problems analysis by means of elliptic integrals, International Journal for Numerical Methods in Engineering. (1981) 17, no. 1, 145–153, 2-s2.0-0019381989, https://doi.org/10.1002/nme.1620170113, ZBL0453.73088.
10.1002/nme.1620170113
Web of Science® Google Scholar
25 Byrd P. F. and Friedman M. D., Handbook of Elliptic Integrals for Engineers and Scientists, 1971, 2nd edition, Springer, New York, NY, USA, 0277773.
10.1007/978-3-642-65138-0
Google Scholar
26 Dutka J., The early history of the hypergeometric function, Archive for History of Exact Sciences. (1984) 31, no. 1, 16–34, https://doi.org/10.1007/BF00330241, 769538, ZBL0554.01013.
10.1007/BF00330241
Web of Science® Google Scholar
27 Saran S., Hypergeometric functions of three variables, Ganita. (1954) 5, 77–91, 0087777, ZBL0058.29602.
Google Scholar
28 Lauricella G., Sulle funzioni ipergeometriche a più variabili, Rendiconti del Circolo Matematico di Palermo. (1893) 7, no. 1, 111–158, 2-s2.0-11644322139, https://doi.org/10.1007/BF03012437.
10.1007/BF03012437
Google Scholar
29 Navaee S. and Elling R. E., Equilibrium configurations of cantilever beams subjected to inclined end loads, Journal of Applied Mechanics. (1992) 59, no. 3, 572–579, 2-s2.0-0026912090, https://doi.org/10.1115/1.2893762.
10.1115/1.2893762
Web of Science® Google Scholar
30 Landau L. and Lifchitz E., Théorie de l′Élasticité, 1967, MIR, Moscow, Russia.
Google Scholar
31 Mathieu E., Dynamique Analytique, 1876, Gauthier Villars, Paris, Farnce.
Google Scholar
32 Saalschütz L., Der Belastete Stab unter Einwirkung einer Seitlichen Kraft, 1880, B.G. Teubner, Leipzig, Germany.
Google Scholar
33 Zakharov Y. V. and Okhotkin K. G., Nonlinear bending of thin elastic rods, Journal of Applied Mechanics and Technical Physics. (2002) 43, 739–744, https://doi.org/10.1023/A:1019800205519, ZBL1002.74055.
10.1023/A:1019800205519
Google Scholar
34 Rao B. N. and Rao V. G., On the large deflection of cantilever beams with end rotational load, Zeitschrift für Angewandte Mathematik und Mechanik. (1986) 66, no. 10, 507–508.
10.1002/zamm.19860661027
Web of Science® Google Scholar
35 Mingari Scarpello G. and Ritelli D., Elliptic integral solutions of spatial elastica of a thin straight rod bent under concentrated terminal forces, Meccanica. (2006) 41, no. 5, 519–527, https://doi.org/10.1007/s11012-006-9000-3, 2284832, ZBL1163.74525.
10.1007/s11012-006-9000-3
Web of Science® Google Scholar
36 Kiepert L., Grundriss der Differential-und Integral-Rechnung II. Teil, 1918, Hannover Helwingsche Verlagsbuchhandlung.
Google Scholar
37 Belluzzi O., Scienza delle Costruzioni, 1970, 1, Zanichelli, Bologna, Italy.
Google Scholar

Citing Literature

All articles

Exact Solutions of Nonlinear Equation of Rod Deflections Involving the Lauricella Hypergeometric Functions

Abstract

1. Introduction

1.1. A Literature′s Overview

1.2. Aim of the Paper

1.3. Special Functions Tools

2. Bent Slender Rod: A Large Deflections 2D-Model

2.1. Rod Inflected by a Constant Bending Couple at Its Tip

2.2. The Horizontal Heavy Rod

2.3. A Tip-Sheared Horizontal Rod

2.4. The Rod Inflected by Hydrostatic Pressure

2.5. The Rod Loaded by a Sinusoidal Bending Moment

3. How to Compute the Tip Position after the Strain

4. Conclusions

Acknowledgments

Endnotes

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exact Solutions of Nonlinear Equation of Rod Deflections Involving the Lauricella Hypergeometric Functions

Abstract

1. Introduction

1.1. A Literature′s Overview

1.2. Aim of the Paper

1.3. Special Functions Tools

2. Bent Slender Rod: A Large Deflections 2D-Model

2.1. Rod Inflected by a Constant Bending Couple at Its Tip

2.2. The Horizontal Heavy Rod

2.3. A Tip-Sheared Horizontal Rod

2.4. The Rod Inflected by Hydrostatic Pressure

2.5. The Rod Loaded by a Sinusoidal Bending Moment

3. How to Compute the Tip Position after the Strain

4. Conclusions

Acknowledgments

Endnotes

References

Citing Literature

Figures

References

Related

Information