International Journal of Mathematics and Mathematical Sciences
Volume 2011, Issue 1 746918
Research Article
Open Access

A New Solution for the Director Relaxation Problem in Twisted Nematic Film Based on Wavelet Analysis

Aleksey Kudreyko, 

Corresponding Author

Aleksey Kudreyko

Department of Mathematics and Computer Science, University of Salerno, Via Ponte Don Melillo, 84084 Fisciano (SA), Italy unisa.it

Search for more papers by this author
Nail Migranov, 

Nail Migranov

Department of Engineering Physics, Bashkir State University, 100 Mingazheva Street, Ufa 450014, Russia bsunet.ru

Search for more papers by this author
First published: 22 March 2011
https://doi.org/10.1155/2011/746918
Academic Editor: Hari Srivastava

Abstract

The present research considers and explains the application of the Haar wavelets as basis functions in solution of the propagation of perturbations in low-dimensional anisotropic media. The computations of the relaxation problem in the form of traveling waves have shown that the present approach possesses several advantages over regular methods.

1. Introduction

Not to mention that the study of such non-Newtonian fluids as liquid crystals (LC) has lead to the commercial production of widely used electronic devices, the theory of LC still has a few problems, whose solution presents a difficulty. The problem of a director relaxation in twisted nematic cells (TNCs) in the form of nonlinear waves still remains unsolved. TNCs are integral parts of liquid crystal displays, which are used in laptops and personal computers. TNC is a drop of LC placed between two parallel surfaces, separated by a spacer, and arranged in such a way that the director in the upper surface n+ of the liquid crystal cell is perpendicular to the director in the lower surface n−; in this case, the director always lies in the plane parallel to the two bounding surfaces. In the absence of an external electric field, a linear director field distribution is characterized by the azimuthal angle Φ = (π/2)z and governed by van der Waals′ forces [1, 2]. Here, Φ is the azimuthal angle formed by the director and the X-axis lying in the same plane, the Z-axis is perpendicular to the bounding surfaces, and the origin of the coordinate system is located at the lower surface of the twisted nematic cell. In response to an external electric field E = Ej aligned parallel to the two bounding surfaces along the Y-axis, the twist re-orientation of the director field occurs toward the external electric field. The threshold value of the external electric field, when nonlinear relaxation mechanisms of the director field can occur, we will denote as Ecr.

The use of TNC in production of LC monitors provided a strong encouraging stimulus for intensive research in this field. The present paper shows that angular moments acting on a unit element of nematic LC can generate traveling waves along the Z-axis. This problem can be easily reduced to the solution of dimensionless parabolic partial differential equation.

The goal of the paper is to present the director relaxation problem using the Haar wavelet method [3]. The earlier effort for the solution of this problem was realized in [2]. However, the considered mathematical model does not take into account the perpendicularity of the directors′ orientations located in the plane of bounded plates at the initial moment t = 0.

Methods of wavelet analysis adapted for the solution of partial differential equations have been actively developing in the past 15 years. The advantages of the application of wavelets for the solution of differential problems over regular numerical methods consist of linearly increasing computational costs because of the sparsity of intermediate matrices. Moreover, the quality of solutions obtained by analytically defined basis functions always exceeds classical numerical methods.

2. Problem Formulation

The dynamic equation based on the balance of elastic, electric, and hydrodynamic torques [2, 4] is written as follows:
(2.1)
where Δ = ɛ0ɛaE2/2, ɛ0 is the vacuum permittivity and ɛa-dielectric anisotropy coefficient of nematic LC, K2 is the twist elastic constant.
In order to study the problem of propagation of the traveling wave from the top plate to the bottom plate, it is convenient to present (2.1) with respect to dimensionless coordinates
(2.2)
where t = τγ1/ɛ0ɛaE2, τ-dimensionless time and , -dimensionless coordinate [2].
The purpose of our approach consists of the study of the generation process of a traveling wave running between bounded plates by means of wavelet basis. In the coordinate system, connected with the motion of disturbance in the media, we can introduce , where v is the dimensionless velocity of wave propagation. Taking into account the rule of differentiation for complex functions, the left-hand side of (2.2) generates two terms. Thus, this equation takes the form
(2.3)
In the case of strong anchoring of LC molecules with bounding surfaces, the torque balance for these surfaces leads to the following boundary and initial conditions:
(2.4)
where H presents the Heaviside step function. The main feature of such an initial condition is that the solution strongly satisfies the upper boundary condition by adding sin (which was not fulfilled in [2]). Otherwise, the initial condition means that at the initial moment, , which is physically wrong. The location of the external disturbance is set at our choice. The number 8.9999 means that the Gaussian cannot belong to two intervals of the Heaviside step function. Such form of the initial condition can be generated by a laser pulse [2].

3. Haar Wavelets

From all families of wavelets, we can distinguish a few easily defined functions, which represent a powerful tool in the solution of partial differential equations. Such wavelets are: Shannon wavelets [5], harmonic wavelets [6], and Haar wavelets. The latter wavelets are wellstudied in [3, 7, 8] and references therein.

The family of Haar wavelets for q ∈ [0; 1] is defined as follows:
(3.1)
where integer numbers m = 2j, j = 0,1, …, J show the approximation level of a wavelet k = 0,1, …, m − 1 is the dilation parameter. Index i can be computed as follows: i = m + k + 1, and its minimum value is 2. The maximum value of i is 2M = 2J+1. The scaling function corresponds to i = 1
(3.2)
In order to proceed the solution of (2.3), we must compute [3] the following integrals:
(3.3)
Thus, Haar wavelets are transformed into piecewise polynomials of the second order. To get the solution of (2.3) with initial and boundary conditions (2.4), we will employ the collocation method. The idea of this method consists of the following: differential equation (2.3) is fulfilled in equally spaced points (the so-called collocation points) within the space bounded by the plates. Define the location of collocation points as follows:
(3.4)
Also, let us introduce matrices H, P, R with its elements H(i, l) = hi(ql), P(i, l) = pi(ql), and R(i, l) = ri(ql). It is necessary to underline that the dimension of these matrices equals to 2M × 2M.

4. Solution of the Base Equation

The unknown function in (2.3) is searched within the interval τ ∈ [τs, τs+1] as the following series:
(4.1)
where the wavelet coefficients as(i) represent coordinates of a vector of dimension 2M. If τ differs from [τs, τs+1], then coefficients as(i) change their values.

It is obvious to present a question about our choice of basis functions. As we know, many other bases exist, which could be suitable for the solution of this problem. The answer to this question should be originated from the limited opportunities of disclosure of the angle between two directors located in parallel planes, and separated by distance Δz(Δq*). It thus appears the discretization of the space variable, and the plot of Φ(τs, q) can be presented by means of scaling functions pi(q) and ri(q) without any losses of the corresponding data.

Since the Haar wavelets are defined for q ∈ [0; 1], then we must present (2.3) in new variables, that is,
(4.2)
In view of formulae (4.2), (2.3) takes the form
(4.3)
At this point we have everything to proceed to the study of the relaxation process in a TNC governed by the external electric field E = Ej. Let us integrate (3.1) with respect to τ on interval [τs, τs+1], and twice with respect to q on [0; q]. Then, we get
(4.4)
The boundary condition on the bottom plate yields , while the one on the top plate gives . Then, we obtain
(4.5)
The substitution of (4.5) into (4.4) and the corresponding discretization of independent variables gives the following system of equations:
(4.6)
The initial values of Φ1(l), can be computed from the initial condition (2.4) and the corresponding change of variables (4.2).

The solution of (2.3) with initial and boundary conditions (2.4) in the moving coordinate system was obtained by the Haar wavelet method and was illustrated in Figure 1. The initial disturbance of the director′s field in a TNC was generated close to the top plate.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Propagation of the traveling wave Φ(τ, q) in a TNC for the moving coordinate system. Parameters of the method: J = 7, Δτ = 0.005; parameters of the problem: v = 2, q1 = 0, 2q2 = 10, σ = 0.25, q3 = 8.

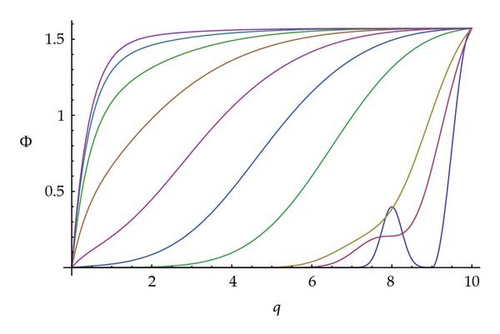
The simulations have shown that this approach for the problem of relaxation of a director toward its equilibrium position allows its the computation of different dynamic modes in TNC. The relaxation of a director with respect to the laboratory coordinate system is shown in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Propagation of the traveling wave with respect to the laboratory coordinate system Φ((E/Ecr)(z/d) − vτ) versus z/d*10−1. Parameters of the method: J = 7, Δτ = 0.005; parameters of the problem: q1 = 7 − vτ, q2 = 10, v = 2, σ = 0.25, E/Ecr = 10.

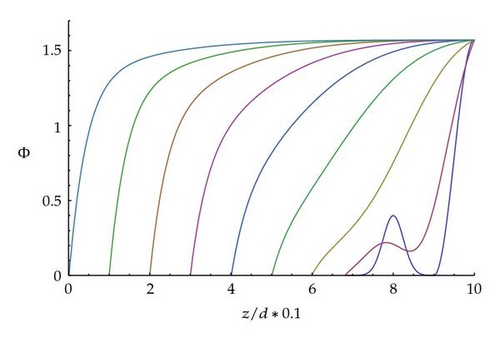
The criterion for relaxation of a director was chosen in the form: ɛ = |Φ(τs+1) − Φ(τs)| ≤ 10−4. In other words, if the azimuthal angle between two time steps is less than ɛ, then the algorithm stops. It is worth emphasizing that the Haar wavelet method permits to get solutions with a smaller error. However, in this case, lower values of ɛ do not play any significant role and only increase the CPU load.

5. Conclusions

The present paper describe the phenomenon of spatial relaxation in a TNC for the case of strong anchoring of LC molecules with the bounded plates. It was suggested to employ the Haar wavelet method for getting a function, which describes the evolution of the azimuthal angle. The advantage of such an approach over regular methods is that the unknown function is searched as a superposition of analytically defined functions, which constitute a complete basis in the L2[0; 1] space. Another reason for our choice of basis functions is low computational costs conditioned [8] by the sparsity of matrix as(i).

Acknowledgments

The work of A. A. Kudreyko is supported by the Istituto Nazionale di Alta Matematica Francesco Severi (Rome-IT) under scholarship U 2010/000139, 1 October 2010. A. A. Kudreyko is thankful to Professor Carlo Cattani (University of Salerno) for many valuable discussions.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.