Probabilistic Modeling of Fatigue Damage Accumulation for Reliability Prediction
Abstract
A methodology for probabilistic modeling of fatigue damage accumulation for single stress level and multistress level loading is proposed in this paper. The methodology uses linear damage accumulation model of Palmgren-Miner, a probabilistic S-N curve, and an approach for a one-to-one transformation of probability density functions to achieve the objective. The damage accumulation is modeled as a nonstationary process as both the expected damage accumulation and its variability change with time. The proposed methodology is then used for reliability prediction under single stress level and multistress level loading, utilizing dynamic statistical model of cumulative fatigue damage. The reliability prediction under both types of loading is demonstrated with examples.
1. Introduction
Most of the mechanical components are subjected to fatigue due to random loading as well as constant amplitude loading during their usage. Fatigue is also recognized as one of the main reasons for failure of mechanical components [1]. This has led to a need for developing new approaches to predict the reliability and useful life of mechanical components, which are subjected to fatigue damage. This has been the primary focus of designers for many years, and the field still presents many challenges, even though extensive progress has been made in the past few decades [2].
Earlier models of fatigue damage accumulation reported in the literature focus on deterministic nature of the process whereas in practice, damage accumulation is of stochastic nature. This stochasticity results from the randomness in fatigue resistance of material as well as that of the loading process [3]. As a result of this, even under constant amplitude fatigue test at any given stress level, the fatigue life shows stochastic behavior with a specific distribution. The literature shows that fatigue life data follows either normal or log-normal distribution under constant amplitude or random loading [4–6]. Weibull distribution has also been reported to fit fatigue life data [7, 8], though there are no apparent physical or mathematical phenomenon explained for this [9]. Researchers have proposed different modeling approaches to the probabilistic damage accumulation paradigm. Shen et al. [3] developed a probabilistic distribution model of stochastic fatigue damage, wherein they have considered the randomness of loading process as well as the randomness of fatigue resistance of material by introducing a random variable of single cycle fatigue damage. Liu and Mahadevan [2] proposed a general methodology for stochastic fatigue life under variable amplitude loading by combining a nonlinear fatigue damage accumulation rule and stochastic S-N curve representation technique. Nagode and Fajdiga [10] have modeled a probability density function (PDF) of failure cycles at any stress level as a normal distribution based on the DeMoivre-Laplace principle to reliably predict endurance limit of a randomly loaded structural component. Liao et al. [11] proposed a new cumulative fatigue damage dynamic interference model assuming that cumulative damage follows normal or lognormal distribution. Wu and Huang [12] modeled fatigue damage and fatigue life of structural components subjected to variable loading as a Gaussian random process. Ben-Amoz [13] developed a cumulative damage theory based on the concept of bounds on residual fatigue life in two-stage cycling. Castillo et al. [14] developed a general model for predicting fatigue behavior for any stress level and range by generalizing the Weibull model. Sethuraman and Young [15] have developed a cumulative damage threshold crossing model. This model considers a multicomponent product which undergoes deterioration/damage at regular intervals of time and failure occurs as soon as the maximum damage to some component crosses a certain threshold. Time to failure data is used to estimate the model parameters. A comprehensive review of cumulative fatigue damage and life prediction theories can be found in Fatemi and Yang [16].
Two aspects are significantly important from the point of view of modeling probabilistic fatigue damage. First, an accurate physical damage accumulation model needs to be in place to predict expected or nominal fatigue damage. Second, an appropriate uncertainty modeling technique is required to account for stochasticity [2]. A review of literature has indicated that handling of stochasticity in modeling uncertainty involve complex mathematics. This fact is the primary motivation behind the development of a simpler approach for handling stochasticity in fatigue damage accumulation modeling in the proposed research work. This paper proposes a simpler approach to deduce the distribution of a fatigue damage accumulation from the fatigue life distribution using a one-to-one transformation methodology and to a certain extent attempts to minimize the mathematical complexity. It also proposes a simple and unique way to model the damage accumulation process treating it as a nonstationary probabilistic process to capture damage accumulation and its variability at any given point of time. The proposed methodology can be effectively used to predict reliability of mechanical components subjected to fatigue loading due to single stress level and multi-stress level.
An outline of this paper is as follows. Section 2 elaborates an approach for modeling probabilistic damage accumulation to capture expected values of damage and its variability. Section 3 presents a reliability prediction approach utilizing dynamic model of cumulative fatigue damage. The applicability of proposed methodology and its implications are illustrated with help of examples in Section 4. The conclusion is presented in Section 5.
2. Modeling Probabilistic Fatigue Damage Accumulation
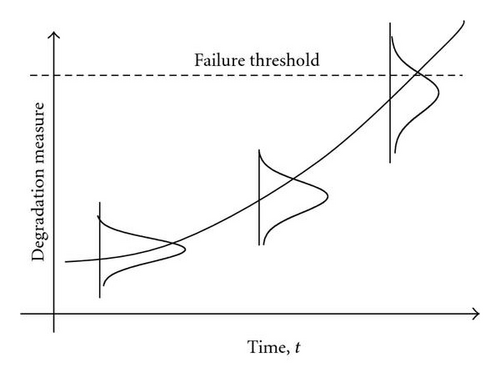
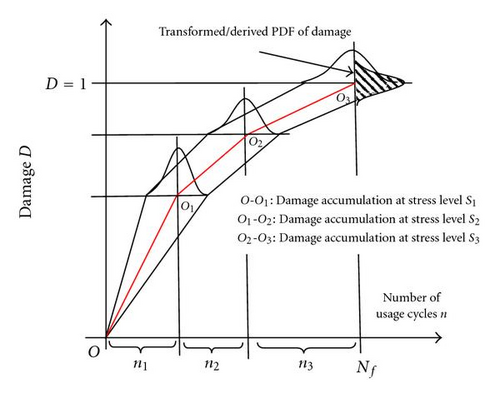
Damage accumulation is a complex and irreversible phenomenon, wherein the damage of the product under consideration gradually accumulates and over a period of time leads to its failure. Therefore, damage accumulation can be treated as a measure of degradation in fatigue resistance of materials. Moreover, the damage accumulation is probabilistic in nature and it can be depicted graphically as shown in Figure 1. The Figure shows monotonically increasing degradation path where the degradation measure is increasing probabilistically with time.
2.1. Modeling Expected Value of Damage Accumulation

2.2. Distribution of Fatigue Damage Accumulation
In order to establish the PDF of the damage accumulation measure (D) and to estimate distribution parameters, first the fatigue failure life is treated as random variable which follows certain distribution. Thereafter, the distribution of D is derived using the one-to-one PDF transformation methodology proposed by Benjamin and Cornell [18]. As per Benjamin and Cornell [18], the unknown PDF of a random variable can be derived using this transformation technique, if that variable is directly or functionally related to another random variable whose PDF is already known. Since cumulative damage accumulation is a function of usage life (or fatigue failure life), the PDF transformation methodology provides an effective means to establish distribution of damage accumulation measure. In Figure 3, line l1 is the trend line of expected damage accumulation as given by (5) at a given stress level (S). The straight line depicts a linear relation between the damage accumulation measure and usage cycles (n). Now assuming that the PDF of usage cycles is known, Figure 3 provides the basic understanding of how this known PDF of fatigue life can be used to obtain the PDF of the damage accumulation measure. It must be noted, as shown in Figure 3, that initial variability of usage cycles is zero and it follows increasing trend in variability with increase in usage cycle. It is further assumed that this increase in variability also follows a linear trend as suggested by Coit et al. [20].
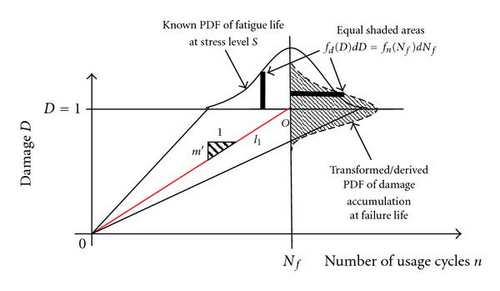
From the above discussion, it is clear that in order to derive the distribution of D using Benjamin and Cornell’s [18] PDF transformation technique, there are two basic requirements that need to be fulfilled: (i) a clearly defined relation between damage accumulation and usage cycles and (ii) the knowledge of the distribution or PDF of the usage cycle.
2.2.1. Application of the PDF Transformation Technique for Deriving the PDF of the Damage Accumulation Measure
Assuming that slope of the damage accumulation trend line is constant for any given stress level, the variability in damage accumulation can be treated as a function of the variability in usage cycle. Equations (17) and (18) derived using one-to-one transformation approach clearly explain that the PDF of damage accumulation will be the same as usage life distribution because of linear relationship between these two variables. However, the resulting PDF of damage accumulation is scaled down by factor m′.
2.3. Modeling Trend Line of Variance
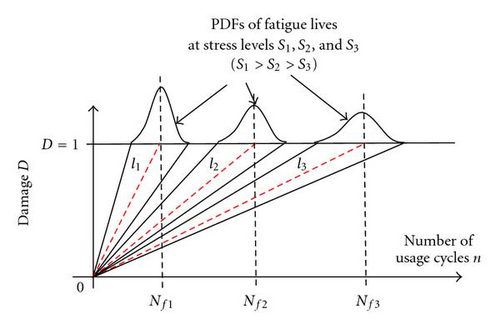
As already discussed, the damage accumulation increases linearly with usage cycles at a given stress level. Further, Figure 4 shows increasing trend in variability or standard deviation of fatigue lives with decrease in stress levels as well. It must also be noted that the variability is zero at the initial stage (i.e., at n = 0) for all the stress levels. This indicates the presence of a trend of increasing variance in fatigue lives as stress level decreases, that is, there is low variability in fatigue life at higher stress level and higher variability in fatigue life when product is subjected to lower stress levels as shown in Figure 4. The challenge is to capture this increasing trend in variability with stress levels as well as usage cycle and model it into total variability of damage accumulation.
- (1)
At constant stress level, the variability in damage accumulation increases monotonically with increase in usage cycles as explained by Wang and Coit [17] and Coit et al. [20].
- (2)
The variability in fatigue life is lower at higher stress levels, whereas it monotonically increases with decrease in stress levels as shown in Figures 2 and 4. Pascual and Meeker [21] have also stated that in most fatigue experiments, the variance of the fatigue life increases as stress decreases, and therefore the standard deviation of fatigue life can be modeled as monotonic function of stress. In fact, the variability in fatigue life of a product subjected to multiple stress levels is another major source of variability in damage accumulation.
In order to model total variability in damage accumulation, these two sources of variability need to be considered. The following section elaborates the modeling of variability in damage accumulation considering these two aspects.
2.3.1. Deriving the Equation for the Variance Trend Line
Given the fact that the variability in usage cycles continuously increases from zero to a certain value at fatigue failure life, its rate of change can be interpreted using geometric reasoning. This is shown diagrammatically in Figure 5.
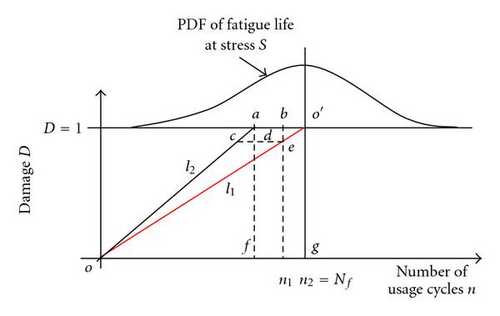
As shown in Figure 5, l1 represents the mean damage accumulation trend line and line l2 connects the origin with 1σ point (i.e., point a in Figure 5) of the fatigue life distribution. Therefore, ao′ represents one standard deviation distance from center point of the fatigue life distribution, and hence, . Let us assume that slopes of these two lines l1 and l2 are represented as m′ and m′′, respectively.
The above equation represents a model that can be used to capture the variability in damage accumulation for a single stress level. The same model can be extended to capture the variability in damage accumulation if the product is subjected to multi-stress level as well. Figure 6 illustrates the concept of how variance of usage cycles changes in a multilevel stress loading scenario.
In the next section, the models developed for capturing damage accumulation and its variability are used in conjunction with the dynamic statistical model for predicting the reliability of mechanical components.
3. Reliability Prediction
- (1)
Fatigue failure occurs when damage accumulation (D) reaches the threshold damage (Dc), where E(Dc) = 1.
- (2)
The threshold damage or critical damage has the same distribution as the damage accumulation measure.
- (3)
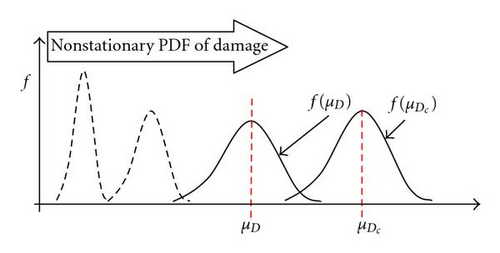
When usage life is equal to the fatigue failure life (n = Nf), the variability of threshold damage accumulation is equal to the variability of damage accumulation measure. The variability of damage accumulation measure continuously increases with usage life but when usage cycle reaches to fatigue failure level, the corresponding variability is assumed to be the same as variability of threshold damage accumulation. However, it is statistically independent of (D).
A diagrammatic representation of the above concept is shown in Figure 7. It is important to note that when usage cycle is equal to failure life (n = Nf), the variability of threshold damage accumulation will be equal to the variability of damage accumulation ().
4. Example
To demonstrate the applicability of the proposed reliability assessment approach, fatigue test data required to model S-N curve is adopted from Zaccone [7], which were obtained after conducting fatigue tests on helical compression springs used in compressors. Table 1 shows the fatigue test data at different amplitude stress levels and corresponding standard deviation considered.
| Constant amplitude stress (MPa) (Si) | Mean number of cycle to failure (Nf) | Standard deviation |
|---|---|---|
| 470 | 33581 | 4785 |
| 435 | 64616 | 9692 |
| 395 | 146101 | 23291 |
| 360 | 320222 | 53947 |
| 320 | 867130 | 156303 |
4.1. Reliability Prediction for a Single Stress Level
Using these values of variables and parameters, the variability at threshold damage is obtained as .
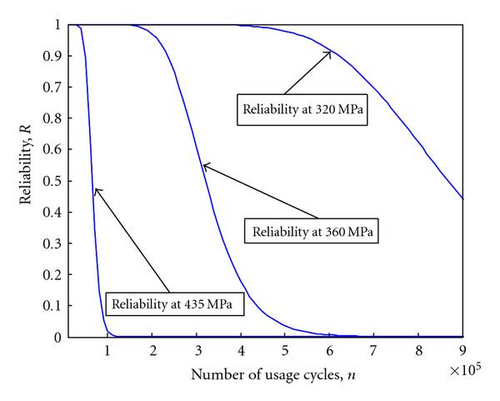
Considering reliability function equation (39), Figure 8 illustrates a reliability plot for single stress level at 435 MPa, 360 MPa, and 320 MPa. These reliability plots clearly reveal the trend of reliability loss with increase in usage cycles. The careful analysis of these reliability plots indicate that reliability remains higher (almost constant) for initial period and later on starts declining with usage cycle. This phenomenon explains existing understanding of crack initiation and crack propagation periods. The higher and stable reliability phase, although it varies with stress levels, represents crack initiation period, and reliability loss phase is indicative of crack propagation period. It is clear from these plots that crack initiation period is smaller for higher stress level and loss of reliability is faster during crack propagation indicating faster degradation or higher rate of damage accumulation. The total life of the product also varies with stress levels and therefore supports out argument that dynamic behavior or degradation phenomenon needs to be captured in design optimization models to provide more realistic solutions.
4.2. Reliability Prediction for Multi-Stress Levels
To demonstrate multi-stress loading scenarios, let’s consider a helical compression spring subjected to three successive stress levels of 435 MPa, 360 MPa, and 320 MPa for 40000, 60000 and remaining number of usages cycles up to fatigue failure, respectively. To estimate reliability under multi-stress level loading, the fatigue life of spring needs to be predicted under multi-stress loading conditions.
4.2.1. Prediction of Fatigue Life
4.2.2. Prediction of Reliability
Using the appropriate values of variables and parameters, the variability at the threshold damage is.
4.3. Reliability Prediction for Multi-Stress Levels by Changing Sequence of Loading
To study the effect of change in sequence of loading on reliability behavior of the helical compression spring, the sequence of multi-stress levels loading is reversed (i.e., 320 MPa, 360 MPa, and 435 MPa for successive usage cycles 167750, 60000, and 40000, resp.).
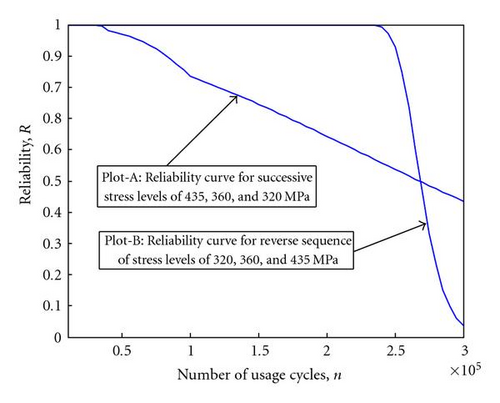
The reliability plot for this reversed multilevel stress loading is plotted as plot-B in Figure 9. In multi-stress loading scenario, reversal of loading sequence will not affect the fatigue life of spring much, as the fraction of life consumed at different stress level remains the same in light of linear damage accumulation theory. But reliability plot-B indicates considerable change in its shape. The initial higher reliability phase is considerably longer due to low-high stress sequence. This is an indication of longer crack initiation phase and slower rate of damage accumulation because of slow propagation of crack at lower stress levels. However, as soon as spring is subjected to higher stress level, the reliability starts declining sharply due to faster propagation of cracks and hence higher rate of damage accumulation at higher stress level. In other words, the implications of change in sequence of loading can be observed in the duration of crack initiation phase and the rate of loss of reliability with usage time (as shown in Figure 9). It can be observed that the rate of loss of reliability is generally higher for high-low sequence of loading compared to low-high sequence but it changes later.
Authors believe these two scenarios represent two extremes but ideal cases of loading phenomenon of multilevel stress loading. In real life applications, the loading pattern is not necessarily sequential but could be any combination of stress levels in any sequence of loading. Therefore, these two extreme scenarios provide a band of reliability behavior for multilevel stress loading, and actual reliability behavior, for any given real life loading pattern, could be somewhere within this band.
5. Conclusion
The proposed approach provides an easy methodology for modeling the probabilistic distribution of the damage accumulation measure and hence capturing real life behavior of the product. It proposes a simple and unique way to model the damage accumulation process treating it as a nonstationary process to capture damage accumulation and its variability at any given point of time. The proposed approach can be extended to consider other fatigue failure distributions such as lognormal and Weibull distributions to model probabilistic damage accumulation.
The major limitation of the proposed approach is that it treats damage accumulation as linear phenomenon whereas in actual practice damage accumulation could be a nonlinear phenomenon especially in multi-stress loading scenarios. Our future research efforts are directed towards developing an understanding to capture nonlinear damage accumulation phenomenon in multi-stress loading conditions. Another potential research area for future research can be towards capturing and incorporating degradation behavior (dynamic degradation phenomenon) into design optimization models to capture life-cycle issues and provide more realistic solutions.




