Journal of Applied Mathematics
Volume 2011, Issue 1 715087
Research Article
Open Access

Asymptotic Analysis of Transverse Magnetic Multiple Scattering by the Diffraction Grating of Penetrable Cylinders at Oblique Incidence

Ömer Kavaklıoğlu, 

Corresponding Author

Ömer Kavaklıoğlu

Department of Electrical and Computer Engineering, School of Engineering and Applied Science, The George Washington University, Washington, DC 20052, USA gwu.edu

Search for more papers by this author
Roger Henry Lang, 

Roger Henry Lang

Department of Electrical and Computer Engineering, School of Engineering and Applied Science, The George Washington University, Washington, DC 20052, USA gwu.edu

Search for more papers by this author
First published: 20 December 2011
https://doi.org/10.1155/2011/715087
Citations: 1
Academic Editor: Yongkun Li

Abstract

We have presented a derivation of the asymptotic equations for transverse magnetic multiple scattering coefficients of an infinite grating of penetrable circular cylinders for obliquely incident plane electromagnetic waves. We have first deducted an “Ansatz” delineating the asymptotic behavior of the transverse magnetic multiple scattering coefficients associated with the most generalized condition of oblique incidence (Kavaklıoğlu, 2000) by exploiting Schlömilch series corresponding to the special circumstance that the grating spacing is much smaller than the wavelength of the incident electromagnetic radiation. The validity of the asymptotic equations for the aforementioned scattering coefficients has been verified by collating them with the Twersky′s asymptotic equations at normal incidence. Besides, we have deduced the consequences that the asymptotic forms of the equations at oblique incidence acquired in this paper reduce to Twersky′s asymptotic forms at normal incidence by expanding the generalized scattering coefficients at oblique incidence into an asymptotic series as a function of the ratio of the cylinder radius to the grating spacing.

1. Introduction

Rayleigh [1] first treated the problem of the incidence of plane electric waves on an insulating dielectric cylinder as long ago as 1881. He published the classical electromagnetic problem of the diffraction of a plane wave at normal incidence by a homogeneous dielectric cylinder [2]. His solution was later generalized for obliquely incident plane waves when the magnetic vector of the incident wave is transverse to the axis of the cylinder by Wait [3]. Moreover, Rayleigh [4, 5] adduced the first theoretical investigation for the problem of diffraction by gratings. His results have been extended by Wait [6] for the treatment of scattering of plane waves by parallel-wire grids with arbitrary angle of incidence. Wait [6] developed the solution of the problem of the scattering of plane electromagnetic waves incident upon a parallel-wire grid that was backed by a plane-conducting surface. He generalized this result subsequently to a plane wave, incident obliquely with arbitrary polarization on a planar grid [7]. Wait did not treat the scattering of obliquely incident plane electromagnetic waves by the infinite array of thick dielectric cylinders. This configuration has recently been studied by Kavaklıoğlu [8–10], and an analytic expression for the generalized multiple scattering coefficients of the infinite grating at oblique incidence was captured in the form of a convergent infinite series [11].

The formal analytical solution for the scattering of a plane acoustic or electromagnetic wave by an arbitrary configuration of parallel cylinders of different radii and physical parameters in terms of cylindrical wave functions was obtained by Twersky [12] who considered all possible contributions to the excitation of a particular cylinder by the radiation scattered by the remaining cylinders in the grating and extended this solution to expound the case where all the axes of cylinders lie in the same plane [13]. Twersky [14] subsequently introduced the formal multiple scattering solution of a plane wave by an arbitrary configuration of parallel cylinders to the finite grating of cylinders. He later employed Green’s function methods to represent the multiple scattering amplitude of one cylinder within the grating in terms of the functional equation and the single-scattering amplitude of an isolated cylinder [15]. Furthermore, Twersky [16] acquired a set of algebraic equations for the multiple scattering coefficients of the infinite grating in terms of the elementary function representations of Schlömilch series [17] and the well-known scattering coefficients of an isolated cylinder.

In the area of acoustics, Millar [18] studied the problem of scattering of a plane wave by finite number of cylinders equispaced in a row that are associated with scatterers both “soft” and “hard” in the acoustical sense. The solutions in the form of series in powers of a small parameter, essentially the ratio of cylinder dimension to wavelength, were obtained. Besides, Millar [19] investigated the scattering by an infinite grating of identical cylinders. In a more recent investigation, Linton and Thompson [20] formulated the diffracted acoustic field by an infinite periodic array of circles and determined the conditions for resonance by employing the expressions which enable Schlömilch series to be computed accurately and efficiently [21–23].

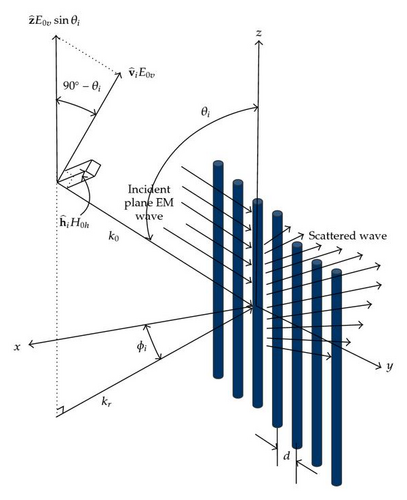
Previous investigations mentioned above do not include the most general case of oblique incidence although the grating is illuminated by an incident plane E-polarized electromagnetic wave at an arbitrary angle ϕi to the x-axis, whereas in the generalized oblique incidence solution presented in this investigation, the direction of the incident plane wave makes an arbitrary oblique angle θi with the positive z-axis as indicated in Figure 1. As far as can be ascertained by the writers, Sivov [24, 25] first treated the diffraction by an infinite periodic array of perfectly conducting cylindrical columns for the most generalized case of obliquely incident plane-polarized electromagnetic waves in order to determine the reflection and transmission coefficients of the infinite grating of perfectly conducting cylinders in free space under the assumption that the period of the grating spacing was small compared to a wavelength. The configuration of a greater relevance to the problem has recently been investigated by many other researchers. For instance, Lee [26] studied the scattering of an obliquely incident electromagnetic wave by an arbitrary configuration of parallel, nonoverlapping infinite cylinders and acquired the solution for the scattering of an obliquely incident plane wave by a collection of closely spaced radially stratified parallel cylinders that can have an arbitrary number of stratified layers [27]. Moreover, Lee [28] presented a general treatment of scattering of arbitrarily polarized incident light by a collection of radially stratified circular cylinders at oblique incidence, described the solution to the problem of scattering of obliquely incident light by a closely spaced parallel radially stratified cylinders embedded in a semi-infinite dielectric medium [29], and developed a general scattering theory for obliquely incident plane-polarized monochromatic waves on a finite slab containing closely spaced radially stratified circular cylinders [30]. In addition, the formulation for the extinction and scattering cross-sections of closely spaced parallel infinite cylinders in a dielectric medium of finite thickness is presented [31]. In the area of modeling photonic crystal structures, Smith et al. [32] developed a formulation for cylinder gratings in conical incidence using a multipole method and studied scattering matrices and Bloch modes in order to investigate the photonic band gap properties of woodpile structures [33]. This area of research has recently received a lot of attention due to potential applications to microcircuitry, nanotechnology, and optical waveguides.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The schematic of the scattering by an infinite grating at oblique incidence.

Three-dimensional generalization of Twersky’s solution [15, 16] for scattering of waves by the infinite grating of dielectric circular cylinders was originally developed by Kavaklıoğlu [8–10] by employing the separation-of-variables method for both TM and TE polarizations, and the reflected and transmitted fields were derived for obliquely incident plane H-polarized waves in [34]. Kavaklıoğlu and Schneider [35] presented the asymptotic solution of the multiple scattering coefficients for obliquely incident and vertically polarized plane waves as a function of the ratio of the cylinder radius to grating spacing when the grating spacing, d, is small compared to a wavelength.

Furthermore, Kavaklıoğlu and Schneider [11] acquired the exact analytical solution for the multiple scattering coefficients of the infinite grating for obliquely incident plane electromagnetic waves by the application of the direct Neumann iteration technique to two infinite sets of equations describing the exact behavior of the multiple scattering coefficients, which was originally published in [8, 10], in the form of a convergent infinite series and obtained the generalized form of Twersky’s functional equation for the infinite grating in matrix form for obliquely incident waves [11].

The purpose of this paper is to elucidate the derivation of the equations pertaining to the asymptotic behavior of the transverse magnetic multiple scattering coefficients of an infinite array of infinitely long circular dielectric cylinders illuminated by obliquely incident plane electromagnetic waves. The arbitrarily polarized obliquely incident plane wave depicted in Figure 1 can be decomposed into two different modes of polarization. The asymptotic representation associated with the transverse magnetic (TM) mode that is also defined as vertical polarization, for which the incident electric field Einc has a component parallel to the constituent cylinders of the grating, will be treated in this investigation.

2. Problem Formulation

“An infinite number of infinitely long identical dielectric circular cylinders,” which are separated by a distance “d,” are placed parallel to each other in the y-z plane and positioned perpendicularly to the x-y plane as indicated in Figure 1. For TM mode; is the unit vector associated with the vertical polarization and has a component parallel to the cylinders of the grating. The fact that “the incident E-field has a component parallel to all the cylinders of the dielectric grating” does not mean that we deal with the TM mode as it does not exclude the existence of other components of E-field. The incident plane wave depicted in Figure 1 makes an angle of obliquity θi with the positive z-axis.

Lemma 2.1 (multiple scattering representation for an infinite grating of dielectric circular cylinders for obliquely incident E-polarized plane electromagnetic waves [3, 7, 8]). A vertically polarized plane electromagnetic wave, which is obliquely incident upon the infinite array of identical insulating dielectric circular cylinders with radius “a,” dielectric constant “εr,” and relative permeability “μr,” can be expanded in “the individual cylindrical coordinate system (Rs, ϕs, z) of the sth cylinder” in terms of the cylindrical waves referred to the axis of sth cylinder as

()

The origin of each individual cylindrical coordinate system, namely, (Rs, ϕs, z), is located at the center of the corresponding cylinder. In the above description of the incident field, is a unit vector that denotes the vertical polarization having a component parallel to all the cylinders, ϕi is the angle of incidence in x-y plane measured from the x-axis in such a way that ψi = π + ϕi, implying that the wave is obliquely incident in the first quadrant of the coordinate system, and “Jn(x)” stands for a Bessel function of order n. In addition, we have the following definitions:
()
“e−iωt” time dependence is suppressed throughout the paper, where “ω” stands for the angular frequency of the incident wave in radians per second, “k0” is the free-space wave number, “c” denotes the speed of light in free space, and “t” represents time in seconds. The centers of the cylinders in the infinite grating are located at the positions r0, r1, r2, …, and so forth. The exact solution for the z-component of the electric field in the exterior of the grating belonging to this configuration can be expressed in terms of the incident electric field in the coordinate system of the sth cylinder located at rs, plus a summation of cylindrical waves outgoing from each individual mth cylinder located at rm, as |r − rm| → ∞, that is,
()

Lemma 2.2 (expressions for the z-components of the exterior fields [8]). Let for all n ∈ Z, where “Z” stands for the set of all integers, denote the set of all multiple scattering coefficients corresponding to the exterior electric and magnetic fields of the infinite grating associated with obliquely incident plane E-polarized electromagnetic waves, respectively. Then, the exterior electric and magnetic field intensities associated with vertically polarized obliquely incident plane electromagnetic waves are given as

()
()

In this representation, depicts the set of all undetermined multiple scattering coefficients associated with exterior electric fields defined by the expressions (29) and (34)–(37) in [8], and delineates the set of all undetermined multiple scattering coefficients associated with exterior magnetic fields defined by the expressions (40)–(42) in [8], respectively. In expressions (2.4a) and (2.4b), we have
()
()
where  Δ ≡ krd/2π and “” denotes the nth order Hankel function of first kind, for all n ∈ Z. The series ℐn−m(krd) in expression (2.4b) is the generalization of the “Schlömilch series for obliquely incident electromagnetic waves” [10, 17] and converges provided that krd(1 ± sin ψi)/2π does not equal integers. The integral values of krd(1 ± sin ψi)/2π are known as the “grazing modes” or “Rayleigh values” [17]. The convergence of the series for the scattering coefficients can be found on page 342 in [11]. Moreover, the convergence of the Schlömilch series has been discussed by Twersky [17] in detail, who also gives additional references. The exact expressions corresponding to the radial and angular components of the electric and magnetic field intensities have already been obtained in [8] by employing the z-component of the external field in the expressions (2.4a) and (2.4b).

3. Derivation of the Asymptotic Equations for the Multiple Scattering Coefficients of the Infinite Grating at Oblique Incidence

This section is devoted to the formal derivation of the asymptotic equations for the exterior electric and magnetic multiple scattering coefficients of the infinite grating of dielectric cylinders for obliquely incident vertically polarized plane waves. Since the wavelength of the incident radiation is much larger than the grating spacing, the condition max {(krd/2π)(1 ± sin ψi)} ≡ krd/π < krd ≪ 1 is automatically satisfied thereby excluding any special case associated with the grazing modes. In order to demonstrate the procedure of obtaining the asymptotic equations for the TM multiple scattering coefficients of the infinite grating at oblique incidence, we will first introduce the exact equations corresponding to the transverse magnetic multiple scattering coefficients associated with the exterior electric and magnetic fields of the infinite grating of dielectric circular cylinders at oblique incidence by asserting the following lemma.

Lemma 3.1 (exact equations of the transverse magnetic multiple scattering coefficients of the infinite grating of insulating dielectric cylinders at oblique incidence [8]). Exact equations corresponding to the transverse magnetic multiple scattering coefficients of an infinite grating of insulating dielectric cylinders associated with obliquely incident plane electromagnetic waves are first presented by the equations (85a) and (85b) in [8] as

()
The coefficients arising in this infinite set of linear algebraic equations are defined as
()
Two sets of constants and , in which ζr ∈ {εr, μr} stands for the relative permittivity and permeability of the dielectric cylinders, respectively, are given as
()
for ζ ∈ {ε, μ}, and for all n ∈ Z; where k1 is defined as , and
()
for ζ ∈ {ε, μ} and for all n ∈ Z, where  F in the expression above is a constant and given as
()
In these equations εr and μr denote the relative dielectric constant and the relative permeability of the insulating dielectric cylinders; ε0 and μ0 stand for the permittivity and permeability of the free space, respectively. In addition, , and in expressions (3.2) and (3.3) are defined as
()
which imply the first derivatives of the Bessel and Hankel functions of first kind and of order n with respect to their arguments.

Theorem 3.2 (approximate equations for the scattering coefficients of the infinite grating at oblique incidence when krd ≪ 1). The asymptotic form of the exact equations for the transverse magnetic multiple scattering coefficients of an infinite grating at oblique incidence can be inferred by two different sets, in which the first one contains only the odd coefficients and the second set contains only the even coefficients. Odd multiple scattering coefficients associated with the infinite grating of dielectric circular cylinders at oblique incidence satisfy the following two sets of asymptotic equations:

()
Similarly, the even multiple scattering coefficients satisfy the following two infinite sets of asymptotic equations associated with the transverse magnetic multiple scattering coefficients of the infinite grating of dielectric circular cylinders at oblique incidence as
()
where N denotes the set of all natural numbers.

Proof. The exact equations in (3.1) can be solved for An, and when the distance between the cylinders of the infinite grating is smaller than the wavelength of the incident wave, that is, for krd ≪ 1 the exact equations take the following form:

()
where is a (2   ×   2) matrix defined as
()
and “ℋn(krd)” connotes the approximation to the “exact form of the Schlömilch series ℐn(krd)” in the limiting case when for krd ≪ 1. Introducing (3.10)) into (3.9), the approximate set of equations for the scattering coefficients of the infinite grating at oblique incidence can explicitly be written as
()
In the above, we have
()
The n-dependent constants appearing in (3.10) and (3.11) are defined as
()
()
()
()
The various constants appearing in the definitions (3.13a)–(3.13d) are expressed as
()
The elements of the matrix of coefficients in ((3.11) can be calculated using the expressions (3.14), for instance (sεμ/D) and (sμε/D) terms can be written as
()
In terms of the definitions of (3.13a)–(3.13d), the approximate set of equations for the multiple scattering coefficients of the infinite grating at oblique incidence given in ((3.11) takes the following form:
()
Statement of Theorem 3.2 follows immediately upon decomposition of (3.16) into its odd and even components as it is designated by (3.7) and (3.8).

The elementary function representations of the Schlömilch series ℐn(krd) in (2.5b) have originally been derived by Twersky [17] for the normal incidence and modified by Kavaklıoğlu [10] for the oblique incidence. We will employ these elementary function representations for the evaluation of the asymptotic forms of the Schlömilch series ℋn = 𝒥n + i𝒩n in the limit of krd ≪ 1. Twersky’s forms [16, 17] are still valid for the case of obliquely incident waves [10] with a slight modification in their arguments.

Lemma 3.3 (approximate expressions for the “Schlömilch series ℋn = 𝒥n + i𝒩n” in the limit of krd ≪ 1 [10, 17]). We have obtained ℋ0 for the special case of n = 0 as

()
where γ = 1.781…. In (3.17), cos ϕμ is defined by the following relationship:
()
The angles ϕμ are the usual “diffraction angles” of  the grating, and (3.18) that provides these discrete angles is called the “grating equation”. “Propagating modes” are determined by |sin ϕμ| < 1, and they correspond to |μ| ≤ μ±, the μ±’s being the closest integers to the m±’s for which |sin ϕμ| < 1 should be satisfied, that is, μ± < m±, such that
()
“Evanescent modes” are determined by |sin ϕμ| > 1, and they correspond to integer values of μ such that |μ| ≥ m± + 1, we have , and are determined by . For this case the “grating equation” takes the form of
()
For the general case, we have ℋn, for all n ∈ N  as
()
Finally, Bn(x) is the Bernoulli polynomial of argument “x” and power “n”, in ((3.21).

Remark 3.4 (Bessel series 𝒥0, 𝒥2n, and 𝒥2n+1). The propagating range of the Schlömilch series ℋn, for all n ∈ Z+, where Z+ = {0,1, 2,3, …} in (3.17) and ((3.21), is described by “𝒥n” Bessel series, which can explicitly be written as

()

Remark 3.5 (Neumann series 𝒩0, 𝒩2n, and 𝒩2n+1). The evanescent range of the Schlömilch series ℋn, for all n ∈ Z+ in (3.17) and (3.21), is described by “i𝒩n” where 𝒩n is known as the Neumann series. 𝒩n in (3.17) and ((3.21) can be put into the following form for this limiting case (krd ≪ 1) as

()
In addition, we can obtain the simplified expressions for 𝒩2n and 𝒩2n+1 as
()
()

Remark 3.6 (special case when μ+ = μ− = 0). The physical problem under consideration corresponds to the special case for which there is only one propagating mode and the scattering of wavelengths is larger than the grating spacing, that is, (krd/2π)(1 ± sin ψi) < 1. Then the Bessel series for ϕ0 = π + ψi, which implies that the plane wave is incident onto the grating in the first quadrant, for all n ∈ Z+, reduces to

()
where δnm stands for the Kronecker delta function.

Remark 3.7 (approximations for Neumann series𝒩0, 𝒩2n, and 𝒩2n+1 in the limit of Δ ≪ 1). Inserting μ+ = μ− = 0 in (3.23a), (3.23b), and (3.23c), the expression for 𝒩0 in (3.23a)) reduces to

()
The approximation of the Neumann series 𝒩0, for ϕ0 = π + ψi, up to terms of the order can be obtained from (3.25a) as
()
where ζ(s), for all s ∈ ℜ, denotes the Riemann zeta function. In the same range, the Neumann series 𝒩n reduces to
()
where ℱ’s in (3.26) are given as
()

Remark 3.8 (approximations for Schlömilch series, ℋn = 𝒥n + i𝒩n in the limit of Δ ≪ 1). If  krd is small, that is to say if (krd/2π)(1 ± sin ψi) < 1, then there is only one discrete propagating mode. Employing the expansions for the Bessel and Neumann Series obtained in the previous sections for ϕ0 = π + ψi; the Schlömilch Series in this range can be expressed as

()

Remark 3.9 (leading terms of the Schlömilch series,  ℋn = 𝒥n + i𝒩n in the limit of  Δ ≪ 1). The leading terms of ℋ’s for large “n”, for all n ∈ N is given as

()
where Bn(x) corresponds to the Bernoulli Polynomial. From (3.28) and (3.29), we can determine the leading terms of the Schlömilch series as
()
The leading terms of ℋn for large “n” are given by
()
where  h2n’s and  h2n+1’s for large "n" are given as
()
()
In the above expressions, Bξ’s are the Bernoulli numbers, and the relationship between Bernoulli polynomial and Bernoulli numbers is given as
()

4. Asymptotic Expansions for the Scattering Coefficients of the Infinite Grating at Oblique Incidence in the Limiting Case of “(a/d) ≪ 1”

In order to find a solution for the set of equations given in (3.15) and (3.16), we have introduced an “Ansatz” [36] for the scattering coefficients of the electric and magnetic fields of the infinite grating assuming (kra) ≪ 1, and (kra/krd) ≡ ξ < 1/2, as
()
()
for all n ∈ N, for the odd multiple coefficients corresponding to the electric and magnetic field intensities of the infinite grating associated with obliquely incident plane electromagnetic waves, and
()
()
for all n ∈ Z+ for the even multiple coefficients. In the above expressions, we have delineated the wavelength-independent parts of the multiple scattering coefficients associated with the exterior electric and magnetic field intensities as .

Theorem 4.1 (asymptotic equations for the multiple scattering coefficients corresponding to the exterior electric and magnetic field intensities associated with obliquely incident vertically polarized plane electromagnetic waves). The multiple scattering coefficients corresponding to the exterior electric and magnetic field intensities associated with obliquely incident vertically polarized plane electromagnetic waves satisfy two infinite sets of asymptotic equations described by

()
for the odd multiple scattering coefficients, and
()
for the even multiple scattering coefficients.

Proof. We have defined the overall effect of the multiple scattering terms when the wavelength is much larger than the grating spacing, that is, (krd) ≪ 1, and (kra/krd) ≡ ξ < 1/2 as

()
for the electric field coefficients, and
()
for the magnetic field coefficients. Employing the approximations of Schlömilch series given in (3.27) in the expressions (4.3a) and (4.3b), we can write the overall effect of the multiple scattering terms when the wavelength is much larger than the grating spacing, that is, (krd) ≪ 1, and (kra/krd) ≡ ξ < 1/2 as
()
()
for all n ∈ N, for the odd coefficients,
()
()
for all n ∈ N, for the even coefficients; and the special case for n = 0 is given by
()
Defining the wavelength independent parts of the scattering matrices from (3.10)) as
()
()
()
for all n ∈ N, corresponding to the odd, and
()
corresponding to the even part. Using the definitions in (4.6a)–(4.6d), and introducing (4.4a)–(4.4d) into (3.7) and (3.8), we have obtained the following set of equations for the approximations of the scattering coefficients:
()
corresponding to the odd scattering coefficients, and
()
corresponding to the even scattering coefficients. Splitting the matrices in (4.7a) and (4.7b) into two parts, we have
()
for the odd scattering coefficients, and
()
for even scattering coefficients. From (4.4a)–(4.4d), we have established the following terms:
()
for the multiple interactions corresponding to the scattering coefficients of the electric field, and
()
for the multiple interactions corresponding to the scattering coefficients of the magnetic field, for all n ∈ N, for the odd scattering coefficients, and
()
for the multiple interactions corresponding to the scattering coefficients of the electric field,
()
for the multiple interactions corresponding to the scattering coefficients of the magnetic field, for all n ∈ N, for the even scattering coefficients. Inserting (4.9a)-(4.9b) and (4.10a)-(4.10b) into (4.8a)-(4.8b), we have finally obtained the infinite set of asymptotic equations for the multiple scattering coefficients corresponding to the exterior electric and magnetic field intensities of an infinite grating of dielectric circular cylinders associated with obliquely incident and vertically polarized electromagnetic waves as it is proposed by the statement of Theorem 4.1 introduced in (4.2a) and (4.2b). In addition, we have noticed that the scattering coefficients of the electric and magnetic fields appeared as coupled to each others.

5. Discussion and Comparison of the Generalized Transverse Magnetic Multiple Scattering Coefficients of the Infinite Grating with Twersky’s Normal Incidence Case

Remark 5.1 (Twersky’s asymptotic solution for the multiple scattering coefficients at normal incidence). The exact equations for the multiple scattering coefficients of the infinite grating associated with the vertically polarized normally incident waves [16] can be solved by truncation as

()
where, the numerator terms are given as
()
()
()
()
and the denominator terms are given as
()
()
The bn’s, for all n ∈ N, are given by
()
Finally, an’s appearing in (5.2) represent the asymptotic forms of the single-scattering coefficients associated with an isolated cylinder within the grating at normal incidence and can be approximated for (kra) ≪ 1 as
()
for all n ∈ N,where
()
()
for all n ∈ N.  Inserting (5.3), (3.29), and (3.30) into (5.2), bn’s can be evaluated as
()
()
()
()
Expressions in (5.5a)–(5.5d) are valid for kra ≪ 1, and krd ≪ 1. In general, bn’s can be expressed as
()
Obviously, (5.5a) and (5.6) will asymptotically be written as
()
for all  n ∈ N,  where
()
()
represent kra-independent parts of bn’s for wavelengths larger than the radii, that is, (kra) ≪ 1. The numerator terms appearing in (5.1b)–(5.1e) can be approximated as
()
The denominator terms appearing in (5.1c) can be approximated as
()
Inserting (5.5a)–(5.5d) to (5.10) into (5.1a)–(5.1g), we have
()
From (5.11), we have deduced that when the grating spacing is much smaller than a wavelength, that is, for the range of kra ≪ 1 and krd ≪ 1, the asymptotic form of the transverse magnetic multiple scattering coefficients of the infinite grating associated with the exterior electric field, An, can asymptotically be represented as
()
An,0’s represent the wavelength-independent parts of the multiple scattering coefficient An, and the first four of them are given in terms of previously defined constants as
()
()
()
()
In the expressions (5.13a)–(5.13d), an,0 denotes the wavelength-independent parts of the scattering coefficients associated with an isolated cylinder within the grating at normal incidence [16]. From the set of equations in (5.12), we have observed that they conform to the “Ansatz” statement of (3.7) and (3.8). Inserting (5.8b) into (5.13b), we have obtained
()
()
We can equivalently deduct the same result from the “asymptotic equations of the infinite grating at oblique incidence” in ((3.11) for the special case of normal incidence as
()
()
Keeping those terms up to (a/d)6 in both numerator and denominator of (5.14b), we have obtained
()
()
and expanding the denominator of (5.15a) in the form of a geometric series, that is, 1/(1 − x) = 1 + x + x2 + x3 + ⋯, |x| < 1 we have derived an asymptotic expansion for A1,0 as
()
()
()
Thereby, employing the definition of the first-order multiple scattering coefficient when the radius of the cylinders is small compared to a wavelength, we have obtained Twersky’s solution for the normal incidence. Similarly, inserting (5.8b) into (5.13c) for n = 2, we have
()
()
()
Expanding the denominator of (5.17b) in the form of a geometric series, we have obtained
()
or neglecting terms of the order of (a/d)6, we have
()
()
()
This substantiates the validity of the second-order multiple scattering coefficients, which reduces to Twersky’s form for normal incidence. For the asymptotic expansion of A3,0 in powers of (a/d), we have inserted (5.8b) into (5.13d) for n = 3 and obtained
()
()
()
Employing (5.15a) in (5.19b), we have
()
()
Equation (5.20b) can be deducted from the oblique coefficients as
()
Expanding the denominator of (5.20b) in the form of a geometric series, we have obtained
()
Keeping terms up to the order of (a/d)4, we have
()
Using the definition of the single-scattering coefficients in (3.13a) at oblique incidence, an,0 at normal incidence [16] can be acquired as
()
and the third-order scattering coefficient at normal incidence can then be acquired as
()

Lemma 5.2 (generalized asymptotic solution of the multiple scattering coefficients at oblique incidence [11, 34, 35]). The generalized asymptotic solution for the multiple scattering coefficients of an infinite grating of dielectric circular cylinders for obliquely incident vertically polarized waves has already been acquired in [35] by solving the asymptotic matrix equations of the infinite grating at oblique incidence as

()
()
()
()
()
()
()
()

Twersky’s asymptotic solution for the transverse magnetic multiple scattering coefficients of the infinite grating at normal incidence can then be acquired by exploiting the generalized asymptotic equations at oblique incidence derived in this investigation, thereby verifying the validity of the proposed “Ansatz” in Section 4.

Remark 5.3 (reduction of the generalized asymptotic solution at oblique incidence to Twersky’s asymptotic solution for the multiple scattering coefficients at normal incidence). In order to reduce Twersky’s results at normal incidence from the generalized multiple scattering coefficients at oblique incidence given in (5.22a)–(5.25b), we have used ψi = 0, θi = π/2, sin  θi = 1, and F = 0 in (5.22a)–(5.25b) and acquired the following results: (a) a comparison of (5.22a), which determines the generalized scattering coefficient for n = 0, with (5.4a) and (5.13a) proves that the generalized multiple scattering coefficient at oblique incidence reduces to the Twersky’s coefficient for the normal incidence case; (b) the following term, namely, , which represents the wavelength-independent part of the (1,1) element of the scattering matrix in (3.10)), reduces to the Twersky’s an,0 for the normal incidence case as

()
With this identification, the generalized scattering coefficient of (5.23a) reduces to Twersky’s A1,0 normal incidence case as given in (5.16c). Similarly, the generalized scattering coefficient of (5.24a) becomes identical with the Twersky’s A2,0 scattering coefficient of the normal incidence case as it is given in (5.18d); and finally, the generalized scattering coefficient of (5.25a) conforms to Twersky’s A3,0 as it is given by (5.21d).

6. Conclusion

In this investigation, we have presented a rigorous derivation of the asymptotic equations associated with the multiple scattering coefficients of an infinite grating of dielectric circular cylinders for obliquely incident vertically polarized plane electromagnetic waves. We have predicted the asymptotic behavior of the multiple scattering coefficients of the infinite grating at oblique incidence when the wavelength of the incident radiation is much larger than the distance between the constituent cylinders of the grating, that is, (dsin θi)(1 ± sin ψi) ≪ λ0 ≡ 2π/k0. Furthermore, we have predicated that our results are nothing but the generalizations of those acquired by [16] for the nonoblique incidence case. We have inferred that these equations can be solved by a technique described by Kavaklıoğlu and Schneider [35], which reduces to Twersky’s asymptotic solution at normal incidence, as well.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.