Convergence of GAOR Iterative Method with Strictly α Diagonally Dominant Matrices
Abstract
We discuss the convergence of GAOR method for linear systems with strictly α diagonally dominant matrices. Moreover, we show that our results are better than ones of Darvishi and Hessari (2006), Tian et al. (2008) by using three numerical examples.
1. Introduction
In [2–4], some people studied the convergence of GAOR method for solving linear systems Hy = f. In [2], Yuan and Jin studied the convergence of GAOR method and show that the GAOR method is better than the GSOR method under certain conditions. In [3], Darvishi and Hessari studied the convergence of GAOR method for diagonally dominant coefficient matrices and gave the regions of convergence. In [4], Tian et al. studied the convergence of GAOR method for strictly diagonally dominant coefficient matrices and gave the regions of convergence.
Sometimes, the coefficient matrices of linear systems Hy = f are not strictly diagonally dominant. In this paper, we will discuss the convergence of GAOR method for linear systems Hy = f with strictly α diagonally dominant matrices which need not to be strictly diagonally dominant.
Definition 1.1 (see [5].)Let A = (aij) ∈ Cn×n. If there exists α ∈ [0,1],
Obviously, if A is a strictly diagonally dominant matrix (A ∈ SD), then A ∈ D(α). But not vice versa.
In [3], Darvishi and Hessari obtained the following result.
Theorem 1.2. Let H ∈ SD and assume that ω ≥ r ≥ 0. Then the sufficient condition for convergence of the GAOR method is
In [4], Tian et al. obtained the following result.
Theorem 1.3. If H ∈ SD, then the sufficient conditions for the convergence of the GAOR method are either
- (i)
0 ≤ r ≤ 1 and 0 < ω ≤ 1 or
- (ii)
|r | ≤ min i{(1 − Ji)/Ki} and 0 < ω < 2/(1 + max i(J + rK) i).
This work is organized as follows. In Section 2, we obtain bound for the spectral radius of the iterative matrix Lω,r of GAOR iterative method. In Section 3, we present two convergence theorems of GAOR method. In Section 4, we present three numerical examples to show that our results are better than ones of Theorems 1.2 and 1.3.
2. Upper Bound of the Spectral Radius of Lω,r
In this section, we obtain upper bound of the spectral radius of iterative matrix Lω,r.
Theorem 2.1. Let H ∈ D(α), then ρ(Lω,r) satisfies the following inequality:
Proof. Let λ be an arbitrary eigenvalue of iterative matrix Lω,r, then
When λ is an eigenvalue of iterative matrix Lω,r, then there exists at least one i (i ∈ N), such that
3. Convergence of GAOR Method
In this section, we investigate the convergence of GAOR method to solve linear system (1.1). We assume that H is a strictly α diagonally dominant coefficient matrix and get some sufficient conditions for the convergence of GAOR method.
Theorem 3.1. Let H ∈ D(α), then GAOR method is convergent if ω, r satisfy either
- (I)
0 < ω ≤ 1 and
()
- (II)
and
()
Proof. Since H ∈ D(α), then GAOR method is convergent if we have ρ(Lω,r) < 1, that is,
Firstly, when 0 < ω ≤ 1, then
Secondly, when 1 < ω, then
When r = 0, we can get the following theorem.
Theorem 3.2. Let H ∈ D(α), then ρ(Lω,0) < 1 if
4. Examples
In the following examples, we give the regions of convergence of GAOR method to show that our results are better than ones of Theorems 1.2 and 1.3.
Example 4.1. Let
Obviously, H is not a strictly diagonally dominant matrix, so we cannot use the results of Theorems 1.2 and 1.3. But H ∈ D(1/2), and
- (I)
0 < ω ≤ 1 and |r| < 1/10
- (II)
1 < ω < 24/23 and |r| < (2 − (23/12)ω)(6/5ω).
Example 4.2 (Example 1 of paper [4]). Let
- (I)
0 < ω ≤ 1 and |r| < 3/4
- (II)
1 < ω < 1.2 and |r| < ((18 − 5ω)/4ω).
In addition, H is a strictly diagonally dominant matrix.
By Theorem 1.3, we obtain the following regions of convergence:
- (I)
0 ≤ r ≤ 1 and 0 < ω ≤ 1,
- (II)
0 ≤ r < 0.3 and 0 < ω < 1.2,
- (III)
−0.3 < r < 0 and 0 < ω < (18/(15 − 10r)).
By Theorem 1.2, we obtain the following region of convergence:
0 ≤ r ≤ ω and 0 < ω < (18/(15 + 10r)).
And we get Figure 1, where the regions of convergence got by Theorems 3.1 and 1.3, Theorem 1.2 are bounded by blue lines, red lines, green lines, respectively.
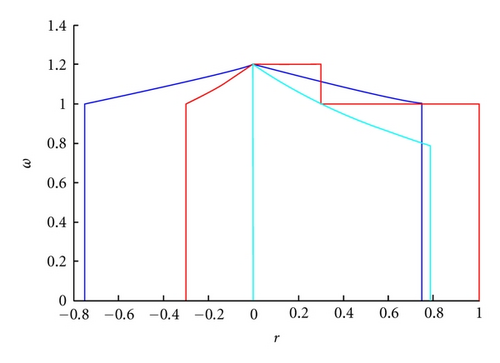
This figure shows that the regions of convergence got by Theorem 3.1 are larger than ones got by Theorems 1.2 and 1.3.
Example 4.3. Consider
Obviously, H is not a strictly diagonally dominant matrix, so we cannot use the results of Theorems 1.2 and 1.3. But H ∈ D(1/2), and
- (I)
0 < ω ≤ 1 and |r| < (2208/3481)
- (II)
1 < ω < (192/169) and |r| < ((18432 − 16224ω)/3481ω).
Acknowledgments
The authors would like to thank the referees for their valuable comments and suggestions, which greatly improved the original version of this paper. This work was supported by the National Natural Science Foundation of China (Grant no. 11001144) and the Science and Technology Program of Shandong Universities of China (J10LA06).




