Vortex Streets on a Sphere

1. Introduction

For fluid flow on a two-dimensional plane, the vorticity at a point is twice the angular rotation. A point vortex is a model of a flow in which the vorticity is zero except at the point itself where the vorticity is infinite, so that there is a nonzero circulation around the point. The study of point vortices on the plane, and other two-dimensional manifolds such as the cylinder, sphere, and torus, has a long history, dating back to the 19th century with Helmholtz [1] initiating the point vortex model and Kirchhoff [2] and Lin [3] formulating it as a Hamiltonian dynamical system. In this paper, we are concerned primarily with vortex streets, which consist of one or more periodic rows of point vortices, the simplest of which is a single infinite row of identical vortices [4]. These have important applications in engineering and geophysics, with a single row having been used to model the quasisteady large-scale vortices arising following the roll-up of a shear layer, and double rows, or von Kármán vortex streets [5], having been used to model the shedding of eddies behind a bluff body. An overview of two-dimensional vortex streets can be found in standard texts on hydrodynamics such as IN [6, 7].

In this paper, we are interested in transporting these well-known vortex streets from the plane to a curved two-dimensional manifold, the surface of a sphere. Flows on a sphere are important because of applications to planetary atmospheres. In his classic monograph, Lamb [6] briefly outlines a method of determining the motion of vortices on a curved manifold and discusses how some of the 19th century work on electrical conduction, such as charge-on-a-sphere problems, by Boltzmann, Kirchhoff, Töpler, and others could be applied to the problem of point vortices on the sphere although Gromeka [8] appears to have been the first to study vortices on a sphere specifically. More recently, the formulation of the motion of vortex streets on curved manifolds has been examined in more detail by Hally [9], with several subsequent studies [10–12] delving more deeply into the formulation of vortex motion on a sphere. A review of some of the work on point vortices on vortices on a sphere can be found in [13]. One interesting thread of research [14–16] has involved using numerical methods, such as contour surgery, to study the motion of vortex patches on a sphere, and although these results were numerical rather than the closed-form expressions sought in the current work, they serve to reveal the richness of vortex motion on a sphere.

The outline of the rest of the paper is as follows. In Section 2, we present our analysis, giving a brief overview of two-dimensional vortex streets in Section 2.1 and then transporting these streets to the sphere in Section 2.2, where we look at two vortex streets in detail, a row of corotating vortices and a row of counterrotating vortices. Finally, in Section 3, we make some closing remarks.

2. Analysis

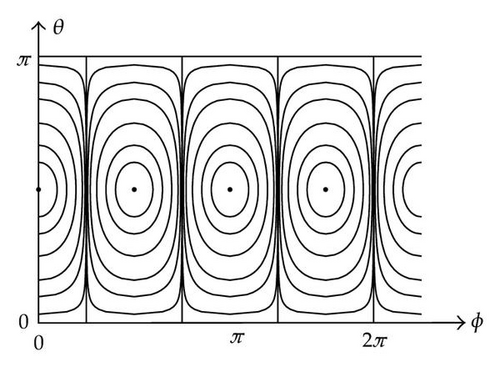
2.1. Two-Dimensional Vortex Streets

In plane two-dimensional hydrodynamics, the equation governing the motion of an inviscid incompressible fluid can be written in terms of a streamfunction ψ(x, y, t) as

$$ ()

where ∂(a, b)/∂(x, y) = (∂a/∂x)(∂b/∂y) − (∂a/∂y)(∂b/∂x) is a Jacobian and ∇² = (∂²/∂x²) + (∂²/∂y²) is the two-dimensional Laplacian. The streamfunction (2.1) admits steady-state solutions of the form

$$ ()

for any function ℱ, and a number of solutions are known for two-dimensional hydrodynamics. If we set ℱ ≡ 0, (2.2) becomes the two-dimensional Laplace equation ∇²ψ = 0, the fundamental solution of which has the form

$$ ()

where $$ is the distance from the fixed point x = x₀, y = y₀, which represents a point vortex of strength κ at x = x₀,   y = y₀, for which ∇²ψ = 0 except at the point itself with a circulation around the vortex of κ. Because ∇²ψ = 0 except at the point vortex itself, it is possible to construct steady-state solutions to (2.2) consisting of more than one vortex although for such a combination of vortices to be a steady-state solution, each vortex much be located at a point where the velocities induced by the other vortices sum to zero. A number of well-known steady-state vortex street solutions are given in Table 1, and an overview of vortex streets can be found in standard texts on hydrodynamics such as [6, 7]. The first solution in the table, which dates back to [4], is an infinite row of identical vortices, each of strength κ, located along y = 0 at the points x = ±π, ±3π, ±5π, … which is sketched in Figure 1(a). If we combine a row of vortices of strengths κ at x = ±π, ±3π, ±5π, … with a row of vortices of strengths −κ at x = 0, ±2π, ±4π, …, we have a row of vortices of alternating sign, which is sketched in Figure 1(b). There are also two combinations due to von Kármán [5] which propagate at constant speed in the negative x-direction: the symmetrical double row and the staggered double row, both of which consist of two rows of vortices, one along y = d and the other along y = −d, with the symmetrical row propagating at speed c = (κ/2π)coth d and the staggered row at speed c = (κ/2π)tanhd. It is straightforward to verify that the single rows in Table 1 are stationary and that the double rows propagate at constant speed. To calculate the velocity of a vortex in a vortex street, we must subtract the contribution for an isolated vortex from the streamfunction for the vortex street and then evaluate the resulting expression at the location of the vortex, so that, for example, for the vortex at (x, y) = (π, 0) in the corotating single row,

$$ ()

With this approach, it can be shown that the corotating and counterrotating rows are stationary, while the symmetrical and staggered double rows propagate in the x-direction with velocities −(κ/2π)coth d and −(κ/2π)tanhd, respectively.

Table 1. Some two-dimensional vortex streets.

Single corotating row	$$
Single counterrotating row	$$
Symmetrical double row	$$
Staggered double row	$$

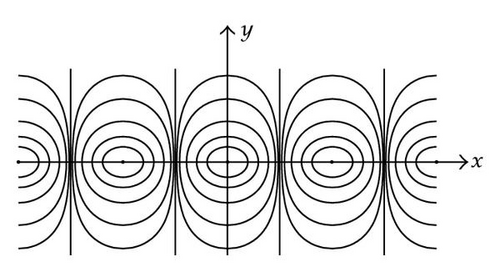
For the plane case, the corotating single row was generalized to smooth finite-amplitude vortices satisfying Liouville’s equation by [17] and the counterrotating row to finite-amplitude vortices satisfying the sinh-Poisson equation by [18].

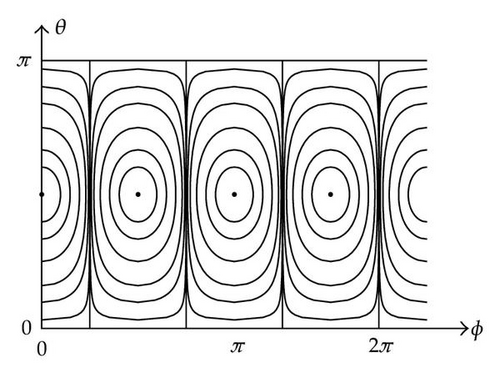
2.2. Vortex Streets on a Sphere

If we have a two-dimensional vortex street which is periodic in at least one direction, such as those in Table 1, it is possible to transport that street to the surface of a sphere, which to the best of our knowledge has not been done previously. In what follows, we will work in spherical polars (r, θ, ϕ) with associated velocities (u_r, u_θ, u_ϕ). If we consider only motions on the surface of a sphere of radius R, we will have r = R and the radial velocity will be zero, u_r = 0. If we introduce a streamfunction via u_θ = (∂ψ/∂ϕ)csc θ and u_ϕ = −∂ψ/∂θ, the inviscid incompressible equations of motion become

$$ ()

together with a radial pressure gradient $$. In the above, ∇² ≡ R⁻²[csc²θ(∂²/∂ϕ²) + cot θ(∂/∂θ) + (∂²/∂θ²)] is the Laplacian on the sphere, known as the Laplace-Beltrami operator. The streamfunction (2.5) admits steady-state solutions of the form

$$ ()

This formulation is of course not new and has been used by a number of authors to study vortices on a sphere in the past. At this point, however, we will depart from previous studies and make the change of variable η = ln  tan(θ/2), so that the interval 0 ≤ θ ≤ π is mapped onto −∞ < η < ∞. With this change of variable, ∇² ≡ R⁻²cosh ²η[(∂²/∂ϕ²) + (∂²/∂η²)]. Since we can write the surface of the sphere as 0 ≤ θ ≤ π,   0 ≤ ϕ ≤ 2π, or equivalently −∞ < η < ∞,   0 ≤ ϕ ≤ 2π, it follows that if ψ = Ψ(x, y) is a point vortex solution on the plane which is 2π-periodic in x, then the transformation x → ϕ,   y → η will produce a point vortex solution on the sphere, ψ = Ψ(ϕ, ln  tan(θ/2)). If we apply this transformation to the two-dimensional vortex streets in Table 1, we obtain the corresponding vortex streets on a sphere given in Table 2. We will examine a couple of these vortex streets in more detail.

Table 2. Some vortex streets on the sphere; m = 1,2, 3, ….

Single corotating row	$$
Single counterrotating row	$$
Symmetrical double row	$$
Staggered double row	$$

It is straightforward to verify that the single rows in Table 2 are stationary and that the double rows propagate at constant speed. To calculate the velocity of a vortex in a vortex street, we must subtract the contribution of that vortex itself from the streamfunctions in Table 2 and then evaluate the resulting expression at the location of the vortex. Since dη/dθ = csc θ,   u_θ = (∂ψ/∂ϕ)csc θ and u_ϕ = −(∂ψ/∂η)csc θ, and therefore it follows from the velocities of the two-dimensional vortex streets in Section 2.1 that the corotating and counterrotating rows are stationary, while the symmetrical and staggered double rows propagate in the ϕ-direction with velocities κcoth dcosh d/2π and κsinh d/2π, respectively, since dη/dθ|_η=d = cosh d and are therefore rotating steadily about the axis.

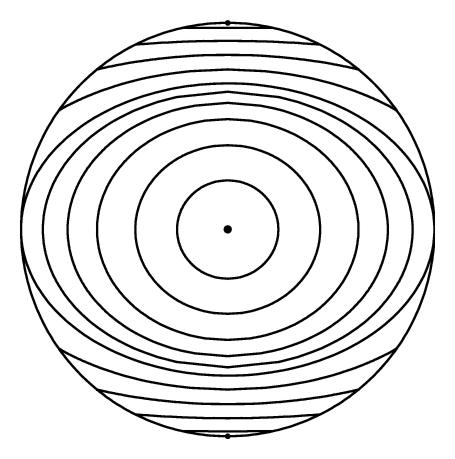
2.2.1. Single Corotating Row

The streamfunction and velocity components for a single row of identical vortices are given by

$$ ()

for m = 1,2, 3, …. This streamfunction is plotted in Figure 2 for m = 4. When m = 1, the streamfunction (2.7) reduces to ψ = ln [cos ϕ + csc θ], which is part of a larger family of solutions ψ = ln [cos ϕ + (1/2)(ctan(θ/2) + (1/c)cot(θ/2))], while when m = 2, we have ψ = ln [2 cot²θ + 2 cos ²ϕ].

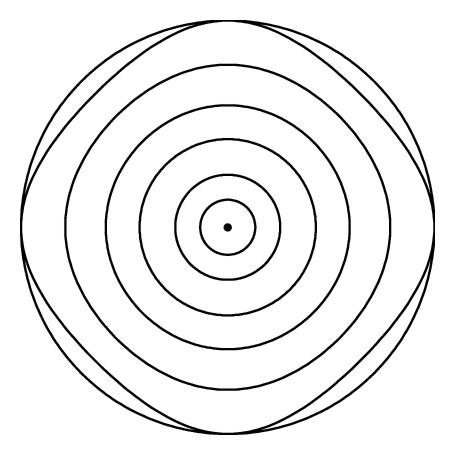
The points θ = 0 and π, which are the poles of the sphere, correspond to y = −∞ and +∞ on the plane, and ψ → ∞ as θ → 0+ and π−. We can see from Figure 2(b) that the flow at each of the poles looks like a vortex, and (2.7) confirms that there are point vortices at the two poles, with ψ ~ −(κm/2π)ln θ as θ → 0 and −(κm/2π)ln (π − θ) as θ → π. Close to the poles, we have u_ϕ ~ −mκ/2πθ as θ → 0 and mκ/2π(π − θ) as θ → π, so that u_ϕ is singular at the poles, while u_θ ~ −(mκθ^m−1/2^mπ)sin mϕ as θ → 0 and −(mκ(π−θ)^m−1/2^mπ)sin mϕ as θ → π, so that u_θ → −(κ/2π)sin ϕ as θ → 0, π for m = 1 and u_θ → 0 as θ → 0, π for m > 1.

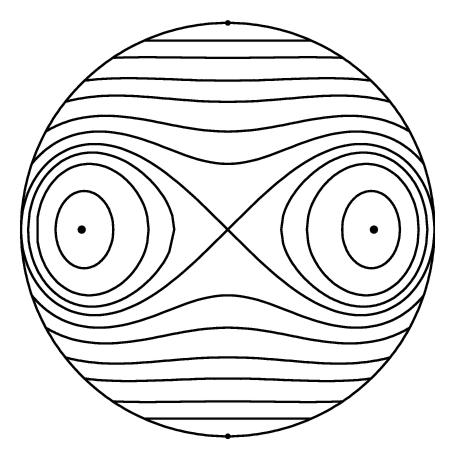
2.2.2. Single Counterrotating Row

The streamfunction and velocity components for a single row of alternating vortices are given by

$$ ()

for m = 1,2, 3, …. This streamfunction is plotted in Figure 3 for m = 2. When m = 1, the streamfunction (2.8) reduces to ψ = ln [(1 + cos ϕsin θ)/(1 − cos ϕsin θ)], which is the point vortex limit of a solution given in [19], while when m = 2, we have ψ = ln [(cos ²θ + cos ²ϕ sin ²θ)/(1 − cos ²ϕ sin ²θ)].

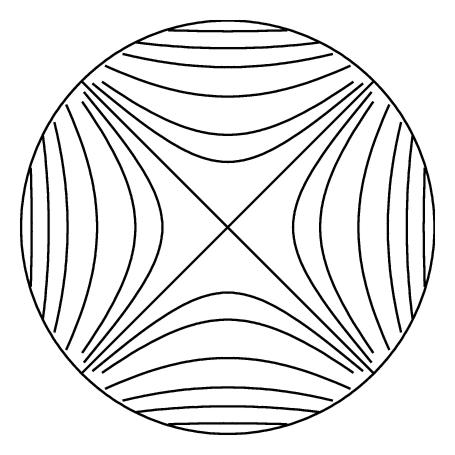
The spherical arcs ϕ = π/2m, 3π/2m, …, (2m − 1)π/2m are streamlines since ψ = 0 on these lines. The points θ = 0 and π, which are the poles of the sphere, correspond to y = −∞ and +∞ on the plane, and ψ → 0 as θ → 0+ and π−. We can see from Figure 3(b) that the flow at each of the poles looks like flow in a corner of angle π/2m, with the streamlines ϕ = π/2m, 3π/2m, …, (2m − 1)π/2m acting like rigid walls, and (2.8) confirms that ψ ~ (κθ^m/π2^m−1)cos mϕ as θ → 0 and (κ(π−θ)^m/π2^m−1)cos mϕ as θ → π. Close to the poles, we have u_ϕ ~ −(mκθ^m−1/2^m−1π)cos mϕ as θ → 0 and (mκ(π−θ)^m−1/2^m−1π)cos mϕ as θ → π, while u_θ ~ −(mκθ^m−1/2^m−1π)sin mϕ as θ → 0 and −(mκ(π−θ)^m−1/2^m−1π)sin mϕ as θ → π, so that for m = 1,   u_ϕ ~ −(κ/π)cos ϕ as θ → 0 and (κ/π)cos ϕ as θ → π and u_θ ~ −(κ/π)sin ϕ as θ → 0 or π, and for m > 1, both u_ϕ and u_θ→0 as θ → 0 or π.

2.2.3. Symmetrical and Staggered Double Rows

Near to the poles, the streamfunction for the symmetrical double row, ψ ~ (κ/π)(md − 2^1−msinh mdcos mϕθ^m) as θ → 0 and −(κ/π)(md − 2^1−msinh mdcos mϕ(π−θ)^m) as θ → π, with u_ϕ ~ (mκθ^m−1/2^m−1π)sinh mdcos mϕ as θ → 0 and (mκ(π−θ)^m−1/2^m−1π)sinh mdcos mϕ as θ → π, while u_θ ~ (mκθ^m−1/2^m−1π)sinh mdsin mϕ as θ → 0 and −(mκ(π−θ)^m−1/2^m−1π)sinh mdsin mϕ as θ → π, so that for m = 1,   u_ϕ ~ (κ/2π)sinh dcos ϕ as θ → 0 or π and u_θ ~ −(κ/π)sinh dsin ϕ as θ → 0 and −(κ/π)sinh dsin ϕ as θ → π, and for m > 1, both u_ϕ and u_θ→0 as θ → 0 or π.

Near to the poles, the streamfunction for the staggered double row, ψ ~ (κ/π)(md + 2^1−mcosh mdcos mϕθ^m) as θ → 0 and −(κ/π)(md − 2^1−mcosh mdcos mϕ(π−θ)^m) as θ → π, with u_ϕ ~ −(mκθ^m−1/2^m−1π)cosh mdcos mϕ as θ → 0 and (mκ(π−θ)^m−1/2^m−1π)cosh mdcos mϕ as θ → π, while u_θ ~ −(mκθ^m−1/2^m−1π)cosh mdsin mϕ as θ → 0 and −(mκ(π−θ)^m−1/2^m−1π)cosh mdsin mϕ as θ → π, so that for m = 1,   u_ϕ ~ −(κ/π)cosh dcos ϕ as θ → 0 and (κ/π)cosh dcos ϕ as θ → π and u_θ ~ −(κ/2π)cosh dsin ϕ as θ → 0 or π, and for m > 1, both u_ϕ and u_θ→0 as θ → 0 or π.

2.2.4. Gauss’ Constraint on the Vorticity

Since a sphere is a closed compact surface, it follows from Gauss’ theorem that the integral of the scalar vorticity field over the spherical surface must be zero. This is a global constraint on the vorticity distribution. In order to satisfy this constraint and simultaneously have an irrotational flow, each point vortex must be counterbalanced by another point vortex on the sphere. By inspection, the single counterrotating row and the symmetrical and staggered double rows satisfy this constraint because for these vortex streets the total vorticity on the spherical surface is the sum of the circulations of the point vortices, and for each point vortex, there is a point vortex of opposite strength, so that the circulations sum to zero. For the single corotating row (2.7), the situation is slightly more complex. There are m point vortices along the equator θ = π/2, and close to the vortex at θ = π/2 and ϕ = π/m, the streamfunction behaves like $$, with similar behavior at the other vortices along the equator. There are also two point vortices at the poles: close to the vortex at θ = 0, the streamfunction behaves like −(κm/2π)ln θ, while close to the vortex at θ = π, the streamfunction behaves like −(κm/2π)ln (π − θ), so that the circulations sum to zero and the constraint is satisfied for the single corotating row, and it would appear that the two polar vortices are generated to satisfy this constraint.

3. Discussion

In the previous section, we saw that if we had a vortex street ψ = Ψ(x, y) on the plane which was 2π-periodic in x, then the transformation x → ϕ, y → ln  tan (θ/2) would produce a vortex street on the sphere, ψ = Ψ(ϕ, ln  tan(θ/2)). We would mention that in [20], we used a much simpler transformation to transport vortices from the plane to the cylinder. Perhaps surprisingly, this very simple approach of transporting vortex streets from the plane to the sphere does not appear to have been used previously, with most previous studies having instead used a stereographic projection, an approach which Lamb [6] mentions was used by Kirchhoff as far back as 1875 to study electrical conduction in a spherical sheet. As an illustration, we applied this transformation to the two-dimensional vortex streets in Table 1 to obtain the corresponding vortex streets on a sphere given in Table 2, and the vortex streets corresponding to rows of corotating and counterrotating vortices were plotted in Figures 2 and 3. For the corotating row, two polar vortices are generated, presumably to satisfy the Gauss constraint on the vorticity.

As to the direction of possible future research, we mentioned in Section 1 that for the plane case, some of the vortex streets have been generalized to smooth finite amplitude vortices, resulting in Stuart vortices [17] and Mallier-Maslowe vortices [18]. We saw in Section 2.2 that when m = 1, the streamfunction (2.8) for the counterrotating row reduced to the point vortex limit of a solution given in [19], where we presented some finite-amplitude vortex solutions for the sphere, so conversely it follows that the m = 1 counterrotating case can be generalized to smooth finite-amplitude vortices. It would be interesting to see if the remaining vortex streets presented here could be generalized as well although we note that this is somewhat harder for the sphere, because the equation for nonlinear solutions on the sphere, [(∂²/∂ϕ²) + (∂²/∂η²)]ψ = r²  sech²ηℱ(ψ), has a sech²η factor on the right hand side which is not present in the corresponding equation on the plane, [(∂²/∂x²) + (∂²/∂y²)]ψ = ℱ(ψ). Perhaps because of this additional factor, very few exact smooth solutions are known for flow on a sphere, and apart from [19], the only exact distributed vortex equilibria (as opposed to point vortices) on a sphere appear to be the exact solutions on a rotating sphere presented in [21, 22] and two studies by Crowdy, one involving a generalization of Stuart vortices to the sphere [23], the other involving a combination of vortex patches and point vortices [24].

We would not claim that the present study is exhaustive, and another possible direction for future research was suggested by an anonymous referee, who wondered whether any vortex street solutions might be found consisting of double rows with different strengths.