Graphs Based on BCK/BCI-Algebras

Proposition 3.1. Let A and B be subsets of X, then

• (1)

  A⊆l(r(A)) and A⊆r(l(A)),

• (2)

  If A⊆B, then l(B)⊆l(A) and r(B)⊆r(A),

• (3)

  l(A) = l(r(l(A))) and r(A) = r(l(r(A))).

Proof. Let a ∈ A and x ∈ l(A), then x*a = 0, and so a ∈ r(l(A)). This says that A⊆r(l(A)). Dually, A⊆l(r(A)). Hence, (1) is valid.

Assume that A⊆B and let x ∈ l(B), then x*b = 0 for all b ∈ B, which implies from A⊆B that x*b = 0 for all b ∈ A. Thus, x ∈ l(A), which shows that l(B)⊆l(A). Similarly, we have r(B)⊆r(A). Thus, (2) holds.

Using (1) and (2), we have l(r(l(A)))⊆l(A) and r(l(r(A)))⊆r(A). If we apply (1) to l(A) and r(A), then l(A)⊆l(r(l(A))) and r(A)⊆r(l(r(A))). Hence, l(A) = l(r(l(A))) and r(A) = r(l(r(A))).

Definition 3.2. A nonempty subset I of X is called a quasi-ideal of X if it satisfies

Example 3.3. Let X = {0, a, b, c, d} be a set with the *-operation given by Table 1, then (X; *, 0) is a BCK-algebra (see [4]). The set I : = {0, a, b} is a quasi-ideal of X.

Obviously, every quasi-ideal I of a BCK-algebra X contains the zero element 0. The following example shows that there exists a quasi-ideal I of a BCI-algebra X such that 0 ∉ I.

Example 3.4. Let X = {0, 1, a, b, c} be a set with the *-operation given by Table 2, then (X; *, 0) is a BCI-algebra (see [3]). The set I : = {0, 1, a} is a quasi-ideal of X containing the zero element 0, but the set J : = {a, b, c} is a quasi-ideal of X which does not contain the zero element 0.

Obviously, every ideal of X is a quasi-ideal of X, but the converse is not true. In fact, the quasi-ideal I : = {0, a, b} in Example 3.3 is not an ideal of X. Also, quasi-ideals I and J in Example 3.4 are not ideals of X.

Definition 3.5. A (quasi-) ideal I of X is said to be l-prime if it satisfies

• (i)

  I is proper, that is, I ≠ X,

• (ii)

  (∀x, y ∈ X)  (l({x, y})⊆I⇒x ∈ I  or  y ∈ I).

Example 3.6. Consider the BCK-algebra X = {0, a, b, c, d} with the operation * which is given by the Table 3, then the set I = {0, a, c} is an l-prime ideal of X.

Theorem 3.7. A proper (quasi-) ideal I of X is l-prime if and only if it satisfies

for all x₁, …, x_n ∈ X.

Proof. Assume that I is an l-prime (quasi-) ideal of X. We proceed by induction on n. If n = 2, then the result is true. Suppose that the statement holds for n − 1. Let x₁, …, x_n ∈ X be such that l({x₁, …, x_n−1, x_n})⊆I. If y ∈ l({x₁, …, x_n−1}), then l({y, x_n})⊆l({x₁, …, x_n−1, x_n})⊆I. Assume that x_n ∉ I, then y ∈ I by the l-primeness of I, which shows that l({x₁, …, x_n−1})⊆I. Using the induction hypothesis, we conclude that x_i ∈ I for some i ∈ {1, …, n − 1}. The converse is clear.

Lemma 3.8. If X is a BCK-algebra, then l({x, 0}) = {0} for all x ∈ X.

Proof. Let x ∈ X and a ∈ l({x, 0}), then a*x = 0 = a*0 = a, and so l({x, 0}) = {0} for all x ∈ X.

Corollary 3.9. If X is a BCI-algebra, then l({x, 0}) = {0} for all x ∈ X with l({x, 0}) ≠ ∅.

Lemma 3.10. If X is a BCI-algebra, then l({x, 0}) = {0} for all x ∈ X₊, where X₊ is the BCK-part of X.

Proof. Straightforward.

Lemma 3.11. For any elements a and b of a BCK-algebra X, if a*b = 0, then l({a})⊆l({b}) and Z_b⊆Z_a.

Proof. Assume that a*b = 0. Let x ∈ l({a}), then x*a = 0, and so

Thus, x ∈ l({b}), which shows that l({a})⊆l({b}). Obviously, Z_b⊆Z_a.

Theorem 3.12. For any element x of a BCK-algebra X, the set of zero divisors of x is a quasi-ideal of X containing the zero element 0. Moreover, if Z_x is maximal in {Z_a∣a ∈ X, Z_a ≠ X}, then Z_x is l-prime.

Proof. By Lemma 3.8, we have 0 ∈ Z_x. Let a ∈ X and b ∈ Z_x be such that a*b = 0. Using Lemma 3.11, we have

and so l({x, a}) = {0}. Hence, a ∈ Z_x. Therefore, Z_x is a quasi-ideal of X. Let a, b ∈ X be such that l({a, b})⊆Z_x and a ∉ Z_x, then l({a, b, x}) = {0}. Let 0 ≠ y ∈ l({a, x}) be an arbitrarily element, then l({b, y})⊆l({a, b, x}) = {0}, and so l({b, y}) = {0}, that is, b ∈ Z_y. Since y ∈ l({a, x}), we have y*x = 0. It follows from Lemma 3.11 that Z_x⊆Z_y ≠ X so from the maximality of Z_x it follows that Z_x = Z_y. Hence, b ∈ Z_x, which shows that Z_x is l-prime.

Definition 3.13. By the associated graph of a BCK/BCI-algebra X, denoted Γ(X), we mean the graph whose vertices are just the elements of X, and for distinct x, y ∈ Γ(X), there is an edge connecting x and y, denoted by x − y if and only if l({x, y}) = {0}.

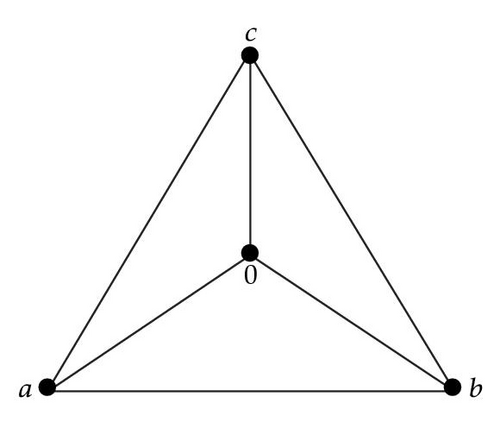
Example 3.14. Let X = {0, a, b, c} be a set with the *-operation given by Table 5, then X is a BCK-algebra (see [4]). The associated graph Γ(X) of X is given by the Figure 1.

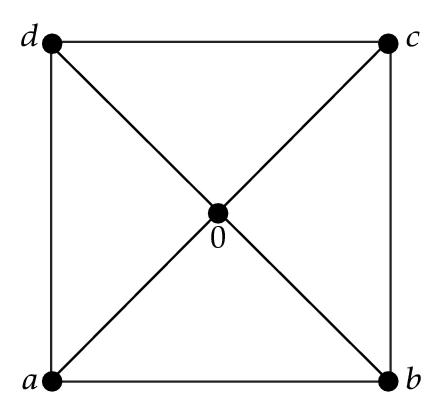
Example 3.15. Let X = {0, a, b, c, d} be a set with the *-operation given by Table 6, then X is a BCK-algebra (see [4]). By Lemma 3.8, each nonzero point is adjacent to 0. Note that l({a, b}) = l({a, d}) = l({b, c}) = l({c, d}) = {0}, l({a, c}) = {0, a}, and l({b, d}) = {0, b}. Hence the associated graph Γ(X) of X is given by the Figure 2.

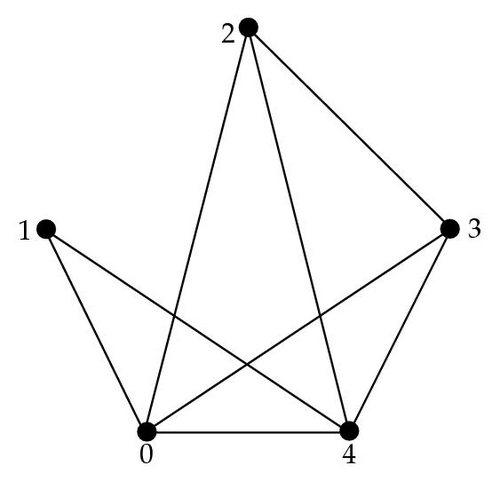
Example 3.16. Let X = {0, 1,2, 3,4} be a set with the *-operation given by Table 7, then X is a BCK-algebra (see [4]). By Lemma 3.8, each nonzero point is adjacent to 0. Note that l({1,2}) = {0, 1}, that is, 1 is not adjacent to 2 and l({1,3}) = l({1,4}) = l({2,3}) = l({2,4}) = l({3,4}) = {0}. Hence, the associated graph Γ(X) of X is given by Figure 3.

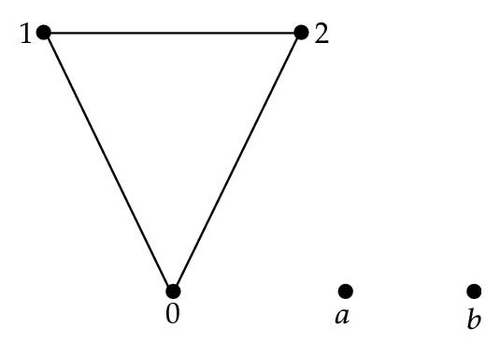
Example 3.17. Consider a BCI-algebra X = {0, 1,2, a, b} with the *-operation given by Table 4, then

l({a, b}) = {a}, and l({1,2}) = {0}. Since X₊ = {0, 1,2}, we know from Lemma 3.10 that two points 1 and 2 are adjacent to 0. The associated graph Γ(X) of X is given by Figure 4.

Theorem 3.18. Let Γ(X) be the associated graph of a BCK-algebra X. For any x, y ∈ Γ(X), if Z_x and Z_y are distinct l-prime quasi-ideals of X, then there is an edge connecting x and y.

Proof. It is sufficient to show that l({x, y}) = {0}. If l({x, y})≠{0}, then x ∉ Z_y and y ∉ Z_x. For any a ∈ Z_x, we have l({x, a}) = {0}⊆Z_y. Since Z_y is l-prime, it follows that a ∈ Z_y so that Z_x⊆Z_y. Similarly, Z_y⊆Z_x. Hence, Z_x = Z_y, which is a contradiction. Therefore, x is adjacent to y.

Theorem 3.19. The associated graph of a BCK-algebra is connected in which every nonzero vertex is adjacent to 0.

Proof. It follows from Lemma 3.8.