Nondimensional Analysis of Fractional-Order PDD1/2 Control of Purely Inertial Systems
Abstract
The paper discusses the performance of the PDD1/2 control scheme, which is an extension of the classical PD scheme with the introduction of the half-derivative term. The comparison between the PD and the PDD1/2 schemes is performed with reference to a second-order purely inertial system, using a dimensionless approach for the sake of generality. The influences of the sampling time and of the saturation are taken into account. The results show that the introduction of the half-derivative term, in proper combination with the derivative term, reduces the settling time under the same conditions of maximum control output and null overshoot.
1. Introduction
Even though the introduction of Fractional Calculus dates back to the eighteenth century, in the last years there is a revival of interest about this theoretical issue, and new possible fields of application are emerging.
Fractional Calculus is an extension of classical mathematics which considers derivatives and integrals to an order which is not necessarily integer but can be rational, irrational, or complex [1–3]. The theoretical possibility of this extension was already discussed by Euler and Liouville; nevertheless, most practical applications are recent and cover many different areas: not only science and engineering but also economics and finance. At present, researchers’ efforts have two distinct aims: investigating the mathematical aspects of Fractional Calculus and widening the range of its possible applications [4].
As regards physics, Fractional Calculus has been recognized as a powerful tool in modelling multiscale problems, characterized by wide time or length scales. An interesting physical interpretation of fractional derivatives is proposed in [5].
In the area of variational principles, it is possible to replace the classical derivatives with the fractional ones; fractional formulations of the Euler-Lagrange equations, of the Hamilton equations, and of the Dirac equations have been proposed and applied [6–8]. The recently introduced Nambu dynamics is a generalization of Hamiltonian mechanics involving multiple Hamiltonians [9]. Other applications of Fractional Calculus in physics are described in [10].
In biology and bioengineering, Fractional Calculus is used to predict macroscale behaviour from microscale observations [11] and to model the neuron behaviour [12, 13].
In economics, Fractional Calculus can be applied to technological change models to obtain generalized solutions [14].
As regards engineering, Fractional Calculus plays an important role, for example, in control system design [15–19], electronics [20], and robotics [21–23].
Focussing on control system design, the most widespread approach consists in generalizing the classical PID scheme by introducing derivatives and integrals to an arbitrary order, giving rise to the PIλDμ controller [24]: with this approach there are two additional parameters (the orders λ and μ) to tune the system behaviour besides the proportional, derivative, and integral gains.
An alternative approach is not substituting a differential-order derivative term for the first-order derivative term, but using them in combination, giving rise to the PIDD1/2 scheme [25, 26]. The main justification of this approach is practical: control system designers are unlikely to discard completely the universally used PID scheme, but probably they will accept to add the half-derivative term as optional if it brings significant benefits.
The positive effects of the introduction of the half-derivative term have already been discussed in [25, 26], with reference to second-order purely inertial linear systems and to position control of some simple robotic architectures; in these works the attention is focused on the comparison between the PD scheme and the PDD1/2 scheme in the transient state, and the integral term, which reduces the steady state error, is not considered. In the present paper the comparison between PD and PDD1/2 schemes is deepened using a nondimensional approach for the sake of generality, taking into account the influence of saturation and sampling time.
2. Definition of Fractional-Order Derivative
There are different possible theoretical approaches to generalize the concepts of derivative and integral to a noninteger order α. The definitions that correspond to these approaches are proved to be equivalent; nevertheless, the different definitions lead to different discrete-time implementations, with different performance in real-time control system applications [27].
The discrete-time implementations that are based on the Letnikov, Tustin, and Simpson definitions are compared in [27]; these implementations are characterized by an infinite number of terms, which requires a proper truncation. The comparison shows that the definition by Letnikov has several computational advantages in the discrete-time implementation and is more robust in what concerns the series truncation.
Moreover, (4) is characterized by an infinite number of terms; in the real implementation the number of terms must be truncated. The influence of this truncation is discussed in [27].
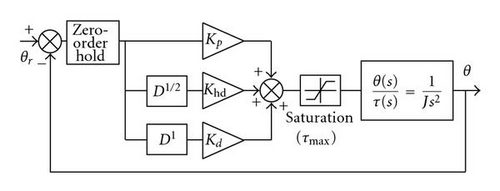
3. Discrete-Time PDD1/2 Control with Saturation of a Second-Order Linear System
- (i)
a zero-order hold,
- (ii)
a PDD1/2 control with proportional gain Kp, derivative gain Kd, and half-derivative gain Khd,
- (iii)
a saturation block which limits the control torque τ in the interval [−τmax , τmax ], where τmax is the output saturation value,
- (iv)
a continuous-time second-order linear rotational system.
| Parameter | Symbol | SI unit |
|---|---|---|
| mass moment of inertia of the rotor | J | kg·m2 |
| proportional gain | Kp | Nm/rad |
| derivative gain | Kd | Nms/rad |
| half-derivative gain | Khd | Nms1/2/rad |
| saturation torque | τmax | Nm |
| sampling time | Ts | s |
- (i)
ζ corresponds to the damping ratio of the second-order mechanical systems; if we consider that in this case, the elastic return force and the damping force are, respectively, applied by the proportional and derivative terms; therefore ζ represents nondimensionally the derivative gain Kd;
- (ii)
ψ represents nondimensionally the half-derivative gain Khd;
- (iii)
λ (dimensionless sampling time) represents nondimensionally the sampling time Ts;
- (iv)
σ (dimensionless saturation torque) represents nondimensionally the saturation torque τmax .
4. Discrete-Time PDD1/2 Control with Saturation of a Second-Order Linear System: Simulation Results
- (i)
Section 4.1 shows the effects of saturation (parameter σ) on the step response of the system with PD control (ψ = 0).
- (ii)
Section 4.2 shows the effects of the introduction of the half-derivative term, keeping constant the derivative term (ζ), the sampling rate (λ), and the maximum control output (σ).
- (iii)
Section 4.3 shows that a proper combination of the half-derivative and derivative terms (parameters ψ and ζ) allows to reduce remarkably the settling time keeping constant λ and σand respecting the condition of null overshoot (“null-overshoot/minimum settling time ψ-ζ combination, n.o.m.s.t. ψ-ζ combination ).
- (iv)
Section 4.4 discusses the influence of the parameter σ on the system behaviour and on the n.o.m.s.t ψ-ζ combination.
- (v)
Section 4.5 discusses the influence of the sampling time (parameter λ) on the n.o.m.s.t. ψ-ζ combination.
All the simulations are performed using the Matlab package Simulink.
4.1. Effects of Saturation on the PD Control
First of all, we analyze the system behaviour without half-derivative term (ψ = 0) in order to discuss the influence of the dimensionless parameters σ and ζ; since ψ = 0, λ does not influence the system behaviour, provided that it is sufficiently small: in fact if λ tends to zero (i.e., the sampling time tends to be negligible with respect to the system dynamics), the discrete-time evaluation of the derivative tends to the continuous time derivative; as we will see, this is not true if ψ > 0, because of the approximation of the z-transfer function (5), which has a finite number of terms.
Figure 2 shows the system step response (null initial conditions: θ(0) = 0, ) with σ = 1 and five different values of ζ: 0.4, 0.6, 0.8, 1, 1.2; for the first three values of ζ the system has overshoot.
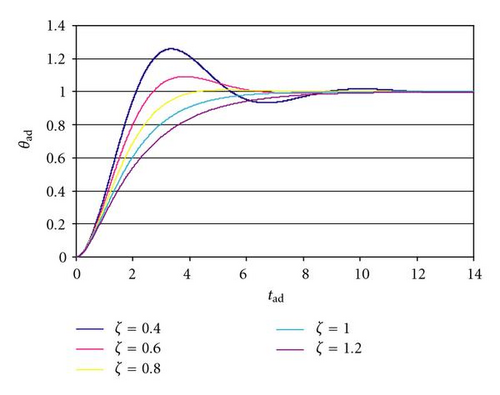
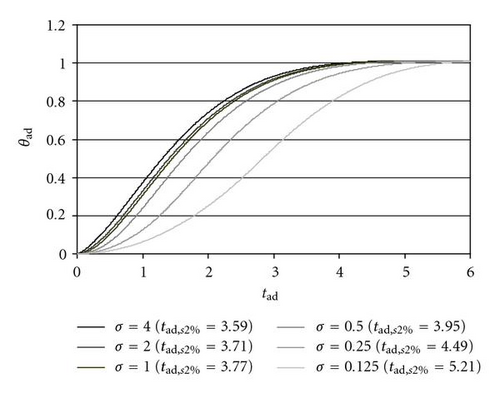
Table 2 shows the dimensionless settling time to within 2% (tad,s2%) as a function of ζ and σ; five values of ζ (0.4, 0.6, 0.8, 1, 1.2) and six values of σ (4, 2, 1, 0.5, 0.25, 0.125) are considered. The simulations show that the system has overshoot only for ζ = 0.4, 0.6, 0.8, and that for ζ = 0.8 there are the lower settling times, independently from σ. Moreover, it is possible to note that tad,s2% increases with the decrease of σ: in particular, Figure 3 shows the time histories of θad for the six systems of the third column of Table 2(ζ = 0.8).
| σ↓ ξ→ | 0.4 | 0.6 | 0.8 | 1 | 1.2 |
|---|---|---|---|---|---|
| 4 | 8.09(o.s.) | 5.61(o.s.) | 3.60(o.s.) | 5.81 | 7.87 |
| 2 | 8.19(o.s.) | 5.72(o.s.) | 3.72(o.s.) | 5.92 | 7.97 |
| 1 | 8.24(o.s.) | 5.77(o.s.) | 3.77(o.s.) | 5.97 | 8.03 |
| 0.5 | 8.50(o.s.) | 5.99(o.s.) | 3.96(o.s.) | 6.13 | 8.15 |
| 0.25 | 9.41(o.s.) | 6.54(o.s.) | 4.49(o.s.) | 6.54 | 8.50 |
| 0.125 | 14.66(o.s.) | 8.41(o.s.) | 5.21(o.s.) | 7.30 | 9.16 |
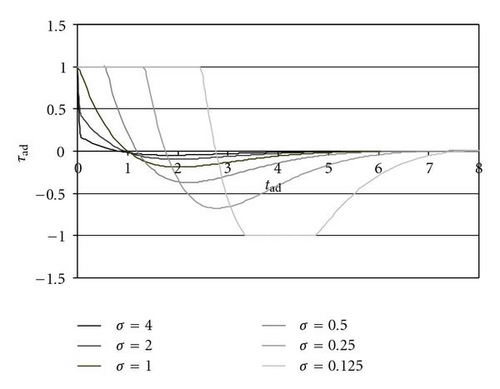
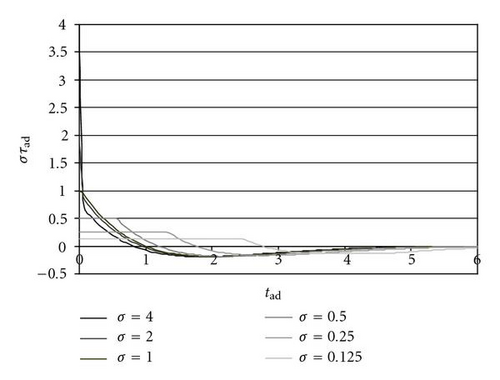
The increase of settling time with the decrease of σ is due to the lower saturation torque; it can be observed by the time histories of τad (Figure 4) and στad = τ/(Kpθr) (Figure 5); the second dimensionless value is more significant in this comparison because it is not nondimensionalized using the saturation torque.
4.2. Effects of the Introduction of the Half-Derivative Term
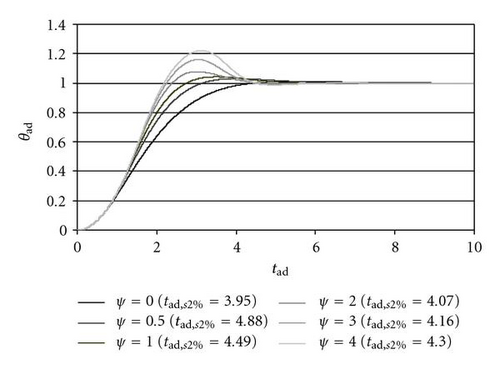
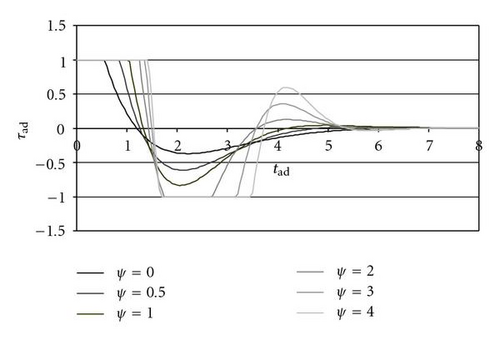
Let us consider now the system behaviour keeping constant the derivative term (ζ = 0.8) and the saturation (σ = 0.5), but introducing the half-derivative term (ψ ≠ 0); the dimensionless sampling time is constant (λ = 0.05). The introduction of ψ causes an increase of the overshoot and higher settling times (Figure 6), with a more oscillating input torque (Figure 7); therefore the half-derivative term in this comparison is not advantageous.
4.3. Combined Effects of the Half-Derivative and Derivative Terms (“Null-Overshoot/Minimum Settling Time” ψ-ζ Combination)
On the other hand, the introduction of the half-derivative term with a proper adjustment of the derivative term can lead to benefits when it is necessary to minimize the settling time while avoiding overshoot (two frequent requirements). Let us consider the system with the same saturation level and sampling time of Section 4.2 (σ = 0.5; λ = 0.05); now we determine the minimum derivative coefficient ζ that provides stabilization without overshoot as function of the half-derivative coefficient ψ. This minimum value is ζ = 0.96 for the PD control (ψ = 0); for ψ > 0 the value of ζ has to be properly increased to avoid overshoot, and it is possible to associate a value of ζ to any value of ψ; in the following this ψ-ζ combination will be named n.o.m.s.t. ψ-ζ combination (null-overshoot/minimum settling time). This combination depends on σ and λ, as will be discussed in Sections 4.4 and 4.5.
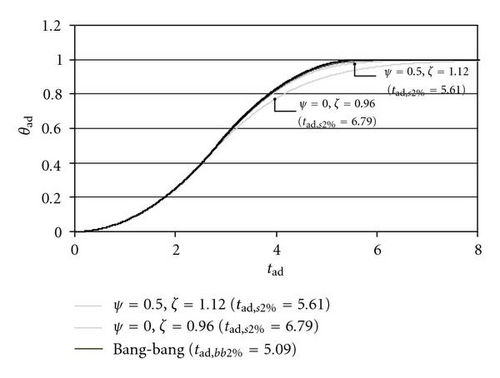
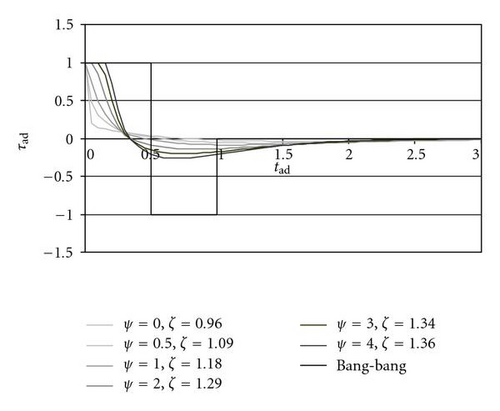
Figure 8 shows the time histories of θad as a function of tad in case of seven n.o.m.s.t. ψ-ζ combinations (ψ = 0 (PD), 0.5, 1, 2, 3, 4, 8) and the corresponding dimensionless settling times tad,s2%: the reduction of settling time that corresponds to the increase of ψ is remarkable (up to −55% for ψ = 8 with respect to ψ = 0). This reduction is due to the fact that with high half-derivative gain the control output tends to be similar to the one of a bang-bang control (Figure 9), and the bang-bang control (maximum positive torque for acceleration and maximum negative torque for deceleration) minimizes the settling time of a second-order linear system for a given maximum control output.
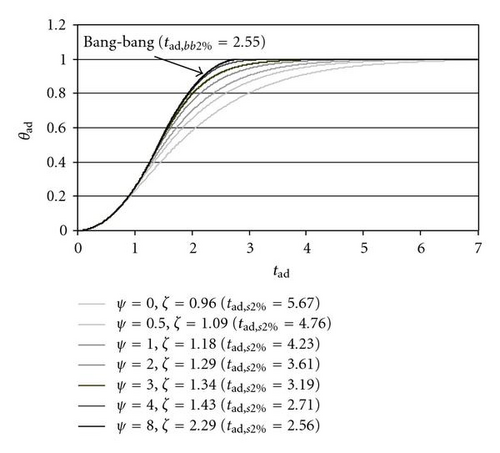
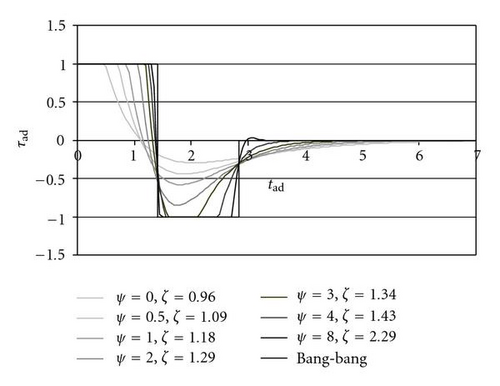
With ψ ≥ 4 the dimensionless settling time is very close to the theoretical minimum tad,bb2% (2.55 for σ = 0.5); therefore a further increase of ψ and ζ is not profitable, also because high values of the damping coefficient lead to instability in the real implementation.
4.4. Effects of σ on the n.o.m.s.t. ψ-ζ Combination
Figures 10 and 11 show the system behaviour with σ = 0.125 (lower saturation torque than in the case of Section 4.3) and λ = 0.05, with the n.o.m.s.t. ψ-ζ combinations corresponding to ψ = 0, 0.5, 1, 2, 3, 4. In Figure 10 the graphs with ψ ≥ 1 are very similar and superimposed to the bang-bang graph. Let us note that the values of ζ in the ψ-ζ combinations are changed with respect to the case of Section 4.3 (σ = 0.5; λ = 0.05) due to the different values of σ (Table 3).
| ψ | ζ | |||||
|---|---|---|---|---|---|---|
| σ = 0.125 | σ = 0.25 | σ = 0.5 | σ = 1 | σ = 2 | σ = 4 | |
| 0 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 |
| 0.5 | 1.12 | 1.09 | 1.09 | 1.09 | 1.09 | 1.09 |
| 1 | 1.38 | 1.18 | 1.18 | 1.18 | 1.18 | 1.18 |
| 2 | 1.94 | 1.38 | 1.29 | 1.29 | 1.29 | 1.29 |
| 3 | 2.52 | 1.72 | 1.34 | 1.34 | 1.34 | 1.34 |
| 4 | 3.11 | 2.09 | 1.43 | 1.36 | 1.36 | 1.36 |
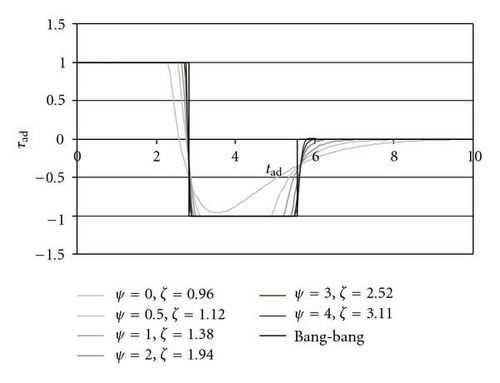
Since the saturation torque is low, all the systems with the exception of the one with ψ = 0 reach the saturation in both directions (Figure 11); all the settling times are close to the minimum value tad,bb2% = 5.09, (17), with moderate influence of ψ (Figure 10).
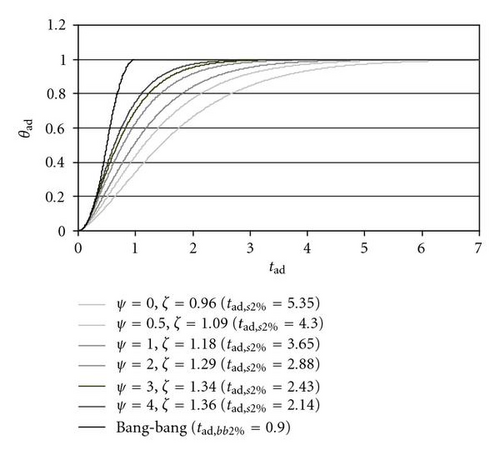
On the contrary, the influence of ψ on the settling time increases with higher values of σ. Figures 12 and 13 show the system behaviour with σ = 4, λ = 0.05, and different n.o.m.s.t. ψ-ζ combinations (ψ = 0, 0.5, 1, 2, 3, 4): the increment of ψ causes a remarkable reduction of settling time (−60% with respect to ψ = 0 for ψ = 4).
The histogram of Figure 14 shows the influence on the settling time of the parameters σ and ψ adopting the corresponding n.o.m.s.t. ψ-ζ combinations and keeping constant λ = 0.05: for all the values of σ, the increment of ψ causes a reduction of the settling time, but this reduction is larger for high values of σ, that is, when the saturation torque is relatively high.
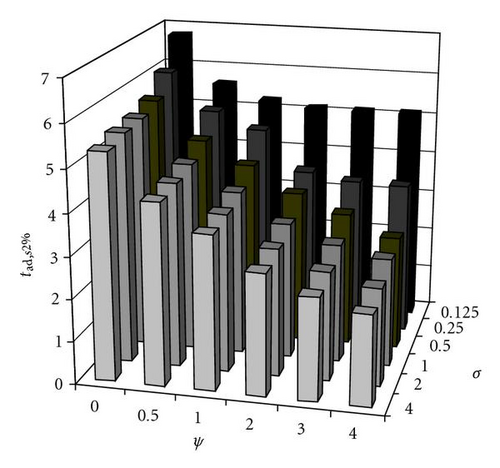
Let us note that for σ ≥ 1 the n.o.m.s.t. ψ-ζ combinations are equal (Table 3); also the n.o.m.s.t. ψ-ζ combination with σ = 0.5 is very similar to the ones with σ ≥ 1. This means that for all the operative conditions in which σ ≥ 1 the PDD1/2 control can be tuned optimally with a unique n.o.m.s.t. ψ-ζ combination. Since σ is usually higher than 1 in normal operative conditions, because τmax ≫ Kpθr, we can neglect the influence of σ and adopt always the ψ-ζ combination for σ ≥ 1; this combination will be named in the following “n.o.m.s.t.(hσ) ψ-ζ combination” for brevity.
4.5. Effects of λ on the n.o.m.s.t. ψ-ζ Combination
The previous simulations have shown that the n.o.m.s.t. ψ-ζ combination tends to the constant n.o.m.s.t.(hσ) ψ-ζ combination when σ tends to high values. Nevertheless, all the considered simulations are characterized by a constant value of λ; then it is necessary to study the influence of this parameter on the system behaviour. As a matter of fact, the half-derivative term is calculated by (5), which is a discrete-time approximation with a finite number of terms; therefore the influence of the sampling time is not negligible.
- (i)
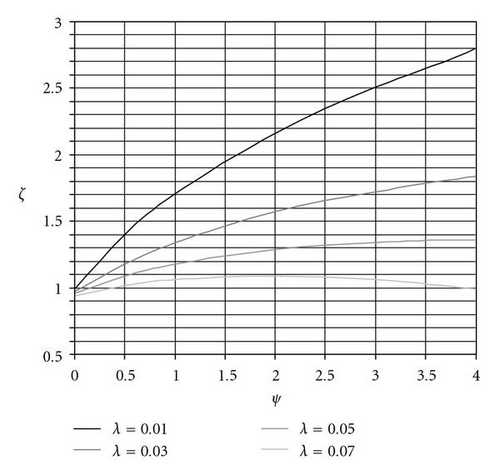
λ influences the n.o.m.s.t.(hσ) ψ-ζ combination: Figure 15 shows the n.o.m.s.t.(hσ) ψ-ζ combination for λ = 0.01, 0.03, 0.05, 0.07;
- (ii)
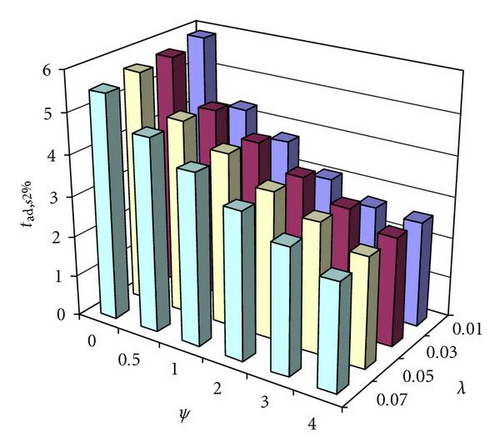
for the same value of ψ, variations of λ do not affect significantly the sampling time if the n.o.m.s.t.(hσ) ψ-ζ combination is properly changed according to λ, as shown in Figure 16 (the small fluctuations are due to the numerical approximations of (5)).
5. Conclusions
A comparison between the classical PD and the proposed PDD1/2 control scheme has been performed with reference to a linear second-order inertial system. The PDD1/2 control scheme derives from the PD control scheme with the addition of the half-derivative term. The effects of the saturation and of the sampling time have been considered.
A dimensionless approach has been adopted for sake of generality, by introducing four dimensionless parameters: ζ, which represents the derivative gain; ψ, which represents the half-derivative gain; λ, which represents the sampling time; and σ, which represents the control saturation.
- (i)
The introduction of the half-derivative term (ψ) in proper combination with the derivative term (ζ) allows to reduce the settling time of a step response under the same limitation of maximum torque (σ) respecting the condition of null overshoot.
- (ii)
The reduction of settling time is higher for high values of maximum torque (σ).
- (iii)
The null overshoot/minimum settling time (n.o.m.s.t.) ψ-ζ combination is characterized by the minimum value of ζ that provides stabilization without overshoot as function of ψ, while keeping constant σ and λ; for higher values of ζ the settling time increases; for lower values of ζ there is overshoot, which is unwanted. Therefore we consider this combination as the optimum combination of the derivative and half-derivative terms.
- (iv)
The n.o.m.s.t. ψ-ζ combination depends on σ and λ; nevertheless, the n.o.m.s.t. combination tends to be constant if σ tends to high values, and σ is usually high in normal operative conditions (τmax ≫ Kpθr); therefore the influence of σ on the tuning of the gains can be neglected. This leads to the n.o.m.s.t.( hσ ) ψ-ζ combination.
- (v)
On the contrary, the influence of λ on the n.o.m.s.t. ψ-ζ combination is not negligible; fortunately, λ depends on the sampling time, on the system inertia (which are constant), and on the proportional gain, but not on the operative conditions (i.e., the amplitude of the commanded step).
- (vi)
For all of these reasons, the n.o.m.s.t. ψ-ζ combination can be selected only on the basis of λ.
In conclusion, the results show that the introduction of the half-derivative term can reduce the settling time of a second-order linear system under the same conditions of maximum control output and null overshoot; moreover, the selection of the half-derivative gain is quite simple and can be based on the graph of Figure 15, which provides the n.o.m.s.t.(hσ) ψ-ζ combinations for different values of λ.
These advantages of the PDD1/2 scheme with respect to the PD scheme in the control of the transient behaviour of purely inertial systems are quite interesting from a technical and industrial point of view: as a matter of fact, the systems that are (exactly or approximately) purely inertial are remarkably widespread (e.g., rotors).
Another common case is when a rotor is connected to a viscous load, proportional to the angular speed; also in this case it is possible to use the proposed control scheme adopting the same criteria to select the half-derivative gain: the viscous load and the derivative control term have the same mathematical expression and can be added up to obtain the overall system damping; as a consequence, the system model and the corresponding control tuning criteria are the same.
Also in case of more complex mechanical systems, characterized by nonlinear inertial effects (e.g., serial robots) the introduction of the half-derivative term can improve the dynamic performance [25, 26].
In the following of the research the application of the half-derivative term will be experimentally tested on a physical system; moreover, there are several issues that must be investigated, such as the extension to the PIDD1/2 scheme and the control stability in presence of disturbances and nonlinear friction effects. Moreover, although the nondimensional approach provides general results, an analytical study of the influence of the half-derivative term is necessary. However, the introduction of the halfderivative term seems to be an interesting option to improve the performance of the classical PID control in terms of settling time, with potential benefits in a wide range of automation and mechatronic applications.




