International Journal of Differential Equations
Volume 2010, Issue 1 764738
Research Article
Open Access

He′s Variational Iteration Method for Solving Fractional Riccati Differential Equation

H. Jafari, 

Corresponding Author

H. Jafari

Department of Mathematics and Computer Science, University of Mazandaran, P.O. Box 47416-95447, Babolsar, Iran umz.ac.ir

Search for more papers by this author
H. Tajadodi, 

H. Tajadodi

Department of Mathematics and Computer Science, University of Mazandaran, P.O. Box 47416-95447, Babolsar, Iran umz.ac.ir

Search for more papers by this author
First published: 29 March 2010
https://doi.org/10.1155/2010/764738
Citations: 32
Academic Editor: Shaher M. Momani

Abstract

We will consider He′s variational iteration method for solving fractional Riccati differential equation. This method is based on the use of Lagrange multipliers for identification of optimal value of a parameter in a functional. This technique provides a sequence of functions which converges to the exact solution of the problem. The present method performs extremely well in terms of efficiency and simplicity.

1. Introduction

The fractional calculus has found diverse applications in various scientific and technological fields [1, 2], such as thermal engineering, acoustics, electromagnetism, control, robotics, viscoelasticity, diffusion, edge detection, turbulence, signal processing, and many other physical processes. Fractional differential equations (FDEs) have also been applied in modeling many physical, engineering problems, and fractional differential equations in nonlinear dynamics [3, 4].

The variational iteration method was proposed by He [5] and was successfully applied to autonomous ordinary differential equation [6], to nonlinear partial differential equations with variable coefficients [7], to Schrodinger-KdV, generalized Kd and shallow water equations [8], to linear Helmholtz partial differential equation [9], recently to nonlinear fractional differential equations with Caputo differential derivative [10, 11], and to other fields, [12]. The variational iteration method gives rapidly convergent successive approximations of the exact solution if such a solution exists; otherwise a few approximations can be used for numerical purposes. The method is effectively used in [6–8, 13–15] and the references therein. Jafari et al. applied the variational iteration method to the Gas Dynamics Equation and Stefan problem [13, 14]. We consider here the following nonlinear fractional Riccati differential equation:

(1.1)
subject to the initial conditions
(1.2)
where α is fractional derivative order, n is an integer, A(t), B(t), and C(t) are known real functions, and ck is a constant. There are several definitions of a fractional derivative of order α > 0. The two most commonly used definitions are the Riemann-Liouville and Caputo. Each definition uses Riemann-Liouville fractional integration and derivatives of whole order. The difference between the two definitions is in the order of evaluation. Riemann-Liouville fractional integration of order a is defined as
(1.3)
The following two equations define Riemann-Liouville and Caputo fractional derivatives of order α, respectively:
(1.4)
(1.5)
where m − 1 < α ⩽ m and m ∈ N. We have chosen to use the Caputo fractional derivative because it allows traditional initial and boundary conditions to be included in the formulation of the problem, but for homogeneous initial condition assumption, these two operators coincide. For more details on the geometric and physical interpretation for fractional derivatives of both the Riemann-Liouville and Caputo types, see [1].

2. Analysis of the Variational Iteration Method

We consider the fractional differential equation

(2.1)
with initial condition y(0) = 0, where Dα = dα/dtα. According to the variational iteration method [5], we construct a correction functional for (2.1) which reads
(2.2)
To identify the multiplier, we approximately write (2.2) in the form
(2.3)
where λ is a general Lagrange multiplier, which can be identified optimally via the variational theory, and is a restricted variation, that is, .
The successive approximation yn+1, n⩾0 of the solution y(t) will be readily obtained upon using Lagrange′s multiplier, and by using any selective function y0. The initial value y(0) and yt(0) are usually used for selecting the zeroth approximation y0. To calculate the optimal value of λ, we have
(2.4)
This yields the stationary conditions λ′(ξ) = 0, and 1 + λ(ξ) = 0, which gives
(2.5)
Substituting this value of Lagrangian multiplier in (2.3), we get the following iteration formula
(2.6)
and finally the exact solution is obtained by
(2.7)

3. Applications and Numerical Results

To give a clear overview of this method, we present the following illustrative examples.

Example 3.1. Consider the following fractional Riccati differential equation:

(3.1)
subject to the initial condition y(0) = 0.

The exact solution of (3.1) is y(t) = (e2t − 1)/(e2t + 1), when α = 1.

In view of (2.6) the correction functional for (3.1) turns out to be

(3.2)
Beginning with y0(t) = tα/Γ(1 + α), by the iteration formulation (3.2), we can obtain directly the other components as
(3.3)
and so on. The nth Approximate solution of the variational iteration method converges to the exact series solution. So, we approximate the solution y(t) = lim n→∞yn(t).

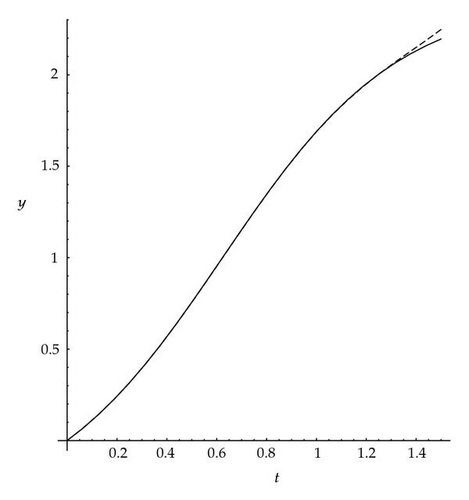
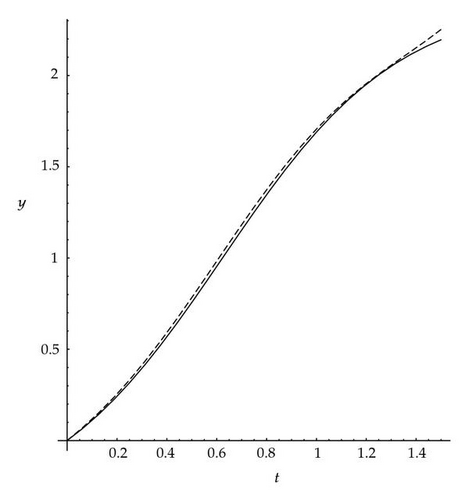
In Figure 1, Approximate solution (y(t)≅y3(t)) of (3.4) using VIM and the exact solution have been plotted for α = 1. In Figure 2, Approximate solution (y(t)≅y3(t)) of (3.4) using VIM and the exact solution have been plotted for α = 0.98.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Dashed line: Approximate solution.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Dashed line: Approximate solution.

Comment 3. This example has been solved using HAM, ADM, and HPM in [16–18]. It should be noted that these methods have given same result after applying the Padé approximants on y(t).

Example 3.2. Consider the following fractional Riccati differential equation:

(3.4)
subject to the initial condition y(0) = 0.

The exact solution of (3.4) is , when α = 1.

Expanding y(t) using Taylor expansion about t = 0 gives

(3.5)
The correction functional for (3.4) turns out to be
(3.6)
Beginning with y0(t) = tα/Γ(1 + α), by the iteration formulation (3.6), we can obtain directly the other components as
(3.7)
and so on. In Figure 3, Approximate solution (y(t)≅y3(t)) of (3.4) using VIM and the exact solution have been plotted for α = 1. In Figure 4, Approximate solution (y(t)≅y3(t)) of (3.4) using VIM and the exact solution have been plotted for α = 0.98.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Dashed line: Approximate solution.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Dashed line: Approximate solution.

4. Conclusion

In this paper the variational iteration method is used to solve the fractional Riccati differential equations. We described the method, used it on two test problems, and compared the results with their exact solutions in order to demonstrate the validity and applicability of the method.

Acknowledgments

The authors express their gratitude to the referees for their valuable suggestions and corrections for improvement of this paper. Mathematica has been used for computations in this paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.