Cluster State Computation with Quantum-Dot Charge Qubits
Abstract
Quantum computers are expected to far surpass the capabilities of today′s most powerful supercomputers, particularly in areas such as the theoretical simulation of quantum systems, cryptography, and information processing. The cluster state is a special, highly entangled quantum state that forms the universal resource on which measurement-based quantum computation can be performed. This paper provides a brief review of the theoretical foundations of cluster state quantum computation and how it evolved from the traditional model of digital computers. It then proposes a scheme for the generation of such entanglement in a solid-state medium through the suppression of resonant tunneling of a ballistic electron by a single-electron charge qubit. To investigate the viability of the scheme for the creation of cluster states, numerical calculations are performed in which the entanglement interaction is modeled in detail.
1. Introduction
The simulation of quantum systems is an integral part of modern science. Such simulations are difficult, however, due to the massive computational resources they require. Quantum computers [1] offer a unique solution to this problem by explicitly using quantum mechanics to perform computation more efficiently. While they promise much, building practical quantum computers using implementations analogous to those of digital computing has proved extremely challenging. In 2001, Raussendorf and Briegel [2] proposed a more robust implementation that used a highly entangled cluster state as a universal resource on which to perform measurement-based quantum computation. The systematic generation of entanglement suitable for the creation of such cluster states is consequently of great importance in the realization of a viable quantum computer.
We begin this paper by giving a brief review of the theoretical foundations of cluster state quantum computation and how it evolved from the traditional model of digital computers. In the next section, we outline a scheme to generate controlled entanglement in a solid-state system using resonant tunneling and give details of the simulation and numerical techniques used to test it. In Section 3, we present the results from our simulation and, in Section 4, discuss the possible difficulties of using such a scheme to generate a cluster state.
1.1. Computation and Physical Simulations
It was Turing, in his revolutionary 1936 paper “On Computable Numbers, with an Application to the Entscheidungsproblem’’ [3], who first proposed the computational model used by all modern computers. He showed that any mathematical operation with an arithmetic formulation, called a computable function, could be performed with finite means by a simple physical device. This theoretical device, known as the universal Turing machine, used a set of basic mechanical actions to manipulate symbols on an infinite one-dimensional paper tape. During each step of computation, the machine would address only a single symbol on the tape and perform a single action that depended on the symbol’s value and the machine’s variable internal state. The particular action taken at each step was controlled by an internal table of conditional instructions, called an algorithm. By constructing a suitable algorithm, such a machine could be made to automatically perform any arithmetic operation on numbers encoded on the tape using only a finite number of steps. What made the universal Turing machine so powerful was that a small set of basic actions, symbols, and instructions could be used with only local information about the system to perform all arithmetic operations in a finite time. While constructing such a mechanical device proved impractical, Turing’s model formed the template for all modern computers.
Unlike the universal Turing machine, a modern computer is a digital device based on the laws of electrodynamics. In place of paper tape, computers use binary digits, called bits, to store and process information. Physically, bits are addressable electronic systems that can have only one of two possible computational states labeled 0 and 1. Information, known as input, is encoded onto a number of bits via some binary discretizing schema. Computation is then performed by sequentially switching the bits between their 0 and 1 states using simple one- and two-bit operations called Boolean logic gates. The final state of the bits is then read off and decoded to give the result, or output, of the computation. While this implementation appears significantly different from Turing’s, a set of just two two-bit Boolean logic gates, the universal gates NAND and NOR, can perform all binary boolean algebraic operations using only finite means. This allows a digital computer to deterministically transform a set of input bits into any possible output and so act as a universal Turing machine.
It is the universality of digital computers that has made them such an invaluable tool in modern life and enabled complex simulations of physical systems to be performed. This has led scientists to ask an important question: “what kind of physical systems can be efficiently simulated on a digital computer?’’ Turing envisaged his universal machine performing computations using an infinite paper tape over some finite, but arbitrarily long, amount of time. As infinite computational resources are impossible, the efficiency with which a computer uses its resources and the time a computation takes to complete impose a physical limit on what can and can not be “reasonably’’ simulated. This constraint, called tractability, can be formalized by demanding that the number of bits and gate operations of a digital computation scales polynomially with the complexity of the system being simulated. Unfortunately for physicists, the simulation of systems governed by the laws of quantum mechanics is generally intractable and so cannot be efficiently performed using digital computers. This becomes apparent by considering that the size of the Hilbert space characterizing a quantum system grows exponentially with the number of particles in it. For example, to simulate a system of only 500 spin 1/2 particles a digital computer must posses enough bits to represent 2500 complex numbers just to describe its general state.
1.2. Quantum Computation
It was the question of efficiency, and in particular the intractability of simulating quantum systems, that lead Feynman in 1982 [4] to propose a model for a universal quantum simulator. He realized that the inefficiency of digital computers in simulating quantum systems was due to the underlying electrodynamic laws used in their implementation. Feynman argued that by basing a computer explicitly on the laws of quantum mechanics more efficient simulations could be performed. In 1985, Deutsch [1] took the final step in defining a model of quantum computation by combining Feynman’s simulator with the universal Turing machine and showed it was possible to construct a universal quantum Turing machine that could perform these simulations using only finite means. This machine was not only truly universal but possessed unique quantum properties that allowed it to compute certain problems more efficiently.
One of the defining features of quantum computation is quantum parallelism. As a quantum system can exist in a linear superposition of its basis states, the universal quantum Turing machine can, at any step in the computation, represent all possible computational states simultaneously. If this superposition is preserved, then by applying suitable unitary operators to the system it can, in a single step, perform a computation on all these states that scales exponentially with the required physical resources. This would be equivalent to running computation on massively paralleled digital computers; however such a simple comparison is deceptive as to obtain classical output from the quantum system it must first be measured. When this measurement is performed, the system randomly collapses into one of its basis states destroying the superposition. This means that quantum computation is probabilistic. Only by designing algorithms that take advantage of interference effects the probability of a particular result can be made arbitrarily high and so deterministic computations performed. Useful quantum algorithms have already been designed for solving, as yet, intractable problems such as the factoring of large numbers [5] and list searching [6]. These algorithms, as well as efficient simulation of quantum systems, mean that a practical quantum computer would be hugely beneficial to modern science.
1.2.1. The Qubit
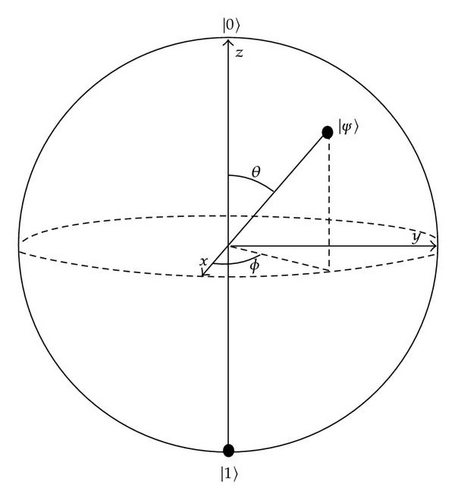
1.2.2. The Quantum Circuit Model
Due to its similarity with traditional digital circuits, the most widely used representation of quantum computation is the quantum circuit model. In this model, a sequence of noninteracting qubits, called the quantum register, is first prepared in the desired input state. Computation is then performed by sequentially applying one- and two-qubit unitary operations, called quantum logic gates, before the qubits are measured to obtain the output. Just as Boolean logic circuits can be shown to be equivalent to the universal Turing machine, such quantum circuits have been shown to be equivalent to the universal quantum Turing machine [7].
An important example of a quantum circuit is the single-qubit “teleporter’’ which is represented by the following circuit diagram:
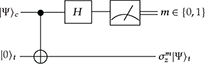
In quantum circuit diagrams, time flows from left to right with the horizontal lines, called quantum wires, representing the separate qubits that comprise the quantum register. One-qubit operations and gates are represented on single quantum wires and two-qubit gates are represented by using perpendicular lines to show interaction, and so entanglement, between the relevant qubits. The “teleporter’’ circuit functions by first entangling the control qubit (top wire) with a target qubit prepared in the |0〉 state (bottom wire) using the two-qubit CNOT gate. This applies a NOT operation to the target-qubit if and only if the control-qubit is in the |1〉 state. Once entangled, the control-qubit passes through a single-qubit Hadamard gate and its observable state is measured. The resulting state of the target-qubit will then be , where m ∈ {0,1} is the outcome of the measurement on the control-qubit. This circuit is called the single-qubit “teleporter’’ as the state of the control-qubit is “teleported,’’ with a possible additional factor σz (the Pauli spin matrix), to the target-qubit via their entanglement.
It is a remarkable property of the quantum circuit model that any unitary evolution operator needed for quantum computation can be perfectly simulated using only two-qubit gates {U2 : U2 ∈ U(22)} [8]. This can be further simplified into just the two-qubit CNOT gate and the set of single-qubit gates {U1 : U1 ∈ U(2)} [9] with which all two-qubit gates can be simulated. While these are truly universal quantum gates, allowing for the exact simulation of any unitary evolution operator, it is often more convenient to work with sets of gates that are only approximately universal. An approximately universal set of gates can efficiently simulate, to an arbitrary accuracy, any unitary evolution operator. One such set of approximately universal quantum gates is formed by only three gates {H, W = eπ/8Z(−π/8), CNOT} [10].
The universality, both exact and approximate, of one- and two-qubit gates makes the quantum circuit model a powerful tool for the design and analysis of quantum algorithms. Practically, however, efficient physical implementations of the model have proved difficult to construct. Problems arise due to the need for both fault tolerant multiqubit gates and robust scalable qubits within a single system. For systems with strongly interacting qubits, multiqubit gates are more easily constructed; however, the qubits tend to experience high levels of decoherence making them less robust. Conversely, for systems with weakly interacting qubits, the qubits are more robust but multiqubit gates are much harder to construct. This has lead physicists to consider a new model of quantum computation that can be more easily implemented—the cluster state or one-way computation model.
1.2.3. The Cluster State
The cluster state model for quantum computation was proposed by Raussendorf and Briegel in 2001 [2] as a scheme for performing quantum computing based on entanglement. Their model consisted of an ensemble of entangled qubits, known as the cluster state, on which computation and readout is performed by an adaptive sequence of single-qubit measurements. These measurements propagate quantum correlations through the system and, by combining their results via some tractable classical computation, generate the output. As measuring the individual qubits removes their entanglement and so destroys the original state, cluster state computation is also referred to as one-way computation. The great advantage of a cluster state computer is that in requiring only single qubit measurements it avoids many of the practical problems associated with the quantum circuit implementation.
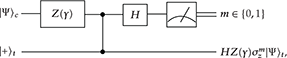
where the CNOT gate has been replaced by the CZ gate using the relation CZ = (Ic ⊗ Ht)CNOT(Ic ⊗ Ht) and the additional Hadamard gates have been absorbed by the initial and final state of the target qubit (|+〉 = H|0〉). As the Z(γ) gate commutes with the CZ gate, the H and Z(γ) gates can be combined and four of these circuits concatenated to give


where the measurement basis is given in each vertex and the measurement round denoted by the subscript. By adapting the sign of the rotations based on the results of the previous measurements and compensating for any prefactor using a classical computation, an operation equivalent, modulo a global phase, to any single-qubit rotation W ∈ SU(2) can be performed. In a similar manner it is possible to show that the CNOT gate can also be constructed [11] and so cluster state computation is computationally equivalent to the quantum circuit model where both inputs and outputs are classical.
The cluster state model of quantum computation offers a unique way of designing quantum algorithms. More than this, it provides a robust scheme for implementing a practical computing device. Such a device does not suffer from many of the disadvantages associated with a quantum circuit implementation as it uses only single qubit measurements to perform computation. Furthermore, it has been shown that a cluster state quantum computer would be more resilient to decoherence effects [12], can function efficiently even with only probabilistic entanglement [13], and provides the ability for efficient error correction [14, 15]. Before cluster state computation can be practically implemented, the controlled generation of entanglement necessary for the formation of the cluster state must be realized and this is the focus of this work.
2. Physical Implementation and Simulation
Multiqubit entanglement forms the universal resource on which all cluster state quantum computation is performed. To date, many physical systems have been proposed for the generation of such states including photons [16], cavity quantum electrodynamics [17], ions [18], optical lattices [19], and superconducting quantum circuits [20]. Schemes for generating cluster states in solid-state coupled double quantum dots (DQD) have also been proposed [21–23] and such a scheme is the focus here. A solid-state implementation is desirable for several key reasons; DQDs are highly scalable, allow for good control of charge and spin characteristics, and can have large spatial separations between qubits. Practically, a solid-state implementation would also benefit from the current expertise of the semiconductor industry.
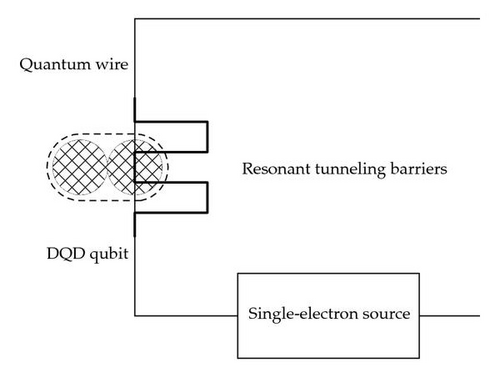
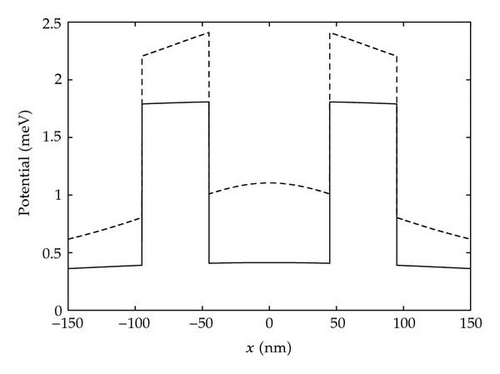
In this paper, we present a detailed analysis on the entanglement generated between a single-electron charge qubit and a ballistic electron based on resonant tunneling. The modeled system consists of a charge qubit formed by a single-electron confined to a GaAs DQD. A GaAs quantum wire containing symmetric rectangular resonant tunneling barriers, formed by InAs slices, is positioned near to the centre of one of the dots and a ballistic electron pumped through the wire by a single-electron source [24]. The computational basis states of the qubit are then defined by the localization of the qubit electron to one of the two quantum dots with the state |1〉 corresponding to that closest to the quantum wire. A schematic diagram of this scheme is shown in Figure 2. By numerically simulating the system in detail, rather than assuming a simple interaction based on Pauli operators, a realistic determination of the systems suitability for cluster state generation can be made.
2.1. Approximations
Both the qubit and quantum wire being modeled are confined to the conduction band of a GaAs semiconductor heterostructure. Lattice and screening effects are accounted for by using a linear approximation for the effective electron mass and permittivity of m* = 0.0667me and ϵ = 12.9ϵ0 [25], respectively. Throughout the simulation, the ballistic and qubit electrons are well separated in space and so distinguishable. Consequently, only Coulombic interactions between the electrons are modeled with spin-orbit and spin-spin coupling effects considered negligible in comparison. Decoherence and thermal effects are also ignored as, to a first approximation, the system is considered to be well isolated from the environment and operating in the low-temperature regime. The total system is then completely described by a Hamiltonian composed of the kinetic energy operators of both electrons, the Coulombic interaction between them, the potential of the resonant tunneling barriers experienced by the ballistic electron, and the confinement potential for the electron in the qubit. As the electron energies being considered are small (E ≪ mec2 = 0.511 MeV) and only light elements (GaAs) are involved, relativistic effects are ignored and the system dynamics are given by solution to the time-dependent Schrödinger equation (2.15). For convenience all equations are given in atomic units with ℏ = me = e = 1/(4πϵ0) = 1 and t is used throughout to represent time.
2.2. Theory
2.2.1. The Qubit
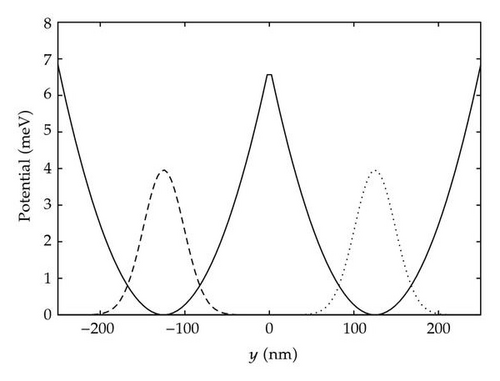
2.2.2. The Ballistic Electron
2.2.3. Total System
2.3. Numerical Simulation
3. Results and Discussion
The quantum mechanical phenomenon of coherent resonant tunneling describes the complete transmission of a ballistic electron through a set of barriers that is classically disallowed. It occurs when the incident energy of the ballistic electron closely matches one of the virtual energy eigenstates of the potential well formed by the barriers. At these specific energies the transmission probability is sharply peaked and the barriers are effectively “transparent’’ to the ballistic electron’s wavefunction. The particular energies at which these peaks occur is determined solely by the geometry of the barrier potential and for the one-dimensional case of an isolated ballistic electron and symmetric rectangular double barriers analytic solutions can be derived [34]. To demonstrate the sensitivity of the resonant tunneling system, transmission profiles were calculated using the analytic solution for varying barrier widths and separations and these can be seen in Figures 4 and 5, respectively. Due to the extreme sensitivity, small changes in the geometry of the barrier potential will cause large changes in the transmission probabilities of the ballistic electron. In our system, the localization of the qubit electron to one of the two basis states alters the strength of the Coulombic interaction with the ballistic electron and so affects the transmission probability causing entanglement.
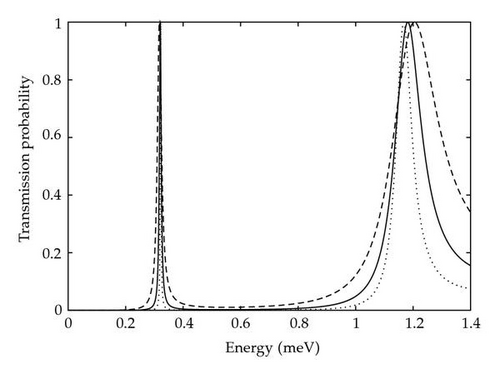
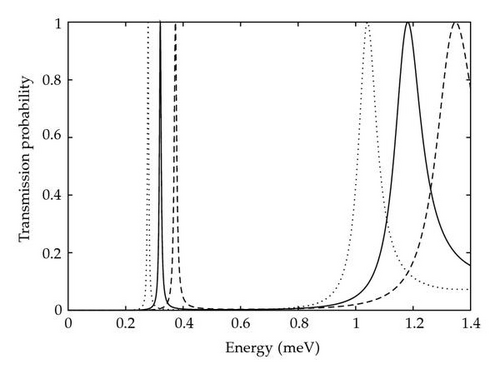
It has been shown [35] that, while the particular mechanism of entanglement is unimportant, for any arbitrary quantum system to be used as a cluster state the localized entanglement between pairs of nearest neighbor qubits must be at a maximum. If this is not the case, then measurements on the individual qubits will result in the incomplete transfer of quantum information and computational errors will occur. For our scheme to create entanglement suitable for the generation of a cluster state in a single step it is necessary that after a tunneling event there is maximum entanglement between the electrons and that the state of the qubit is unchanged.
To optimize the entanglement generated by a single resonant tunneling event, a simplex minimization method was used to alter the separation and width of the resonant tunneling barriers. For each set of barrier parameters, a series of simulations were run using the maximally mixed pure qubit state over a range of ballistic electron energies. The total time for each simulation was dynamically set to ensure that the final position of the electrons was well separated and the concurrence for each calculated. The difference between unity and the maximum concurrence across the complete energy range was then used as the measure of fitness in the optimization. Using this technique, a maximum concurrence of 0.998 was achieved for a barrier width of 50 nm, separation of 90 nm, and with a ballistic electron energy of 1.585 meV.
Using the optimized system parameters, the probability of the ballistic electron becoming trapped was found to be negligible, the final state of the ballistic electron can be seen in Figure 6, and the tunneling was effectively elastic. Furthermore, the resonant tunneling event takes just 445 ps and so the qubit can be considered as static during entanglement (see (2.7)).
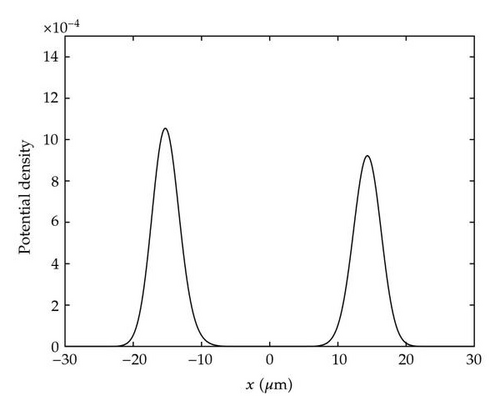
To investigate how resonant tunneling leads to this high level of entanglement, the transmission probabilities for the initial qubit states |0〉 and |1〉 were calculated using the optimized barrier parameters. The transmission profiles, as well as the corresponding concurrence values for an initial qubit state |+〉, are shown in Figure 7. As expected, there is a strong correlation between the difference in transmission probability of the two states and the concurrence of the system. Aside from the small secondary peak in the |1〉 profile at around 2.3 meV, both transmission profiles strongly resemble the analytic case for an isolated ballistic electron seen in Figure 5. This implies that resonant tunneling is being suppressed by the change in the ballistic electrons energy due to the Coulombic interaction with the qubit and not because of distortions in the potential of the resonant tunneling barriers themselves. The total potential experienced by the ballistic electron from both the resonant barriers and the overall Coulombic interaction of the qubit in each basis state can be seen in Figure 8. When the qubit is in the |0〉 state, there is very little change in the potential compared to the resonant barriers alone but there is an increase in the baseline energy of on average 0.41 meV (see Figure 8). Fitting the analytic solution to the calculated transmission peak gives good agreement across the whole probability profile with an increase in the baseline energy of 0.40 meV. For the qubit in the |1〉 state the situation is not as straightforward as the shape of the potential is being noticeably distorted by the Coulombic interaction between the electrons (see Figure 8). Here the average increase in baseline energy is 0.99 meV compared to the value found by fitting the analytic solution of 0.97 meV. While the change in energy is similar, the analytic profile does not agree across the whole calculated probability profile and so distortions in the barrier shape do affect the transmission probabilities at certain ballistic energies.
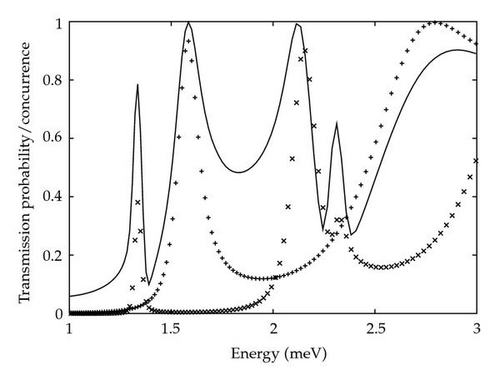
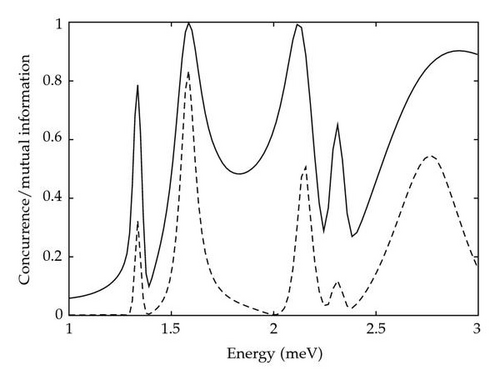
The generation of a cluster state requires not only maximal entanglement but also entanglement between all nearest neighboring qubits. If the resonant tunneling system is to be used to perform such entanglement in a single step, then it should not disrupt the state of the qubit and so allow multiple entanglement operations to be performed. From the reduced density matrix of the qubit, the probabilities after entanglement were found to be 0.50 and 0.50 for the |0〉 and |1〉 basis states, respectively. This means that there is no change in the probability density of the qubit compared to its initial maximally mixed state . Unlike the probability, the relative phase of the qubit basis states after entanglement is dependent on the basis state of the ballistic electron. As we are free to choose this basis, a state is selected that preserves the relative phase of the qubit. Simulations were then run using the optimized system parameters and maximally mixed initial qubit states with a range of relative and global phases. It was found that changes in the phase of the qubit do not affect the concurrence of the system and, by applying the selected ballistic electron basis state, that these phases were preserved after entanglement. This means that the resonant tunneling event does not introduce any relative phase in the state of the qubit and so the initial state of the qubit is completely preserved, as required.
To test the stability of the system, a series of simulations were run using small perturbations in each of the optimized parameters and the linear response of the concurrence calculated. It was found that a 1 nm change in the width and separation of the barriers gives an average change in the concurrence of −0.006 and −0.041, respectively and that a 1 μeV change in the initial energy of the ballistic electron gives an average change of −0.002.
4. Conclusions
In this paper we have provided a brief review of the theoretical foundations of cluster state quantum computation and how it evolved from the traditional model of digital computers. We also reported on numerical simulations of a solid-state system for generating controlled entanglement between a single-electron charge qubit and a ballistic electron using the suppression of coherent resonant tunneling in a quantum wire. It was found that a high level of entanglement could be achieved, with a concurrence of 0.998, and that the state of the qubit was unaffected by the process. The primary mechanism of entanglement was the difference in the transmission probabilities corresponding to the two localized basis states of the qubit. These differences occurred due to the Coulombic interaction between the electrons changing the ballistic electron’s energy which shifted the resonance peaks. If the ballistic electron can be used to entangle further qubits, then this scheme provides a viable method for the generation of cluster states.
The concurrence was found to be highly sensitive to the system parameters especially the barrier separation. This poses a significant limitation on any practical implementation of this scheme as it requires the precise fabrication of the resonant tunneling barriers and means that the system will be heavily affected by imperfections in their interface. The stability may be improved by using a different geometry for the barriers or a greater number but the effect this would have on the concurrence is unclear and more work needs to be done in this area. Furthermore, while the simulation was closely modeled on experimentally realizable components and treated the ballistic and qubit electrons and their interactions in detail, it did not include decoherence effects that would be present in a real system. This means that our results provide an idealized upper limit for the possible entanglement that such a practical implementation could produce.
Acknowledgments
The authors would like to thank N. Menicucci and C. Hines for valuable discussions. This work was supported by iVEC—The hub of advanced computing in Western Australia, The University of Western Australia, and the Australian Research Council.




