Volume 2010, Issue 1 307209

Research Article

Open Access

Constraint Consensus Methods for Finding Interior Feasible Points in Second-Order Cones

Anna Weigandt,

Anna Weigandt

Department of Mathematics, Illinois State University, Normal, IL 61790-4520, USA illinoisstate.edu

Search for more papers by this author

Kaitlyn Tuthill,

Kaitlyn Tuthill

Department of Mathematics, Saint Michael′s College, Colchester, VT 05439, USA smcvt.edu

Search for more papers by this author

Shafiu Jibrin,

Corresponding Author

Shafiu Jibrin

[email protected]

Department of Mathematics and Statistics, Northern Arizona University, Flagstaff, AZ 86011-5717, USA nau.edu

Search for more papers by this author

Anna Weigandt,

Anna Weigandt

Department of Mathematics, Illinois State University, Normal, IL 61790-4520, USA illinoisstate.edu

Search for more papers by this author

Kaitlyn Tuthill,

Kaitlyn Tuthill

Department of Mathematics, Saint Michael′s College, Colchester, VT 05439, USA smcvt.edu

Search for more papers by this author

Shafiu Jibrin,

Corresponding Author

Shafiu Jibrin

[email protected]

Department of Mathematics and Statistics, Northern Arizona University, Flagstaff, AZ 86011-5717, USA nau.edu

Search for more papers by this author

First published: 06 February 2011

https://doi.org/10.1155/2010/307209

Citations: 1

Academic Editor: Tak-Wah Lam

Share a link

Email
Wechat
Bluesky

Abstract

Optimization problems with second-order cone constraints (SOCs) can be solved efficiently by interior point methods. In order for some of these methods to get started or to converge faster, it is important to have an initial feasible point or near-feasible point. In this paper, we study and apply Chinneck′s Original constraint consensus method and DBmax constraint consensus method to find near-feasible points for systems of SOCs. We also develop and implement a new backtracking-like line search technique on these methods that attempts to increase the length of the consensus vector, at each iteration, with the goal of finding interior feasible points. Our numerical results indicate that the new methods are effective in finding interior feasible points for SOCs.

1. Introduction

We consider a system of second-order cone inequalities as follows:

(1.1)

where x ∈ ℝⁿ, A_i is an m_i × n matrix, b_i is a vector in

, c_i is a vector in ℝⁿ, and d_i is a scalar. The norm is the standard Euclidean norm. We assume the interior of the feasible region

is nonempty.

Second-order cones (SOCs) are important to study because there exist many optimization problems where the constraints can be written in this form. For instance, SOCs can be used to easily represent problems dealing with norms, hyperbolic constraints, and robust linear programming. There are also a huge number of real world applications in areas such as antenna array weight design, grasping force optimization, and portfolio optimization (see [1] for more information on these and other applications). Furthermore, there exist efficient interior point methods for solving optimization problems with SOC constraints, such as the primal-dual interior-point method. Because of these applications and the success of interior point methods when applied to SOCs, there exists a need to be able to efficiently find a near-feasible or feasible point for a system of SOCs [1–4]. One approach to feasibility is given in [5].

In this paper, we will describe two of Chinneck′s constraint consensus algorithms and apply them to SOCs to find near-feasible points. These are the Original constraint consensus method and DBmax constraint consensus method. One could of course add a small value to the final consensus vector of these methods to make it enter the interior of the feasible region [6]. However, this would not work if the final consensus vector is far away from the boundary. We propose a different approach, one which increases the step size of the consensus vector at each iteration using a backtracking technique. The goal is to find interior feasible points and to reduce the number of iterations and amount of time. The technique works by extending the consensus vector by a given value and then backtracking until it is as close as possible to the feasible region at a point where the number of satisfied constraints does not decrease. Finally, we investigate the effectiveness of the modification on applied to Original and DBmax methods by testing them upon randomly generated problems. The results show that the backtracking technique is effective at finding interior feasible points. It also greatly reduces the number of necessary iterations and time of the methods.

We also study how our work for SOCs apply to the special case of convex quadratic constraints (CQCs). More information on the importance of CQCs in the field of optimization can be found in [7, 8]. Our results for CQCs show that backtracking also significantly reduces the number of necessary iterations and time of the Original method. It also was able to find interior feasible points on many of the test problems. However, backtracking does not work well with the DBmax method in the case of CQCs. We note that in both constraint types (SOCS or CQCs), DBmax method outperforms the Original method, as expected.

2. The Constraint Consensus Methods Applied to Second-Order Cones

In this section, we study and apply Chinneck′s Original constraint consensus and DBmax constraint consensus methods to SOCs in order to find near-feasible points of the system (1.1).

The first constraint consensus method, hereby, called Original was developed by Chinneck in [3] (see Algorithm 1). The method starts from an infeasible point x₀. The method associates each constraint f_i(x) ≥ 0 with a feasibility vector fv_i (i = 1,2, …, q). In the case of our SOCs, . The feasibility vector is defined by , where v = max {0, −f_i(x₀)} is the constraint violation at x₀ and ∇f_i(x₀) is the gradient of f_i(x) ≥ 0 at point x₀. We assume that ∇f_i(x) exists. Note that if f_i(x) is linear, x₀ + fv_i extends from x₀ to its orthogonal projection on the constraint f_i(x) ≥ 0. The length of the feasibility vector ∥fv_i∥ = v/∥∇f_i(x₀)∥ is called the feasibility distance. We define x₀ to be near feasible with respect to f_i(x) ≥ 0 if ∥fv_i∥ < α, where α is a preassigned feasibility tolerance. We say that x₀ is feasible with respect to f_i(x) ≥ 0 if f_i(x₀) ≥ 0 and is an interior feasible point if f_i(x₀) > 0.

Algorithm 1: Original constraint consensus algorithm.

INPUTS: set of q constraints (1.1), an initial point x, a feasibility distance tolerance α,
a movement tolerance β, maximum number of iterations μ.
while steps <μ do
NINF = 0, for all j : n_j = 0, s_j = 0
for every constraint i do
if constraint i is violated then
Calculate feasibility vector fv_i and feasibility distance ∥fv_i∥
if ∥fv_i∥>α then
NINF = NINF + 1
for every variable x_j do
n_j ← n_j + 1, s_j ← s_j + fv_ij
If NINF = 0 then
exit successfully
for every variable x_j: do
if n_j ≠ 0 then
t_j = s_j/n_j
else
t_j = 0
if ∥t∥ ≤ β then
exit unsuccessfully
x = x + t, steps = steps + 1

The feasibility vectors are then combined to create a single consensus vector which reflects the movements suggested by all the feasibility vectors. The consensus vector, t, is created by averaging the nonzero components of the feasibility vectors. Each component of t is given by t_j = s_j/n_j (the average of the jth components of the violated feasibility vectors) with s_j being the sum of the jth components of the feasibility vectors for each constraint that is violated at the point x₀, and n_j being the number of constraints that are violated (not near feasible) at point x₀. The consensus vector is then added to x₀ to get a new iterate x₁, and the algorithm is repeated until the number of violated constraints (NINF) at the current iterate is zero. The algorithm will also stop looping if the consensus vector becomes too short and not enough progress towards the feasible region is being made quickly enough—if the movement tolerance β is reached.

Ibrahim et al. gave several modifications of the Original method in [9]. While the Original method treats all eligible feasibility vectors equally, the variations they develop place emphasis on feasibility vectors that have a stronger influence on the consensus vector. They generate two different types of improved constraint consensus algorithms. They generally found a direction-based algorithm, called DBmax, to be the most successful among all the variations, see Algorithm 2.

Algorithm 2: DBmax constraint consensus algorithm.

INPUTS: set of q constraints (1.1), an initial point x, a feasibility distance tolerance α,
a movement tolerance β, maximum number of iterations μ.
while steps <μ do
NINF = 0, for all , , ,
for every constraint i do
if constraint i is violated then
Calculate feasibility vector fv_i and feasibility distance ∥fv_i∥
if ∥fv_i∥ > α then
NINF = NINF + 1
for every variable x_j do
if fv_ij > 0 then
if then
else if fv_ij < 0 then
if then
if NINF = 0 then
exit successfully
for every variable x_j: do
if n⁺ = n⁻ then
else if then
else
if ∥t∥ ≤ β then
exit unsuccessfully
x = x + t, steps = steps + 1

DBmax looks at the jth component of every valid feasibility vector and takes the maximum value for the sign with the most votes, which then becomes the jth entry of the consensus vector. If there are equal number of positive and negative jth components, t_j becomes the average of the most positive and most negative jth component of the valid feasibility vectors. Let be the value of the most positive jth component of the feasibility vectors, be the value of the most negative jth component of the feasibility vectors, be the number of violated constraints that vote for a positive movement for the variable x_j, and be the number of violated constraints that vote for a negative movement for the variable x_j.

For a more specific example, we consider a system of 3 SOCs in ℝ², pictured in Figure 1. We will refer to this system when demonstrating concepts throughout this paper.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The feasible region S for Example 2.1.

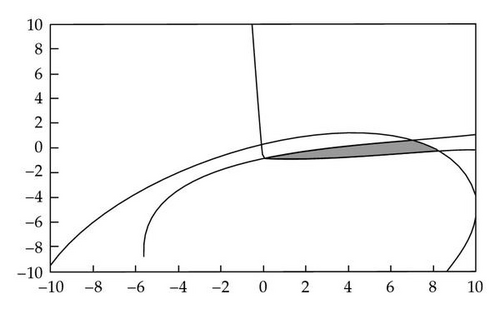
Example 2.1. A system of q = 3 second-order cones (SOCs) with n = 2 variables:

(1) ,

(2) ,

(3) ,

where

(2.1)

We define the function

(2.2)

Note that f(x) = 0 gives the boundary of the cone, f(x) is nonnegative inside the feasible region of the cone and negative outside of the cone. We can see in Figure 2, an example of the contours of f(x) for Cone (1) of Example 2.1.

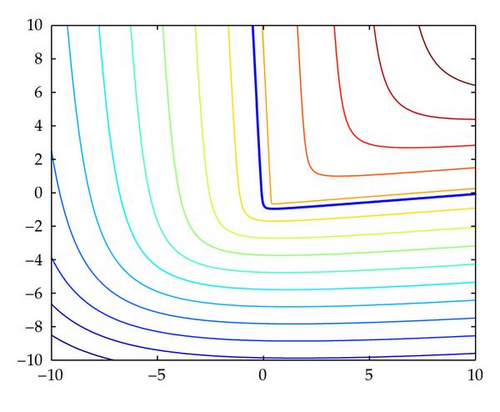
The following theorem is well known. An elementary proof can be given using the triangle inequality as shown. It will be used to discuss the convergence of the Original and DBmax methods.

Theorem 2.2. f(x) is concave over ℝⁿ.

Proof. For convenience, we will consider two separate functions, f₁(x) = c^Tx + d and f₂(x) = −∥Ax + b∥. The sum of two concave functions is also concave, so it suffices to show that f₁(x) and f₂(x) are both concave. f₁(x) is linear, so it is concave. In order to show f₂(x) is concave in ℝⁿ, it suffices to prove that f₂(tx + (1 − t)y) ≥ tf₂(x) + (1 − t)f₂(y) for 0 ≤ t ≤ 1 and x, y ∈ ℝⁿ.

By the triangle inequality, we have that

(2.3)

This means that f₂(tx + (1 − t)y) ≥ tf₂(x) + (1 − t)f₂(y), so f₂(x) is concave. The sum of two concave functions is also concave, so f₁(x) + f₂(x) is concave. Therefore f(x) is also concave.

Projection algorithms such as the Original and DBmax constraint consensus methods have been proven to converge, when the functions f_i(x) are concave [3, 10, 11]. So, Theorem 2.2 guarantees convergence in the case of SOCs. Theorem 2.2 shows that the feasible region S of our system (1.1) is convex.

The main task in adapting the consensus methods to SOCs is computing the gradient ∇f(x) of f(x) = c^Tx + d − ∥Ax + b∥. It is given by

(2.4)

When calculating the gradient, there exist two potential problems. First of all, there are times when the gradient may fail to exist. When Ax + b = 0 the gradient is undefined. For example, in our first cone, the solution to Ax + b = 0 is x = (0.4375, −0.625). As shown in Figure 3, this point happens to be within the feasible region of our cone. This will not always be the case, but the probability of picking a solution to Ax + b = 0 within our algorithm is very slim. Another potential problem is when the gradient is zero, the feasibility vector will be undefined. If ∇f(x) = 0 or undefined at an iteration, the algorithm fails and one should pick a different starting point. For cone (1) our example there does not exist a point where the gradient is zero, as shown below

(2.5)

The only possible solution to this system happens to be x₁ = 0.4375 and x₂ = −0.625, which is where the gradient is undefined. This means that there is no solution to ∇f(x) = 0 for this particular example.

We know from Theorem 2.2 that f(x) is concave. A nice result is that if f(x) is strictly concave, then the only potential place for the gradient to be zero occurs inside of the feasible region, as shown in Theorem 2.3.

Theorem 2.3. Suppose f(x) is strictly concave. If ∇f(x) = 0, then x is inside of the feasible region of f(x) ≥ 0.

Proof. If the gradient is zero, f(x) must be at a critical point. Since f(x) is strictly concave, the only potential critical point will be the maximum of f(x). Since f(x) < 0 outside the feasible region and f(x) ≥ 0 inside the feasible region, it follows that the maximum of f(x) must also be nonnegative. Therefore the gradient can only be zero inside of the feasible region.

As a consequence of this result, for strictly concave constraints, the gradient will only be zero inside of the feasible region, and so the feasibility vector exists at all iterates of our algorithms.

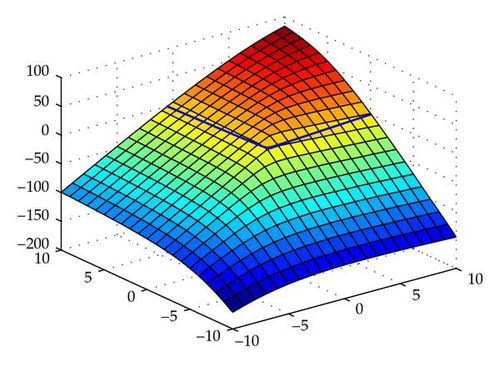
Let g(γ) = f(x_k + γs_k), where s_k is the feasibility vector at x_k. Figure 4 is an example of g(γ). The graph of g(γ) is a slice of the graph of f(x). It follows from Theorem 2.2 that g(γ) is concave in γ over ℝ.

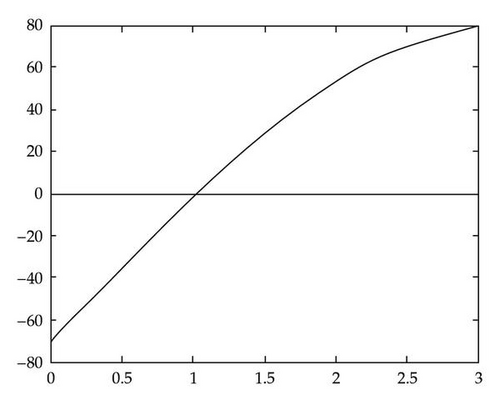
The following results show that in each iteration of the algorithm, we move closer to the boundary of the feasible region.

Theorem 2.4. Suppose the line {x_k + γs_k∣ γ ∈ ℝ} intersects the boundary of {x∣f(x) ≥ 0} at γ^*. Then g(γ) is nondecreasing over [0, γ^*].

Proof. g(γ) is negative over [0, γ^*) and is zero at γ^*. Since g(γ) is concave over ℝ, then g(γ) is increasing over [0, γ^*].

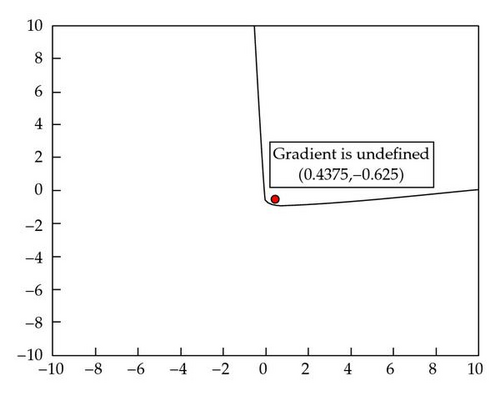
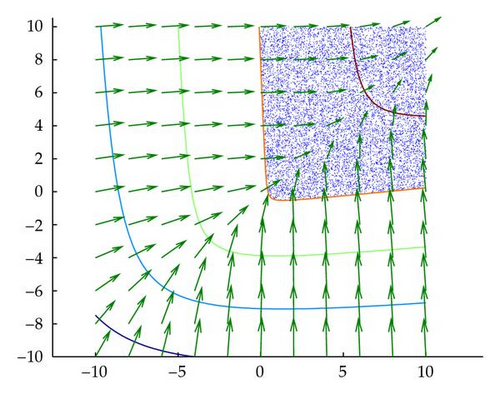
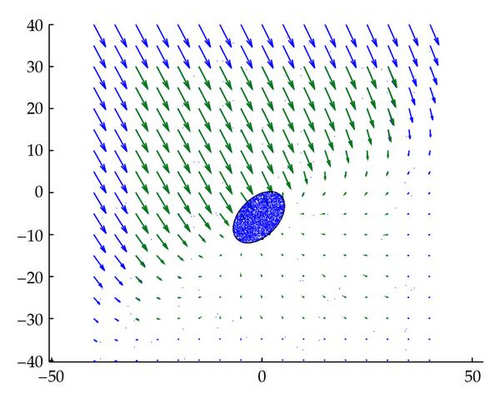
For concave f(x), approximations of the feasibility vector will most often fall short of reaching the boundary of f(x) ≥ 0. As such the consensus vector will also fall short of the boundary. It may be desirable to increase the length of the consensus vector as much as possible towards the boundary. From Figure 5, we can see that for all points that lie outside of the feasible region of the cone, the direction of the gradient points is the direction of the boundary. However, this is not the case for all SOCs. As seen in Figure 6, some iterates may not have a gradient that points directly at the feasible region. Hence, there is a limit to how much to increase the length of the consensus vector in general. This point is noted when we discuss the backtracking technique later.

3. The Case of Convex Quadratic Constraints

In this section, we study how the discussions in the previous section apply to the special case of convex quadratic constraints (CQCs). This study will be limited to results that are different and relevant to CQCs.

We consider a system of CQCs:

(3.1)

where x ∈ ℝⁿ, A_i is an m_i × n matrix, b_i is a vector in

, c_i is a vector in ℝⁿ, and d_i is a scalar.

For ease of presentation, consider the single CQC

(3.2)

It is nice to note that a CQC is also SOC. To see this, note that

(3.3)

where

(3.4)

For simplicity and without a loss of generalization, we assume that P is positive definite. So, P^1/2 exists and is invertible. Then, the CQC (3.2) is equivalent to

(3.5)

This is equivalent to the SOC

(3.6)

The above result implies that all our results on concavity and convergence on SOCs also extend to the CQC system (3.1). It suffices to compute the gradient ∇f(x) and Hessian H_f(x) of f(x) = c^Tx + d − (Ax+b)^T(Ax + b). They are given by

(3.7)

The feasibility vector does not exist when the gradient is zero. Note that the gradient ∇f(x) = 0 is given by the solution to the linear system

(3.8)

To use as an illustration, consider the following example.

Example 3.1. A convex quadratic constraint (CQC) with n = 2 variables.

, where

(3.9)

For Example 3.1, the linear system (3.8) is

(3.10)

with the solution x₁ = −27/176 and x₂ = −47/176, which is in the feasible region. See Figure 7.

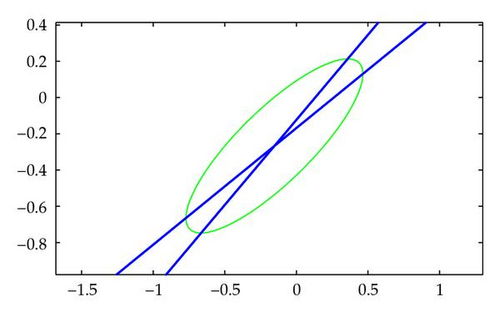
Since the Hessian H_f(x) = −2A^TA, f(x) is strictly convex if A^TA is positive definite. So, similar to Theorem 2.3, if A^TA is positive definite, then the gradient can only be zero at a point inside the feasible region. This means, in this case, the feasibility vector exists at all iterates of the consensus algorithms.

4. New Variation of the Constraint Consensus Methods

In this section, we propose a modification to the Original and DBmax constraint consensus methods. It extends the length of the consensus vector at each iteration of the methods with the goal of finding a point in the interior of the feasible region S of our system (1.1).

The Backtracking Line Search Technique (Algorithm 3) is a step in the constraint consensus methods (Algorithms 1 and 2) that attempts to extend the length the consensus vector t to a closer near-feasible point. It goes to a point where the number of satisfied constraints does not decrease. The backtracking technique seeks to provide rapid convergence by inexpensively testing to see if we can increase the size of the consensus vector. Starting by computing the consensus vector in the usual way (either using the Original method or DBmax), it tests to see if it can successfully increase the size of the consensus vector, in the hope of getting closer to the feasible region in less iterations and time. The technique has the added benefit that it is possible for the final point to be actually in the interior instead of being a near-feasible point.

Algorithm 3: Backtracking line search technique.

INPUTS: set of q constraints (1.1) or (3.1), a point x, the consensus vector t
Compute the binary word b at x
count = 0
while count < 3 do
α = 1 + 0.5^count
xtemp = x + α*t
Compute the binary word bcomp at xtemp
if (bcomp) ≤ sum(b) then
x = xtemp; Exit Function
else
count = count+1
if count = loop then
x = x + t

The Backtracking Line Search Technique uses the concept of a binary word.

Definition 4.1. Define δ(x) = δ₁(x), …, δ_q(x) to be the binary word for the set of constraints (1.1) or (3.1), given by

(4.1)

If δ(x) = [0 ⋯ 0], then x is a feasible point. We can easily check the feasibility of x by taking the sum of the components of the binary word. When the sum is 0, we know that x is feasible and we can allow the algorithm to exit. We can define an equivalence relation on ℝⁿ, where x₁ is related to x₂ if the binary word of x₁ is the same as the binary word of x₂. The equivalence classes form a partition of ℝⁿ.

We start by computing the consensus vector t. Then we scale the consensus vector by an initial scalar factor. We add this consensus vector to x. Using this new point, we count the number of constraints that are violated with the binary word. We consider the new consensus vector to be successful if the resulting point violates the same number or fewer constraints than the previous point did. If this is not the case, the algorithm backtracks and tries a smaller increase in the consensus vector. If the point still has not found an improvement in the number of satisfied constraints after backtracking three times, then it returns to the starting consensus vector. In our tests, we scale the consensus vector by 2, 1.5, 1.25, and if none of those are satisfactory then we return to a step size of 1. Algorithm 3 could easily be varied to use other step sizes, based on the type of constraint or problem.

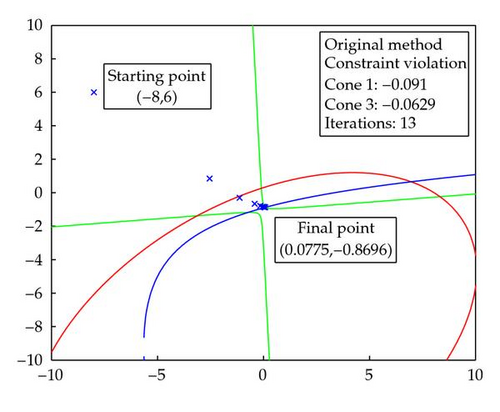
In Figure 8, we can see a comparison of the Original method and Original method with backtracking applied to Example 2.1. Given the same initial starting point of (−8,6), the Original method with backtracking reached feasibility in fewer iterations and less time. Furthermore, the final point obtained by using the Original method with backtracking was actually feasible for all three constraints, as opposed to being near feasible. The final point obtained by the Original method was only feasible for the second constraint, and within a feasibility distance tolerance 0.01 for the other two constraints.

5. Numerical Experiments

In this section, we use numerical experiments to test the Original method and DBmax method with and without the backtracking line search technique on random test problems.

For each SOC test problem, we first generate integer values q, m_i = m, and n uniformly in the intervals [1,50], [1,10], and [2,10], respectively. Then, a random point is chosen with the values of each entry being in uniform in [−10,10]. After this, q SOCs are generated using m and n, where each entry of A, b, c, and d is uniform in the interval [−10,10]. We check to ensure that all the q SOCs are satisfied at the random point. Table 1 lists the SOC test problems. The CQC test problems are generated like the SOC test problems. However, the q CQCs are generated so that each is satisfied at the origin and the entries of b are uniform in [−0.5,0.5]. The CQC test problems are given in Table 1.

Table 1. Test problems.

Problem	SOCs			CQCs
Problem	n	m_i = m	q	n	m_i = m	q
1	10	9	7	9	7	7
2	6	2	48	3	9	15
3	3	8	15	7	3	25
4	8	1	37	4	9	28
5	7	3	27	10	4	8
6	3	7	50	2	10	41
7	3	8	5	5	8	47
8	9	7	7	8	4	34
9	7	5	20	6	6	17
10	10	7	37	2	8	44
11	9	2	36	8	2	19
12	10	4	42	2	4	16
13	5	3	36	2	6	3
14	3	10	6	10	9	46
15	9	8	6	5	5	10
16	8	7	1	5	7	2
17	6	6	5	7	9	25
18	10	9	43	7	10	48
19	8	9	30	8	2	41
20	10	5	42	10	3	41
21	7	9	37	7	1	32
22	6	2	37	3	3	48
23	9	2	47	2	9	24
24	4	9	10	2	4	1
25	10	7	26	4	2	25

For each test problem and method, we chose a random infeasible point x₀ as our starting point with entries uniform in [−100,100]. We set our feasibility distance tolerance to be α = 0.01 and our movement tolerance to be β = 0.001. We chose our maximum number of iterations to be μ = 500. All codes were written in MATLAB^© 7.9.0 and ran on Dell OptiPlex GX280.

5.1. Second-Order Cones

Tables 3 and 4 give the results for the SOC test problems. If the number (Iter) of iterations is 500, it means the method did not converge. The last column shows whether or not the method converged to an interior feasible point. Table 2 gives the success rate over all the 25 problems in finding an interior feasible point and average time per problem (where converged). Both the Original method and DBmax method failed in Problem 6 and Problem 13.

Table 2. Success rates and average times on SOCs.

Algorithm	Success rate %	Average time (sec)
Original	0	0.131
Original (Backtrack)	64	0.075

DBmax	4	0.055
DBmax (Backtrack)	84	0.033

Table 3. SOCs: comparison of Original method and Original method with backtracking.

Problem	Original			Original with backtracking
Problem	Iter	Time (sec)	Interior feas Pt?	Iter	Time (sec)	Interior feas Pt?
1	34	0.055	N	4	0.023	Y
2	83	0.194	N	33	0.162	N
3	121	0.094	N	51	0.086	Y
4	53	0.117	N	14	0.059	Y
5	98	0.135	N	30	0.085	N
6	500	1.195	N	500	2.506	N
7	40	0.013	N	4	0.003	Y
8	81	0.034	N	24	0.021	N
9	78	0.082	N	32	0.071	N
10	42	0.080	N	15	0.059	Y
11	140	0.252	N	61	0.228	N
12	127	0.269	N	60	0.258	N
13	500	0.870	N	500	1.842	N
14	7	0.003	N	3	0.003	Y
15	23	0.009	N	4	0.003	Y
16	5	0.001	N	3	0.001	Y
17	12	0.004	N	3	0.002	Y
18	85	0.189	N	5	0.025	Y
19	95	0.148	N	10	0.033	Y
20	66	0.139	N	22	0.096	Y
21	43	0.083	N	32	0.126	Y
22	339	0.610	N	10	0.040	Y
23	197	0.448	N	69	0.327	N
24	10	0.006	N	4	0.005	Y
25	27	0.037	N	7	0.020	Y

Table 4. SOCs: comparison of DBmax method and DBmax method with backtracking.

Problem	DBmax			DBmax with Backtracking
Problem	Iter	Time (sec)	Interior feas Pt?	Iter	Time (sec)	Interior feas Pt?
1	16	0.014	N	5	0.014	Y
2	145	0.332	N	16	0.100	Y
3	101	0.077	N	30	0.061	Y
4	14	0.030	N	5	0.025	Y
5	25	0.035	N	6	0.021	Y
6	500	1.196	N	500	3.313	N
7	6	0.002	N	7	0.005	Y
8	52	0.022	N	8	0.008	Y
9	13	0.014	N	18	0.040	Y
10	20	0.038	N	8	0.038	Y
11	35	0.063	N	8	0.036	Y
12	87	0.179	N	17	0.091	Y
13	500	0.866	N	500	2.408	N
14	3	0.001	N	3	0.003	Y
15	5	0.002	N	4	0.003	Y
16	5	0.001	N	3	0.001	Y
17	14	0.004	N	4	0.003	Y
18	37	0.082	N	9	0.055	N
19	35	0.054	N	9	0.039	N
20	87	0.181	N	12	0.065	Y
21	8	0.016	N	7	0.036	Y
22	5	0.010	N	5	0.023	Y
23	31	0.072	N	10	0.057	Y
24	4	0.003	Y	4	0.007	Y
25	20	0.027	N	7	0.024	Y

As expected, on average the DBmax method took fewer iterations and less time than the Original method. Also, note that DBmax found an interior feasible point in Problem 24. It is interesting to note that the backtracking technique showed general improvement in iterations and processing time in the methods over all the test problems, where there was convergence.

On average the Original method with backtracking took less time than the Original method. Similarly, the DBmax method with backtracking took less time than the DBmax method. The Original method with backtracking has a strict feasibility success rate of 64% while the DBmax with backtracking has a success of 84%.

5.2. Convex Quadratic Constraints

Tables 6 and 7 give the results for the CQC test problems. Table 5 gives the success rate over all the 25 problems in finding an interior feasible point and average time per problem (where converged). Again, as expected, on average the DBmax method took less number of iterations and less time than the Original method.

Table 5. Success rates and average times on CQCs.

Algorithm	Success rate %	Average time (sec)
Original	0	0.110
Original (Backtrack)	44	0.061

DBmax	0	0.041
DBmax (Backtrack)	36	0.114

Table 6. CQCs: comparison of the Original method and Original method with backtracking.

Problem	Original			Original with backtracking
Problem	Iter	Time (sec)	Interior feas Pt?	Iter	Time (sec)	Interior feas Pt?
1	55	0.050	N	19	0.028	N
2	16	0.022	N	7	0.016	Y
3	51	0.129	N	16	0.060	Y
4	18	0.049	N	6	0.028	N
5	158	0.127	N	53	0.070	N
6	16	0.060	N	9	0.056	Y
7	25	0.109	N	6	0.042	N
8	48	0.151	N	14	0.072	N
9	31	0.051	N	11	0.032	Y
10	15	0.061	N	8	0.052	Y
11	130	0.236	N	42	0.121	N
12	19	0.028	N	6	0.015	Y
13	14	0.005	N	8	0.005	Y
14	32	0.143	N	8	0.057	N
15	24	0.024	N	7	0.011	N
16	21	0.005	N	11	0.005	Y
17	28	0.068	N	7	0.027	N
18	26	0.119	N	6	0.043	N
19	86	0.325	N	29	0.181	N
20	77	0.291	N	30	0.183	N
21	135	0.451	N	50	0.286	N
22	24	0.115	N	8	0.059	N
23	17	0.042	N	8	0.031	Y
24	15	0.002	N	14	0.003	Y
25	39	0.101	N	12	0.050	Y

Table 7. CQCs: comparison of DBmax method and DBmax method with backtracking.

Problem	DBmax			DBmax with backtracking
Problem	Iter	Time (sec)	Interior feas Pt?	Iter	Time (sec)	Interior feas Pt?
1	25	0.017	N	96	0.110	N
2	11	0.015	N	253	0.601	N
3	21	0.049	N	58	0.231	Y
4	13	0.035	N	500	2.071	N
5	36	0.028	N	45	0.060	Y
6	11	0.042	N	27	0.170	N
7	14	0.060	N	500	3.467	N
8	18	0.057	N	500	2.537	N
9	16	0.026	N	500	1.317	N
10	11	0.044	N	27	0.181	N
11	31	0.054	N	31	0.095	Y
12	13	0.019	N	25	0.061	N
13	12	0.004	N	23	0.012	Y
14	16	0.069	N	500	3.521	N
15	11	0.011	N	21	0.034	Y
16	21	0.005	N	24	0.009	Y
17	15	0.035	N	500	1.895	N
18	14	0.062	N	500	3.572	N
19	23	0.084	N	500	3.083	N
20	27	0.100	N	500	3.049	N
21	28	0.089	N	29	0.199	Y
22	12	0.057	N	500	3.711	N
23	12	0.030	N	27	0.103	Y
24	15	0.002	N	14	0.004	Y
25	13	0.032	N	500	2.001	N

As can be seen from the tables, applying the backtracking technique to the Original method dramatically reduces the number of iterations and time. In addition, the Original method with backtracking has a strict feasibility success rate of 44%. With DBmax, the backtracking technique did not work well. There is significant increase in both iterations and time to reach feasibility and 11 out of the 25 problems diverged. This is most likely due to the fact that the consensus vector in DBmax is already long. This means that an extension of the consensus vector might move it too far and bring it right over the feasible region. We suspect that this is due to the nature of the CQC constraints, which tend to form bounded feasible regions.

6. Conclusion

We study the Chinneck′s Original constraint consensus and DBmax methods as they apply to second-order cones (SOCs) and the special case of convex quadratic constraints (CQCs) to find near-feasible points. We also present a new backtracking line search technique that increases the size of the consensus vector with the goal of finding interior feasible points.

Given a set of SOCs, we adapt the Original and DBmax constraint consensus methods to find near-feasible points. These methods alone rarely can find an interior feasible point with SOCs. We develop a backtracking line search technique to find interior feasible points. We test the methods both with and without the backtracking technique over a variety of test problems and compare them with the time and number of iterations it takes to converge.

Before applying backtracking, the method known to reach feasibility in the least amount of time, with the fewest number of iterations was consistently DBmax. The Original with backtracking method is still not as fast as DBmax. However, the Original with backtracking reaches feasibility in fewer number of iterations than DBmax and is able to find interior feasible points in most of the test problems. The Original with backtracking method works well with SOCs and with CQCs. But, while DBmax with backtracking method works very well with SOCs, it does not work well with CQCs. It might be that with CQCs, the consensus vector in the backtracking step is increased too far.

Overall and considering both SOCs and CQCs, we find the backtracking line search to be most successful in reducing time and iterations needed to reach the feasible region when applied to the Original consensus method. As mentioned before, DBmax with backtracking method is not successful with CQCs. In the future it would be interesting to try more variations of the backtracking line search technique. We could compare the effectiveness of different initial step sizes and reductions in the backtracking technique, especially with DBmax when applied to CQCs. It would also be nice to investigate the effect of the backtracking technique on the other variants of the Original method given in [9].

Acknowledgment

The work of A. Weigandt and K. Tuthill was supported by the Department of Mathematics and Statistics at Northern Arizona University under the REU program of the National Science Foundation in Summer 2010.

References

1 Lobo M. S., Vandenberghe L., Boyd S., and Lebret H., Applications of second-order cone programming, Linear Algebra and Its Applications. (1998) 284, no. 1–3, 193–228, https://doi.org/10.1016/S0024-3795(98)10032-0, 1655138.
10.1016/S0024-3795(98)10032-0
Web of Science® Google Scholar
2 Alizadeh F. and Goldfarb D., Second-order cone programming, Mathematical Programming. (2003) 95, no. 1, 3–51, https://doi.org/10.1007/s10107-002-0339-5, 1971381.
10.1007/s10107-002-0339-5
Web of Science® Google Scholar
3 Chinneck J. W., The constraint consensus method for finding approximately feasible points in nonlinear programs, Informs Journal on Computing. (2004) 16, no. 3, 255–265, 2075807.
10.1287/ijoc.1030.0046
Web of Science® Google Scholar
4 Nesterov Y. and Nemirovsky A., Interior-Point polynomial methods in convex programming, Studies in Applied Mathematics, 1994, 13, SIAM, Philadelphia, Pa, USA.
Google Scholar
5 Caron R. J., Traynor T., and Jibrin S., Feasibility and constraint analysis of sets of linear matrix inequalities, Informs Journal on Computing. (2010) 22, no. 1, 144–153, 2663500.
10.1287/ijoc.1090.0323
Web of Science® Google Scholar
6 Chinneck J. W., Private communication with S. Jibrin, 2010.
Google Scholar
7 den Hertog D., Interior Point Approach to Linear, Quadratic and Convex Programming, 1994, 277, Kluwer Academic Publishers, Dordrecht, The Netherlands, Mathematics and Its Applications, 1282714.
10.1007/978-94-011-1134-8
Google Scholar
8 Vanderbei R. J., Linear Programming: Foundations and Extensions, 2001, Second edition, Kluwer Academic Publishers, Boston, Mass, USA, 1845638.
10.1007/978-1-4757-5662-3
Web of Science® Google Scholar
9 Ibrahim W. and Chinneck J. W., Improving solver success in reaching feasibility for sets of nonlinear constraints, Computers & Operations Research. (2008) 35, no. 5, 1394–1411, https://doi.org/10.1016/j.cor.2006.08.002, 2578315.
10.1016/j.cor.2006.08.002
Web of Science® Google Scholar
10 Censor Y. and Zenios S. A., Parallel Optimization: Theory, Algorithms, and Applications, 1997, Oxford University Press, New York, NY, USA, Numerical Mathematics and Scientific Computation, 1486040.
Google Scholar
11 Butnariu D., Censor Y., and Reich S., Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications, 2001, 8, North-Holland Publishing, Amsterdam, The Netherlands, Studies in Computational Mathematics, 1853247.
Google Scholar

Citing Literature

All articles

Constraint Consensus Methods for Finding Interior Feasible Points in Second-Order Cones

Abstract

1. Introduction

2. The Constraint Consensus Methods Applied to Second-Order Cones

3. The Case of Convex Quadratic Constraints

4. New Variation of the Constraint Consensus Methods

5. Numerical Experiments

5.1. Second-Order Cones

5.2. Convex Quadratic Constraints

6. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Constraint Consensus Methods for Finding Interior Feasible Points in Second-Order Cones

Abstract

1. Introduction

2. The Constraint Consensus Methods Applied to Second-Order Cones

3. The Case of Convex Quadratic Constraints

4. New Variation of the Constraint Consensus Methods

5. Numerical Experiments

5.1. Second-Order Cones

5.2. Convex Quadratic Constraints

6. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information