The aim of this paper is to study the dynamics of predator-prey interaction in a chemostat to determine whether including a discrete delay to model the time between the capture of the prey and its conversion to viable biomass can introduce oscillatory dynamics even though there is a globally asymptotically stable equilibrium when the delay is ignored. Hence, Holling type I response functions are chosen so that no oscillatory behavior is possible when there is no delay. It is proven that unlike the analogous model for competition, as the parameter modeling the delay is increased, Hopf bifurcations can occur.

1. Introduction

The chemostat, also known as a continuous stir tank reactor (CSTR) in the engineering literature, is a basic piece of laboratory apparatus used for the continuous culture of microorganisms. It has potential applications for such processes as wastewater decomposition and water purification. Some ecologists consider it a lake in a laboratory. It can be thought of as three vessels, the feed bottle that contains fresh medium with all the necessary nutrients, the growth chamber where the microorganisms interact, and the collection vessel. The fresh medium from the feed bottle is continuously added to the growth chamber. The growth chamber is well stirred and its contents are then removed to the collection vessel at a rate that maintains constant volume. For a detailed description of the importance of the chemostat and its application in biology and ecology, one can refer to [1, 2].

The following system describes a food chain in the chemostat where a predator population feeds on a prey population of microorganisms that in turn consumes a nonreproducing nutrient that is assumed to be growth limiting at low concentrations

(1.1)

Here s(t) represents the concentration of the growth limiting nutrient, x(t) the density of the prey population, and y(t) the density of the predator population. Parameter s⁰ denotes the concentration of the growth limiting nutrient in the feed vessel, D₀ the dilution rate, η(ξ) the growth yield constant, D(Δ) the sum of the dilution rate D₀ and the natural species specific death rate of the prey (predator) population, respectively. Here f(s) denotes the functional response of the prey population on the nutrient and g(x) denotes the functional response of the predator on the prey.

Butler et al. [3] considered the coexistence of two competing predators feeding on a single prey population growing in the chemostat. As a subsystem of their model, they studied the global stability of system (1.1) with both f(s) and g(x) taking the form of Holling type II. They proved that under certain conditions the interior equilibrium is globally asymptotically stable with respect to the interior of the positive cone. However, they also proved that for certain ranges of the parameters there is at least one nontrivial limit cycle and conjectured that the limit cycle is unique and would be a global attractor with respect to the noncritical orbits in the open positive octant. This conjecture was partially solved by Kuang [4]. He showed that there is a range of parameters for which a unique periodic orbit exists and roughly located the position of the limit cycle.

Bulter and Wolkowicz [5] studied predator mediated coexistence in the chemostat assuming D₀ = D = Δ. Model (1.1) was studied as a submodel. For general monotone response functions, Bulter and Wolkowicz showed that (1.1) is uniformly persistent if the sum of the break even concentrations of substrate and prey is less than the input rate of the nutrient s⁰. However they showed that it is necessary to specify the form of the response functions in order to discuss the global dynamics of the model. If f(s) is modelled by Holling type I or II and g(x) by Holling type I, Bulter and Wolkowicz proved that (1.1) could have up to three equilibrium points and that there is a transfer of global stability from one equilibrium point to another as different parameters are varied making conditions favorable enough for a new population to survive. In this case, there are no periodic solutions. However, even if f(s) is given by Holling type I, if g(x) is given by Holling type II, they showed that a Hopf bifurcation can occur in (1.1), and numerical simulations indicated that the bifurcating periodic solution was asymptotically stable.

We include a time delay in (1.1) to model the time between the capture of the prey and its conversion to viable biomass. Our aim is to show that such a delay can induce nontrivial periodic solutions in a model where there is always a globally asymptotically stable equilibrium when delay is ignored, and hence no such periodic solutions are possible otherwise. For this reason we select the response functions of the simplest form; that is, we choose the Holling type I form for both f(s) and g(x), so that (1.2) always has a globally asymptotically stable equilibrium when the conversion process is assumed to occur instantaneously. It is interesting to note that in the analogous model of competition between two species in the chemostat, delay cannot induce oscillatory behavior for any reasonable monotone response functions (see Wolkowicz and Xia [6]).

With delay modelling the time required for the predator to process the prey after it has been captured, the model is given by

(1.2)

For t ∈ [−τ, 0],

(1.3)

Here variables s(t), x(t), y(t), and parameters s⁰, D₀, η, ξ, D₀, D, and Δ have the same interpretation as for model (1.1). Note therefore that D⩾D₀, and Δ⩾D₀. The additional parameter τ is a nonnegative constant modelling the time required for the conversion process. Hence, e^−Δτy(t − τ) represents the concentration of the predator population in the growth chamber at time t that were available at time t − τ to capture prey and were able to avoid death and washout during the τ units of time required to process the captured prey.

We analyze the stability of each equilibrium and prove that the coexistence equilibrium can undergo Hopf bifurcations. Numerical simulations appear to show that (1.2) can have a stable periodic solution bifurcating from the coexistence equilibrium as the delay parameter increases from zero. This periodic orbit can then disappear through a secondary Hopf bifurcation as the delay parameter increases further.

2. Scaling of the Model and Existence of Solutions

Suppose that functions f(s) and g(s) are of Holling type I form, that is, f(s) = αs (α > 0) and g(x) = kx (k > 0). System (1.2) reduces to

(2.1)

Introducing the following change of variables gives:

(2.2)

With this change of variables, omitting the

’s for convenience, system (2.1) becomes

(2.3)

where Δ⩾1 and D⩾1, with initial data given by (1.3). For biological significance, a point is assumed to be an equilibrium point of (2.3) only if all of its components are nonnegative.

Let τ = 0. Model (2.3) reduces to a special case of the model considered in [7]. If D > α, the model has only one equilibrium point (1,0, 0) and it is globally asymptotically stable. If D < α and 1 − D/α − ΔD/k < 0, the model has a second equilibrium point (D/α, (α − D)/αD, 0) and it is globally asymptotically stable. When 1 − D/α − ΔD/k > 0, the model has a third equilibrium point (k/(k + αΔ), Δ/k, α/(k + αD) − D/k) and it is the global attractor. Therefore, model (2.3) has no periodic solutions when the time delay is ignored. If g(x) is of Holling type II form, Butler and Wolkowicz [5] proved that a Hopf bifurcation is possible resulting in a periodic solution for a certain range of parameter values. We emphasize again here, that it is for this reason that in this paper we restrict our attention to the simplest case for both response functions, that is, Holling type I, in order to see whether delay can be responsible for periodic solutions in (1.2).

Theorem 2.1. Assuming , then there exists a unique solution (s(t), x(t), y(t)) of (2.3) passing through (s₀, ϕ(θ), ψ(θ)) with s(t) > 0, x(t) > 0 and y(t) > 0 for t ∈ [0, ∞). The solution is bounded. In particular, given any ϵ₀ > 0, x(t) < 1 + ϵ₀ for all sufficiently large t.

Proof. For t ∈ [0, τ], one has t − τ ∈ [−τ, 0], x(t − τ) = ϕ(t − τ), and y(t − τ) = ψ(t − τ). System (2.3) becomes

(2.4)

a system of nonautonomous ordinary differential equations with initial conditions s(0) = s₀, x(0) = ϕ(0), and y(0) = ψ(0). Since the right-hand side of (2.4) is differentiable in both x and y, by Theorems 2.3, 3.1, and Corollary 4.3 in Miller and Michel [8], there exists a unique solution defined on [0, τ] satisfying (2.4). By using the method of steps in Bellman and Cooke [9], it can be shown that the solution through (s₀, ϕ(θ), ψ(θ)) is defined for all t⩾0.

Now we prove s(t) > 0 for all t > 0. From the first equation of (2.3),

(2.5)

Proceed using the method of contradiction. Suppose that there exists a first t^⋆ such that s(t^⋆) = 0 and s(t) > 0 for t ∈ [0, t^*). Then

. But from the first equation of (2.3)

(2.6)

a contradiction.

To prove x(t) > 0 for t ∈ [0, ∞), assume there is a first such that , and x(t) > 0 for . Divide both sides of the second equation of (2.3) by x(t) and integrate from 0 to , to obtain

(2.7)

contradicting

To show that y(t) is positive on [0, ∞), suppose that there exists t^⋆ > 0 such that y(t^⋆) = 0, and y(t) > 0 for t ∈ [0, t^*). Then From the third equation of (2.3), we have

(2.8)

a contradiction.

To prove the boundedness of solutions, define

(2.9)

It follows that

(2.10)

where the first inequality holds since D⩾1, Δ⩾1, x(t) > 0 and y(t + τ) > 0. It follows that

(2.11)

Therefore, the solution (s(t), x(t), y(t)) is bounded, and given any ϵ₀ > 0, x(t) < 1 + ϵ₀ for all sufficiently large t.

3. Equilibria and Stability

Model (2.3) has three equilibrium points: E₁ = (1,0, 0), E₂ = (D/α, (α − D)/αD, 0), and

(3.1)

We call E₁ the washout equilibrium, E₂ the single species equilibrium, and E₊ the coexistence equilibrium. For the sake of biological significance, E₊ exists (distinct from E₂) if and only if its third coordinate y₊(τ) = (αs₊(τ) − D)/k > 0, that is, s₊(τ) > D/α, or equivalently, τ lies between 0 and τ_c, where

(3.2)

Note that if (k/Δ)(1/D − 1/α) ⩽ 1, the equilibrium E₊ does not exist for any τ (⩾0), and if (k/Δ)(1/D − 1/α) = 1, then E₊ = E₂.

The linearization of (2.3) about an equilibrium (s, x, y) is given by

(3.3)

The associated characteristic equation is given by

(3.4)

Direct calculation of the left-hand side of (3.4) gives

(3.5)

For convenience, define

(3.6)

Theorem 3.1. Equilibrium E₁ is stable if α < D and unstable if α > D.

Proof. Evaluating the characteristic equation at E₁ gives

(3.7)

The eigenvalues −1 and −Δ are both negative. The third eigenvalue is −D + α. Therefore the equilibrium E₁ is stable if α < D and unstable if α > D.

Remark 3.2. If α < D, then there is only one equilibrium, E₁. If α > D, equilibrium E₂ also exists.

Lemma 3.3. Assume α > D. The characteristic equation evaluated at E₂ has two negative eigenvalues, and the remaining eigenvalues are solutions of

(3.8)

In addition, the characteristic equation evaluated at E₂ has zero as an eigenvalue if and only if τ = τ_c.

Proof. Assume α > D. Equilibrium E₂ exists. Consider the characteristic equation at E₂. Since (α − D)/αD = (1 − s)/αs at E₂,

(3.9)

where λ₁ + λ₂ = −α/D and λ₁λ₂ = α − D > 0. Therefore, λ₁ and λ₂ have negative real parts. The rest of the eigenvalues are roots of (3.8).

Assuming that λ = 0 is a root of (3.8), we have

(3.10)

Solving for τ gives

(3.11)

Theorem 3.4. Assume that D⩾1, Δ⩾1, k > 0, α > 0, and (k/Δ)(1/D − 1/α)⩾1 so that τ_c⩾0. Equilibrium E₂ is locally asymptotically stable if τ > τ_c and unstable if τ < τ_c. If D = 1, then equilibrium E₂ is globally asymptotically stable for τ > (1/Δ)ln (k/Δ).

Proof. Assume that τ > τ_c. Assumptions k > 0, Δ⩾1, and (k/Δ)(1/D − 1/α)⩾1 imply 1/D > 1/α, or equivalently α > D. By Lemma 3.3, to prove that equilibrium E₂ is locally asymptotically stable, one only needs to show that (3.8) admits no root with nonnegative real part.

Consider the real roots of (3.8) first. Note that 1/D > 1/α. Equation (3.8) has no solution for λ ⩽ −Δ. Otherwise the left-hand side would be less than zero, but the right-hand side would be greater than zero. Assume λ > −Δ. The left-hand side of (3.8) is a monotone increasing function in both λ and τ, takes value 0 at λ = −Δ, and goes to positive infinity as λ → +∞ or τ → +∞. By Lemma 3.3, when τ = τ_c, then λ = 0 is a solution of (3.8). Thus for τ > τ_c, any real root λ of (3.8) must satisfy −Δ < λ < 0.

For any , we have and . Therefore there exists at least one such that is a solution of (3.8). Equilibrium E₂ is unstable if τ < τ_c.

In what follows, we prove that if τ > τ_c all complex eigenvalues of (3.8) have negative real parts. Suppose that λ + Δ = γ + iβ (β > 0) is a solution of (3.8). Using the Euler formula, we have

(3.12)

Equating the real parts and imaginary parts of the equation, we have

(3.13)

Squaring both equations, adding, and taking the square root on both sides give

(3.14)

The left-hand side of (3.14) is monotonically increasing in γ, β, and τ provided that γ > 0. Since (3.14) has solution γ = Δ, β = 0 at τ = τ_c, any roots of (3.14) must satisfy γ < Δ since τ > τ_c. Hence Re{λ} = γ − Δ < 0. Therefore (3.8) has no complex eigenvalue with nonnegative real part and so E₂ is locally asymptotically stable for τ > τ_c.

Assume that D = 1. Now we prove that E₂ is globally asymptotically stable when τ > (1/Δ)ln (k/Δ), or equivalently ke^−Δτ < Δ. In this case, choose ϵ₀ > 0 small enough such that ke^−Δτ(1 + ϵ₀) < Δ. By Theorem 2.1, for such ϵ₀, there exists a T > 0 so that 0 < x(t) < 1 + ϵ₀ for t > T. Hence, for t > T + τ, ke^−Δτx(t − τ) < Δ. In Example 5.1 of Kuang ([10, page 32]), choose ρ(t) = τ, a(t) = Δ, b(t) = ke^−Δτx(t − τ), and α = Δ/2. We obtain . Therefore y(t) → 0 as t → ∞. Let z(t) = s(t) + x(t). Noting D = 1, from (2.3), we have . Multiply by the integrating factor e^t, . Integrating both sides from 0 to t gives

(3.15)

, then

. Therefore lim _t→∞z(t) = 1. If

, by L′Hôspital′s rule,

(3.16)

since x(t) is bounded and lim _t→∞y(t) = 0. It again follows that lim _t→∞z(t) = 1. Hence

(3.17)

We show that lim _t→∞s(t) = 1/α and lim _t→∞x(t) = (α − 1)/α. First assume that the limits exist, that is, and . From (2.3), we know that and are uniformly continuous since s(t), x(t), and y(t) are bounded. By Theorem A.3, it follows that and . Note that lim _t→∞y(t) = 0. Letting t → ∞ in (2.3) gives

(3.18)

Either

. Assume that

, that is, lim _t→∞s(t) = 1 and lim _t→∞x(t) = 0. Note that α > D. There exists ϵ > 0 such that α − D − (α + k)ϵ > 0. For such ϵ, there exists a sufficiently large t so that s(t) > 1 − ϵ and 0 < y(t) < ϵ. Recalling that x(t) > 0, by (2.3)

(3.19)

for all sufficiently large t. Therefore it is impossible for x(t) to approach 0 from above giving a contradiction. Therefore, we must have

Now suppose that the limits do not exist. In particular if x(t) does not converge, then let and . By Lemma A.2 in the appendix, there exists {t_m}↑∞ and {s_m}↑∞ such that

(3.20)

From (2.3),

(3.21)

Noting that x(t_m) > 0, we have s(t_m) = (1 − ky(t_m))/α. Since lim _t→∞y(t) = 0, lim _t→∞s(t_m) = 1/α. By (3.17), lim _t→∞x(t_m) = lim _t→∞(x(t_m) + s(t_m)) − s(t_m) = 1 − 1/α = (α − 1)/α. Therefore

. Similarly we can show that

. This implies that lim _t→∞x(t) = (α − 1)/α, a contradiction.

Since s(t) + x(t) converges and x(t) converges, then s(t) must also converge. Hence lim _t→∞s(t) = 1/α and lim _t→∞x(t) = (α − 1)/α. It follows that E₂ is globally asymptotically stable.

4. Hopf Bifurcations at E₊ Assuming D = Δ = 1

Now consider the stability of E₊. The characteristic equation at E₊ is

(4.1)

By assumption Δ = D = 1, and so

(4.2)

where

(4.3)

The characteristic equation at E₊ has one eigenvalue equal to −1 and the others are given by solutions of the equation

(4.4)

Lemma 4.1. Assuming k > 0, α > 0, and k(1 − 1/α)⩾1 so that τ_c = ln (k(1 − 1/α))⩾0, then E₊ has no zero eigenvalue for τ ∈ (0, τ_c).

Proof. Assume that τ ∈ (0, τ_c). By the method of contradiction, suppose that there exists a zero root of (4.4). Therefore

(4.5)

Noting that τ_c > 0 if and only if k(1 − 1/α) > 1, for any 0 < τ < τ_c,

(4.6)

a contradiction.

Lemma 4.2. Assume k > 0, α > 0, k(1 − 1/α) > 1. Equilibrium E₊ is asymptotically stable when τ = 0.

Proof. For τ = 0, (4.4) reduces to

(4.7)

Both coefficients are positive, since

(4.8)

and k(1 − 1/α) > 1 implies 1 − 1/α > 1/k. Therefore, all the roots of the characteristic equation have negative real parts.

Lemma 4.3. As τ is increased from 0, a root of (4.4) with positive real part can only appear if a root with negative real part crosses the imaginary axis.

Proof. Taking n = 2 and g(λ, τ) = p(τ)λ + (qλ + c(τ))e^−λτ + β(τ) in Kuang [10, Theorem 1.4, page 66] gives

(4.9)

Therefore, no root of (4.4) with positive real part can enter from infinity as τ increases from 0. Hence roots with positive real part can only appear by crossing the imaginary axis.

For τ ≠ 0, assuming λ = iω (ω > 0) is a root of ,

(4.10)

Substituting e^iθ = cos θ + isinθ into (4.10) gives

(4.11)

Separating the real and imaginary parts, we obtain

(4.12)

Solving for cos (ωτ) and sin(ωτ) gives

(4.13)

Noting sin²(ωτ) + cos ²(ωτ) = 1, squaring both sides of equations (4.13), adding, and rearranging gives

(4.14)

Solving for ω, we obtain two roots ω₁(τ) and ω₂(τ):

(4.15)

Define conditions (H₁) and (H₂) as follows:

(4.16)

(4.17)

Lemma 4.4. If (H₁) holds for all τ in some interval I, then (4.14) has two positive roots ω₁(τ)⩾ω₂(τ) for all τ ∈ I with ω₁(τ) > ω₂(τ) when all the inequalities in (H₁) are strict. If (H₂) holds for all τ in some interval I, then (4.14) has only one positive root, ω₁(τ) for all τ ∈ I. If no interval exists where either (H₁) or (H₂) holds, then there are no positive real roots of (4.14).

Define the interval

(4.18)

When the end points of J are real and J ≠ ∅, define

(4.19)

We prove that (H₁) holds for any τ ∈ I₁.

From D = Δ = 1,

(4.20)

If α > 1, then

. It follows that

(4.21)

Therefore,

(4.22)

Theorem 4.5. Assume and , then I₁ is not empty, and for any τ ∈ I₁, but , condition (H₁) holds and ω₁(τ) > ω₂(τ) > 0. If , then ω₁(τ) > ω₂(τ) = 0.

Proof. For any , we have , and therefore

(4.23)

Hence,

(4.24)

Therefore,

. Since

, it follows that

(4.25)

Hence,

(4.26)

From

, we have

. Therefore,

(4.27)

and so I₁ is not empty. Noting s₊(τ) = 1/(1 + (αΔ/k)e^Δτ) and Δ = 1, for any τ ∈ I₁, but

, we have

In what follows, we intend to show that for any such τ, condition (H₁) holds. From (4.3),

(4.28)

Since s₊(τ) < 1, to show that the first inequality in (H₁) holds, it suffices to show that the factor on the right-hand side of the above expression is positive. Since

, and

(4.29)

Since

for

(4.30)

For any

(4.31)

Hence,

(4.32)

Next consider the second inequality in (H₁). For

, since

. Therefore, αs₊(τ) > 1. For

(4.33)

Finally,

(4.34)

where

(4.35)

Since s₊(τ) < 1,

(4.36)

It follows that 0 < α₂ < α₁. Again noting that s₊(τ) < 1,

(4.37)

Hence, for any

, we have

. This leads to

(4.38)

Therefore, (H₁) holds for any τ ∈ I₁. By Lemma 4.4, both ω₁(τ) > 0 and ω₂(τ) > 0.

If , we have . Noting (4.25), we obtain

(4.39)

By (4.15), it follows that ω₁(τ) > 0 and ω₂(τ) = 0.

Now we define interval I₂ and prove that (H₂) holds on I₂

(4.40)

In the following theorem, we consider the case that parameters are chosen so that

(4.41)

Theorem 4.6. Assume α > 1 and . Interval I₂ given by (4.41) is not empty. For any τ ∈ I₂, (H₂) holds and hence ω₁(τ) > 0.

Proof. Assume α > 1. Letting

(4.42)

then

(4.43)

G(α) is an increasing function of α and G(1) = 0. G(α) > G(1) implies that

Therefore

(4.44)

This gives

(4.45)

By assumption

, we obtain

(4.46)

Noting that D = Δ = 1 and recalling the definition of τ_c given in (3.2),

(4.47)

Therefore, I₂ given by (4.41) is not empty. For any τ ∈ I₂, noting s₊(τ) = 1/(1 + (αΔ/k)e^Δτ) and Δ = 1, we have

In what follows, we intend to show for any τ ∈ I₂, or equivalently , (H₂) holds. For any , by (4.44), it follows that s₊(τ) > 1/α and so αs₊(τ) > 1. Hence,

(4.48)

For any

, we have

, since 1/4 > 1/(4α) and 1/16 > 1/(16α²) imply that

(4.49)

Therefore,

(4.50)

Condition (H₂) holds. By Lemma 4.4, ω₁(τ) > 0.

Next, to determine whether (4.2) has a pair of pure imaginary eigenvalues, we consider

(4.51)

We obtain

(4.52)

If there exists (τ, ω) satisfying (4.52), then (4.2) has a pair of pure imaginary roots ±iω. A necessary condition for (4.52) to have solutions is . Otherwise, , and the second equation of (4.52) becomes cos (ωτ) = αs₊(τ). However, for any τ ∈ (0, τ_c), we have αs₊(τ) > 1, since

(4.53)

Hence, the second equation of (4.52) has no solution. Assume

for ω⩾0 and τ ∈ [0, τ_c] and denote the right-hand sides of (4.52) by

(4.54)

Define functions

(4.55)

Lemma 4.7. Assume and . For any τ ∈ I₁ given by (4.19), there exists ϵ_j > 0 and θ_j(τ) with ϵ_j ⩽ θ_j(τ) ⩽ π (j=1,2) such that

(4.56)

Proof. For any τ ∈ I₁, by Theorem 4.5, ω₁(τ) > 0 and ω₂(τ)⩾0. It is easy to see that h₁(0, τ) = 0 and lim _ω→+∞h₁(ω, τ) = −∞. There are two roots of h₁(z, τ) = 0, z₁ = 0 and

(4.57)

Hence, h₁(ω, τ) > 0 for 0 < ω < z₂(τ). For any τ ∈ I₁, as shown in Theorem 4.5,

. This implies

. Therefore,

and αs₊(τ) > 1. The function h₂(ω, τ) is monotonically increasing for ω⩾0, since

(4.58)

Since s₊(τ) < 1,

(4.59)

Also, lim _ω→∞h₂(ω, τ) = αs₊(τ) > 1. Therefore, there exists a unique

, such that h₂(l_max(τ), τ) = 1. Solving h₂(l_max, τ) = 1 for l_max and noting that

, it is easy to see that

(4.60)

Then, h₂(ω, τ) ⩽ 1 for any ω ∈ [0, l_max(τ)]. Since s₊(τ) < 1, l_max(τ) < z₂(τ). Therefore, h₁(ω, τ) > 0 for any ω ∈ [0, l_max(τ)]. Since ω₁(τ) is a positive root of

, we have h₂(ω₁(τ), τ) ⩽ 1, which implies that 0 < ω₁(τ) ⩽ l_max(τ) < z₂(τ). Therefore, h₁(ω₁(τ), τ) > 0, and so

. In fact,

(4.61)

since

(4.62)

Thus, θ₁(τ) is defined and 0 ⩽ θ₁(τ) ⩽ π. Since cos (θ₁(τ) + 2nπ) = h₂(ω₁(τ), τ),

(4.63)

Hence, θ₁(τ) satisfies (4.56). From (4.61), h₂(ω₁(τ), τ) < h₂(l_max(τ), τ) = 1, and so θ₁(τ) > 0. Since θ₁(τ) is continuous on the interval I₁ and I₁ is closed, there exists ϵ₁ > 0 such that θ₁(τ)⩾ϵ₁. Similarly we can prove the existence of θ₂(τ).

Lemma 4.8. Assume α > 1 and . For any τ ∈ I₂ given by (4.41), there exists ϵ > 0 and θ₁(τ) such that ϵ ⩽ θ₁(τ) < π and θ₁(τ) satisfies (4.56) for j = 1.

Proof. For any τ ∈ I₂, by Theorem 4.6, only ω₁(τ) > 0.

As in Lemma 4.7, we have h₁(ω, τ) > 0 for 0 < ω < z₂(τ). For any τ ∈ I₂, as shown in Theorem 4.6, . Letting

(4.64)

we have

(4.65)

G(α) is an increasing function and G(1) = 0. Since G(α) > G(1), it follows that

. Therefore, for any

, we obtain

, or equivalently

. Since

(4.66)

h₂(ω, τ) is monotonically increasing for any ω⩾0. For any

(4.67)

which implies that

. Hence,

(4.68)

For τ ∈ [0, τ_c), lim _ω→∞h₂(ω, τ) = αs₊(τ) > 1, since

(4.69)

As in the proof of Lemma 4.7, there exists a unique

such that h₂(l_max(τ), τ) = 1. Then l_max(τ) < z₂(τ). Therefore, h₁(ω, τ) > 0 for any ω ∈ [0, l_max(τ)]. The rest of the proof is similar to the proof of Lemma 4.7. Furthermore, θ₁(τ) < π, since h₂(ω₁(τ), τ)>−1 for any ω₁(τ)∈[0, l_max(τ)).

Theorem 4.9. Consider system (2.3) with D = Δ = 1.

(1)
Suppose , , and τ ∈ I₁ given by (4.22). For τ ∈ I₁ and j = 1,2, ω_j(τ) is nonnegative and there exists ϵ_j > 0 and θ_j(τ) such that ϵ_j ⩽ θ_j(τ) ⩽ π and θ_j(τ) satisfies (4.56). If there exists n⩾0 such that θ_j(τ) + 2nπ intersects τω_j(τ) at some , then (4.4) has a pair of pure imaginary eigenvalues . System (2.3) undergoes a Hopf bifurcation at provided .
(2)
Suppose α > 1, , and τ ∈ I₂ given by (4.41). For τ ∈ I₂, only ω₁(τ) is positive and there exists ϵ > 0 and θ₁(τ) such that ϵ ⩽ θ₁(τ) < π and θ₁(τ) satisfies (4.56) for j = 1. If there exists n⩾0 such that θ₁(τ) + 2nπ intersects τω₁(τ) at some , then (4.4) has a pair of pure imaginary eigenvalues . System (2.3) undergoes a Hopf bifurcation at provided .

Proof. Assume D = Δ = 1 in system (2.3).

Case 1. Suppose τ ∈ I₁. By Theorem 4.5, ω_j(τ)⩾0 for j = 1,2. By Lemma 4.7, there exists ϵ_j > 0 and θ_j(τ) such that ϵ_j ⩽ θ_j(τ) ⩽ π and θ_j(τ) satisfies (4.56). Assume that there exists a positive integer such that for some integer n⩾0. Then system (4.52) has one solution . Equation (4.4) has a pair of pure imaginary eigenvalues .

In what follows, we show that the conditions required for a Hopf Bifurcation (see Theorem A.1 in the appendix) are satisfied by the linearization (3.3) of (2.3) at E₊. In (A.1), choosing τ as the bifurcation parameter and letting

(4.70)

the linearization (3.3) of (2.3) at E₊ is of the form (A.1). Taking a to be any positive real number and b = 1/2, hypothesis (S₁) in the Hopf Bifurcation Theorem holds, since

(4.71)

for all τ ∈ ℝ and |Reλ | < a.

The characteristic equation (4.4) of (3.3) at E₊ has a pair of pure imaginary eigenvalues and no other root of (4.4) is an integral multiple of . Hence the hypothesis (S₂) in the Hopf Bifurcation Theorem holds. Therefore, (2.3) undergoes a Hopf bifurcation at E₊ when provided .

Case 2. Suppose τ ∈ I₂. By Theorem 4.5, only ω₁(τ) > 0. By Lemma 4.8, there exists ϵ > 0 and θ₁(τ) such that ϵ ⩽ θ₁(τ) < π and θ₁(τ) satisfies (4.56). Assume there exists such that for some integer n⩾0. Then system (4.52) has one solution . Equation (4.4) has a pair of pure imaginary eigenvalues . The rest of the proof is similar to that of Case 1 when j = 1.

Corollary 4.10. Consider system (2.3) with D = Δ = 1.

(1)
Suppose , , and τ ∈ I₁ given by (4.22). For τ ∈ I₁, ω_j(τ) is nonnegative and there exists ϵ_j > 0 and θ_j(τ) such that ϵ_j ⩽ θ_j(τ) ⩽ π and θ_j(τ) satisfies (4.56) for j = 1,2. If there exists a positive integer n_j⩾0 such that and , then θ_j(τ) + 2n_jπ intersects τω_j(τ) at least once at some . System (2.3) undergoes a Hopf bifurcation at provided .
(2)
Suppose α > 1, , and τ ∈ I₂ defined in (4.41). For τ ∈ I₂, only ω₁(τ) is positive. There exists ϵ > 0 and θ₁(τ) such that ϵ ⩽ θ₁(τ) < π and θ₁(τ) satisfies (4.56) for j = 1. If there exists a positive integer N⩾0 such that , then for any 0 ⩽ n ⩽ N, θ₁(τ) + 2nπ intersects τω₁(τ) at least once at some . System (2.3) undergoes a Hopf bifurcation at provided .

Proof. Assume D = Δ = 1 in system (2.3).

(4.72)

By the Mean Value Theorem, there exists

such that

. By Theorem 4.9. Case 1, the conclusion follows.

Case 2. Suppose τ ∈ I₂. By Theorem 4.5, only ω₁(τ) > 0. By Lemma 4.8, there exists ϵ > 0 and θ₁(τ) such that ϵ ⩽ θ₁(τ) < π and θ₁(τ) satisfies (4.56). Assume that there exists a positive integer N⩾0 such that . By (4.41), 0 ∈ I₂. Therefore . For 0 ⩽ n ⩽ N,

(4.73)

By the Mean Value Theorem, there exists

such that

. By Theorem 4.9. Case 2, the conclusion follows.

Corollary 4.11. Consider system (2.3) with D = Δ = 1. Assume and . If , then , where I₁ was defined in (4.22). For any τ ∈ I₁, ω_j(τ) is nonnegative and there exists ϵ_j > 0 and θ_j(τ) such that ϵ_j ⩽ θ_j(τ) ⩽ π and θ_j(τ) satisfies (4.56) for j = 1,2. If there exists a positive integer N_j⩾0 (j = 1,2) such that , then for any 0 ⩽ n ⩽ N_j, θ_j(τ) + 2nπ intersects τω_j(τ) at least once at some . System (2.3) undergoes a Hopf bifurcation at provided .

Proof. Assume . Then By (4.22),

(4.74)

For any τ ∈ I₁, by Theorem 4.5, ω_j(τ)⩾0 for j = 1,2. By Lemma 4.7, there exists ϵ_j > 0 and θ_j(τ) such that ϵ_j ⩽ θ_j(τ) ⩽ π and θ_j(τ) satisfies (4.56). Noting 0 ∈ I₁,

. Assume there exists a positive integer N_j⩾0 (j = 1,2) such that

. For any 0 ⩽ n ⩽ N_j,

and

. By Corollary 4.10, the conclusion follows.

5. Numerical Results

This section includes bifurcation diagrams involving the interior equilibrium E₊ and numerical simulations of periodic solutions of the predator-prey model in the chemostat.

5.1. Variation of Eigenvalues

To study the stability switches of E₊, DDEBIFTOOL (see [11, 12]) was chosen to illustrate how the real part of the eigenvalues of (4.2) changes as parameters α and τ vary.

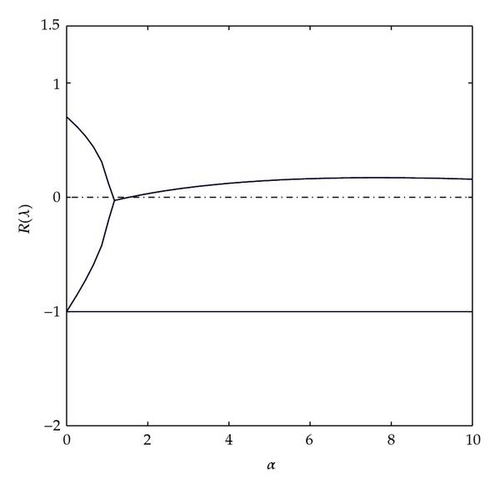
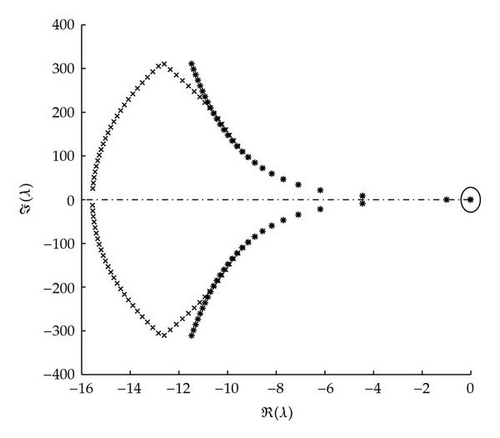
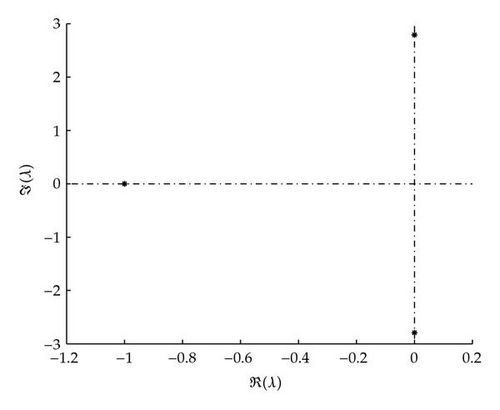
First fix parameters D = Δ = 1, k = 24, and τ = 0.5. Taking α as the bifurcation parameter and varying it from 0 to 10, the real part of the eigenvalues with largest real part of (4.2) was plotted in Figure 1. At α ≈ 1.15 and α ≈ 1.5, there is either a zero eigenvalue or a pair of pure imaginary roots. For α ∈ (1.15,1.5), all eigenvalues have negative real parts. For example, taking α = 1.3, Figure 2(a) shows that the eigenvalues of (4.2) with largest real parts (the ones in the circle) have negative real parts. Note that due to the scaling, the eigenvalues in the circle seem to be indistinguishable from zero. But in fact, they are a pair of complex eigenvalues with real parts slightly less than zero. DDEBIFTOOL can keep track of the occurrence of a pair of pure imaginary eigenvalues as α varies in the neighborhood of α = 1.5. Figure 2(b) clearly shows that there is a pair of pure imaginary eigenvalues. Hence, Hopf bifurcation is possible. Note that by continuation, the pair of eigenvalues with largest real parts in Figure 2(a) for α = 1.3 becomes the pair of pure imaginary eigenvalues in Figure 2(b) for α ≈ 1.5.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Variation of the largest real part of the eigenvalues as the bifurcation parameter α is varied. At α ≈ 1.15 and 1.5, the largest real part crosses zero and it seems that there is a zero eigenvalue for α ≈ 1.15 and a pair of pure imaginary eigenvalues for α ≈ 1.5. The largest real part becomes positive as α increases through 1.5. But as α increases further, for α ≈ 17, the largest real part crosses zero again and remains negative thereafter. There is a second Hopf bifurcation at α ≈ 17. This is consistent with what is observed in Figure 3 when τ = 0.5 and α varies from 0 to 30. Parameters are D = Δ = 1, k = 24, and τ = 0.5.

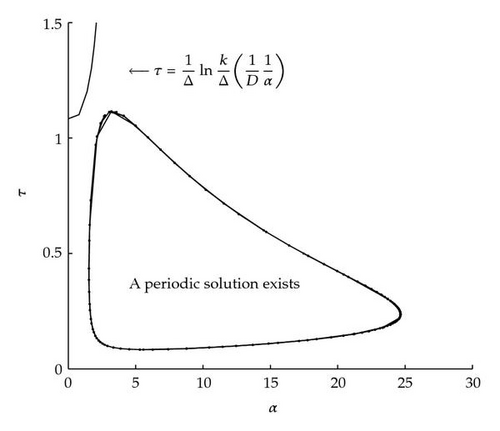
Finally fix all parameters as before and vary both τ and α. In Figure 3, we plot the Hopf bifurcation diagram in α and τ parameter space. The curve at the left upper corner is τ = τ_c. For any pair (α, τ) below that curve, a coexistence equilibrium E₊ exists (i.e., all components are positive). For any pair (α, τ) on the closed curve, there is a Hopf bifurcation. Inside the closed curve, there is a periodic solution surrounding E₊. For any (α, τ) outside the closed curve and below τ = τ_c, the coexistence equilibrium E₊ is stable.

5.2. Simulations Demonstrating Hopf Bifurcations

In this section, we illustrate Theorem 4.9 for system (2.3). Take D = Δ = 1 and let τ vary. We choose parameters α = 100 and k = 100 for Case 1 (see Figures 4–12), and α = 2 and k = 20 for Case 2 (see Figures 13–18).

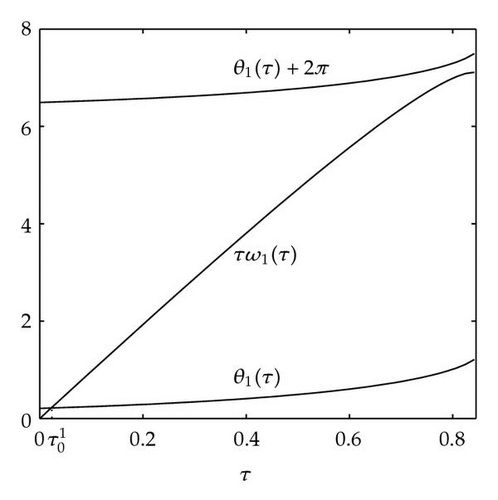
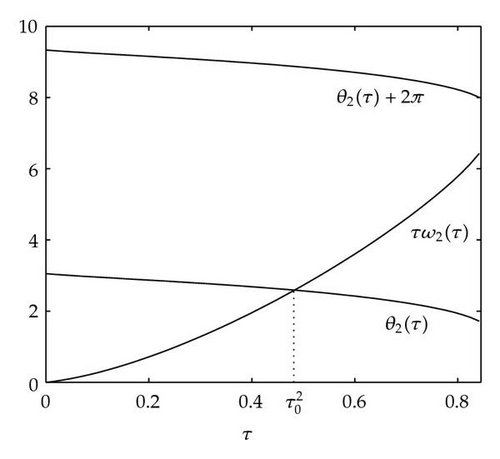
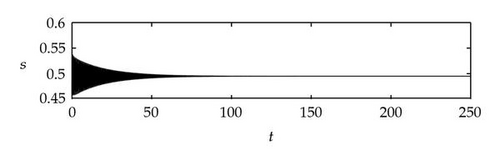
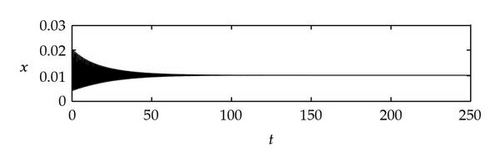
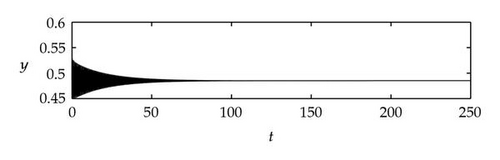
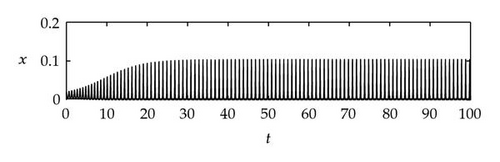
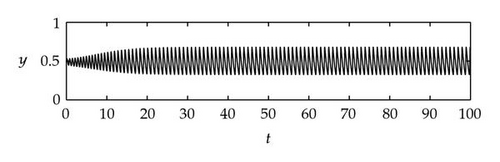
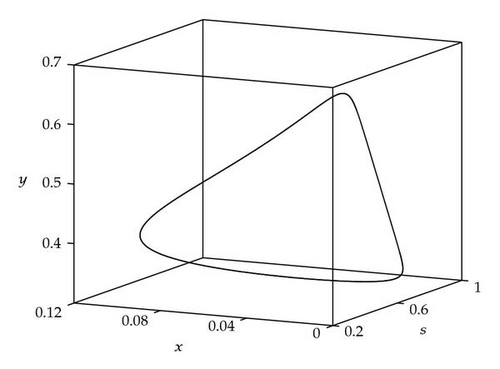
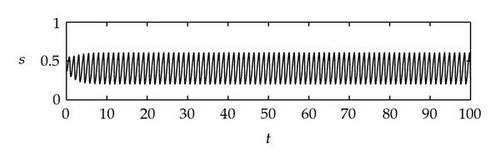
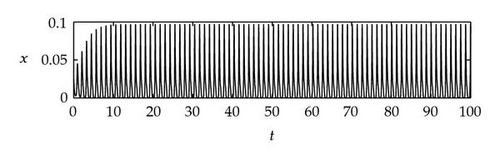
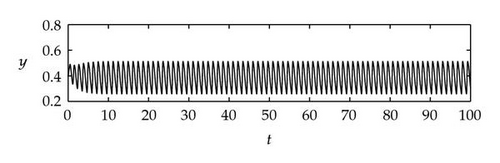
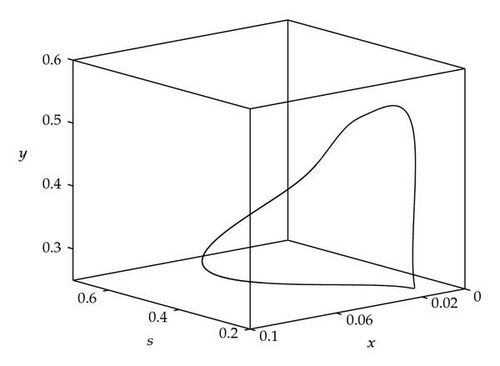
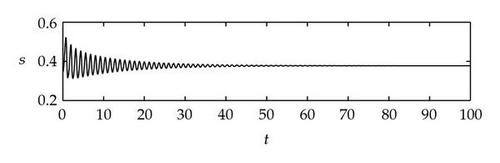
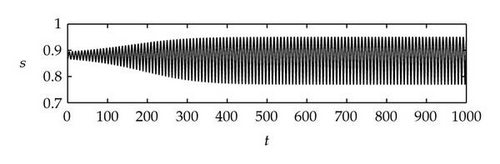
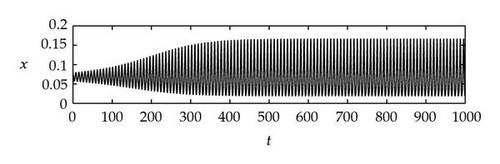
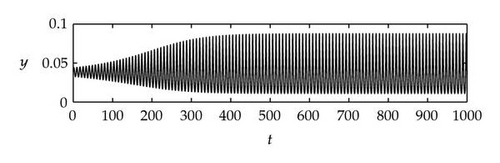
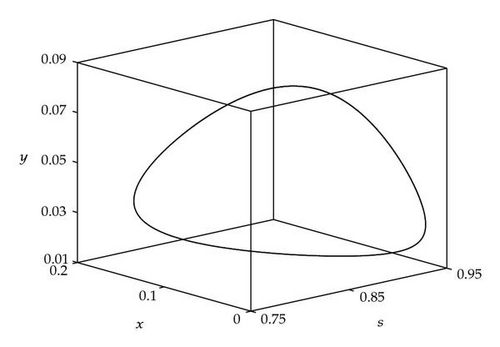
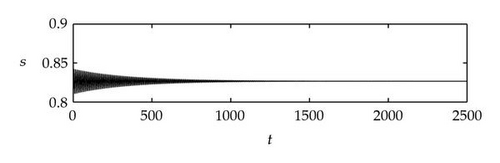
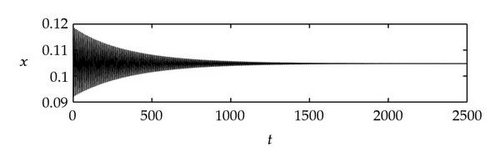
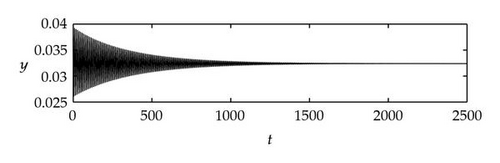
Case 1. Note that I₁ is given by (4.22). Since ,

(5.1)

Also,

. Therefore I₁ ≈ [0, 0.77]. By Theorem 4.9, ω_j(τ) is positive and θ_j(τ) satisfies (4.56) for any τ ∈ I₁ and j = 1,2.

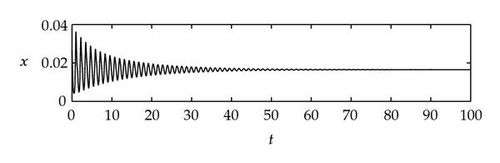
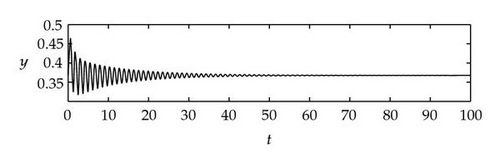
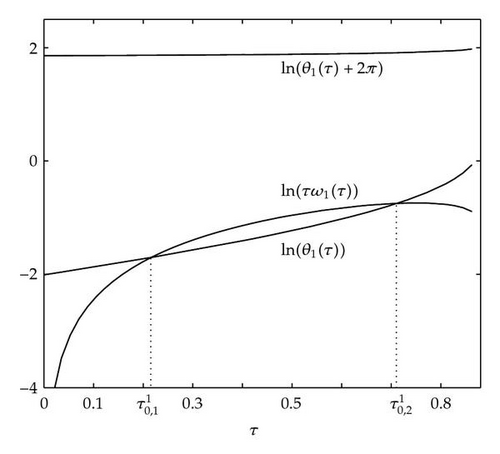
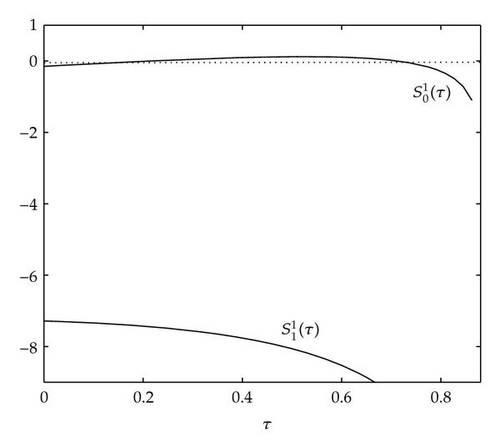
Figure 4 shows that θ_j(τ) intersects τω_j(τ) at some with and . We see that θ_j(τ) + 2nπ has no intersection with τω_j(τ) for n⩾2 and j = 1,2. By Theorem 4.9, (4.4) has two distinct pairs of pure imaginary eigenvalues . Next we need to check if .

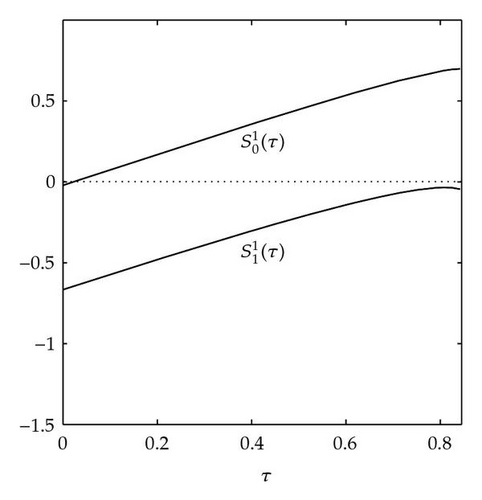
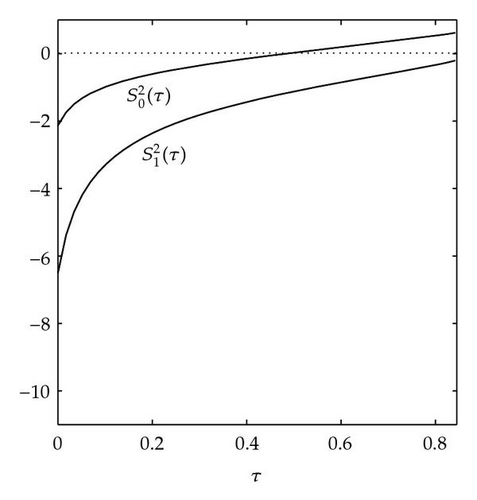
As in Beretta and Kuang [13], we can define

(5.2)

Any zero

is an intersection of θ_j(τ) + 2nπ and τω_j(τ) and vice versa. By (4.10) in Beretta and Kuang [13] and noting that

, we have the relation

(5.3)

where we take + for j = 1 and − for j = 2.

From Figure 5(a), it is observed that has only one zero at n = 0 with Hence, By Theorem 4.9, system (2.3) undergoes a Hopf bifurcation at . Similarly from Figure 5(b), has only one zero for n = 0 and (2.3) undergoes a Hopf bifurcation at .

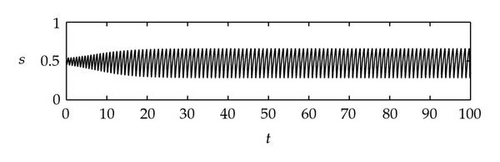
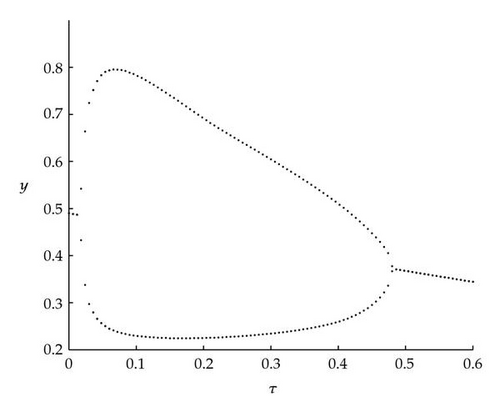
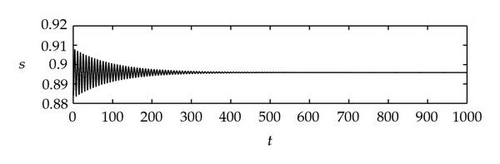
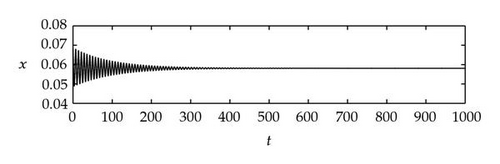
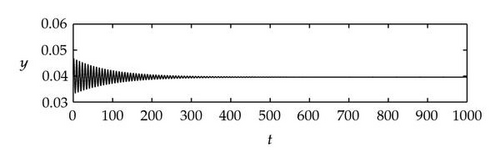
Next we used MATLAB to simulate solutions of model (2.3) for several values of τ. For each fixed delay τ, we chose initial data s(t) = s₊(τ) − 0.01, x(t) = x₊(τ) + 0.01, and y(t) = y₊(τ) + 0.001 for t ∈ [−τ, 0]. From Figure 6, we can see that the equilibrium E₊ is stable if . As delay τ increases past , where a Hopf bifurcation occurs, a pair of complex eigenvalues of (4.4) enters the right-half plane. The equilibrium E₊ loses its stability and a periodic solution bifurcates from E₊ (see Figures 7 and 8). As we increase the delay further to , the periodic solution still exists and remains stable (see Figures 9 and 10). However, as the delay τ increases further, past , the stable periodic solution disappears in a second Hopf bifurcation, and E₊ regains stability (see Figure 11). We provide a bifurcation diagram illustrating the change in dynamics as τ varies (see Figure 12). For any , there is an orbitally asymptotically stable periodic solution.

Case 2. Take k = 20 and α = 2. For such parameters, I₂ ≈ [0,0.85]. By Theorem 4.9, ω₁(τ) is positive and θ₁(τ) satisfies (4.56) for j = 1 and τ ∈ I₂. Figure 13 shows that θ₁(τ) intersects τω₁(τ) twice. To distinguish these intersections, denote them as and . On the other hand, θ₁(τ) + 2π has no intersection with τω₁(τ).

From Figure 14,

(5.4)

By (5.3),

(5.5)

By Theorem 4.5, system (2.3) undergoes a Hopf bifurcation at

and at

. For τ less than

, the equilibrium E₊ is asymptotically stable (see Figure 15). For τ greater than

, but less than

, there is an orbitally asymptotically stable periodic solution surrounding the equilibrium E₊ (see Figures 16 and 17). At

, there is a second Hopf bifurcation, where the periodic solution coalesces with E₊. For

, the periodic orbit no longer exists and E₊ regains stability (see Figure 18) until it disappears when τ > τ_c.

Acknowledgment

This research is partially supported by NSERC.

Appendix

Preliminary Results

To establish the existence of periodic solutions in autonomous delay differential equations, one of the simplest ways is through Hopf Bifurcation. Below is a general Hopf Bifurcation theorem for delay differential equations due to De Oliveira [14]. Before stating the theorem we require some notation.

Consider a one parameter family of neutral delay differential equations:

(A.1)

where D, L, f, and g are continuously differentiable in α and x_t ∈ ℂ([−r, 0], ℝⁿ) (r is a constant), f(α, 0) = g(α, 0), ∂f(α, 0)/∂x_t = ∂g(α, 0)/∂x_t = 0, D(α, x_t) and L(α, x_t) are linear in x_t, and

(A.2)

for x_t ∈ ℂ([−r, 0], ℝⁿ). Assume α ∈ ℝ, where r₀(α) = 0, r_k(α)∈(0,1], and A_k(α), B_k(α), A(α, θ), and B(α, θ) satisfy

(A.3)

It is easy to see that the characteristic matrix

(A.4)

is continuously differentiable in α ∈ ℝ and Δ(α, λ) is an entire function of λ. Making the following assumptions on (A.1).

S₁ There exist constants a > 0, b > 0 such that, for all complex values λ such that |Reλ | < a and all α ∈ ℝ, the following inequalities hold:
(A.5)
S₂ The characteristic equation det Δ(α, λ) = 0 has, for α = α₀, a simple purely imaginary root λ₀ = iv₀, v₀ > 0, and no root of det Δ(α₀, λ) = 0, other than ±iv₀, is an integral multiple of λ₀.
S₃ Re(∂λ(α₀)/∂α) ≠ 0.

Now we are ready to state the Hopf bifurcation theorem for (A.1).

Theorem A.1 (Hopf bifurcation theorem, see Kuang [10, page 60]). In (A.1), assume that (S₁)–(S₃) hold. Then there is an ϵ > 0 such that, for a ∈ ℝ, |a | ⩽ ϵ, there are functions α(a) ∈ ℝ, ω(a) ∈ ℝ, α(0) = α₀, ω(0) = 2π/v₀, such that (A.1) has an ω(α)-periodic solution x^*(a)(t), that is continuously differentiable in t, and a with x^*(0) = 0. Furthermore, for |α − α_o | < ϵ, |ω − (2π/v₀)| < ϵ, every ω-periodic solution x(t) of (A.1) with |x(t)| < ϵ must be of this type, except for a translation in phase; that is, there exists a ∈ (−ϵ, ϵ) and b ∈ ℝ such that x(t) = x^*(a)(t + b) for all t ∈ ℝ.

The following lemma is usually called the Fluctuation Lemma. For a proof, see Hirsh et al. [15].

Lemma A.2. Let f : ℝ⁺ → ℝ be a differentiable function. If lim inf _t→∞f(t) < lim sup _t→∞f(t), then there are sequences t_m↑∞ and s_m↑∞ such that for all m

(A.6)

The proof of the following useful lemma can be found in [16].

Theorem A.3. Let a ∈ (−∞, ∞) and f : [a, ∞) → ℝ be a differentiable function. If lim _t→∞f(t) exists (finite) and the derivative function is uniformly continuous on (a, ∞), then .

References

1 Hsu S. B., Hubbell S., and Waltman P., A mathematical theory for single-nutrient competition in continuous cultures of micro-organisms, SIAM Journal on Applied Mathematics. (1977) 32, no. 2, 366–383, MR0434492, https://doi.org/10.1137/0132030, ZBL0354.92033.
10.1137/0132030
Web of Science® Google Scholar
2 Smith H. L. and Waltman P., The Theory of the Chemostat: Dynamics of Microbial Competition, 1995, 13, Cambridge University Press, Cambridge, UK, Cambridge Studies in Mathematical Biology, MR1315301.
10.1017/CBO9780511530043
Google Scholar
3 Butler G. J., Hsu S. B., and Waltman P., Coexistence of competing predators in a chemostat, Journal of Mathematical Biology. (1983) 17, no. 2, 133–151, MR714265, https://doi.org/10.1007/BF00305755, ZBL0508.92019.
10.1007/BF00305755
Web of Science® Google Scholar
4 Kuang Y., Limit cycles in a chemostat-related model, SIAM Journal on Applied Mathematics. (1989) 49, no. 6, 1759–1767, MR1025959, https://doi.org/10.1137/0149107, ZBL0683.34021.
10.1137/0149107
Web of Science® Google Scholar
5 Butler G. J. and Wolkowicz G. S. K., Predator-mediated competition in the chemostat, Journal of Mathematical Biology. (1986) 24, no. 2, 167–191, https://doi.org/10.1007/BF00275997, MR853832, ZBL0604.92019.
10.1007/BF00275997
Web of Science® Google Scholar
6 Wolkowicz G. S. K. and Xia H., Global asymptotic behavior of a chemostat model with discrete delays, SIAM Journal on Applied Mathematics. (1997) 57, no. 4, 1019–1043, MR1462050, https://doi.org/10.1137/S0036139995287314, ZBL0902.92023.
10.1137/S0036139995287314
Web of Science® Google Scholar
7 Wolkowicz G. S. K., Successful invasion of a food web in a chemostat, Mathematical Biosciences. (1989) 93, no. 2, 249–268, MR984280, https://doi.org/10.1016/0025-5564(89)90025-4, ZBL0676.92014.
10.1016/0025-5564(89)90025-4
CAS PubMed Web of Science® Google Scholar
8 Miller R. K. and Michel A. N., Ordinary Differential Equations, 1982, Academic Press, New York, NY, USA, MR660250.
Google Scholar
9 Bellman R. and Cooke K. L., Differential-Difference Equations, 1963, Academic Press, New York, NY, USA, MR0147745, ZBL0226.76030.
10.1063/1.3050672
Google Scholar
10 Kuang Y., Delay Differential Equations with Applications in Population Dynamics, 1993, 191, Academic Press, Boston, Mass, USA, Mathematics in Science and Engineering, MR1218880.
Google Scholar
11 Engelborghs K., Luzyanina T., and Roose D., Numerical bifurcation analysis of delay differential equations using DDE-BIFTOOL, Transactions on Mathematical Software. (2002) 28, no. 1, 1–21, https://doi.org/10.1145/513001.513002, MR1918642, ZBL1070.65556.
10.1145/513001.513002
Web of Science® Google Scholar
12 Verheyden K., New functionality in dde-biftool v.2.03., Addendum to the manual of DDE-BIFTOOL v. 2.00 (and v.2.02), unpublished, 2007.
Google Scholar
13 Beretta E. and Kuang Y., Geometric stability switch criteria in delay differential systems with delay dependent parameters, SIAM Journal on Mathematical Analysis. (2002) 33, no. 5, 1144–1165, https://doi.org/10.1137/S0036141000376086, MR1897706, ZBL1013.92034.
10.1137/S0036141000376086
Web of Science® Google Scholar
14 De Oliveira J. C. F., Hopf bifurcation for functional differential equations, Nonlinear Analysis. (1980) 4, no. 2, 217–229, MR563805, https://doi.org/10.1016/0362-546X(80)90050-4, ZBL0456.34044.
10.1016/0362-546X(80)90050-4
Google Scholar
15 Hirsch W. M., Hanisch H., and Gabriel J.-P., Differential equation models of some parasitic infections: methods for the study of asymptotic behavior, Communications on Pure and Applied Mathematics. (1985) 38, no. 6, 733–753, MR812345, https://doi.org/10.1002/cpa.3160380607, ZBL0637.92008.
10.1002/cpa.3160380607
Web of Science® Google Scholar
16 Golpalsalmy K., Stability and Oscillations in Delay Differential Equations of Population Dynamics, 1985, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar

Citing Literature

All articles

A Predator-Prey Model in the Chemostat with Time Delay

Abstract

1. Introduction

2. Scaling of the Model and Existence of Solutions

3. Equilibria and Stability

4. Hopf Bifurcations at E₊ Assuming D = Δ = 1

5. Numerical Results

5.1. Variation of Eigenvalues

5.2. Simulations Demonstrating Hopf Bifurcations

Acknowledgment

Appendix

Preliminary Results

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Predator-Prey Model in the Chemostat with Time Delay

Abstract

1. Introduction

2. Scaling of the Model and Existence of Solutions

3. Equilibria and Stability

4. Hopf Bifurcations at E+ Assuming D = Δ = 1

5. Numerical Results

5.1. Variation of Eigenvalues

5.2. Simulations Demonstrating Hopf Bifurcations

Acknowledgment

Appendix

Preliminary Results

References

Citing Literature

Figures

References

Related

Information

4. Hopf Bifurcations at E₊ Assuming D = Δ = 1