Journal of Artificial Evolution and Applications
Volume 2009, Issue 1 803973
Research Article
Open Access

An Evolutionary Method for Combining Different Feature Selection Criteria in Microarray Data Classification

Nicoletta Dessì, 

Nicoletta Dessì

Dipartimento di Matematica e Informatica, Università degli Studi di Cagliari, Via Ospedale 72, 09124 Cagliari, Italy unica.it

Search for more papers by this author
Barbara Pes, 

Corresponding Author

Barbara Pes

Dipartimento di Matematica e Informatica, Università degli Studi di Cagliari, Via Ospedale 72, 09124 Cagliari, Italy unica.it

Search for more papers by this author
First published: 22 July 2009
https://doi.org/10.1155/2009/803973
Citations: 11
Academic Editor: Stephen Smith

Abstract

The classification of cancers from gene expression profiles is a challenging research area in bioinformatics since the high dimensionality of microarray data results in irrelevant and redundant information that affects the performance of classification. This paper proposes using an evolutionary algorithm to select relevant gene subsets in order to further use them for the classification task. This is achieved by combining valuable results from different feature ranking methods into feature pools whose dimensionality is reduced by a wrapper approach involving a genetic algorithm and SVM classifier. Specifically, the GA explores the space defined by each feature pool looking for solutions that balance the size of the feature subsets and their classification accuracy. Experiments demonstrate that the proposed method provide good results in comparison to different state of art methods for the classification of microarray data.

1. Introduction

Microarray technologies provide an unprecedented opportunity for uncovering the molecular basis of cancer and other pathologies. Any microarray experiment assays the expression levels of a large number of genes in a biological sample. These assays provide the input to a wide variety of computational efforts aiming at defining global gene expression profiles of pathological tissues and comparing them with corresponding normal tissues. Generally, this process is carried on by selecting a small informative set of genes that can distinguish among the various classes of pathology, by choosing an appropriate mathematical model (i.e., a classifier), by estimating the parameters of the model based on a training set of samples whose classification is known in advance.

A relevant problem in microarray data classification, and in machine learning in general, is the risk of “overfitting” that arises when the number of training samples is small and the number of attributes or features (i.e., the genes) is comparatively large. In such a situation, we can easily learn a classifier that correctly describes the training data but performs poorly on an independent set of data. In order to improve the performance of learning algorithms [1–3], it is of paramount importance to reduce the dimensionality of the data by deleting unsuitable features [4].

Indeed, the selection of an optimal subset of features by exhaustive search is impractical and computationally intensive when the number of attributes is high, as it is for microarray data, and a proper learning strategy must thus be devised. The relevance of good feature selection methods has been discussed by [5], but the recommendations in literature do not give evidence for a single best method for either the feature selection or the classification of microarray data [6].

Recent studies on evolutionary algorithms (EAs) have revealed their success on microarray classification. Particularly, these methods not only converge to high quality solutions, but also search for the optimal set of features on complex and large spaces of possible genes [7, 8]. One of the most influential factors in the quality of the solutions found by an evolutionary algorithm is a suitable definition of the search space of the potential solutions.

This paper proposes an evolutionary approach that combines results from different ranking methods to assess the merits of the individual features by evaluating their strength of class predictability. This gives us the ability to find feature subsets with small size and high classification performance that we call feature pools (FPs). Each FP is assumed as an initial set of informative genes and is further refined by a wrapper approach involving a genetic algorithm (GA) and SVM classifier. Specifically, the GA explores the space defined by each FP looking for solutions that balance the size of the feature subsets and their classification accuracy.

Our extensive experiments on a public microarray dataset, namely the Leukemia dataset (Available at http://www.broad.mit.edu/cgi-bin/cancer/publications/.), demonstrate that the proposed approach is highly effective in selecting features and outperforms some proposed methods in literature.

The rest of the paper is organized as follows. In Section 2, we provide background information on microarray data analysis and discuss some related works. Section 3 illustrates the rationale for the proposed approach and describes the adopted evolutionary algorithm. We provide our extensive results and their interpretations in Section 4. Section 5 contains a detailed discussion as well a comparison with the results of different state-of-art methods from the literature. Finally, in Section 6 we conclude with some final remarks and suggest future research directions.

2. Background and Related Work

The “curse of dataset sparsity” [9, 10] is a major concern in microarray analysis, since microarray data include a large number of gene expression values per experiment (several thousands of features), and a relatively small number of samples (a few dozen of patients). Giving a large number of features to learning algorithms can make them very inefficient for computational reasons. In addition, irrelevant data may confuse algorithms making them to build inefficient classifiers while correlation between feature sets causes the redundancy of information and may result in the counter effect of overfitting [5]. Therefore, it is more important to explore data and utilize independent features to train classifiers, rather than increase the number of features we use.

The problem of feature selection has received a thorough treatment in machine learning and pattern recognition. Most of the feature selection algorithms approach the task as a search problem, where each state in the search specifies a distinct subset of the possible features [11]. The search problem is combined with a criterion in order to evaluate the merit of each candidate subset of features. There are a lot of possible combinations between each search procedure and each feature evaluation measure [12].

Based on the evaluation measure, feature selection algorithms can broadly fall into the filter model and the wrapper model [13]. The filter model relies on general characteristics of the training data to select predictive features (i.e., features highly correlated to the target class) without involving any mining algorithm. Conversely, the wrapper model uses the predictive accuracy of a predetermined mining algorithm to give the quality of a selected feature subset, generally producing features better suited to the classification task at hand. However, it is computationally expensive for high-dimensional data [11, 13]. As a consequence, the filter model is often preferred in gene selection due to its computational efficiency.

Hybrid and more sophisticated feature selection techniques have been explored in recent microarray research efforts [14]. Among the most promising approaches, evolutionary algorithms have been applied to microarray analysis in order to look for the optimal or near optimal set of predictive genes on complex and large search spaces [15]. For example, references [16–18] address the problem of gene selection using a standard genetic algorithm which evolves populations of possible solutions, the quality of each solution being evaluated by an SVM classifier. Genetic algorithms have been employed in conjunction with different classifiers, such as k-Nearest Neighbor in [19] and Neural Networks in [20]. Moreover, evolutionary approaches enable the selection problem to be treated as a multiobjective optimization problem, minimizing simultaneously the number of genes and the number of misclassified examples [18, 21].

3. The Evolutionary Method

Most of the evolutionary algorithms approach the task of microarray classification as a search problem where each state in the search specifies a distinct subset of the possible relevant features. If the search space is too large, it is possible that the evolutionary algorithm cannot discover the most selective genes within the search space. Moreover, having too many redundant or irrelevant genes increases computational complexity and cost and degrades estimation in classification error. On the other hand, if the initial gene space is too small, it is possible that some predictive genes are not included in the search space.

Feature ranking (FR) is a traditional evaluation criterion that is used by most popular search methods for assessing individual features and assigning them weights according to their relevance to the target class. Often the top-ranked genes are selected and evaluated by search algorithms in order to find the best feature subset. Although several search strategies exist, most of them cannot be applied to microarray datasets due to the large number of genes. Furthermore FR algorithms cannot discover redundancy and correlation among genes.

These limitations suggest us to pursue a hybrid method that attempts to take advantage from the combination of FR and evolutionary algorithms by exploiting their best performance in two steps. First, different FR methods are used for ranking genes. Since it is unfeasible to search for every possible subset of genes through the search space, only the top ranked genes are considered; they provide distinct lists of ordered genes that are combined in subsets, namely feature pools, of potentially “good” features. Second, each feature pool is further reduced by a genetic algorithm (GA) that tries to discover gene subsets having smaller size and/or better classification performance.

The use of different ranking methods promotes the selection of important subsets without losing informative genes while reducing the search space for the genetic algorithm. Being hard to apply evolutionary methods directly to high-dimensional datasets [22], reduced feature pools provide the possibility of putting into practice genetic algorithms, usually effective for small or middle scale datasets, for micro-array data classification. In the rest of this section, we give a description of these steps.

3.1. First Step: Ranking Genes and Building Feature Pools

Algorithm 1 describes the first step that aims to reduce the dimensionality of the initial problem by identifying pools of candidate genes to be further selected by the GA.

    Algorithm 1: Pseudocode describing the first step of the proposed evolutionary method

  • INPUT: D—Dataset of N features

  •    M—Number of ranking methods to be considered

  •    Met—Ranking method

  •    T—Threshold

  • OUTPUT: FeaturePools—A list of M sets of features

  • –––––––––––––––––––––––––––––-

  • (1) list RankedSets = { }

  • (2) AllFeatures = { }

  • (3) for  k = 1 to M

  • (4)   Setk = { }

  • (5)   for  each feature fi  ε  D

  • (6)     score = rank(fi,  Metk,  D)

  • (7)     append fi to Setk according to score

  • (8)   end for

  • (9)   Setk = top (Setk,  T)

  • (10)     AllFeatures = AllFeatures ∪ Setk

  • (11)     append Setk to RankedSets

  • (12)   end for

  • (13)   list FeaturePools = { }

  • (14)   FP0 = { }

  • (15)   list Combinations = { }

  • (16)   for  k = M to 2

  • (17)     Combinations = Combine(M,  k)

  • (18)     shared = CommonFeatures(RankedSets,

  •     Combinations)

  • (19)     FPM+1−k = shared ∪ FPM−k

  • (20)     append FPM+1−k to FeaturePools

  • (21)   end for

  • (22)   FPM = AllFeatures

  • (23)   append FPM to FeaturePools

Firstly, the genes are ranked using M ranked methods (lines 1–8). Ranking is carried out separately by each method and results in M ranked sets of genes each of ones contains all the genes in descending order of relevance. Then, we reduce the dimensionality by considering only the T top-ranked genes from each set (line 9), where T is a fixed threshold. This process results in a list of M ranked sets (line 11).

The basic idea of our approach is to absorb useful knowledge from these M sets and to fuse their information by considering the features they share (lines 13–23). In more detail, given a positive integer k (2 ≤ k ≤ M), we build a list of all possible k-combinations of the first M integers starting from 1 (line 17). For example, if M = 4 and k = 2, the list of combinations is as follows: {(1,2) (1,3) (1,4) (2,3) (2,4) (3,4)}. Each integer indexes a ranked set and we use these combinations (line 18) for determining the features shared by M,  M − 1, …, 2 of the M sets, respectively.

Next (lines 19–23), the shared features are employed for building a list of nested feature pools FP1⊆FP2 ⋯ ⊆FPM, where FP1 contains the features shared by all the M sets, FP2 the features shared by at least M − 1 of the M sets, FP3 the features shared by at least M − 2 of the M sets, …, FPM−1 the features shared by at least 2 of the M sets. Finally, FPM contains all the features belonging to the M sets.

3.2. Second Step: Gene Selection by GA/SVM

In the second step, we implement a wrapper model that combines GA and SVM. The latter is a popular classification technique, however other classifiers could be incorporated in our approach. To sum up, the GA selects some features as an individual and SVM evaluates them by classification, and the result is used for estimating the fitness of the individual. The possible choices of feature pools FPi define the evolutionary search space.

Figure 1 shows the whole structure of this second step. This is carried out separately on each FPi. At the start of the search, a population of individuals (i.e., feature subsets) is randomly initialized from the feature pool FPi. Each individual of the current population is evaluated according to a fitness function. Each time the fitness is evaluated, an SVM classifier is built and tested on the feature subset under investigation. Then, a new population is generated by applying genetic operations (selection, crossover and mutation) and the fitness is again evaluated until a prespecified number of generations G is reached. This evolution process results in a best individual that we try to further refine by initializing from it a new population that is used as a starting point of a new evolution process. The refinement is iterated until a pre-specified stopping criterion is met. When the entire round of search is completed, the final feature subset is returned.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The architecture of the GA/SVM algorithm.

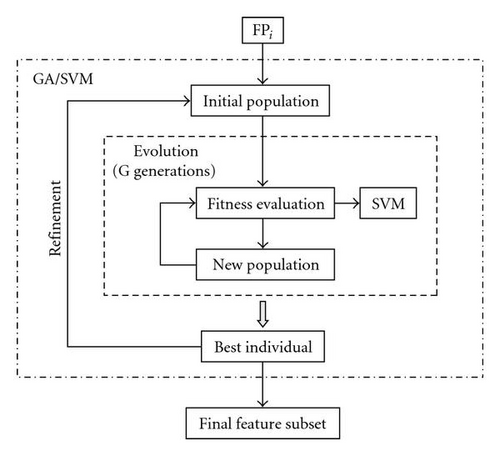
The basic components of our GA are as follows.

3.2.1. Representation of Individuals

Generally, a genetic algorithm represents the individual as a string or a binary array. Considering the large number of genes, if we represent all the genes as a binary vector, this results in a very long chromosome. Since the pre-processing step reduces the dimensionality of initial gene set, we limit the maximum size of each individual, that is, the length of chromosome, to a predetermined parameter size M*T that denotes the maximum cardinality of a feature pool. The individuals are encoded by n-bit binary vectors. If a bit is “1” it means that the corresponding feature is included in the gene subset, while the bits with value 0 mean the opposite.

3.2.2. Fitness Function

The fitness function is a key factor which affects the performance of GAs. Our aim is to define a function to scale the merit of a feature subset in terms of both classification accuracy and degree of dimensionality in order to see how good your approach is in situations where there is a large number of genes. The main idea is to achieve a tradeoff between the accuracy and the size of the obtained feature subsets. As a compromise between these two evaluation criteria, the fitness is defined as follows:
()
where w is a parameter between 0 and 1, x is a feature vector representing an individual, C(x) is the classification accuracy of a classifier built on x, and S(x) is the x size, that is, the number of genes included into x.

Here, the first term measures the weighted classification accuracy from a classifier and the second one evaluates the weighted size of the feature subset x. The parameter w is a fitness scaling mechanism for assessing the relevance of each term. Increasing the value of w will give more relevance to accuracy and reducing it will set more penalties on the size.

This multiobjective fitness makes it possible to obtain diverse solutions of high accuracy, while conventional approaches tend to be converged to a local optimum. We will analyze systematically the usefulness of the adopted function in our experiments.

3.2.3. Genetic Operators

Selection Roulette wheel selection is used to probabilistically select individuals from a population for later breeding. The probability P(hi) of selecting the individual hi is proportional to its own fitness F(hi) and inversely proportional to the fitness of other competing hypotheses in the current population. It is defined as follows:

()

Crossover We use the single point crossover, which is enough for our application. One crossover point i is chosen at random so that the first i bits are contributed by one parent and the remaining bits by the second parent.

Mutation Each individual has a probability pm to mutate. We randomly choose a number of n bits to be flipped in every mutation stage.

3.2.4. Stopping Criteria

A single evolution process is terminated when a predefined number of generations G is reached or an individual of maximum accuracy (100%) and minimum size (1) is obtained. The best individual produced by the evolution is iteratively refined by starting a new evolution process (Figure 1) until the fitness cannot be further improved (or a predefined number of iterations I is reached): the results show the possibility of improvement even if in few cases.

P trails of search are carried out using the GA/SVM approach previously described. The resulting gene subsets, as well as the partial results of the refinement process in each trail of search, are recorded in an archive for further analysis. All recorded gene subsets will be used in further evaluation and compared with respect to dimensionality and classification accuracy. This allows the identification of optimal subsets along with summary information such as the average classification accuracy and the average size of the gene subsets selected in different rounds of search.

4. Experimental Results

We verify the proposed method with Leukaemia [2] which is a popular public microarray dataset. Leukemia contains 72 samples among which 25 samples are collected from acute myeloid leukaemia (AML) patients and 47 samples are from acute lymphoblastic leukaemia (ALL) patients. Gene expression levels of 7129 genes are reported.

4.1. Methods and Parameters Settings

In the first step (see Section 3.1) we used the following ranking methods:
  • (i)

    information Gain (IG),

  • (ii)

    chi-squared (CHI),

  • (iii)

    symmetrical Uncert (SU),

  • (iv)

    one Rule (OR).

CHI measures the degree of independence between the feature and the target class. Inspired by information theory, IG evaluates the reduction of uncertainty (entropy) in classification prediction when knowing the feature. SU allows the discriminatory power of each feature to be found and OR operates by using a one rule classifier to evaluate each feature.

For genetic operations (see Section 3.2) the parameters were set as follows:
  • (i)

    population size: 25,

  • (ii)

    number of generations: G = 10,  G = 20,  G = 30,

  • (iii)

    probability of crossover: 1,

  • (iv)

    probability of mutation : 0.001,

  • (v)

    number of refinement iterations: I = 10.

SVM error estimation was by using leave-one-out cross validation (LOOCV). That is, one of the samples was left out to be a pseudotest data and the classifier was built based on all but the left out sample. This evaluation was repeated for each sample, and the estimated accuracy is a mean over all considered samples. We notice that LOOCV is a straightforward technique for estimating error rates and it is also an almost unbiased estimator.

The ranking methods and the SVM classifier were provided by the Weka library [4]. In particular, we must take account that in the Weka library SVM is trained using the SMO algorithm [23].

The evolutionary algorithm is run using GALib [24], a C++ library of genetic algorithm objects. The library includes tools for using genetic algorithms to do optimization in any C++ program using any representation and any genetic operators.

4.2. First Step

As already mentioned, the first step is done over ranking genes and, in the experiments, four (M = 4) ranking methods (IG, CHI, SU, OR) were used for it. First, each ranking method was applied to Leukemia and four ranked lists were generated. Then, we carried through preliminary experiments to compare the effectiveness of the considered methods.

Specifically, we ordered features according to their predictive power within each list and studied the behavior of SVM classifier on nested subsets of top-ranked features (i.e., top-2, top-4, top-8, etc.) from each list. Table 1 shows the LOOCV accuracy of SVM, respectively, by each nested subset and each ranking method. We note the similarity between results obtained with the four methods. The maximum accuracy (i.e., 98,6%) was reached by running SVM on 1024 features, except for CHI method where a peak was achieved on 32 features. We observe that when the number of selected features further increases, the accuracy does not improve, due to the inclusion of uninformative or redundant genes.

Table 1. LOOCV accuracy (%) of different groups of top ranked features.
Top-ranked features IG CHI SU OR
2 93.1 93.1 93.1 91.7
4 93.1 93.1 93.1 88.9
8 93.1 93.1 93.1 94.4
10 94.4 93.1 93.1 93.1
16 94.4 94.4 94.4 95.8
20 94.4 94.4 95.8 97.2
25 95.8 97.2 97.2 95.8
32 97.2 98.6 97.2 97.2
64 95.8 97.2 97.2 97.2
128 94.4 97.2 97.2 97.2
256 97.2 97.2 97.2 97.2
512 97.2 97.2 97.2 97.2
1024 98.6 98.6 98.6 98.6
2048 98.6 98.6 98.6 98.6
4096 98.6 98.6 98.6 98.6
7129 98.6 98.6 98.6 98.6

Results in Table 1 seem to suggest that no single feature selection criterion is optimal in identifying a small subset of highly discriminative features. This may be caused by the complex interactions, correlations, and redundancy between features and the biases embedded in the feature ranking criteria. On this premise, our experimental study aims to explore the effectiveness of combining useful outcomes from different methods, according to the methodology presented in Section 3.

As a first step, we cut off the T = 20 top ranked genes from each list, where the threshold of 20 is chosen based on a common practice in microarray studies. Table 2 shows the index of the 20 top-ranked genes (i.e., features) ordered by the relevance that each gene is assigned by each single ranking method. As we can see, some genes are shared by two or more ranking methods while some genes are specific to a single method.

Table 2. The 20 top-ranked genes from each ranking method.
Top-20 IG Top-20 CHI Top-20 SU Top-20 OR
1 3252 1834 1834 4847
2 4847 4847 4847 760
3 1834 1882 1882 6041
4 1882 3252 3252 1882
5 6041 6855 760 1685
6 2288 2288 2288 6376
7 760 760 6041 6855
8 6855 6041 6855 2288
9 1685 1685 1685 3252
10 1779 6376 6376 1834
11 2128 4373 2354 1779
12 6376 2128 4373 4366
13 2354 4377 4377 4328
14 4366 2354 4366 2402
15 4377 1779 2402 4196
16 4373 2402 758 1745
17 4328 1144 4328 1144
18 758 4366 1144 2020
19 1144 6281 3320 1928
20 2642 2121 2642 6347
Table 3 shows the composition of the feature pools FPi (i = 1, …, 4) as well as the LOOCV accuracy of the SVM classifier trained on each FPi (baseline model). The letter following each feature denotes the corresponding feature colour defined as follows:
  • (i)

    r marks the red features, that is, genes selected by all methods;

  • (ii)

    b marks the blue features, that is, genes selected by three methods;

  • (iii)

    g marks the green features, that is, genes selected by two methods;

  • (iv)

    y marks the yellow features, that is, genes selected by just one method.

Table 3. FPi composition and accuracy of the corresponding baseline model.
FP1 FP2 FP3 FP4
1 3252r 3252r 3252r 3252r
2 4847r 4847r 4847r 4847r
3 1834r 1834r 1834r 1834r
4 1882r 1882r 1882r 1882r
5 6041r 6041r 6041r 6041r
6 2288r 2288r 2288r 2288r
7 760r 760r 760r 760r
8 6855r 6855r 6855r 6855r
9 1685r 1685r 1685r 1685r
10 6376r 6376r 6376r 6376r
11 4366r 4366r 4366r 4366r
12 1144r 1144r 1144r 1144r
13 1779b 1779b 1779b
14 2354b 2354b 2354b
15 4377b 4377b 4377b
16 4373b 4373b 4373b
17 4328b 4328b 4328b
18 2402b 2402b 2402b
19 2128g 2128g
20 758g 758g
21 2642g 2642g
22 6281y
23 2121y
24 3320y
25 4196y
26 1745y
27 2020y
28 1928y
29 6347y
  
Accuracy 94.4% 94.4% 94.4% 98.6%

The choice of different colours is a useful heuristic we adopted for revealing the features shared by different ranking methods.

4.3. Second Step

Starting from the different feature pools obtained in the previous step, we performed a further gene selection according to the evolutionary approach described in Section 3.2. Specifically, we studied the behavior of the proposed algorithm in four ways: with respect to the parameter w (ranging from 0.70 to 0.95), with respect to the number of generations (G = 10, G = 20, G = 30), with respect to the classification accuracy, and with respect to the dimensionality of the feature subset.

Since the evolutionary algorithm performs a stochastic search, we consider the average accuracy and the average dimensionality of the selected subsets over a number P = 5 of trials. Within each FPi (i = 1, …, 4), Tables 4, 5, 6, and 7 report the accuracy (average and maximum) and the number of selected genes (average and minimum), respectively, by each value of w and the number of generations.

Table 4. Performance of GA on the feature pool FP1.
w Number of generations Average accuracy (%) Maximum accuracy (%) Average size Minimum size
0.70 10 94.2 95.8 4 3
20 94.2 95.8 4 3
30 93.3 95.8 3 2
  
0.75 10 94.4 97.2 4 3
20 94.4 97.2 3 2
30 93.9 97.2 3 2
  
0.80 10 96.4 98.6 5 4
20 95.5 97.7 4 4
30 95.0 97.2 4 2
  
0.85 10 95.0 97.2 4 3
20 96.7 98.6 4 4
30 95.8 98.6 4 2
  
0.90 10 96.9 98.6 4 3
20 96.4 97.2 6 3
30 96.9 98.6 5 3
  
0.95 10 95.8 97.2 4 3
20 96.9 98.6 4 2
30 97.2 98.6 4 3
Table 5. Performance of GA on the feature pool FP2.
w Number of generations Average accuracy (%) Maximum accuracy (%) Average size Minimum size
0.70 10 95.3 97.2 6 5
20 98.1 100 6 4
30 97.5 98.6 5 4
  
0.75 10 97.2 98.6 7 5
20 97.2 98.6 7 6
30 96.9 97.2 5 3
  
0.80 10 95.8 97.2 6 4
20 96.1 97.2 5 3
30 96.9 98.6 6 3
  
0.85 10 97.2 98.6 6 3
20 97.8 98.6 5 3
30 98.1 98.6 6 3
  
0.90 10 98.3 100 4 3
20 97.5 98.6 4 3
30 97.2 100 4 3
  
0.95 10 97.8 98.6 4 3
20 97.5 98.6 4 3
30 98.1 98.6 4 3
Table 6. Performance of GA on the feature pool FP3.
w Number of generations Average accuracy (%) Maximum accuracy (%) Average size Minimum size
0.70 10 96.7 98.6 6 3
20 96.4 97.2 6 3
30 97.8 100 7 5
  
0.75 10 96.7 98.6 8 7
20 97.8 100 8 4
30 97.8 100 10 5
  
0.80 10 96.9 98.6 7 3
20 98.9 100 5 3
30 98.1 98.6 10 5
  
0.85 10 97.8 100 5 3
20 98.3 100 5 3
30 98.9 100 6 4
  
0.90 10 98.6 100 6 3
20 98.6 100 4 3
30 98.9 100 4 3
  
0.95 10 99.4 100 5 3
20 98.3 100 4 3
30 98.6 100 4 3
Table 7. Performance of GA on the feature pool FP4.
w Number of generations Average accuracy (%) Maximum accuracy (%) Average size Minimum size
0.70 10 98.6 98.6 12 11
20 98.3 98.6 12 6
30 98.3 98.6 9 4
  
0.75 10 98.6 100 10 6
20 98.9 100 9 6
30 98.6 98.6 11 10
  
0.80 10 98.6 98.6 12 7
20 98.6 98.6 9 3
30 98.6 98.6 8 5
  
0.85 10 98.6 98.6 7 5
20 98.6 98.6 9 3
30 98.6 98.6 9 6
  
0.90 10 98.9 100 5 5
20 99.2 100 9 4
30 98.9 100 6 3
  
0.95 10 98.3 98.6 10 7
20 98.6 98.6 5 4
30 98.9 100 6 3

Compared with the baseline model of FP1 (red features in Table 3), whose accuracy is 94,4% on 12 features, we can see from Table 4 that the proposed evolutionary approach results in gene subsets of smaller size for each combination of w and number of generations. As well, the average accuracy outperforms the baseline model only if w ≥ 0.80, meaning that we should give more priority on the classification accuracy over the size when evaluating the fitness of each feature subset. Moreover, the number of generations seems to not significantly affect the performance of the algorithm, suggesting that few generations are sufficient for GA to converge on the best individual.

Compared with the baseline model (accuracy: 94,4%, size: 18) of FP2 (red and blue features in Table 3), Table 5 shows a clear improvement in terms of both classification accuracy and dimensionality for each combination of w and number of generations. Interestingly enough, increasing w (that means the fitness is evaluated giving more priority on the accuracy over the size) does not significantly increase the accuracy of the selected subset, while the size of the selected subset tends to decrease as w increases. This seems to suggest that the optimization of the accuracy (first term in the fitness function) implies optimizing the dimensionality too. As in the case of FP1, the performance does not improve when increasing the number of generations.

Our GA achieves the best results on the feature pool FP3 (red, blue, and green features in Table 3), as we can see in Table 6. Indeed, the comparison with the baseline model (accuracy: 94,4%, size: 21) shows an improved performance for each combination of w and number of generations. Moreover, for 13 different settings of parameters, a classifier with 100% accuracy is identified by the algorithm. Higher values of w, in particular w ≥ 0.85, lead to the best performance not only in terms of accuracy but also in terms of dimensionality, confirming that optimizing the accuracy means automatically reducing the size of the selected subset. Again, the number of generations seems to be not important, especially for higher values of w.

Finally, in the case of FP4 (red, blue, green, and yellow features in Table 3), each combination of parameters results in the selection of gene subsets whose classification accuracy is, on average, the same as the baseline model (98,6%) and no further improvement was achieved by the evolutionary algorithm in terms of accuracy. On the other hand, the dimensionality of the selected subsets is much lower than the initial number of features (29), which reveals a high degree of correlation and redundancy between the genes belonging to FP4.

5. Discussion

A basic question is to discuss the change in accuracy when varying the number of selected features and their combinations. In general, we believe that there is not a rule to determine an optimal number of features to get the best accuracy even for a specific classifier since that number may change from data to data and also may vary from different feature selection methods as our experiments demonstrate.

The threshold of 20 used to cut off top-ranked features is an arbitrary number, though it is based on our experience as we consider that biologists like a small number of features to separate two classes of cells and building a classifier would need a long time if many discriminatory features are selected.

However, this arbitrary choice does not pay when we simply consider use SVM on the 20 top-ranked features (baseline model) or on nested subsets of top-ranked features (i.e., top-2, top-4, top-8, etc.): accuracy is poor but this is not surprising and means that many features interact closely.

Our method demonstrated its efficiency in discovering the size of optimal subsets selected on the subsets of common features. Results show that the SVM classifier performs better on these optimal subsets. However, features common to all ranking methods (i.e., the red features belonging to FP1) define a search space that is too small and the performance of the classifier did not increase when the search was refined by an additional number of generations. When this search space was enlarged by adding blue, green, and yellow features our approach shows an excellent performance, not only at providing a very good average accuracy, but also with respect to the number of selected features and the computational cost. Resulting from the union of red, blue, and green features, the pool FP3 seems to define the most effective search space for the GA.

Table 8 summarizes our results with the results of seven state-of-art methods from the literature. The conventional criteria are used to compare the results, the classification accuracy in terms of the rate of correct classification (first number) and the number of used genes (the number in parenthesis, “-” indicating that the number of genes is not available). For our approach, the classification rate we presented is the maximum accuracy obtained on FP3 and the corresponding number of genes (see Table 6 for details). As it can be observed, we obtain a maximum classification rate of 100% using 3 genes (the corresponding average accuracy was 99,4%) which is much better than that reported in [25, 26]. This same performance is achieved by [3, 16, 17, 21, 27]. However, the number of genes selected by [16, 17, 21, 27] is greater than the one obtained by our method whose number of selected genes is greater than the one reported in [3].

Table 8. The proposed method versus seven state-of-art methods.
The proposed method 100 (3)
[25] 94.10 (-)
[27] 100 (8)
[16] 100 (6)
[26] 95.0 (-)
[21] 100 (4)
[3] 100 (2)
[17] 100 (25)

We also observe that increasing the number of generations does not greatly affect the performance of the algorithm. This may be because the size of the initial gene pool FP3 gives search space enough to the evolutionary algorithm. As well, the performance increases within high values of the parameter w. This means that the tradeoff between the two objectives of the fitness function is best represented when we give more importance to the accuracy since a high level of accuracy was automatically reached with a low number of features.

Another topic to address is the number of features subsets that reach the 100% accuracy (perfect predictors) and the frequency of selection of the genes that are member of the best predictors. Table 10 shows the perfect predictors discovered by the proposed approach. Interesting, no perfect predictor was discovered on the search space defined by FP1. It seems to confirm that this space is not large enough and contains groups of correlated features. Blue and green features mitigate the presence of this correlation by enlarging the search space. As well, the presence of yellow features in FP4 seems to influence the size of the optimal predictors since there is a notable difference when we consider the size of optimal predictors originated by FP2 and FP3. We observe that all features belonging to a perfect predictor are multicoloured, that is, they denote top-ranked genes shared by different groups of ranking methods. This indicates that combinations of features are beneficial.

Table 9 shows the frequency of the genes belonging to the optimal predictors (the number in parenthesis indicates the total number of perfect predictor within each feature pool). These results can be used by biologists for further evaluation.

Table 9. Features belonging to the perfect predictors in Table 10.
FP Selected feature Frequency
FP2 1144r 3 (3)
6855r 2 (3)
1834r 1 (3)
6376r 1 (3)
2354b 3 (3)
4377b 2 (3)
4373b 1 (3)
  
FP3 1144r 15 (18)
1834r 10 (18)
6855r 5 (18)
1685r 4 (18)
760r 3 (18)
1882r 1 (18)
2288r 1 (18)
6376r 1 (18)
2354b 12 (18)
4377b 9 (18)
4373b 7 (18)
2402b 1 (18)
4328b 1 (18)
2642g 8 (18)
758g 7 (18)
  
FP4 1685r 3 (7)
6855r 3 (7)
1144r 2 (7)
1834r 2 (7)
4366r 2 (7)
1882r 1 (7)
2288r 1 (7)
6041r 1 (7)
2354b 6 (7)
4377b 3 (7)
2402b 2 (7)
4373b 1 (7)
2642g 4 (7)
758g 2 (7)
2128g 1 (7)
2020y 5 (7)
6281y 5 (7)
6347y 5 (7)
1928y 4 (7)
2121y 1 (7)
4196y 1 (7)
Table 10. Perfect predictors identified by the proposed approach.
FP Size Features
FP2 4 1144r  2354b  4373b  4377b
4 1144r  1834r  6855r  2354b
5 1144r  6855r  6376r  2354b  4377b
  
FP3 3 1144r  1834r  2642g  (4 times)
4 1144r  2354b  4373b  4377b  (3times)
4 1144r  1834r  2354b  758g   (2times)
4 1834r  2354b  4328b  2642g
4 1834r  1685r  2354b  2642g
5 1144r  1834r  1685r  4373b  758g
5 1144r  1834r  2354b  4377b  758g
6 2288r  6855r  2354b  4377b  758g  2642g
6 1144r  1685r  6855r  2354b  4373b  4377b
7 760r  1144r  6376r  6855r  2354b  4373b  4377b
8 760r  1144r  1685r  1882r  6855r  4373b  4377b  758g
8 760r  1144r  6855r  2354b  2402b  4377b  758g  2642g
  
FP4 5 2354b  4377b  2020y  6281y  6347y
5 2354b  2642g  2020y  6281y  6347y
5 1685r  2354b  1928y  2020y  6347y
6 2354b  2128g  2642g  2020y  6281y  6347y
6 6855r  2354b  2402b  4377b  2642g  1928y
14 1144r  1834r  1882r  1685r  4366r  6855r  2354b  2402b 4373b  758g  2642g  1928y  2121y  6281y
14 1144r  1685r  1834r  2288r  4366r  6041r  6855r  4377b  758g  1928y  2020y  4196y  6281y  6347y

6. Conclusions

We presented a new evolutionary approach to select relevant features subsets in order to use them for the classification task. With respect to speeding-up the EA evaluation, we worked in proposing the combination of different ranking methods with two goals: to incorporate information to the GA to be used by genetic operators, and to reduce the computational time of the classification process by means of a pre-processing step from the data. The EA incorporates information in the early stage, when different ranking methods are applied before running the classification process, by organizing the top-ranked features into different feature pools. The main concern is the formulation of the feature selection issue as an optimization problem so that the predictors with maximum accuracy and minimum size can be found. We demonstrated that the proposed approach solves this optimization problem in efficient way and experimental results show that our method outperforms different state-of-art methods for the classification of microarray data. As future work, we will apply the proposed method to a variety of datasets and study the feature overlapping.

Acknowledgment

The authors are very grateful to anonymous reviewers for the useful comments and suggestions.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.