Underdominance, Multiscale Interactions, and Self-Organizing Barriers to Gene Flow

1. Introduction

Charles Darwin referred to speciation as the “mystery of mysteries” [1] and nearly 150 years later the mechanisms involved in speciation remain an important topic of debate in evolutionary biology (for recent reviews of this topic, see [2–8]). Historically, models of speciation have commonly invoked geographical isolation as a means for divergent evolution [9–11]. However, empirical evidence [12–14] suggests that speciation can also occur in the absence of geographical barriers to gene flow, and there has been a recent flurry of theoretical models providing support for these observations [15–24]. These models typically assume divergent evolution leading to speciation, subsequent to some form of premating reproductive isolating mechanism. For example, disruptive natural selection toward use of different parts of the available resource spectrum [17, 19] could alter the timing and/or location of mating events, resulting in two or more effectively reproductively isolated subpopulations that then continue to diverge, despite continuing to share the same geographic range. Similarly, assortative mating (due to sexual selection, e.g., where like prefers to mate with like) has also been proposed as a premating isolating mechanism [15, 18, 20], with several models employing a combination of these factors [15, 16, 21–24].

Spatially localized breeding interactions have been observed in a variety of both plant (e.g., [25–29]) and animal (e.g., [30–32]) populations, and the spatially explicit nature of these interactions has often been recognized as potentially important in speciation processes. Wright [33] derived statistical predictions that showed how spatially localized mating within interbreeding populations leads to nonadaptive differentiation in different parts of the population which are isolated from each other by distance. He felt that this process could be important for evolution within a species, but would only rarely represent first steps toward speciation itself. Subsequent spatially explicit individual-based models with localized mating have been employed to show how patches with distinct gene frequencies become quickly established and persist for many generations, even in the absence of selection [34, 35]. When selection is present, such evolving spatial self-organization of genotypes can help maintain high levels of genetic variation at multiple loci, when multiple genotypes have the same fitness [36]. Similarly, when male dispersal is dependent on mating success, theoretical models have demonstrated that populations will self-organize into groups of similar genotypes, promoting the evolution of assortative mating and thus facilitating the emergence of reproductively isolated groups [37]. Further, computational simulations have shown that environmental heterogeneity, such as the presence of gradual environmental gradients, can facilitate evolution of reproductive isolation [16]. Even with no assortative mating or environmental heterogeneity, simulated two-locus haploid populations experiencing disruptive selection (which are functionally equivalent to diploid populations with inviable heterozygotes, a.k.a. complete underdominance) will self-organize into two reproductively isolated species [38]. However, this occurs only if the hybrids are completely inviable, and such models have often been dismissed as unrealistic on the grounds that it is difficult to explain how the incompatible alleles became established in the same population in the first place.

If an ancestral diploid population is homozygous for a single allele at a given locus, it is difficult to envision how a new mutant allele with even mild underdominance (i.e., slight heterozygote disadvantage) could become established in the gene pool. In panmictic populations, the probability that an underdominant mutation becomes fixed decreases exponentially with both population size and the degree of underdominance [7], since this requires crossing a maladaptive valley in moving between fitness “peaks”. However, several possible mechanisms for the successful introduction of underdominance have been put forth. Conceivably, environmental changes could alter the fitness effects of previously fixed alleles so that they later become underdominant [38]. Alternatively, if there is strong disruptive selection toward different niches within the habitat, then a mutant hybrid may experience a transient fitness advantage by exploiting underutilized resources in a new niche, but then exhibit underdominance once the population stabilizes [39, 40]. Bateson [9], Dobzhansky [10], and Muller [11] proposed a means by which hybrid incompatibilities could evolve via epistatic (i.e., nonlinear gene-gene) interactions between mutations occurring at separate loci in allopatric (i.e., geographically isolated) populations, and Kondrashov [41] showed how this same process could also occur if mutations arise nearly simultaneously in different regions in a single interbreeding population where individuals have limited movement. Despite the theoretical difficulties regarding the introduction of underdominance, there is no question that natural populations do maintain a great deal of genetic variation, and there is ample empirical evidence of underdominance and even complete hybrid sterility [42–45]. For example, in a recent comprehensive genetic study in maize, direct evidence was found for several types of within locus nonadditivity, including allelic underdominance at multiple loci [46].

Epistasis has long been recognized as important in evolutionary processes [9], and our rapidly growing understanding of the complex interconnectedness of genetic [47–49] and metabolic [50] regulatory networks is spawning a new appreciation for the ubiquity of nonlinear gene-gene interactions [51, 52]. Empirical evidence suggests that epistasis may be an important factor leading to speciation [44] and some form of epistasis is a common assumption in theoretical models of speciation [9–11, 21]. Recent molecular evidence indicates that the distribution of genetic polymorphisms associated with complex diseases (i.e., diseases that are caused by epistatic interactions of many genetic polymorphisms) is not significantly different from the distribution of normal human variation (comprising apparently neutral polymorphisms) [53], indicating that some polymorphisms may be individually nearly neutral but become significantly deleterious only in certain combinations, or in response to certain environmental conditions.

In this paper, we use simulated diploid populations evolving on two-dimensional spatial grids to explore the specific question as to whether the cumulative effects of incomplete underdominance (mild heterozygote disadvantage) at multiple epistatically interacting loci can potentially drive speciation events, even in the absence of other premating isolation mechanisms, such as allopatry, environmental heterogeneity, or assortative mating. Two primary questions are tackled: (1) how can underdominant alleles become initially established in a single interbreeding population in a homogeneous environment?, (2) assuming that multiple mildly underdominant alleles exist in a population, can self-organization of genotypes result in a coalescence of mild incompatibilities such that two reproductively isolated species emerge?

2. Methods

2.3. Fitness Models

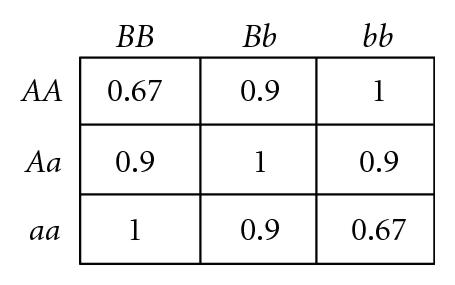
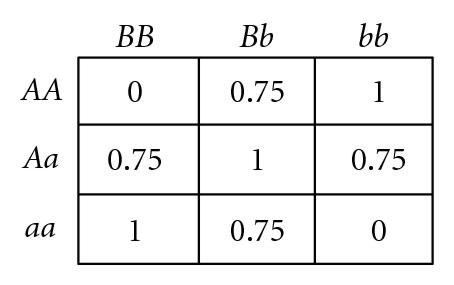
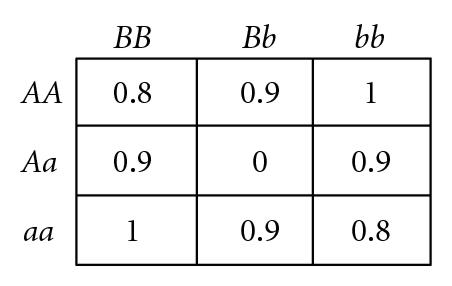
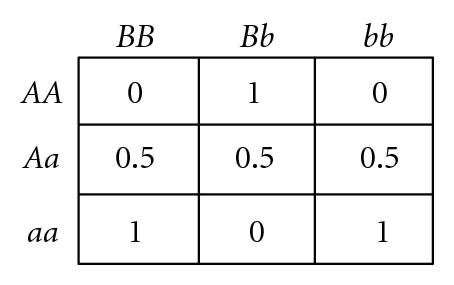
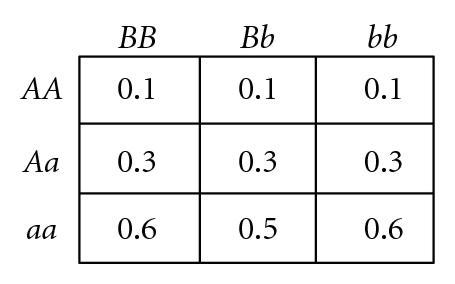
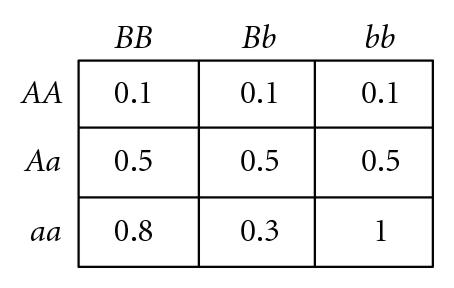
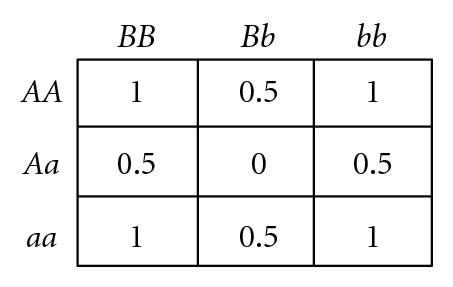
Several different fitness models are discussed in this study, incorporating various types and degrees of additivity (linear within-locus fitness, where the heterozygote has fitness intermediate to that of the two homozygotes), dominance (nonlinear within-locus fitness), and epistatic (nonlinear between-locus fitness) interactions, including the two-locus fitness tables shown in Figure 1. In these fitness tables, a value of 0 means inviability, and positive values simply indicate relative fitnesses of the various genotypes. Before discussing the fitness functions used in our experiments, we briefly review two fitness functions used in related literature, for comparison.

2.3.1. Review of Fitness Models of Goldstein and Holsinger

Goldstein and Holsinger [36] employed two types of multilocus fitness functions in their study exploring the effects of self-organization in populations with localized mating, as exemplified by the two-locus fitness functions shown in Figures 1(a) and 1(b). These functions actually exhibit within-locus overdominance (i.e., the average fitness of each single-locus heterozygote (Aa or Bb) is higher than either single-locus homozygote (AA, aa, BB, or bb), for both loci), so polymorphism is maintained through selection, even though directional selection will favor homozygotes aa in combination with BB, or bb in combination with AA. Our study differs from theirs in that they were exploring self-organization under this form of stabilizing selection (due to heterozygote advantage), while we explore self-organization under disruptive selection (due to heterozygote disadvantage).

2.3.2. Review of Bateson, Dobzhansky, Muller Incompatibilities

Bateson [9], Dobzhansky [10], and Muller [11] proposed a mechanism for the introduction of hybrid incompatibilities between allopatric populations (commonly referred to as BDM incompatibilities). An example of a BDM type incompatibility is illustrated by the two-locus fitness table shown in Figure 1(c). If a common ancestral population includes only AABB, it is easy to see that mutations to a and b are each individually beneficial and so could each become fixed if they arise in allopatric populations, resulting in only aaBB in one population and AAbb in the other. The hybrid between these two populations AaBb is inviable, so speciation has occurred, even if the geographic barriers between the two populations are subsequently removed. This model is extendible to multiple loci with cumulative effects [56]. However, BDM incompatibilities require multiple allopatric mutations (or nearly simultaneous mutations in populations with localized mating [41]), and so cannot be used to explain the introduction of underdominance at individual bi-allelic loci. In this study, we demonstrate the introduction of within-locus underdominance at multiple loci in interbreeding populations with localized mating, from individual mutational events that may be simultaneous or sequential.

The remainder of the specific fitness models shown in Figure 1 are discussed in the next section in the context of the relevant experiments.

3. Experiments

3.1. Introducing within-Locus Underdominance

3.1.1. Additive by Dominance Epistasis

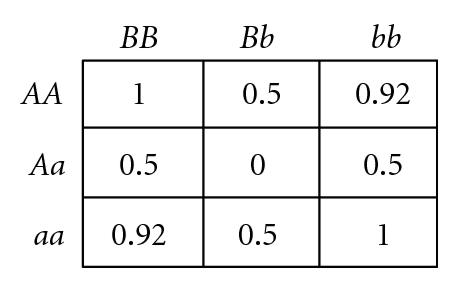
Goodnight [55] suggested, but did not demonstrate, that certain types of two-locus epistasis could result in the introduction of complete within-locus underdominance with a single mutation. For example, consider the fitness table for two loci shown in Figure 1(d) (which exhibits what Goodnight [55] refers to as pure “additive by dominance” epistasis). An ancestral population with only A, B, and b alleles will experience stabilizing selection, since the hybrid AABb genotype is the most fit, so both B and b alleles will be maintained in the population. As long as randomly interbreeding populations remain in Hardy-Weinberg equilibrium (where both alleles B and b have equal frequency, so the relative frequencies of diploid genotypes BB : Bb : bb are 1 : 2 : 1) a newly introduced a allele will be selectively neutral and could become fixed due to drift. However, any deviation away from a frequency of 0.5 at the B locus will result in directional selection for the a allele. In a panmictic population, either aaBB or aabb will take over the population, depending on which of B or b is most prevalent as a result of drift. However, in a population with localized mating, both aaBB and aabb can become established in different parts of the population, causing disruptive selection and subsequent self-organizing reproductive isolation (speciation) of these two genotypes. We have confirmed that such events can occur in simulated populations that were randomly initialized with spatially uncorrelated distributions of equal numbers of the B and b alleles but only a single randomly located a allele in a sea of A alleles, as illustrated by a representative simulation depicted in Figure 2. If the mutant a allele is not lost due to early drift, it quickly begins to increase due to directional selection in its local environment, which almost inevitably leads to patches of reproductively isolated species with genotypes aaBB and aabb. In a 100 × 100 grid, such speciation events were observed in 30% of 20 trials when using 3 × 3 localized mating neighborhoods, whereas fixation to either aabb or aaBB occurred 100% of the time when mating was panmictic. This example is of interest because of the fact that complete underdominance at the B locus is the result of a single mutational event, resulting in speciation when mating is localized, despite the fact that all alleles and loci have identical average effects when the population is in Hardy-Weinberg equilibrium. However, the existence of perfect transient “additive by dominance” epistasis (Figure 1(d)) in natural populations is expected to be very rare, at best, given the very specific requirements that the B locus exhibit perfect underdominance, perfect neutrality, and perfect overdominance in AA, Aa, and aa backgrounds, respectively.

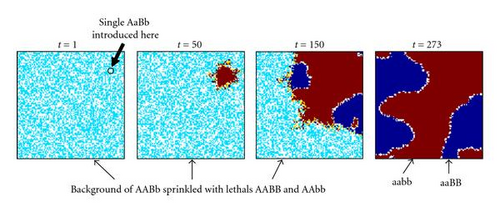
3.1.2. Directional Selection for within-Locus Underdominance at a Single Locus

It actually turns out to be quite simple to introduce within-locus underdominance into interbreeding populations via single mutational events and directional selection, when we allow for both additive and epistatic genetic variance. Consider a two-locus fitness table, where the (nonnegative) entries are calculated by the formulas below:

where η > α > β > δ   ≥ 0 and η ≥ δ + γ. This fitness table has the following properties: (i) polymorphisms at the B locus are neutral when in AA or Aa backgrounds, (ii) the maximum fitness is η, (iii) the predominant component of fitness variance at the A locus is additive (i.e., there is directional selection for the a allele, since η − α < η − β < η − δ), and (iv) there are varying degrees of epistatic additivity and underdominance at the B locus in combination with aa, depending on the values of δ (the degree of asymmetry in fitness between aaBB and aabb) and γ (the degree of underdominance of aaBb relative to aaBB), respectively. Two example instantiations of the fitness formulas in (2) are shown in Figure 1(e) (δ = 0, so there is no additive component to fitness at the B locus, so bb and BB have equal fitness) and Figure 1(f) (δ   = 0.2, so there is an additive component for the B locus, with bb being more fit than BB).

To illustrate how easily within-locus underdominance, even when asymmetric (i.e., δ > 0), can be introduced, we ran the following experiments using η = 1.0, α = 0.9, β = 0.5, γ ∈ {0,0.1,0.2,0.3,0.4,0.5,0.6}, and δ ∈ {0,0.1,0.2,0.3,0.4}. Populations of 100 × 100 individuals were randomly initialized in spatially uncorrelated Hardy-Weinberg frequencies for the B and b alleles, but initially contained only the A allele at the A locus, so all genotypes in the ancestral population were of equal fitness. A single beneficial mutant a allele was then introduced into each population in a random location and the population was allowed to evolve until one of three events occurred: (i) the a allele was lost due to early drift (unsuccessful trial), (ii) only one genotype remained, usually aaBB but occasionally aabb, (unsuccessful trial), or (iii) the A allele was lost due to directional selection and both B and b remained, so that within-locus asymmetric underdominance has been established at the B locus (successful trial). The probability that the mutant a allele will become fixed is governed by α − β (i.e., how immediately beneficial the mutation is). However, once the a allele starts to increase in frequency, directional selection takes over and the A allele is soon lost, after which time either outcome (ii) or (iii) will occur.

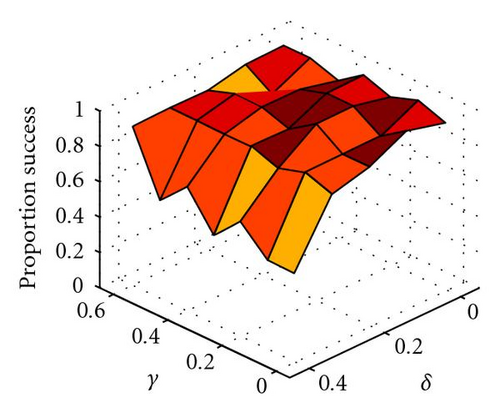
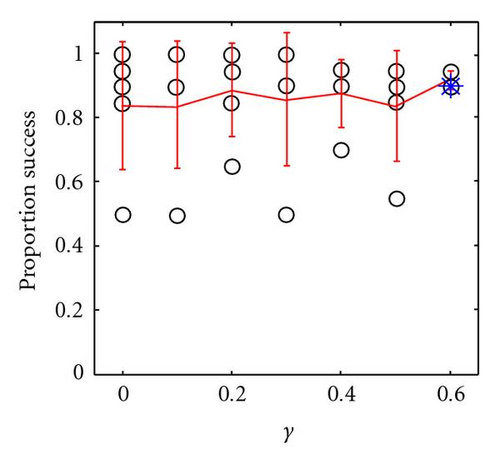
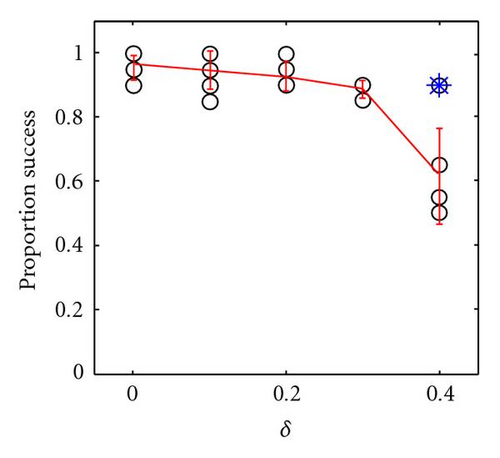
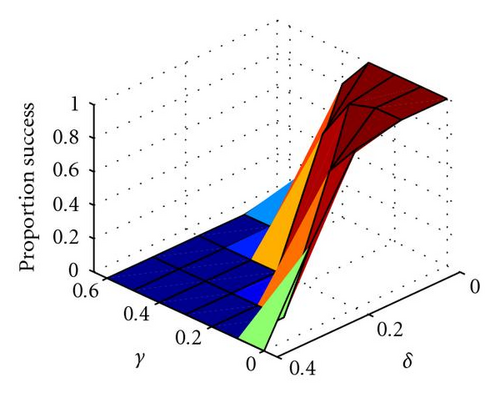
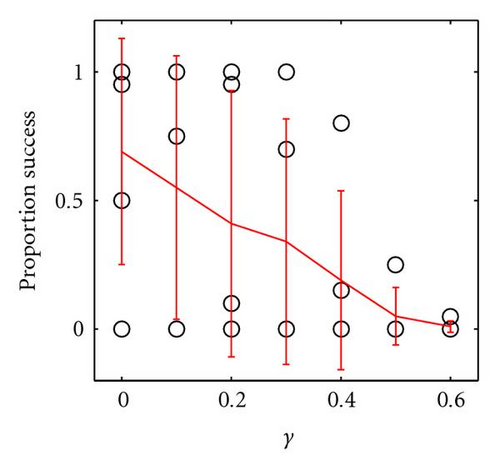
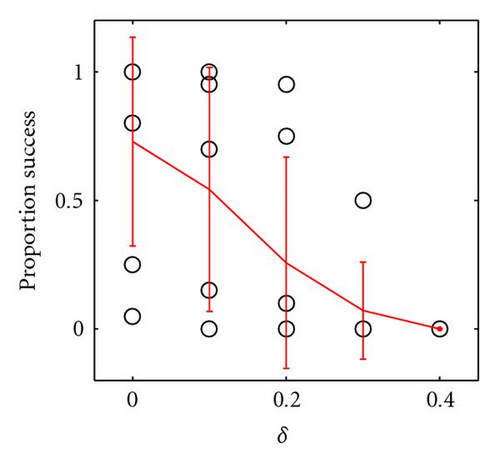
In Figure 3 we show how the proportion of successful introductions (out of 20 attempts at each parameter combination) of within-locus underdominance varies with 3 × 3 localized mating on a 100 × 100 grid, as a function of γ and δ, where the probability of fixation of the a allele is close to 1 (because α − β = 0.4, so directional selection for a is strong). Somewhat surprisingly, the success of introduction of underdominance at the B locus is essentially independent of the degree of underdominance γ (Figure 3(b)). Indeed, even with complete underdominance (i.e., heterozygote inviability at η − δ − γ = 0) shown by the asterisks in Figures 3(b) and 3(c), a single mutational event can cause speciation into reproductively isolated populations of aaBB and aabb. This is similar to the speciation event caused by the table in Figure 1(d) and shown in Figure 2, although in this case speciation can occur even when the aaBB genotype is less fit than the aabb genotype, because boundaries of inviable hybrids between clusters of these two genotypes act as barriers to gene flow that help to protect the less fit species. Thus, perfect genetic redundancy, where multiple homozygotes are equally fit, is not a strict requirement for self-organized speciation to occur. However, the frequency of successful trials is reduced as the asymmetry in fitness (δ) between aaBB and aabb is increased, because this increases the probability that the entire population converges on aabb (Figure 3(c)). In summary, when mating is localized, even strong underdominance with mild asymmetry between homozygotes can be easily introduced into the population through a single mutational event, when simple and biologically feasible forms of additivity and epistasis are considered. The fitness formulas in (2) are just one of many forms of epistatic fitness that can have this effect, as long as there is directional selection toward the newly introduced allele.

When mating is panmictic, weak underdominance and asymmetry can still be introduced in this manner, but the frequency of success is very sensitive to both γ and δ and unless these are both very weak the population rapidly converges to either aaBB or aabb, resulting in the failure to introduce within-locus underdominance at the B locus. This is shown by the results of an identical set of experiments to those described above, except where mating was panmictic (Figure 4). Even when underdominance is successfully introduced, it is not likely to persist for long in panmictic populations, as discussed later.

3.1.3. Directional Selection for Introducing Underdominance at Multiple Loci

The method described in Section 3.1.2 for introducing underdominance within loci can be easily extended to introducing both within-locus and epistatic underdominance at two or more loci. For example, consider the 4-locus fitness table shown in Figure 5, where the ancestral population is in Hardy-Weinberg proportions for alleles A, a, B, and b but has only alleles C and D present.

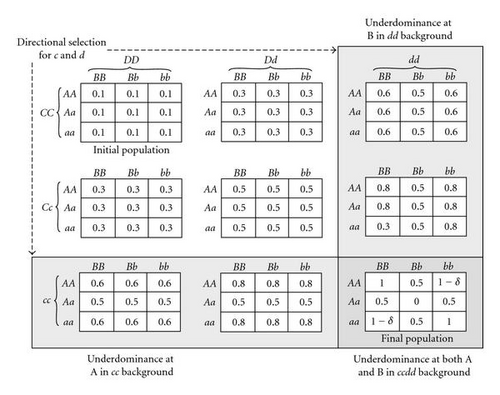
Introduction of a mutant c allele will introduce underdominance at the A locus, through the directional selection process described in Section 3.1.2, and illustrated in the first column of 2-locus tables of Figure 5. Similarly, introduction of a mutant d allele will introduce underdominance at the B locus, as illustrated in the first row of 2-locus tables of Figure 5. Introduction of both c and d alleles can lead the population to the fitness table shown in the lower right 2-locus table of Figure 5, which is equivalent to Figure 1(g) (if δ = 0) or Figure 1(h) (if δ = 0.08). In order to test how frequently this occurs, we performed the following set of experiments, using the fitness table shown in Figure 5 with δ = 0.08. In each case, a 100 × 100 population was randomly initialized in spatially uncorrelated Hardy-Weinberg proportions for A, a, B, and b but with only C and D alleles present. Then, c and d alleles were introduced in random locations; in one set of experiments, these two mutations were introduced simultaneously, whereas in another set of experiments the c allele was introduced first and, if it became fixed (i.e., if it replaced the C allele entirely), then the d allele was subsequently introduced. Both simultaneous and sequential introductions were tested in conjunction with both 3 × 3 localized mating and with panmixia, in 100 random trials for each of these four possible combinations. A trial was considered successful if and only if both C and D alleles disappeared while all of the A, a, B, b, c, and d alleles remained, so that the resulting fitnesses were as shown in Figure 1(h). In the case of panmixia, none of the trials were successful. However, with 3 × 3 localized mating 80% of the simultaneous introduction trials were successful and 32% of the sequential introduction trials were successful in introducing the two-locus underdominance, even though in this example the underdominance is fairly strong and the homozygotes in the resulting population are not all equally fit. This process is easily generalizable to introducing underdominance at more than two loci, especially when the underdominance is mild.

3.2. Self-Organization in 2 Locus Systems Due to Multiscale Interactions

In the previous section, we established that underdominant polymorphisms, such as shown in Figures 1(g) and 1(h), can be easily introduced into populations with localized mating interactions. In this section, we tackle the question as to what happens in populations with multiple underdominant loci. Specifically, we wanted to see if self-organization of the genotypes would occur in spatially structured populations and if so, how this would affect the evolutionary dynamics.

Populations of 100 × 100 individuals with two bi-allelic loci were subject to fitnesses according to either the table shown in Figure 1(g) (within-locus underdominance with no epistasis) or the table shown in Figure 1(h) (within-locus underdominance with mild epistasis). The populations were randomly initialized in Hardy-Weinberg equilibrium, with all alleles having initially equal frequencies and spatially uncorrelated random uniform distribution across the spatial domain (e.g., Figure 6(a), to preclude the introduction of initial bias in average effects or spatial organization. The random Hardy-Weinberg initialization is conservative when examining self-organization, since any initial clustering or local biases in fitness will only serve to nucleate cluster formation more quickly and speed up the process of self-organization. Groups of individuals are considered different species only if all hybrids between the groups are inviable. Experiments consisted of 10 random replications from each of 10 random starting domains, for both 3 × 3 localized mating and panmictic mating neighborhoods.

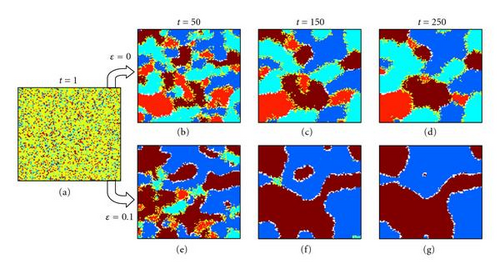
With panmixia, populations without epistasis (fitness as in Figure 1(g)) became completely fixed to one of the four possible homozygotes, with equal probability. With epistasis (fitness as in Figure 1(h)), panmictic populations became fixed to one of the two fittest homozygotes, with equal probability. These results are consistent with mean field predictions that underdominance cannot be maintained in populations with random mating.

When populations experience 3 × 3 localized mating, however, the results are more interesting. Without epistasis (fitness as in Figure 1(g)), the populations quickly self-organize into a patchy structure of the four possible homozygotes and the sizes of these clusters coarsens over time (e.g., Figures 6(b), 6(c), and 6(d). In this case, speciation does not occur since gene flow remains possible between all four homozygotes (Figure 1(g)). In contrast, with disruptive epistasis present (where the most fit genotypes are genetically incompatible with each other, such as with fitness in Figure 1(h)), populations with localized mating invariably self-organize into reproductively isolated clusters of the two fittest genotypes (e.g., Figures 6(e), 6(f), and 6(g), despite the absence of any environmental heterogeneity, externally imposed barriers to gene flow, or assortative mate preference. Thus, multiscale interactions comprising within-locus underdominance, between-locus epistasis, and localized mating interactions between individuals can result in self-organized speciation.

It should be noted that if allowed to run indefinitely, stochastic events in these finite and homogeneous simulated spatial domains ultimately favor one or the other species. However, real ecological domains are heterogeneous and once reproductive isolation has occurred, it is likely that two species will continue to diverge and, therefore, may not continue to be in direct competition for the same set of resources.

3.3. Extension to More than 2 Loci

For speciation to occur due to self-organization of only two underdominant loci, the degree of underdominance must be significant, so that the double heterozygote is completely inviable. However, we now consider a more biologically realistic scenario in which mild underdominance exists at several loci. Will such populations still exhibit self-organized speciation? In order to tackle this question we created a generalized fitness function exhibiting underdominance with optional epistasis, as follows:

$$ ()

where f_i is the fitness of individual i. Genotypes of individuals comprised L bi-allelic underdominant loci, where the two alleles at a given locus are identified by uppercase or lowercase letters. In (3) a maximum potential fitness of 1 is reduced by an underdominance penalty U, increased by an epistatic bonus E, and then renormalized so that the maximum possible fitness is brought back to 1. The underdominance penalty U is computed as the proportion of underdominant loci that are heterozygous. Thus, the more loci in the genotype, the milder the underdominance, and only genotypes heterozygous at all underdominant loci are inviable. Note that this strict inverse dependence of the degree of individual within-locus underdominance on the number of interacting loci is the most conservative approach for examining whether speciation will occur, since we construct these genomes so that, in all cases, there is only one possible genotype that is completely inviable. Speciation would be more likely to occur if there were multiple inviable genotypes, and would never occur if the within-locus underdominance penalty U were less than 1.0 for all genotypes. The epistatic bonus E is computed as the product of an epistatic coefficient ε and the maximum of the number of homozygous loci with the same case (upper or lower), such that only the two most genetically distinct homozygous genotypes (e.g., AABBCC and aabbcc) experience equal and maximal fitness.

This simple fitness function was employed because it allows easy control of both the degree of underdominance (by changing the number of loci) and the degree of epistasis (by changing ε) being modeled, while still maintaining identical average effects for each locus and each allele in the initial populations (which were randomly initialized in spatially uncorrelated Hardy-Weinberg equilibrium for all alleles). Note that for a 2-locus system, the fitnesses for the 9 genotypes shown in the tables in Figures 1(g) and 1(h) can be generated from (3), where ε = 0 and ε = 0.1, respectively (note that these same fitnesses could have resulted from the evolutionary process described in Section 3.1.3 and illustrated in Figure 5). Experiments were performed with L ∈ {2,4, 6,8, 10} underdominant loci and epistasic coefficients of ε ∈ {0.01,0.1}, with both panmixia and 3 × 3 localized mating. Each experimental configuration was run for 100 trials (10 random runs from each of 10 random initial populations).

As before, when mating is panmictic, the population rapidly fixes to one of the two fittest genotypes with equal probability, and speciation does not occur (Figure 7, bottom line). However, with 3 × 3 localized mating, speciation was observed in 100% of the trials for both values of epistasis tested, (Figure 7, top two lines). As the number of loci increases (and consequently the degree of within-locus underdominance decreases) the fitness valleys of heterozygotes at each locus become less pronounced, allowing increasingly easy traversal of fitness valleys and enabling underdominant polymorphisms to persist longer in the population. For example, with mild epistasis (ε = 0.1), the number of generations to speciation events increased exponentially (R² = 0.72) with the number of interacting loci L (Figure 7, middle line). Decreasing the epistasis coefficient by an order of magnitude (to ε = 0.01) increased the mean of the log of time to speciation by an order of magnitude (P < .0001, ANOVA) but also increased the variance (P < .0001, O’Brien’s test), with a corresponding drop in correlation (R² = 0.11, Figure 7, top line). In the latter case, the asymmetry in fitness between any of the homozygotes is almost negligible, enabling the underdominant polymorphisms to persist longer before speciation occurs.

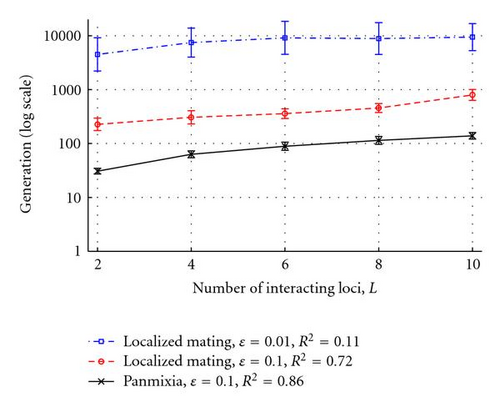
The results of these experiments demonstrate that, with localized mating and mild underdominance, clusters of homozygous genotypes spontaneously form and can coexist for long periods of time. With even a small amount of disruptive epistasis, leaky genetic boundaries between these clusters tend to coalesce over time to form impermeable genetic barriers to gene flow, even when individual loci are nearly neutral. Thus, speciation can occur as an emergent property from the self-organization of multiple underdominant polymorphisms in populations with localized mating.

3.4. The Effect of External Barriers to Gene Flow

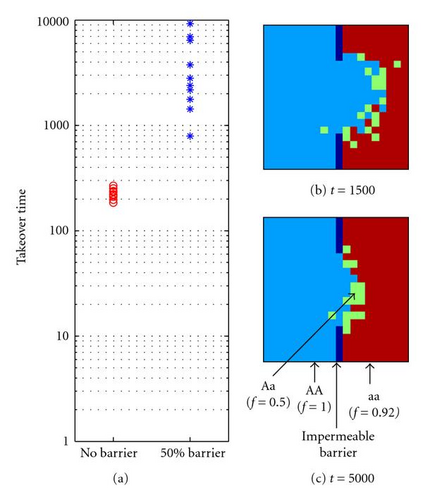
As shown in Figure 7, underdominant alleles and less fit genotypes can persist for long periods in a single interbreeding population, if mating is spatially localized, even when the domain is completely homogeneous and no niche differentiation occurs. However, the presence of external barriers to gene flow can further enhance the persistence of underdominance and less fit genotypes in an interbreeding population. If even partial external (e.g., geographic) barriers to gene flow are present, self-organized cluster boundaries will tend to become stabilized at external boundaries [57]. Consider a simple single-locus 20 × 20 population, where the left half of the domain is initially populated with the homozygote AA with fitness 1.0, while the right half is populated with the homozygote aa with fitness 0.92, and the heterozygote Aa has fitness 0.5 (i.e., fitness is as in column 1 of the table shown in Figure 1(h)). When there is no physical barrier between them, the more fit AA takes over the entire domain in an average of only 224 generations (10 trials, standard deviation = 25), whereas when 10 of the 20 cells are blocked by an impermeable external boundary, leaving a 10-cell window in the center, the takeover time increases by over an order of magnitude to an average of 3777 (10 trials, standard deviation = 2809), with one takeover time as high as 9254 generations (Figure 8(a). The reason for this dramatic slowdown in takeover by the more fit genotype is illustrated by snapshots from a representative run. At 1500 generations (Figure 8(b), the more fit AA genotype has made a bulge into the half if the domain initially occupied by aa. However, the fitness advantage of AA is countered by the fact that the local mating neighborhoods at the convex cluster boundary have a larger proportion of aa genotypes, which increases their probability of being selected by (1). In fact, the bulge tends to grow and shrink in size over time; in this example it was much smaller at 5000 generations (Figure 8(c) than it was at 1500 generations (Figure 8(b). Ultimately, if given enough time, a fitter genotype will “break through” the barrier and then rapidly take over the rest of the domain (this particular run took 7166 generations for complete takeover).

4. Discussion and Conclusions

Underdominance can conceivably enter the genome of an interbreeding population via a variety of potential mechanisms. Previously proposed mechanisms include environmental change [38], disruptive selection caused by niche differentiation [39, 40], and “additive by dominance” epistasis [55]. Here, we demonstrate a simple alternative and biologically reasonable mechanism by which within-locus underdominance can easily become established at one or more loci, either simultaneously or sequentially. Specifically, the proposed mechanism requires (i) an initial condition comprising a preexistent neutral polymorphism at a locus (ii) an advantageous mutation at a second locus (which thus becomes fixed by directional selection), and (iii) an epistatic interaction between the two loci, such that the first (previously neutral) locus becomes underdominant in the background of the newly fixed favorable allele at the second locus. We note that these requirements are consistent with the existence of a large amount of observed neutral polymorphism, occasional advantageous mutations, and pervasive epistatic genetic interactions in biological organisms [47]. Our simulations show that, if mating is panmictic, then only mild underdominance can be introduced in this manner and is not likely to persist for long. However, when mating is spatially localized, even strong underdominance with mild asymmetry can be easily introduced and maintained in interbreeding populations for long durations. Our model thus illustrates how underdominance at multiple loci can easily be introduced into interbreeding populations with localized interactions.

We also demonstrate that in locally mating populations exhibiting mild underdominance at multiple loci, the populations self-organize into clusters of compatible genotypes. Gene flow persists between clusters unless the hybrids between clusters are completely inviable. Even in the extreme case, where boundaries for different underdominant loci are initially independent of each other, over time they become aligned. Thus, leaky genetic boundaries coalesce to form harder genetic boundaries (deeper fitness valleys). When certain forms of mild epistasis are present, speciation can be an emergent property in this model, arising as the result of multiscale interactions (within-locus, between-locus, and between individuals) without any geographic, niche-based, mate preference, or other premating isolating mechanisms. In contrast, self-organization cannot occur when mating is panmictic, in which case the populations invariably converge on a single genotype.

Just as localized mating can promote maintenance of genetic polymorphisms at multiple diploid loci in patchy structures when selection is stabilizing [36], we have shown that a similar process can occur when selection is disruptive. In both cases, genetic redundancy (where multiple genotypes have the same fitness) help to stabilize the polymorphisms. However, under disruptive selection even clusters of unequal fitness can persist long enough for speciation to occur, since the fitness valleys in the hybrid zones between unequally fit genotypes slow the takeover by the fitter genotype. If external barriers to gene flow are also present, then these can increase persistence of even asymmetric underdominant polymorphisms by further stabilizing cluster boundaries.

In the experiments reported here, mating interactions were either panmictic or used overlapping 3 × 3 localized mating neighborhoods. However, even when mating is generally localized in natural populations, there are still likely to be occasional long range interactions (e.g., long range migration events in animals or unusually long dispersal of pollen or seeds in plants). In a separate set of experiments reported elsewhere [58], we assessed the sensitivity of simulated self-organized speciation to relaxations in the assumption of strictly localized mating. Specifically, we altered the interaction topology from nearest neighbor interactions to panmictic interactions in two ways: (i) by increasing the size of the contiguous mating neighborhoods and (ii) by allowing for long-distance dispersal of individuals with increasing probability. The results of that study [58] show self-organized speciation to be robust to mating neighborhood sizes significantly larger than nearest neighbor interactions (relative neighborhood size to domain size is actually shown to be the governing parameter, as in cellular evolutionary algorithms [59]) and to probabilities of long-distance dispersal that fall well into the range of so called “small-world” [60] interaction topologies.

Spatially explicit models, such as employed here, are not generally analytically tractable, and the lack of closed form solutions has led some to claim that this limits the generality of theoretical conclusions [6]. However, in complex biological systems, the generality of theoretical conclusions may be even more severely limited by the assumptions necessary for analytical tractability, and by the principle of computational irreducibility [61] simulations can be necessary in order to gain insight into complex multiscale spatiotemporal evolutionary processes. We do not dispute that analytical solutions based on assumptions such as panmixia or haploidy can certainly lead to useful generalizations in some circumstances. Yet, as demonstrated in this contribution as well as a variety of other studies of both simulated and natural populations (e.g., [16, 34, 36, 38, 54, 57, 62–65]), essential evolutionary dynamics often emerge as a consequence of spatially-constrained interactions. While the model employed herein is highly idealized, it nonetheless manifests properties observed in natural populations, while removing the confounding effects of differences in initial average effects of different alleles or different loci, heterogeneity in the environment, or premating isolation of similar genotypes due to mate selection or geographic isolation. The three primary assumptions in our model of self-organized speciation are that populations can exhibit (i) underdominant polymorphisms, (ii) epistatic genetic interactions, and (iii) spatially localized mating, all of which have been widely observed in natural populations, as discussed in the introduction. These simulations yield potentially useful generalizations and insights, demonstrate the sensitivity of evolutionary processes to spatial and multiscale aspects of interactions, and underscore the importance of taking these complexities into account.

The degree to which epistatic underdominance is a significant driving force in natural evolution is difficult to say. Certainly, hybrid zones of reduced fitness are commonly observed between closely related species, but when and how these hybrid incompatibilities evolved is impossible to determine in retrospect. However, while this study cannot answer the question of whether or not recombination and self-organization of many nearly neutral underdominant alleles has led to emergent intrinsic barriers to gene flow in natural systems, we argue that it does indicate that such processes may be feasible and even parsimonious mechanisms for genetic divergence without premating isolation. We conclude that multiscale interactions can potentially help to maintain underdominant polymorphisms and may contribute to speciation events. This model shows one way that the emergent properties in complex biological communities can drive evolutionary change. It is probable that, in natural systems, many mechanisms are operating simultaneously to cause speciation.