Volume 2009, Issue 1 483079

Research Article

Open Access

Rotations in the Space of Split Octonions

Corresponding Author

Merab Gogberashvili

[email protected]

Particle Physics Department, Andronikashvili Institute of Physics, 6 Tamarashvili Street, 0177 Tbilisi, Georgia acnet.ge

Department of Physics, Faculty of Exact and Natural Sciences, Javakhishvili Tbilisi State University, 3 Chavchavadze Avenue, 0128 Tbilisi, Georgia tsu.ge

Department of Physics, California State University, 2345 E. San Ramon Avenue, M/S MH37, Fresno, CA 93740, USA calstate.edu

Search for more papers by this author

Merab Gogberashvili,

Corresponding Author

Merab Gogberashvili

[email protected]

Particle Physics Department, Andronikashvili Institute of Physics, 6 Tamarashvili Street, 0177 Tbilisi, Georgia acnet.ge

Department of Physics, Faculty of Exact and Natural Sciences, Javakhishvili Tbilisi State University, 3 Chavchavadze Avenue, 0128 Tbilisi, Georgia tsu.ge

Department of Physics, California State University, 2345 E. San Ramon Avenue, M/S MH37, Fresno, CA 93740, USA calstate.edu

Search for more papers by this author

First published: 01 July 2009

https://doi.org/10.1155/2009/483079

Citations: 1

Academic Editor: Fedele Lizzi

Share a link

Email
Wechat
Bluesky

Abstract

The geometrical application of split octonions is considered. The new representation of products of the basis units of split octonionic having David′s star shape (instead of the Fano triangle) is presented. It is shown that active and passive transformations of coordinates in octonionic “eight-space” are not equivalent. The group of passive transformations that leave invariant the pseudonorm of split octonions is SO(4, 4), while active rotations are done by the direct product of O(3, 4)-boosts and real noncompact form of the exceptional group G₂. In classical limit, these transformations reduce to the standard Lorentz group.

1. Introduction

Nonassociative algebras may surely be called beautiful mathematical entities. However, they have never been systematically utilized in physics, only some attempts have been made toward this goal. Nevertheless, there are some intriguing hints that nonassociative algebras may play essential role in the ultimate theory, yet to be discovered.

Octonions are one example of a nonassociative algebra. It is known that they form the largest normed algebra after the algebras of real numbers, complex numbers, and quaternions [1–3]. Since their discovery in 1844/1845 by Graves and Cayley there have been various attempts to find appropriate uses for octonions in physics (see reviews [4–7]). One can point to the possible impact of octonions on: Color symmetry [8–11]; GUTs [12–15]; Representation of Clifford algebras [16–19]; Quantum mechanics [20–24]; Space-time symmetries [25, 26]; Field theory [27–29]; Formulations of wave equations [30–32]; Quantum Hall effect [33]; Kaluza-Klein program without extra dimensions [34–36]; Strings and M-theory [37–40]; and so forth.

In this paper we study rotations in the model, where geometry is described by the split octonions [41–43].

2. Octonionic Geometry

Let us review the main ideas behind the geometrical application of split octonions presented in our previous papers [41–43]. In our model some characteristics of physical world (such as dimension, causality, maximal velocities, and quantum behavior) can be naturally described by the properties of split octonions. Interesting feature of the geometrical interpretation of the split octonions is that their pseudonorms, in addition to some other terms, already contain the ordinary Minkowski metric. This property is equivalent to the existence of local Lorentz invariance in classical physics.

To any physical signal we correspond eight-dimensional number, the element of split octonions,

(2.1)

Here we have one scalar basis unit (denoted as 1), the three vector-like objects J_n, the three pseudovector-like elements j_n, and one pseudoscalar-like unit I. The eight real parameters that multiply basis elements we treat as the time t, the special coordinates xⁿ, some quantities λⁿ with the dimensions momentum⁻¹, and the quantity ω having the dimension energy⁻¹. We suppose also that (2.1) contains two fundamental constants of physics: the velocity of light c and the Planck constant ℏ.

The squares of basis units of split octonions are inner product resulting unit element, but with the opposite signs,

(2.2)

Multiplications of different hypercomplex basis units are defined as skew products (n, m, k = 1,2, 3),

(2.3)

where ϵ_nmk is the fully antisymmetric tensor.

From (2.3) we notice that to generate complete basis of split octonions the multiplication and distribution laws of only three vector-like elements J_n are needed. In geometrical application this can explain why classical space has three dimensions. The three pseudovector-like basis units j_n can be defined as the binary product

(2.4)

and thus can describe oriented orthogonal planes spanned by two vector-like elements J_n. The seventh basic unit I (the oriented volume) is formed by the products of all three fundamental basis elements J_n and has three equivalent representation:

(2.5)

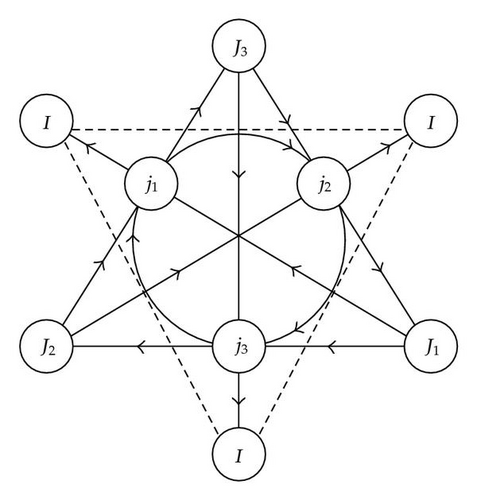
The multiplication table of octonionic units is most transparent in graphical form. To visualize the products of ordinary octonions the Fano triangle is used [1–3], where the seventh basic unit I is place at the center of the graph. In the algebra of split octonions we have less symmetry, and for a proper description of the products (2.3) the Fano graph should be modified by shifting I from the center of the Fano triangle. Also we will use three equivalent representations of I, (2.5), and, instead of the Fano triangle, we arrive at David′s star shaped duality plane for products of the split octonionic basis elements.

On this graph the product of two basis units is determined by following the oriented solid line connecting the corresponding nodes. Moving opposite to the orientation of the line contributes a minus sign to the result. Dashed lines just show that the corners of the triangle with I nodes are identified.

Conjugation, which can be understand as a reflection of the vector-like basis units J_n, reverses the order of octonionic basis elements in any given expression, thus

(2.6)

there is no summing in the last formula. So the conjugation of (2.1) gives

(2.7)

Using (2.2) one can find that the pseudonorm of (2.1),

(2.8)

has (4 + 4) signature. If we consider s as the interval between two octonionic signals we see that (2.8) reduces to the classical formula of Minkowski space-time in the limit ℏ → 0.

Using the algebra of basis elements (2.3) the octonion (2.1) can be written in the equivalent form

(2.9)

We notice that the pseudoscalar-like element I introduces the ′quantum′ term corresponding to some kind of uncertainty of space-time coordinates. For the differential form of (2.9) the invariance of the pseudonorm (2.8) gives the relation:

(2.10)

where v_n = dx_n/dt denotes 3-dimensional velocity measured in the frame (2.1). The generalized Lorentz factor (2.10) contains extra terms that vanish in the limit ℏ → 0. So the dispersion relation in our model has a form similar to that of double-special relativity models [44, 45].

From the requirement to have the positive pseudonorm (2.8) from (2.10) we obtain several relations

(2.11)

Recalling that λ and ω have dimensions of momentum⁻¹ and energy⁻¹, respectively, we conclude that the Heisenberg uncertainty principle in our model has the same geometrical meaning as the existence of the maximal velocity in Minkowski space-time.

3. Rotations

To describe rotations in 8-dimensional octonionic space (2.1) with the interval (2.8) we need to define exponential maps for the basis units of split octonions.

Since the squares of the pseudovector-like elements j_n are negative,

, we can define

(3.1)

where θ_n are some real angles.

At the same time for the other basis elements J_n, I, which have the positive squares

, we have

(3.2)

where m_n and σ are real numbers.

In 8-dimensional octonionic “space-time’’ (2.1) there is no unique plane orthogonal to a given axis. Therefore for the operators (3.1) and (3.2) it is not sufficient to specify a single rotation axis and an angle of rotation. It can be shown that the left multiplication of the octonion s by one of the operators (3.1), (3.2) (e.g., ) yields four simultaneous rotations in four mutually orthogonal planes. For simplicity we consider only the left products since it is known that one side multiplications generate the whole symmetry group that leaves the octonionic norms invariant [46].

So rotations naturally provide splitting of an octonion in four orthogonal planes. To define these planes note that one of them is formed by the hypercomplex element that we chose to define the rotation (j₁ in our example), together with the scalar unit element of the octonion. The rest orthogonal planes are given by the three pairs of other basis elements that lie with the considered basis unit (j₁ in the example) on the lines emerged it in David′s star (see Figure 1). Thus the pairs of basis units that are rotated into each other are the pairs that form associative triplets with the considered basis unit. For example, the basis unit j₁, according to Figure 1, has three different representations in the octonionic algebra:

(3.3)

So the planes orthogonal to (1 − j₁) are (J₂ − J₃), (j₂ − j₃), and (J₁ − I). Using (3.3) and the representation (3.1) it is possible to “rotate out’’ the four octonionic axes, and (2.1) can be written in the equivalent form

(3.4)

where

(3.5)

are the norms in four orthogonal octonionic planes. The corresponding angles are given by

(3.6)

This decomposition of split octonion is valid only if the full pseudonorm of the octonion (2.8) is positive, that is,

(3.7)

A decomposition similar to (3.4) exists if the another pseudovector-like basis unit, j₂ or j₃, is fixed.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Split octonion multiplication as David′s star.

In contrast with uniform rotations giving by the operators j_n we have limited rotations in the planes orthogonal to (1 − J_n) and (1 − I). However, we can still perform a decomposition similar to (3.4) of s using expressions of the exponential maps (3.2). But now, unlike on (3.5), the norms of the corresponding planes are not positively defined and, instead of the condition (3.7), we should require positiveness of the norms of each four planes. For example, the pseudoscalar-like basis unit I has three different representations (2.5), and it can provide the hyperbolic rotations (3.2) in the orthogonal planes (1 − I), (J₁ − j₁), (J₂ − j₂), and (J₃ − j₃). The expressions for the 2 norms (3.5) in this case are: , , , and .

Now let us consider active and passive transformations of coordinates in 8-dimensional space of signals (2.1). With a passive transformation we mean a change of the coordinates t, x_n, λ_n, and ω, as opposed to an active transformation which changes the basis 1, J_n, j_n, and I.

The passive transformations of the octonionic coordinates t, x_n, λ_n, and ω, which leave invariant the norm (2.8) form SO(4,4). We can represent these transformations of (2.1) by the left products

(3.8)

where R is one of (3.1), (3.2). The operator R simultaneously transforms four planes of s. However, in three planes R can be rotated out by the proper choice of octonionic basis. Thus R can represent rotations separately in four orthogonal planes of s. Similarly we have some four angles for the other six operators (3.1), (3.2) and thus totally 4 × 7 = 28 parameters corresponding to SO(4,4) group of passive coordinate transformations. For example, in the case of the decomposition (3.4) we can introduce four arbitrary angles ϕ_t, ϕ_x, ϕ_λ, and ϕ_ω, and

(3.9)

Obviously under these transformations the pseudonorm (2.8) is invariant. By the fine tuning of the angles in (3.9) we can define rotations in any single plane from four.

Now let us consider active coordinate transformations, or transformations of basis units 1, J_n, j_n, and I. For them, because of nonassociativity, the results of two different rotations (3.1) and (3.2) are not unique. This means that not all active octonionic transformations (3.1) and (3.2) form a group and can be considered as a real rotation. Thus in the octonionic space (2.1) not to the all passive SO(4,4)-transformations we can make corresponding active ones, only the transformations that have a realization as associative multiplications should be considered. It is known that associative transformations can be done by the combined rotations of special form in two octonionic planes that form a subgroup of SO(4,4), known as the automorphism group of split octonions (the real noncompact form of Cartan′s exceptional Lie group G₂). Some general results on and its subgroup structure can be found in [47,16b].

Let us recall that the automorphism A of a algebra is defined as the transformations of the hypercomplex basis units x and y under which the multiplication table of the algebra is invariant, that is,

(3.10)

Associativity of these transformations is obvious from the second relation, and the set of all automorphisms of composition algebras form a group. In the case of quaternions, because of associativity, active and passive transformations, SU(2) and SO(3), respectively, are isomorphic and quaternions are useful to describe rotations in 3-dimensional space. One has a different situation for octonions. Each automorphism in the octonionic algebra is completely defined by the images of three elements that do not form quaternionic subalgebras, that is, they all not lie on the same David′s line [49]. Consider one such set, say (j₁, j₂, J₁). Then there exists an automorphism

(3.11)

where α₁ and β₁ are some independent real angles. By the definition (3.10) the automorphism does not affect unit scalar 1. The images of the other basis elements under automorphism (3.11) are determined by the conditions

(3.12)

It can easily be checked that transformed bases

, I^′ satisfy the same multiplication rules as J_n, j_n, I.

There exist similar automorphisms with fixed j₂ and j₃ axes, which are generated by the angles α₂, β₂ and α₃, β₃, respectively.

One can define also hyperbolic automorphisms for the vector-like units J_n by the angles u_n, k_n. For example, for fixed J₁ similar to (3.11) and (3.12) transformations are

(3.13)

Analogously in the case of fixed I we find that

(3.14)

So for each octonionic basis there are seven independent automorphisms each introducing two angles that correspond to 2 × 7 = 14 generators of the algebra

. For our choice of basis the infinitesimal passive transformation of the coordinates, corresponding to

, has the form

(3.15)

where U_ik is the symmetric matrix

(3.16)

In the limit (ℏλ, ℏω → 0) the transformations (3.15) reduce to the standard O(3) rotations of Euclidean 3-space by the Euler angles ϕ_n = α_n − β_n.

The formulas (3.15) represent rotations of (3,4)-sphere that is orthogonal to the time coordinate t. To define the boosts note that active and passive forms of mutual transformations of t with x_n, λ_n, and ω are isomorphic and can be described by the seven operators (3.1) and (3.2) (e.g., the first term in (3.9), which form the group O(3,4). In the case (ℏλ, ℏω → 0) we recover the standard O(3) Lorentz boost in the Minkowski space-time governing by the operators , where m_n = arctanv_n/c.

4. Conclusion

In this paper the David′s star duality plane, which describes the multiplication table of the basis units of split octonions (instead of the Fano triangle of ordinary octonions), was introduced. Different kind of rotations in the split octonionic space was considered. It was shown that in octonionic space active and passive transformations of coordinates are not equivalent. The group of passive coordinate transformations, which leave invariant the pseudonorms of split octonions, is SO(4,4), while active rotations are done by the direct product of the seven O(3,4)-boosts and fourteen -rotations. In classical limit these transformations give the standard 6-parametrical Lorentz group.

Acknowledgment

The author would like to acknowledge the support of a 2008-2009 Fulbright Fellowship.

References

1 Schafer R., Introduction to Non-Associative Algebras, 1995, Dover, New York, NY, USA, ZBL0875.62584.
Google Scholar
2 Springer T. A. and Veldkamp F. D., Octonions, Jordan Algebras and Exceptional Groups, 2000, Springer, Berlin, Germany, Springer Monographs in Mathematics, ZBL1087.17001, MR1763974.
10.1007/978-3-662-12622-6
Google Scholar
3 Baez J. C., The octonions, Bulletin of the American Mathematical Society. (2002) 39, no. 2, 145–205, https://doi.org/10.1090/S0273-0979-01-00934-X, ZBL1026.17001, MR1886087.
10.1090/S0273-0979-01-00934-X
Web of Science® Google Scholar
4 Finkelstein D., Quantum Relativity: A Synthesis of the Ideas of Einstein and Heisenberg, 1996, Springer, Berlin, Germany, MR1384538.
10.1007/978-3-642-60936-7
Google Scholar
5 Emch G., Algebraic Methods in Statistical Mechanics and Quantum Field Theory, 1972, John Wiley & Sons, New York, NY, USA.
Google Scholar
6 Gürsey F. and Tze C., On the Role of Division, Jordan and Related Algebras in Particle Physics, 1996, World Scientific, Singapore, MR1626607.
10.1142/3282
Google Scholar
7 Lõhmus J., Paal E., and Sorgsepp L., Nonassociative Algebras in Physics, 1994, Hadronic Press, Palm Harbor, Fla, USA, MR1320709.
10.29083/Monograph1
Google Scholar
8 Günaydin M. and Gürsey F., Quark statistics and octonions, Journal of Mathematical Physics. (1973) 14, no. 11, 1651–1667.
10.1063/1.1666240
Web of Science® Google Scholar
9 Günaydin M. and Gürsey F., Quark statistics and octonions, Physical Review D. (1974) 9, no. 12, 3387–3391, https://doi.org/10.1103/PhysRevD.9.3387.
10.1103/PhysRevD.9.3387
CAS Web of Science® Google Scholar
10 Adler S. L., Quaternionic chromodynamics as a theory of composite quarks and leptons, Physical Review D. (1980) 21, no. 10, 2903–2915, https://doi.org/10.1103/PhysRevD.21.2903.
10.1103/PhysRevD.21.2903
CAS Web of Science® Google Scholar
11 Morita K., Octonions, quarks and QCD, Progress of Theoretical Physics. (1981) 65, no. 2, 787–790.
10.1143/PTP.65.787
CAS Google Scholar
12 Kugo T. and Townsend P., Supersymmetry and the division algebras, Nuclear Physics B. (1983) 221, no. 2, 357–380, MR0709052.
10.1016/0550-3213(83)90584-9
Web of Science® Google Scholar
13 Sudbery A., Division algebras, (pseudo)orthogonal groups and spinors, Journal of Physics A. (1984) 17, no. 5, 939–955, https://doi.org/10.1088/0305-4470/17/5/018, ZBL0544.22010, MR0743176.
10.1088/0305-4470/17/5/018
Google Scholar
14 Dixon G., Derivation of the standard model, Il Nuovo Cimento B. (1990) 105, no. 3, 349–364, MR1050882, https://doi.org/10.1007/BF02726106.
10.1007/BF02726106
Google Scholar
15 De Leo S., [email protected], Quaternions for GUTs, International Journal of Theoretical Physics. (1996) 35, no. 9, 1821–1837, MR1408548, ZBL0873.15009.
10.1007/BF02302418
CAS Web of Science® Google Scholar
16 Porteous I. R., Clifford Algebras and the Classical Groups, 1995, Cambridge University Press, Cambridge, UK, MR1369094.
10.1017/CBO9780511470912
Google Scholar
17 Okubo S., Introduction to Octonions and Other Non-Associative Algebras in Physics, 1995, Cambridge University Press, Cambridge, UK, MR1356224.
10.1017/CBO9780511524479
Google Scholar
18 Lounesto P., Clifford Algebras and Spinors, 2001, Cambridge University Press, Cambridge, UK, MR1834977.
10.1017/CBO9780511526022
Web of Science® Google Scholar
19 Carrion H. L., [email protected], Rojas M., and [email protected], Toppan F., [email protected], Quaternionic and octonionic spinors. A classification, Journal of High Energy Physics. (2003) 7, no. 4, 901–928, MR1989560.
Google Scholar
20 Finkelstein D., Jauch J. M., Schiminovich S., and Speiser D., Foundations of quaternion quantum mechanics, Journal of Mathematical Physics. (1962) 3, no. 2, 207–220, MR0137500.
10.1063/1.1703794
Web of Science® Google Scholar
21 Horwitz L. P. and Biedenharn L. C., Quaternion quantum mechanics: second quantization and gauge fields, Annals of Physics. (1984) 157, no. 2, 432–488, MR0768240, ZBL0558.46039.
10.1016/0003-4916(84)90068-X
CAS Web of Science® Google Scholar
22 Günaydin M., Piron C., and Ruegg H., Moufang plane and octonionic quantum mechanics, Communications in Mathematical Physics. (1978) 61, no. 1, 69–85, MR0503050, https://doi.org/10.1007/BF01609468, ZBL0409.22018.
10.1007/BF01609468
Web of Science® Google Scholar
23 De Leo S. and Rotelli P., Translations between quaternion and complex quantum mechanics, Progress of Theoretical Physics. (1994) 92, no. 5, 917–926, MR1312814.
10.1143/ptp/92.5.917
Google Scholar
24 Dzhunushaliev V., [email protected], A non-associative quantum mechanics, Foundations of Physics Letters. (2006) 19, no. 2, 157–167, MR2214389, https://doi.org/10.1007/s10702-006-0373-2, ZBL1099.81004.
10.1007/s10702-006-0373-2
Google Scholar
25 Gürsey F., Symmetries in physics (1600–1980), Proceedings of the 1st International Meeting on the History of Scientific Ideas, 1987, Barcelona, Spain, Seminario d′Història de las Cièncias, MR1116556.
Google Scholar
26 De Leo S., [email protected], Quaternions and special relativity, Journal of Mathematical Physics. (1996) 37, no. 6, 2955–2968, MR1390246, https://doi.org/10.1063/1.531548, ZBL0870.53061.
10.1063/1.531548
Web of Science® Google Scholar
27 Morita K., Quaternionic Weinberg-Salam theory, Progress of Theoretical Physics. (1982) 67, no. 6, 1860–1876.
10.1143/PTP.67.1860
CAS Google Scholar
28 Nash C. and Joshi G. C., Spontaneous symmetry breaking and the Higgs mechanism for quaternion fields, Journal of Mathematical Physics. (1987) 28, no. 2, 463–467, MR0872029.
10.1063/1.527627
CAS Web of Science® Google Scholar
29 Adler S. L., Quaternion Quantum Mechanics and Quantum Field, 1995, Oxford University Press, New York, NY, USA.
Google Scholar
30 Kurdgelaidze D. F., Fundamentals of nonassociative classical field theory, Soviet Physics Journal. (1986) 29, no. 11, 883–887, https://doi.org/10.1007/BF00898439.
10.1007/BF00898439
Google Scholar
31 Davies A. J. and Joshi G. C., A bimodular representation of ten-dimensional fermions, Journal of Mathematical Physics. (1986) 27, no. 12, 3036–3039, MR0866607, ZBL0614.17001.
10.1063/1.527232
Web of Science® Google Scholar
32 De Leo S. and [email protected], Rotelli P., [email protected], The quaternionic Dirac Lagrangian, Modern Physics Letters A. (1996) 11, no. 5, 357–366, MR1385639, ZBL1022.81518.
10.1142/S0217732396000400
Web of Science® Google Scholar
33 Bernevig B. A., Hu J., Toumbas N., and Zhang S.-C., Eight-dimensional quantum hall effect and “octonions”, Physical Review Letters. (2003) 91, no. 23, 236803.
10.1103/PhysRevLett.91.236803
CAS PubMed Web of Science® Google Scholar
34 SmithF. D.Jr., Spin(8) gauge field theory, International Journal of Theoretical Physics. (1986) 25, no. 4, 355–403, MR0841690, ZBL0603.58047, https://doi.org/10.1007/BF00670765.
10.1007/BF00670765
CAS Web of Science® Google Scholar
35 Pavšič M., [email protected], A novel view on the physical origin of E₈, Journal of Physics A. (2008) 41, no. 33, 332001, https://doi.org/10.1088/1751-8113/41/33/332001.
10.1088/1751-8113/41/33/332001
Google Scholar
36 Castro C., [email protected], On the noncommutative and nonassociative geometry of octonionic space time, modified dispersion relations and grand unification, Journal of Mathematical Physics. (2007) 48, no. 7, 073517, https://doi.org/10.1063/1.2752013, MR2337698, ZBL1144.81321.
10.1063/1.2752013
Web of Science® Google Scholar
37 Fairlie D. B. and Manogue C. A., Lorentz invariance and the composite string, Physical Review D. (1986) 34, no. 6, 1832–1834, MR0857920, https://doi.org/10.1103/PhysRevD.34.1832.
10.1103/PhysRevD.34.1832
CAS Web of Science® Google Scholar
38 Chung K.-W. and Sudbery A., Octonions and the Lorentz and conformal groups of ten-dimensional space-time, Physics Letters B. (1987) 198, no. 2, 161–164, MR0919128.
10.1016/0370-2693(87)91489-4
CAS Web of Science® Google Scholar
39 Lukierski J. and [email protected], Toppan F., [email protected], Generalized space-time supersymmetries, division algebras and octonionic M-theory, Physics Letters B. (2002) 539, no. 3-4, 266–276, MR1918690, ZBL0996.17002, https://doi.org/10.1016/S0370-2693(02)02073-7.
10.1016/S0370-2693(02)02073-7
CAS Web of Science® Google Scholar
40 Boya L., GROUP 24: Physical and Mathematical Aspects of Symmetries, 2002, CRC Press, Paris, France.
Google Scholar
41 Gogberashvili M., [email protected], Octonionic electrodynamics, Journal of Physics A. (2006) 39, no. 22, 7099–7104, MR2233274, ZBL1122.78001, https://doi.org/10.1088/0305-4470/39/22/020.
10.1088/0305-4470/39/22/020
Google Scholar
42 Gogberashvili M., [email protected], Octonionic version of Dirac equations, International Journal of Modern Physics A. (2006) 21, no. 17, 3513–3523, MR2250518, ZBL1095.81022, https://doi.org/10.1142/S0217751X06028436.
10.1142/S0217751X06028436
CAS Web of Science® Google Scholar
43 Gogberashvili M., [email protected], Octonionic geometry, Advances in Applied Clifford Algebras. (2005) 15, no. 1, 55–66, MR2236624, ZBL1110.51300, https://doi.org/10.1007/s00006-005-0003-2.
10.1007/s00006-005-0003-2
Google Scholar
44 Amelino-Camelia G., Relativity in spacetimes with short-distance structure governed by an observer-independent (Planckian) length scale, International Journal of Modern Physics D. (2002) 11, no. 1, 35–59, MR1883132, ZBL1062.83500, https://doi.org/10.1142/S0218271802001330.
10.1142/S0218271802001330
Web of Science® Google Scholar
45 Magueijo J. and Smolin L., Lorentz invariance with an invariant energy scale, Physical Review Letters. (2002) 88, no. 19, 190403.
10.1103/PhysRevLett.88.190403
CAS PubMed Web of Science® Google Scholar
46 Manogue C. A. and [email protected], Schray J., [email protected], Finite Lorentz transformations, automorphisms, and division algebras, Journal of Mathematical Physics. (1993) 34, no. 8, 3746–3767, MR1230549, ZBL0797.53075.
10.1063/1.530056
Web of Science® Google Scholar
47 Beckers J., Hussin V., and Winternitz P., Nonlinear equations with superposition formulas and the exceptional group G₂. I. Complex and real forms of g₂ and their maximal subalgebras, Journal of Mathematical Physics. (1986) 27, no. 9, 2217–2227, MR0854752, https://doi.org/10.1063/1.526993.
10.1063/1.526993
Web of Science® Google Scholar
48 Beckers J., Hussin V., and Winternitz P., Nonlinear equations with superposition formulas and the exceptional group G₂. II. Classification of the equations, Journal of Mathematical Physics. (1987) 28, no. 3, 520–529, MR0877223, https://doi.org/10.1063/1.527636.
10.1063/1.527636
Web of Science® Google Scholar
49 Zorn M., The automorphisms of Cayley′s non-associative algebra, Proceedings of the National Academy of Sciences of the United States of America. (1935) 21, no. 6, 355–358, ZBL0011.38903.
10.1073/pnas.21.6.355
CAS PubMed Google Scholar

Citing Literature

All articles

Rotations in the Space of Split Octonions

Abstract

1. Introduction

2. Octonionic Geometry

3. Rotations

4. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Rotations in the Space of Split Octonions

Abstract

1. Introduction

2. Octonionic Geometry

3. Rotations

4. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information