A discrete version of particle swarm optimization (DPSO) is employed to solve uncapacitated facility location (UFL) problem which is one of the most widely studied in combinatorial optimization. In addition, a hybrid version with a local search is defined to get more efficient results. The results are compared with a continuous particle swarm optimization (CPSO) algorithm and two other metaheuristics studies, namely, genetic algorithm (GA) and evolutionary simulated annealing (ESA). To make a reasonable comparison, we applied to same benchmark suites that are collected from OR-library. In conclusion, the results showed that DPSO algorithm is slightly better than CPSO algorithm and competitive with GA and ESA.

1. Introduction

Efficient supply chain management has led to increased profit, increased market share, reduced operating cost, and improved customer satisfaction for many businesses. One strategic decision in supply chain management is facility location [1]. Location problems are classified into categories with some assumptions such as limiting the capacity and open number of sites. The uncapacitated facility location (UFL) problem assumes the cost of satisfying the client requirements has two components: a fixed cost of setting up a facility in a given site, and a transportation cost of satisfying the customer requirements from a facility. The capacities of all the facilities are assumed to be infinite [2].

1.1. Literature Review

There are many different titles for the UFL problem in the literature: the problem of a nonrecoverable tools optimal system [3], the standardization and unification problem [4], the location of bank accounts problem [5], warehouse location problem [6], uncapacitated facility location problem [7], and so on. The academic interest to investigate this mathematical model reasoned different interpretations. UFL problem is one of the most widely studied problems in combinatorial optimization problems thus there is a very rich literature in operations research (OR) for this kind of problem [8]. All important approaches relevant to UFL problems can be classified into two main categories: exact algorithms and metaheuristics-based methods.

There is a variety of exact algorithms to solve the UFL problem, such as branch and bound [6, 9], linear programming [10], Lagrangean relaxation algorithms [11], dual approach (DUALLOC ) of Erlenkotter [12], and the primal-dual approaches of Körkel [13]. Although Erlenkotter [12] developed this dual approach as an exact algorithm, it can also be used as a heuristic to find good solutions. It is obvious that since the UFL problem is NP-hard [14], exact algorithms may not be able to solve large practical problems efficiently. There are several studies to solve UFL problem with heuristics and metaheuristics methods. Alves and Almeida [15] proposed a simulated annealing algorithms and reported they produce high-quality solutions, but quite expensive in computation times. A new version of evolutionary simulated annealing algorithm (ESA) called distributed ESA presented by Aydin and Fogarty [16]. They stated that with implementing it they get good quality of solutions within short times. Another popular metaheuristic, tabu search algorithm, is applied by Al-Sultan and Al-Fawzan in [17]. Their application produces good solutions, but takes significant computing time and limits the applicability of the algorithm. Michel and Van Hentenryck [18] also applied tabu search and their proposed algorithm generates more robust solutions. Sun [19] examined tabu search procedure against the Lagrangean method and heuristic procedures reported by Ghosh [2]. Genetic algorithms (GA) are also applied by Kratica and Jaramillo [20, 21]. Finally, there are also artificial neural network approaches to solve UFL problems in Gen et al. [22] and Vaithyanathan et al. [23].

The particle swarm optimization (PSO) is one of the recent metaheuristics invented by Eberhart and Kennedy [24] based on the metaphor of social interaction and communication such as bird flocking and fish schooling. On one hand, it can be counted as an evolutionary method with its way of exploration via neighborhood of solutions (particles) across a population (swarm) and exploiting the generational information gained. On the other hand, it is different from other evolutionary methods in such a way that it has no evolutionary operators such as crossover and mutation. Another advantage is its ease of use with fewer parameters to adjust. In PSO, the potential solutions, the so-called particles, move around in a multidimensional search space with a velocity, which is constantly updated by the particle′s own experience and the experience of the particle′s neighbors or the experience of the whole swarm. PSO has been successfully applied to a wide range of applications such as function optimization, neural network training [25], task assignment [26], and scheduling problem [27, 28].

Since PSO is developed for continuous optimization problem initially, most existing PSO applications are resorting to continuous function value optimization [29–32]. Recently, a few researches applied PSO for discrete combinatorial optimization problems [26–28, 33, 34, 35, 36, 37].

1.2. UFL Problem Definition

In a UFL problem, there are a number of customers, m, to be satisfied by a number of facilities, n. Each facility has a fixed cost, fc_j. A transport cost, c_ij, is accrued for serving customer, i, from facility, j. There is no limit of capacity for any candidate facility and the whole demand of each customer has to be assigned to one of the facilities. We are asked to find the number of facilities to be established and specify those facilities such that the total cost will be minimized (1). The mathematical formulation of the problem can be stated as follows [14]:

()

subject to

()

where i = 1, …, m; j = 1, …, n; x_ij represents the quantity supplied from facility i to customer j; y_j indicates whether facility j is established (y_j = 1) or not (y_j = 0).

Constraint (2) makes sure that all customers demands have been met by an open facility and (3) is to keep integrity. Since it is assumed that there is no capacity limit for any facility, the demand size of each customer is ignored, and therefore (2) established without considering demand variable.

It is obvious that since the main decision in UFL is opening or closing facilities, UFL problems are classified in discrete problems. On the other hand, PSO is mainly designed for continuous problem thus it has some drawbacks when applying PSO for a discrete problem. This tradeoff increased our curiosity to apply PSO algorithm for solving UFL problem.

The organization of the paper is as follows: in Section 2, the implementation of both continuous and discrete PSO algorithms for UFL problem is given with the details of how a local search procedure is embedded. Section 3 reports the experimental settings and results. There are three sets of comparisons: the first is between CPSO and DPSO algorithms; the second is between CPSO with local search (CPSO_LS) and DPSO with local search (DPSO_LS) algorithms; and the third is among DPSO_LS with two other algorithms from the literature. Finally, Section 4 provides with the conclusion.

2. PSO Algorithms for UFL Problem

As mentioned Section 1, PSO is one of the population-based optimization technique inspired by nature. It is a simulation of social behaviour of a swarm, that is, bird flocking, fish schooling. Suppose the following scenario: a flock of bird is randomly searching for food in an area, where there is only one piece of food available and none of them knows where it is, but they can estimate how far it would be at each iteration. The problem here is “what is the best strategy to find and get the food?”. Obviously, the simplest strategy is to follow the bird known as the nearest one to the food. PSO inventers were inspired of such natural process-based scenarios to solve the optimization problems. In PSO, each single solution, called a particle, is considered as a bird, the group becomes a swarm (population) and the search space is the area to explore. Each particle has a fitness value calculated by a fitness function, and a velocity of flying towards the optimum, the food. All particles fly across the problem space following the particle nearest to the optimum. PSO starts with initial population of solutions, which is updated iteration-by-iteration. Therefore, PSO can be counted as an evolutionary algorithm besides being a metaheuristics method, which allows exploiting the searching experience of a single particle as well as the best of the whole swarm.

2.1. Continuous PSO Algorithm for UFL Problem

The continuous particle swarm optimization (CPSO) algorithm used here is proposed by the authors, Sevkli and Guner [33]. The CPSO considers each particle has three key vectors: position (X_i), velocity (V_i), and open facility (Y_i). X_i denotes the ith position vector in the swarm, X_i = [x_i1, x_i2, x_i3, …, x_in], where x_ik is the position value of the ith particle with respect to the kth dimension (k = 1, 2, 3, …n). V_i denotes the ith velocity vector in the swarm, V_i = [v_i1, v_i2, v_i3, …, v_in], where v_ik is the velocity value of the ith particle with respect to the kth dimension. Y_i represents the opening or closing facilities based on the position vector (X_i), Y_i = [y_i1, y_i2, y_i3, …, y_in], where y_ik represents opening or closing kth facility of the ith particle. For an n-facility problem, each particle contains n number of dimensions.

Initially, the position and the velocity vectors are generated as continuous uniform random variables, using the following rules:

()

where x_min⁡ = −10.0, x_max⁡ = 10.0, v_min⁡ = −4.0, v_max⁡ = 4.0 which are consistent with the literature [38], and r₁ and r₂ are uniform random numbers in [0, 1] for each dimension and particle. The position vector X_i = [x_i1, x_i2, x_i3, …, x_in] corresponds to the continuous position values for the n facilities, but it does not represent a candidate solution to calculate a total cost (fitness value). In order to create a candidate solution, a particle, the position vector is converted to a binary variable, Y_i ← X_i, which is also a key element of a particle. In other words, a continuous set is converted to a discrete set for the purpose of creating a candidate solution, particle. The fitness of the ith particle is calculated by using open facility vector (Y_i). For simplicity, let f_i(Y_i ← X_i) be denoted as f_i.

In order to ascertain how to derive an open facility vector from position vector, an instance of 5-facility problem is illustrated in Table 1. Position values are converted to binary variables using following formula:

()

Table 1. An illustration of deriving open facility vector from position vector for a 6-customer 5-facility problem.

ith particle vectors	Particle dimension (k)
	1	2	3	4	5

Position vector (X_i)	1.8	3.01	−0.99	0.72	−5.45
Velocity vector (V_i)	−0.52	2.06	3.56	2.45	−1.44
Open facility vector (Y_i)	1	1	0	0	1

In (5), the absolute value of a position value is first divided by 2 and then the remainder is floored to nearest integer number. Then it is assigned to corresponding element of the open facility vector. For example, fifth element of the open facility vector, y₅, can be calculated as follows:

()

Considering the 5-facility to 6-customer example shown in Table 2, the total cost of open facility vector (Y_i) can be calculated as follows:

Table 2. An example of 5-facility to 6-customer.

Facility locations		1	2	3	4	5

Fixed cost		12	5	3	7	9

Customers	1	2	3	6	7	1
	2	0	5	8	4	12
	3	11	6	14	5	8
	4	19	18	21	16	13
	5	3	9	8	7	10
	6	4	7	9	6	0

()

For each particle in the swarm, let define P_i = [p_i1, p_i2, …, p_in], as the personal best, where p_ik denotes the position value of the ith personal best with respect to the kth dimension. The personal bests are determined just after generating Y_i vectors and their corresponding fitness values. In every generation, the personal best of each particle is updated based on its position vector and fitness value. Regarding the objective function, f_i(Y_i ← X_i), the fitness values for the personal best of the ith particle, P_i, is denoted by . At the beginning, the personal best values are equal to position values (P_i = X_i), explicitly P_i = [p_i1 = x_i1, p_i2 = x_i2, p_i3 = x_i3, …, p_in = x_in] and the fitness values of the personal bests are equal to the fitness of positions, .

Then the best particle in the whole swarm is selected as the global best. G = [g₁, g₂, g₃, …, g_n] denotes the best position of the globally best particle, f_g = f(Y ← G), achieved so far in the whole swarm. At the beginning, global best fitness value is determined as the best of personal bests over the whole swarm, , with its corresponding position vector X_g, which is to be used for G = X_g, where G = [g₁ = x_g1, g₂ = x_g2, g₃ = x_g3, …, g_n = x_gn] and corresponding Y_g = [y_g1, y_g2, y_g3, …, y_gn] denotes the open facility vector of the global best found.

The velocity of each particle is updated based on its personal best and the global best in the following way:

()

where w is the inertia weight used to control the impact of the previous velocities on the current one , t is generation index, r₁ and r₂ are different random numbers for each dimension and particle in [0, 1], and c₁ and c₂ are the learning factors which are also called social and cognitive parameters. The next step is to update the positions.

()

After updating position values for all particles, the corresponding open facility vectors can be determined by their fitness values in order to start a new iteration if the predetermined stopping criterion has not met yet. In this study, we employed the gbest model of Kennedy et al. [38] for CPSO , which is elaborated in the pseudocode given below.

2.2. Discrete PSO Algorithm for UFL Problem

The discrete PSO (DPSO) algorithm used here is first proposed by Pan et al. [37] for the no-wait flowshop scheduling problem. We employed the DPSO algorithm for UFL problem. In DPSO, each particle is based on only the open facility vector Y_i = [y_i1, y_i2, y_i3, …, y_in], where y_ik represents opening or closing kth facility of the ith particle. For an n-facility problem, each particle contains n number of dimensions. The dimensions of Y_i are binary random numbers. The fitness of the ith particle is calculated by f_i(Y_i).

The open facility vector (Y_i) of the particle i at iteration t can be updated as follows [37]:

()

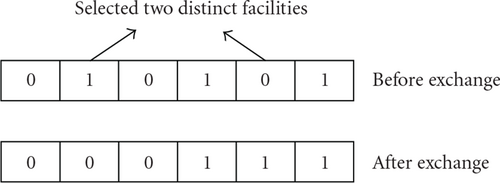
Equation (10) consists of three components: the first component (11) is the velocity of the particle. F₁ represents the exchange operator (Figure 1) which is selecting two distinct facilities from the open facility vector, , of particle and swapping randomly with the probability of w . In other words, a uniform random number, r, is generated between 0 and 1. If r is less than w then the exchange operator is applied to generate a perturbed Y_i vector of the particle by , otherwise current Y_i is kept as .

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Exchange operator.

()

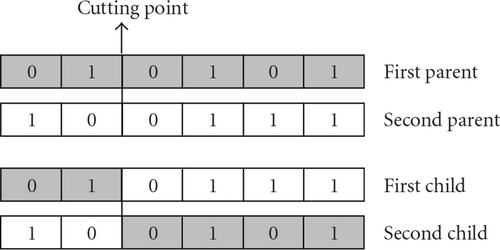
The second component (12) is the cognition part of the particle representing particle’s own experience. F₂ represents the one-cut crossover (Figure 2) with the probability of c₁. Note that and will be the first and second parents for the crossover operator, respectively. It is resulted either in or in depending on the choice of a uniform random number

()

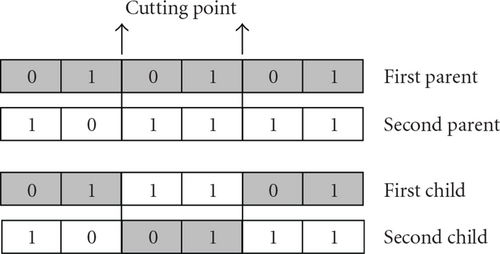
The third component (13) is the social part of the particle representing experience of whole swarm. F₃ represents the two-crossover (Figure 3) operator with the probability of c₂. Note that and G^t−1 will be the first and second parents for the crossover operator, respectively. It is resulted either in or in depending on the choice of a uniform random number. In addition, one-cut and two-cut crossovers produce two children. In this study, we selected one of the children randomly.

The corresponding Y_i vectors are determined with their fitness values so as to start a new iteration if the predetermined stopping criterion has not met yet. We apply the gbest model of Kennedy and Eberhart for DPSO. The pseudocode of DPSO is given in Algorithm 2.

Algorithm 1: Pseudocode of CPSO algorithm for UFL problem.

Begin
Initialize particles (population) randomly
For each particle
Calculate open facility vectors (1)
Calculate fitness value using open facility vector
Set to position vector and fitness value
as personal best ()
Select the best particle and its position
vector as global(G^t)
End
Do {
Update inertia weight
For each particle
Update velocity (8)
Update position(9)
Find open facility vectors
Calculate fitness value using open
facility vector (1)
Update personal best()
Update the global best (G^t) value with
position vector
End
Apply local search (for CPSO_LS) to global best
} While (Maximum Iteration is not reached)
End

Algorithm 2: Pseudocode of DPSO algorithm for UFL problem.

Begin
Initialize open facility vector
Calculate fitness value using Y_i(1)
Do
Find personal best ()
Find global best (G^t)
For Each Particle
Apply velocity component (11)
Apply cognition component (12)
Apply social component (13)
Calculate fitness value using Y_i(1)
Apply local search (for DPSO_LS)
to global best
While (Maximum Iteration is not reached)
End

2.3. Local Search for CPSO and DPSO Algorithm

Apparently, CPSO and DPSO conduct such a rough search that they produce premature results, which do not offer satisfactory solutions. For this reason, it is inevitable to embed a local search algorithm to CPSO and DPSO so as to produce more satisfactory solutions. In this study, we have applied a simple local search method to neighbours of the global best particle in every generation. In CPSO global best has three vectors, so local search is applied to the position vector (X_i). Since DPSO has one vector. Local search is applied only this vector (Y_i).

The neighbourhood structure with which neighbour solutions are determined to move is one of the key elements in metaheuristics. The performance of the hybrid algorithm depends on the efficiency of the neighbourhood structure. For both algorithms, flip operator is employed as a neighbourhood structure. It is defined as: picking randomly one position value (i) of the global best, then changing its value with using formula (14) for CPSO_LS and formula (15) for DPSO_LS. Since binary and continuous values are stored in Y_i and X_i vectors, respectively, the equations are slightly different

()

The local search algorithm applied in this study is sketched in Algorithm 3. The global best found at the end of each iteration of CPSO and DPSO is adopted as the initial solution by the local search algorithm. In order not to lose the best found and to diversify the solution, the global best is modified with two facilities (η and κ) which are randomly chosen. Then flip operator is applied to as long as it gets a better solution. The final produced solution, s, is replaced with the old global best if its fitness value is better than the initial one.

Algorithm 3: Pseudocode for local search.

Begin
Set globalbest open facility vector (Yg)
to s0 (for DPSO_LS)
Set globalbest position vector (Xg)
to s0 (for CPSO_LS)
Modify s0 based on η,κ and set to s
Set 0 to loop
Repeat:
Apply Flip to s and get s1
if (f(s1)≤f(s0))
Replace s with s1
else
loop = loop + 1
Until loop < n is false.
if (f(s)≤f(s0)) Replace Yg with s (for DPSO_LS)
if (f(s)≤f(s0)) Replace Xg with s (for CPSO_LS)
End.

3. Experimental Results

The experimental study has been completed in three stages; first, we compared the CPSO and DPSO algorithms without local search, then we compared these algorithms with local search (CPSO_LS and DPSO_LS) with respect to their solution quality; finally, DPSO_LS results are compared with other two metaheuristics, namely, genetic algorithm (GA) and evolutionary simulated annealing algorithm (ESA). Experimental results provided in this section are carried out over 15 benchmark problems well-known by the researchers of UFL problem . The benchmarks are undertaken from the OR library [39], a collection of benchmarks for operations research (OR) studies. There are currently 15 UFL test problems in the OR-library. Among these test problems, 12 are relatively small in size ranging from m × n = 50 × 16 to m × n = 50 × 50. The other three are relatively large with m × n = 1000 × 100. The benchmarks are introduced in Table 3 with their optimum values. Although the optimum values are known, it is really hard to hit the optima in every attempt of optimization. Since the main idea is to test the performance of CPSO and DPSO algorithm with UFL benchmark, the results of both algorithms are provided in Table 4 as the solution quality: average relative percent error (ARPE),hit to optimum rate, (HR) and average computational processing time (ACPU) in seconds . ARPE is the percentage of difference from the optimum and defined as following:

()

where H_i denotes the ith replication solution value, U is the optimal value provided in the literature, and R is the number of replications. HR provides the ratio between the number of runs yielded the optimum and the total numbers of experimental trials.

Table 3. Benchmarks tackled with the sizes and the optimum values.

Benchmarks
Problems	Size (m × n)	Optimum

Cap71	16×50	932615.75
Cap72	16×50	977799.40
Cap73	16×50	1010641.45
Cap74	16×50	1034976.98
Cap101	25×50	796648.44
Cap102	25×50	854704.20
Cap103	25×50	893782.11
Cap104	25×50	928941.75
Cap131	50×50	793439.56
Cap132	50×50	851495.33
Cap133	50×50	893076.71
Cap134	50×50	928941.75
CapA	100×1000	17156454.48
CapB	100×1000	12979071.58
CapC	100×1000	11505594.33

Table 4. Experimental results gained for CPSO and DPSO without local search.

	CPSO			DPSO
Problem	ARPE	HR	ACPU	ARPE	HR	ACPU

Cap71	0.026	0.83	0.1218	0.000	1.00	0.0641
Cap72	0.050	0.83	0.1318	0.000	1.00	0.0651
Cap73	0.034	0.73	0.1865	0.000	1.00	0.0708
Cap74	0.095	0.00	0.1781	0.000	1.00	0.0693
Cap101	0.183	0.00	0.8818	0.000	1.00	0.3130
Cap102	0.135	0.33	0.7667	0.000	1.00	0.3062
Cap103	0.145	0.00	0.9938	0.000	1.00	0.3625
Cap104	0.286	0.60	0.6026	0.002	0.93	0.2021
Cap131	0.911	0.00	3.6156	0.173	0.13	2.5464
Cap132	0.756	0.00	3.5599	0.090	0.17	2.6328
Cap133	0.496	0.00	3.7792	0.042	0.43	2.5292
Cap134	0.691	0.23	3.3333	0.000	1.00	1.7167
CapA	21.242	0.00	29.5739	8.654	0.00	24.8972
CapB	10.135	0.00	27.1318	4.918	0.00	22.0652
CapC	8.162	0.00	27.6149	4.545	0.00	23.1340

Obviously, the higher the HR the better quality of solution, while the lower the ARPE the better quality. The computational time spent for CPSO [33] and DPSO cases are obtained as time to get best value over 1000 iterations, while for CPSO_LS and DPSO_LS cases are obtained as time to get best value over 250 iterations. All algorithms and other related software were coded with Borland C++ Builder 6 and run on an Intel Centrino 1.7 GHz PC with 512 MB memory.

There are fewer parameters used for the DPSO and DPSO_LS algorithms and they are as follows: the size of the population (swarm) is the number of facilities, the social and cognitive probabilities, c₁ and c₂, are set as c₁=c₂ = 0.5, and inertia weight, w, is set to 0, 9. Each problem solution run is conducted for 30 replications. There were two termination criteria that have been applied for every run: first, one is getting the optimum solution, the other is reaching the maximum iteration number that is chosen for obtaining the result in a reasonable CPU time.

The performance of CPSO algorithm looks not very impressive as the results produced within the range of time over 1000 iterations. The CPSO search found 6 optimal solutions, whereas the DPSO algorithm found 12 among 15 benchmark problems. The ARPE index which is expected lower for good solution quality is very high for CPSO when applied CapA, CapB, and CapC benchmarks and none of the attempts for these benchmarks hit the optimum value. As come to the ARPE index of DPSO, it is better than the ARPE index of CPSO, but not satisfactory as expected. In term of CPU, DPSO is better than CPSO as well. When the results are investigated statistically with using the t-test with 99% levels of confidence, the DPSO produced significantly better fitness results than CPSO when CapA, CapB, and CapC fitness results are excluded. It may be possible to improve the solutions quality by carrying on with algorithms for a further number of iterations, but, then the main idea and useful motivation of employing the heuristics, that is, getting a better quality within shorter time, will be lost. This fact imposed that it is essential to empower CPSO and DPSO with hybridizing with a local search algorithm. Thus a simple local search algorithm is employed in this case for that purpose, as mentioned before.

The results of CPSO_LS and DPSO_LS are shown in Table 5. The performance of CPSO_LS and DPSO_LS looks very impressive compared to the CPSO and the DPSO algorithms with respect of all three indexes. HR is 1.00 which means 100% of the runs yield with optimum for all benchmark except CapB and CapC for CPSO_LS and except CapA, CapB, and CapC for DPSO_LS. On the other hand, it should be mentioned that DPSO_LS found optimum solutions of all instances, while CPSO_LS found optimums except for CapC. The ARPE index results of CPSO_LS and DPSO_LS are very small for both algorithms and very similar to each other thus there is no meaningful difference. When the results are compared statistically with using the t-test with 99% levels of confidence, the CPSO_LS and DPSO_LS can be considered as equal. In term of CPU, CPSO_LS consumed 18% more time than DPSO_LS thus we can say that the results of DPSO_LS are slightly better than CPSO_LS.

Table 5. Experimental results of CPSO_LS and DPSO_LS.

	CPSO_LS			DPSO_LS
Problem	ARPE	HR	ACPU	ARPE	HR	ACPU

Cap71	0.000	1.00	0.0146	0.000	1.00	0.0130
Cap72	0.000	1.00	0.0172	0.000	1.00	0.0078
Cap73	0.000	1.00	0.0281	0.000	1.00	0.0203
Cap74	0.000	1.00	0.0182	0.000	1.00	0.0109
Cap101	0.000	1.00	0.1880	0.000	1.00	0.1505
Cap102	0.000	1.00	0.0906	0.000	1.00	0.0557
Cap103	0.000	1.00	0.2151	0.000	1.00	0.1693
Cap104	0.000	1.00	0.0370	0.000	1.00	0.0344
Cap131	0.000	1.00	1.4281	0.000	1.00	0.4922
Cap132	0.000	1.00	1.0245	0.000	1.00	0.2745
Cap133	0.000	1.00	1.3651	0.000	1.00	0.4516
Cap134	0.000	1.00	0.3635	0.000	1.00	0.0594
CapA	0.037	1.00	16.3920	0.051	0.53	14.5881
CapB	0.327	0.63	19.6541	0.085	0.40	17.6359
CapC	0.091	0.00	17.4234	0.036	0.13	15.7685

The experimental study is also carried out as a comparative work in Table 6. A genetic algorithm (GA) introduced by Jaramillo et al. [21] and an evolutionary simulated annealing algorithm (ESA) proposed by Aydin and Fogarty [16] are taken for the comparison. These algorithms were coded and run under the same condition with the DPSO_LS algorithm. The performance of DPSO_LS algorithm looks slightly better than GA in both two indexes. Especially, in respect of CPU time DPSO_LS much more better than GA. Comparing with ESA, both algorithms deviations from optimum are very similar. However, especially for CapA, CapB, and CapC; GA and ESA consume more CPU time than DPSO_LS algorithm.

Table 6. Summary of results gained from different algorithms for comparison.

	Deviation from optimum [33]			Average CPU
Problem	GA [21]	ESA [16]	DPSO_LS	GA [21]	ESA [16]	DPSO_LS

Cap71	0.00	0.00	0.000	0.287	0.041	0.0130
Cap72	0.00	0.00	0.000	0.322	0.028	0.0078
Cap73	0.00033	0.00	0.000	0.773	0.031	0.0203
Cap74	0.00	0.00	0.000	0.200	0.018	0.0109
Cap101	0.00020	0.00	0.000	0.801	0.256	0.1505
Cap102	0.00	0.00	0.000	0.896	0.098	0.0557
Cap103	0.00015	0.00	0.000	1.371	0.119	0.1693
Cap104	0.00	0.00	0.000	0.514	0.026	0.0344
Cap131	0.00065	0.00008	0.000	6.663	2.506	0.4922
Cap132	0.00	0.00	0.000	5.274	0.446	0.2745
Cap133	0.00037	0.00002	0.000	7.189	0.443	0.4516
Cap134	0.00	0.00	0.000	2.573	0.079	0.0594
CapA	0.00	0.00	0.051	184.422	17.930	14.5881
CapB	0.00172	0.00070	0.085	510.445	91.937	17.6359
CapC	0.00131	0.00119	0.036	591.516	131.345	15.7685

4. Conclusion

In this paper, one of the recent metaheuristics algorithms called DPSO is applied to solve UFL benchmark problems. The algorithm has been tested on several benchmark problem instances and optimal results are obtained in a reasonable computing time. The results of DPSO with local search (DPSO_LS) are compared with results of a CPSO [33] with local search (CPSO_LS) and two other metaheuristics approaches, namely, GA [21] and ESA [16]. It is concluded that the DPSO_LS is slightly better than the CPSO_LS and competitive with GA and ESA.

The main purpose of this paper is testing performance of CPSO and DPSO algorithms under the same condition. When compared CPSO, DPSO proves to be a better algorithm for UFL problems. It also should be noted that, since CPSO considers each particle based on three key vectors; position (X_i), velocity (V_i), and open facility (Y_i). So, CPSO allocates more memory than DPSO for each particle. In addition, to the best our knowledge, this is the first application of discrete PSO algorithm applied to the UFL problem.

References

1 Simchi-Levi D., Kaminsky P., and Simchi-Levi E., Designing and Managing the Supply Chain, Concepts, Strategies and Case Studies, 2000, McGraw-Hill, Boston, Mass, USA.
Google Scholar
2 Ghosh D., [email protected], Neighborhood search heuristics for the uncapacitated facility location problem, European Journal of Operational Research. (2003) 150, no. 1, 150–162, https://doi.org/10.1016/S0377-2217(02)00504-0.
10.1016/S0377-2217(02)00504-0
Web of Science® Google Scholar
3 Beresnev V. L., Gimady E. H., and Dementev V. T., Extremal Problems of Standardization, 1978, Nauka, Novosibirsk, Russia.
Google Scholar
4 Gimady E. H., The Choice of Optimal Scales in One Problem Class of Location or Standartization, 1970, 6th edition, Nauka, Novosibirsk, Russia, Manage Systems.
Google Scholar
5 Corneuéjols G., Fisher M. L., and Nemhauser G. L., Location of bank accounts to optimize float: an analytic study of exact and approximate algorithms, Management Science. (1977) 23, no. 8, 789–810.
10.1287/mnsc.23.8.789
Web of Science® Google Scholar
6 Khumawala B. M., An efficient branch and bound algorithm for the warehouse location problem, Management Science. (1972) 18, no. 12, B718–B733.
10.1287/mnsc.18.12.B718
Web of Science® Google Scholar
7 Krarup J. and Pruzan P. M., The simple plant location problem: survey and synthesis, European Journal of Operation Research. (1983) 12, no. 1, 36–81, https://doi.org/10.1016/0377-2217(83)90181-9.
10.1016/0377-2217(83)90181-9
Web of Science® Google Scholar
8 P. B. Mirchandani and R. L. Francis, Discrete Location Theory, 1990, Wiley-Interscience, New York, NY, USA.
Google Scholar
9 Klose A., A branch and bound algorithm for an UFLP with a side constraint, International Transactions in Operational Research. (1998) 5, no. 2, 155–168, https://doi.org/10.1111/j.1475-3995.1998.tb00111.x.
10.1111/j.1475-3995.1998.tb00111.x
Google Scholar
10 Van Roy T. J., A cross decomposition algorithm for capacitated facility location, Operations Research. (1986) 34, no. 1, 145–163.
10.1287/opre.34.1.145
Web of Science® Google Scholar
11 Barcelo J., Hallefjord Å., Fernandez E., and Jörnsten K., Lagrangean relaxation and constraint generation procedures for capacitated plant location problems with single sourcing, OR Spektrum. (1990) 12, no. 2, 79–88, https://doi.org/10.1007/BF01784983.
10.1007/BF01784983
Web of Science® Google Scholar
12 Erlenkotter D., A dual-based procedure for uncapacitated facility location, Operations Research. (1978) 26, no. 6, 992–1009.
10.1287/opre.26.6.992
Web of Science® Google Scholar
13 Köerkel M., On the exact solution of large-scale simple plant location problems, European Journal of Operational Research. (1989) 39, no. 2, 157–173, https://doi.org/10.1016/0377-2217(89)90189-6.
10.1016/0377-2217(89)90189-6
Web of Science® Google Scholar
14 Cornuéjols G., Nemhauser G. L., and Wolsey L. A., The uncapacitated facility location problem, Discrete Location Theory, 1990, John Wiley & Sons, New York, NY, USA, 119–171.
Google Scholar
15 Alves M. L. and Almeida M. T., Simulated annealing algorithm for the simple plant location problem: a computational study, Revista Investigaćão Operacional. (1992) 12.
Google Scholar
16 Aydin M. E. and [email protected], Fogarty T. C., [email protected], A distributed evolutionary simulated annealing algorithm for combinatorial optimisation problems, Journal of Heuristics. (2004) 10, no. 3, 269–292, https://doi.org/10.1023/B:HEUR.0000026896.44360.f9.
10.1023/B:HEUR.0000026896.44360.f9
Web of Science® Google Scholar
17 Al-Sultan K. S. and [email protected], Al-Fawzan M. A., A tabu search approach to the uncapacitated facility location problem, Annals of Operations Research. (1999) 86, 91–103, https://doi.org/10.1023/A:1018956213524.
10.1023/A:1018956213524
Web of Science® Google Scholar
18 Michel L. and Van Hentenryck P., [email protected], A simple tabu search for warehouse location, European Journal of Operational Research. (2004) 157, no. 3, 576–591, https://doi.org/10.1016/S0377-2217(03)00247-9.
10.1016/S0377-2217(03)00247-9
Web of Science® Google Scholar
19 Sun M., [email protected], Solving the uncapacitated facility location problem using tabu search, Computers & Operations Research. (2006) 33, no. 9, 2563–2589, https://doi.org/10.1016/j.cor.2005.07.014.
10.1016/j.cor.2005.07.014
Web of Science® Google Scholar
20 Kratica J., Tošic D., Filipović V., and Ljubić I., Solving the simple plant location problem by genetic algorithm, RAIRO Operations Research. (2001) 35, no. 1, 127–142, https://doi.org/10.1051/ro:2001107.
10.1051/ro:2001107
Web of Science® Google Scholar
21 Jaramillo J. H., Bhadury J., and Batta R., On the use of genetic algorithms to solve location problems, Computers & Operations Research. (2002) 29, no. 6, 761–779, https://doi.org/10.1016/S0305-0548(01)00021-1.
10.1016/S0305-0548(01)00021-1
Web of Science® Google Scholar
22 Gen M., [email protected], Tsujimura Y., and [email protected], Ishizaki S., [email protected], Optimal design of a star-LAN using neural networks, Computers & Industrial Engineering. (1996) 31, no. 3-4, 855–859, https://doi.org/10.1016/S0360-8352(96)00279-3.
10.1016/S0360-8352(96)00279-3
Web of Science® Google Scholar
23 Vaithyanathan S., [email protected], Burke L. I., and [email protected], Magent M. A., [email protected], Massively parallel analog tabu search using neural networks applied to simple plant location problems, European Journal of Operational Research. (1996) 93, no. 2, 317–330, https://doi.org/10.1016/0377-2217(96)00047-1.
10.1016/0377-2217(96)00047-1
Web of Science® Google Scholar
24 Eberhart R. C. and Kennedy J., New optimizer using particle swarm theory, Proceedings of the 6th International Symposium on Micro Machine and Human Science (MHS ′95), October 1995, Nagoya, Japan, 39–43, https://doi.org/10.1109/MHS.1995.494215.
10.1109/MHS.1995.494215
Google Scholar
25 Van den Bergh F. and Engelbecht A. P., Cooperative learning in neural networks using particle swarm optimizers, South African Computer Journal. (2000) 26, 84–90.
Google Scholar
26 Salman A., Ahmad I., and Al-Madani S., Particle swarm optimization for task assignment problem, Microprocessors and Microsystems. (2002) 26, no. 8, 363–371, https://doi.org/10.1016/S0141-9331(02)00053-4.
10.1016/S0141-9331(02)00053-4
Web of Science® Google Scholar
27 Allahverdi A. and [email protected], Al-Anzi F. S., [email protected], A PSO and a Tabu search heuristics for the assembly scheduling problem of the two-stage distributed database application, Computers & Operations Research. (2006) 33, no. 4, 1056–1080, https://doi.org/10.1016/j.cor.2004.09.002.
10.1016/j.cor.2004.09.002
Web of Science® Google Scholar
28 Tasgetiren M. F., [email protected], Liang Y.-C., Sevkli M., and Gencyilmaz G., A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem, European Journal of Operational Research. (2007) 177, no. 3, 1930–1947, https://doi.org/10.1016/j.ejor.2005.12.024.
10.1016/j.ejor.2005.12.024
Web of Science® Google Scholar
29 Eberhart R. C. and Shi Y., Comparison between genetic algorithms and particle swarm optimization, Evolutionary Programming VII, 1998, 1447, Springer, Berlin, Germany, 611–616, Lecture Notes in Computer Science, https://doi.org/10.1007/BFb0040812.
10.1007/BFb0040812
Google Scholar
30 Kennedy J. and Eberhart R. C., Particle swarm optimization, 4, Proceedings of IEEE International Conference on Neural Networks (ICNN ′95), November-December 1995, Perth, Australia, 1942–1948.
Google Scholar
31 Naka S., Genji T., Yura T., and Fukuyama Y., [email protected], A hybrid particle swarm optimization for distribution state estimation, IEEE Transactions on Power Systems. (2003) 18, no. 1, 60–68, https://doi.org/10.1109/TPWRS.2002.807051.
10.1109/TPWRS.2002.807051
Web of Science® Google Scholar
32 Yoshida H., Kawata K., Fukuyama Y., and Nakanishi Y., A particle swarm optimization for reactive power and voltage control considering voltage stability, Proceedings of the International Conference on Intelligent System Application to Power System (ISAP ′99), April 1999, Rio de Janeiro, Brazil, 117–121.
Google Scholar
33 Sevkli M. and Guner A. R., A continuous particle swarm optimization algorithm for uncapacitated facility location problem, Ant Colony Optimization and Swarm Intelligence, 2006, 4150, Springer, Berlin, Germany, 316–323, Lecture Notes in Computer Science, https://doi.org/10.1007/11839088_28.
10.1007/11839088_28
Google Scholar
34 Kennedy J. and Eberhart R. C., A discrete binary version of the particle swarm algorithm, 5, Proceedings of IEEE International Conference on Systems, Man and Cybernetics (SMC ′97), October 1997, Orlando, Fla, USA, 4104–4108, https://doi.org/10.1109/ICSMC.1997.637339.
10.1109/ICSMC.1997.637339
Google Scholar
35 Yin P.-Y., [email protected], A discrete particle swarm algorithm for optimal polygonal approximation of digital curves, Journal of Visual Communication and Image Representation. (2004) 15, no. 2, 241–260, https://doi.org/10.1016/j.jvcir.2003.12.001.
10.1016/j.jvcir.2003.12.001
Web of Science® Google Scholar
36 Liao C.-J., Tseng C.-T., and Luarn P., A discrete version of particle swarm optimization for flowshop scheduling problems, Computers & Operations Research. (2007) 34, no. 10, 3099–3111.
10.1016/j.cor.2005.11.017
Web of Science® Google Scholar
37 Pan Q.-K., [email protected], Tasgetiren M. F., and [email protected], Liang Y.-C., [email protected], A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem, Computers & Operations Research. (2008) 35, no. 9, 2807–2839, https://doi.org/10.1016/j.cor.2006.12.030.
10.1016/j.cor.2006.12.030
Web of Science® Google Scholar
38 Kennedy J., Eberhart R. C., and Shi Y., Swarm Intelligence, 2001, Morgan Kaufmann, San Francisco, Calif, USA.
Google Scholar
39 Beasley J. E., OR-Library, 2005, http://people.brunel.ac.uk/~mastjjb/jeb/info.html.
Google Scholar

Citing Literature

All articles

A Discrete Particle Swarm Optimization Algorithm for Uncapacitated Facility Location Problem

Abstract

1. Introduction

1.1. Literature Review

1.2. UFL Problem Definition

2. PSO Algorithms for UFL Problem

2.1. Continuous PSO Algorithm for UFL Problem

2.2. Discrete PSO Algorithm for UFL Problem

2.3. Local Search for CPSO and DPSO Algorithm

3. Experimental Results

4. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Discrete Particle Swarm Optimization Algorithm for Uncapacitated Facility Location Problem

Abstract

1. Introduction

1.1. Literature Review

1.2. UFL Problem Definition

2. PSO Algorithms for UFL Problem

2.1. Continuous PSO Algorithm for UFL Problem

2.2. Discrete PSO Algorithm for UFL Problem

2.3. Local Search for CPSO and DPSO Algorithm

3. Experimental Results

4. Conclusion

References

Citing Literature

Figures

References

Related

Information