Performance of Single and Double Shaft Disk Separators

1. Introduction

Shear-enhanced or dynamic filtration consisting of rotating disks relies on the presence of a shear stress at the filter media surface to reduce the accumulation of the particles. The reason for its good performance is that very high shear rates are produced with a low inlet flow, thereby resulting in low pressure drop in the module. In the classical cross flow filtration with membrane modules, the shear stress is linked to the feed flow rate which leads to the pressure drop. High shear stress is produced by increasing the tangential flow along the membrane surface and continuous circulation of the feed flow. In rotating filters, the shear stress and flow rate are unlinked because the shear stress is a function of the rotating filter disk. Dynamic filters which create relative motion between the filter media and the suspension producing high shear rate are compared with conventional cross flow filtration [1]. In this study, the average shear stress is estimated based on the power consumed by the rotating disk filter. Rotating disk within an enclosed housing has been investigated extensively in the past decades [2]. It was found that the hydrodynamics of the system is governed by the Reynolds number Re  = ω · r²/υ and the axial clearance s_c where ω is the rotational speed, r is the disk radius, υ is the fluid kinematics viscosity, and s_c is the axial clearance between the disk and a stationary wall.

With relatively large axial gap between the disk and a stationary wall, the boundary layers are separated by a core of fluid moving at an angular velocity of (kω_d), where k = ω_f/ω_d is a velocity coefficient and has a value of almost less than one. In recent papers [3–7], the coef-ficient k for various disks is determined by regression from peripheral pressure measurements taken on the housing rim at various angular velocities using Bernoulli’s equation. The velocity coefficient is found to be in the range 0.4-0.5 for a smooth disk. Many disks with different modification on the surface types are recently developed to increase the velocity coefficient, thereby enhancing the dynamic fil-tration performance. With eight radial vanes on the rotating disc, Schiele got k = 0.9, resulting in a dramatic in-crease of the shear stress and, of course, the power input [8].

The main objective of this study is to estimate andvalidate the average velocity coefficient, both for single and double shaft disk separators and the dynamic filtrationperformance, respectively. Additionally, we want to assess the contribution of filter overlapping by estimating the average shear stress based on electrical powerconsumption. Lastly, we would like to compare the single and double shaft disk separators based on filtration experiments.

2. Experimental Setup

Two different geometries have been used as shown in Figure 1. The first consists of five filter disks (dp = 40 μm, r_o = 45 mm, r_i = 15 mm) mounted on a single hollow shaft with axial gap between two successive filter disks s_g = 14 mm, see Figure 1(a). The second geometry consists also of five filter disks but mounted on two hollow shafts rotating with the same speed direction. The axial shear gap between two overlapped disks is s_s = 4 mm and s_g = 14 mm between nonoverlapping disks; see Figure 1(b). The whole system is placed in stainless steel housing. Permeate is collected inside each disk by a hollow shaft. The filtration unit is provided with two pressure sensors, one of which is installed inside the housing close to disk periphery while the second is mounted on the shaft where the filtrate exits. Permeate and concentrate flow rates are measured by magnetic-inductive flow meters. The filtration pressure difference can be estimated by the pressure sensors.

The filtration experiments are carried out using asuspension of sphere glass (mean particle size 10 μm), which is easy to prepare. The suspensions behave as a Newtonian fluid at low concentration (13.4 g/l).

3. Results and Discussion

3.1. Determination of Velocity Factor k with Water

The clearance inside the filter disk where the filtrate collects is small and divided in radial flow channel (about 2 mm). Therefore, the filtrate rotates as a solid body at the same rotation speed of the filter, that is, k = 1 and its pressure p_f varies as the square of angular velocity due to centrifugal force according to

$$ ()

Here, $$ denotes its pressure when it enters the hollow shaft. Its average value over the membrane area is given by integrating (1) over the membrane area as

$$ ()

In the single shaft configuration, the axial gap between two rotating filter disks is relatively large. The concentrate flow is assumed to present an inviscid core rotating at a velocity kω, where ω is the disk angular velocity and k is the average velocity coefficient. The parameter k = ω_f/ω_d is always less than 1. The concentrate radial pressure in the boundary layer is equal to the inviscid core and is given by

$$ ()

Here, $$ is the concentrate pressure inside the housing at the center, which is also equal to the pressure when the disk is at rest. By averaging the concentrate pressure over the filter surface to eliminate the radial dependence of the pressure, we can get

$$ ()

Since the permeate is collected at atmospheric pressure, the mean pressure difference along the filter surface is obtained by

$$ ()

Filtrate flow rate was measured using filter disks with average pore size 40 μm and clean water as a test fluid at various rotation speeds. The pressure $$ was measured when the filter disk at rest was 6 kPa (see Figure 2). In general, by increasing the rotation speeds permeate flux decreases due to the centrifugal forces acting on permeate side. We can determine the rotations speeds via extrapolation at which permeate flux vanish, $$, that is, the pressure difference is zero. By using (5) we will be able to estimate the average velocity coefficient $$ for the two configurations. The average velocity coefficient was found to be 0.898 and 0.875 for single and double shafts disk separator, respectively.

In order to check the consistency of the filtration data with the averaged pressure difference (5), we calculate the water filtration rate from

$$ ()

The comparison between calculated and measured filtration flow rates at various rotation speeds is plotted in Figure 3, with $$ = 0.898 and 0.875 for single and double shaft disk separators. The agreement was excellent and confirms the validity of (5) for the estimated average velocity coefficient $$ which must be independent of radial.

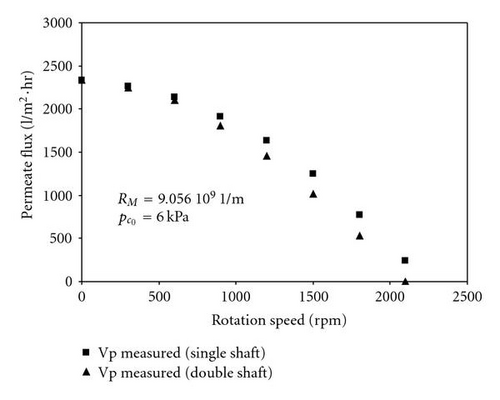
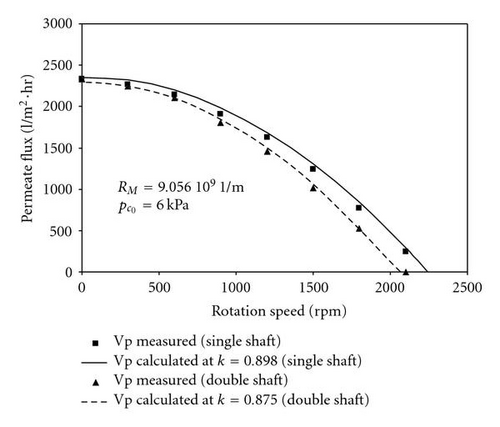
The variation of the measured filtrate flux rate with rotation speed is represented in Figure 2 for single and double shaft disk separators. The filtrate flux rate is seen to be larger using single shaft disk separator. In fact, the difference in permeate flux rate using single and double shaft disk separators refers to the average velocity coefficient $$. Thus, the coefficient $$ may also be good criteria for configuration performance with absence filter cake, since higher value of $$ will produce higher permeate flux rate according to (6). Moreover, we can expect that the torque is necessary to rotate the disk and thus the shear stress over the disks will be varied in terms of the average velocity coefficient $$.

3.2. Energetic Consideration

It is important to estimate the energy that is necessary to drive the disk especially in an industrial sized system.Therefore, we have measured the electrical power consumed by the single and double shaft disk separators under consideration. In our small scale device, a large part of the electrical power supplied is consumed by friction of the rotating shaft. Thus, to eliminate the shaft friction, we have subtracted the electrical power necessary to drive the system without disks from the power at the same speed in the filtration test (with filters). The power difference corresponds to the friction forces (shear stress) exerted by the fluid on the disks, which, in a large scale system, will be the most dominating forces. This power difference is shown in Figure 4 for clean water. It increases nonlinearly with speed and is larger for double shaft disk separators due to filter disks overlapping. The electrical efficiency for 0.75 kW motor sizes is assumed 60% at average rate (independent on the load rate). To estimate the mechanical power P_m developed by friction forces on the two sides of the disk, we use

$$ ()

where P_e is the electrical power, η the output efficiency without discs, ω the angular velocity of the motor, τ the shear stress over disk surface.

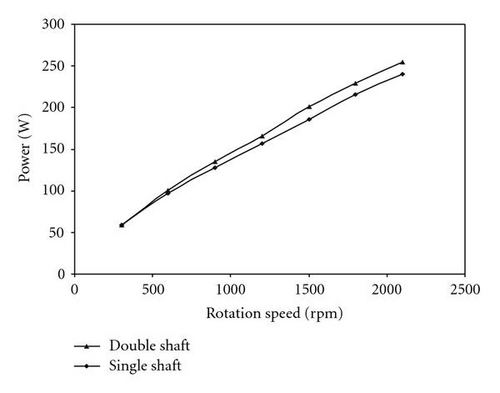
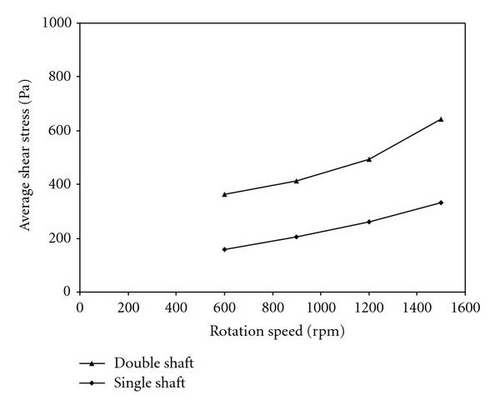
The power difference consumed by single and double shaft disk separators is converted into shear forces exerted on the disks. Thus, we were able to estimate the average shear stress over the filter surface for single and double shaft disk separators according to (7). Figure 5 shows the average shear stress for different rotation speeds using single and double shaft disk separators. It is clear that the estimated average shear stress for the double shaft filter disk is about twice as much as shear stress for the single shaft filter disk. This is due to the filter disk overlapping.

3.3. Filtration Experiments

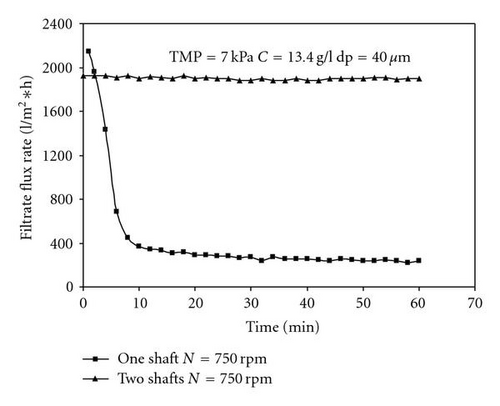
We have shown that the average shear stress for the filter disk overlapping is almost twice as large as compared to the single shaft disk separator. Thus, it is legitimate to investigate its ability in avoiding cake formation under filtration process. Therefore, filtration experiments were carried out using single and double shaft disk separators at N = 750 rpm, C = 13.4 g/l, and TMP = 7 kPa. The time dependency of the permeate flux rate were recorded for single and double shafts disk separator (Figure 6). It was found that permeate flux remains constant (steady state filtration) over time for the double shaft disk separator and decays sharply using the single shaft disk separator. The higher shear stress produced by using double shaft disk filter as shown before is mainly the reason for the free cake filter disk. The single shaft showed unsteady state filtration under the same filtration conditions. The shapes of the filter cakes, for single and double shaft disk separators, are depicted in Figure 7. The filter cake in the single shaft disk was observed to be denser and homogenously distributed over the filter surface as compared to the double shaft disk filter.

4. Conclusion

The performance of single and double shaft disk separators has been investigated. Permeate flux rate is found to decrease as the rotation speed increases for both configurations. The average velocity coefficient $$ was estimated for both configurations and also confirmed under the filtrationprocess. It was found that the average velocity coefficient $$ is thecriterion for configuration performance. Shear stress is enhanced by decreasing the average velocity coefficient. The power consumption is not only a function of rotation speed but is also affected by the filter geometry. It is possible to obtain steady state filtration (without cake formation) using double shaft disk separator.