A Markov chain approach to the study of randomly grown graphs is proposed and applied to some popular models that have found use in biology and elsewhere. For most randomly grown graphs used in biology, it is not known whether the graph or properties of the graph converge (in some sense) as the number of vertices becomes large. Particularly, we study the behaviour of the degree sequence, that is, the number of vertices with degree 0, 1, …, in large graphs, and apply our results to the partial duplication model. We further illustrate the results by application to real data.

1. Introduction

Over the past decade, networks have played a prominent role in many different disciplines including theoretical physics, technology, biology, and sociology [1–9]. Particularly in biology, networks have become fundamental for the description of complex data structures. The appeal of networks may, at least partly, be due to the fact that in addition to being based on a rigorous mathematical base [10–14], they also provide a convenient graphical representation of the data which allows for visual interpretation. Examples of complex data structures that can be described by networks include food webs in ecology, sexual partner networks in sociology, and protein interaction networks in biology.

The canonical model in random graph theory has been Erdös-Renyi random graphs, where each of a fixed number of vertices has a Poisson-distributed number of links to other vertices. A Poisson number of links have turned out barely to be realistic for many empirically observed networks, and other models have been suggested to accomodate the discrepancies between theory and observation. Barabási and Albert [2] proposed a simple stochastic model, the preferential attachment (PA) model, whereby the network gradually is built up by adding one vertex at a time until the network reaches the desired size. This model is able to account for the scale-free degree distribution that is observed in some empirical networks, but not many of the other features and motifs that are found in real networks (e.g., [15–18]). Therefore, for mathematical and statistical analysis of network data, many other stochastic models have been proposed, in particular models that fall in the class of randomly grown graphs (RGGs; see next section for a definition) which share the property of the PA model of gradual growth. Overviews of different models and their properties can be found in [13, 16, 19, 20].

While the PA model has been under close mathematical scrutiny (e.g., [20]), other RGGs have been treated less extensively (e.g., [19, 21]) and mostly in the context of considering a continuous time approximation to the original discrete time Markov process (e.g., [13, 22, 23]). In this paper, we specifically address the question of the behavior of the vertex degrees as the number of vertices grows large. For a class of RGGs (including the PA model), the existence of a limiting degree distribution has been proven and its analytical form has been derived [21]. However, for most RGGs applied in biology, it is not known whether a limiting distribution exists, letting alone its form.

Biologically, it is of great interest to know whether the network stabilizes as it grows, or whether the degree distribution is a function of the size of the network, even for large network sizes. It relates to the question whether the network in an evolutionary perspective reaches an equilibrium, such that adding new vertices does not change the overall connectivity of the network. For example, in relation to protein interaction networks where vertices represent proteins and edges represent physical interactions between proteins, both scenarios seem a priori possible. Proteins may be able to engage in an unlimited number of interactions, or the number of interactions may be restricted by a number of factors such as space, time, and protein production rates. With the increasing statistical interest in analyzing complex biological networks with respect to evolutionary and functional properties [1, 5, 9, 13, 14, 24], it is also becoming of interest to understand the mathematical properties of the models.

We study a large class of RGGs that allows the construction of a simple, but time-inhomogeneous, Markov chain. For a given RGG, the corresponding Markov chain can be used to address questions about the RGG, for example, questions about the degree distribution. In particular, we focus on a special RGG, the partial duplication model, which has recently been used in the study of biological protein interaction networks [16, 18, 25, 26] and has formed the basis for new and more biologically realistic models (e.g., [16, 27]). The partial duplication model has two parameters (p and q) and we give conditions under which the chain is ergodic or transient. Further, based on the time-inhomogeneous Markov chain, we define a time-homogeneous Markov chain and a continuous time, time-homogeneous Markov process, and demonstrate that these, in general, are easier to study and apply than the original chain. Proofs rely on general theory of discrete Markov processes, which makes it easy to prove similar results for other RGGs.

Finally, we apply our results to a collection of real protein interaction data.

2. RGGs

An RGG is a Markov chain on undirected graphs such that G_t has exactly t vertices, and the set of vertices of G_t is a subset of the set of vertices of G_t+1 for all t ≥ s. Note that we do not require the set of edges of G_t to be a subset of the set of edges of G_t+1.

Denote by n_t(k) the expected number of vertices of degree k at time t. Since, by assumption, the graph G_t has exactly t vertices, the expected relative frequency of vertices of degree k at time t is f_t(k) = n_t(k)/t. For many RGGs, one can derive a recursive formula for n_t(k), often referred to as the master equation [13]. Here, we consider a very general class of master equations given by

(2.1)

where A(t) for all t ≥ s is an infinite real matrix with A(t) _k,j = 0 for k > j + 1, and such that all columns sum to the same number a(t). Furthermore, assume for suitable real numbers b_k,j that

(2.2)

with b_k,j = 0 for k > j + 1. The latter condition guarantees that the vertex degree can increase by at most one. By construction, n_t(k) = 0 for k + 1 > t, and hence A(t) is effectively a t × (t − 1) matrix. We assume that the entries (2.2) in this submatrix are positive.

One particular example of a model fulfilling the conditions above is the partial duplication model (details are found in Section 4). The master equation is given by

(2.3)

For several other models, the master equation takes a similar form. Among these models are the duplication-divergence model [16], an approximation to the duplication-mutation model [22, 23], and the models discussed in [21] after a suitable modification (see Section 5.2). Generally, (2.1) is fulfilled whenever the expected degree change in a vertex depends on the degree only, and not on the degrees of the other vertices.

It follows immediately from (2.1) that

(2.4)

where B(t) is the transpose of (t/(t + 1))A(t), and by assumption all rows of B(t) sum to b(t) = (t/(t + 1))a(t). It follows that

(2.5)

that is, b(t) = 1 and the matrices {B(t)} _t≥s describe a Markov chain with time-dependent transition probabilities.

Proposition 2.1. Assume that ∑_k≥0b_j,k < ∞ for all j ≥ 0. If f_t(j) → f(j) pointwise for all j ≥ 0, then {f(j)} _j≥0 satisfies

(2.6)

Proof. The second part of the proposition is a simple application of Fatou′s lemma. By using (2.4), the definition of B(t), and ∑_k≥0b_j,k < ∞, it follows that

(2.7)

for some real number d_j, and it remains to prove that d_j = 0. Note that

(2.8)

and by using Cesaro′s lemma, we get

(2.9)

Consider the jump chain corresponding to the Markov chain {B(t)} _t≥s, that is, the Markov chain with transition probabilities B(t) _j,k/(1 − B(t) _j,j) for j ≠ k, unless B(t) _j,j = 1 in which case the probability is put to 0. The jump chain has time-independent transition probabilities given by

(2.10)

and p_j,j = 0 for all j ≥ 0. If 1 + b_j,j = 0, then p_j,k = 0. Occasionally, we consider a slightly modified jump chain (still with time-independent transition probabilities) which is allowed to stay in the same state with positive probability.

If a stationary distribution

for the jump chain exists, it fulfills

(2.11)

Assume that inf _j≥0(1 + b_j,j) > 0 and put

. Then we obtain that

(2.12)

and hence

is a solution to the equation in Proposition 2.1. Furthermore, we may normalize

to get a distribution, and hence (2.11) and (2.12) may be used to transfer a stationary distribution for the jump chain to the limit of the time-inhomogeneous Markov chain and vice versa.

In our main example, the partial duplication model (see Section 4 for details), we have b_0,0 = 2q − 1 and

(2.13)

and hence the assumption inf _j≥0(1 + b_j,j) > 0 is fulfilled if q > 0.

3. A Continuous Time Approximation

In this section, we show that the time-inhomogeneous Markov chain converges to a continuous time, time-homogeneous Markov process after a suitable time transformation.

Denote by T_i the time of the ith jump in the time-inhomogeneous chain after a given time t₀, and let J_i be the state to which it jumps. Set T₀ = t₀ and J₀ = j₀, the state of the chain at time t₀. To simplify notation further, introduce s_i = (t_i, j_i) and S_i = (T_i, J_i).

Note that at time t, the probability of staying in state j is B(t) _j,j = 1 − (b_j,j + 1)/(t + 1). In particular, if we let

, then

(3.1)

for large t_i−1 and t_i. Now consider the transformation Z_i = log T_i − log T_i−1 = log T_i/T_i−1. It follows that

(3.2)

as t_i−1 → ∞. That is, in the limit, the transformed waiting time is exponentially distributed with parameter α_i.

Proposition 3.1. Let , z ≥ 0, take the value of the time-inhomogeneous Markov chain at time t, where t = ⌊t₀e^z⌋ and ⌊x⌋ denotes the integer part of x. At time 0, . For fixed j₀, the process converges to a continuous time, time-homogeneous Markov process as t₀ → ∞.

Proof. Clearly, the process , z ≥ 0, is Markovian by definition. Let be the time of the ith jump, that is, and in the notation above. It follows from (3.2) that

(3.3)

for t₀ → ∞. (Subscript s₀ in

is used to underline the implicit dependency of s₀ = (t₀, j₀).) Recall the transition probabilities (2.10) in the original jump chain. It follows immediately that

(3.4)

where

. Combined with (3.3) this shows that, in the limit as t₀ → ∞, the rate of jumping to j_i from j_i−1 is β_i. More precisely, it demonstrates that

, z ≥ 0, converges to a continuous time, time-homogeneous Markov process with transition rate matrix Q = {q_j,k} _j,k≥0 given by q_j,k = b_k,j for j ≠ k, and q_j,j = −q_j = ∑_k≠jq_j,k. This sum is indeed finite because by assumption b_k,j = 0 for k > j + 1 (see Section 2).

Note that a stationary equation for the continuous-time Markov chain fulfills the equation in Proposition 2.1 with f(j) replaced by π_j.

4. The Partial Duplication Model

Consider the model , where G_s is a simple graph with s vertices, and where G_t+1 is obtained from G_t in the following way: introduce a new vertex v and choose u ∈ G_t uniformly. With probability q, connect v and u. Independently of each other, connect each neighbor of u to v with probability p.

In this section, we follow the path outlined in the previous section. That is, we first find the jump chain corresponding to the partial duplication model. As already stated in Section 1, the master equation is given by

(4.1)

It can be seen in the following way: the first term corresponds to the case where a vertex of degree k keeps its degree, and this is the case unless one of two things happens: (i) the vertex is copied and receives a link to the new vertex, or (ii) it receives a link because one of its k neighbors is copied. The probabilities of these two events are q/t and kp/t, respectively. Similarly, the third term corresponds to the case where a vertex of degree k − 1 gets a new link in one of the above-mentioned ways. The two remaining terms correspond to the cases where the new vertex has degree k. The new vertex has degree k when a vertex of degree ≥k is copied and receives exactly k links to the neighbors of the copied vertex and no link to the copied vertex, or if a vertex of degree ≥k − 1 is copied and receives a link to the copied vertex and exactly k − 1 links to the neighbors of the copied vertex.

The cases q = 0 and q = 1 have been studied in [19, 26], respectively. Note, however, that the master equation given in [26] is incorrect. For general q, the model has been discussed in [18]. It follows immediately that

(4.2)

where we, in order to simplify notation, define

(4.3)

From (4.2), we may read off the description of the matrix B(t). Its entries satisfy that

(4.4)

and B(t) _j,k = 0 otherwise. An easy calculation shows that

(4.5)

from which it follows that the probability of jumping from state j is

(4.6)

Motivated by this formula, we allow the jump chain to stay in state j with probability (1 − q)b_j(j) + qb_j(j − 1), and it follows that the transition probabilities p_j,k in the modified jump chain satisfy that

(4.7)

and p_j,k = 0 otherwise.

In particular, the chain is irreducible if and only if 0 < q < 1. If q = 0, the state 0 is absorbing, and if q = 1, the state 0 is not reachable from any other state. If state 0 is ignored, the resulting chain is irreducible for q = 1.

4.1. Classification of States

We first recall a theorem from [28]. The theorem is reformulated in [29], and we will use that formulation. If q = 1, then we ignore the state 0, and since in this case all p_j,0 are zero, the conditions stated in theorems below stay the same.

Theorem 4.1. Let be a Markov chain. If there exist a sequence of non-negative real numbers and an integer N ≥ 1 such that

(4.8)

then the chain is ultimately recurrent.

Applied to the partial duplication model the theorem states that if there is a sequence

of nonnegative real numbers with x_j → ∞ such that

(4.9)

then, if q = 0, the probability of ultimate absorption in 0 is 1. If q ≠ 0, the conclusion of the theorem is that all states are persistent.

The solution p of log (p) + p = 0, where log denotes the natural logarithm, is known as the omega constant, and we denote it by Ω. We have Ω ≈ 0.5671.

Proposition 4.2. Let p < Ω in the partial duplication model. If q = 0, the probability of ultimate absorption in 0 is 1, and if q > 0, the Markov chain is persistent.

In [26] it is claimed that for q = 0 there exists a limiting distribution different from the one we find.

Proof. Let x_j = log (j + 1). Then is a nonnegative sequence of real numbers with x_j → ∞, and hence it suffices to show that, for the choices of p and q in the proposition, the sequence satisfies (4.9). Since log is a concave function, Jensen′s inequality implies that E(log (X + 1)) ≤ log (E(X) + 1) for a positive random variable X. In particular, using this for binomially distributed random variables, we get

(4.10)

and hence we need only prove that the right-hand side of this inequality is less than or equal to log (j + 1) for j ≫ 0. This may, for j ≫ 0, be rewritten as

(4.11)

and here the first two log -terms converge to 0, while the two remaining terms converge to log (p) and p, respectively. Here we have used that

(4.12)

Note that since p < Ω by assumption, we have log (p) + p < 0, and hence the inequality in (4.11) holds for all j ≫ 0.

Since zero is the only absorbing state, it follows that for p ≥ Ω, a limiting distribution takes the form (a₀, 0, 0, …), with a₀ ≤ 1. To infer the behaviour of the Markov chain for other values of q, we first recall a result proved in [30].

Theorem 4.3. Let be an irreducible, aperiodic Markov chain. If there exist a sequence of positive real numbers and an integer N ≥ 1 with

(4.13)

then the chain is transient.

Let Φ denote the golden ratio conjugate. That is, Φ is the unique positive real number p satisfying that 1/p = p + 1. We have Φ ≈ 0.6180.

Proposition 4.4. Let q > 0 in the partial duplication model. Then the Markov chain is transient for all p > Φ.

Proof. Put x_j = 1/(j + 1) for all j ≥ 0. Then x_j > 0 for all j ≥ 0, and x_j → 0. Thus, in order to apply Theorem 4.3, we only need to verify that is a solution to the inequalities in (4.9).

It follows from a straightforward calculation that

(4.14)

such that

is a solution if the right-hand side of this inequality is less than or equal to (1 + q + jp)/(j + 1) for j ≫ 0. This is equivalent to

(4.15)

and the left-hand side converges to 1/p − p as j → ∞. Since p > Φ, it follows that 1/p − p < 1, and hence the inequality in (4.15) holds for all j ≫ 0.

Let q > 0 such that the chain is irreducible. One may ask for which p the chain is ergodic. By Proposition 4.4, a necessary condition is p < Φ. However, as we will see, this may not be sufficient. To see this, we first recall another theorem from [28].

Theorem 4.5. Let be an irreducible, aperiodic Markov chain. If there exist an N ≥ 1 and a nonnegative sequence of real numbers such that

(4.16)

then the chain is ergodic.

In the partial duplication model, the second condition in the theorem is always fulfilled since p_j,k = 0 for k > j + 1. Let X_t denote the state of the chain at time t. If there exists N ≥ 0 and ε > 0 such that

(4.17)

then this N, together with x_j = j/ε, will work in Theorem 4.5. This is pointed out in [28].

Proposition 4.6. Let q > 0. Then the Markov chain is ergodic for all p < 1/2.

Proof. We find

(4.18)

Note that p < 1/2 implies 2 − 1/p < 0, and hence 2 − 1/p ≤ −ε for all sufficiently small ε > 0. That is, for a large N, (4.17) is fulfilled.

In general, it is not an easy task to actually find the stationary distribution of the jump chain or the time-inhomogeneous Markov chain. For q = 1, an attempt to solve (2.4) has been made in [19]. They assume that converges and show that, under this assumption, the limit (for p > 0) has a power-law tail. However, this does not establish the existence of a stationary distribution. Further, the power-law they provide for p > Ω is in fact not a distribution. In the special case p = 0, the stationary distribution is π_j = (1/2) ^j for j ≥ 1.

It is natural to ask what happens for the values of p not covered in the propositions above. In general, this is difficult. However, if Ω is not the maximal upper bound in Proposition 4.2, the culprit must be the particular choice of . Indeed, the damage provided by the use of Jensen′s inequality is not severe. This may be seen in the following way: denote by μ_k(j) the kth central moment of a binomially distributed random variable X with parameters j and p. From [31], we get μ_k(j) = O(j^−k/2), and by expanding log (X + 1) as a Taylor series around jp, it follows that E[log (X + 1)] = log (jp + 1) + O(j⁻¹).

4.2. Application to Protein Interaction Networks

We used the computer program developed for [18] to estimate the parameters under the partial duplication model for different protein interaction networks. The Plasmodium falciparum (P. falciparum) dataset is obtained from [32], and the remaining datasets are downloaded from the Database of Interacting Proteins (http://dip.doe-mbi.ucla.edu). Curiously, we note that according to Proposition 4.6, all pairs of p and q correspond to ergodic Markov chains, indicating that the networks stabilize as the number of vertices becomes large.

For one of the networks, P. falciparum, we conducted some further experiments where 50 networks were simulated with the same number of vertices as in P. falciparum (1271) and the degree distribution was computed. All simulations were started from an initial network of two vertices connected by an edge. Furthermore, 1271 runs of the corresponding Markov chain were performed, and the degree distribution was calculated and compared to the degree distribution obtained from the simulated networks. Here, the initial state of the Markov chain is 1. The length of the runs was varied, as shown in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Shown is the distribution of vertex degrees of 50 simulated networks (solid) and that of numbers simulated from the corresponding Markov chain (dashed), using parameters estimated for the *P. falciparum* dataset. In addition, the observed degree distribution for *P. falciparum* is shown (dot-dashed).

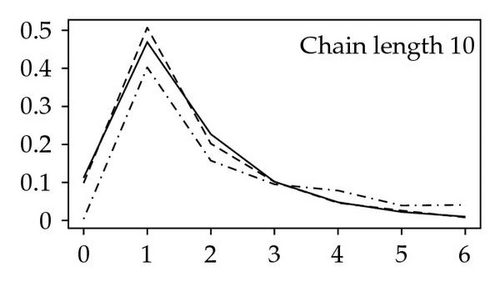
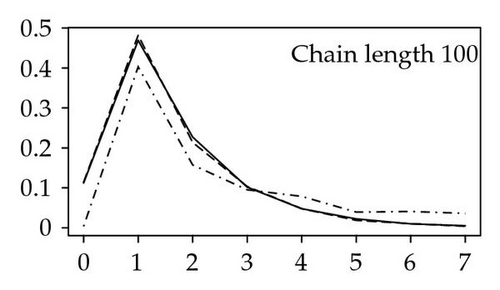
The simulations indicate that the Markov chain approach may be used to approximate the degree distribution. This is particularly useful for simulation of large networks in terms of memory usage; storing the connections between vertices requires memory capacity proportional to the number of vertices times the average number of connections. Simulation of the corresponding Markov chain requires memory capacity proportional to the current value of the chain.

The empirical degree distribution for P. falciparum shows that the partial duplication model does not provide a perfect fit. For example, no zero-degree vertices are included in the dataset (experimenter′s choice), and this needs to be incorporated into the model.

5. Other Models

We have applied the Markov chain approach to other models, and in this section we briefly present some of the results.

5.1. The Duplication-Divergence Model

The duplication-divergence model is an extension of the partial duplication model, and it has been used for analysis of protein interaction networks as well [15, 16, 27, 33]. However, the model is slightly more complicated than the partial duplication model, and it has three parameters p, q, and r. A step in this model is as follows: pick a vertex u in the graph uniformly, and add a new vertex v. Connect u and v with probability q, and create an edge e_w between v and w whenever there is an edge between the vertices u and w. Now modify the pairs independently of each other in the following way: with probability p, keep both edges; otherwise, with probability r, keep e_w and delete , and with probability 1 − r, keep and delete e_w.

One can derive a master equation and go through the construction of the modified jump chain. In this case, the transition probabilities p_j,k satisfy that

(5.1)

and p_j,k = 0 otherwise. Here ψ = (1 − p)(1 − r), and b_j(k, s) is the binomial probability from (4.3) with p replaced by s.

In order to apply Theorem 4.1, we put x_j = log (j + 1). It follows from simple calculations, again using Jensen′s inequality, that

is a solution to (4.9) if p and r satisfy that

(5.2)

Note that in the special cases r = 0 and r = 1, the left-hand side of the inequality reduces to log (p) + p, the same inequality as seen earlier. Actually, for r = 0 the model is the partial duplication model. It follows that if r = 0 or r = 1, a solution p of (5.2) must satisfty that p < Ω. For 0 < r < 1 an exact upper bound on p is harder to derive. For these values of r, the solution p is less than Ω and attains a minimum p ≈ 0.5235 for r = 1/2.

5.2. Another Class of Models

We believe that the Markov chain approach presented in this paper may be used to infer the behavior of other classes of models. In [21], simple models with master equations on the form

(5.3)

where a_k and c_k are nonnegative numbers, are studied. The resulting master equation for the relative frequencies f_t(k) may be written in matrix form as

(5.4)

where

, and c and f_t are the column vectors consisting of all the numbers c_k and f_t(k), respectively. The matrix A(t) is given by

(5.5)

Note that columns of the partitioned matrix in (5.4) sum to t + 1. That is, when divided by t + 1, the transpose of this matrix represents a Markov chain with time-dependent transition probabilities. We identify the countable set of states with N ∪ {−∞} where the artificial state −∞ accounts for the first row and the first column in the partitioned matrix.

We may compute the corresponding jump process, and again it turns out that its transition probabilities p_j,k are time-independent. We may get rid of the state −∞ by simply forgetting the time we spend there. That is, for j, k ≥ 0, we replace p_j,k by the sum

, and this leads to a Markov chain with transition probabilities given by

(5.6)

These jump chains are in fact all ergodic, and the stationary distribution of the time-inhomogeneous Markov chains has been derived in [21].

5.3. Other Extentions

Still other models do not fall under the conditions and assumptions introduced in this paper. For example, the master equation of the most general form of the duplication-mutation model [22, 23] depends on terms O(1/t²), and the columns of A(t) do not sum to the same number a(t) because of O(1/t²) terms, and because the requirement A(t) _k,j = 0 for k > j + 1 is not fulfilled.

Some of these problems may be circumvented at the cost of a more technical and elaborate exposition, but often the results need to be stated as limiting results. For example, if the columns of A(t) do not sum to the same number, the jump chain in (2.10) should be considered as emerging in the limit t → ∞.

Furthermore, one may choose to ignore terms of order O(1/t²) in the master equation. As t → ∞, the influence from higher-order terms often becomes insignificant, justifying such an approximation. This is, for example, the case for the duplication-mutation model.

Table 1. Parameters estimated from protein interaction data.

Species	Vertices	Edges	p	q
H. pylori	675	1291	0.263	0.052
P. falciparum	1271	2642	0.026	0.789
C. elegans	2368	3767	0.315	0.105
S. cerevisiae	4968	17530	0.131	0.263

Acknowledgments

M. Knudsen is supported by the Centre for Theory in the Natural Sciences, University of Aarhus. C. Wiuf is supported by the Danish Cancer Society and the Danish Research Councils. They would like to thank an anonymous reviewer for valuable suggestions that improved the clarity of the paper.

References

1 Alm E. and Arkin A. P., Biological networks, Current Opinion in Structural Biology. (2003) 12, no. 2, 193–202, https://doi.org/10.1016/S0959-440X(03)00031-9.
10.1016/S0959-440X(03)00031-9
Google Scholar
2 Barabási A.-L. and Albert R., Emergence of scaling in random networks, Science. (1999) 286, no. 5439, 509–512, https://doi.org/10.1126/science.286.5439.509, MR2091634.
10.1126/science.286.5439.509
CAS PubMed Web of Science® Google Scholar
3 Burda Z., Correia J. D., and Krzywicki A., Statistical ensemble of scale-free random graphs, Physical Review E. (2001) 64, no. 4, 9, 046118, https://doi.org/10.1103/PhysRevE.64.046118.
10.1103/PhysRevE.64.046118
CAS Web of Science® Google Scholar
4 Cork J. and Purugganan M., The evolution of molecular genetic pathways and networks, Bioessay. (2004) 26, no. 5, 479–484, https://doi.org/10.1002/bies.20026.
10.1002/bies.20026
CAS PubMed Web of Science® Google Scholar
5 Evans T., Complex networks, Contemporary Physics. (2004) 45, no. 6, 455–474, https://doi.org/10.1080/00107510412331283531.
10.1080/00107510412331283531
Web of Science® Google Scholar
6 Newman M. E. J. and Park J., Why social networks are different from other types of networks, Physical Review E. (2003) 68, no. 3, 8, 036122, https://doi.org/10.1103/PhysRevE.68.036122.
10.1103/PhysRevE.68.036122
CAS PubMed Web of Science® Google Scholar
7 Padgett J., Robust action and the rise of the medici, American Journal of Sociology. (1993) 98, no. 6, 1259–1319, https://doi.org/10.1086/230190.
10.1086/230190
Web of Science® Google Scholar
8 Scott J., Social Network Analysis, 2000, Sage, Beverly Hills, Calif, USA.
Google Scholar
9 de Silva E. and Stumpf M., Complex networks and simple models in biology, Journal of the Royal Society Interface. (2005) 2, no. 5, 419–430, https://doi.org/10.1098/rsif.2005.0067.
10.1098/rsif.2005.0067
CAS PubMed Web of Science® Google Scholar
10 Albert R. and Barabási A.-L., Statistical mechanics of complex networks, Reviews of Modern Physics. (2002) 74, no. 1, 47–97, https://doi.org/10.1103/RevModPhys.74.47, MR1895096.
10.1103/RevModPhys.74.47
CAS PubMed Web of Science® Google Scholar
11 Bollobas B., Random Graphs, 1998, Academic Press, New York, NY, USA.
10.1007/978-1-4612-0619-4_7
Google Scholar
12 Bollobas B. and Riodan O., S. Bornholdt and H. Schuster, Mathematical results on scale-free graphs, Handbook of Graphs and Networks, 2003, Wiley & Sons, New York, NY, USA, 1–34.
Web of Science® Google Scholar
13 Dorogovtsev S. N. and Mendes J. F. F., Evolution of networks, From Biological Nets to the Internet and WWW, 2003, Oxford University Press, Oxford, UK, MR1993912, ZBL1109.68537.
10.1093/acprof:oso/9780198515906.001.0001
Google Scholar
14 Newman M. E. J., The structure and function of complex networks, SIAM Review. (2003) 45, no. 2, 167–256, https://doi.org/10.1137/S003614450342480, ZBL1029.68010, MR2010377.
10.1137/S003614450342480
Web of Science® Google Scholar
15 Middendorf M., Ziv E., Adams C. et al., Discriminative topological features reveal biological network mechanisms, BMC Bioinformatics. (2004) 5, https://doi.org/10.1186/1471-2105-5-181.
10.1186/1471-2105-5-181
PubMed Web of Science® Google Scholar
16 Middendorf M., Ziv E., and Wiggins C. H., Inferring network mechanisms: the drosophila melanogaster protein interaction network, Proceedings of the National Academy of Sciences of the United States of America. (2005) 102, no. 9, 3192–3197, https://doi.org/10.1073/pnas.0409515102.
10.1073/pnas.0409515102
CAS PubMed Web of Science® Google Scholar
17 Milo R., Shen-Orr S., Itzkovitz S., Kashtan N., Chklovskii D., and Alon U., Network motifs: simple building blocks of complex networks, Science. (2002) 298, no. 5594, 824–827, https://doi.org/10.1126/science.298.5594.824.
10.1126/science.298.5594.824
CAS PubMed Web of Science® Google Scholar
18 Wiuf C., Brameier M., Hagberg O., and Stumpf M. P. H., A likelihood approach to analysis of network data, Proceedings of the National Academy of Sciences of the United States of America. (2006) 103, no. 20, 7566–7570, https://doi.org/10.1073/pnas.0600061103, MR2221040.
10.1073/pnas.0600061103
CAS PubMed Web of Science® Google Scholar
19 Chung F. and Lu L., Complex Graphs and Networks, 2006, 107, American Mathematical Society, Providence, RI, USA, CBMS Regional Conference Series in Mathematics, ZBL1114.90071, MR2248695.
10.1090/cbms/107
Google Scholar
20 Durrett R., Random Graph Dynamics, 2006, 20, Cambridge University Press, New York, NY, USA, Cambridge Series in Statistical and Probabilistic Mathematics, ZBL1116.05001, MR2271734.
10.1017/CBO9780511546594
Google Scholar
21 Hagberg O. and Wiuf C., Convergence properties of the degree distribution of some growing network models, Bulletin of Mathematical Biology. (2006) 68, no. 6, 1275–1291, https://doi.org/10.1007/s11538-006-9085-9, MR2249751.
10.1007/s11538-006-9085-9
PubMed Web of Science® Google Scholar
22 Raval A., Some asymptotic properties of duplication graphs, Physical Review E. (2003) 68, no. 6, 10, 066119, MR2060979.
10.1103/PhysRevE.68.066119
Web of Science® Google Scholar
23 Solé R. V., Pastor-Satorras R., Smith E. D., and Kepler T., A model of large-scale proteome evolution, Advances in Complex Systems. (2002) 5, no. 1, 43–54, ZBL1020.92024.
10.1142/S021952590200047X
Google Scholar
24 Stumpf M. P. H., Kelly W., Thorne T., and Wiuf C., Evolution at the system level: the natural history of protein interaction networks, Trends in Ecology & Evolution. (2007) 22, no. 7, 366–373, https://doi.org/10.1016/j.tree.2007.04.004.
10.1016/j.tree.2007.04.004
PubMed Web of Science® Google Scholar
25 Bhan A. B., Galas D. J., and Dewey T. G., A duplication growth model of gene expression networks, Bioinformatics. (2002) 18, no. 11, 1486–1493, https://doi.org/10.1093/bioinformatics/18.11.1486.
10.1093/bioinformatics/18.11.1486
CAS PubMed Web of Science® Google Scholar
26 Chung F., Lu L., Dewey T. G., and Galas D. J., Duplication models for biological networks, Journal of Computational Biology. (2003) 10, no. 5, 677–688, https://doi.org/10.1089/106652703322539024.
10.1089/106652703322539024
CAS PubMed Web of Science® Google Scholar
27 Ratmann O., Jørgensen O., Hinkley T., Stumpf M. P. H., Richardson S., and Wiuf C., Using likelihood-free inference to compare evolutionary dynamics of the protein networks of H. pylori and P. falciparum, PLoS Computational Biology. (2007) 3, no. 11, https://doi.org/10.1371/journal.pcbi.0030230.
10.1371/journal.pcbi.0030230
PubMed Web of Science® Google Scholar
28 Tweedie R. L., Sufficient conditions for regularity, recurrence and ergodicity of Markov processes, Mathematical Proceedings of the Cambridge Philosophical Society. (1975) 78, 125–136, ZBL0331.60047, MR0391269.
10.1017/S0305004100051562
Web of Science® Google Scholar
29 Samuel-Cahn E. and Zamir S., Algebraic characterization of infinite Markov chains where movement to the right is limited to one step, Journal of Applied Probability. (1977) 14, no. 4, 740–747, https://doi.org/10.2307/3213347, ZBL0389.60050, MR0461669.
10.2307/3213347
Web of Science® Google Scholar
30 Harris C. M. and Marlin P. G., A note on feedback queues with bulk service, Journal of the Association for Computing Machinery. (1972) 19, no. 4, 727–733, https://doi.org/10.1145/321724.321735, ZBL0251.60054, MR0346936.
10.1145/321724.321735
Web of Science® Google Scholar
31 Romanovsky V., Note on the moments of a binomial (p+q)ⁿ about its mean, Biometrika. (1923) 15, no. 3-4, 410–412, https://doi.org/10.2307/2331875.
10.2307/2331875
Web of Science® Google Scholar
32 LaCount D. J., Vignali M., Chettier R. et al., A protein interaction network of the malaria parasite plasmodium falciparum, Nature. (2005) 438, no. 7064, 103–107, https://doi.org/10.1038/nature04104.
10.1038/nature04104
CAS PubMed Web of Science® Google Scholar
33 Wagner A., How the global structure of protein interaction networks evolves, Proceedings of the Royal Society B. (2003) 270, no. 1514, 457–466, https://doi.org/10.1098/rspb.2002.2269.
10.1098/rspb.2002.2269
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

A Markov Chain Approach to Randomly Grown Graphs

Abstract

1. Introduction

2. RGGs

3. A Continuous Time Approximation