This paper presents an approach to single-position, intraday automated trading based on a neurogenetic algorithm. An artificial neural network is evolved to provide trading signals to a simple automated trading agent. The neural network uses open, high, low, and close quotes of the selected financial instrument from the previous day, as well as a selection of the most popular technical indicators, to decide whether to take a single long or short position at market open. The position is then closed as soon as a given profit target is met or at market close. Experimental results indicate that, despite its simplicity, both in terms of input data and in terms of trading strategy, such an approach to automated trading may yield significant returns.

1. Introduction

Trading is the activity of buying and selling financial instruments for the purpose of gaining a profit [1]. Usually, such operations are carried out by traders by making bids and offers, by using orders to convey their bids and offers to the brokers or, more interestingly, by developing automated trading systems that arrange their trades.

Several works have been carried out in the literature by considering market simulators for program trading. Recently, Brabazon and O′Neill [2] explained that, in program trading, the goal is usually to uncover and eliminate anomalies between financial derivatives and the underlying financial assets which make up those derivatives. Trading rules are widely used by practitioners as an effective mean to mechanize aspects of their reasoning about stock price trends. However, due to their simplicity, individual rules are susceptible of poor behavior in specific types of adverse market conditions. Naive combinations of rules are not very effective in mitigating the weaknesses of component rules [3]. As pointed out in [3], recent developments in the automation of exchanges and stock trading mechanisms have generated substantial interest and activity within the machine learning community. In particular, techniques based on artificial neural networks (ANN′s) [4, 5] and evolutionary algorithms (EAs) [2, 6, 7] have been investigated, in which the use of genetic algorithms and genetic programs has proven capable of discovering profitable trading rules. The major advantages of the evolutionary algorithms over conventional methods mainly regard their conceptual and computational simplicity, their applicability to broad classes of problems, their potential to hybridize with other methods, and their capability of self-optimization. Evolutionary algorithms can be easily extended to include other types of information such as technical and macroeconomic data as well as past prices. For example, genetic algorithms become useful to discover technical trading rules [8] or to find optimal parameter values for trading agents [9]. Some works focused on investigating the relationship between neural network optimization for financial trading and the efficient market hypothesis [10]; others examined the relationships between economic agents′ risk attitude and the profitability of stock trading decisions [11]; others focused on modeling the mutual dependencies among financial instruments [4], and recently, other works construct predictive models for financial time series by employing evolutionary neural network modeling approaches [12, 13].

This work is based on an evolutionary artificial neural network approach (EANN), already validated on several real-world problems [4, 5]. It is applied to providing trading signals to an automated trading agent, performing joint evolution of neural network weights and topology.

The matter is organized as follows. Section 2 describes the trading problem, which is the focus of this work, and the main characteristics of the trading rules and the simulator implemented in this work. Section 3 introduces the artificial neural networks and the evolutionary artificial neural networks, together with some of their previous applications to real-world problems. Then in Section 4, the neurogenetic approach is presented, together with the main aspects of the evolutionary process and information related to the considered financial data. Section 6 presents the experiments carried out on some financial instruments: the stock of Italian car maker FIAT, the Dow Jones Industrial Average (DJIA), the Financial Times Stock Exchange (FTSE 100), and the Nikkei, a stock market index for the Tokyo Stock Exchange (Nikkei 225), together with a comparison with other traditional methods. Finally, Section 7 concludes with a few remarks.

2. Problem Description

A so-called single-position automated day-trading problem is the problem of finding an automated trading rule for opening and closing a single position within a trading day. In such a scenario, either short or long positions are considered, and the entry strategy is during the opening auction at market price. A profit-taking strategy is also defined in this work, by waiting until market close unless a stop-loss strategy is triggered. A trading simulator is used to evaluate the performance of a trading agent.

While for the purpose of designing a profitable trading rule R, that is, solving any static automated day trading problem, the more information is available the better it is, whatever the trading problem addressed, for the purpose of evaluating a given trading rule, the quantity and granularity of quote information required vary depending on the problem. For instance, for one problem, daily open, high, low, and close data might be enough, while for another tick-by-tick data would be required. Such a problem does not happen in this approach, because, in order to evaluate the performance of the rules, the trading simulator only needs the open, high, low, and close quotes for each day of the time series.

An important distinction that may be drawn is the one between static and dynamic trading problems. A static problem is when the entry and exit strategies are decided before or on market open and do not change thereafter. A dynamic problem allows making entry and exit decisions as market action unfolds. Static problems are technically easier to approach, as the only information that has to be taken into account is the information available before market open. This does not mean, however, that they are easier to solve than their dynamic counterparts. The aim of the approach implemented in this work considers the definition of an automated trader in the static case.

2.1. Evaluating Trading Rules

What one is really trying to optimize when approaching a trading problem is the profit generated by applying a trading rule. Instead of looking at absolute profit, which depends on the quantities traded, it is a good idea to focus on returns.

2.1.1. Measures of Profit and Risk-Adjusted Return

For mathematical reasons, it is convenient to use log-returns instead of the usual returns, because they are additive under compounding. The annualized log-return of rule R when applied to time series X of length N is

()

where r(R,X,i) is the log-return generated by the rule R on the ith day of time series X, and Y is the number of market days in a year. This is the most obvious performance index for a trading rule. However, as a performance measure, average log-return completely overlooks the risk of a trading rule.

Following the financial literature on investment evaluation, the criteria for evaluating the performance of trading rules, no matter for what type of trading problem, should be measures of risk-adjusted investment returns. The reason these are good metrics is that, in addition to the profits, consistency is rewarded, while volatile patterns are not. Common measures within this class are the Sharpe ratio [14] and its variants. An extension of the Sharpe ratio implemented in this approach is the Sortino ratio [15],

()

where DSR corresponds to the downside risk of rule R on time series X and is defined by (3). The Sortino ratio is a measure of a risk-adjusted return of an investment asset. While the Sharpe ratio takes into account any volatility in return of an asset, Sortino ratio differentiates volatility due to up and down movements, since the up movements are considered desirable and not accounted in the volatility. For this reason, the Sortino ratio does not penalize a fund for its upside volatility:

()

where θ corresponds to the minimum acceptance level of the log-return.

2.2. Trading Simulator

Static trading problems could be classified according to four different features: the type of positions allowed, the type of entry strategy, the type of profit-taking strategy, and, finally, the strategy for stop-loss or exit.

In this approach, either short or long positions are considered, and the entry strategy is during the opening auction at market price. An open position is closed if predefined profit is attained (profit-taking strategy) or, failing that, at the end of the day at market price. No stop-loss strategy is used, other than automatic liquidation of the position when the market closes.

A trading simulator is used to evaluate the performance of a trading agent. The trading simulator supports sell and buy operations, and allows short selling. Only one open position is maintained during each trading process.

In this approach, in order to evaluate the performance of the rules, the trading simulator only requires the open, high, low, and close quotes for each day of the time series. The data set X used for trading agent optimization consists of such data, along with a selection of the most popular financial instrument technical indicators.

Each record consists of the inputs to the network calculated on a given day, considering only past information, and the desired output, namely, which action would have been most profitable on the next day.

As explained in detail in Section 4.6, the overall data set has been divided into three sets, respectively, training, test, and validation set, referring to three different time intervals, in order to avoid overlapping of the considered time period, as explained in (4):

()

All entries of the data set will be described in detail in Section 5; the three data sets show some of the input data used in this problem. All the input data are also summarized in Table 4.

The log-return generated by rule R on the ith day of time series X depends on a fixed take-profit return r_TP. This is a parameter of the algorithm that corresponds to the maximum performance that can be assigned by the automated trading simulation. The constant value of r_TP is defined, together with all other parameters, when the population of traders is generated for the first time, and does not change during the entire evolutionary process.

The main steps of the trading simulator are shown by the following pseudocode.

For all days, i of the time series:

(i)
opens a single day-trading position,
(ii)
calculates signal_i with neurogenetic approach,
(iii)
sends to the trading simulator the order decoded from the neurogenetic approach,
(iv)
calculates the profit r(R,X,i),
(v)
closes the position.

The measure of the profit obtained from each day is defined by

()

Different positions, previously generated by the neural network simulation, are considered in order to obtain the measure of the log-returns on the time series.

Equation (6) defines the signal generated by decoding the output of the ANNs processed by the evolutionary approach. For each day, this is defined through two different operation thresholds θ_buy and θ_sell, that correspond, respectively, to the maximum value of a network output for buying and to the minimum value for selling. In this automated trader application, these threshold are set, respectively, to 0.34 and 0.66, in order to avoid introducing a bias toward one or the other alternative operation the trader can execute:

()

The trading rules defined in this approach use past information to determine the best current trading action, and return a buy/sell signal for the current day depending on the information available on the previous day. Such a rule is then used to define the log-returns of the financial trading on the current day.

In the trading simulation, the log-returns obtained are then used, together with the risk free rate r_f and the downside risk DSR, given by (3), to calculate the Sortino ratio SR_d. This value represents the measure of the risk-adjusted returns of the simulation, and it will be used by the neurogenetic approach, together with a measure of the network computational cost, in order to evaluate the fitness of an individual trading agent.

At the beginning of the trading day, the trader sends to the trading simulator the order decoded from the output of the neural network. During the trading day, if a position is open, the position is closed as soon as the desired profit (indicated by a log-return r_TP) is attained (in practice, this could be obtained by placing a reverse limit order at the same time as the position-opening order); if a position is still open when the market closes, it is automatically closed in the closing auction at market price.

3. Artificial Neural Networks

Artificial neural networks (ANN′s) are well-defined computational models belonging to Soft Computing. The attractiveness of ANNs comes from the remarkable information processing characteristics of the biological system such as nonlinearity, high parallelism, robustness, fault and failure tolerance, learning, ability to handle imprecise information, and their capability to generalize.

Among the different kinds of neural networks, feedforward multilayer perceptron (MLP) neural networks receive great attention due to their relative simplicity and computational capabilities. In a feedforward neural network, an input pattern is transformed into an output pattern through the processing performed by a series of layers of interconnected nodes, defining layers of neurons. The layers between inputs and outputs are defined “hidden layers” and the neurons that belong to these layers are called “hidden nodes,” because they are not directly connected to the external system through the inputs and the outputs. Each node computes a transfer function, represented by the following equation:

()

where g(w · x) is called the activation function. Commonly used continuous transfer functions are linear, hyperbolic tangent, and Gaussian, even if most researchers prefer to use the sigmoid function, whose analytic form is

()

The sigmoid, as the tangent hyperbolic, is a popular activation function because it is differentiable and it saturates to the horizontal asymptotic axes y = 0 and y = 1. The transfer function implemented in the neurogenetic approach, described in the following chapters, is a kind of sigmoid function, the tan-sigmoid function, that tends asymptotically to −1 and +1 at the extremes. Figure 1 shows the shape of this function. As indicated in [16], networks of neurons with real-valued inputs and sigmoid transfer function can be used to approximate mathematical functions, allowing the parametrization of the latter. This is very useful in situations where the exact expression of the function is unknown.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Tangent sigmoidal function.

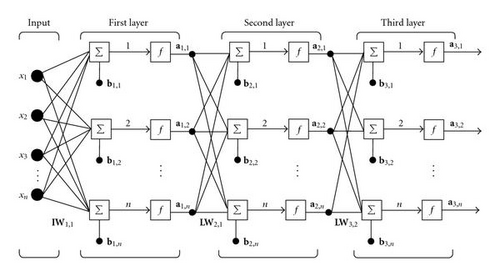
An example of architecture of a feedforward MLP neural network is depicted in Figure 2, where each activation function a_i depends on the contribution of the previous subnetwork topology.

The expressions of the activation values defined for the example reported in Figure 2 are here defined:

()

The activation function obtained at each hidden layer will become the input for the successive layer, with the expression reported in (10):

()

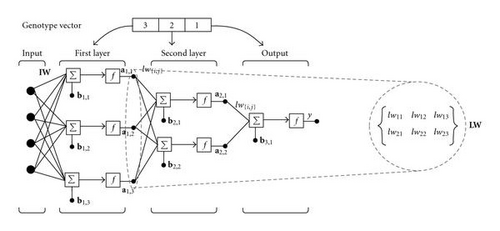
3.1. Evolutionary Artificial Neural Networks

The success of an ANN application usually requires a high number of experiments. Moreover, several parameters of an ANN, set during the design phase, can affect how easy a solution is to be found. In this sense, a particular type of evolving systems, namely, neurogenetic systems, has become a very important topic of study in neural network design. They make up so-called Evolutionary Artificial Neural Networks (EANNs) [36, 47, 48], that is, biologically-inspired computational models that use evolutionary algorithms in conjunction with neural networks to solve problems in a synergetic way.

Several approaches presented in the literature have been developed to apply evolutionary algorithms to neural network design. Some consider the setting of the weights in a fixed topology network. Others optimize network topologies, or evolve the learning rules, the input feature selection, or the transfer function used by the network. Several systems also allow an interesting conjunction of the evolution of network architecture and weights, carried out simultaneously.

Table 1 summarizes some of the approaches presented in the literature for the different EANN techniques.

Table 1. Synoptic table of some evolving ANNs techniques presented in the literature.

Evolutionary ANNs
Techniques	Examples in the literature
Weight optimization	GA with real encoding (Montana et al. [17])
	GENITOR (Whitley et al. [18])
	Mutation-based EAs (Keesing et al. [19])
	Improved GA (Yang et al. [20])
	NN weight evolution (Zalzala et al. [21])
	MLP training using GA (Seiffert [22])
	STRE (Pai [23])

Parameter optimization	GA for competitive learning NNs
	(Merelo Guervós et al. [24])
	G-prop II/III (Merelo Guervós et al. [25])
	ANOVA (Castillo et al. [26])

Rule optimization	GA for learning rules (Chalmers [27])
Rule optimization	GP for learning rules (Poli et al. [28])

Transfer function optimization	EANNs through EPs (Yao et al. [29])
Transfer function optimization	Hybrid method with GP (Poli et al. [30])

Input data selection	EAs for fast data selection (Brill et al. [31])
Input data selection	Selecting Training set (Reeves et al. [32])

Architeture optimization: constructive and destructive algorithms	Design of ANN (Yao et al. [33])
	Design NN using GA (Miller et al. [34])
	NEAT (Stanley and Miikkulainen [35])
	EP-Net (Yao [36])
	Evo-design for MLP (Filho et al. [37])
	genetic design of NNs (Harp et al. [38])
	Constructing/Pruning with GA (Wang et al. [20])
	Network Size Reduction (Moze et al. [39])

Simultaneous evolution of architecture and weights	ANNA ELEONORA (Maniezzo [40])
	EP-Net (Yao et al. [36])
	Improved GA (Leung et al. [41])
	COVNET (Pedrajas et al. [42])
	CNNE (Yao et al. [43])
	SEPA, MGNN (Palmes et al. [44])
	GNARL (Angeline et al. [45])
	GAEPNet (Tan [46])
	NEGE Approach (Azzini and Tettamanzi [5])
	Structure Evolution and
	Parameter Optimization (Palmes et al. [44])

The last technique reported in this table also corresponds to that considered in this work. Important aspects of the simultaneous evolution underline that an evolutionary algorithm allows all aspects of a neural network design to be taken into account at once, without requiring any expert knowledge of the problem. Furthermore, the conjunction of weights and architecture evolution overcomes the possible drawbacks of each single technique and joins their advantages. The main advantage of weight evolution is to simulate the learning process of a neural network, avoiding the drawbacks of the traditional gradient descent techniques, such as the backpropagation algorithm (BP). Given then some performance optimality criteria about architectures, as momentum, learning rate, and so on, the performance level of all these forms a surface in the design space. The advantage of such representation is that determining the optimal architecture design is equivalent to finding the highest point on this surface. The simultaneous evolution of architecture and weights limits also the negative effects of a noisy-fitness evaluation in an ANN structure optimization, by defining a one-to-one mapping between genotypes and phenotypes of each individual.

This neurogenetic approach restricts the attention to a specific subset of feedforward neural networks, namely, MLP, presented above, since they have features such as the ability to learn and generalize smaller training set requirements, fast operation, ease of implementation, and simple structures.

4. The Neurogenetic Approach

The approach implemented in this work defines a population of traders, the individuals, encoded through neural network representations. The improvements of the joint evolution of architecture and weights make the evolutionary algorithm considered in this approach to evolve a traders population by using this technique, taking advantage of the backpropagation (BP) as a specialized decoder [5].

The general idea implemented is similar to other approaches presented in the literature, but it differs from them in the novel aspects implemented in the genetic evolution. This work can be considered a hybrid algorithm, since a local search based on the gradient descent technique, backpropagation, can be used as local optimization operator on a given data set. The basic idea is to exploit the ability of the EA to find a solution close enough to the global optimum, together with the ability of the BP algorithm to finely tune a solution and reach the nearest local minimum.

BP becomes useful when the minimum of the error function currently found is close to a solution but not close enough to solve the problem; BP is not able to find a global minimum if the error function is multimodal and/or nondifferentiable. Moreover, the adaptive nature of NN learning by examples is a very important feature of these methods, and the training process modifies the weights of the ANN, in order to improve a predefined performance criterion, that corresponds to an objective function over time. In several methods to train neural networks, BP has emerged as a suitable solution for finding a set of good connection weights and biases.

4.1. Evolutionary Algorithm

The idea proposed in this work is close to the solution presented in EPNet [36]: a new evolutionary system for evolving feedforward ANNs, that puts emphasis on evolving ANNs behaviors. This neurogenetic approach evolves ANNs architecture and connection weights simultaneously, as EPNet, in order to reduce noise in fitness evaluation.

Close behavioral link between parent and offspring is maintained by applying different techniques, like weight mutation and partial training, in order to reduce behavioral disruption. Genetic operators defined in the approach include the following.

(i)
Truncation Selection.
(ii)
Mutation, divided into
- (a)
  weight mutation,
- (b)
  topology mutation.

In this context, the evolutionary process attempts to mutate weights before performing any structural mutation; however, all different kinds of mutation are applied before the training process. Weight mutation is carried out before topology mutation, in order to perturb the connection weights of the neurons in a neural network. After each weight mutation, a weight check is carried out, in order to delete neurons whose contribution is negligible with respect to the overall network output. This allows to obtain, if possible, a reduction of the computational cost of the entire network before any architecture mutation.

Particular attention has to be given to all these operators, since they are defined in order to emphasize the evolutionary behavior of the ANNs, reducing disruptions between them.

It is well known that recombination of neural networks of arbitrary structure is a very hard issue, due to the detrimental effect of the permutation problem. No satisfactory solutions have been proposed so far in the literature. As a matter of facts, the most successful approaches to neural network evolution do not use recombination at all [36]. Therefore, in this approach the crossover operator is not applied either, because of the disruptive effects it could have on the neural models, after the cut and recombination processes on the network structures of the selected parents.

4.2. Individual Encoding

For each simulation a new population of MLPs is created. As described in detail in [5], individuals are not constrained to a preestablished topology, and the population is initialized with different hidden layer sizes and different numbers of neurons for each individual according to two exponential distributions, in order to maintain diversity among all the individuals in the new population. Such dimensions are not bounded in advance, even though the fitness function may penalize large networks. A normal distribution is also applied to determine the weights and bias values, and variance is initialized to one for all weights and biases. Variances are applied in conjunction with evolutionary strategies in order to perturb network weights and bias. Each individual is encoded in a structure in which basic information is maintained as illustrated in Table 2.

Table 2. Individual representation.

Element	Description
l	Length of the topology string, corresponding to the number of layers
Topology	String of integer values that represent the number of neurons in each layer
W⁽⁰⁾	Weights matrix of the input layer neurons of the network
Var⁽⁰⁾	Variance matrix of the input layer neurons of the network
W⁽ⁱ⁾	Weights matrix for the ith layer, i = 1, …,l
Var⁽ⁱ⁾	Variance matrix for the ith layer, i = 1, …,l
b_ij	Bias of the jth neuron in the ith layer
Var(b_ij)	Variance of the bias of the jth neuron in the ith layer

The values of all these parameters are affected by the genetic operators during evolution, in order to perform incremental (adding hidden neurons or hidden layers) and decremental (pruning hidden neurons or hidden layers) learning.

Table 3 lists all the parameters of the algorithm, and specifies the values that they assume in this problem.

Table 3. Parameters of the algorithm.

Symbol	Meaning	Default value
n	Population size	60
	Probability of inserting a hidden layer	0.05
	Probability of deleting a hidden layer	0.05
	Probability of inserting a neuron in a hidden layer	0.05
r	Parameter used in weight mutation for neuron elimination	1.5
h	Mean for the exponential distribution	3
N_in	Number of network inputs	24
N_out	Number of network outputs	1
α	Cost of a neuron	2
β	Cost of a synapsis	4
λ	Desired tradeoff between network cost and accuracy	0.2
k	Constant for scaling cost and MSE in the same range	10⁻⁶

Table 4. Input technical indicators.

Index	Input technical indicators	Description
1	Open(i)	Opening value of the financial instrument on day i
2	High(i)	High value of the financial instrument on day i
3	Low(i)	Low value of the financial instrument on day i
4	Close(i)	Closing value of the financial instrument on day i
5	MA5(i)	5-day Moving Average on day i
6	MA10(i)	10-day Moving Average on day i
7	MA20(i)	20-day Moving Average on day i
8	MA50(i)	50-day Moving Average on day i
9	MA100(i)	100-day Moving Average on day i
10	MA200(i)	200-day Moving Average on day i
11	EMA5(i)	5-day Exponential Moving Average on day i
12	EMA10(i)	10-day Exponential Moving Average on day i
13	EMA20(i)	20-day Exponential Moving Average on day i
14	EMA50(i)	50-day Exponential Moving Average on day i
15	EMA100(i)	100-day Exponential Moving Average on day i
16	EMA200(i)	200-day Exponential Moving Average on day i
17	MACD(i)	Moving Average Convergence/Divergence on day i
18	SIGNAL(i)	Exponential Moving Average on MACD on day i
19	MOMENTUM(i)	Rate of price change on day i
20	ROC(i)	Rate of change on day i
21	K(i)	Stochastic oscillator K on day i
22	D(i)	Stochastic oscillator D on day i
23	RSI(i)	Relative Strength Index on day i
24	Close(i − 1)	Closing value of the financial instrument on day i − 1

The setting of the mutation probability parameters , , and is defined in this work equal to the default values shown in Table 3, since, as indicated by previous experiences [4, 49, 50], their setting is not critical for the performance of the evolutionary process.

4.3. The Evolutionary Process

The general framework of the evolutionary process can be described by the following pseudocode. Individuals in a population compete and communicate with other individuals through genetic operators applied with independent probabilities, until termination conditions are not satisfied.

(1)
Initialize the population by generating new random individuals.
(2)
Create for each genotype the corresponding MLP, and calculate its cost and its fitness values.
(3)
Save the best individual as the best-so-far individual.
(4)
While not termination condition do,
- (a)
  apply the genetic operators to each network,
- (b)
  decode each new genotype into the corresponding network,
- (c)
  compute the fitness value for each network,
- (d)
  save statistics.

The application of the genetic operators to each network is described by the following pseudocode.

(1)
Select from the population (of size n) ⌊n/2⌋ individuals by truncation and create a new population of size n with copies of the selected individuals.
(2)
For all individuals in the population,
- (a)
  mutate the weights and the topology of the offspring,
- (b)
  train the resulting network using the training set,
- (c)
  calculate f on the test set (see Section 4.6),
- (d)
  save the individual with lowest f as the best-so-far individual if the f of the previously saved best-so-far individual is higher (worse).
(3)
Save statistics.

For each generation of the population, all the information of the best individual is saved.

4.4. Selection

The selection method implemented in this work is taken from the breeder genetic algorithm [51], and differs from natural probabilistic selection in that evolution considers only the individuals that best adapt to the environment. Elitism is also used, allowing the best individual to survive unchanged in the next generation and solutions to monotonically get better over time.

The selection strategy implemented is truncation. This kind of selection is not a novel solution, indeed, several approaches consider evolutionary approaches describing the truncation selection, in order to prevent the population from remaining too static and perhaps not evolving at all. Moreover, this kind of selection is a very simple technique and produces satisfactory solutions through conjunction with other strategies, like elitism.

In each new generation a new population has to be created, and the first half of such new population corresponds to the best parents that have been selected with the truncation operator, while the second part of the new population is defined by creating offspring from the previously selected parents.

4.5. Mutation

The main function of this operator is to introduce new genetic materials and to maintain diversity in the population. Generally, the purpose of mutation is to simulate the effect of transcription errors that can occur with a very low probability, the mutation rate, when a chromosome is duplicated. The evolutionary process applies two kinds of neural network perturbations.

(i) Weights mutation, that perturbs the weights of the neurons before performing any structural mutation and applying BP. This kind of mutation defines a Gaussian distribution for the variance matrix values Var⁽ⁱ⁾ of each network weight W⁽ⁱ⁾, defined in Table 2. This solution is similar to the approach implemented by Schwefel [52], who defined evolution strategies, algorithms in which the strategy parameters are proposed for self-adapting the mutation concurrently with the evolutionary search. The main idea behind these strategies is to allow a control parameter, like mutation variance, to self-adapt rather than changing their values by some deterministic algorithm. Evolution strategies perform very well in numerical domains, since they are dedicated to (real) function optimization problems.

This kind of mutation offers a simplified method for self-adapting each single value of the variance matrix , whose values are defined as log-normal perturbations of their parent parameter values. The weight perturbation implemented in this neurogenetic approach allows network weights to change in a simple manner, by using evolution strategies.

(ii) Topology mutation, that is defined with four types of mutation by considering neurons and layer addition and elimination. It is implemented after weight mutation because a perturbation of weight values changes the behavior of the network with respect to the activation functions; in this case, all neurons whose contribution becomes negligible with respect to the overall behavior are deleted from the structure. The addition and the elimination of a layer and the insertion of a neuron are applied with independent probabilities, corresponding, respectively, to three algorithm parameters , , and . Also these parameters are set at the beginning and maintained unchanged during the entire evolutionary process.

All the topology mutation operators are aimed at minimizing their impact on the behavior of the network; in other words, they are designed to be as little disruptive, and as much neutral, as possible, preserving the behavioral link between the parent and the offspring better than by adding random nodes or layers.

4.6. Fitness

An important aspect that has to be considered in the overall evolutionary process is that the depth of the network structure could in principle increase without limits under the influence of some of the topology mutation operators, defining a so-called bloating effect. In order to avoid this problem, some penalization parameters are introduced in the fitness function in order to control the structure growth, reducing the corresponding computational cost.

In this application, the fitness function depends on the risk-adjusted return obtained by the considered trader, and is calculated, at the end of the training and evaluation process, by

()

where λ corresponds to the desired tradeoff between network cost and accuracy, and has been set to 0.2 after some preliminary experiments. This parameter also represents the measure of the correlation between the fitness value and the measure of the risk-adjusted return considered

. k is a scaling constant set to 10⁻⁶, and c models the computational cost of a neural network, defined by

()

where N_hn is the number of hidden neurons, N_syn is the number of synapses, and α = 2 and β = 4 represent, respectively, the costs of each hidden neuron and of each synapsis. This term has been introduced to keep the demand of computational resources at a reasonable level by penalizing large networks. In this work, we have assumed these values in order to give more weight to the number of synapses of the neural network.

It is important to emphasize that the Sortino ratio used in the fitness function defines “risk” as the risk of loss.

Following the commonly accepted practice of machine learning, the problem data are partitioned into three sets, respectively, training set, for network training, test set, used to decide when to stop the training and avoid overfitting, and validation set, used to test the generalization capabilities of a network. There is no agreement in the literature on the way test and validation sets are named, and here the convention that validation set is used to assess the quality of the neural networks is adopted, while test set is used to monitor network training.

The fitness is calculated according to (11) over the test set. The training set is used for training the networks with BP and the test set is used to stop BP.

5. Input and Output Settings

The data set of the automated trader simulation is created by defining input data and the corresponding target values for the desired output.

The input values of the data set are defined by considering the quotes of the daily historical prices and 24 different technical indicators for the same financial instrument, that correspond to the most popular indicators used in technical analysis. These indicators also summarize important features of the time series of the financial instrument considered, and they represent useful statistics and technical information that otherwise should be calculated by each individual of the population, during the evolutionary process, increasing the computational cost of the entire algorithm.

The list of all the inputs of a neural network is shown in Table 4, and a detailed discussion about all these technical indicators can be easily found in the literature [53]. In this approach, the values of all these technical indicators are calculated for each day based on the time series up to and including the day considered.

In all the time series considered, for each day i one target value is defined, corresponding to the operation that would have been most profitable to carry out for a trader on the next day. In the output definition, only two possible operations are taken into account, namely to buy and sell, respectively, encoded with the values 0 (for buy) and 1 (for sell):

()

The choice between them depends on the value of the corresponding return for buy and sell operations, as follows:

()

6. Experiments and Results

The automated trader presented in this work has been applied to four financial instruments: the stock of Italian car maker FIAT, traded at the Borsa Italiana stock exchange, the Dow Jones Industrial Average (DJIA), the Financial Times Stock Exchange (FTSE 100), and a stock market index for the Tokyo Stock Exchange Nikkei, namely the Nikkei 225. All the four databases were created by considering all daily quotes and the 24 technical indicators described in Table 4.

Each database has been divided into three sets, in order to define the training, test, and validation sets for the neurogenetic process. In each of the considered financial instrument, training, test, and validation sets have been created by considering, respectively, the 66, 27, and 7% of all available data. All time series of the three data sets are preprocessed by rescaling them so that they are normally distributed with mean 0 and standard deviation σ equal to 1.

The risk free rate r_f has been set for all runs to the relevant average discount rate during the time span covered by the data. Different settings have been also considered for the log-return values of the take profit, for both target output and trading simulator settings, in order to define the combination that better suits to the results obtained by the evolutionary process to provide the best automated trader. For each of the considered financial instrument, three settings are considered and set, respectively, to 0.0046, 0.006, and 0.008, in order to more or less cover the range of possible target daily returns.

A first round of experiments, whose results are summarized in Table 5, was aimed at determining the most promising setting of the neurogenetic algorithm parameters for three distinct settings of the take-profit log-return. Indeed, the neurogenetic parameters are set to the constant values defined in the evolutionary approach, previously reported in Table 3. In order to find out optimal settings of the genetic parameters , , and , several runs of the trading application have been carried out by using FIAT, the first financial instrument considered in this work. For each run of the evolutionary algorithm, up to 800 000 network evaluations (i.e., simulations of the network on the whole training set) have been allowed, including those performed by the backpropagation algorithm. In the automatic trading of FIAT instrument, all the daily data are related to the period from the 31st of March, 2003, through the 1st of December, 2006.

Table 5. A comparison of experimental results for different settings of the neurogenetic algorithm parameters.

Setting	Parameter setting			Take-profit log-returns
				r_TP = 0.0046			r_TP = 0.006			r_TP = 0.008
				f_avg	Std. Dev.	SR_d	f_avg	Std. Dev.	SR_d	f_avg	Std. Dev.	SR_d
1	0.05	0.05	0.05	0.3909	0.0314	0.0311	0.2514	0.0351	0.2731	0.1207	0.0196	0.3950
2	0.05	0.1	0.05	0.4052	0.0486	−0.0620	0.2574	0.0258	1.2290	0.1200	0.0252	0.2091
3	0.1	0.1	0.05	0.4118	0.0360	−0.6211	0.2711	0.064	−0.0627	0.1172	0.0187	0.0407
4	0.1	0.2	0.05	0.4288	0.0418	0.1643	0.2541	0.0386	0.2843	0.1200	0.0153	0.3287
5	0.2	0.05	0.05	0.4110	0.0311	1.2840	0.2697	0.0447	0.4199	0.1188	0.0142	0.0541
6	0.2	0.1	0.2	0.4023	0.0379	0.7685	0.2811	0.0194	0.3215	0.1187	0.0197	1.2244
7	0.2	0.2	0.2	0.4346	0.0505	−0.0612	0.2393	0.0422	0.3612	0.1089	0.0111	0.3290

Table 5 reports the average and standard deviation of the test fitness of the best solutions found for each parameter setting over 10 runs, as well as their Sortino ratio, for reference.

What these results tell us is that for each different setting of the genetic parameters there is no high difference of the mean fitness f_avg. The choice has been carried out by considering the solution that could satisfy the aim of low fitness, maintaining satisfactory values for the Sortino Ratio. However, as indicated in previous works [4, 49, 50], the actual setting of the neurogenetic parameters is not critical; therefore, from that point on, we decided to adopt the standard setting corresponding to row 1 in the table, with , , and , also for the other financial instruments considered in this approach.

A second round of experiments was aimed at determining whether using a different take-profit log-return for generating the target in the learning data set used by backpropagation than the one used for simulating and evaluating the trading rules could bring about any improvement of the results. For this reason, in this second round of experiments, the best individual found for each setting is saved, and the Sortino ratio and the correlated log-returns on the validation set are reported.

The time series considered for each of the four financial instruments are shown in Table 6. Note that the time series considered for these instruments also cover the recent credit crunch bout of volatility, as it is the case for the last 90 days of the DJIA and FTSE validation sets (cf., Table 13). Nevertheless, the strategy implemented has shown satisfactory performance and robustness with respect to such a volatility crisis.

Table 6. Financial instruments and time series.

Time series period	Instruments
Time series period	DJIA	FTSE	Nikkei	FIAT
From	10/16/2002	10/16/2002	10/23/2002	03/28/2003
To	11/09/2007	11/09/2007	11/09/2007	12/01/2006

The values of worst, average, and best Sortino Ratio and log-returns found are shown in Tables 7, 8, 9, and 10, respectively for FIAT, DJIA, FTSE, and Nikkei instruments.

Table 7. Comparison of validation Sortino ratio and log-return for different combinations of target and simulation take profits for FIAT instrument.

Target take profit	Validation set	Simulation take profit
		0.0046			0.006			0.008
		Worst	Avg.	Best	Worst	Avg.	Best	Worst	Avg.
0.0046	SR_d	−0.6210	0.2149	1.2355	−0.3877	−0.0027	0.5294	−0.3605	0.0050	0.5607
0.0046	Log-return	−0.3336	0.1564	0.6769	−0.1973	0.0628	0.3192	−0.1770	0.0225	0.3424
0.006	SR_d	−0.1288	−0.0303	0.0712	−0.0620	0.4035	1.2289	−0.0043	0.3863	1.2432
0.006	Log-return	0	0.0218	0.0737	0.0363	0.2559	0.6768	0.0320	0.3041	0.6773
0.008	SR_d	−0.0620	0.2137	0.7859	−0.0620	0.2803	0.9327	0.0395	0.3683	1.2237
0.008	Log-return	0	0.1484	0.4531	0	0.1850	0.5312	0.0562	0.2311	0.6695

Table 8. Comparison of validation Sortino ratio and log-return for different combinations of target and simulation take profits for DJIA instrument.

Target take profit	Validation set	Simulation take profit
		0.0046			0.006			0.008
		Worst	Avg.	Best	Worst	Avg.	Best	Worst	Avg.
0.0046	SR_d	0.6506	0.9829	1.4956	0.8920	1.0829	1.4822	1.1464	1.6260	1.8516
0.0046	Log-return	0.3862	0.5511	0.7939	0.51059	0.610	0.7953	0.6431	0.8646	0.9735
0.006	SR_d	0.50425	0.7682	1.1365	0.1171	0.7034	1.3417	0.5854	1.471	2.2098
0.006	Log-return	0.3101	0.4451	0.6287	0.1009	0.4104	0.7289	0.3594	0.7900	1.1255
0.008	SR_d	0.1380	0.5131	0.7024	0.1974	1.0860	1.7617	0.9162	1.3306	2.0015
0.008	Log-return	0.1125	0.3140	0.4131	0.1459	0.6003	0.9209	0.5236	0.7256	1.0383

Table 9. Comparison of validation Sortino ratio and log-return for different combinations of target and simulation take profits for FTSE instrument.

Target take profit	Validation set	Simulation take profit
		0.0046			0.006			0.008
		Worst	Avg.	Best	Worst	Avg.	Best	Worst	Avg.
0.0046	SR_d	0.6820	1.1627	1.4193	1.5262	1.7075	1.9199	1.8717	2.0766	2.3146
0.0046	Log-return	0.4041	0.6384	0.7599	0.8142	0.8964	0.9902	0.9831	1.0682	1.1694
0.006	SR_d	0.4914	1.1476	1.4922	1.4852	1.6725	1.8357	1.8266	2.1439	2.3312
0.006	Log-return	0.3033	0.6299	0.7947	0.7943	0.8808	0.9543	0.9618	1.0977	1.1792
0.008	SR_d	1.0992	1.2297	1.5179	1.5320	1.7565	2.0262	1.7763	2.1589	2.3961
0.008	Log-return	0.6086	0.6708	0.8056	0.8183	0.9187	1.0372	0.9427	1.1039	1.2050

Table 10. Comparison of validation Sortino ratio and log-return for different combinations of target and simulation take profits for Nikkei instrument.

Target take profit	Validation set	Simulation take profit
		0.0046			0.006			0.008
		Worst	Avg.	Best	Worst	Avg.	Best	Worst	Avg.
0.0046	SR_d	6.0964	7.1855	8.9124	6.5291	7.6685	8.8954	7.6012	9.1406	10.5916
0.0046	Log-return	0.4833	0.5349	0.6115	0.4909	0.5523	0.5938	0.6506	0.7286	0.7968
0.006	SR_d	5.1195	7.3389	9.2933	6.2432	7.5702	8.5831	8.4128	9.3151	10.7664
0.006	Log-return	0.4530	0.5485	0.6221	0.5330	0.6141	0.6763	0.7199	0.7674	0.8372
0.008	SR_d	4.3248	6.9352	10.2934	6.4700	7.8899	9.9229	8.9438	9.6727	10.7350
0.008	Log-return	0.3773	0.5179	0.6694	0.5533	0.6224	0.7556	0.7539	0.7843	0.8214

The conclusion is that runs in which the take profit used to construct the target is greater than or equal to the actual target used by the strategy usually lead to more profitable trading rules, with few exceptions.

6.1. Tenfold Crossvalidation

To further validate the generalization capabilities of the automated trading rules found by the approach, a tenfold crossvalidation has been carried out as follows.

The training and test sets have been merged together into a set covering the period from March 31, 2003 to August 30, 2006. That set has been divided into 10 equal-sized intervals. Each interval has been used in turn as the validation set, while the remaining 9 intervals have been used to create a training set (consisting of 6 intervals) and a test set (3 intervals).

Each record of the sets can be regarded as independent of the others, since it contains a summary of the whole past history of the time series, as seen through the lens of the technical indicators used. Therefore, any subset of the records can be used to validate models trained on the rest of the set, without violating the constraint that only past data be used by a model to provide a signal for the next day.

The 10 (training, test, and validation) data sets thus obtained have been used to perform 10 runs each of the evolutionary algorithm, for a total of 100 runs. The best performing take-profit settings found during the previous round of experiments have been used for all 100 runs, namely, a target take profit of 0.006 and a simulation take profit of 0.008. Table 11 reports the average and standard deviation of the best fitness obtained during each run; the best individual found in each run was applied to its relevant validation set, and the resulting Sortino ratio and log-return are reported in the table.

Table 11. Tenfold validation: experimental results for different settings of the neurogenetic algorithm parameters.

Setting	Parameter setting			Take-profit log-return = 0.008
Setting				f_avg	Std. Dev.	Log-return	SR_d
1	0.05	0.05	0.05	0.1518	0.0101	0.7863	1.4326
	0.05	0.1	0.05	0.1491	0.0267	4840	0.8105
	0.1	0.1	0.05	0.1598	0.0243	0.2012	0.2899
	0.1	0.2	0.05	0.1502	0.0190	0.7304	1.3235
	0.2	0.05	0.05	0.1494	0.0256	0.7399	1.3307
	0.2	0.1	0.2	0.1645	0.0115	0.9002	1.6834
	0.2	0.2	0.2	0.1532	0.0129	0.3186	0.5037

2	0.05	0.05	0.05	0.1892	0.0251	0.9920	1.8991
	0.05	0.1	0.05	0.1768	0.0293	0.6362	1.1229
	0.1	0.1	0.05	0.1786	0.0342	0.9726	1.8707
	0.1	0.2	0.05	0.1749	0.0274	0.7652	1.3965
	0.2	0.05	0.05	0.1765	0.0188	0.7391	1.3340
	0.2	0.1	0.2	0.1864	0.0210	0.5362	0.9355
	0.2	0.2	0.2	0.1799	0.0306	0.7099	1.2751

3	0.05	0.05	0.05	0.1780	0.0290	0.6655	1.2008
	0.05	0.1	0.05	0.1790	0.1003	1.0537	2.0371
	0.1	0.1	0.05	0.1880	0.1364	0.8727	1.6569
	0.1	0.2	0.05	0.1858	0.1683	0.3767	0.6347
	0.2	0.05	0.05	0.1894	0.1363	0.5434	0.9474
	0.2	0.1	0.2	0.1845	0.1013	0.6544	1.1784
	0.2	0.2	0.2	0.1840	0.1092	0.6882	1.2551

4	0.05	0.05	0.05	0.1909	0.0315	0.7800	1.4484
	0.05	0.1	0.05	0.2026	0.0234	0.8400	1.5745
	0.1	0.1	0.05	0.1866	0.0300	0.9303	1.7543
	0.1	0.2	0.05	0.1831	0.0293	0.8194	1.5384
	0.2	0.05	0.05	0.2011	0.0379	1.0497	2.0417
	0.2	0.1	0.2	0.2212	0.0283	0.5146	0.8842
	0.2	0.2	0.2	0.1923	0.0340	0.9758	1.8647

5	0.05	0.05	0.05	0.2520	0.0412	0.6825	1.2430
	0.05	0.1	0.05	0.2237	0.0245	0.5403	0.9552
	0.1	0.1	0.05	0.2213	0.0327	0.4932	0.8545
	0.1	0.2	0.05	0.2169	0.0331	0.4748	0.8201
	0.2	0.05	0.05	0.2295	0.0416	0.5796	1.0335
	0.2	0.1	0.2	0.2364	0.0316	0.4449	0.7644
	0.2	0.2	0.2	0.2200	0.0287	0.5799	1.0251

6	0.05	0.05	0.05	0.1932	0.0478	0.3892	0.6407
	0.05	0.1	0.05	0.2183	0.0339	0.8521	1.5979
	0.1	0.1	0.05	0.2303	0.0312	0.6858	1.2407
	0.1	0.2	0.05	0.2094	0.0444	0.6375	1.1418
	0.2	0.05	0.05	0.2168	0.0268	0.6776	1.2254
	0.2	0.1	0.2	0.2320	0.0445	0.8312	1.5614
	0.2	0.2	0.2	0.2186	0.0495	0.3634	0.6671

7	0.05	0.05	0.05	0.2020	0.0268	0.5196	0.8740
	0.05	0.1	0.05	0.2171	0.0227	0.6727	1.1781
	0.1	0.1	0.05	0.2081	0.0184	0.9178	1.7002
	0.1	0.2	0.05	0.2042	0.0381	0.6905	1.2214
	0.2	0.05	0.05	0.2050	0.0375	0.6653	1.1619
	0.2	0.1	0.2	0.2187	0.0235	0.8449	1.5530
	0.2	0.2	0.2	0.2153	0.0353	0.8321	1.5207
8	0.05	0.05	0.05	0.2109	0.0370	0.3534	0.5823
	0.05	0.1	0.05	0.2018	0.0460	0.6068	1.0832
	0.1	0.1	0.05	0.1845	0.0369	0.8938	1.6860
	0.1	0.2	0.05	0.1956	0.0338	0.5846	1.0402
	0.2	0.05	0.05	0.2172	0.0300	0.4137	0.6968
	0.2	0.1	0.2	0.1856	0.0365	0.5516	0.9617
	0.2	0.2	0.2	0.1888	0.0366	0.8130	1.5059

9	0.05	0.05	0.05	0.2010	0.0263	0.9420	1.7953
	0.05	0.1	0.05	0.1997	0.0252	0.2538	0.4051
	0.1	0.1	0.05	0.2007	0.0312	0.7444	1.3792
	0.1	0.2	0.05	0.2300	0.0373	0.8998	1.6987
	0.2	0.05	0.05	0.2170	0.0429	0.7192	1.3175
	0.2	0.1	0.2	0.2252	0.0248	0.9606	1.8470
	0.2	0.2	0.2	0.1930	0.0441	0.9813	1.8860

10	0.05	0.05	0.05	0.2161	0.0168	0.4443	0.7558
	0.05	0.1	0.05	0.2017	0.0312	0.8144	1.5233
	0.1	0.1	0.05	0.2154	0.0333	0.8133	1.5007
	0.1	0.2	0.05	0.2138	0.0424	0.9079	1.7118
	0.2	0.05	0.05	0.2079	0.0230	0.6604	1.1749
	0.2	0.1	0.2	0.2063	0.0288	0.6148	1.0804
	0.2	0.2	0.2	0.2113	0.0323	0.7083	1.2787

It can be observed that the results are consistent for all ten data sets used in the cross-validation, with Sortino ratios often greater than one, meaning that the expected return outweighs the risk of the strategy. This is a positive indication of the generalization capabilities of the neurogenetic approach.

6.2. Discussion

The approach to automated intraday trading described above is minimalistic in two respects:

(i)
the data considered each day by the trading agent to make a decision about its action is restricted to the open, low, high, and close quotes of the last day, plus the close quote of the previous day; any visibility of the rest of the past time series is filtered through a small number of popular and quite standard technical indicators;
(ii)
the trading strategy an agent can follow is among the simplest and most accessible even to the unsophisticated individual trader; its practical implementation does not even require particular kinds of information technology infrastructures, as it could very well be enacted by placing a couple of orders with a broker on the phone before the market opens; there is no need to monitor the market and react in a timely manner.

Nonetheless, the results clearly indicate that, despite its simplicity, such an approach may yield, if carried out carefully, significant returns, in the face of a risk that is, to be sure, probably higher than the one the average investor would be eager to take, but all in all proportionate with the returns expected.

By simulating individual trading rules, we observed that the signal given by the neural network is correct most of the times; when it is not, the loss (or draw-down) tends to be quite severe—which is the main reason for the low Sortino ratios exhibited by all the evolved rules.

However, a simple but effective technique to greatly reduce the risk of the trading rules is to pool a number of them, discovered in independent runs of the algorithm, perhaps using different parameter settings, and adopt at any time the action suggested by the majority of the rules in the pool. In case of tie, it is safe to default to no operation.

Table 12 shows the history of a simulation of a trading strategy carried out on the FIAT instrument, combining by majority vote the seven best trading rules discovered when using a target take profit of 0.006 and a simulation take profit of 0.008 on the validation set. Only days in which the majority took a position are shown.

Table 12. A simulation of the strategy dictated by the majority of the best trading rules (one for each of the 7 parameter settings of Table 5) obtained by running the algorithm with a combination of target take profit of 0.006 and a simulation take profit of 0.008. The action in the Action column refers to the (short)-selling or buying of FIAT. The r column shows the log-return realized by the strategy for each day. Only days in which the strategy took a position are shown. As previously defined, each ANN output has been decoded into one of the three operations buy, no operation, and sell, corresponding, respectively, to the three output ranges: output <0.34, 0.34≤ output ≤0.66, and output >0.66.

Date	Output of the best ANN found with each parameter setting							Action FIAT	r
Date	1	2	3	4	5	6	7	Action FIAT	r
09/08/2006	No Op.	Buy	No Op.	Buy	Buy	No Op.	Buy	Buy	−0.00087
09/11/2006	No Op.	Buy	Buy	Buy	No Op.	Buy	Buy	Buy	0.00605
09/12/2006	No Op.	Buy	Buy	Buy	Buy	Buy	Buy	Buy	0.008
09/13/2006	No Op.	Buy	Buy	Buy	Buy	Buy	Buy	Buy	0.008
09/14/2006	Buy	Buy	No Op.	Buy	No Op.	No Op.	Buy	Buy	0.008
09/26/2006	No Op.	Buy	No Op.	Buy	No Op.	Buy	Buy	Buy	0.008
10/18/2006	No Op.	Buy	Buy	Buy	No Op.	Buy	Buy	Buy	0.008
10/19/2006	No Op.	Buy	Buy	Buy	Buy	Buy	Buy	Buy	0.008
11/02/2006	No Op.	Buy	No Op.	Buy	Buy	No Op.	Buy	Buy	0.008
11/03/2006	No Op.	Buy	No Op.	Buy	Buy	Buy	Buy	Buy	0.008
11/06/2006	No Op.	Buy	No Op.	Buy	Buy	Buy	Buy	Buy	0.008
11/07/2006	No Op.	Buy	No Op.	Buy	Buy	No Op.	Buy	Buy	0.008

Table 13. Volatility of the time series considered, expressed as the standard deviation of daily log-returns calculated on the training, test, and validation sets of each time series.

Data set	Volatility
Data set	DJIA	FTSE	Nikkei	FIAT
Training	0.0085	0.0091	0.0121	0.0179
Test	0.0063	0.0079	0.0108	0.0200
Validation	0.0112	0.0138	0.0139	0.0178

The compounded return is really attractive: the annualized log-return of the above strategy, obtained with target take profit of 0.006 and actual take profit of 0.008, corresponds to a percentage annual return of 39.87%, whereas the downside risk is almost zero (0.003). Similar results are obtained when applying the same technique to the other instruments considered, as shown in the bottom line of Table 14. This table shows a comparison of the percentage annual returns obtained by the automated trader of this approach with a “Buy & Hold” strategy, which opens a long position on the first day at market open and closes it on the last day at market close.

Table 14. Percentage annual return of the strategy.

Strategy	Percentage return
Strategy	DJIA	FTSE	Nikkei	FIAT
Buy & Hold	−3.80	−4.98	−14.30	23.94
Neurogenetic approach	37.92	48.67	5.35	39.87

7. Conclusion

An application of a neurogenetic algorithm to the optimization of a simple trading agent for static, single-position, intraday trading has been described. The approach has been validated on time series of four diverse financial instruments, namely, the stock of Italian car maker FIAT, the Dow Jones Industrial Average, which is an index designed to reflect the New York Stock Exchange, the FTSE index of the London Stock Exchange, and the Nikkei 225 index of the Tokyo Stock Exchange.

Experimental results indicate that, despite its simplicity, both in terms of input data and in terms of trading strategy, such an approach to automated trading may theoretically yield significant returns while effectively reducing risk.

Traditional finance theory asserts that investors can buy/sell any quantity of stock without affecting price. Contemporary microstructure literature [1] provides a wealth of evidence that this is not the case and that trade size and other important determinants like trade type, trading strategy, industry sector, and trading time can have significant price impact and affect the profitability of trading [54]. This is evidenced by the recent growth in large brokers providing trading platforms to clients to access dark liquidity pools and specialist firms promising trade execution services which minimize price impact. In this work no price impact has been assumed, mainly due to difficulties in correctly estimating it, even if, in the real world, a strategy trading significant volumes of shares or contracts will influence the market [55], thus reducing its effectiveness. Therefore, the performance data presented should not been construed to reflect the performance of those strategies when applied to the market, but to provide evidence of the capability of the neurogenetic approach to extract useful knowledge from data. A realistic assessment of risks and returns associated with applying such knowledge goes beyond the scope of our work.

The main contribution of this work is demonstrating that it is possible to extract meaningful and reliable models of financial time series from a collection of popular technical indicators by means of evolutionary algorithms coupled with artificial neural networks.

The introduction of a neurogenetic approach to the modeling of financial time series opens up opportunities for many extensions, improvements, and sophistications both on the side of input data and indicators, and of the technicalities of the trading strategy.

A natural extension would consist of enriching the data used for modeling with more sophisticated technical indicators. Novel indicators might be evolved or coevolved by means of other evolutionary techniques like genetic programming.

Other extensions could involve applying the approach to more complex trading problems. These might be dynamic intraday trading problems, or static problems that require higher-resolution data to be evaluated.

Finally, it would be interesting to compare the neurogenetic approach with other evolutionary modeling approaches, for example using fuzzy logic to express models [56].

References

1 Harris L., Trading and Exchanges, Market Microstructure for Practitioners, 2003, Oxford University Press, New York, NY, USA.
Google Scholar
2 Brabazon A. and O′Neill M., Biologically Inspired Algorithms for Financial Modelling, 2006, Springer, Berlin, Germany.
Google Scholar
3 Subramanian H., [email protected], Ramamoorthy S., [email protected], Stone P., and [email protected], Kuipers B. J., [email protected], Designing safe, profitable automated stock trading agents using evolutionary algorithms, 2, Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ′06), July 2006, Seattle, Wash, USA, 1777–1784, https://doi.org/10.1145/1143997.1144285.
10.1145/1143997.1144285
Google Scholar
4 Azzini A. and Tettamanzi A. G. B., Neuro-genetic single position day trading, Proceedings of the Workshop Italiano di Vita Artificiale e Computazione Evolutiva (WIVACE ′07), September 2007, Sicily, Italy.
Google Scholar
5 Azzini A. and [email protected], Tettamanzi A. G. B., [email protected], A neural evolutionary approach to financial modeling, 2, Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ′06), July 2006, Seattle, Wash, USA, 1605–1612, https://doi.org/10.1145/1143997.1144263.
10.1145/1143997.1144263
Google Scholar
6 Dempster M. A. H. and Jones C., A real-time adaptive trading system using genetic programming, Quantitative Finance. (2001) 1, no. 4, 397–413, https://doi.org/10.1088/1469-7688/1/4/301.
10.1088/1469-7688/1/4/301
Google Scholar
7 Dempster M. A. H., Payne T. W., Romahi Y., and Thompson G. W. P., Computational learning techniques for intraday FX trading using popular technical indicators, IEEE Transactions on Neural Networks. (2001) 12, no. 4, 744–754, https://doi.org/10.1109/72.935088.
10.1109/72.935088
CAS PubMed Web of Science® Google Scholar
8 Allen F. and [email protected], Karjalainen R., Using genetic algorithms to find technical trading rules, Journal of Financial Economics. (1999) 51, no. 2, 245–271, https://doi.org/10.1016/S0304-405X(98)00052-X.
10.1016/S0304-405X(98)00052-X
Web of Science® Google Scholar
9 Cliff D., [email protected], Explorations in evolutionary design of online auction market mechanisms, Electronic Commerce Research and Applications. (2003) 2, no. 2, 162–175, https://doi.org/10.1016/S1567-4223(03)00017-6.
10.1016/S1567-4223(03)00017-6
Google Scholar
10 Skabar A. and Cloete I., Neural networks, financial trading and the efficient markets hypothesis, 4, Proceedings of the 25th Australasian Conference on Computer Science, January-February 2002, Melbourne, Victoria, Australia, Australian Computer Science, 241–249.
Google Scholar
11 Hayward S., [email protected], Evolutionary artificial neural network optimisation in financial engineering, Proceedings of the 4th International Conference on Hybrid Intelligent Systems (HIS ′04), December 2005, Kitakyushu, Japan, 210–215, https://doi.org/10.1109/ICHIS.2004.42.
10.1109/ICHIS.2004.42
Google Scholar
12 Yi-Hui L., [email protected], Evolutionary neural network modeling for forecasting the field failure data of repairable systems, Expert Systems with Applications. (2007) 33, no. 4, 1090–1096, https://doi.org/10.1016/j.eswa.2006.08.032.
10.1016/j.eswa.2006.08.032
Web of Science® Google Scholar
13 Armano G., [email protected], Marchesi M., and Murru A., A hybrid genetic-neural architecture for stock indexes forecasting, Information Sciences. (2005) 170, no. 1, 3–33, https://doi.org/10.1016/j.ins.2003.03.023.
10.1016/j.ins.2003.03.023
Web of Science® Google Scholar
14 Sharpe W., The Sharpe ratio, Journal of Portfolio Management. (1994) 1, 49–58.
10.3905/jpm.1994.409501
Web of Science® Google Scholar
15 Sortino F. and van der Meer R., Downside risk, Capturing what′s at stake in investment situations, Journal of Portfolio Management. (1991) 17, 27–31.
10.3905/jpm.1991.409343
Web of Science® Google Scholar
16 Tettamanzi A. G. B. and Tomassini M., Soft Computing: Integrating Evolutionary, Neural, and Fuzzy Systems, 2001, Springer, Berlin, Germany.
10.1007/978-3-662-04335-6
Google Scholar
17 Montana D. and Davis L., Training feedforward neural networks using genetic algorithms, Proceedings of the 11th International Conference on Artificial Intelligence (IJCAI ′89), August 1989, Detroit, Mich, USA, Morgan Kaufmann, 762–767.
Google Scholar
18 Whitley D. and Kauth J., GENITOR: a different genetic algorithm, 1988, Colorado State University, Fort Collins, Colo, USA.
Google Scholar
19 Keesing R. and Stork D. G., Evolution and learning in neural networks: the number and distribution of learning trials affect the rate of evolution, Proceedings of the Conference on Advances in Neural Information Processing Systems 3, November 1990, Denver, Colo, USA, 804–810.
Google Scholar
20 Yang B., [email protected], Su X.-H., and [email protected], Wang Y.-D., BP neural network optimization based on an improved genetic algorithm, 1, Proceedings of the International Conference on Machine Learning and Cybernetics, November 2002, Beijing, China, 64–68, https://doi.org/10.1109/ICMLC.2002.1176710.
10.1109/ICMLC.2002.1176710
Google Scholar
21 Mordaunt P. and Zalzala A. M. S., Towards an evolutionary neural network for gait analysis, 2, Proceedings of the Congress on Evolutionary Computation (CEC ′02), May 2002, Honolulu, Hawaii, USA, 1238–1243, https://doi.org/10.1109/CEC.2002.1004537.
10.1109/CEC.2002.1004537
Google Scholar
22 Seiffert U., Multiple layer perceptron training using genetic algorithms, Proceedings of the European Symposium on Artificial Neural Networks (ESANN ′01), April 2001, Bruges, Belgium, 159–164.
Google Scholar
23 Vijayalakshmi Pai G. A., [email protected], A fast converging evolutionary neural network for the prediction of uplift capacity of Suction Caissons, 1, Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems (CIS ′04), December 2004, Singapore, 654–659.
Google Scholar
24 Merelo Guervós J. J., Patón M., Cañas A., Prieto A., and Morán F., J. Mira, J. Cabestany, and A. Prieto, Optimization of a competitive learning neural network by genetic algorithms, 686, Proceedings of the International Workshop on Artificial Neural Networks: New Trends in Neural Computation (IWANN ′93), June 1993, Sitges, Spain, Springer, 185–192, Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-56798-4_145.
10.1007/3-540-56798-4_145
Google Scholar
25 Castillo-Valdivieso P. A., Rivas Santos M. R., Merelo Guervós J. J., Gonzalez J., Prieto A., and Romero G., W. Banzhaf, J. Daida, A. E. Eiben et al., G-prop-III: global optimization of multilayer perceptrons using an evolutionary algorithm, 1, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′99), July 1999, Orlando, Fla, USA, Morgan Kaufmann.
Google Scholar
26 Castillo-Valdivieso P. A., [email protected], Merelo Guervós J. J., Prieto A., Rojas I., and Romero G., Statistical analysis of the parameters of a neuro-genetic algorithm, IEEE Transactions on Neural Networks. (2002) 13, no. 6, 1374–1394, https://doi.org/10.1109/TNN.2002.804281.
10.1109/TNN.2002.804281
CAS PubMed Google Scholar
27 Chalmers D. J., D. S. Touretzky, J. L. Elman, T. J. Sejnowski, and G. E. Hinton, The evolution of learning: an experiment in genetic connectionism, Proceedings of the Connectionist Summer School Workshop, 1990, San Mateo, Calif, USA, Morgan Kaufmann, 81–90.
Google Scholar
28 Radi A. and Poli R., Discovering efficient learning rules for feedforward neural networks using genetic programming, 2002, JanuaryDepartment of Computer Science, University of Essex, Essex, UK.
Google Scholar
29 Yao X. and Liu Y., Evolving artificial neural networks through evolutionary programming, Proceedings of the 5th Annual Conference on Evolutionary Programming, February-March 1996, San Diego, Calif, USA, MIT Press, 257–266.
Google Scholar
30 Figueira Pujol J. C. and Poli R., W. Banzhaf, J. Daida, A. E. Eiben et al., Evolution of neural networks using weight mapping, 2, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′99), July 1999, Orlando, Fla, USA, Morgan Kaufmann, 1170–1177.
Google Scholar
31 Brill F. Z., Brown D. E., and Martin W. N., Fast genetic selection of features for neural network classifiers, IEEE Transactions on Neural Networks. (1992) 3, no. 2, 324–328, https://doi.org/10.1109/72.125874.
10.1109/72.125874
CAS PubMed Web of Science® Google Scholar
32 Reeves C. R. and Taylor S. J., A. Eiben, D. Back, M. Schoenauer, and H. P. Schwefel, Selection of training data for neural networks by a genetic algorithm, 1498, Proceedings of the 5th International Conference on Parallel Problem Solving from Nature (PPSN ′98), September 1998, Amsterdam, The Netherlands, Springer, 633–642, Lecture Notes in Computer Science, https://doi.org/10.1007/BFb0056843.
10.1007/BFb0056843
Google Scholar
33 Yao X. and [email protected], Liu Y., Towards designing artificial neural networks by evolution, Applied Mathematics and Computation. (1998) 91, no. 1, 83–90, https://doi.org/10.1016/S0096-3003(97)10005-4.
10.1016/S0096-3003(97)10005-4
Web of Science® Google Scholar
34 Miller G. F., Todd P. M., and Hegde S. U., J. D. Schaffer, Designing neural networks using genetic algorithms, Proceedings of the 3rd International Conference on Genetic Algorithms, June 1989, Fairfax, Va, USA, 379–384.
Google Scholar
35 Stanley K. O. and [email protected], Miikkulainen R., [email protected], Evolving neural networks through augmenting topologies, Evolutionary Computation. (2002) 10, no. 2, 99–127, https://doi.org/10.1162/106365602320169811.
10.1162/106365602320169811
PubMed Web of Science® Google Scholar
36 Yao X. and Liu Y., A new evolutionary system for evolving artificial neural networks, IEEE Transactions on Neural Networks. (1997) 8, no. 3, 694–713, https://doi.org/10.1109/72.572107.
10.1109/72.572107
CAS PubMed Web of Science® Google Scholar
37 Filho E. F. M. and de Carvalho A. C. P., Evolutionary design of MLP neural network architectures, Proceedings of the 4th Brazilian Symposium on Neural Networks (SBRN ′97), December 1997, Goiania, Brazil, 58–65, https://doi.org/10.1109/SBRN.1997.645849.
10.1109/SBRN.1997.645849
Google Scholar
38 Harp S., Samad T., and Guha A., J. D. Schaffer et al., Towards the genetic synthesis of neural networks, Proceedings of the 3rd International Conference on Genetic Algorithms, June 1989, Fairfax, Va, USA, Morgan Kaufmann, 360–369.
Google Scholar
39 Moze M. C. and Smolensky P., Using relevance to reduce network size automatically, Connection Science. (1989) 1, no. 1, 3–16, https://doi.org/10.1080/09540098908915626.
10.1080/09540098908915626
Google Scholar
40 Maniezzo V., Genetic evolution fo the topology and weight distribution of neural networks, IEEE Transactions on Neural Networks. (1994) 5, no. 1, 39–53, https://doi.org/10.1109/72.265959.
10.1109/72.265959
CAS PubMed Web of Science® Google Scholar
41 Leung F. H. F., Lam H. K., Ling S. H., and Tam P. K. S., Tuning of the structure and parameters of a neural network using an improved genetic algorithm, IEEE Transactions on Neural Networks. (2003) 14, no. 1, 79–88, https://doi.org/10.1109/TNN.2002.804317.
10.1109/TNN.2002.804317
CAS PubMed Web of Science® Google Scholar
42 García-Pedrajas N., [email protected], Hervás-Martínez C., and [email protected], Muñoz-Pérez J., [email protected], COVNET: a cooperative coevolutionary model for evolving artificial neural networks, IEEE Transactions on Neural Networks. (2003) 14, no. 3, 575–596, https://doi.org/10.1109/TNN.2003.810618.
10.1109/TNN.2003.810618
CAS PubMed Web of Science® Google Scholar
43 Islam M. M., Yao X., and Murase K., [email protected], A constructive algorithm for training cooperative neural network ensembles, IEEE Transactions on Neural Networks. (2003) 14, no. 4, 820–834, https://doi.org/10.1109/TNN.2003.813832.
10.1109/TNN.2003.813832
PubMed Web of Science® Google Scholar
44 Palmes P. P., [email protected], Hayasaka T., and [email protected], Usui S., [email protected], Mutation-based genetic neural network, IEEE Transactions on Neural Networks. (2005) 16, no. 3, 587–600, https://doi.org/10.1109/TNN.2005.844858.
10.1109/TNN.2005.844858
PubMed Web of Science® Google Scholar
45 Angeline P. J., Saunders G. M., and Pollack J. B., An evolutionary algorithm that constructs recurrent neural networks, IEEE Transactions on Neural Networks. (1994) 5, no. 1, 54–64, https://doi.org/10.1109/72.265960.
10.1109/72.265960
CAS PubMed Web of Science® Google Scholar
46 Tan Z.-H., [email protected], Hybrid evolutionary approach for designing neural networks for classification, Electronics Letters. (2004) 40, no. 15, 955–957, https://doi.org/10.1049/el:20045250.
10.1049/el:20045250
Web of Science® Google Scholar
47 Yao X., Evolving artificial neural networks, Proceedings of the IEEE. (1999) 87, no. 9, 1423–1447, https://doi.org/10.1109/5.784219.
10.1109/5.784219
Web of Science® Google Scholar
48 Yao X., Evolutionary Optimization, 2002, Kluwer Academic Publishers, Norwell, Mass, USA.
Google Scholar
49 Azzini A., [email protected], Cristaldi L., [email protected], Lazzaroni M., [email protected], Monti A., [email protected], Ponci F., and [email protected], Tettamanzi A. G. B., [email protected], Incipient fault diagnosis in electrical drives by tuned neural networks, Proceedings of the IEEE Instrumentation and Measurement Technology Conference (IMTC ′06), April 2006, Sorrento, Italy, 1284–1289, https://doi.org/10.1109/IMTC.2006.328495.
10.1109/IMTC.2006.328495
Google Scholar
50 Azzini A. and [email protected], Tettamanzi A. G. B., [email protected], A neural evolutionary classification method for brain-wave analysis, 3907, Proceedings of the European Workshop on Evolutionary Computation in Image Analysis and Signal Processing (EVOIASP ′06), April 2006, Budapest, Hungary, 500–504, Lecture Notes in Computer Science, https://doi.org/10.1007/11732242_45.
10.1007/11732242_45
Google Scholar
51 Muhlenbein H. and Schlierkamp-Voosen D., The science of breeding and its application to the breeder genetic algorithm (bga), Evolutionary Computation. (1993) 1, no. 4, 335–360.
10.1162/evco.1993.1.4.335
Web of Science® Google Scholar
52 Schwefel H., Numerical Optimization for Computer Models, 1981, John Wiley & Sons, Chichester, UK.
Google Scholar
53 Colby R., The Encyclopedia of Technical Market Indicators, 2002, 2nd edition, McGraw-Hill, New York, NY, USA.
Google Scholar
54 Bikker J. A., [email protected], Spierdijk L., and [email protected], van der Sluis P. J., [email protected], Market impact costs of institutional equity trades, Journal of International Money and Finance. (2007) 26, no. 6, 974–1000, https://doi.org/10.1016/j.jimonfin.2007.01.007.
10.1016/j.jimonfin.2007.01.007
Web of Science® Google Scholar
55 Chen J., Hong H., Huang M., and Kubik J. D., Does fund size erode mutual fund performance? the role of liquidity and organization, American Economic Review. (2004) 94, no. 5, 1276–1302, https://doi.org/10.1257/0002828043052277.
10.1257/0002828043052277
Web of Science® Google Scholar
56 da Costa Pereira C. and Tettamanzi A. G. B., A. Brabazon and M. O′Neill, Fuzzy-evolutionary modeling for single-position day trading, Natural Computing in Computational Economics and Finance, 2008, 100, Springer, Berlin, Germany.
10.1007/978-3-540-77477-8_8
Google Scholar

Citing Literature

All articles

Evolving Neural Networks for Static Single-Position Automated Trading

Abstract

1. Introduction