A contribution to a multidimensional analysis of trade competition
Abstract
International trade grew substantially throughout the last decades and international relations became more important for the economic performance of the countries. Simultaneously, new poles emerged in the international arena leading to growing competition for higher market shares. Therefore, trade competition is a critical dimension of analysis for applied international trade studies. We propose a conceptual framework for measuring this phenomenon by combining some critical previous contributions to build a multidimensional and more comprehensive concept, which defines trade competition as a function of the degree of both structural similarity and total exports overlap. Moreover, structural similarity should take into account three elements: sectoral shares similarity, inter-sectoral similarity (evaluating how different the distinct sectors are) and intra-sectoral similarity (proximity in terms of quality ranges exported). Several measures are proposed to empirically capture the concept suggested. Finally, we present an example including the exports of six European economies (Germany, France, the United Kingdom, Greece, Hungary and Sweden) to 124 destination markets (in 2007, 2011, 2015) in order to illustrate the application of the concept and measures suggested.
1 Introduction
Economic globalisation and the emergence of new poles in the world economy are among the most critical trends of (at least) the last three decades (Head & Mayer, 2013; Riad et al., 2012). As described by Kaplinsky and Messner (2008, p. 197), “the global economy is undergoing a profound and momentous shift.” This geographical reconfiguration of international economic relations was driven by technological progress and the reduction of trade costs generated by the evolution in the transport sector and the liberalisation trend that characterised the world economy in the second half of the twentieth century (Carter & Li, 2004). As a consequence of these transformations, international trade grew dramatically during the last decades and we are faced with a new scenario characterised by much more open and interdependent economies (Berthelon & Freund, 2008). Given the magnitude of actual trade flows and their importance for the overall economic performance of the countries (and the firms), the phenomenon of trade competition requires special attention and needs to be seen as a priority in the agenda of international trade research.
More specifically, particular emphasis should be directed to the development of new ways to evaluate the phenomenon, providing not only a detailed view of the actual situation but also some insights on critical dynamic elements, capturing the main trends and highlighting the challenges that they raise. Some efforts are already in place aiming the analysis of the threat imposed by the emergence of new important players in the international trade arena. A major example is of course the case of China (Kaplinsky & Messner, 2008), with several studies analysing the impact of the Chinese trade growth for other countries in several destination markets (e.g., Blázquez-Lidoy, Rodríguez, & Santiso, 2006; Giovannetti, Sanfilippo, & Velucchi, 2013; Greenaway, Mahabir, & Milner, 2008; Jenkins, 2012; Jenkins, Peters, & Moreira, 2008; Lall & Albaladejo, 2004; Lall, Weiss, & Oikawa, 2005; Schott, 2008).
The most common approach to this subject evaluates the similarity in sectoral shares (structural similarity) as a proxy of trade competition (Blázquez-Lidoy et al., 2006; Duboz & Le Gallo, 2011; Langhammer & Schweickert, 2006; Schott, 2008; Vandenbussche, Comite, Rovegno, & Viegelahn, 2013; Wu & Chen, 2004). The Krugman Specialization Index (KSI; Krugman, 1991) and the Finger–Kreinin index (Finger & Kreinin, 1979) are commonly used as baseline indicators (Palan, 2010). Retaining this spirit but using an even simpler approach, other studies calculate correlation coefficients between the sectoral shares, the ranking of these sectoral shares or the ranking of revealed comparative advantage measures (De Benedictis & Tajoli, 2007; Lall & Albaladejo, 2004; Shafaeddin, 2004).
Another dimension considered in the empirical literature is the level of intra-sectoral similarity, that is, the proximity in terms of quality ranges exported. In fact, the growing pattern of vertical specialisation (Fontagné, Gaulier, & Zignago, 2008; Kaitila, 2010; Vandenbussche et al., 2013) leads some researchers to consider measures that capture the similarity in terms of sectoral shares and quality ranges simultaneously (Antimiani & Henke, 2007).
Crespo and Simões (2012) propose an even larger measure of structural similarity, which besides sectoral shares similarity and intra-sectoral similarity also incorporates inter-sectoral similarity (evaluating how different the distinct sectors are). The basic argument is that sectors have distinct levels of dissimilarity among them in what concerns their production requirements. Let us illustrate this idea with a simple example. To that end, we consider three countries—countries 1, 2 and 3—totally specialised in one sector: country 1 in potatoes, country 2 in tomatoes and country 3 in computers. It is reasonable to assume that potatoes and tomatoes have more similar production requirements than tomatoes and computers. Therefore, the index of structural similarity should be able to reflect this situation, making clear that the level of structural similarity is higher in the first case. However, the KSI is not able to capture this aspect as it indicates maximum dissimilarity whenever the countries under comparison export different sectors, as occurs in the example above. To overcome this problem, Crespo and Simões (2012) propose the consideration of an average of the Krugman Index calculated at different levels of sectoral disaggregation in order to evaluate not only the level of actual competition (traditionally evaluated through the Krugman Index) but also the potential one.
Finally, in another important milestone in this literature, Jenkins (2008) puts the emphasis on the concept of competitive threat and highlights that a measure that attends only to structural similarity and ignores the level of overlap between total exports of the two countries under comparison is strongly affected in its capacity to evaluate the critical aspects that are at the heart of the trade competition reality at the world level.
The empirical studies produced in this area do not benefit however from a global conceptual framework. Instead, these studies use partial measures that capture some important dimension of trade competition between two countries but lack the consideration of other important elements. They are therefore, at best, partial measures, making clear the need for new contributions in this research area, namely with the objective of providing innovative insights regarding the measurement of trade competition between two countries. The development of such framework is the main goal of this paper.
The approach developed in this study takes the KSI as starting point and incorporates the two main contributions of the study by Crespo and Simões (2012), thereby leading to a measure of structural similarity that accounts for the three critical dimensions of this phenomenon simultaneously: sectoral shares similarity, inter-sectoral similarity and intra-sectoral similarity. By doing so, we are able to obtain a richer measure of structural similarity. However, this is not enough to capture the real concept of trade competition. For that, we need to add to our measure of structural similarity a way to incorporate the overlap between total exports of the two countries (i.e., the ratio between the value of exports from the smaller country and the value of exports from the larger country). Inspired by Jenkins (2008), we propose an adjustment to our previous indicator, obtaining distinct indexes for each of the two countries under analysis.
In addition, while the common approach evaluates trade competition between two countries in a specific destination market, we complement our methodological proposal by considering not only a set of measures that correspond to this perspective but also indicators that aim to quantify the overall level of competition between two countries, that is, in a group of countries to which they export.
With the framework developed in the present study, we aim to contribute to applied international trade literature by providing important tools to answer some critical questions, for example: (i) What are the main competitors of each country in the different destination markets? (ii) What are the sources of the competition dynamics identified? (iii) What has been the evolution of trade competition between two specific countries along the last years? A correct and rigorous answer to these questions could provide useful guidance for economic policy actions that may impact the specialisation patterns of the exports, in both sectoral and geographical terms.
The remainder of the paper is structured as follows. Section 2 presents our measure of structural similarity and introduces the overlap between total exports in the analysis of trade competition. Section 3 extends the previous approach by considering the level of trade competition between two countries in a group of destination markets. Section 4 illustrates our methodological proposal through an empirical example considering export data for Germany, France, the United Kingdom, Greece, Hungary and Sweden, along the period 2007–15. Section 5 presents some final remarks.
2 Methodology
In this section, we present the critical aspects of the methodology that we propose to capture a broad concept of trade competition. In subsection 2.1, we discuss the baseline index which only considers sectoral shares. Next, we extend the analysis through the inclusion of inter-sectoral similarity (subsection 2.2) and intra-sectoral similarity (subsection 2.3). In subsection 2.4, we take the contributions from the previous subsections as support in order to present an overall index of structural similarity. Finally, in subsection 2.5 we discuss a measure of trade competition that includes not only the three dimensions of structural similarity but also the level of trade overlap.
2.1 Sectoral shares similarity
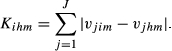 (1)
(1)The weights of sector j in the export structure of i and h to m are expressed, respectively, as vjim and vjhm. Additionally, vjim = xjim/xim, where xjim are the exports of sector j from i to m and xim are the total exports from i to m. The same definitions apply to vjhm. Kihm ranges between 0 (perfect similarity between the two export structures) and 2 (maximum dissimilarity).
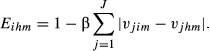 (2)
(2)The most common value for β is 0.5. We assume this value for β throughout. Therefore, Eihm ranges between 0 and 1. In this perspective, the level of structural similarity is maximum (i.e., Eihm = 1) when the weights of each sector are equal in the exports of countries i and h to market m.
2.2 Inter-sectoral similarity
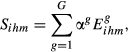 (3)
(3)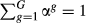 .
.  is calculated as in Equation 2 for each level g. The main difference between the index proposed in Crespo and Simões (2012) and the measure that we suggest in this paper is the fact that Crespo and Simões (2012) assume equal weights for all levels of sectoral disaggregation (i.e., a simple average) while we generalise that measure by allowing the weights to be defined according to the objectives of each study.
is calculated as in Equation 2 for each level g. The main difference between the index proposed in Crespo and Simões (2012) and the measure that we suggest in this paper is the fact that Crespo and Simões (2012) assume equal weights for all levels of sectoral disaggregation (i.e., a simple average) while we generalise that measure by allowing the weights to be defined according to the objectives of each study.This procedure allows us to take into account that some sectors are more similar in terms of their characteristics and production requirements. In comparison with Eihm, Sihm allows that distinct sectors at a higher level of sectoral disaggregation are classified as more similar if, when lower levels of disaggregation are considered, they belong to the same sector than when that does not occur.
The weights assigned to each level of disaggregation depend, as stated above, on the importance that the researcher wants to give to this dimension of structural similarity. Greater importance to this dimension implies more weight to less disaggregated levels of sectoral analysis. Of course, we should bear in mind that this option corresponds to assume a concept of trade competition based, in a higher proportion, on the level of potential competition instead of present competition, as explained in the Introduction.2
2.3 Intra-sectoral similarity
Several studies have reported an increasing specialisation by quality ranges at the international level, suggesting that besides inter-sectoral differences between the specialisation patterns of the countries, there are important intra-sectoral differences (Fontagné et al., 2008; Kaitila, 2010; Vandenbussche et al., 2013). In order to incorporate this aspect in the evaluation of the degree of structural similarity, it is necessary to measure the quality of the goods, which, by definition, is a complex task. When we consider trade data, the use of unit export values as a quality proxy is the usual procedure to overcome this problem (Stiglitz, 1987).
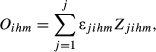 (4)
(4)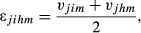 (5)
(5)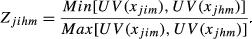 (6)
(6)For sector j, UV(xjim) and UV(xjhm) are the unit values of the exports from i and h to m, respectively.
Oihm works as an adjustment factor that reduces the level of structural similarity between i and h according to the average degree of intra-sectoral dissimilarity. In its turn, the degree of intra-sectoral similarity is calculated considering a weighted average of the differences, in each sector, in terms of quality ranges. The weights—expressed by ɛjihm—are the average share of j in the exports from i and h to m.
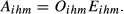 (7)
(7)When the unit export values of i and h to m are exactly the same, Zjihm = 1. If this is the case for all products, Oihm = 1 and, therefore, Aihm = Eihm. A greater difference in the unit export values implies a greater penalisation on Eihm, indicating a lower degree of structural similarity between i and h.
2.4 Structural similarity—an overall index
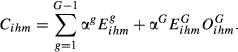 (8)
(8)Cihm is calculated in same way as Sihm (Equation 3) but now incorporating the adjustment suggested in the previous subsection in order to consider the intra-sectoral similarity. This adjustment is introduced only at the most disaggregated level of sectoral analysis because we need such level of detail to allow the assumption of prices as quality proxy. An important consequence of this aspect is however the fact that the importance given to intra-sectoral similarity depends on the weight given to the most disaggregated level of sectoral analysis (αG). Therefore, the value of αG should be high enough to account for intra-sectoral similarity and low enough to capture inter-sectoral similarity. The concrete values are of course a subjective decision of the researcher but, in our opinion, αG should range between 0.5 and 0.9.3
The index Cihm takes its maximum value (i.e., Cihm = 1) when the exports of i and h to market m are equal in terms of the three dimensions of structural similarity considered.
2.5 Total exports overlap
All the indexes discussed until now are (partial or overall) measures of structural similarity. In this subsection, we argue that the competition between two countries in a given market depends not only on the level of structural similarity but also on the value of total exports and, more specifically, on the degree of overlap between these two flows. A simple example illustrates the point. Let us consider three countries—A, B and C—and assume that the weights of all sectors are equal in the three countries, the only difference being the overall value of their exports, which is similar between A and B but very different between these countries and C. Although Eihm indicates a similar level of structural similarity between all pairs of countries (in this case, maximum similarity), these situations are distinct and express different levels of trade competition.
This question was introduced by Jenkins (2008) by referring that structural similarity indexes capture only the composition of the exports of the two countries under comparison and that this procedure implies obtaining a single value for a pair of countries. According to Jenkins (2008, p. 1355), “no index which implies that Honduras is as much a competitive threat to China's export markets as China is for Honduran exports is credible.” To overcome this limitation, Jenkins (2008) introduces two new indicators: the static and the dynamic index of competitive threat. These indexes reflect the proportion of total exports of a country concentrated in products in which the other country is globally competitive.
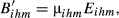 (9)
(9)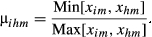 (10)
(10)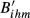 in which the adjustment of the structural similarity index depends on the importance given to this dimension. In this case, we have:4
in which the adjustment of the structural similarity index depends on the importance given to this dimension. In this case, we have:4
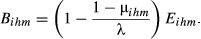 (11)
(11)The influence of the total exports overlap decreases as the parameter λ increases (λ ≥ 1), with Bihm converging to Eihm.
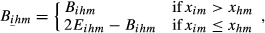 (12)
(12)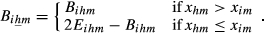 (13)
(13)Bihm and Bihm range between 0 and 2.
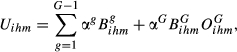 (14)
(14)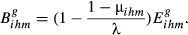 (15)
(15)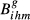 varies by country, we can also obtain indicators Uihm for each country. Uihm and Uihm are calculated using the same logic of Uihm:
varies by country, we can also obtain indicators Uihm for each country. Uihm and Uihm are calculated using the same logic of Uihm:
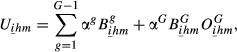 (16)
(16)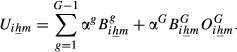 (17)
(17)3 Trade competition in a group of countries
In the previous section, we discussed our proposal for the measurement of trade competition between two countries in a given market. Table 1 summarises the indicators presented until this moment, highlighting the dimensions captured by each of them (Table 1). Each of these indicators is a trade competition index between i and h in market m and hereinafter will be designated in generic terms as TCIihm.
| TCI ihm | Structural similarity | Total exports overlap | Parameters | ||
|---|---|---|---|---|---|
| Sectoral shares similarity | Inter-sectoral similarity | Intra-sectoral similarity | |||
| E ihm | x | β | |||
| S ihm | x | x | β, αG(g = 1, …, G) | ||
| A ihm | x | x | β | ||
| C ihm | x | x | x | β, αG(g = 1, …, G) | |
| B ihm | x | x | β, λ | ||
| U ihm | x | x | x | x | β, αG(g = 1, …, G), λ |
In this section, we take a step forward by evaluating the overall level of trade competition between two countries in a group of markets (instead of only one).5 By broadening the spectrum of analysis, we gain an overall picture about the competitive threat that one country represents to another in all markets in which they compete.
Going from TCIihm to TCIih indicators introduces a new methodological challenge. Each country (potentially) exports to (M − 1) countries. However, this group of destination countries is not equal; there is one element that is different. In fact, while country i can export to country h, country h can export to country i. Our suggestion to overcome this problem involves the direct comparison of the bilateral flows between countries i and h.
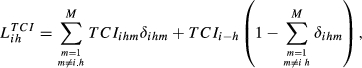 (18)
(18)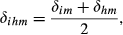 (19)
(19)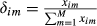 and
and 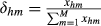 .
.In this case, maximum overall competition requires the existence of maximum similarity in the trade flows for each destination market.
Lih can be based on any of the TCIihm discussed in the previous sections. We will designate the Lih obtained from Eihm as  , from Aihm as
, from Aihm as 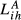 and so on.
and so on.
4 An example
Throughout the previous sections, we proposed a conceptual framework to measure the degree of trade competition between two countries. In order to illustrate the methodology, we now present an empirical example. We analyse the trade competition among six European economies—Germany (DE), France (FR), the United Kingdom (GB), Greece (GR), Hungary (HU) and Sweden (SE)—in 2007, 2011 and 2015. As destination markets, we include, in addition to these six countries, a total of 118 markets (i.e., M = 124), corresponding to the near totality of the trade flows from these countries (Germany: 99.28%; France: 98.22%; the United Kingdom: 98.46%; Greece: 98.15%; Hungary: 99.67%; and Sweden: 99.15%). An overview of the countries included in our sample is given in Table A1 in the Appendix.
Trade data (in value and volume) is drawn from Eurostat using the Harmonized Commodity Description and Coding System (HS nomenclature). The largest level of sectoral disaggregation is HS6. Additionally, for incorporating inter-sectoral similarity, exports data (in value) classified in terms of HS2 and HS4 are also considered.
Applying the methodological proposal presented in sections 2 and 3 to these data produces a large amount of very rich evidence. We will focus the analysis on the index described in section 3 (Lih) because this is built from the previous ones, and it is therefore possible to see how the different dimensions add to the understanding of the level of competition between each of the 15 pairs of countries.
4.1 Sectoral shares similarity
We will start with the Lih based on Eihm which is the index most frequently used in the literature to analyse structural similarity and which, for this reason, will provide a benchmark to measure the impact of the remaining dimensions of trade competition. To compute this index, we consider data at the most disaggregated level (HS6).
The results in Table 2 allow us to retain some important conclusions. First, a significant degree of heterogeneity is detected. In fact, considering the evidence for 2015, the values for the 15 country pairs range between 0.09 (GR-HU) and 0.426 (DE-FR).
| TCI ihm | E ihm | S ihm (1) | S ihm (2) | S ihm (3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | |

|
0.444 | 0.435 | 0.426 | 0.460 | 0.448 | 0.439 | 0.488 | 0.475 | 0.466 | 0.533 | 0.515 | 0.506 |
| (1.035) | (1.032) | (1.032) | (1.100) | (1.093) | (1.094) | (1.199) | (1.186) | (1.189) | ||||
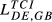
|
0.387 | 0.356 | 0.388 | 0.401 | 0.370 | 0.402 | 0.431 | 0.397 | 0.428 | 0.475 | 0.438 | 0.468 |
| (1.039) | (1.039) | (1.035) | (1.114) | (1.115) | (1.102) | (1.228) | (1.231) | (1.205) | ||||
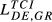
|
0.129 | 0.118 | 0.127 | 0.139 | 0.128 | 0.136 | 0.160 | 0.148 | 0.156 | 0.191 | 0.177 | 0.185 |
| (1.079) | (1.081) | (1.074) | (1.241) | (1.247) | (1.230) | (1.481) | (1.495) | (1.459) | ||||

|
0.248 | 0.264 | 0.309 | 0.266 | 0.280 | 0.326 | 0.301 | 0.314 | 0.360 | 0.354 | 0.363 | 0.410 |
| (1.069) | (1.061) | (1.054) | (1.213) | (1.186) | (1.165) | (1.426) | (1.372) | (1.329) | ||||
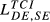
|
0.344 | 0.312 | 0.321 | 0.360 | 0.326 | 0.336 | 0.392 | 0.356 | 0.366 | 0.440 | 0.401 | 0.411 |
| (1.046) | (1.047) | (1.047) | (1.139) | (1.143) | (1.140) | (1.277) | (1.286) | (1.280) | ||||
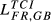
|
0.360 | 0.331 | 0.335 | 0.376 | 0.345 | 0.350 | 0.407 | 0.374 | 0.379 | 0.454 | 0.417 | 0.422 |
| (1.044) | (1.045) | (1.044) | (1.130) | (1.131) | (1.129) | (1.260) | (1.261) | (1.258) | ||||
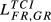
|
0.154 | 0.146 | 0.141 | 0.165 | 0.157 | 0.151 | 0.188 | 0.178 | 0.172 | 0.221 | 0.211 | 0.202 |
| (1.070) | (1.072) | (1.070) | (1.216) | (1.220) | (1.217) | (1.432) | (1.441) | (1.434) | ||||
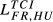
|
0.226 | 0.223 | 0.241 | 0.240 | 0.237 | 0.256 | 0.269 | 0.266 | 0.285 | 0.312 | 0.300 | 0.330 |
| (1.063) | (1.066) | (1.062) | (1.192) | (1.195) | (1.185) | (1.383) | (1.346) | (1.369) | ||||

|
0.282 | 0.264 | 0.248 | 0.299 | 0.278 | 0.264 | 0.332 | 0.307 | 0.296 | 0.382 | 0.351 | 0.343 |
| (1.060) | (1.056) | (1.064) | (1.177) | (1.165) | (1.191) | (1.353) | (1.331) | (1.381) | ||||
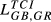
|
0.128 | 0.127 | 0.124 | 0.139 | 0.137 | 0.133 | 0.161 | 0.156 | 0.152 | 0.195 | 0.185 | 0.180 |
| (1.086) | (1.075) | (1.073) | (1.265) | (1.228) | (1.226) | (1.530) | (1.456) | (1.451) | ||||
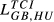
|
0.188 | 0.183 | 0.207 | 0.203 | 0.197) | 0.222 | 0.234 | 0.225 | 0.251 | 0.279 | 0.268 | 0.294 |
| (1.078) | (1.077) | (1.069) | (1.241) | (1.233) | (1.208) | (1.483) | (1.467) | (1.416) | ||||
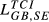
|
0.277 | 0.221 | 0.256 | 0.295 | 0.234 | 0.273 | 0.329 | 0.260 | 0.306 | 0.380 | 0.299 | 0.356 |
| (1.062) | (1.058) | (1.066) | (1.186) | (1.176) | (1.196) | (1.371) | (1.353) | (1.392) | ||||
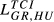
|
0.095 | 0.088 | 0.090 | 0.104 | 0.097 | 0.099 | 0.123 | 0.115 | 0.118 | 0.151 | 0.143 | 0.147 |
| (1.095) | (1.101) | (1.106) | (1.294) | (1.309) | (1.320) | (1.588) | (1.619) | (1.640) | ||||
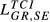
|
0.113 | 0.117 | 0.105 | 0.123 | 0.127 | 0.115 | 0.143 | 0.147 | 0.135 | 0.173 | 0.177 | 0.166 |
| (1.086) | (1.084) | (1.096) | (1.266) | (1.254) | (1.290) | (1.532) | (1.508) | (1.581) | ||||
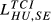
|
0.153 | 0.161 | 0.176 | 0.171 | 0.177 | 0.192 | 0.207 | 0.211 | 0.224 | 0.260 | 0.261 | 0.272 |
| (1.116) | (1.103) | (1.089) | (1.350) | (1.313) | (1.272) | (1.699) | (1.626) | (1.545) | ||||
-
Eihm is the structural similarity index between exporting countries i and h for market m (accounting for similarity in sectoral weights); Sihm is a trade competition index between exporting countries i and h for market m that accounts for sectoral weights similarity and inter-sectoral similarity; the methodological options for Sihm indicators are as follows: for Sihm(1), we have (α1, α2, α3) = (0.025; 0.075; 0.9); Sihm(2)—(α1, α2, α3) = (0.1; 0.15; 0.75); and Sihm(3)—(α1, α2, α3) = (0.2; 0.3; 0.5);
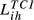 is an overall trade competition index for the country pair i and h. In this table, we have four different
is an overall trade competition index for the country pair i and h. In this table, we have four different  for each country pair (i.e.,
for each country pair (i.e., 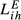 ,
, 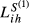 ,
, 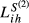 and
and 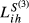 ); numbers between parentheses are the ratios
); numbers between parentheses are the ratios 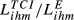 . Bold is used for the country pair having the highest value of the ratio
. Bold is used for the country pair having the highest value of the ratio 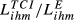 and italics for the pair with the minimum value.
and italics for the pair with the minimum value.
Second, DE-FR and DE-GB are the pairs that show the highest overall level of structural similarity, with values for 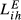 of 0.426 and 0.388, respectively. Other pairs that also reveal high levels of structural similarity are FR-GB (0.335) and DE-SE (0.321). Adding to this last result, we can verify that all the values of
of 0.426 and 0.388, respectively. Other pairs that also reveal high levels of structural similarity are FR-GB (0.335) and DE-SE (0.321). Adding to this last result, we can verify that all the values of 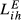 above 0.2 concern country pairs including at least one of the three largest European economies (Germany, France and the United Kingdom). Fourth, the pair that presents the lowest level of structural similarity (GR-HU) reveals an interesting characteristic: there are eight destination markets for which EGR,HU,m = 0. This contrasts with the average number of Eihm = 0 for all pairs which is 0.67. In our sample, Greece is the country that exports the smallest number of products to the 123 destination markets considered. Using the HS6 digit level, Greece exports on average 455 products (out of the 6,280 possible). This number compares with an average of 2,575 for Germany, 2,034 for France, 1,835 for the United Kingdom, 1,067 for Sweden and 677 for Hungary. This evidence means therefore that Greece and Hungary are exporting a small number of different products. Fifth, it is possible to say that the central message emerging from the data for 2015 is also valid for the two other years under analysis.
above 0.2 concern country pairs including at least one of the three largest European economies (Germany, France and the United Kingdom). Fourth, the pair that presents the lowest level of structural similarity (GR-HU) reveals an interesting characteristic: there are eight destination markets for which EGR,HU,m = 0. This contrasts with the average number of Eihm = 0 for all pairs which is 0.67. In our sample, Greece is the country that exports the smallest number of products to the 123 destination markets considered. Using the HS6 digit level, Greece exports on average 455 products (out of the 6,280 possible). This number compares with an average of 2,575 for Germany, 2,034 for France, 1,835 for the United Kingdom, 1,067 for Sweden and 677 for Hungary. This evidence means therefore that Greece and Hungary are exporting a small number of different products. Fifth, it is possible to say that the central message emerging from the data for 2015 is also valid for the two other years under analysis.
4.2 Inter-sectoral similarity
The incorporation of inter-sectoral similarity requires assigning weights to the different levels of sectoral disaggregation (HS2, HS4 and HS6). To minimise the subjectivity in this process, we test three alternative sets of values for these weights (α1, α2 and α3) gradually increasing the importance attributed to less disaggregated levels (HS2 and HS4).6 Each of these alternatives leads to a different Sihm indicator (Sihm(1), Sihm(2) and Sihm(3)) and consequently to a different Lih.
The results shown in Table 2 support two main conclusions. First, in comparison with the evidence drawn from 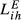 , there is an increase in the level of trade competition for all pairs of countries. This is of course an implication of the adjustment introduced by the consideration of the inter-sectoral dimension. In the extreme case, when α3 = 1 we obtain
, there is an increase in the level of trade competition for all pairs of countries. This is of course an implication of the adjustment introduced by the consideration of the inter-sectoral dimension. In the extreme case, when α3 = 1 we obtain  . The consideration of other levels of sectoral disaggregation obviously leads to an increase in the level of structural similarity. When lower values are assigned to α3, the impact of the inter-sectoral similarity is more pronounced and therefore the differential of
. The consideration of other levels of sectoral disaggregation obviously leads to an increase in the level of structural similarity. When lower values are assigned to α3, the impact of the inter-sectoral similarity is more pronounced and therefore the differential of  vis-à-vis
vis-à-vis 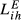 increases. Second, this increase is more pronounced for the pairs with the lowest values of
increases. Second, this increase is more pronounced for the pairs with the lowest values of 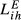 , namely GR-HU, GR-SE and HU-SE. Taken
, namely GR-HU, GR-SE and HU-SE. Taken 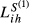 as example, the highest increase occurs in the case GR-HU in which
as example, the highest increase occurs in the case GR-HU in which 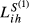 is 10.6% higher than
is 10.6% higher than 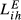 . This result can be compared with increases of 3.2% for the pair DE-FR and 3.5% for DE-GB.
. This result can be compared with increases of 3.2% for the pair DE-FR and 3.5% for DE-GB.
In the Appendix (Table A2), we present some complementary evidence. For each pair, the destination markets were ranked according to their average weight in total exports from the smallest to the largest value and then divided into ten groups (the number of destination markets for each pair is 123 and, except for the first three groups—less relevant markets—which include 13 countries each, the other seven groups have 12 countries each).
For all the 15 pairs considered, the 24 most important markets (groups 9 and 10) absorb more than 75% of total exports. For each group, we selected a set of indicators (Eihm, Sihm(2), Aihm, Bihm(2), Uihm(5)) and present their average values (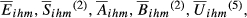 respectively).
respectively).
In Table A2, we present, for each group of destination markets, the ratios between the average values of TCIihm indexes and the average values of Eihm. From this evidence, we obtain a deeper understanding about the causes of the increase of the 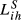 indicators (in comparison with
indicators (in comparison with 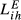 ). It is possible to conclude that, for the majority of the country pairs, the impact of introducing the inter-sectoral dimension is stronger in the first groups of countries, that is, in the case of the less important destination markets. For example, in the case of the pair GR-HU (which registers the highest increase of
). It is possible to conclude that, for the majority of the country pairs, the impact of introducing the inter-sectoral dimension is stronger in the first groups of countries, that is, in the case of the less important destination markets. For example, in the case of the pair GR-HU (which registers the highest increase of 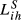 indicators vis-à-vis
indicators vis-à-vis 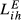 ), the evidence shows that the impact is more pronounced in groups 1–4. This occurs because: (i) since
), the evidence shows that the impact is more pronounced in groups 1–4. This occurs because: (i) since 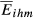 is a very small number, small increases in absolute terms give rise to considerable changes in relative terms; (ii) using the HS6 nomenclature, these countries are exporting different (although relatively similar) products. This means that there is a high likelihood that these products belong to the same category when we use the HS4 or HS2 nomenclatures. As an example, let us consider the case of group 2. The ratio between
is a very small number, small increases in absolute terms give rise to considerable changes in relative terms; (ii) using the HS6 nomenclature, these countries are exporting different (although relatively similar) products. This means that there is a high likelihood that these products belong to the same category when we use the HS4 or HS2 nomenclatures. As an example, let us consider the case of group 2. The ratio between 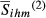 and
and 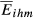 is 4.856. The destination markets that are most responsible for this increase are Costa Rica, Ivory Coast, Venezuela, Tanzania and Ecuador. The case of this last country is illustrative of what occurs with the less important markets. Using the HS6 nomenclature, Greece and Hungary export 39 and 88 products, respectively, for this market but only three products are the same (EGR,HU,m = 0.00001). However, using HS2, exports become concentrated in some categories such as sector 39 “Plastics and Articles Thereof,” sector 84 “Nuclear Reactors, Boilers, Machinery and Mechanical Appliances, Parts Thereof” and sector 90 “Optical, Photographic, Cinematographic, Measuring, Checking, Medical or Surgical Instruments and Apparatus; Parts and Accessories.” As a consequence, SGR,HU,m(2) = 0.017 which means that SGR,HU,m(2)/EGR,HU,m = 1,700.
is 4.856. The destination markets that are most responsible for this increase are Costa Rica, Ivory Coast, Venezuela, Tanzania and Ecuador. The case of this last country is illustrative of what occurs with the less important markets. Using the HS6 nomenclature, Greece and Hungary export 39 and 88 products, respectively, for this market but only three products are the same (EGR,HU,m = 0.00001). However, using HS2, exports become concentrated in some categories such as sector 39 “Plastics and Articles Thereof,” sector 84 “Nuclear Reactors, Boilers, Machinery and Mechanical Appliances, Parts Thereof” and sector 90 “Optical, Photographic, Cinematographic, Measuring, Checking, Medical or Surgical Instruments and Apparatus; Parts and Accessories.” As a consequence, SGR,HU,m(2) = 0.017 which means that SGR,HU,m(2)/EGR,HU,m = 1,700.
4.3 Intra-sectoral similarity
Table 3 contains the results for Lih based on Aihm—accounting for sectoral shares similarity and intra-sectoral similarity—and Cihm—also including inter-sectoral similarity.
| TCI ihm | A ihm | C ihm (1) | C ihm (2) | C ihm (3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | |

|
0.203 | 0.272 | 0.262 | 0.242 | 0.302 | 0.292 | 0.307 | 0.353 | 0.343 | 0.412 | 0.434 | 0.424 |
| (0.457) | (0.626) | (0.615) | (0.546) | (0.695) | (0.685) | (0.692) | (0.813) | (0.805) | (0.928) | (0.999) | (0.996) | |
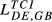
|
0.215 | 0.201 | 0.212 | 0.247 | 0.230 | 0.243 | 0.302 | 0.281 | 0.296 | 0.389 | 0.361 | 0.380 |
| (0.557) | (0.564) | (0.545) | (0.640) | (0.647) | (0.625) | (0.782) | (0.788) | (0.762) | (1.007) | (1.012) | (0.978) | |
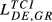
|
0.055 | 0.050 | 0.051 | 0.072 | 0.066 | 0.068 | 0.104 | 0.096 | 0.099 | 0.154 | 0.142 | 0.147 |
| (0.424) | (0.419) | (0.404) | (0.561) | (0.558) | (0.538) | (0.809) | (0.812) | (0.783) | (1.193) | (1.204) | (1.161) | |

|
0.128 | 0.141 | 0.164 | 0.157 | 0.169 | 0.196 | 0.211 | 0.221 | 0.251 | 0.294 | 0.301 | 0.338 |
| (0.513) | (0.534) | (0.532) | (0.631) | (0.641) | (0.633) | (0.848) | (0.836) | (0.814) | (1.182) | (1.139) | (1.095) | |
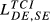
|
0.192 | 0.173 | 0.178 | 0.223 | 0.202 | 0.208 | 0.277 | 0.252 | 0.259 | 0.363 | 0.331 | 0.339 |
| (0.557) | (0.555) | (0.556) | (0.647) | (0.647) | (0.647) | (0.806) | (0.809) | (0.807) | (1.056) | (1.063) | (1.058) | |
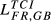
|
0.143 | 0.170 | 0.167 | 0.181 | 0.201 | 0.199 | 0.244 | 0.254 | 0.252 | 0.345 | 0.337 | 0.338 |
| (0.397) | (0.515) | (0.498) | (0.502) | (0.609) | (0.592) | (0.678) | (0.767) | (0.752) | (0.959) | (1.019) | (1.007) | |
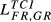
|
0.054 | 0.068 | 0.060 | 0.075 | 0.086 | 0.078 | 0.112 | 0.120 | 0.111 | 0.171 | 0.172 | 0.162 |
| (0.349) | (0.466) | (0.428) | (0.484) | (0.591) | (0.556) | (0.727) | (0.820) | (0.788) | (1.106) | (1.174) | (1.148) | |
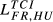
|
0.071 | 0.112 | 0.116 | 0.101 | 0.138 | 0.144 | 0.153 | 0.184 | 0.192 | 0.235 | 0.248 | 0.268 |
| (0.314) | (0.502) | (0.483) | (0.446) | (0.619) | (0.597) | (0.677) | (0.825) | (0.797) | (1.040) | (1.115) | (1.111) | |

|
0.108 | 0.130 | 0.118 | 0.142 | 0.158 | 0.147 | 0.201 | 0.207 | 0.198 | 0.295 | 0.284 | 0.278 |
| (0.383) | (0.491) | (0.475) | (0.505) | (0.598) | (0.592) | (0.714) | (0.784) | (0.797) | (1.045) | (1.076) | (1.118) | |
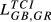
|
0.046 | 0.051 | 0.045 | 0.065 | 0.069 | 0.062 | 0.100 | 0.099 | 0.093 | 0.154 | 0.147 | 0.140 |
| (0.358) | (0.404) | (0.365) | (0.508) | (0.538) | (0.501) | (0.783) | (0.781) | (0.749) | (1.208) | (1.158) | (1.134) | |
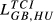
|
0.078 | 0.078 | 0.086 | 0.103 | 0.102 | 0.112 | 0.151 | 0.147 | 0.159 | 0.224 | 0.216 | 0.233 |
| (0.412) | (0.426) | (0.414) | (0.548) | (0.560) | (0.542) | (0.800) | (0.803) | (0.769) | (1.188) | (1.180) | (1.123) | |
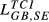
|
0.126 | 0.101 | 0.112 | 0.159 | 0.126 | 0.143 | 0.216 | 0.170 | 0.198 | 0.305 | 0.239 | 0.284 |
| (0.456) | (0.456) | (0.438) | (0.572) | (0.569) | (0.561) | (0.778) | (0.769) | (0.775) | (1.099) | (1.081) | (1.111) | |
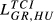
|
0.033 | 0.035 | 0.035 | 0.048 | 0.049 | 0.050 | 0.076 | 0.076 | 0.078 | 0.120 | 0.116 | 0.120 |
| (0.343) | (0.400) | (0.395) | (0.503) | (0.561) | (0.561) | (0.801) | (0.859) | (0.867) | (1.259) | (1.319) | (1.338) | |
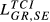
|
0.036 | 0.047 | 0.037 | 0.053 | 0.064 | 0.054 | 0.085 | 0.094 | 0.084 | 0.134 | 0.142 | 0.132 |
| (0.318) | (0.401) | (0.352) | (0.472) | (0.545) | (0.512) | (0.755) | (0.804) | (0.804) | (1.191) | (1.208) | (1.256) | |
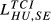
|
0.058 | 0.065 | 0.068 | 0.085 | 0.091 | 0.095 | 0.135 | 0.139 | 0.143 | 0.213 | 0.213 | 0.218 |
| (0.378) | (0.403) | (0.389) | (0.556) | (0.566) | (0.539) | (0.883) | (0.865) | (0.814) | (1.388) | (1.327) | (1.239) | |
-
Aihm is a trade competition index between exporting countries i and h for market m that accounts for sectoral weights similarity and intra-sectoral similarity; Cihm is a trade competition index between exporting countries i and h for market m that accounts for sectoral weights similarity, inter-sectoral similarity and intra-sectoral similarity; the methodological options for the Cihm indicators are as follows: for Cihm(1), we have (α1, α2, α2) = (0.025; 0.075; 0.9); Cihm(2)—(α1, α2, α2) = (0.1; 0.15; 0.75); and Cihm(3)—(α1, α2, α2) = (0.2; 0.3; 0.5);
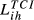 is an overall trade competition index for the country pair i and h. In this table, we have four different
is an overall trade competition index for the country pair i and h. In this table, we have four different  for each country pair (i.e.,
for each country pair (i.e., 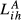 ,
, 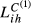 ,
, 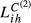 and
and 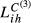 ); numbers between parentheses are the ratios
); numbers between parentheses are the ratios 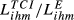 . Bold is used for the country pair having the highest value of the ratio
. Bold is used for the country pair having the highest value of the ratio 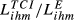 and italics for the pair with the minimum value.
and italics for the pair with the minimum value.
Let us consider, once again, 2015 as reference year. A first important finding is that there is a strong similarity in the quality ranges of the products exported by the following country pairs: DE-FR (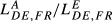 = 0.615), DE-SE (
= 0.615), DE-SE ( = 0.556), DE-GB (
= 0.556), DE-GB (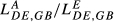 = 0.545) and DE-HU (
= 0.545) and DE-HU (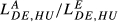 = 0.532). While the results for the first three pairs are expected, the fourth is less obvious. However, this evidence should be understood in a historical context where Hungary has been showing a strong improvement in terms of quality of exports. This evolution is not new. Crespo and Fontoura (2007) conclude that, in 2003, Hungary is one of the Central and Eastern European Countries where the weight of the higher categories in terms of quality ranges is the highest. Moreover, this study concludes that, in the case of Estonia, Slovakia and Hungary, “exports of a higher quality correspond to sectors with a higher weight on trade” (Crespo and Fontoura, 2007, pp. 625–626). This idea also helps to explain the evidence obtained in our analysis. In fact, in the present case, we can say that Germany and Hungary, despite some differences in terms of sectoral shares, have some important sectors in which the unit values of exports are similar, conducing to high values for Zjihm. This occurs, for example, in the following sectors: sector 84 “Nuclear Reactors, Boilers, Machinery and Mechanical Appliances; Parts Thereof,” sector 85 “Electrical Machinery and Equipment and Parts Thereof; Sound Recorders and Reproducers; Television Image and Sound Recorders and Reproducers, Parts and Accessories of such Articles” and sector 87 “Vehicles; Other than Railway or Tramway Rolling Stock, and Parts and Accessories Thereof.”
= 0.532). While the results for the first three pairs are expected, the fourth is less obvious. However, this evidence should be understood in a historical context where Hungary has been showing a strong improvement in terms of quality of exports. This evolution is not new. Crespo and Fontoura (2007) conclude that, in 2003, Hungary is one of the Central and Eastern European Countries where the weight of the higher categories in terms of quality ranges is the highest. Moreover, this study concludes that, in the case of Estonia, Slovakia and Hungary, “exports of a higher quality correspond to sectors with a higher weight on trade” (Crespo and Fontoura, 2007, pp. 625–626). This idea also helps to explain the evidence obtained in our analysis. In fact, in the present case, we can say that Germany and Hungary, despite some differences in terms of sectoral shares, have some important sectors in which the unit values of exports are similar, conducing to high values for Zjihm. This occurs, for example, in the following sectors: sector 84 “Nuclear Reactors, Boilers, Machinery and Mechanical Appliances; Parts Thereof,” sector 85 “Electrical Machinery and Equipment and Parts Thereof; Sound Recorders and Reproducers; Television Image and Sound Recorders and Reproducers, Parts and Accessories of such Articles” and sector 87 “Vehicles; Other than Railway or Tramway Rolling Stock, and Parts and Accessories Thereof.”
On the other extreme, showing higher levels of dissimilarity in terms of quality ranges exported (with ratios between 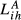 and
and 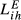 below 0.4), we can identify the pairs GR-SE, GB-GR, HU-SE and GR-HU. Despite some obvious differences in quantitative terms, the key ideas emerging from
below 0.4), we can identify the pairs GR-SE, GB-GR, HU-SE and GR-HU. Despite some obvious differences in quantitative terms, the key ideas emerging from  remain valid for all the years considered.
remain valid for all the years considered.
Complementing this result with the evidence from Table A2, we see that the difference (in relative terms) between 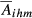 and
and 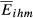 is smaller for the pair DE-FR than for the other pairs and that this higher similarity is found for all ten groups of countries with the exception of groups 3 and 4.
is smaller for the pair DE-FR than for the other pairs and that this higher similarity is found for all ten groups of countries with the exception of groups 3 and 4.
Turning now to Lih based on Cihm, what occurs in this case is a consequence of what we concluded from the pieces we have gathered until this moment. When we consider 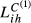 , the conclusions are very similar to those derived from
, the conclusions are very similar to those derived from 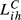 , which is not surprising because in this specific case α3 is 0.9 and therefore the inter-sectoral dimension has a small impact on the overall measure of structural similarity. When lower values for α3 are considered, which occurs with
, which is not surprising because in this specific case α3 is 0.9 and therefore the inter-sectoral dimension has a small impact on the overall measure of structural similarity. When lower values for α3 are considered, which occurs with 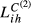 and even more with
and even more with 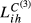 , the impact of the several dimensions changes. For example, in this last case, the conclusions obtained from
, the impact of the several dimensions changes. For example, in this last case, the conclusions obtained from 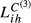 reveal the high influence of the inter-sectoral dimension. In all the cases, however, the ranking of the country pairs does not change significantly in terms of their degree of structural similarity, allowing to retain some of the key ideas presented above, namely the high level of structural similarity registered among the largest European economies.
reveal the high influence of the inter-sectoral dimension. In all the cases, however, the ranking of the country pairs does not change significantly in terms of their degree of structural similarity, allowing to retain some of the key ideas presented above, namely the high level of structural similarity registered among the largest European economies.
4.4 Total exports overlap
The 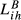 indexes attend simultaneously to sectoral shares similarity and total exports overlap (Table 4). We use three alternative values for the parameter λ involved in these indexes. With λ = 1 (full incorporation of the total exports overlap dimension), from
indexes attend simultaneously to sectoral shares similarity and total exports overlap (Table 4). We use three alternative values for the parameter λ involved in these indexes. With λ = 1 (full incorporation of the total exports overlap dimension), from 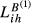 it is possible to conclude that, in all years under analysis, there is a less pronounced decrease in the index for the pair FR-GB (
it is possible to conclude that, in all years under analysis, there is a less pronounced decrease in the index for the pair FR-GB (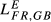 = 0.335 drops to
= 0.335 drops to  = 0.190, in 2015)7 due to the fact that these countries have the most similar global dimension (in terms of total exports).
= 0.190, in 2015)7 due to the fact that these countries have the most similar global dimension (in terms of total exports).
| TCI ihm | B ihm (2) | U ihm (2) | U ihm (5) | U ihm (8) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | |

|
0.330 | 0.317 | 0.307 | 0.179 | 0.221 | 0.212 | 0.227 | 0.258 | 0.248 | 0.304 | 0.316 | 0.306 |
| (0.742) | (0.728) | (0.722) | (0.403) | (0.509) | (0.498) | (0.511) | (0.593) | (0.583) | (0.685) | (0.726) | (0.718) | |
|
0.261 | 0.241 | 0.263 | 0.167 | 0.156 | 0.165 | 0.204 | 0.190 | 0.201 | 0.263 | 0.244 | 0.258 |
| (0.675) | (0.677) | (0.677) | (0.432) | (0.438) | (0.424) | (0.528) | (0.534) | (0.516) | (0.680) | (0.685) | (0.663) | |
|
0.073 | 0.068 | 0.071 | 0.041 | 0.038 | 0.038 | 0.059 | 0.054 | 0.055 | 0.086 | 0.080 | 0.081 |
| (0.568) | (0.572) | (0.557) | (0.319) | (0.318) | (0.299) | (0.456) | (0.460) | (0.432) | (0.669) | (0.679) | (0.639) | |

|
0.157 | 0.164 | 0.193 | 0.101 | 0.106 | 0.124 | 0.134 | 0.138 | 0.158 | 0.185 | 0.186 | 0.211 |
| (0.633) | (0.622) | (0.624) | (0.407) | (0.402) | (0.401) | (0.540) | (0.521) | (0.511) | (0.746) | (0.704) | (0.682) | |
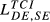
|
0.212 | 0.193 | 0.196 | 0.138 | 0.126 | 0.128 | 0.171 | 0.157 | 0.158 | 0.223 | 0.204 | 0.206 |
| (0.617) | (0.620) | (0.612) | (0.402) | (0.405) | (0.399) | (0.498) | (0.503) | (0.494) | (0.649) | (0.656) | (0.643) | |
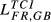
|
0.281 | 0.259 | 0.263 | 0.141 | 0.158 | 0.156 | 0.191 | 0.199 | 0.198 | 0.269 | 0.264 | 0.265 |
| (0.779) | (0.785) | (0.783) | (0.392) | (0.477) | (0.464) | (0.530) | (0.602) | (0.589) | (0.748) | (0.799) | (0.789) | |
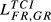
|
0.086 | 0.084 | 0.080 | 0.041 | 0.051 | 0.044 | 0.062 | 0.069 | 0.062 | 0.094 | 0.098 | 0.091 |
| (0.557) | (0.574) | (0.564) | (0.267) | (0.346) | (0.314) | (0.401) | (0.473) | (0.443) | (0.610) | (0.670) | (0.642) | |
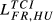
|
0.148 | 0.148 | 0.161 | 0.066 | 0.091 | 0.096 | 0.100 | 0.120 | 0.128 | 0.152 | 0.167 | 0.177 |
| (0.655) | (0.663) | (0.666) | (0.293) | (0.408) | (0.399) | (0.442) | (0.541) | (0.530) | (0.675) | (0.748) | (0.735) | |

|
0.179 | 0.168 | 0.156 | 0.090 | 0.100 | 0.092 | 0.127 | 0.131 | 0.124 | 0.186 | 0.180 | 0.174 |
| (0.634) | (0.636) | (0.627) | (0.320) | (0.379) | (0.370) | (0.452) | (0.498) | (0.498) | (0.660) | (0.684) | (0.699) | |
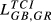
|
0.075 | 0.077 | 0.073 | 0.038 | 0.042 | 0.037 | 0.058 | 0.060 | 0.055 | 0.089 | 0.087 | 0.082 |
| (0.585) | (0.602) | (0.593) | (0.298) | (0.327) | (0.298) | (0.455) | (0.467) | (0.441) | (0.699) | (0.686) | (0.665) | |
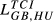
|
0.126 | 0.121 | 0.138 | 0.070 | 0.068 | 0.076 | 0.101 | 0.097 | 0.106 | 0.148 | 0.141 | 0.154 |
| (0.669) | (0.663) | (0.668) | (0.370) | (0.374) | (0.365) | (0.534) | (0.531) | (0.512) | (0.788) | (0.773) | (0.743) | |
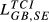
|
0.185 | 0.146 | 0.164 | 0.106 | 0.083 | 0.092 | 0.144 | 0.113 | 0.127 | 0.204 | 0.158 | 0.181 |
| (0.666) | (0.661) | (0.640) | (0.382) | (0.377) | (0.360) | (0.520) | (0.510) | (0.495) | (0.735) | (0.717) | (0.708) | |
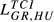
|
0.060 | 0.054 | 0.056 | 0.030 | 0.031 | 0.032 | 0.048 | 0.047 | 0.049 | 0.076 | 0.072 | 0.076 |
| (0.629) | (0.618) | (0.628) | (0.317) | (0.348) | (0.354) | (0.505) | (0.532) | (0.547) | (0.794) | (0.816) | (0.845) | |
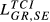
|
0.065 | 0.070 | 0.064 | 0.031 | 0.039 | 0.033 | 0.049 | 0.057 | 0.052 | 0.078 | 0.085 | 0.081 |
| (0.577) | (0.597) | (0.610) | (0.273) | (0.332) | (0.316) | (0.437) | (0.487) | (0.495) | (0.693) | (0.727) | (0.772) | |
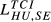
|
0.111 | 0.115 | 0.125 | 0.062 | 0.066 | 0.067 | 0.098 | 0.099 | 0.101 | 0.153 | 0.152 | 0.153 |
| (0.722) | (0.719) | (0.708) | (0.403) | (0.409) | (0.380) | (0.638) | (0.619) | (0.572) | (1.000) | (0.944) | (0.868) | |
-
Bihm is a trade competition index between exporting countries i and h for market m that accounts for sectoral weights similarity and total exports overlap; Uihm is a trade competition index between exporting countries i and h for market m that accounts for sectoral weights similarity, inter-sectoral similarity, intra-sectoral similarity and total exports overlap; the methodological option for Bihm(2) is λ = 2; the methodological options for the Uihm indicators are as follows: for Uihm(2), we have (α1, α2, α2, λ) = (0.025; 0.075; 0.9; 2); Uihm(5)—(α1, α2, α2, λ) = (0.1; 0.15; 0.75; 2); and Uihm(8)—(α1, α2, α2, λ) = (0.2; 0.3; 0.5; 2);
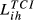 is an overall trade competition index for the country pair i and h. In this table, we have four different
is an overall trade competition index for the country pair i and h. In this table, we have four different 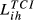 for each country pair (i.e.,
for each country pair (i.e., 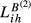 ,
, 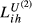 ,
, 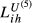 and
and 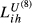 ); numbers between parentheses are the ratios
); numbers between parentheses are the ratios 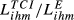 . Bold is used for the country pair having the highest value of the ratio
. Bold is used for the country pair having the highest value of the ratio 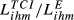 and italics for the pair with the minimum value.
and italics for the pair with the minimum value.
In the case of 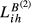 and
and 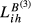 , the indicators suffer a lower decrease when compared with the impact on
, the indicators suffer a lower decrease when compared with the impact on 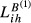 . Nevertheless, the qualitative impact is similar in what concerns the ranking of the most penalised country pairs. Considering once again the evidence presented in Table A2, we can see that, with the exception of groups 4 and 5, it is for the pair FR-GB that we find a narrower gap between
. Nevertheless, the qualitative impact is similar in what concerns the ranking of the most penalised country pairs. Considering once again the evidence presented in Table A2, we can see that, with the exception of groups 4 and 5, it is for the pair FR-GB that we find a narrower gap between 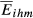 and
and 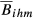 (2).
(2).
Regarding 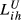 , the overall trade competition indexes capturing simultaneously the three dimensions of structural similarity and total exports overlap, we calculate nine alternatives resulting from varying the values given to α1, α2, α3 and λ. In Table 4, we present three of these alternatives which are developed assuming λ = 2 and three alternative sets of parameters for α1, α2, and α3: Uihm(2) is based on (α1, α2, α3) = (0.025, 0.075, 0.9); Uihm(5)—(α1, α2, α3) = (0.1, 0.15, 0.75); and Uihm(8)—(α1, α2, α3) = (0.2, 0.3, 0.5). The remaining alternatives are presented in the Appendix (Table A3).
, the overall trade competition indexes capturing simultaneously the three dimensions of structural similarity and total exports overlap, we calculate nine alternatives resulting from varying the values given to α1, α2, α3 and λ. In Table 4, we present three of these alternatives which are developed assuming λ = 2 and three alternative sets of parameters for α1, α2, and α3: Uihm(2) is based on (α1, α2, α3) = (0.025, 0.075, 0.9); Uihm(5)—(α1, α2, α3) = (0.1, 0.15, 0.75); and Uihm(8)—(α1, α2, α3) = (0.2, 0.3, 0.5). The remaining alternatives are presented in the Appendix (Table A3).
From the results presented in Table 4, we conclude that, with the exception of 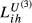 in 2007, the three country pairs comparing the largest European economies reveal the highest values in all the measures considered, that is, for all years and combination of parameters, despite some obvious quantitative differences. This evidence arises from a combination of effects: (i) less accentuated difference in terms of total exports; (ii) the highest similarity in terms of sectoral shares; and (iii) similarity in the quality ranges exported.
in 2007, the three country pairs comparing the largest European economies reveal the highest values in all the measures considered, that is, for all years and combination of parameters, despite some obvious quantitative differences. This evidence arises from a combination of effects: (i) less accentuated difference in terms of total exports; (ii) the highest similarity in terms of sectoral shares; and (iii) similarity in the quality ranges exported.
4.5 An analysis by exporting country
Finally, Table 5 contains evidence concerning the idea introduced in subsection 2.5 that to measure competition for one pair of countries, instead of only one index we should have a different value for each of the countries under consideration. For this analysis, we have selected some 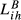 and
and 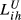 indicators with different values for the parameters.
indicators with different values for the parameters.
| Pairs | TCI ihm = B ihm (2) | TCI ihm = U ihm (2) | TCI ihm = U ihm (5) | TCI ihm = U ihm (8) |
|---|---|---|---|---|
| DE,FR |  = 0.307 = 0.307 |
 = 0.212 = 0.212 |
 = 0.248 = 0.248 |
 = 0.306 = 0.306 |
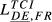 = 0.314 = 0.314 |
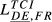 = 0.216 = 0.216 |
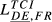 = 0.253 = 0.253 |
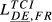 = 0.312 = 0.312 |
|
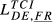 = 0.537 = 0.537 |
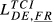 = 0.368 = 0.368 |
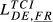 = 0.433 = 0.433 |
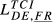 = 0.536 = 0.536 |
|
| DE,GB | 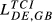 = 0.263 = 0.263 |
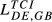 = 0.165 = 0.165 |
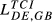 = 0.201 = 0.201 |
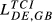 = 0.258 = 0.258 |
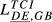 = 0.274 = 0.274 |
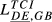 = 0.171 = 0.171 |
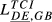 = 0.208 = 0.208 |
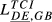 = 0.267 = 0.267 |
|
 = 0.503 = 0.503 |
 = 0.315 = 0.315 |
 = 0.384 = 0.384 |
 = 0.492 = 0.492 |
|
| DE,GR | 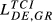 = 0.071 = 0.071 |
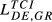 = 0.038 = 0.038 |
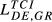 = 0.055 = 0.055 |
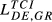 = 0.081 = 0.081 |
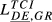 = 0.077 = 0.077 |
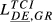 = 0.041 = 0.041 |
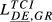 = 0.059 = 0.059 |
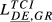 = 0.087 = 0.087 |
|
 = 0.176 = 0.176 |
 = 0.095 = 0.095 |
 = 0.139 = 0.139 |
 = 0.207 = 0.207 |
|
| DE,HU |  = 0.193 = 0.193 |
 = 0.124 = 0.124 |
 = 0.158 = 0.158 |
 = 0.211 = 0.211 |
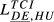 = 0.203 = 0.203 |
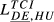 = 0.131 = 0.131 |
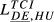 = 0.166 = 0.166 |
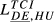 = 0.222 = 0.222 |
|
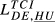 = 0.415 = 0.415 |
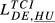 = 0.260 = 0.260 |
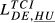 = 0.336 = 0.336 |
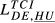 = 0.455 = 0.455 |
|
| DE,SE |  = 0.196 = 0.196 |
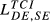 = 0.128 = 0.128 |
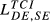 = 0.158 = 0.158 |
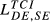 = 0.206 = 0.206 |
 = 0.205 = 0.205 |
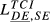 = 0.134 = 0.134 |
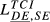 = 0.166 = 0.166 |
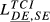 = 0.215 = 0.215 |
|
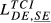 = 0.437 = 0.437 |
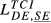 = 0.281 = 0.281 |
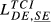 = 0.352 = 0.352 |
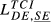 = 0.464 = 0.464 |
|
| FR,GB | 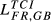 = 0.263 = 0.263 |
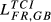 = 0.156 = 0.156 |
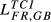 = 0.198 = 0.198 |
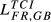 = 0.265 = 0.265 |
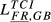 = 0.321 = 0.321 |
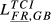 = 0.189 = 0.189 |
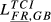 = 0.240 = 0.240 |
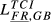 = 0.322 = 0.322 |
|
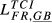 = 0.350 = 0.350 |
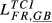 = 0.208 = 0.208 |
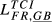 = 0.264 = 0.264 |
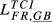 = 0.353 = 0.353 |
|
| FR,GR | 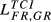 = 0.080 = 0.080 |
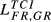 = 0.044 = 0.044 |
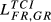 = 0.062 = 0.062 |
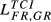 = 0.091 = 0.091 |
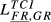 = 0.094 = 0.094 |
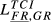 = 0.052 = 0.052 |
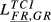 = 0.073 = 0.073 |
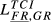 = 0.105 = 0.105 |
|
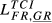 = 0.188 = 0.188 |
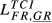 = 0.105 = 0.105 |
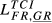 = 0.150 = 0.150 |
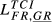 = 0.219 = 0.219 |
|
| FR,HU | 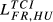 = 0.161 = 0.161 |
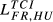 = 0.096 = 0.096 |
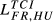 = 0.128 = 0.128 |
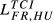 = 0.177 = 0.177 |
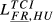 = 0.175 = 0.175 |
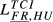 = 0.104 = 0.104 |
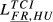 = 0.139 = 0.139 |
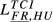 = 0.192 = 0.192 |
|
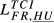 = 0.307 = 0.307 |
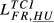 = 0.183 = 0.183 |
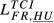 = 0.246 = 0.246 |
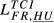 = 0.343 = 0.343 |
|
| FR,SE |  = 0.156 = 0.156 |
 = 0.092 = 0.092 |
 = 0.124 = 0.124 |
 = 0.174 = 0.174 |
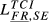 = 0.189 = 0.189 |
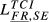 = 0.113 = 0.113 |
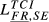 = 0.151 = 0.151 |
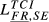 = 0.210 = 0.210 |
|
 = 0.308 = 0.308 |
 = 0.181 = 0.181 |
 = 0.245 = 0.245 |
 = 0.346 = 0.346 |
|
| GB,GR | 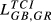 = 0.073 = 0.073 |
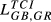 = 0.037 = 0.037 |
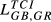 = 0.055 = 0.055 |
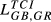 = 0.082 = 0.082 |
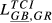 = 0.083 = 0.083 |
 = 0.042 = 0.042 |
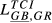 = 0.061 = 0.061 |
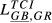 = 0.092 = 0.092 |
|
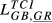 = 0.165 = 0.165 |
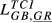 = 0.083 = 0.083 |
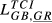 = 0.124 = 0.124 |
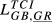 = 0.189 = 0.189 |
|
| GB,HU | 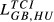 = 0.138 = 0.138 |
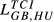 = 0.076 = 0.076 |
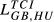 = 0.106 = 0.106 |
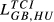 = 0.154 = 0.154 |
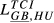 = 0.163 = 0.163 |
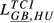 = 0.089 = 0.089 |
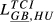 = 0.125 = 0.125 |
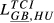 = 0.182 = 0.182 |
|
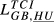 = 0.251 = 0.251 |
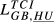 = 0.136 = 0.136 |
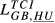 = 0.194 = 0.194 |
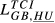 = 0.284 = 0.284 |
|
| GB,SE | 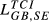 = 0.164 = 0.164 |
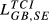 = 0.092 = 0.092 |
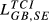 = 0.127 = 0.127 |
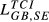 = 0.181 = 0.181 |
 = 0.199 = 0.199 |
 = 0.112 = 0.112 |
 = 0.153 = 0.153 |
 = 0.218 = 0.218 |
|
 = 0.312 = 0.312 |
 = 0.174 = 0.174 |
 = 0.243 = 0.243 |
 = 0.351 = 0.351 |
|
| GR,HU |  = 0.056 = 0.056 |
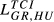 = 0.032 = 0.032 |
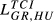 0.049 0.049 |
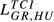 = 0.076 = 0.076 |
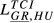 = 0.115 = 0.115 |
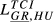 = 0.065 = 0.065 |
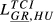 = 0.100 = 0.100 |
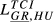 = 0.153 = 0.153 |
|
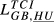 = 0.065 = 0.065 |
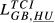 = 0.036 = 0.036 |
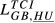 = 0.056 = 0.056 |
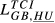 = 0.087 = 0.087 |
|
| GR,SE | 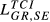 = 0.064 = 0.064 |
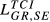 = 0.033 = 0.033 |
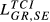 = 0.052 = 0.052 |
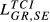 = 0.081 = 0.081 |
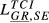 = 0.129 = 0.129 |
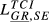 = 0.065 = 0.065 |
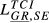 = 0.104 = 0.104 |
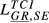 = 0.164 = 0.164 |
|
 = 0.080 = 0.080 |
 = 0.042 = 0.042 |
 = 0.065 = 0.065 |
 = 0.090 = 0.090 |
|
| HU,SE | 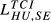 = 0.125 = 0.125 |
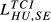 = 0.067 = 0.067 |
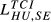 = 0.101 = 0.101 |
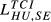 = 0.153 = 0.153 |
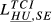 = 0.183 = 0.183 |
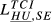 = 0.099 = 0.099 |
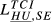 = 0.151 = 0.151 |
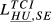 = 0.231 = 0.231 |
|
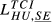 = 0.169 = 0.169 |
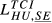 = 0.091 = 0.091 |
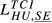 = 0.136 = 0.136 |
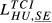 = 0.206 = 0.206 |
-
The methodological options concerning the TCIihm indicators are explained in Table 4;
 and
and 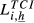 are the trade competition indexes for countries i and h, respectively.
are the trade competition indexes for countries i and h, respectively.
There are interesting results to highlight from Table 5. First, the evidence obtained with 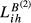 emphasises the fact that the smaller country may suffer an important increase in its country-specific index. This makes clear that the larger countries are stronger competitors than we can infer from the analysis of the baseline index (
emphasises the fact that the smaller country may suffer an important increase in its country-specific index. This makes clear that the larger countries are stronger competitors than we can infer from the analysis of the baseline index (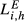 ). The results provided in the first column of Table 5 allow us to conclude that Greece is the country that suffers the strongest competition from the three larger European economies. In fact, when we compare the
). The results provided in the first column of Table 5 allow us to conclude that Greece is the country that suffers the strongest competition from the three larger European economies. In fact, when we compare the 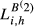 with
with 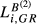 (i = DE, GB, FR), it is possible to see very high increases in the country-specific index for Greece. The ratios between the country-specific index and the baseline index are 2.48 for the pair DE-GR, 2.35 for the pair FR-GR and 2.26 for the pair GB-GR. Second, other pairs with a very significant impact for the smaller country include DE-SE (with a ratio of 2.23) and DE-HU (with a ratio of 2.15). Third, the gap between
(i = DE, GB, FR), it is possible to see very high increases in the country-specific index for Greece. The ratios between the country-specific index and the baseline index are 2.48 for the pair DE-GR, 2.35 for the pair FR-GR and 2.26 for the pair GB-GR. Second, other pairs with a very significant impact for the smaller country include DE-SE (with a ratio of 2.23) and DE-HU (with a ratio of 2.15). Third, the gap between 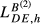 and the correspondent
and the correspondent 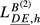 is small for all the countries h considered (France, the United Kingdom, Greece, Hungary and Sweden). For example, with data for 2015, the gap between
is small for all the countries h considered (France, the United Kingdom, Greece, Hungary and Sweden). For example, with data for 2015, the gap between 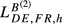 and
and 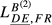 is very small (
is very small (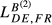 = 0.307;
= 0.307; 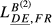 = 0.314). The same occurs, in qualitative terms, for the remaining countries. In fact, the increases registered by the indexes for Germany are always inferior to 10%. This result arises because German exports are higher than the values presented by France in 95 markets, the United Kingdom in 106 markets, Greece in 120 markets, Hungary in 122 markets and Sweden in 121 markets. Fourth, the other pair presenting a gap of similar magnitude between
= 0.314). The same occurs, in qualitative terms, for the remaining countries. In fact, the increases registered by the indexes for Germany are always inferior to 10%. This result arises because German exports are higher than the values presented by France in 95 markets, the United Kingdom in 106 markets, Greece in 120 markets, Hungary in 122 markets and Sweden in 121 markets. Fourth, the other pair presenting a gap of similar magnitude between 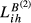 and the indicator for the larger exporter is FR-HU (
and the indicator for the larger exporter is FR-HU (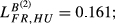
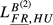 = 0.175, with an increase of 8.7%). Fifth, FR-GB and HU-SE reveal the smallest gap between
= 0.175, with an increase of 8.7%). Fifth, FR-GB and HU-SE reveal the smallest gap between 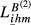 and
and 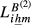 (
(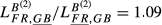 and (
and ( ). These are the two pairs with closest values of total exports (xFR/xGB = 1.11 and xSE/xHU = 1.41). However, France exports more than the United Kingdom to 81 markets while Sweden exports more than Hungary for 95 markets. Finally, the findings for the indicators
). These are the two pairs with closest values of total exports (xFR/xGB = 1.11 and xSE/xHU = 1.41). However, France exports more than the United Kingdom to 81 markets while Sweden exports more than Hungary for 95 markets. Finally, the findings for the indicators 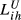 are, in general terms, similar to those using the
are, in general terms, similar to those using the 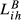 indicators.
indicators.
5 Conclusion
The main goal of the present study was the methodological discussion of a set of measures that allow a broader understanding of the concept of trade competition. We defined this concept as being a function of both structural similarity and total exports overlap while, in turn, the first concept encapsulates three dimensions: (i) sectoral shares similarity, as in the standard KSI or similar measures; (ii) intra-sectoral similarity; and (iii) inter-sectoral similarity. Building on this multidimensional concept, we propose indexes that allow the quantification of the trade competition phenomenon both in a specific destination market and in a group of markets. Of course, as we propose several measures, each one including different dimensions of similarity, the evidence obtained concerning the ranking of country pairs in terms of trade competition depends on the specific measure considered in the analysis. Therefore, a correct interpretation of the evidence produced requires a clear identification of the index used in each empirical exercise.
In order to provide an empirical example of the methodology proposed, we considered evidence from six European economies—Germany, France, the United Kingdom, Greece, Hungary and Sweden—in 2007, 2011 and 2015. The results obtained in the empirical example emphasise the high level of trade competition among the largest European economies, namely Germany, France and the United Kingdom. The evidence obtained with the multidimensional measures suggested in this study also leads to the conclusion that trade competition may arise from different sources, making clear that partial evidence resulting from a unidimensional analysis may provide an incomplete picture of the complex reality of trade competition.
As our main contribution is a methodological one, the challenge now concerns the application of the measures suggested in this paper to a broad range of different countries and time periods. This is a critical step towards a better understanding of a complex and dynamic phenomenon with evident implications for the countries in terms of competitiveness and growth. In the methodological sphere, further research must be devoted to a detailed identification of the contribution of the different dimensions considered to the final level of trade competition between the countries. However, perhaps the main idea to retain from this study is that the study of trade competition is a fundamental issue in the context of the empirical analysis of international trade and that the development of better measures for this concept is a critical task for international trade researchers.
Notes
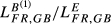 = 0.567).
= 0.567).
Appendix A
| Afghanistan | Gibraltar | Oman |
| Albania | Georgia | Pakistan |
| Algeria | Greece | Panama |
| Andorra | Guinea | Peru |
| Angola | Hong Kong | The Philippines |
| Argentina | Hungary | Poland |
| Australia | Iceland | Portugal |
| Austria | India | Qatar |
| Azerbaijan | Indonesia | Romania |
| Bahrain | Iran | Russian Federation |
| Bangladesh | Iraq | Saudi Arabia |
| Belarus | Ireland | Senegal |
| Belgium | Israel | Serbia |
| Benin | Italy | Singapore |
| Bosnia and Herzegovina | Ivory Coast | Slovakia |
| Brazil | Japan | Slovenia |
| Bulgaria | Jordan | South Africa |
| Cameroon | Kazakhstan | Spain |
| Canada | Kenya | Sri Lanka |
| Cayman Islands | South Korea | Sudan |
| Chile | Kuwait | Sweden |
| China | Latvia | Switzerland |
| Colombia | Lebanon | Syria |
| Congo | Liberia | Taiwan |
| Democratic Republic of Congo | Libya | Tanzania |
| Costa Rica | Liechtenstein | Thailand |
| Croatia | Lithuania | Togo |
| Cuba | Luxembourg | Tunisia |
| Cyprus | Macedonia | Turkey |
| Czech Republic | Malaysia | Turkmenistan |
| Denmark | Mali | Ukraine |
| Dominican Republic | Malta | United Arab Emirates |
| Ecuador | Mauritania | The United Kingdom |
| Egypt | Mauritius | United States |
| Equatorial Guinea | Mexico | Uruguay |
| Estonia | Moldova | Uzbekistan |
| Ethiopia | Morocco | Venezuela |
| Finland | The Netherlands | Vietnam |
| France | New Caledonia | British Virgin Islands |
| Gabon | New Zealand | Yemen |
| Germany | Nigeria | |
| Ghana | Norway |
| TCI ihm |
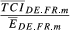
|
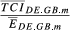
|
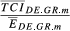
|

|
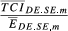
|
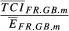
|
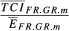
|
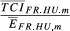
|

|
|
|---|---|---|---|---|---|---|---|---|---|---|
| Group 1 | S ihm (2) | 1.186 | 1.333 | 1.498 | 1.307 | 1.500 | 1.280 | 1.508 | 1.502 | 1.578 |
| A ihm | 0.394 | 0.241 | 0.182 | 0.291 | 0.155 | 0.199 | 0.204 | 0.244 | 0.144 | |
| B ihm (2) | 0.728 | 0.728 | 0.513 | 0.519 | 0.550 | 0.816 | 0.536 | 0.588 | 0.605 | |
| U ihm (5) | 0.540 | 0.547 | 0.451 | 0.401 | 0.473 | 0.551 | 0.483 | 0.541 | 0.569 | |
| Weight | 0.188% | 0.091% | 0.073% | 0.046% | 0.072% | 0.135% | 0.178% | 0.140% | 0.131% | |
| Group 2 | S ihm (2) | 1.226 | 1.281 | 1.932 | 1.321 | 1.428 | 1.286 | 1.554 | 1.745 | 1.378 |
| A ihm | 0.346 | 0.302 | 0.108 | 0.339 | 0.274 | 0.269 | 0.172 | 0.188 | 0.220 | |
| B ihm (2) | 0.661 | 0.717 | 0.513 | 0.528 | 0.556 | 0.741 | 0.528 | 0.558 | 0.588 | |
| U ihm (5) | 0.483 | 0.541 | 0.649 | 0.433 | 0.491 | 0.543 | 0.491 | 0.619 | 0.463 | |
| Weight | 0.371% | 0.231% | 0.237% | 0.134% | 0.206% | 0.364% | 0.413% | 0.334% | 0.342% | |
| Group 3 | S ihm (2) | 1.191 | 1.235 | 1.355 | 1.592 | 1.366 | 1.249 | 1.633 | 1.365 | 1.327 |
| A ihm | 0.350 | 0.278 | 0.291 | 0.280 | 0.254 | 0.365 | 0.186 | 0.240 | 0.219 | |
| B ihm (2) | 0.735 | 0.733 | 0.511 | 0.520 | 0.535 | 0.758 | 0.521 | 0.651 | 0.612 | |
| U ihm (5) | 0.511 | 0.517 | 0.421 | 0.547 | 0.430 | 0.592 | 0.532 | 0.504 | 0.453 | |
| Weight | 0.595% | 0.459% | 0.531% | 0.288% | 0.365% | 0.750% | 0.842% | 0.573% | 0.606% | |
| Group 4 | S ihm (2) | 1.189 | 1.171 | 1.501 | 1.259 | 1.303 | 1.199 | 1.472 | 1.647 | 1.309 |
| A ihm | 0.380 | 0.404 | 0.219 | 0.282 | 0.291 | 0.412 | 0.221 | 0.206 | 0.360 | |
| B ihm (2) | 0.636 | 0.774 | 0.522 | 0.544 | 0.594 | 0.747 | 0.525 | 0.531 | 0.711 | |
| U ihm (5) | 0.461 | 0.561 | 0.475 | 0.389 | 0.456 | 0.565 | 0.461 | 0.554 | 0.592 | |
| Weight | 0.887% | 0.832% | 1.053% | 0.527% | 0.609% | 0.999% | 1.302% | 0.825% | 0.993% | |
| Group 5 | S ihm (2) | 1.157 | 1.185 | 1.421 | 1.336 | 1.233 | 1.164 | 1.463 | 1.386 | 1.252 |
| A ihm | 0.430 | 0.401 | 0.227 | 0.335 | 0.390 | 0.356 | 0.204 | 0.340 | 0.278 | |
| B ihm (2) | 0.656 | 0.706 | 0.523 | 0.539 | 0.612 | 0.756 | 0.578 | 0.661 | 0.625 | |
| U ihm (5) | 0.476 | 0.518 | 0.437 | 0.447 | 0.471 | 0.515 | 0.503 | 0.565 | 0.444 | |
| Weight | 1.358% | 1.243% | 1.700% | 0.962% | 1.223% | 1.348% | 2.004% | 1.294% | 1.493% | |
| Group 6 | S ihm (2) | 1.120 | 1.166 | 1.314 | 1.285 | 1.245 | 1.209 | 1.292 | 1.294 | 1.226 |
| A ihm | 0.463 | 0.446 | 0.267 | 0.350 | 0.383 | 0.345 | 0.279 | 0.309 | 0.295 | |
| B ihm (2) | 0.708 | 0.664 | 0.543 | 0.540 | 0.555 | 0.805 | 0.538 | 0.637 | 0.641 | |
| U ihm (5) | 0.504 | 0.501 | 0.410 | 0.430 | 0.434 | 0.581 | 0.401 | 0.487 | 0.452 | |
| Weight | 2.331% | 1.835% | 3.388% | 1.786% | 2.089% | 2.083% | 3.648% | 2.355% | 2.261% | |
| Group 7 | S ihm (2) | 1.107 | 1.157 | 1.325 | 1.252 | 1.212 | 1.157 | 1.271 | 1.304 | 1.279 |
| A ihm | 0.505 | 0.446 | 0.262 | 0.373 | 0.430 | 0.417 | 0.301 | 0.350 | 0.330 | |
| B ihm (2) | 0.701 | 0.666 | 0.535 | 0.539 | 0.596 | 0.822 | 0.600 | 0.558 | 0.606 | |
| U ihm (5) | 0.515 | 0.493 | 0.411 | 0.420 | 0.466 | 0.589 | 0.445 | 0.456 | 0.467 | |
| Weight | 4.798% | 3.436% | 6.179% | 3.853% | 3.807% | 4.470% | 5.907% | 4.391% | 4.584% | |
| Group 8 | S ihm (2) | 1.110 | 1.127 | 1.258 | 1.238 | 1.217 | 1.151 | 1.219 | 1.266 | 1.231 |
| A ihm | 0.532 | 0.515 | 0.310 | 0.418 | 0.445 | 0.483 | 0.382 | 0.384 | 0.365 | |
| B ihm (2) | 0.682 | 0.659 | 0.557 | 0.541 | 0.540 | 0.755 | 0.565 | 0.651 | 0.631 | |
| U ihm (5) | 0.516 | 0.504 | 0.408 | 0.433 | 0.432 | 0.576 | 0.430 | 0.521 | 0.477 | |
| Weight | 8.463% | 9.047% | 9.576% | 7.061% | 7.687% | 7.710% | 9.035% | 7.201% | 7.891% | |
| Group 9 | S ihm (2) | 1.109 | 1.122 | 1.220 | 1.170 | 1.180 | 1.156 | 1.200 | 1.186 | 1.214 |
| A ihm | 0.567 | 0.513 | 0.398 | 0.493 | 0.483 | 0.452 | 0.410 | 0.443 | 0.385 | |
| B ihm (2) | 0.658 | 0.673 | 0.576 | 0.608 | 0.532 | 0.846 | 0.630 | 0.685 | 0.631 | |
| U ihm (5) | 0.513 | 0.509 | 0.435 | 0.476 | 0.421 | 0.630 | 0.473 | 0.526 | 0.478 | |
| Weight | 14.496% | 17.140% | 22.393% | 19.071% | 19.603% | 14.170% | 16.767% | 16.397% | 14.581% | |
| Group 10 | S ihm (2) | 1.090 | 1.090 | 1.214 | 1.151 | 1.120 | 1.114 | 1.204 | 1.180 | 1.174 |
| A ihm | 0.637 | 0.563 | 0.430 | 0.543 | 0.594 | 0.514 | 0.442 | 0.482 | 0.506 | |
| B ihm (2) | 0.702 | 0.649 | 0.566 | 0.586 | 0.655 | 0.755 | 0.563 | 0.683 | 0.645 | |
| U ihm (5) | 0.575 | 0.496 | 0.441 | 0.475 | 0.534 | 0.566 | 0.441 | 0.540 | 0.515 | |
| Weight | 66.513% | 65.686% | 54.871% | 66.272% | 64.340% | 67.971% | 59.904% | 66.491% | 67.119% |
| TCI ihm |
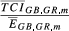
|
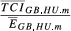
|
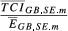
|
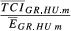
|
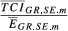
|
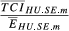
|
|
|---|---|---|---|---|---|---|---|
| Group 1 | S ihm (2) | 1.549 | 1.647 | 1.879 | 1.713 | 1.425 | 2.142 |
| A ihm | 0.069 | 0.189 | 0.101 | 0.187 | 0.140 | 0.131 | |
| B ihm (2) | 0.518 | 0.544 | 0.636 | 0.691 | 0.588 | 0.640 | |
| U ihm (5) | 0.442 | 0.566 | 0.739 | 0.760 | 0.467 | 0.958 | |
| Weight | 0.083% | 0.059% | 0.073% | 0.047% | 0.063% | 0.042% | |
| Group 2 | S ihm (2) | 1.337 | 1.185 | 1.578 | 4.856 | 2.032 | 1.733 |
| A ihm | 0.042 | 0.285 | 0.162 | 0.042 | 0.074 | 0.188 | |
| B ihm (2) | 0.549 | 0.545 | 0.688 | 0.700 | 0.647 | 0.669 | |
| U ihm (5) | 0.345 | 0.357 | 0.670 | 2.828 | 0.869 | 0.760 | |
| Weight | 0.263% | 0.197% | 0.167% | 0.159% | 0.219% | 0.146% | |
| Group 3 | S ihm (2) | 1.632 | 1.467 | 1.480 | 2.574 | 2.319 | 2.061 |
| A ihm | 0.164 | 0.271 | 0.196 | 0.051 | 0.038 | 0.124 | |
| B ihm (2) | 0.537 | 0.588 | 0.632 | 0.739 | 0.593 | 0.698 | |
| U ihm (5) | 0.538 | 0.541 | 0.551 | 1.452 | 0.944 | 0.937 | |
| Weight | 0.655% | 0.422% | 0.450% | 0.363% | 0.541% | 0.319% | |
| Group 4 | S ihm (2) | 1.649 | 1.449 | 1.320 | 1.748 | 1.453 | 1.670 |
| A ihm | 0.144 | 0.229 | 0.254 | 0.131 | 0.156 | 0.147 | |
| B ihm (2) | 0.571 | 0.545 | 0.627 | 0.660 | 0.599 | 0.670 | |
| U ihm (5) | 0.559 | 0.472 | 0.478 | 0.763 | 0.484 | 0.687 | |
| Weight | 1.030% | 0.724% | 0.808% | 0.688% | 1.099% | 0.584% | |
| Group 5 | S ihm (2) | 1.406 | 1.449 | 1.341 | 1.690 | 1.527 | 1.460 |
| A ihm | 0.177 | 0.201 | 0.275 | 0.161 | 0.144 | 0.162 | |
| B ihm (2) | 0.565 | 0.614 | 0.626 | 0.777 | 0.586 | 0.656 | |
| U ihm (5) | 0.444 | 0.501 | 0.502 | 0.809 | 0.521 | 0.544 | |
| Weight | 1.686% | 1.023% | 1.236% | 1.288% | 1.860% | 1.043% | |
| Group 6 | S ihm (2) | 1.329 | 1.373 | 1.238 | 1.467 | 1.537 | 1.496 |
| A ihm | 0.236 | 0.278 | 0.354 | 0.228 | 0.121 | 0.169 | |
| B ihm (2) | 0.634 | 0.632 | 0.719 | 0.721 | 0.664 | 0.595 | |
| U ihm (5) | 0.470 | 0.521 | 0.540 | 0.619 | 0.569 | 0.514 | |
| Weight | 3.143% | 1.703% | 1.789% | 2.463% | 3.321% | 1.769% | |
| Group 7 | S ihm (2) | 1.320 | 1.397 | 1.278 | 1.322 | 1.214 | 1.430 |
| A ihm | 0.225 | 0.306 | 0.314 | 0.235 | 0.396 | 0.259 | |
| B ihm (2) | 0.607 | 0.575 | 0.667 | 0.692 | 0.640 | 0.701 | |
| U ihm (5) | 0.446 | 0.497 | 0.505 | 0.521 | 0.487 | 0.602 | |
| Weight | 5.535% | 4.030% | 3.366% | 4.669% | 5.401% | 4.009% | |
| Group 8 | S ihm (2) | 1.235 | 1.261 | 1.226 | 1.336 | 1.455 | 1.384 |
| A ihm | 0.356 | 0.350 | 0.353 | 0.272 | 0.175 | 0.290 | |
| B ihm (2) | 0.614 | 0.597 | 0.672 | 0.646 | 0.614 | 0.629 | |
| U ihm (5) | 0.455 | 0.459 | 0.497 | 0.505 | 0.515 | 0.539 | |
| Weight | 9.641% | 8.516% | 7.454% | 8.762% | 8.622% | 6.739% | |
| Group 9 | S ihm (2) | 1.229 | 1.255 | 1.231 | 1.288 | 1.169 | 1.293 |
| A ihm | 0.343 | 0.393 | 0.381 | 0.349 | 0.484 | 0.352 | |
| B ihm (2) | 0.668 | 0.675 | 0.633 | 0.567 | 0.656 | 0.711 | |
| U ihm (5) | 0.487 | 0.538 | 0.486 | 0.452 | 0.511 | 0.575 | |
| Weight | 20.750% | 19.054% | 18.426% | 20.650% | 21.389% | 20.476% | |
| Group 10 | S ihm (2) | 1.213 | 1.181 | 1.185 | 1.319 | 1.294 | 1.269 |
| A ihm | 0.383 | 0.418 | 0.458 | 0.418 | 0.341 | 0.393 | |
| B ihm (2) | 0.568 | 0.627 | 0.640 | 0.653 | 0.579 | 0.710 | |
| U ihm (5) | 0.425 | 0.467 | 0.497 | 0.578 | 0.470 | 0.572 | |
| Weight | 57.213% | 64.272% | 66.230% | 60.911% | 57.485% | 64.875% |
-
For each pair, the destination markets were ranked according to their average weight in total exports from the smallest to the largest value and then divided into ten groups (the number of destination markets for each pair is 123 and, except for the first three groups—less relevant markets—which include 13 countries each, the other seven groups have 12 countries each); for the methodological options concerning the indicators Sihm(2), Aihm, Bihm(2) and Uihm(5), see the notes on Tables 2 to 4;
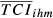 designate the average value of each index for each group of countries. Bold is used for the country pair having the highest value of the ratio
designate the average value of each index for each group of countries. Bold is used for the country pair having the highest value of the ratio 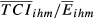 and italics for the pair with the minimum value.
and italics for the pair with the minimum value.
| TCI ihm | B ihm (1) | B ihm (3) | U ihm (1) | U ihm (3) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | |

|
0.215 | 0.198 | 0.189 | 0.368 | 0.356 | 0.347 | 0.115 | 0.140 | 0.132 | 0.200 | 0.248 | 0.238 |
| (0.485) | (0.457) | (0.444) | (0.828) | (0.819) | (0.815) | (0.259) | (0.323) | (0.310) | (0.450) | (0.571) | (0.560) | |
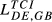
|
0.136 | 0.126 | 0.138 | 0.303 | 0.280 | 0.305 | 0.087 | 0.082 | 0.086 | 0.194 | 0.181 | 0.191 |
| (0.351) | (0.355) | (0.355) | (0.784) | (0.785) | (0.785) | (0.225) | (0.229) | (0.222) | (0.501) | (0.507) | (0.491) | |
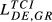
|
0.018 | 0.017 | 0.014 | 0.092 | 0.085 | 0.089 | 0.010 | 0.009 | 0.008 | 0.052 | 0.047 | 0.048 |
| (0.137) | (0.144) | (0.114) | (0.712) | (0.715) | (0.705) | (0.076) | (0.079) | (0.059) | (0.399) | (0.398) | (0.379) | |

|
0.066 | 0.064 | 0.077 | 0.188 | 0.198 | 0.232 | 0.045 | 0.043 | 0.052 | 0.120 | 0.127 | 0.148 |
| (0.265) | (0.244) | (0.249) | (0.755) | (0.748) | (0.750) | (0.182) | (0.164) | (0.169) | (0.482) | (0.482) | (0.479) | |
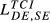
|
0.081 | 0.075 | 0.072 | 0.256 | 0.233 | 0.238 | 0.054 | 0.051 | 0.048 | 0.167 | 0.151 | 0.154 |
| (0.234) | (0.240) | (0.223) | (0.745) | (0.747) | (0.741) | (0.158) | (0.163) | (0.150) | (0.484) | (0.485) | (0.481) | |
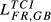
|
0.201 | 0.188 | 0.190 | 0.307 | 0.283 | 0.287 | 0.102 | 0.115 | 0.112 | 0.154 | 0.172 | 0.170 |
| (0.559) | (0.569) | (0.567) | (0.853) | (0.856) | (0.856) | (0.283) | (0.346) | (0.335) | (0.429) | (0.521) | (0.506) | |
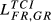
|
0.018 | 0.022 | 0.018 | 0.109 | 0.105 | 0.100 | 0.008 | 0.015 | 0.010 | 0.052 | 0.063 | 0.056 |
| (0.114) | (0.148) | (0.129) | (0.705) | (0.716) | (0.710) | (0.051) | (0.101) | (0.073) | (0.339) | (0.428) | (0.395) | |
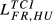
|
0.070 | 0.074 | 0.080 | 0.174 | 0.175 | 0.187 | 0.032 | 0.046 | 0.049 | 0.078 | 0.106 | 0.112 |
| (0.310) | (0.330) | (0.332) | (0.770) | (0.784) | (0.777) | (0.141) | (0.206) | (0.202) | (0.344) | (0.478) | (0.465) | |

|
0.075 | 0.072 | 0.063 | 0.213 | 0.200 | 0.187 | 0.038 | 0.043 | 0.037 | 0.108 | 0.119 | 0.110 |
| (0.267) | (0.272) | (0.254) | (0.756) | (0.757) | (0.751) | (0.134) | (0.161) | (0.149) | (0.381) | (0.452) | (0.444) | |
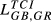
|
0.022 | 0.026 | 0.023 | 0.092 | 0.094 | 0.090 | 0.011 | 0.015 | 0.012 | 0.047 | 0.051 | 0.045 |
| (0.170) | (0.204) | (0.185) | (0.723) | (0.735) | (0.728) | (0.088) | (0.115) | (0.094) | (0.368) | (0.397) | (0.365) | |
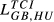
|
0.064 | 0.059 | 0.070 | 0.147 | 0.142 | 0.161 | 0.036 | 0.035 | 0.039 | 0.081 | 0.080 | 0.088 |
| (0.337) | (0.326) | (0.336) | (0.779) | (0.775) | (0.779) | (0.193) | (0.189) | (0.188) | (0.430) | (0.436) | (0.424) | |
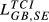
|
0.092 | 0.071 | 0.072 | 0.216 | 0.171 | 0.194 | 0.053 | 0.041 | 0.041 | 0.124 | 0.097 | 0.109 |
| (0.332) | (0.323) | (0.281) | (0.777) | (0.774) | (0.760) | (0.193) | (0.185) | (0.158) | (0.446) | (0.441) | (0.427) | |
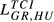
|
0.024 | 0.021 | 0.023 | 0.072 | 0.066 | 0.068 | 0.012 | 0.012 | 0.013 | 0.036 | 0.037 | 0.038 |
| (0.257) | (0.236) | (0.257) | (0.752) | (0.745) | (0.752) | (0.130) | (0.135) | (0.146) | (0.379) | (0.419) | (0.423) | |
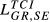
|
0.017 | 0.023 | 0.023 | 0.081 | 0.086 | 0.078 | 0.008 | 0.014 | 0.013 | 0.038 | 0.047 | 0.040 |
| (0.154) | (0.195) | (0.220) | (0.718) | (0.732) | (0.740) | (0.073) | (0.120) | (0.119) | (0.339) | (0.403) | (0.381) | |
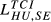
|
0.068 | 0.070 | 0.073 | 0.125 | 0.130 | 0.142 | 0.038 | 0.040 | 0.039 | 0.070 | 0.074 | 0.076 |
| (0.443) | (0.438) | (0.416) | (0.814) | (0.813) | (0.805) | (0.251) | (0.252) | (0.221) | (0.454) | (0.461) | (0.433) | |
| TCI ihm | U ihm (4) | U ihm (6) | U ihm (7) | U ihm (9) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | 2007 | 2011 | 2015 | |

|
0.146 | 0.162 | 0.153 | 0.254 | 0.289 | 0.280 | 0.196 | 0.197 | 0.187 | 0.340 | 0.355 | 0.345 |
| (0.329) | (0.373) | (0.360) | (0.571) | (0.666) | (0.657) | (0.442) | (0.454) | (0.440) | (0.766) | (0.817) | (0.811) | |
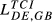
|
0.106 | 0.099 | 0.105 | 0.237 | 0.220 | 0.232 | 0.137 | 0.128 | 0.135 | 0.305 | 0.283 | 0.298 |
| (0.275) | (0.279) | (0.271) | (0.613) | (0.618) | (0.598) | (0.353) | (0.358) | (0.348) | (0.789) | (0.794) | (0.768) | |
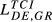
|
0.013 | 0.013 | 0.010 | 0.074 | 0.068 | 0.070 | 0.019 | 0.018 | 0.015 | 0.109 | 0.101 | 0.103 |
| (0.103) | (0.108) | (0.082) | (0.574) | (0.577) | (0.549) | (0.146) | (0.154) | (0.118) | (0.844) | (0.854) | (0.813) | |

|
0.058 | 0.054 | 0.064 | 0.160 | 0.165 | 0.189 | 0.077 | 0.071 | 0.083 | 0.221 | 0.224 | 0.253 |
| (0.232) | (0.205) | (0.208) | (0.643) | (0.626) | (0.612) | (0.310) | (0.268) | (0.269) | (0.892) | (0.849) | (0.820) | |
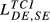
|
0.065 | 0.061 | 0.058 | 0.207 | 0.188 | 0.192 | 0.083 | 0.077 | 0.073 | 0.270 | 0.247 | 0.251 |
| (0.190) | (0.196) | (0.180) | (0.601) | (0.605) | (0.598) | (0.241) | (0.248) | (0.228) | (0.784) | (0.792) | (0.781) | |
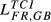
|
0.137 | 0.144 | 0.143 | 0.208 | 0.217 | 0.216 | 0.194 | 0.192 | 0.192 | 0.295 | 0.289 | 0.289 |
| (0.381) | (0.436) | (0.427) | (0.579) | (0.657) | (0.644) | (0.538) | (0.580) | (0.571) | (0.818) | (0.873) | (0.862) | |
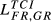
|
0.012 | 0.018 | 0.014 | 0.079 | 0.086 | 0.079 | 0.018 | 0.024 | 0.019 | 0.120 | 0.123 | 0.114 |
| (0.075) | (0.127) | (0.098) | (0.510) | (0.589) | (0.558) | (0.114) | (0.167) | (0.137) | (0.775) | (0.838) | (0.811) | |
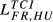
|
0.047 | 0.060 | 0.063 | 0.117 | 0.142 | 0.149 | 0.070 | 0.082 | 0.086 | 0.180 | 0.192 | 0.207 |
| (0.207) | (0.270) | (0.263) | (0.520) | (0.636) | (0.619) | (0.310) | (0.369) | (0.359) | (0.797) | (0.862) | (0.860) | |

|
0.053 | 0.056 | 0.050 | 0.152 | 0.156 | 0.149 | 0.078 | 0.077 | 0.070 | 0.222 | 0.215 | 0.208 |
| (0.189) | (0.212) | (0.200) | (0.539) | (0.593) | (0.598) | (0.276) | (0.291) | (0.280) | (0.789) | (0.815) | (0.839) | |
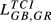
|
0.016 | 0.020 | 0.017 | 0.072 | 0.073 | 0.067 | 0.024 | 0.027 | 0.024 | 0.111 | 0.107 | 0.102 |
| (0.128) | (0.154) | (0.134) | (0.565) | (0.572) | (0.544) | (0.190) | (0.215) | (0.195) | (0.869) | (0.843) | (0.821) | |
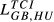
|
0.051 | 0.047 | 0.053 | 0.117 | 0.114 | 0.124 | 0.073 | 0.067 | 0.075 | 0.174 | 0.166 | 0.180 |
| (0.269) | (0.258) | (0.256) | (0.623) | (0.621) | (0.598) | (0.387) | (0.367) | (0.362) | (0.921) | (0.909) | (0.870) | |
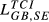
|
0.073 | 0.055 | 0.055 | 0.168 | 0.132 | 0.150 | 0.103 | 0.078 | 0.078 | 0.238 | 0.185 | 0.215 |
| (0.262) | (0.251) | (0.216) | (0.606) | (0.596) | (0.588) | (0.371) | (0.354) | (0.306) | (0.857) | (0.839) | (0.843) | |
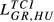
|
0.020 | 0.018 | 0.020 | 0.057 | 0.056 | 0.059 | 0.031 | 0.028 | 0.032 | 0.090 | 0.087 | 0.091 |
| (0.208) | (0.206) | (0.226) | (0.603) | (0.641) | (0.653) | (0.328) | (0.314) | (0.351) | (0.949) | (0.984) | (1.009) | |
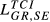
|
0.014 | 0.020 | 0.019 | 0.061 | 0.070 | 0.063 | 0.022 | 0.029 | 0.030 | 0.097 | 0.104 | 0.098 |
| (0.120) | (0.169) | (0.186) | (0.543) | (0.593) | (0.598) | (0.194) | (0.247) | (0.288) | (0.859) | (0.887) | (0.934) | |
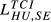
|
0.060 | 0.060 | 0.058 | 0.110 | 0.113 | 0.115 | 0.094 | 0.090 | 0.088 | 0.173 | 0.172 | 0.175 |
| (0.392) | (0.373) | (0.330) | (0.719) | (0.701) | (0.653) | (0.613) | (0.562) | (0.497) | (1.130) | (1.072) | (0.992) | |
-
For the definition of the Bihm and Uihm indicators, see Table 4; the methodological option for Bihm indicators is as follows: for Bihm(1), we have λ = 1; for Bihm(3), we have λ = 3; the methodological options for Uihm indicators are as follows: for Uihm(1), we have (α1, α2, α3, λ) = (0.025; 0.075; 0.9; 2); Uihm(3)—(α1, α2, α3, λ) = (0.025; 0.075; 0.9; 3); Uihm(4)—(α1, α2, α3, λ) = (0.1; 0.15; 0.75; 1); Uihm(6)—(α1, α2, α3, λ) = (0.1; 0.15; 0.75; 3); Uihm(7)—(α1, α2, α3, λ) = (0.2; 0.3; 0.5; 1); and Uihm(9)—(α1, α2, α3, λ) = (0.2; 0.3; 0.5; 3);
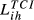 is an overall trade competition index for the country pair i and h. In this table, we have eight different
is an overall trade competition index for the country pair i and h. In this table, we have eight different 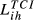 for each country pair (i.e.,
for each country pair (i.e., 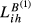 ,
, 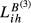 ,
,  ,
, 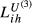 ,
, 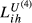 ,
, 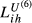 ,
, 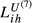 and
and 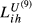 ); numbers between parentheses are the ratios
); numbers between parentheses are the ratios 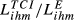 . Bold is used for the country pair having the highest value of the ratio
. Bold is used for the country pair having the highest value of the ratio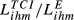 and italics for the pair with the minimum value.
and italics for the pair with the minimum value.




