Examining Determinants of Foreign Wage Premiums in China
Abstract
We estimate foreign wage premiums for every 3-digit manufacturing industry in China and discover a wide range of premiums both for ‘foreign’ ownership and for overseas Chinese ownership. Foreign ownership generates larger and more prevalent wage premiums than overseas Chinese ownership, but both produce premiums that respond similarly in estimates of determinants. Using the number of computers per worker to measure firms' technology levels, we find evidence consistent with the hypothesis that foreign firms pay higher wages to reduce the risk of worker turnover and the accompanying technology leakage in 76 to 78 per cent of industries. However, this determinant explains only 5 to 6 per cent of the foreign wage premium. We find the most intensive support for the ‘fair wage’ hypothesis that foreign firms pay higher wages because they are more profitable than domestic firms and workers in more profitable firms expect to be paid more, otherwise they will shirk. This hypothesis explains an average of 8 to 9 per cent of the foreign wage premiums, with support found in 72 to 75 per cent of the industries. When we consider the best combination of explanatory variables to include in each industry's wage regression, we find evidence consistent with our combined hypotheses in most industries, but we still find large residual foreign wage premiums.
1 Introduction
The empirical literature documenting wage premiums paid by foreign-invested enterprises relative to domestic enterprises is extensive and so are the accompanying hypotheses on why these wage premiums exist. What are much more limited, however, are tests of these hypotheses. Of the many reasons why foreign firms might pay more than domestic firms, which have empirical support and which do not? With worldwide foreign direct investment (FDI) inflows totalling over $1 trillion every year since 2006, it is vital for policymakers to understand fully the various host-country effects of FDI, including labour market effects.1 In this paper, we begin to address this gap in the literature by examining two hypotheses to explain foreign ownership wage premiums using firm-level data for China.
Lipsey and Sjoholm (2004) suggest four possible hypotheses to explain foreign ownership wage premiums: (i) host-country requirements or pressures; (ii) workers' preferences for working for a domestic, rather than foreign, employer; (iii) foreign firms' disadvantage relative to domestic firms in identifying high-quality workers without paying wage premiums; and (iv) foreign firms' stronger aversion to worker turnover due to higher training costs or fear of technology leakage to domestic rivals. The last of these hypotheses is the most amenable to quantitative exploration with firm-level data, so we chose that one to pursue. This hypothesis is based on efficiency wage models.2 Firms will pay above market-clearing wages to reduce worker turnover, and their willingness to pay higher wages increases with the costs of replacing workers. If worker turnover is more costly for foreign firms than for domestic firms, foreign firms should pay higher wages. Another variation of the efficiency wage concept involves the ‘fair wage’ hypothesis developed in Akerlof and Yellen (1990). Workers at more productive and profitable firms expect to be paid more, otherwise they shirk. This hypothesis helps to explain the foreign wage premium if foreign firms are more profitable than their domestic counterparts. We also seek support for this hypothesis using firm-level data from China.
Lipsey and Sjoholm (2004) were among the first to confirm that foreign ownership wage premiums exist even after controlling for region, industry, plant size and worker characteristics. They found a 12 per cent wage premium paid by foreign firms to blue-collar workers and a 22 per cent wage premium paid to white-collar workers in Indonesian factories. Aitken et al. (1996) find substantial foreign wage residuals for Mexico and Venezuela as host countries, but not for the USA as a host country, when they control for plant size, location, type of industry and skill mix. Some studies have gone further in trying to control for differences in worker characteristics using matched employer–employee data. Martins (2011) uses matched data from Portugal to show that some of the pay differential between foreign and domestic firms is explained by the foreign firms' tendency to hire more able workers. Heyman et al. (2007) use matched data from Sweden to conclude that foreign firms' higher wages mostly can be explained by firm and worker characteristics.
Egger and Kreickemeier (2013) argue that differences in observable firm-level characteristics such as capital intensity and worker quality provide only partial explanations of the foreign wage premium. They develop a heterogeneous firms model in which firm-specific and country-specific factors interact to explain the foreign wage premium. If firms in more developed economies have higher productivities on average, then foreign investment by these firms into less developed economies produces one source of a wage premium (i.e. more productive firms pay more). Another source of a wage premium is generated by multinational firms that earn ‘global profits’ and share them with their workers worldwide. In a less developed economy, domestic firms with identical productivities to foreign-invested firms from a more developed economy can coexist but the foreign firms will pay higher wages due to their larger global profits. Our exploration of the fair wage hypothesis relates only indirectly to the Egger and Kreickemeier (2013) model because we are not able to observe the global profits of the foreign firms in our data set. Instead, we examine whether foreign firms pay higher wages in China due to their higher profits earned in China.
Greaney and Li (2013) examine wage differences across manufacturing firms in the same 2-digit industry in a single industrial region in China, the Yangtze River Delta. After controlling for firms' exporter status, location, subsector, capital intensity, size, workforce education and gender, they find foreign ownership wage premiums of 36 per cent and 15 per cent in the general equipment and textiles industries, respectively. That research also finds overseas Chinese-ownership wage premiums of 18 per cent and 12 per cent for the two industries, respectively. Those findings of disparate foreign wage premiums across two different industries in a single region prompted the more extensive inquiry in this paper. Using an efficiency wages perspective, we seek to understand why foreign ownership generates such different wage premiums in different industries in China.
We contribute to the literature by estimating foreign wage premiums for each 3-digit manufacturing industry in China, while controlling for the standard set of observable firm and workforce characteristics (i.e. firm capital-intensity, size, workforce education and gender, location and industry subsector), plus exporter status.3 We are among the first to estimate foreign wage premiums while controlling for exporter status, which should tend to reduce our foreign wage premiums relative to other estimates as foreign firms are more export-oriented than domestic firms and exporter wage premiums are widely acknowledged as a stylised fact (See Bernard and Jensen, 1995, 1997; Schank et al., 2007). Even after controlling for all of these firm-level differences, we find a wide range of foreign ownership wage premiums across the manufacturing industries. We use the cross-industry variation in wage premiums to look for commonalities across industries that generate high or low foreign wage premiums, and we explore the determinants of the foreign wage premiums. To our knowledge, our research is the first to systematically examine the determinants of foreign wage premiums while allowing for variations across industries. This allows us to examine the applicability of our hypotheses at both the intensive and extensive margins. Other studies that identify foreign wage premiums tend to assume that industry fixed effects can capture all sources of variation across industries in wage determination, which means hypotheses can be examined only at the intensive margin. Instead, our study allows for idiosyncratic differences across industries in the responsiveness of wages to various determinants, including firm ownership.4
We tally our results along both extensive and intensive margins using the numbers of industries providing supportive evidence of our hypotheses for the former, and quantifying the strength of our supportive evidence for the latter. Using firm-level data from China, we are able to compare wage premiums across two groups of foreign owners – so-called ‘foreigners’ versus overseas Chinese owners from Hong Kong, Macao or Taiwan. Although we find differences between these two foreign ownership types in the magnitudes and prevalence of wage premia (WP) across industries, we find that both types of foreign ownership produce WP that respond similarly in hypothesis testing of determinants. Next, we provide a description of our data, followed by a discussion of our hypothesis testing methodology, and then our results and conclusions.
2 Data
We use firm-level data from the Financial Information Database for Chinese industrial enterprises provided by the National Bureau of Statistics of China (NBSC). The database covers all industrial firms in China in 2004 with sales of 5 million yuan or more. After data cleaning, we have 264,739 firms in our data set.5 These firms can be divided into 39 industries at the 2-digit level, including 30 manufacturing industries, six mining industries and three utilities and recycling industries. We focus on the manufacturing industries, which include 246,009 firms, and further disaggregate these firms into 168 3-digit industries.
As described in detail in Greaney and Li (2013), the firms in our data set are classified by ownership into five types: state-owned enterprises (SOEs), collectives, private domestic enterprises (PDEs), foreign direct-invested enterprises (FDIEs) and Hong Kong–Macao–Taiwan-invested enterprises (HMTEs). Joint-venture firms are classified according to their largest shareholder's firm type to reflect the managerial control of the firm.6 We estimate wage premiums for FDIEs and HMTEs separately to allow for country-specific ownership effects that might lead to differing wage premiums and determinants thereof. Huang (2004) finds that HMTEs and FDIEs have different technology spillover effects, and Greaney and Li (2012) find evidence suggestive of differing impacts on China's labour market. Potential advantages that HMTEs may have over FDIEs in China include having closer language and cultural linkages, closer geographic proximity, and greater ease in obtaining visas and other government approvals.
Our data set provides firm-level employment numbers for each skill (i.e. education level) and gender group, but not separate wage data for each, only total wages per firm. These wage totals are used along with employment totals to calculate average annual wages per worker for each firm. The strength of our data is the detailed information we have at the firm level to use in explaining the variation in average wages across firms in the same industry. A weakness of our data is that we do not have wages by skill level of workers at each firm. An additional weakness of the NBSC data is that the workforce education statistics are reported only for 2004, not for other years. Due to this data limitation and to our focus on examining a firm-level wage determinant that is, for the most part, time-invariant over several years (i.e. firm ownership), we use a cross-sectional rather than a panel data approach.7
3 Methodology
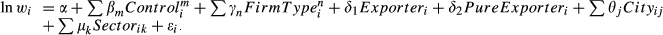(1)Our level of analysis is at the 3-digit industry level, so wi represents average annual wage per worker for firm i in a single 3-digit industry in China. Controli represents m control variables for firm i that are expected to influence its wages, FirmTypei represents n ownership dummy variables for firm i, Exporteri represents an exporter dummy variable for regular exporters (0 < export share of sales ≤ 0.9), and PureExporteri is a dummy variable for pure exporters (export share of sales > 0.9). Cityij is a dummy variable equal to one if firm i is located in city j, and zero otherwise;9 and Sectorik is an industry dummy equal to one if firm i is in 4-digit industry k, and equal to zero otherwise. The control variables include the capital–labour ratio (i.e. fixed assets per worker) to control for differing levels of capital intensity across firms, total employment to control for firm size (i.e. scale economies effects), the weighted average of workers' education years to control for labour quality differences across firms,10 and the share of female workers in the firm's workforce to account for gender wage differentials.11 The expected sign on the first three control variables is positive, and on the last variable is negative due to the gender wage gap.12
The firm-type variables are expressed as dummy variables identifying the legal ownership classification for the firm – SOE, Collective, HMTE or FDIE. A significant coefficient for any of these specified firm types indicates a difference for that firm type relative to the average PDE, which make up the majority of firms in our data set.
The inclusion of Exporter and PureExporter dummy variables is prompted by Defever and Riaño (2012) who find that China's preferential subsidies offered to pure exporters prompts an odd clustering of firms that export almost all of their output, which is not typically observed in other countries.13 They also find that pure exporters tend to be less productive than regular exporters but more productive than non-exporters. We want to identify the firm-type WP separate from any exporter-type WP, so that hypotheses regarding the determinants of each can be separately examined. An added advantage of including the export status dummies is it helps us to control for unobservable worker quality differences that allow more productive firms to become exporters.14
Each wage regression at the 3-digit industry level has a large number of potential independent variables as we have four control variables, four firm types, and two exporter types, plus varying numbers of city and sector dummy variables. To increase our confidence in our estimated coefficients, we set a minimum industry size of 200 firms for inclusion in our wage regressions. Of the 168 manufacturing industries at the 3-digit level, we drop 19 that fall below this sample size criterion, resulting in 149 industries with 244,889 firms for our analysis. Summary statistics for our data are presented in Table S1 in the Appendix for all firms and by firm type.15 On average across all industries, FDIEs, HMTEs and SOEs pay higher wages than PDEs using larger workforces, more educated labour and more capital per labour, but their rankings relative to PDEs differ for our other variables of interest, which is useful for hypothesis testing.
Our first step in analysing the foreign WP across the 149 industries is to use the WP for descriptive analysis.16 We rank the industries by their FDIE, HMTE and SOE WP to see whether the industries at the top share common characteristics that distinguish them from industries at the bottom and to compare the rankings for foreign WP versus state-owned WP. More formally, we examine correlation coefficients between the characteristics of the mean-value firm in each industry and the firm-type WP. Then, we proceed to examine our two hypotheses regarding the sources of the foreign WP.
The first hypothesis links labour productivity to firm wages through managers' fears of costly worker turnover, as follows.
3.1 Hypothesis 1
Worker turnover aversion: due to higher training costs and/or higher fear of technology leakage to domestic rivals, foreign-owned firms have a stronger aversion to worker turnover and therefore pay higher wages than domestic rivals.
Poole (2013) finds support for this hypothesis using matched employer–employee panel data from Brazil. She finds wage spillover evidence of knowledge transfers from multinational to domestic firms. Gorg et al. (2007) use matched employer–employee data for Ghana to show that on-the-job training helps to explain foreign wage premiums. To seek support for the hypothesis with our firm-level data for China, we use three different variables to measure a firm's training costs and/or technology level: training costs per worker, intangible assets per worker and number of computers per worker.17 Firms are asked to report a total for intangible assets based on the value of their patent rights, non-patent technology, trademarks, copyrights, land-use rights and franchise licences. As firms may report zeroes for training costs, intangible assets or computers, these added variables have true zero-value observations. To keep the information embedded in zero-value observations, we add 0.0001 to these variables before taking the logarithm. We use the data to answer the following questions: (i) do foreign firms have higher training costs and/or higher technology than domestic rivals, on average; and (ii) does this differential partially explain the foreign firm wage premium? Each question is posed at the 3-digit industry level to allow for variation across industries, with further details provided after introducing our second hypothesis.
The second hypothesis derived from efficiency wage models is the so-called ‘fair wage’ hypothesis of Akerlof and Yellen (1990). Applied to a market with foreign and domestic firms, this hypothesis can be stated as follows.
3.2 Hypothesis 2
Fair wage: workers at more productive and profitable firms expect to be paid more, otherwise they will shirk. Foreign firms pay more than domestic firms because they are more profitable.
To examine this hypothesis with our data set, we use firm-level total profits per worker and operating profits18 per worker to answer the following questions: (i) do foreign firms on average make higher profits than domestic firms; and (ii) does this differential partially explain the foreign WP? Again, we add 0.0001 to total profit and operating profit before taking the logarithm to keep zero-value observations in the regressions. However, negative values of total profit or operating profit are treated as missing after taking the logarithm.19 As we lose about 22 per cent of our firm observations by dropping those with negative total profits or operating profits reported, we establish two more sets of benchmark regression results to use in making comparisons when either profit variable is involved.20
A potential problem with our profit variables is that corporate tax rules mandate that foreign firms report their profits based on their operations in China, while domestic firms must report their profits based on their operations in China and abroad.21 However, we believe that this data discrepancy is relatively small because only a tiny share of Chinese manufacturing firms had operations abroad in 2004.22 Also, Chinese workers' fair wage expectations might be based primarily on their firms' China operations' profitability, which they presumably know more about than their firms' outside-China profitability, so we focus on firms' China-operations-only profits. However, Egger and Kreickemeier (2013) theorise that one reason why foreign ownership is good for workers in developing countries like China is that these foreign firms share their global profits with their developing country workers. As we do not observe the global profits of the FDIEs or HMTEs with our data, we might be underestimating the relationship between profits and wages for foreign firms operating in China.23
To test each hypothesis, we first answer question (i) using descriptive statistics for each 3-digit industry. As the variance of some of our variables is high and outliers are observed, we use both the per-firm-mean and per-firm-median observation to compare foreign firm types to PDEs within each industry.24 We also use the 75th percentile observation after discovering that the median value for some variables for some firm types is zero, indicating skewed distributions for those variables.
- (A) improved the fit of the regression (i.e. does the adjusted-R2 value increase?);
- (B) caused the estimated foreign WP to become insignificant (i.e. when it had been significant in the benchmark case); and/or
- (C) caused the estimated foreign WP to become smaller but still significant.
To answer question (ii) in the affirmative, we look for cases that satisfy both (A) and (B), or both (A) and (C). By design, criteria (B) and (C) only apply to industries that generate a significant foreign WP in the benchmark regression. Affirmative responses to question (ii) are interpreted as support for a hypothesis, although we acknowledge that these results are merely hypothesis-consistent as we are not able to exclude other possible interpretations for the same results.25 We also look for cases that appear to directly refute question (ii) by tallying cases where the added variable causes the estimated foreign WP to become larger, rather than smaller, while remaining significant. We call these cases (Z). Cases that satisfy (A) and (Z) are interpreted as evidence against our hypotheses. Industries that fail to satisfy (A) and (B), (A) and (C) or (A) and (Z) are simply cases that are neither consistent with nor refute our hypotheses.
We also use the results from the modified wage regressions to quantify how much of the foreign WP can be explained by each determinant individually and in combination with each other. We test for correlations between our determinants (i.e. per worker training costs, intangible assets, numbers of computers, total profits and operating profits) and find strong correlations only between total profits and operating profits (0.90), so those two variables are not included simultaneously into the wage regression.26 We also check for correlations between our determinants and our variables of interest (i.e. the firm-type dummy variables) and do not find strong correlations. The strongest of these correlations is between numbers of computers per worker and the FDIE dummy at 0.24.
4 Results
Table 1 summarises the key results of our benchmark wage regression in equation 1 for 149 3-digit manufacturing industries in China.27 The table shows the WP for different firm types, after controlling for firm capital intensity, size, workforce education and gender, location, subsector and exporter status. It also shows the WP for different exporter statuses after controlling for the control variables, location, subsector and firm type. As seen in the table, the foreign firm types – FDIEs and HMTEs – generate significant, positive coefficients in most industries and these coefficients are larger, on average, than those associated with the two specified domestic firm types – SOEs and Collectives. FDIEs produce significant and positive WP over PDEs in 137 of 149 industries, or 92 per cent of industries, and HMTEs produce significant and positive WP in 93 industries or 62 per cent of industries. In comparison, SOEs produce significant and positive WP in only 47 industries or 32 per cent of industries and collectives produce significant, positive WP in only seven industries, or 5 per cent of industries. Collectives produce significant and negative WP relative to PDEs in 16 industries, and SOEs do the same in 12 industries, while the foreign firm types only produce a significant, negative WP in one industry for FDIEs.
| FDIE | HMTE | SOE | Collective | Exporter | PureExporter | |
|---|---|---|---|---|---|---|
| Number of positive and sig.* | 137 | 93 | 47 | 7 | 68 | 25 |
| Number of negative and sig.* | 1 | 0 | 12 | 16 | 2 | 20 |
| Coefficient mean | 0.261 | 0.181 | 0.100 | −0.037 | 0.101 | 0.032 |
| Coefficient median | 0.250 | 0.155 | 0.141 | −0.078 | 0.094 | 0.043 |
| Coefficient maximum | 1.129 | 0.702 | 0.432 | 0.239 | 0.306 | 0.788 |
| Coefficient minimum | −0.268 | 0.053 | −1.071 | −0.354 | −0.201 | −0.425 |
| Coefficients in percentage terms | ||||||
| Mean | 0.298 | 0.199 | 0.105 | −0.037 | 0.107 | 0.032 |
| Median | 0.284 | 0.168 | 0.152 | −0.075 | 0.099 | 0.044 |
| Maximum | 2.091 | 1.017 | 0.540 | 0.270 | 0.358 | 1.200 |
| Minimum | −0.235 | 0.055 | −0.657 | −0.298 | −0.182 | −0.346 |
Notes
- (i) From 149 3-digit manufacturing industries in China that met a minimum criterion for numbers of firms.
- (ii) The estimated coefficients for control variables in these benchmark regressions are summarised in Table S1, along with regression statistics (i.e. adjusted R2 values, number of observations).
- (iii) FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises; SOEs, state-owned enterprises.
- (iv) *Significant at least at the 10% level.
The estimated WP for the same firm type are quite different across industries, and the ranges are quite large: FDIE (−23.5 to 209.1 per cent), HMTE (5.5 to 101.7 per cent), SOE (−65.7 to 54.0 per cent) and collectives (−29.8 to 27.0 per cent). Due to the large variance in estimated coefficients, we focus on the median estimated WP, rather than the mean, and find that the median WP are 28.4 per cent for FDIEs, 16.8 per cent for HMTEs, 15.2 per cent for SOEs and −7.5 per cent for collectives, all relative to PDEs.28 To directly compare the FDIE and HMTE WP within each industry, we note that 92 of the 93 industries with a significant HMTE WP also report a significant FDIE WP, and 82 of those industries have the FDIE WP larger than the HMTE WP.
We also find that the industry distributions of WP are different across different firm types. Table 2 shows the top 10 and bottom 10 industries ranked by firm-type WP for FDIEs, HMTEs and SOEs relative to PDEs. Industries that appear more than once in the rankings are highlighted to show the common entries. In some cases, industries that appear more than once switch from being a top 10 industry to being a bottom 10 industry depending on which WP is involved. For example, industry 363 (food, beverage, and feed manufacturing equipment) appears as a top 10 industry for FDIE and HMTE WP with 55.3 per cent and 34.3 per cent WP over PDEs, but also appears as a bottom 10 industry for SOE WP, at −25.8 per cent. Industry 322 (steel smelting) appears as a bottom 10 industry for FDIE WP, with the only negative estimated value at −23.5 per cent, but it appears as a top 10 industry for SOE and HMTE WP, with SOEs estimated to pay 46.3 per cent more than PDEs and HMTEs estimated to pay 50.1 per cent more than PDEs. These two extreme examples of SOE WP may be explained by the Chinese government's continuous support of SOEs in the steel industry,29 versus its encouragement of further privatisation and openness in food processing industries.30 Industry 332 (noble metals processing) generates the largest FDIE WP at 209.1 per cent and the second largest HMTE WP at 61.9 per cent. Industry 133 (vegetable oil processing) also appears on both foreign firms' top 10 lists, at 58.4 per cent for FDIEs and 32.3 per cent for HMTEs. Among the bottom 10 lists, FDIEs and HMTEs do not share any common industries, but each shares a common industry with the bottom 10 list for SOEs. Industry 244 (toys) produces only an 8.8 per cent WP for FDIEs, while it produces a −65.7 per cent WP for SOEs, the lowest estimated coefficient for SOEs. Industry 313 (bricks, tiles, stones for construction) produces the lowest WP for HMTEs at 5.5 per cent, while it produces a −9.9 per cent WP for SOEs.
| Top 10 | FDIE | HMTE | SOE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Ind.# | Ind | WP | Ind.# | Ind | WP | Ind.# | Ind | WP | |
| 1 | 332 | Noble metals smelting | 2.091 | 371 | Railway transport equipment | 1.017 | 299 | Other rubber products | 0.540 |
| 2 | 347 | Enamel products | 1.253 | 332 | Noble metals smelting | 0.619 | 334 | Non-ferrous metals | 0.530 |
| 3 | 361 | Mining, metallurgy equipment | 0.653 | 322 | Steel smelting | 0.501 | 282 | Synthetic fibres | 0.469 |
| 4 | 412 | Precision instruments | 0.607 | 299 | Other rubber products | 0.409 | 322 | Steel smelting | 0.463 |
| 5 | 133 | Vegetable oil processing | 0.584 | 276 | Biological, biochemical products | 0.364 | 349 | Miscellaneous metals products | 0.420 |
| 6 | 363 | Food, beverage, feed manufacturing equipment | 0.553 | 363 | Food, beverage, feed manufacturing equipment | 0.343 | 323 | Iron rolling | 0.417 |
| 7 | 353 | Cranes and transporters | 0.549 | 277 | Hygenic, medicinal, pharmacy materials | 0.334 | 429 | Miscellaneous manufacturing | 0.367 |
| 8 | 251 | Refined petroleum products | 0.503 | 295 | Daily-use and medical rubber products | 0.332 | 413 | Watches and timing instruments | 0.338 |
| 9 | 401 | Communication equipment | 0.491 | 263 | Pesticides | 0.328 | 241 | Stationary, pens, educational models | 0.314 |
| 10 | 316 | Fireproof materials | 0.485 | 133 | Vegetable oil processing | 0.323 | 397 | Lighting tools | 0.294 |
| Bottom 10 | |||||||||
| 10 | 405 | Electron devices | 0.128 | 136 | Aquatic products processing | 0.102 | 152 | Beer, wine, spirits | −0.076 |
| 9 | 421 | Handicrafts | 0.128 | 342 | Metallic tools | 0.099 | 135 | Meat processing | −0.080 |
| 8 | 182 | Textile fabric shoes | 0.114 | 272 | Chemical medicines | 0.098 | 313 | Bricks, tiles, stones for construction | −0.099 |
| 7 | 394 | Batteries | 0.108 | 204 | Bamboo, rattan, palm, grass production | 0.096 | 134 | Sugar | −0.099 |
| 6 | 145 | Canned foods | 0.106 | 307 | Plastic parts | 0.094 | 267 | Soaps, toothpaste, perfume | −0.121 |
| 5 | 172 | Wool textile, dyeing and finishing | 0.104 | 175 | Textile products | 0.093 | 345 | Metallic construction and safety products | −0.201 |
| 4 | 414 | Optical instruments, spectacles | 0.104 | 176 | Knitwear and woven products | 0.083 | 315 | Ceramic products | −0.204 |
| 3 | 244 | Toys | 0.088 | 406 | Electronic components | 0.082 | 363 | Food, beverage, feed manufacturing equipment | −0.258 |
| 2 | 137 | Vegetables, fruits, nuts processing | 0.081 | 192 | Leather goods | 0.074 | 374 | Bicycles | −0.349 |
| 1 | 322 | Steel smelting | −0.235 | 313 | Bricks, tiles, stones for construction | 0.055 | 244 | Toys | −0.657 |
Notes
- (i) Only wage premia significant at least at 10% level included in these rankings.
- (ii) WP, wage premium in percentage terms; FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises; SOEs, state-owned enterprises.
In comparing the top half of Table 2 to the bottom half to find common trends across top 10 industries that set them apart from bottom 10 industries, it is surprisingly difficult to make any general statements. Examining each top 10 group or bottom 10 group of industries by their code numbers, we can see at least three, and in some cases, all four of the 1-digit manufacturing sectors represented within each grouping. This simple observation suggests quite a wide diversity of industries can generate high or low firm-type WP. Our next step is to quantify any cross-industry commonalities by generating correlation coefficients between the significant estimated WP and the firm-level means for various statistics for those industries. This can help us to address questions such as: ‘do higher technology industries tend to generate higher FDIE wage premia?’ Table 3 shows the results of this correlation exercise.
| Correlations | FDIE | HMTE | SOE | Collective |
|---|---|---|---|---|
| Firm age | 0.319 | 0.457 | −0.064 | 0.221 |
| Total labour | −0.268 | 0.289 | −0.011 | −0.088 |
| Total assets | −0.135 | 0.330 | 0.210 | −0.075 |
| Gross industrial output | −0.073 | 0.269 | 0.186 | −0.158 |
| Fixed assets | −0.191 | 0.299 | 0.204 | −0.061 |
| Average years of education | 0.332 | 0.330 | 0.189 | 0.118 |
| Higher educated share | 0.313 | 0.292 | 0.174 | 0.078 |
| Female share | −0.386 | −0.373 | −0.176 | −0.178 |
| Export probability | −0.344 | −0.391 | −0.228 | −0.399 |
| Export share of sales | −0.358 | −0.376 | −0.278 | −0.340 |
| Wage per worker | 0.284 | 0.237 | 0.187 | −0.036 |
| Allowance per worker | 0.384 | 0.405 | 0.236 | 0.178 |
| Compensation per worker | 0.325 | 0.297 | 0.208 | 0.027 |
| Fixed Assets per worker | 0.094 | 0.152 | 0.262 | 0.048 |
| Intangible assets per worker | 0.132 | 0.200 | 0.115 | 0.277 |
| Training cost per worker | 0.374 | 0.248 | 0.181 | 0.401 |
| Num of computers per worker | −0.010 | −0.026 | 0.098 | −0.009 |
| Total profit per worker | 0.415 | 0.229 | 0.230 | 0.303 |
| Operating profit per worker | 0.431 | 0.224 | 0.190 | 0.265 |
| No. of significant wage premia | 138 | 93 | 59 | 23 |
Note
- FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises; SOEs, state-owned enterprises.
In Table 3, we highlight correlations that are greater than 0.4 or less than −0.4, of which there are only five cases. FDIE WP tend to be higher in industries that have higher average total profits or operating profits per worker, with correlations of 0.42 and 0.43. FDIE WP show the strongest correlation with our profit variables, although the other firm-type WP also show positive correlations with the profit variables, ranging from 0.19 to 0.30. HMTE WP show the strongest correlation detected, at 0.46, with firm age, implying that industries with older firms on average produce larger HMTE WP. The HMTE WP also tend to increase with the average allowance paid per worker in an industry. SOE WP show no strong correlations with any of our industry averages, but the WP for collectives show a positive correlation with the training costs per worker at 0.41.
A noteworthy result from Table 3 is that all of the firm-type WP are negatively correlated with both export variables. This means that industries that are more export-oriented on both the extensive margin (i.e. export probability) and the intensive margin (i.e. export share of sales) tend to generate smaller firm-type WP. This result might be due to the presence of the exporter and pure exporter dummies in our wage regression, which may account for more wage variation in industries that are more export-oriented. Also of note from Table 3 is the lack of strong correlations between the foreign WP and our technology indicators. The correlations between FDIE and HMTE WP and industries' intangible assets per worker are positive but low at 0.13 and 0.20, while the correlations between these WP and industries' numbers of computers per worker are negative but very small, at −0.01 and −0.03. It does not appear that an industry's average technology level can serve as a good predictor of the size of its foreign wage premiums. Overall in looking at Table 3, we do not get a strong set of correlations between the average firm in each industry and the foreign firms' WP in that industry.
Our next table presents a summary of our results for question (i) for both hypotheses. Do foreign firms have higher training costs, higher technology levels and/or higher profits relative to PDEs, on average? We ask this question for each 3-digit industry using mean, median and 75th percentile values by firm type and then tally the affirmative responses as shown in Table 4. The table shows that for per worker training costs, only 82 industries (or 55 per cent of industries) report a per-firm mean value for FDIEs that exceeds the per-firm mean value for PDEs. Only 30 industries show FDIEs spending more on training costs using the median firm observation within each firm type to make the comparison, and 59 show FDIEs spending more on training costs at the 75th percentile level. One reason for the large disparity between the hypothesis testing using the mean versus the median values for training cost is that in 27 industries, the median value of training costs per worker is zero for all firm types. Over half of all of the firms in our data set report zero training costs per worker.31 Examining the second section of Table 4, we see even smaller numbers of industries that satisfy the hypothesis that HMTEs spend more on training costs than PDEs. Overall we find that we reject the notion that foreign firms tend to spend more than PDEs on worker training in about half of the industries for FDIEs and in the vast majority of industries for HMTEs.
| Per Worker | Intangible | Total Profit | Operating Profit | ||
|---|---|---|---|---|---|
| Training Cost | Assets | Number Computers | |||
| Number of industries where FDIE statistic > PDE statistic | |||||
| Mean | 82 | 110 | 134 | 102 | 107 |
| Median | 30 | 93 | 137 | 105 | 101 |
| 75th percentile | 59 | 131 | 138 | 127 | 124 |
| Number of industries where HMTE statistic > PDE statistic | |||||
| Mean | 31 | 91 | 118 | 69 | 74 |
| Median | 16 | 48 | 132 | 63 | 56 |
| 75th percentile | 24 | 123 | 126 | 90 | 94 |
| Shares of 149 industries where FDIE statistic > PDE statistic | |||||
| Mean | 0.550 | 0.738 | 0.899 | 0.685 | 0.718 |
| Median | 0.201 | 0.624 | 0.919 | 0.705 | 0.678 |
| 75th percentile | 0.396 | 0.879 | 0.926 | 0.852 | 0.832 |
| Shares of 149 industries where HMTE statistic > PDE statistic | |||||
| Mean | 0.208 | 0.611 | 0.792 | 0.463 | 0.497 |
| Median | 0.107 | 0.322 | 0.886 | 0.423 | 0.376 |
| 75th percentile | 0.161 | 0.826 | 0.846 | 0.604 | 0.631 |
Note
- FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises; PDE, private domestic enterprises.
Table 4 shows more affirmative results for question (i) using intangible assets per worker. FDIEs report higher intangible assets per worker than PDEs in 110 industries, and HMTEs do the same in 91 industries. Using median values, the numbers of industries that satisfy the criteria are lower for both foreign firm types, at 93 for FDIEs and 48 for HMTEs. At the 75th percentile, both types of foreign firms report higher intangible assets in most industries, with 131 for FDIEs and 123 for HMTEs. As we found with training costs, intangible assets have a skewed distribution, with over half of the total number of firms reporting zero.
The results using numbers of computers per worker as a proxy of a firm's technology level show more affirmative results than the previously considered variables. A total of 134 industries satisfy the criteria that FDIEs have more computers per worker than PDEs using per firm means for comparison, while 118 industries satisfy the same criteria for HMTEs. The number of industries grows even further using median values, to 137 for FDIEs and 132 for HMTEs. Of our three training and technology measures, computers per worker provides the most consistent support to answer question (i) in the affirmative for the most industries, while training costs per worker failed our test the most often across industries, especially for HMTEs. The differences in results across the three technology and training cost variables at the industry level are not surprising given the low correlations between these variables, mentioned previously.
Table 4 also provides summary statistics for question (i) for Hypothesis 2 regarding the link between profits and firm type. FDIEs on average make more total profit per worker than PDEs in 69 to 71 per cent of industries, depending on whether we use means or medians for comparison, and more operating profit per worker in 68 to 72 per cent of industries. HMTEs do not perform quite as well, earning more total profit per worker on average in only 42 to 46 per cent of industries, and more operating profits per worker in 38 to 50 per cent of industries. As with the training and technology variables, FDIEs tend to satisfy the profitability criterion in more industries than do HMTEs.
Table 5 presents results that address question (ii) for both hypotheses. The first column repeats information from Table 1, the initial benchmark regressions, for the sake of comparison. Columns (2)–(4) summarise our wage regression results after adding the three training and technology determinants one-by-one to the wage regression to see to what extent each of these variables can help to explain the foreign wage premium in each industry. When we add training costs per worker, it produces a significant and positive coefficient in 129 of 149 industries, it never produces a significant and negative coefficient, and it improves the fit of our wage regression in 124 industries (i.e. satisfying criterion (A)). Therefore, we confirm that firms that spend more on worker training tend to pay higher wages in the vast majority of industries. However, differentials in worker training costs do not seem to help to explain the foreign WP in most industries. The table shows that we find no industries that satisfy criterion (A) and (B) and only 22 industries that satisfy (A) and (C) for the FDIE WP. For the HMTE WP, the numbers of industries that satisfy our criteria are even smaller. Only one industry satisfies (A) and (B), and nine industries satisfy (A) and (C).
| Bench Mark | Training Costs | Intangible Assets | Number of Computers | Bench.: Total Profit ≥ 0 | Total Profit | Bench.: Operating Profit ≥ 0 | Operating Profit | Best Fit | |
|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
| Num. ind. w/added variable sig. & positive | 129 | 32 | 122 | 129 | 130 | – | |||
| Num. ind. w/added variable sig. & negative | 0 | 4 | 0 | 0 | 2 | – | |||
| Num. ind. w/improved regression fita (A) | 124 | 66 | 123 | 124 | 123 | 142 | |||
| FDIE coefficients | |||||||||
| Num. ind. w/FDIE coeff. sig. & positive | 137 | 137 | 134 | 133 | 129 | 128 | 129 | 128 | 127 |
| Num.ind. w/FDIE coeff. sig. & negative | 1 | 1 | 2 | 2 | 0 | 1 | 1 | 1 | 0 |
| Num. ind. satisfying (A) & (B) | 0 | 1 | 2 | 1 | 3 | 4 | |||
| Num. ind. satisfying (A) & (C) | 22 | 39 | 106 | 92 | 95 | 100 | |||
| Num. ind. satisfying (A) & (Z) | 94 | 23 | 8 | 17 | 15 | 20 | |||
| Share of ind. satisfying (A) & (B) or (C)b | 0.159 | 0.290 | 0.783 | 0.721 | 0.754 | 0.800 | |||
| Share of ind. satisfying (A) & (Z)b | 0.681 | 0.167 | 0.058 | 0.132 | 0.115 | 0.154 | |||
| HMTE coefficients | |||||||||
| Num. ind. w/HMTE coeff. sig. & positive | 93 | 96 | 95 | 89 | 90 | 90 | 97 | 96 | 94 |
| Num.ind. w/HMTE coeff. sig. & negative | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| Num. ind. satisfying (A) & (B) | 1 | 1 | 2 | 4 | 2 | 4 | |||
| Num. ind. satisfying (A) & (C) | 9 | 22 | 69 | 64 | 73 | 59 | |||
| Num. ind. satisfying (A) & (Z) | 72 | 19 | 9 | 12 | 9 | 24 | |||
| Share of ind. satisfying (A) & (B) or (C)c | 0.108 | 0.247 | 0.763 | 0.756 | 0.773 | 0.649 | |||
| Share of ind. satisfying (A) & (Z)c | 0.774 | 0.204 | 0.097 | 0.133 | 0.093 | 0.247 | |||
| Total #firms | 244,397 | 244,396 | 244,393 | 244,399 | 194,641 | 194,617 | 190,473 | 190,465 | Varies |
Notes
- (i) Criterion (B) = firm type coefficient changed from significant to insignificant with added variable(s) included in the regression.
- (ii) Criterion (C) = firm type coefficient declined but remained significant with added variable(s) included in the regression.
- (iii) Criterion (Z) = firm type coefficient increased but remained significant with added variable(s) included in the regression.
- (iv) FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises.
- (v) aImproved regression fit measured by an increase in adjusted-R2 after new variable added.
- (vi) bShares out of 138 (129 or 130) industries with significant FDIE coefficient in respective benchmark regressions.
- (vii) cShares out of 93 (90 or 97) industries with significant HMTE coefficient in respective benchmark regressions.
The number of cases that appear to refute question (ii) is larger at 94 industries for the FDIE WP and 72 industries for the HMTE WP. For these industries, adding training costs improves the fit of the wage regression while causing the FDIE or HMTE coefficient to increase, rather than decrease. Overall, we see that for training costs our hypothesis is refuted in 68 per cent of industries for the FDIE WP and in 77 per cent of industries for the HMTE WP, while it is supported in only 16 per cent and 11 per cent of industries, respectively. These results are not surprising as we saw in Table 4 that foreign firms do not tend to spend more on worker training than PDEs in most industries. Controlling for training costs, therefore, actually tends to increase rather than decrease the size of our foreign WP in most industries reporting a foreign WP.
Our question (ii) results using intangible assets are somewhat more mixed, as shown in column (3). The variable itself is a significant and positive wage determinant in only 32 industries, while it is a significant and negative determinant in four industries. However, its inclusion improves the fit of our wage regression in 66 industries. For the FDIE WP, adding intangible assets to the wage regressions produces results that satisfy our (A) and (B) criteria in one industry and satisfy our (A) and (C) criteria in 39 industries. The corresponding numbers for HMTE WP are 1 and 22. These numbers are higher than for training costs, in part due to the higher numbers of industries where foreign firms tend to report higher intangible assets than PDEs, as shown in Table 4. Table 5 also shows lower numbers of industries that refute question (ii) by satisfying criteria (A) and (Z), with 23 industries for the FDIE coefficient and 19 industries for the HMTE coefficient. The bottom line results for intangible assets show support for our hypothesis in 29 per cent of industries for the FDIE WP and 25 per cent of industries for the HMTE WP, while contradictory evidence is found in 17 per cent and 20 per cent of industries, respectively.
Table 5 clearly shows that adding the number of computers per worker to our wage regression performs the best out of our added training and technology variables in terms of satisfying our criteria for question (ii). In two industries, adding the number of computers improved the regression fit and caused the FDIE coefficient to lose significance (i.e. satisfied (A) and (B)). In 106 more industries, adding the number of computers improved the regression fit and caused the FDIE coefficient to shrink, while remaining significant (i.e. satisfied (A) and (C)). The corresponding numbers for the HMTE WP are 2 and 69 industries. We find only eight industries for the FDIE WP and nine industries for the HMTE WP that appear to refute our hypothesis by showing a significant increase in the foreign WP after adding the number of computers per worker to the wage regression. These numbers imply support for our hypothesis in 76 to 78 per cent of industries versus contradictory evidence in only 6 to 10 per cent of industries.
To add per worker total profits or operating profits to our wage regressions, we need two new sets of benchmark results to reflect the loss of observations due to negative reported profit values, as described previously. These new benchmark results are summarised in column (5) for all firms with non-negative total profits and in column (7) for firms with non-negative operating profits. Adding total profits per worker as a wage determinant causes the FDIE coefficient to lose significance in one industry and to decrease in size in 92 other industries while also satisfying criterion (A), as shown in column (6). For the HMTE coefficient, four industries satisfy criteria (A) and (B) while 64 satisfy criteria (A) and (C). The results shown in column (8) using operating profits per worker instead of total profits per worker are similar in magnitude to those shown in column (6). Overall, we find support for the fair wage hypothesis in 72 to 75 per cent of industries for FDIE WP and in a similar 76 to 77 per cent of industries for HMTE WP. Evidence contrary to the fair wage hypothesis is found in 12 to 13 per cent of industries for the FDIE WP and 9 to 13 per cent of industries for the HMTE WP.
In column (9) of Table 5, we show the tallied results from using the ‘best-fit’ wage regression for each industry. In 147 of 149 industries, we have a better fit for our wage regression using the non-negative profit restrictions reflected in results shown in columns (5) and (7) rather than the unrestricted benchmark results shown in column (1). For that reason, we use the benchmarks in columns (5) and (7) as our starting point, then sequentially add total (or operating) profit, then number of computers, then intangible assets or training costs, and then all four added variables and compare the fit of the wage regression to select the ‘best-fit’ regression (i.e. the reporting the highest adjusted R2 value). These results allow for variation across industries in wage determinants. We find support for our combined hypotheses32 in 80 per cent of industries to explain the FDIE WP and in 65 per cent of industries to explain the HMTE WP. Contradictory evidence is found in only 15 per cent and 25 per cent of industries, respectively. Across industries, we find the most support on the extensive margin when applying our hypotheses to explain the FDIE WP, followed by the HMTE WP.
As a robustness check, we conduct the same hypothesis testing on the SOE WP, which we do not expect to be well-explained by our two hypotheses. These results are shown in Table S4 in the Appendix. We find support in our ‘best-fit’ regressions for the combined hypotheses applied to SOE WP in only 35 per cent of industries and contradictory evidence in 54 per cent of industries, confirming that the efficiency wage and fair wage hypotheses are less useful in explaining SOE WP.
So far our hypothesis testing has only examined the direction of changes in foreign WP, but we are also interested in the sizes of these changes. Table 6 presents results to address the question: how much of the benchmark foreign WP can be explained by the added wage determinants? We group the results based on the direction of change in the foreign WP and show mean percentage changes for industries with decreases (i.e. those satisfying (A) and (C) criteria) and the corresponding statistic for industries with increases (i.e. those satisfying (A) and (Z) criteria). Of the five variables tested, the two profit variables appear to be the strongest individual determinants of the foreign WP, on average. The FDIE coefficient fell by an average of 8.3 per cent among the 92 industries that saw a decrease in the coefficient when total profits are included in the wage regression. The corresponding result for the HMTE coefficient is an average decline of 8.8 per cent among 64 industries. When operating profits are included, the FDIE coefficient fell by an average of 6.7 per cent across 95 industries and the HMTE coefficient declined by an average of 7.6 per cent across 73 industries.
| Per Worker | Training Costs | Intangible Assets | Intangible Assets – w/out outliera | Number Computers | Total Profit | Operating Profit | Best Fit |
|---|---|---|---|---|---|---|---|
| FDIE coefficients | |||||||
| Mean %Δ in FDIE coeff. for ind. w/decrease | −0.020 | −0.063 | −0.022 | −0.052 | −0.083 | −0.067 | −0.090 |
| Mean %Δ in FDIE coeff. for ind. w/increase | 0.058 | 0.031 | 0.031 | 0.022 | 0.044 | 0.018 | 0.148 |
| Min. %Δ in FDIE coeff. | −0.071 | −1.625 | −0.177 | −0.199 | −0.244 | −0.253 | −0.253 |
| Max. %Δ in FDIE coeff. | 0.694 | 0.147 | 0.147 | 0.064 | 0.494 | 0.062 | 0.966 |
| Num. ind. satisfying (A) & (C) | 22 | 39 | 38 | 106 | 92 | 95 | 100 |
| Num. ind. satisfying (A) & (Z) | 94 | 23 | 23 | 8 | 17 | 15 | 20 |
| HMTE coefficients | |||||||
| Mean %Δ in HMTE coeff. for ind. w/decrease | −0.021 | −0.013 | −0.013 | −0.061 | −0.088 | −0.076 | −0.082 |
| Mean %Δ in HMTE coeff. for ind. w/increase | 0.102 | 0.026 | 0.026 | 0.015 | 0.076 | 0.040 | 0.102 |
| Min. %Δ in HMTE coeff. | −0.060 | −0.030 | −0.030 | −0.235 | −0.298 | −0.285 | −0.248 |
| Max. %Δ in HMTE coeff. | 0.875 | 0.116 | 0.116 | 0.053 | 0.234 | 0.099 | 0.429 |
| Num. ind. satisfying (A) & (C) | 9 | 22 | 22 | 69 | 64 | 73 | 59 |
| Num. ind. satisfying (A) & (Z) | 72 | 19 | 19 | 9 | 12 | 9 | 24 |
Notes
- (i) Mean %change = (coefficient after added variable inclusion − benchmark coefficient)/ABS(benchmark coefficient).
- (ii) ABS, absolute value; FDIE, foreign direct-invested enterprises; HMTE, Hong Kong–Macao–Taiwan-invested enterprises.
- (iii) aOutlier result for industry 332 (Noble metals smelting) with %Δ in FDIE coeff. of −1.625, with coefficient changing from 1.129 to −0.705 with added variable.
Among the training and technology variables, the strongest determinant of the foreign WP is the number of computers per worker. Adding the number of computers to the wage regression reduced the FDIE coefficient by an average of 5.2 per cent across 106 industries, and it reduced the HMTE coefficient by an average of 6.1 per cent across 69 industries. Intangible assets appear to be another strong determinant of the FDIE WP, causing a 6.3 per cent average decline in the coefficient but that average was strongly impacted by a single outlier case where the FDIE coefficient changed signs from positive to negative among the 39 industries showing a coefficient decline. Setting that outlier aside, intangible assets explained only 2.2 per cent of the FDIE coefficient on average across 38 industries, and it explained only 1.3 per cent of the HMTE coefficient on average across 22 industries. Similar to intangible assets, training cost was a weak determinant of the foreign WP, reducing the FDIE WP by only 2 per cent on average in 22 industries and the HMTE WP by only 2.1 per cent on average in only nine industries.
Table 6 also shows the strength of our determinants when used in the best combination for each industry. In these best-fit wage regressions, our hypotheses combined can explain an average of 9 per cent of the FDIE WP in 100 industries, and an average of 8.2 per cent of the HMTE WP in 59 industries. However, we also generate on average 14.8 per cent larger FDIE WP in 20 industries and 10.2 per cent larger HMTE WP in 24 industries in our best-fit regressions. We conclude that our hypotheses combined explain just 9 per cent of the FDIE WP in three-quarters of the industries that produced FDIE WP, and they explain slightly less of the HMTE WP in three-fifths of the industries that produced HMTE WP. Even after controlling for differences in profits, technology and/or training costs, we find large residual WP associated with foreign ownership in China in the vast majority of industries.
As a robustness test of these results on the strengths of WP determinants, we ask how much of the SOE WP is explained by our added technology and profit variables. These results are shown in Table S5 in the Appendix. Contrary to the results above for foreign WP, we find that per worker profit performs poorly as a determinant of the SOE WP while per worker training cost performs well. Total profit (operating profit) reduces the SOE WP in only six (nine) industries by an average of 4.0 per cent (8.5 per cent) while training cost reduces it by 8.3 per cent on average in 40 industries of 59 industries producing a significant SOE WP. These results confirm that the most important determinants for foreign WP (i.e. profits and numbers of computers) differ from the most important determinant of SOE WP (i.e. training costs).33
5 Conclusions
Controlling for observable differences in worker and firm characteristics within each 3-digit manufacturing industry in China, we find a significant wage premium attached to foreign ownership in 92 per cent of industries and a wage premium attached to overseas Chinese ownership in 62 per cent of industries compared to private domestic ownership. FDIEs tended to generate larger WP across industries than HMTEs, but both types of foreign WP responded similarly in our estimates of determinants. By comparison, WP generated by SOEs responded very differently in robustness checks of our results.
We find evidence consistent with both the fair wage and worker turnover aversion (i.e. efficiency wage) hypotheses linking higher profits and higher technology at foreign firms relative to domestic firms to higher wages. Foreign firms tend to earn higher profits per worker and use more computers per worker than private domestic firms in most industries. Controlling for these variables in our wage regression helps to explain some of the foreign wage premium in many industries. We find per worker profit to be the strongest single determinant of foreign WP, explaining 7 to 8 per cent of the FDIE wage premium in 72 to 75 per cent of industries, and 8 to 9 per cent of the HMTE wage premium in 76 to 77 per cent of industries using either total profit or operating profit per worker in our wage regressions. The number of computers per worker helps to explain the foreign wage premium in 78 per cent of industries for the FDIE wage premium and in 76 per cent of industries for the HMTE wage premium, but it explains only 5 to 6 per cent of these WP.
We found mixed evidence for the efficiency wage hypothesis; however, when training costs and intangible assets were used as proxies for firms' worker turnover costs. Foreign firms tended to report higher intangible assets per worker than private domestic firms in most industries but this variable proved to be a significant determinant of firm-level wages in only 21 per cent of industries. As the variable had a direct effect on wages in such a minority of industries, it is unsurprising that it was found to be a weak determinant of foreign wage premiums. Intangible assets were a significant determinant of the FDIE wage premium in only 29 per cent of industries and a significant determinant of the HMTE wage premium in only 25 per cent of industries, while explaining only 1 to 2 per cent of either one on average, aside from one outlier case. Training cost per worker proved to be the worst determinant of foreign WP because foreign firms do not tend to spend more on worker training than private domestic firms in most industries. Instead of finding evidence consistent with our hypothesis using this variable, we find contradictory evidence in most industries; that is, controlling for training costs increased rather than decreased the foreign wage premium in the vast majority of industries. Of the three technology and training variables, the number of computers was the strongest determinant of foreign WP because it was a significant determinant of firm-level wages and foreign firms tended to use more computers than domestic private firms in most industries.
When we combine our fair wage and efficiency wage hypotheses to tally our results using the best-fit wage regression for each industry, we can explain an average of 9 per cent of the FDIE wage premium in 77 per cent of the industries that produced a significant FDIE wage premium, and an average of 8 per cent of the HMTE wage premium in 61 per cent of the industries that produced a significant HMTE wage premium. Even after controlling for differences in profits, technology and/or training costs, we find large residual WP associated with foreign ownership in China in the vast majority of industries. We interpret these results as evidence that additional determinants not only matter for foreign WP but they matter in large ways. Further research is needed to explore these additional determinants of foreign WP.
Notes
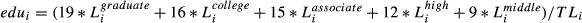, where TLi is the total number of workers in firm i, 
, 
, 
, 
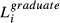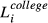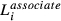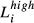and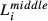 
are number of workers with highest education at graduate, four-year college, three-year college, high school or middle school and below levels in firm i, respectively.
