Identifying Determinants of Branch Performances in Agricultural Bank of China: A Spatial Econometric Approach
We would like to thank the associate editor Eden Yu and two anonymous referees for helpful comments and suggestions.
Abstract
This paper identifies determinants of branches’ performances in Agricultural Bank of China using the spatial econometric approach. Studies on changes of spatial patterns of a financial industry are scarce, especially at the branch level. This paper is the first attempt to take spatial interdependence and urbanisation effects into account to investigate the determinants of China's bank branches’ performances from 1997 to 2011. We have chosen the world's 10th largest bank, the Agricultural Bank of China, because it discloses the most complete panel data of all. Empirical evidence indicates that spatial effects and urbanisation have large, statistically significant impacts on branches’ performances. It highly and positively corresponds to tertiary industry output (domestic consumption) and urbanisation. This signals that the ABC has evolved from a state-owned specialised bank to a listed commercial bank.
1 Introduction
The Agricultural Bank of China (ABC) was resurrected in 1979 to support rural economic development by China's government. The predecessor of the ABC was the Agricultural Cooperative Bank in 1951. The ABC accounted for more than 95 per cent of China's rural credits until the early 1990s (Liu and Wu, 2008). In 1993, the government implemented restructuring policy: Decision on Financial Institutional Reforms. It removed the state-owned banks, including the ABC, from policy financing. In 1994, three new policy banks (the Agricultural Development Bank of China, China Development Bank and Export–Import Bank of China) were set up to replace the original state-owned banks. Furthermore, under the Commercial Banking Law of 1995, the ABC began to operate as commercial banks that were responsible for their profits and losses. Loans were to be made on a commercial basis instead of a policy basis. Thus, the ABC has evolved from a state-owned specialised bank to a wholly state-owned commercial bank and subsequently a state-controlled commercial bank.1 It was then restructured into a joint-stock limited liability company in 2009. It was listed in both Shanghai and Hong Kong Stock Exchanges and became a public shareholding commercial bank in 2010. At the same time, it accepted foreign investment, including Standard Chartered Bank and Seven Group of Australia, as main shareholders. The transformation and privatisation allowed domestic and foreign investment on the bank and has changed the original management goal and nature.
The ABC ranked third in 2013 up from fifth in 2012 by profit in the world according to the annual survey of 2000 in 2012 and 2013. It moved up to 64th in 2013 from 84th in 2012 at the Global 500 (2011 in 2012 and 2013). Geographical dimensions and spatial territorial features of China's financial sector have been omitted in the previous literature. Despite the trend of financial globalisation, however, banking services occur at regional or local levels, still displaying considerable differences from one to another. This leads to the need for better understanding of spatial territorial performances of the ABC.
The location and performances of bank branches are critical to the success of the banking business. The major ingredients for the location decisions and performances of branch banks are often highly sensitive to socioeconomic, demographical, and behavioural factors. Accordingly, the traditional normative approach alone cannot analyse the excessive location-related data associated with the external factors and cannot appropriately evaluate behavioural criteria for branch banking sites (Min, 1989). The spatial econometric model can be applied to overcome the shortcoming in previous literature related to the evaluation of bank branches’ performances (Triki and Maktouf, 2012). Prior studies related to China's banking industry have never taken into account the impacts caused by spatial association effects and factors related to urbanisation.
We are thus motivated to conduct this research and focus the investigation on the ABC due to the data availability. Our analysis constructs a panel of data that combines information on branches’ locations, outputs and local economic, industrial and demographical characteristics. The empirical evidence clearly indicates that spatial autocorrelation exists significantly and highlights spatial effects. There would be a bias if the econometric model excluded spatial effects. Thus, it is important to apply spatial econometric methods, which consider the possibility of spatial effects, to obtain more appropriate empirical results.
Thus, this paper is the first research to assess the performances of one of China's largest banks at the branch level with empirical evidence obtained from employing spatial lag and error models and by underlining the impact of urbanisation. Thus, we emphasise and take factors related to urbanisation into account with the application of the spatial econometric method in evaluating bank branches’ performances. As a result, we conclude that the performances of the ABC concentrated on economically better-developed regions such as east coastal provinces and municipalities. The growth of service sector and urbanisation are contributing factors to the branch performance of the ABC during the period of this study.
The paper is set up as follows. Section 2 reviews existing literature. In Section 3, we present data adopted, introduce the model applied and describe the estimation procedure. Section 4 discusses the empirical results. We conclude in Section 5.
2 Literature Review
Previous literature identified important factors of evaluating bank performances and determinants of bank branches’ performances. There are three main approaches in analysing service industry efficiency: the production, intermediation and the value-added approaches. Berger and Humphrey (1997) regarded that neither the production approach nor the intermediation approach is perfect. Berger and Humphrey (1992) proposed the value-added approach to identify output. In this approach, all liability and asset categories of bank balance sheet are considered to have some output characteristics, to the extent that ‘they have substantial valued added, as judged using an external source of operation cost allocation’. Studies of Doyle et al. (1979), Berger et al. (1987), Min (1989), Berg et al. (1991, 1993), Zardkoohi and Kolari (1994), Berger and Humphrey (1997) and Cook et al. (2000) used total loans and deposits to measure outputs for each branch office. In this paper, we adopt the value-added approach and use both loans and deposits as dependent variables to scrutinise performances of different branches.
The total number of employees in three sectors (primary, secondary and tertiary) was employed in evaluating bank branches’ performances by Doyle et al. (1979), Boufounou (1995) and Crocco et al. (2010). However, the data of the number of employers in the three sectors (primary, secondary and tertiary) and the decomposition of these three sectors at the provincial and municipality level in Mainland China were released incompletely and patchily. Instead, we use outputs of these three sectors at the provincial and municipality levels as proxy variables to assess the impacts of changes of the three sectors on provincial branches’ performances. Thus, outputs of the three sectors stand for different patterns of econ-omic development in each province in Mainland China. Due to the transformation of the ABC mentioned in Section 1, the ABC is now seeking to develop urban and county businesses into the ‘two-engines’ of growth. Based on its branch network restructure, it develops the retail banking business and enhances competitiveness in key urban areas. The bank has been shifting into capitalising urban areas. Therefore, it is assumed that branch performances should be positively and closely related to the higher-developed sectors such as secondary and tertiary industries and relatively less so to the primary sector.
The studies (Graddy and Kyle, 1979; Avery et al., 1999; Bos and Kool, 2006; Crocco et al., 2010) pointed to urbanisation as an important factor in allocating the branch network of banks. Branches in urban areas outperform those in rural areas. In addition, the performances of branches situated in larger urban areas perform even better. Therefore, the number of urban employed workers at the provincial or municipal level stands for the degree of the urbanisation of the province and has positive effects on branch performance.
The population factor is employed in assessing bank branch performances by many studies, such as Clawson (1974), Jackson (1975), Ali and Greenbaum (1977), Doyle et al. (1979, 1981), Graddy and Kyle (1979), Olsen and Lord (1979), Min (1989), Boufounou (1995), Amel and Liang (1997) and Avery et al. (1999). Clearly, population has a positive effect on branch performance.
Prior studies related to China's banking industry have never taken into account the impacts caused by spatial association effects and factors of urbanisation. This paper is therefore the first attempt to investigate the importance of the five determining variables (adopted from the above-existing literature) on China's bank branches’ performances by providing empirical evidence with the application of spatial econometric methods and while underlining the impact of urbanisation.
3 Spatial Econometric Models
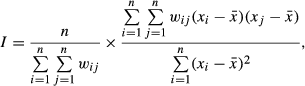
 denotes the mean value of n number of observed values from spatial locations, and wij denotes whether or not there is a spatial neighbourhood between spatial location i and spatial location j of the spatial weight matrix W. Here, wij = 1 if a spatial neighbourhood exists between spatial location i and spatial location j of the spatial weight matrix W, and wij = 0 if there is no spatial neighbourhood between spatial location i and spatial location j of the spatial weight matrix W. In addition, the value of diagonal is equal to zero, that is, wii = 0. There is no spatial correlation between provinces, and therefore, spillover effects among provinces do not exist if W*dependent (or spatial autocorrelation) is not significant. On the contrary, there is spatial correlation between provinces, and spillover effects among provinces exist if W*dependent (or spatial autocorrelation) is significant. The form of spatial weight matrix W can be expressed as follows:
denotes the mean value of n number of observed values from spatial locations, and wij denotes whether or not there is a spatial neighbourhood between spatial location i and spatial location j of the spatial weight matrix W. Here, wij = 1 if a spatial neighbourhood exists between spatial location i and spatial location j of the spatial weight matrix W, and wij = 0 if there is no spatial neighbourhood between spatial location i and spatial location j of the spatial weight matrix W. In addition, the value of diagonal is equal to zero, that is, wii = 0. There is no spatial correlation between provinces, and therefore, spillover effects among provinces do not exist if W*dependent (or spatial autocorrelation) is not significant. On the contrary, there is spatial correlation between provinces, and spillover effects among provinces exist if W*dependent (or spatial autocorrelation) is significant. The form of spatial weight matrix W can be expressed as follows:
The value is between −1 and 1 according to the above formula of Moran's I. There is positive spatial autocorrelation if Moran's I value is larger than 0. There is negative spatial autocorrelation if the value is smaller than 0. There is no spatial autocorrelation, and they are randomly distributed if the value is equal to zero.
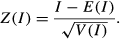
It is a so-called spatial cluster if the test results show that there is a significant spatial autocorrelation. There is a positive spatial autocorrelation if the values of the observed region and the neighbouring region are both high (high–high) or are both low (low–low). Conversely, there is a negative spatial autocorrelation if the value of the observed region is high and that of the neighbouring region is low (high–low) or the value of the observed region is low and that of the neighbouring region is high (low–high).
Despite the substantial difficulties in obtaining adequate and reliable data on China's banks, the volume of deposits and loans in renminbi are consistently available for most provinces and municipalities, as in the case of the ABC. It is suggested that the larger the deposits or loans, the better the performance of the branches. We used two dependent variables in this study: LR (loans in each province or municipality) and DR (deposits in each province or municipality). There are five independent variables: PI, SI, TI (the total value of the primary, secondary or tertiary industries in each province or municipality), UE (the total number of urban employees of the province or municipalities) and POP (the total of population in the province or municipality). The definitions of these variables are displayed in Table 1. The variables are used at the 26 provinces and four municipality levels. All the nominal variables have been transformed with regional consumer price indices into real terms and used under logarithms. The indices data are available from 1994 to 2011 from China Statistical Yearbook (2012). Data on branches’ loans and deposits in 30 provinces and municipalities of the ABC from the year 1997 to 2011 were collected from Almanac of China's Finance and Banking (1990–2012) and Statistical Yearbook of Agricultural Bank of China (1978–2008). Other data were from China Statistical Yearbook (1979–2012). We further group the data into six regions (see also Table 2) referring to the national geography. The six regions, the provinces and municipalities in the study are the Yangtze River Delta (Shanghai city, Jiangsu and Zhejiang provinces), Pearl River Delta (Fujian, Guangdong, Hainan and Guangxi provinces), Bohai Sea region (Beijing city, Tianjing city and Hebei and Shandong provinces), central region (Shanxi, Anhui, Jiangxi, Henan, Hubei and Hunan provinces), western region (Chongqing city, and Guizhou, Sichuan, Yunnan, Shaanxi, Gansu, Qinghai, Ningxia and Xinjiang provinces) and north-east region (Inner Mongolia, Liaoning, Jilin and Heilongjiang provinces).
| Variable Names | Definitions |
|---|---|
| LR i,t | The total amount of loans in renminbi of the province i in year t |
| DR i,t | The total amount of deposits in renminbi of the province i in year t |
| PI i,t | The output of the primary industry of the province i in year t |
| SI i,t | The output of the secondary industry of the province i in year t |
| TI i,t | The output of the tertiary industry of the province i in year t |
| UE i,t | The total number of urban employees of the province i in year t |
| POP i,t | The number of population of the province i in year t |
Notes:
- (i) All the nominal variables have been transformed into real terms and used under logarithms.
- (ii) The output of the primary, secondary and tertiary industry is measured by 100 million yuan.
- (iii) Both DR and LR are measured by the unit of 100 million yuan.
- (iv) Both the variables on UE and POP are measured at the year-end in 10,000 persons according to China Statistical Yearbook.
- (v) The ‘deposits’ are the overall deposits. It covers all types of deposits (a, domestic short-term loans; b, domestic midterm and long-term loans; c, exports and imports finance; d, bill finance) according to the Statistical Yearbook of Agricultural Bank of China (2008).
| Name of the Regions | Provinces and Municipalities Included |
|---|---|
| Yangtze River Delta | Shanghai city, Jiangsu and Zhejiang provinces |
| Pearl River Delta | Fujian, Guangdong, Hainan and Guangxi provinces |
| Bohai Sea region | Beijing city, Tianjing city and Hebei and Shandong provinces |
| Central region | Shanxi, Anhui, Jiangxi, Henan, Hubei and Hunan provinces |
| Western region | Chongqing city, and Guizhou, Sichuan, Yunnan, Shaanxi, Gansu, Qinghai, Ningxia and Xinjiang provinces |
| Northeast region | Inner Mongolia, Liaoning, Jilin and Heilongjiang provinces |
We first employ an exploratory spatial data analysis (ESDA) approach and two methods: the Moran's I and the local indicators of spatial association (LISA) are adopted to evaluate the performances of the ABC at the province and municipality level with the exploration of spatial data.
The results of Moran's I indicate the extent of significant spatial clustering for the outputs (loans and deposits) of totally 30 provinces and municipalities in the sample and evaluate their temporal trends in the period of the study. The measure can be illustrated by Moran scatterplots (Anselin, 1993) to show the decomposition of the association into spatial clusters of similar high or low values and clusters of dissimilar values and to assess the existence of outliers.
The indication provided by the Moran scatterplots is exploratory because it offers no measure of ‘statistical’ significance associated with the individual patterns. We therefore further employ LISA (Anselin, 1995). The data are computed to G* statistics (Getis and Ord, 1992) and can be visualised using geography information system (GIS) or mapping system as triangles pointing up for high–high associated or down for low–low and with varying sizes related to different significant levels.
Our analysis carried out the estimation from 1997 to 2011. To be manageable, we only present tables with the results obtained from Moran's I statistic in years including the beginning 1997 (Asian financial crises), the midyear (subprime crisis occurred in 2007 and 2008) and the end of the year of the observation period in this study, 1997, 2002, 2007, 2008, 2010 and 2011 for renminbi. For consistency's sake and to reduce bias, we further show the maps obtained with the application of LISA as mentioned earlier. The results of LISA analysis identify provinces with either similar, positive associations with their neighbours in terms of their loans or deposits (high–high, low–low) or those with negative association (high–low, low–high). The revealed distribution identifies either regions of concentration or those of dispersal in terms of their loans or deposits relations. Thus, the LISA results can be interpreted as a spatial interaction pattern. These maps confirm and clarify the findings obtained from Moran scatterplots. The temporal trends were deemed sufficient to analyse the long-run evolution of branches’ performances of the ABC from the geospatial perspective.
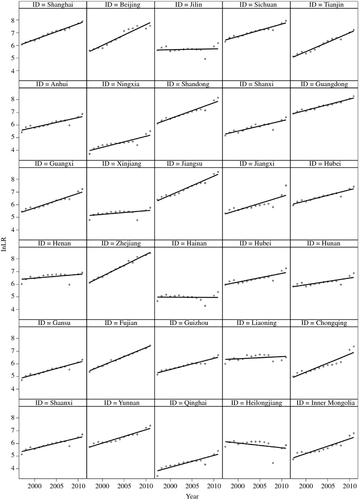
Moran's I test is one of the useful tools in identifying the existence of spatial effects (Chou et al., 2009). The results of Moran's I test presented in Table 3 clearly indicate that spatial autocorrelation exists significantly with the only exception being variable: PI in the years from 2003 to 2007, 2009 and 2010. Thus, the results in Table 3 that highlight spatial effects cannot be ignored. We also recognise the time-period effects in the panel data set of this study by observing scatterplots of each variable. It is regarded that the closer the spots are alongside the curve, the more significant the time-period effects it implies. Almost all of spots are very close to the curve according to the scatterplots of each variable (to be manageable, we only present scatterplots of two variables: LR and DR, in Figures 1 and 2).
| Years | LR | DR | PI | SI | TI | UE | POP |
|---|---|---|---|---|---|---|---|
| 1997 | 0.2388 ** | 0.2185 ** | 0.1805 * | 0.2918 *** | 0.3360 *** | 0.2849 *** | 0.2151 ** |
| (0.0312) | (0.0493) | (0.0638) | (0.0065) | (0.0024) | (0.0017) | (0.0178) | |
| 1998 | 0.20624 * | 0.2156 * | 0.1727 * | 0.1727 * | 0.3420 *** | 0.2587 *** | 0.2150 ** |
| (0.0575) | (0.0541) | (0.0726) | (0.0726) | (0.0020) | (0.0047) | (0.0179) | |
| 1999 | 0.2090 * | 0.2129 * | 0.1764 * | 0.1764 * | 0.3407 *** | 0.2803 *** | 0.2149 ** |
| (0.0535) | (0.0578) | (0.0683) | (0.0683) | (0.0020) | (0.0028) | (0.0179) | |
| 2000 | 0.2121 * | 0.2078 * | 0.1747 * | 0.1747 * | 0.3433 *** | 0.3181 *** | 0.2094 ** |
| (0.0579) | (0.0632) | (0.0746) | (0.0746) | (0.0019) | (0.0009) | (0.0222) | |
| 2001 | 0.2238 ** | 0.2193 ** | 0.1640 * | 0.6940 *** | 0.3299 *** | 0.2757 *** | 0.2149 ** |
| (0.0477) | (0.0490) | (0.081) | (0.0093) | (0.0026) | (0.0036) | (0.0194) | |
| 2002 | 0.2350 ** | 0.2258 ** | 0.1669 * | 0.2860 *** | 0.33292 *** | 0.2419 *** | 0.2143 ** |
| (0.0370) | (0.0441) | (0.0848) | (0.0071) | (0.0027) | (0.0084) | (0.0200) | |
| 2003 | 0.2496 ** | 0.2411 ** | 0.1322 | 0.3027 *** | 0.3390 *** | 0.2164 ** | 0.2170 ** |
| (0.0268) | (0.0309) | (0.1650) | (0.0047) | (0.0023) | (0.0145) | (0.0189) | |
| 2004 | 0.2814 ** | 0.2418 ** | 0.14070 | 0.3040 *** | 0.34197 *** | 0.1201 | 0.2842 *** |
| (0.0121) | (0.0282) | (0.1320) | (0.0046) | (0.0022) | (0.163) | (0.0026) | |
| 2005 | 0.3145 *** | 0.2460 ** | 0.1242 | 0.3113 *** | 0.3119 *** | 0.1927 ** | 0.2081 ** |
| (0.0041) | (0.0244) | (0.1750) | (0.0038) | (0.0049) | (0.0235) | (0.0257) | |
| 2006 | 0.3219 *** | 0.2490 ** | 0.1267 | 0.8951 *** | 0.3075 *** | 0.2046 ** | 0.2077 ** |
| (0.0041) | (0.0210) | (0.1640) | (0.0058) | (0.0053) | (0.0207 | (0.0266) | |
| 2007 | 0.3277 *** | 0.3240 *** | 0.1182 | 0.2978 *** | 0.3094 *** | 0.1840 ** | 0.2070 ** |
| (0.0024) | (0.0064) | (0.1840) | (0.0050) | (0.0051) | (0.0445) | (0.0279) | |
| 2008 | 0.3884 *** | 0.2491 ** | 0.1306 ** | 0.28817 *** | 0.3100 *** | 0.2164 ** | 0.2066 ** |
| (0.0002) | (0.0334) | (0.0138) | (0.00645) | (0.0050) | (0.016) | (0.0290) | |
| 2009 | – | – | 0.1381 | 0.2955 *** | 0.3222 *** | 0.2415 ** | 0.2061 ** |
| (0.115) | (0.0047) | (0.0036) | (0.0109) | (0.0302) | |||
| 2010 | 0.3926 *** | 0.2876 *** | 0.1126 | 0.28140 *** | 0.3371 *** | 0.1580 * | 0.2113 ** |
| (0.0002) | (0.0095) | (0.193) | (00066) | (0.0026) | (0.0961) | (0.0288) | |
| 2011 | 0.4187 * | 0.2477 ** | 0.2153 ** | 0.2729 *** | 0.3366 *** | 0.2406 *** | 0.2123 ** |
| (0.0000) | (0.0215) | (0.0199) | (0.0081) | (0.0027) | (0.0055) | (0.0285) |
Notes:
- (i) Data of LR and DR in 2009 are not available due to the fact that the amounts of deposits and loans of the ABC were not disclosed.
- (ii) The italic values indicate there are significant correlations.
- (iii) *Significance at level 0.1; **significance at level 0.05; ***significance at level 0.01.

With respect to the lag term decision, we adopted Akaike information criterion (AIC) to choose the last lag term. The results are presented in Figure 3. Using either LR or DR as the dependent variable in the spatial econometric model, the values of AIC become larger when the lag time increases (see Figure 3). It is thought that the smaller the value of AIC is, the more appropriate the lag term is. Zero-lag term appears to be the smallest of the test and is therefore the most appropriate in examining the effects of the panel data employed in this paper on LR and DR.
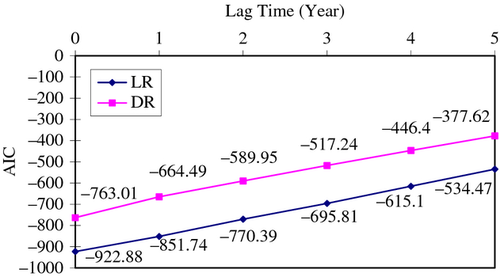
- Note: The horizontal axis stands for the lag time (by year), and the vertical axis stands for the value of AIC.
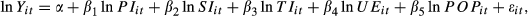 (1)
(1)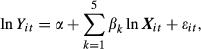 (2)
(2)All five variables are theoretically supposed to have positive signs corresponding to the dependent variables. Thus, the larger the value of PI, SI, TI, UE or POP, the larger the volume of LR or DR would be, and vice versa.
Early literature modelled spatial dependence with regard to spatial weight matrices. The important difference is that the spatial weight matrix is not assumed to be known and is not parameterised. Typical examples of this type of processes include the spatial autoregressive processes and spatial moving average processes. Local non-stationarity and heteroscedasticity are built-in features of these types of processes.2 Spatial dependence exists when the value associated with one location is dependent on those of other locations. The effect of this similarity of values and locations is a loss of information. Spatial dependence can result from spatial interaction effects (e.g. externalities or spillover effects) or from measurement error (e.g. related to a mismatch between the scale at which a phenomenon occurs and how it is measured). Spatial dependence is a property of joint multivariate density functions, while spatial autocorrelation is a moment or characteristic of these functions. Only the latter can be estimated in practice. Spatial heterogeneity exists when structural changes related to location exist in a data set. In such cases, spatial regimes could exist, which are characterised by differing parameter values or functional forms (e.g. patients in some areas can structurally deviate from patients in other areas). Spatial heterogeneity can result in non-constant error variance (heteroscedasticity) across regions, especially when scale-related measurement errors are present. It may be difficult to distinguish from spatial dependence (Chou et al., 2011).
A conventional gravity model explains the variation in the vector of origin–destination flows. It is better that forces leading to flows from an origin region to a destination region may create similar flows to nearby or neighbouring destinations. In contrast to the gravity model, a spatial econometric model of the variation in origin–destination flows would be characterised by: (i) reliance on spatial lags of the dependent variable vector, which is referred to as a spatial autoregressive model, and (ii) spatial lags of the disturbance terms, which is labelled as a spatial error model. The above two models were developed by Anselin et al. (1997). Combining these two models is well known as the SAC model (LeSage and Pace, 2009). Due to the fact that this study relates to spatial and time-specific characteristics, we follow the spatial lag and spatial error models employed by Crocco et al. (2010), Lee and Yu (2010) and Triki and Maktouf (2012). To this end, the two spatial models were modified and used to assess spatial effects and spatial correlation. The two models find consistent results, which is a bias correction procedure of the parameters estimated when adopting the direct method based on maximising the likelihood function with the purpose of adopting the transformation approach. Therefore, the spatial lag model and spatial error model are expressed as equations (3) and (4) representing two dependent variables: LR and DR.
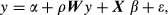 (3)
(3) (4)
(4)The fitness of the panel data used in this paper is the random effects model or the fixed effects model examined by applying the Hausman test. The results of the Hausman test from Tables 4-7 show that the fixed effects model is more appropriate, due to all of the p-values being smaller than 0.05 and therefore statistically significant.
| Types of Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Variables | No Spatial and Time-specific Fixed Effects | Spatial Fixed Effects | Time-period Fixed Effects | Spatial and Time-period Fixed Effects |
| PI i,t | −0.2734 *** | −0.3126 *** | −0.2163 *** | −0.2439 *** |
| (0.000) | (0.0000) | (0.0000) | (0.0032) | |
| SI i,t | −0.1596 *** | −0.0375 | −0.1166 * | 0.2526 *** |
| (0.0106) | (0.6746) | (0.0539) | (0.0044) | |
| TI i,t | 0.9007 *** | 0.5086 *** | 0.9222 *** | 0.6248 *** |
| (0.0000) | (0.0000) | (0.000) | (0.000) | |
| UE i,t | −0.1430 *** | 0.0990 | −0.1757 ** | 0.7128 *** |
| (0.0000) | (0.1480) | (0.0193) | (0.000) | |
| POP i,t | 0.3786 *** | 0.3753 ** | 0.2456 *** | 0.6984 *** |
| (0.0000) | (0.011) | (0.0011) | (0.000) | |
| W*dependent | 0.0200 | 0.5110 *** | 0.0160 | 0.2160 *** |
| (0.1409) | (0.000) | (0.6093) | (0.0002) | |
| Log-likelihood | −122.4441 | 14.8019 | −88.6683 | 80.7244 |
| σ 2 | 0.1049 | 0.0510 | 0.0895 | 0.0405 |
| R 2 | 0.8613 | 0.9325 | 0.8816 | 0.9465 |
| Adjustment R2 | 0.8596 | 0.6544 | 0.8502 | 0.3269 |
| LR test for spatial | 274.4919*** (0.000) | |||
| LR test for time period | 67.5515*** (0.001) | |||
| Hausman test | 156.0360*** (0.000) | |||
Notes:
- (i) Figures in parentheses are the p-value.
- (ii) The italic values indicate there are significant correlations.
- (iii) *Significance at level 0.1; **significance at level 0.05; ***significance at level 0.01.
| Types of Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Variables | No Spatial and time-specific Fixed Effects | Spatial Fixed Effects | Time-period Fixed Effects | Spatial and Time-period Fixed Effects |
| PI i,t | −0.2949 *** | −0.0184 | −0.1582 *** | −0.1577 ** |
| (0.0000) | (0.8000) | (0.0000) | (0.0347) | |
| SI i,t | −0.0589 | −0.2474 *** | −0.0190 | 0.0526 |
| (0.4382) | (0.0056) | (0.7338) | (0.5119) | |
| TI i,t | 1.0292 *** | 0.5391 *** | 0.9469 *** | 0.4767 *** |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| UE i,t | −0.2546 *** | −0.2796 *** | −0.1725 ** | 0.2151 *** |
| (0.0000) | (0.0001) | (0.0127) | (0.0090) | |
| POP i,t | 0.2587 *** | 0.1463 | 0.1378 ** | 0.2577 ** |
| (0.0000) | (0.3307) | (0.0488) | (0.0382) | |
| W*dependent | 0.0440 *** | 0.6520 *** | −0.0220 | 0.0190 |
| (0.0038) | (0.0000) | (0.4154) | (0.7764) | |
| Log-likelihood | −204.9884 | 2.0927 | −55.7862 | 119.3605 |
| σ 2 | 0.1553 | 0.0515 | 0.0760 | 0.0332 |
| R 2 | 0.8587 | 0.9532 | 0.9309 | 0.9698 |
| Adjustment R2 | 0.8527 | 0.7546 | 0.8940 | 0.1267 |
| LR test for spatial | 414.162*** (0.000) | |||
| LR test for time period | 298.40444*** (0.000) | |||
| Hausman test | 58.9736*** (0.000) | |||
Notes:
- (i) Figures in parentheses are the p-value.
- (ii) The italic values indicate there are significant correlations.
- (iii) *Significance at level 0.1; **significance at level 0.05; ***significance at level 0.01.
| Types of Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Variables | No Spatial and time-specific Fixed Effects | Spatial Fixed Effects | Time-period Fixed Effects | Spatial and Time-period Fixed Effects |
| PI i,t | −0.1525 *** | −0.2344 *** | −0.1360 *** | −0.2387 *** |
| (0.0000) | (0.0004) | (0.0000) | (0.0036) | |
| SI i,t | 0.1021 ** | 0.2973 *** | 0.0855 * | 0.3547 *** |
| (0.0450) | (0.0000) | (0.0956) | (0.0000) | |
| TI i,t | 0.6792 *** | 0.5363 *** | 0.8025 *** | 0.6022 *** |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| UE i,t | −0.0546 ** | 0.2161 ** | −0.2080 *** | 0.5490 *** |
| (0.0401) | (0.0159) | (0.0021) | (0.0000) | |
| POP i,t | 0.2078 *** | 0.2788 ** | 0.0582 | 0.5561 *** |
| (0.0000) | (0.0365) | (0.4057) | (0.0000) | |
| Spatial autocorrelation | 0.6880 *** | 0.7320 *** | 0.5870 *** | 0.3990 *** |
| (0.0000) | (0.0000) | (0.0000) | (0.0000) | |
| Log-likelihood | −67.8702 | 53.0891 | −55.6184 | 82.1206 |
| σ 2 | 0.0706 | 0.0387 | 0.0696 | 0.0381 |
| R 2 | 0.8452 | 0.9005 | 0.8758 | 0.9431 |
| Adjustment R2 | 0.8490 | 0.6771 | 0.8441 | 0.3109 |
| LR test for spatial | 76.5743*** (0.000) | |||
| LR test for time period | 66.0998*** (0.0002) | |||
| Hausman test | −69.4051*** (0.0000) | |||
Notes:
- (i) Figures in parentheses are the p-value.
- (ii) The italic values indicate there are significant correlations.
- (iii) *Significance at level 0.1; **significance at level 0.05; ***significance at level 0.01.
| Types of Model | Model I | Model II | Model III | Model IV |
|---|---|---|---|---|
| Variables | No Spatial and time-specific Fixed Effects | Spatial Fixed Effects | Time-period Fixed Effects | Spatial and Time-period Fixed Effects |
| PI i,t | −0.1346 *** | 0.1347 * | −0.1741 *** | −0.1636 ** |
| (0.0000) | (0.0543) | (0.0000) | (0.0285) | |
| SI i,t | 0.1407 ** | 0.0577 | 0.0296 | 0.0575 |
| (0.0114) | (0.4577) | (0.5866) | (0.4731) | |
| TI i,t | 0.8287 *** | 0.7065 *** | 0.9132 *** | 0.4755 *** |
| (0.0000) | (0.0000) | (0.000) | (0.0000) | |
| UE i,t | −0.16677 *** | −0.2013 ** | −0.1578 ** | 0.2153 *** |
| (0.0000) | (0.0348) | (0.0197) | (0.0090) | |
| POP i,t | 0.1203 *** | −0.1166 | 0.1455 ** | 0.2526 ** |
| (0.0042) | (0.4057) | (0.0329) | (0.0522) | |
| Spatial autocorrelation | 0.6970 *** | 0.7720 *** | 0.1270 * | 0.0040 |
| (0.0000) | (0.0000) | (0.0553) | (0.9542) | |
| Log-likelihood | −106.2640 | 27.1761 | −55.1304 | 119.2617 |
| σ 2 | 0.0844 | 0.0428 | 0.0759 | 0.0332 |
| R 2 | 0.8462 | 0.8918 | 0.9302 | 0.9698 |
| Adjustment R2 | 0.8496 | 0.7162 | 0.8932 | 0.1262 |
| LR test for spatial | 464.3291*** (0.000) | |||
| LR test for time period | 299.7161*** (0.001) | |||
| Hausman test | −12.7187** (0.0477) | |||
Notes:
- (i) Figures in parentheses are the p-value.
- (ii) The italic values indicate there are significant correlations.
- (iii) *Significance at level 0.1; **significance at level 0.05; ***significance at level 0.01.
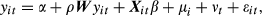 (5)
(5)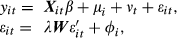 (6)
(6)This study adopts the spatial panel data, so we use LR test to examine whether the data have spatial and time effects. The results of LR test are the same as the Wald test, which is also used for the assessment of the panel data.3
- Model I: the model without both spatial-specific fixed effects μi and time-specific fixed effects νt.
- Model II: the model with the spatial-specific fixed effects μi but without time-specific fixed effects νt.
- Model III: the model with the time-specific fixed effects νt but without spatial-specific fixed effects μi.
- Model IV: the model with both spatial-specific fixed effects μi and time-specific fixed effects νt.
We therefore also conducted the above four types of estimation proposed by Elhorst (2003) to compare and analyse the impacts of spatial-specific and time-specific effects on the parameters of deposits and loans of this study.
The parameters of the above models are estimated by employing maximum likelihood method. Note that LR and DR are used as two dependent variables in this paper. The maximum likelihood estimation (MLE) cannot be applied in estimating the parameters if the probability distribution of the variables does not follow normally distributed. Four of the most frequently adopted techniques used to test the normal distribution of these two dependent variables are Shapiro–Wilk; Kolmogorov–Smirnov; Cramer–von Mises and Anderson–Darling. For instance, the p-values of LR and DR by Shapiro–Wilk age are 0.5198 and 0.6076, respectively. The p-values of these two by Kolmogorov–Smirnov are larger than 0.15. Thus, these p-values are all larger than 0.05. The results signal that both the distributions of LR and DR follow the normal distribution. Therefore, the MLE is used to estimate parameters. Furthermore, the maximum likelihood function adopts the log-likelihood value. Statistically, the larger the log-likelihood value, the better the goodness of fit of the model (Beck et al., 2006).
In addition, both the instrumental variables (IV) and the generalised method of moments (GMM) are consistent estimators (Wooldrige, 2001) in the case of a large sample. They are much less effective in the case of a small sample. On the other hand, the method of IV is useful in resolving endogeneity, but it highly depends on the capability of rigorously selecting relevant explanatory variables such as IV (Angrist and Krueger, 2001). Therefore, the results might not be convincing due to the use of inappropriate IV.
Finally, with respect to the use of the software for spatial lag models with fixed effects panel data proposed by Elhorst (2003, 2010a), the parameter estimated by applying MLE can be inconsistent if the number of the sample (N) is large and the number of the observation time (T) is small. It can still be inconsistent if both N and T of the spatial lag model with spatial and time-period fixed effects are large (Lee and Yu, 2010). However, the above cases pointed out by Lee and Yu (2010) do not apply to the sample of this study because both N and T in this study are not large. In addition, Elhorst (2010b) modified and provided the estimation equations for fixed effects and random effects of both the spatial lag model and spatial error model by MLE method with the software MATLAB code. On the other hand, no source codes are released for IV or GMM.
4 Empirical Results
The empirical results of Moran's I obtained by applying GeoDA software are summarised and presented in Tables 8 and 9. Figures 4 and 5 map the provinces with significant values identified by the LISA approach for the selected years. The analysis adopts the branches’ performances in Beijing, the municipality and the capital of China as the reference region geospatially in comparison with the other performances in all other municipalities and provinces.
| Quadrant | Years | |||||
|---|---|---|---|---|---|---|
| 1997 | 2002 | 2007 | 2008 | 2010 | 2011 | |
| I (high–high) | Shanghai * | Shanghai * | Shanghai ** | Shanghai ** | Shanghai ** | Shanghai ** |
| Beijing | Jiangsu * | Jiangsu * | Jiangsu ** | Jiangsu ** | Jiangsu * | |
| Jiangsu | Fujian * | Fujian * | Fujian * | Fujian * | Fujian * | |
| Zhejiang | Shandong * | Beijing | Beijing | Zhejiang * | Zhejiang * | |
| Shandong | Beijing | Tianjin | Tianjin | Beijing | Beijing | |
| Guangdong | Zhejiang | Zhejiang | Zhejiang | Tianjin | Tianjin | |
| Hebei | Hebei | Shandong | Shandong | Shandong | Shandong | |
| Yunnan | Yunnan | Guangdong | Guangdong | Guangdong | Guangdong | |
| Henan | Henan | Hebei | Hebei | Hebei | Hebei | |
| Hunan | Yunnan | Yunnan | Yunnan | Yunnan | ||
| Jilin | Henan | Guangxi | Guangxi | Guangxi | ||
| Hubei | Guangxi | Chongqing | Chongqing | |||
| Guangxi | Hubei | |||||
| II (low–high) | Anhui * | Anhui * | Anhui * | Anhui * | Anhui ** | Anhui ** |
| Jiangxi * | Jiangxi * | Jiangxi * | Jiangxi * | Hainan ** | Hainan ** | |
| Fujian * | Hainan ** | Hainan ** | Hainan ** | Guizhou | Guizhou | |
| Hainan ** | Guizhou | Guizhou | Guizhou | Hunan | Hunan | |
| Guizhou | Chongqing | Chongqing | Chongqing | Henan | Henan | |
| Chongqing | Hunan | Hunan | Hunan | Jiangxi | Jiangxi | |
| Shanxi | Shanxi | Shanxi | Henan | |||
| Tianjin | Guangxi | |||||
| Tianjin Jilin | ||||||
| III (low–low) | Gansu ** | Gansu ** | Gansu ** | Gansu * | Gansu * | Gansu ** |
| Xinjiang ** | Xinjiang * | Xinjiang * | Xinjiang * | Xinjiang * | Xinjiang * | |
| Shaanxi | Shaanxi | Shaanxi | Inner Mongolia * | Inner Mongolia * | Inner Mongolia * | |
| Inner Mongolia | Inner Mongolia | Inner Mongolia | Shanxi | Shanxi | Shanxi | |
| Ningxia | Ningxia | Ningxia | Shaanxi | Shaanxi | Shaanxi | |
| Qinghai | Qinghai | Qinghai | Ningxia | Liaoning | Liaoning | |
| Jilin | Qinghai | Ningxia | Ningxia | |||
| Heilongjiang | Jilin | Qinghai | Qinghai | |||
| Heilongjiang | Jilin | Jilin | ||||
| Heilongjiang | Heilongjiang | |||||
| IV (high–low) | Sichuan * | Sichuan * | Sichuan Hubei | Sichuan | Sichuan | Sichuan |
| Liaoning | Hubei | Liaoning | Hubei | Hubei | ||
| Heilongjiang | Liaoning | Liaoning | ||||
| Guangdong | ||||||
| Heilongjiang | ||||||
Notes:
- (i) The italic values indicate there are significant correlations.
- (ii) *Significant at the level 0.05; **Significant at the level 0.01.
| Quadrant | Years | |||||
|---|---|---|---|---|---|---|
| 1997 | 2002 | 2007 | 2008 | 2010 | 2011 | |
| I (high–high) | Shanghai * | Shanghai * | Shanghai ** | Shanghai * | Shanghai * | Shanghai ** |
| Jiangsu * | Jiangsu * | Jiangsu ** | Jiangsu * | Jiangsu * | Jiangsu * | |
| Fujian * | Fujian * | Zhejiang * | Fujian * | Shandong * | Shandong * | |
| Shandong | Shandong * | Tianjin * | Zhejiang | Zhejiang | Anhui * | |
| Zhejiang | Zhejiang | Shandong * | Shandong | Beijing | Fujian | |
| Beijing | Beijing | Fujian | Beijing | Hebei | Zhejiang | |
| Hebei | Hebei | Beijing | Hebei | Yunnan | Beijing | |
| Yunnan | Yunnan | Hebei | Yunnan | Guangxi | Hebei | |
| Henan | Guangxi | Yunnan | Anhui | Henan | Yunnan | |
| Hunan | Henan | Anhui | Shanx | Shanxi | Guangxi | |
| Hunan | Shanxi | Henan | ||||
| Shanxi | ||||||
| II (low–high) | Anhui * | Anhui * | Hainan ** | Hainan ** | Hainan ** | Hainan ** |
| Hainan ** | Hainan ** | Jiangxi | Tianjin | Anhui ** | Jiangxi * | |
| Jiangxi * | Jiangxi * | Guangxi | Jiangxi | Fujian * | Tianjin | |
| Tianjin | Tianjin | Henan | Guangxi | Tianjin | Chongqing | |
| Chongqing | Chongqing | Henan | Chongqing | Guizhou | ||
| Guizhou | Guizhou | Guizhou | Hunan | |||
| Guangxi | Shanxi | Jiangxi | ||||
| Shanxi | Hunan | |||||
| III (low–low) | Gansu * | Gansu * | Gansu * | Gansu * | Gansu * | Gansu * |
| Xinjiang * | Xinjiang ** | Xinjiang * | Xinjiang * | Xinjiang * | Xinjiang * | |
| Inner Mongolia | Inner Mongolia | Inner Mongolia | Inner Mongolia | Inner Mongolia | Inner Mongolia | |
| Qinghai | Qinghai | Qinghai | Qinghai | Qinghai | Qinghai | |
| Ningxia | Ningxia | Ningxia | Ningxia | Ningxia | Ningxia | |
| Shaanxi | Shaanxi | Shaanxi | Shaanxi | Shaanxi | Shaanxi Jilin | |
| Jilin | Jilin | Jilin | Jilin Guizhou | Jilin Liaoning | Liaoning | |
| Guizhou | Hunan | Heilongjiang | Heilongjiang | |||
| Chongqing | Chongqing | |||||
| Hubei Hunan | ||||||
| IV (high–low) | Sichuan * | Sichuan * | Heilongjiang | Heilongjiang | Guangdong | Guangdong |
| Heilongjiang | Heilongjiang | Liaoning | Liaoning | Sichuan | Sichuan | |
| Liaoning | Liaoning | Guangdong | Guangdong | Hubei | Hubei | |
| Guangdong | Guangdong | Sichuan | Sichuan | |||
| Hubei | Hubei | Hubei | ||||
Notes:
- (i) The italic values indicate there are significant correlations.
- (ii) *Significant at the level 0.05; **Significant at the level 0.01.
According to empirical findings from Moran I, the spatial pattern of branches’ performances appears to be that there is significant inequality between the coastal and interior regions. The provinces’ and municipalities’ performances of the ABC in terms of renminbi loans and deposits performed better in branches of the coastal region, especially in the Yangtze River Delta and Bohai Sea Region during this period. On the other hand, those provinces were mostly located in the western and north-east region with lower economic growth. Branches in the two regions benefited little from the Open and Reform Policy. Branches’ performances in the western region are the worst.
It is noteworthy that branches in Shanghai, Jiangsu and Zhejiang consistently outperformed others in terms of both renminbi loans and deposits. This can be easily observed from the dark grey areas (68%) in both Figures 4 and 5 with the LISA approach. These three together obviously formed the best-performed region of all during this period. The results confirm the recent strategy of the bank focusing on economically better-developed region: East China coastal region as mentioned in Section 1.
4.1 Results Estimated Using the Spatial Lag Model With Fixed Effects
Results of spatial lag models on LR and DR in Tables 4 and 5, respectively, show that spatial and time-period fixed effects models on LR and DR are more appropriate than the three other (no spatial and time-specific fixed, spatial fixed and time-period fixed effects) models because, by judging, the values of log-likelihood (80.7244) on LR and (119.3605) on DR for spatial and time-period fixed effects models are the largest of all in Tables 4 and 5, respectively.
Table 4 displays the results of using the spatial lag model for the amounts of loans (LR) with fixed effects into four models. Model I shows estimation results for the model with neither region nor time-specific fixed effects. The results come from the geographical features with spatial homogeneity. Model II shows results of the model with spatial-specific fixed effects but not time-specific fixed effects. Model III shows results of the model with time-specific fixed effects but not spatial-specific fixed effects. Model IV shows results of the model with both spatial and time-specific fixed effects. Regarding PI coefficients of provinces or municipalities, the four models exhibit the same negative sign and all appear to be very significant. Thus, the provincial PI coefficient decreased by 1 per cent, and LR increased by 0.2439 per cent. Regarding SI coefficients of provinces or municipalities, the provincial SI has inconsistent effects on bank branch performances. Different from other models, model IV exhibits the positive sign and is very significant. It implies that the development of the secondary industry of the provinces has positive effects on LR with the spatial and time-period effects taken into account. With respect to the provincial TI coefficients, these four models show consistent results: positive sign and all appear to be very significant. Thus, the provincial tertiary industry output has very significant and positive effects on LR. Regarding the UE coefficients of provinces or municipalities, there are mixed results. Taking spatial effects into consideration, results show positive sign. It becomes even more significant in model IV. On the other hand, the result of the other model with no spatial but time-specific effects has very significant impact, but with the opposite sign: negative. This can be attributed to the observation that the industrialisation leads to urbanisation. With continuous rapid economic development and industrialisation during the period of this study, urbanisation deepens. The number of urban employees who tend to work in the tertiary industry plays a more important role on branch performance: LR. Therefore, provincial UE is the most significant determinant of all of branch performances with positive and very significant effects. LR increased by 0.7128 per cent with adding up UE by 1 per cent of the province. Regarding the POP coefficients of provinces and municipalities, these four models all show positive signs with great significance. Model IV appears to be the most significant and has the largest coefficient. In model IV, time-period fixed effects enhance the impact of spatial-specific fixed effects because the coefficient of this factor increases from 0.3753 in model II to 0.6984 in model IV. In other words, the provincial spatial characteristics have a significant effect. Evidence of this is reflected in the process of China's economic and financial development. The population increased in cities and towns versus rural areas. Urbanisation deepened greatly during the process of industrial development (since the Reform and Open Economic Policy in 1978). Workers moved towards manufacturing hubs to obtain jobs in factories as agricultural sector provided less job opportunities and less income. Therefore, Table 4 shows that TI, UE and POP are the three most important factors to bank branch performances in terms of LR. This confirms that the bank branch is theoretically and practically located in a populated area – concentrated in the centre of the city in particular.
Results in Table 5 are similar to those in Table 4. However, TI becomes more significant and has a stronger impact on DR than UE is. POP is still a significant factor.
4.2 Results Estimated Using the Spatial Error Model With Fixed Effects
The estimation results of spatial error models on LR and DR, again models with spatial and time-period fixed effects, have the largest values of log-likelihood: 82.1206 in Table 6 and 119.2617 in Table 7. These results indicate that the spatial and time-specific fixed models are more convincing than the other three models for the panel data analysis. We therefore focus on interpreting results of the spatial and time-period fixed effects model.
Table 6 displays the estimation results of the spatial error model with fixed effects. The patterns illustrated from the first to the fourth models are very similar to those in the spatial lag model in Table 4. The estimation results of each type of model are approximately the same as those of the spatial lag model. It indicates that TI is the most significant and has the highest effects on LR. Meanwhile, provincial POP is the second most significant and has a slightly higher impact on LR than UE does.
Similarly, provincial TI again has the largest coefficient value and is the most significant determinant of DR in Table 7. The provincial POP has a slightly stronger impact than UE does on DR, although to a less significant degree.
4.3 Comparisons
Comparisons of empirical results using the spatial lag model and spatial error model reveal some intriguing similarities and some differences. The estimation results of each type of model in Table 4 are approximately the same as in Table 6. Provincial SI, TI, UE and POP all have positive sign and are at very significant level. UE has the largest coefficient in Table 4, while TI has slightly higher coefficient than UE does in Table 6. Provincial PI is very significant but has negative impacts on LR in both Tables 4 and 6. On the other hand, provincial SI is not significant on DR in Tables 5 and 7, but it is very significant on LR in Tables 4 and 6.
In comparing estimation results in Tables 5 and 7, the provincial TI has the largest positive coefficient and is the most significant factor on DR in both tables. The provincial UE and POP are both at significant level and have positive effects on DR in both tables. In addition, the provincial PI is at significant level but has negative impacts on DR in both tables. The provincial SI is insignificant and has smaller coefficient.
Summarising results from Tables 4-7, we identify that the provincial TI, UE and POP are all consistently very significant and have positive impacts on LR and DR. TI has the largest coefficient in most models, while UE is the second largest and POP is the third. On the other hand, the provincial PI is very significant but has a negative sign in all models, while the provincial SI has mixed signs in different models but is mostly at a less significant level. Thus, these indicate that loans from ABC are no longer made to the agriculture sector and for the government policy.
Reasons of PI and SI that are the negative or less significant contributing factors can be well explained as follows. The ABC was resurrected to support the development of rural infrastructure, particularly key sectors such as transport, telecommunication, public utilities and power in 1979 (Nanto and Sinha, 2002), due to The Opening and Reform policy starting from 1978. The ABC and other three main banks: Bank of China, China Construction Bank and Industrial and Commercial Bank of China, started to play leading roles in China's banking system from the mid-1980s. The functions of these four state-run banks on policy financing were removed in the reform in 1993. Three new banks were set up to take over the above four banks’ functions in implementing government policies in 1994. These three so-called policy banks include the China Development Bank, the Export–Import Bank of China and the Agriculture Development Bank of China. At the same time, shareholding banks and various types of financial institutions such as trust and investment companies, and credit cooperatives were allowed to be established. With the introduction of the Commercial Bank Law of 1995, the four state-run banks began to operate more commercial banks oriented. Loans were to be made on a profitable and no longer government policy basis. The four state-owned banks started to engage consumer credit for purchases of motor vehicles and provide financial support to all-sizes enterprises (Nanto and Sinha, 2002). In other words, the role and the function of the ABC were replaced by the Agriculture Development Bank and the deregulation and the rapid development of local banking system. The PI and SI were not the main sources to the performances of ABC after the government reforms on financial industry.
According to the empirical results above, businesses and profits of the ABC have greatly changed before and after listing in the stock exchanges. It derived from more populated especially urban areas and focused more on tertiary industry during the period of this study. This transformation may also be attributed to the major structural changes and rapid consolidation among China's banking industry to allure domestic and foreign investment in the past two decades. State-owned commercial banks were required to close or merge their small subsidiary saving branches, especially those in lagging rural areas where local savings are small. These changes have greatly influenced the distribution of bank branches, both in number and in location. In the case of the ABC, it had 23,461 branches in 2011. The number was down from 56,539 in 1999.
The research of Hashiguchi and Chen (2012) stated that the remarkable China's economic growth has not been geographically uniform. The regional inequality has generated large industrial agglomerations including the banking industry as well. With accumulated huge foreign investment, China now has three major areas of industrial and economic agglomeration: the Bohai Sea Region centred on Beijing and Tianjin; the Yangtze River Delta extending across Shanghai, Zhejiang and Jiangsu provinces centred on Shanghai; and the Pearl River Delta centred on Guangzhou of Guangdong province.
In the light of the research result of Hashiguchi and Chen (2012), and the consolidation of the location and the number of branches, it does show that branches along the coastal regions – the Yangtze River Delta, Bohai Sea Region, and Pearl River Delta with Shanghai and Beijing cities – play the central-place roles and Guangzhou city, to a lesser degree, outperformed others in inland regions (mostly in central region and especially in the Western region) in terms of loans and deposits. This also applies to the three significant independent variables: TI, UE and POP. Thus, the farther away from the three major central places mentioned above, the less significant the branches’ performances become.
By employing the spatial lag and error models, three major determinants were identified: TI, UE and POP of branch performances of the ABC during this period. We suggest that TI implies the strength of domestic consumption while UE is the proxy for the urbanisation. POP is the fundamental factor for configuration of the bank branch network. In other words, TI reflects the demand side of urbanised economies. The degree of urbanisation of branch efficiency is affected by the demand side urbanised economies, according to Bos and Kool (2006). Thus, TI is also related to urbanisation to certain degree.
5 Conclusions
Geographical dimensions and spatial territorial features of China's financial sector have been omitted in the previous literature. Despite the trend of financial globalisation, however, banking services occur at regional or branch levels, still displaying considerable differences from one to another. This leads to the need for better understanding of spatial territorial performances of China's banking industry. We focus the investigation on the ABC from 1997 to 2011 due to the data availability.
The results of Moran's I tests clearly indicate that the spatial autocorrelation exists significantly. These results also highlight spatial effects cannot be ignored. There will be bias if the econometric model excludes spatial effects. Thus, it is important to apply spatial econometric methods that consider the possibility of spatial effects to obtain more appropriate empirical results. Previous studies related to China's banking industry have never taken the impacts caused by spatial association effects and the urbanisation into account. It would be the first research to evaluate performances of one of China's largest banks at branch level with empirical evidences obtained from employing a spatial econometric model and by underlining the impacts of factors related to urbanisation.
Our empirical results assist management in establishing branches goals, evaluating performances and planning new locations. Spatial lag and error models are employed to produce a set of equations that effectively identify how urbanisation and other factors affect various dimensions of branch performances.
Spatial econometric models are the first time to be applied to identify the determinants of bank branch performances, particularly in the case of the mainland China. It reveals that the models are useful management tools in allocating resources between the branches to achieve higher efficiencies.
Empirical results indicate that spatial effects and urbanisation have statistically significant impacts on branches’ performances. Interestingly, the ABC was resurrected to support rural economic development in 1979, however empirical evidence indicate that its performances were significantly and negatively related to agricultural businesses of rural areas but were highly and positively related to the service industry of populated urban areas. This signals that the ABC has evolved from a state-owned specialised bank to a listed commercial bank.




