Inflation measurement in the presence of stockpiling and consumption smoothing
Abstract
A chained price index is said to suffer from chain drift bias if it indicates an overall price change, even though the prices and quantities in the current period have reverted back to their levels of the base period. The empirical relevance of this bias is well documented in studies that apply sub-annual chaining to scanner data. There it is shown that stockpiling can lead to downward chain drift bias. The present paper draws attention to the fact that smoothing consumption causes substantial upward chain drift. In addition, this study introduces a stochastic simulation approach that is consistent with both, stockpiling and consumption smoothing. A “stress test” is conducted that examines whether rolling window variants of multilateral indices (GEKS, TPD, and GK) effectively curtail the chain drift problem.
1 Introduction
The conventional approach to compute the price change between a base period 0 and a comparison period uses only the prices and quantities of these two periods. Such index formulas are known as bilateral price indices (or direct price indices). In the following, they are denoted by . As an alternative to the bilateral index, , one may compute the price change between periods 0 and from a sequence of overlapping adjacent bilateral price indices. The elements of this sequence can be linked by multiplication: . Such products are known as chain indices and its factors as chain links.
When the item universe remains constant over time and all prices and quantities in the current period revert back to their levels in the base period 0, a price index comparing the current period with the base period should indicate that no price change occurred. All reasonable bilateral price indices, , satisfy this requirement. However, chained bilateral price indices usually violate it. In the present paper, this violation is denoted as chain drift bias. It is usually attributed to sales triggering nonstandard substitution behavior of consumers. Feenstra & Shapiro (2003, p. 135) examine scanner data on canned tuna and compile a weekly chained Törnqvist index that exhibits upward chain drift caused by sales, while de Haan (2008, p. 19), studying scanner data on detergents, finds that sales lead to downward chain drift, even though both studies apply the same index formula and frequency of chaining.
These contradictory results suggest analyzing the causes of chain drift in a more systematic way. The present paper puts its focus on chained bilateral indices that include the quantities of both, the base and the current period (e.g. the indices of Törnqvist, Fisher, Marshall–Edgeworth, and Walsh). It is shown that the chain drift of such chained bilateral price indices is caused by quantity and price changes that are not perfectly synchronized in time.1 Such asynchronous price and quantity changes can arise from different forms of intertemporal optimization behavior of consumers.
A well-known example of such consumer behavior is stockpiling. During a sale, the consumers increase both their consumption and their stocks. Therefore, the purchases “overshoot” consumption. As soon as the price returns to normal, the purchases overshoot consumption in the downward direction because the consumers first use up their extra stocks. When in the subsequent periods the price remains on its normal level, purchased quantities gradually align with consumed quantities. For simplicity, these consequences of stockpiling are denoted here as overshooting quantity reactions to price changes.2 Also temporary price spikes trigger overshooting quantity reactions.
There are other forms of intertemporal optimization behavior leading to asynchronous price and quantity changes. Probably the most important ones are delayed quantity adjustments to price changes. Often, this smoothing is caused by search and adjustment costs. Even so the price of a consumer's favorite product may have permanently increased or the price of a competing product may have permanently fallen, the consumer may show no or only a moderate immediate change in her usual purchasing behavior. Only at some later point of time, after acquiring information about the qualitative features or the handling of alternative products, she may partly or completely switch over to such alternatives. Other reasons for delayed quantity reactions are consumption habits caused by harmful addictions (e.g. nicotine) or by past investments in increased enjoyment from consumed goods (e.g. ability to cook tasty and healthy food).3 For simplicity, all delayed quantity adjustments are denoted here as sticky quantity reactions to price changes.
Several studies of scanner data (e.g. de Haan, 2008, p. 18; de Haan & van der Grient, 2011, p. 43) show that overshooting quantities cause downward chain drift. The chain drift arising from sticky quantities, however, went largely unnoticed.4 Therefore, the present paper's first contribution is to show that sticky quantities lead to upward chain drift.
As a solution to the chain drift problem, Ivancic et al. (2011) advocate a rolling window variant of the Gini–Éltető–Köves–Szulc (GEKS) approach. The GEKS index is free of chain drift. However, its rolling window variant (R-GEKS) involves a mechanism that links the current window to past windows. This special form of chaining is usually denoted as splicing. It cannot be ruled out that splicing generates chain drift.
By now, several variants of such R-GEKS indices have been developed.5 Besides R-GEKS indices, many other multilateral approaches have been proposed to overcome the chain drift problem. These include rolling window variants of the time-product dummy method (R-TPD) and of the Geary–Khamis approach (R-GK).6 Again, these methods require some form of splicing. Consequently, they might also suffer from chain drift bias.
How can one investigate this suspicion? A meaningful examination requires an unassailable benchmark such that the deviation of an index number from that benchmark represents chain drift bias. This benchmark directly follows from the definition of chain drift: when all prices and quantities revert back to their former levels, a price index should indicate that no price change occurred. Unfortunately, the prices and quantities of real world data (e.g. scanner data) never return to their original levels. Therefore, an analysis of chain drift that uses real world data must do without this natural benchmark.
By contrast, in a simulation approach the researcher can generate price–quantity scenarios where all prices and quantities return to their original levels. However, the simulation must ensure that the price–quantity scenarios reflect features of real world purchasing behavior. This requires price scenarios with sales and ordinary price changes as well as quantity scenarios that capture overshooting and sticky quantities arising from consumer behavior such as stockpiling and smoothing of consumption.
Using such a simulation approach, this study's second contribution is a quantitative analysis of the chain drift bias of the R-GEKS, R-TPD, and R-GK approaches. It is shown that these index methods reduce chain drift bias, but they cannot eliminate it. Furthermore, some variants are more effective than others.
As a first step, Section 2 introduces the notion of chain drift and explains why overshooting quantities and sticky quantities cause different directions of chain drift. Section 3 briefly discusses the implications of chain drift for price measurement relying on scanner data and explains why a simulation approach is appropriate for a systematic examination of the various index methods' resilience to chain drift bias. Section 4 presents a simulation-based “stress test” that examines whether the R-GEKS, R-TPD, and R-GK methods curtail chain drift and whether some variants are better suited than others. Section 5 concludes.
2 Chain Drift and Its Sources
Let the integers represent the items of an economy. All items are available during the base period () and the comparison period () and also during all intermediate periods (). The period vector of prices is and the corresponding vector of quantities is . It is customary to interpret a bilateral price index, , as a mapping of the -dimensional vectors , , , and into a single positive number, , that measures the “overall price change” between periods 0 and . All bilateral price indices considered in this study are listed in the Online Appendix A.
Consider some sequence of time periods, .
Definition 1.A chain index that compares period to the base period 0 is defined by
When the prices and quantities in period return to their levels of period 0, the chain index, , should give the same index number as the bilateral index, , namely 1 (e.g. Ivancic et al., 2011, p. 26). Accordingly, in this specific price–quantity scenario, the deviation from unity is an appropriate measure of the extent of chain drift bias (e.g. Ribe, 2012, p. 3; Diewert, 2022; Diewert & Fox, 2022, p. 557). This interpretation of chain drift bias can be formalized in the following way:
Definition 2.The chain drift test of the bilateral price index, , postulates that
Condition (2) can be found in Walsh (1901, p. 401).7 Note that for the chain drift test simplifies to the time reversal test: .8
In standard microeconomic consumer theory, consumers instantaneously adjust their current purchases to the current prices. The usual assumption is that consumers substitute away from products that have become relatively more expensive. The larger the price elasticity of demand, the more pronounced are these quantity reactions. Figure 1 translates this standard theory into a highly stylized example. The figure depicts the prices and quantities of some item during nine consecutive periods, . In the depicted Scenario 1, the prices of the item can take only the values “low”, “normal”, and “high”, and the quantities sold can be “small”, “normal”, or “large”.
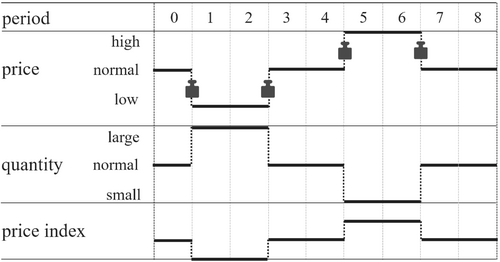
Price changes are marked by the weight icons. The price starts at a normal level, drops in period 1 to the lower level, stays there for another period, returns to normal in period 3, and stays there also during period 4. In period 5, the price increases to high, stays there for another period, before it drops back to normal during period 7, and remains there during period 8. The quantities purchased move exactly inversely to the prices; that is, the consumers' quantity reactions are perfectly synchronous to the price changes. As soon as the price returns to normal, the quantity also returns to normal. In times of constant prices also the quantities remain constant. When the price elasticity of demand is less than unity, expenditure shares and prices are positively correlated.
Many price indices are expenditure-weighted averages of intertemporal price ratios () where the impact of the two periods 0 and on the expenditure weights is symmetric (e.g. Törnqvist, Walsh, Marshall–Edgeworth, Theil, Sato–Vartia).9 Due to this symmetric impact, Scenario 1 generates weights such that the price decline between periods 0 and 1 (its weight is related to the expenditures during periods 0 and 1) and the price increase between periods 2 and 3 (its weight is related to the expenditures during periods 2 and 3) exactly offset each other. Graphically, this balanced weighting is indicated by the equal-sized weight icons located at the price decline between periods 0 and 1 and at the price increase between periods 2 and 3. The same is true for the price increase between periods 4 and 5 and the price decline between periods 6 and 7. As a consequence of this balanced weighting of price increases and price declines, symmetrically weighted indices are immune to chain drift from scenarios like Scenario 1 and one gets .10
Scenario 1 corresponds to standard consumer theory as presented in introductory microeconomics textbooks. Real- world consumer behavior, however, is more complex. One important aspect ignored by standard consumer theory is stockpiling. For example, sales usually lead to increased purchases, part of which are stored. If in the next period the price returns to its normal level, the purchased quantity falls below its normal level, because consumers first use up their extra stock. Only after the extra stock is depleted, the purchased quantity returns to its normal level. In the following, such a scenario is denoted as an overshooting quantity response to sales.11 During the sales period, acquisitions exceed consumption (i.e. stocks increase), while right after the sales period, consumption exceeds acquisitions (stocks decrease).
Periods 0–3 of Scenario 2 (see Figure 2) depict this case in a highly stylized form. In such a scenario, symmetrically weighted indices exhibit chain drift. As a result of the overshooting quantity response, the weight attached to the price reduction between periods 0 and 1 is larger than the weight attached to the price increase between periods 1 and 2. Therefore, the price index level of period 2 is below that of period 0. At the end of period 2, the customers' inventory is back to its normal level. Therefore, the purchases in period 3 increase to their normal level, even though the price is constant. In the literature, there is a rather broad consensus that every valid bilateral index formula must satisfy the identity test. This test says that, in the absence of any price changes, the price index is unity, regardless of any quantity changes. All price indices listed in the Online Appendix A satisfy the identity test. Therefore, the price index level of period 3 remains on the level of period 2 and, thus, below that of period 0. In other words, downward chain drift arises.
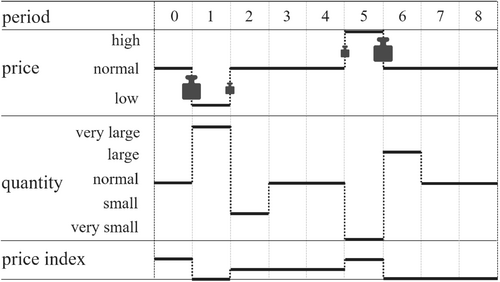
Periods 0–3 of Scenario 2 describe a storable item that consumers keep in stock. In times of unusually low prices (sales) the consumers add to their ordinary stock some extra stock and they deplete that extra stock when the price reverts to its normal level. This is the standard narrative of stockpiling.
However, stockpiling is relevant not only in times of sales but also in times of price spikes. During such spikes, consumers can plunder their ordinary stock and restock it as soon as the price returns to normal. Again, overshooting quantity reactions arise. This is depicted by periods 4–8 of Scenario 2. The price increases in period 5. Many consumers switch to using up their stocks. This leads to a negative quantity reaction that is larger than for items that cannot be stored. In period 6, the price returns to its normal level. This gives the consumers the opportunity to refresh their inventories. At the same time, they return to their normal consumption. Therefore, the total quantity purchased exceeds the normal quantity. As a result of these overshooting quantity responses, the weight attached to the price increase between periods 4 and 5 is smaller than that attached to the price reduction between periods 5 and 6. This leads again to downward chain drift. At the end of period 6, the stock is back to its standard level, such that the purchases in period 7 return to their normal level even though no price change occurs between periods 6 and 7.
In sum, overshooting quantities triggered by sales or by price spikes work in the same direction. Both generate downward chain drift. Overshooting quantities, however, are only one driver of chain drift. Another driver operates in the opposite direction; that is, it causes upward chain drift.
In the field of industrial organization there is extensive literature on search and adjustment costs and their implications for markets.12 Also in the field of price measurement it is well known that search and adjustment costs are relevant in real- world consumption decisions and that they create problems for price measurement purposes (e.g. Reinsdorf, 1994, p. 137; Triplett, 2003, p. 152). Such costs can delay the consumers' substitution behavior, such that part of the quantity response or the complete quantity response happens in a later period than the underlying price change. This is particularly true when the length of a period is relatively short (e.g. 1 week or 1 month). Another cause of delayed quantity responses are harmful or beneficial consumption habits that the consumers have developed over time. Delayed quantity responses are denoted here as sticky quantities.
Figure 3 illustrates the consequences of sticky quantities. In the depicted Scenario 3, demand is completely price inelastic in the short run but price elastic in the long run. More specifically, the complete quantity reaction to each price change is delayed by one period.

In period 1 the price drops, while the quantity remains unchanged. Therefore, the observed expenditure during period 1 is smaller than it would be with the usual quantity reaction of an elastic demand. As a consequence, also the weight attached to the price decline is smaller than it would be with an elastic demand. Graphically, this diminished weight is indicated by the small weight icon at the price decline between periods 0 and 1.
The complete quantity reaction to the reduced price in period 1 occurs one period delayed, that is, in period 2. The price in period 2 remains on the level of period 1. All popular price indices satisfy the identity test. Therefore, their price index level does not change between periods 1 and 2.
Because demand is inelastic in the short run, the price increase between periods 2 and 3 occurs without a quantity reduction. Therefore, the weight attached to this price increase is larger than it would be with the usual quantity reduction. The large weight icon at the transition from periods 2 to 3 highlights this inflated weight. The price increase between periods 4 and 5 is analogous to that between periods 2 and 3. Again, the price increase receives an inflated weight. The price decline between periods 6 and 7 shows the same pattern as that between periods 0 and 1. This price decline receives a diminished weight. Overall, this unbalanced weighting of price declines and price increases leads to upward chain drift.
Theoretically, one can think of quantity reactions that are antedated by one period. This could be regarded as a “negative delay”. The weighting effects are exactly opposite to those of Scenario 3. Price increases receive a diminished weight, whereas price declines receive an inflated weight. As a result, downward chain drift would arise. In reality, such anticipating consumption behavior is unlikely unless stockpiling is involved. Then stocks are depleted in anticipation of the sale. This tends to aggravate the overshooting quantities effect and the resulting downward chain drift. Anticipated price spikes have the same effect.
In summary, sticky quantities (the result of smoothing of consumption) lead to upward chain drift, whereas overshooting quantities (the result of stockpiling) lead to downward chain drift.13 The underlying problem of both cases is the asymmetric weighting of price increases and price reductions.14 This asymmetry is facilitated by quantity changes in times of constant prices. As all popular bilateral price indices satisfy the identity test, they indicate in such periods no overall price change. This suggests that a solution to the chain drift problem may come from price indices that violate the identity test. The R-GEKS indices studied in Sections 3 and 4 are a prominent example. They violate the identity test.15 This could be interpreted as a weakness of the R-GEKS indices. On the contrary, the fact that immunity to chain drift requires price indices that violate the identity test can be interpreted as a weakness of the identity test.16
Overshooting and sticky quantities generate diametrical chain drift bias. For example, Feenstra & Shapiro (2003, p. 133) identify delayed quantity responses in the context of sales.17 In their dataset, the immediate quantity response to a sale is modest, but substantially increased after, in a later period, the sale is advertised. Overall, they identify upward chain drift bias. This suggests that in their dataset the upward bias generated by sticky quantities dominates the downward bias generated by overshooting quantities.18
3 Implications for a Quantitative Analysis of Chain Drift Bias
Storing one's favorite beer when it is on sale may reduce further purchases of beer for some weeks or months but probably not for years. Delayed quantity reactions are also rather a question of weeks than years. This implies that chaining of monthly price indices is more likely to cause chain drift bias than chaining of yearly price indices. Because scanner data allow for the compilation of monthly or even weekly price indices, the issue of chain drift becomes particularly relevant for this type of data source.
GEKS indices offer themselves as a solution because they are transitive and, therefore, free of chain drift.19 However, when the time span covered by a GEKS index becomes too large, the measured price change of neighboring periods is affected by very distant periods. This may reduce the reliability of the results. As a solution, Ivancic et al. (2011, p. 33) propose a rolling window variant of the GEKS approach. This rolling window variant is denoted here as R-GEKS index. In its original form, the GEKS index is based on the bilateral Fisher index, while Caves et al. (1982) propose to use the Törnqvist index. Diewert & Fox (2022, p. 355) denote the latter variant as the Caves–Cristensen–Diewert–Inklaar (CCDI) approach.
When an R-GEKS index is used, the price levels compiled from the most recent window must be linked to the price levels compiled from the earlier windows. Empirical studies show that the choice of the linking procedure (called “splicing”) affects the results of R-GEKS indices (e.g. Fox et al., 2022, pp. 17-22; Lamboray, 2021, pp. 13-17; Melser, 2018, pp. 518-521; Van Loon & Roels, 2018, pp. 9-14). The R-GEKS approach and five different splicing variants are explained in the Online Appendix B. The five mentioned variants are the following: movement splice (Ivancic et al., 2011, p. 33), window splice (Krsinich, 2016, pp. 383-87), half splice (de Haan, 2015, pp. 25–26), mean splice (Diewert & Fox, 2022, pp. 560–561), and direct mean splice (Melser, 2018, p. 518).20 Splicing can be viewed as a special form of chaining. The splicing of chain drift-free GEKS indices can cause chain drift bias.
R-GEKS indices are not the only rolling window indices that have been proposed to solve the issue of chain drift bias. The alternatives include rolling window variants of the time-product dummy method (R-TPD) and of the Geary–Khamis approach (R-GK).21 The available splicing variants are the same as for R-GEKS indices, and the suspicion of chain drift bias also applies to the R-TPD and R-GK approaches.
The diversity of index and splicing methods raises the question of whether one method is more immune to chain drift than others. Does the relative performance of the methods depend on the relative strength of stockpiling (overshooting quantities) and smoothing of consumption (sticky quantities)? The cycle lengths of overshooting quantities and sticky quantities are likely to differ. Therefore, a window length that is suitable for addressing overshooting quantities is unlikely to be adequate for sticky quantities. In other words, a one-size-fits-all window may not exist. In such a situation, should one apply a shorter or rather a longer window length? Do the answers to these questions depend on the consumers' behavioral characteristics (e.g. price elasticity of demand)?
A quantitative analysis of these questions should use an unassailable benchmark for assessing the extent of chain drift bias inherent in the index methods to be compared. To obtain this benchmark, the dataset should be such that, after some periods, all prices and quantities return to their original values. Scanner data and other real- world data cannot be expected to satisfy this postulate.22 Therefore, Goolsbee & Klenow (2018) propose to add to the scanner dataset a hypothetical observation for period where all prices and quantities return to their original values. However, when the prices and quantities move far away from their original values, a sudden return to those original values would constitute a rather unrealistic scenario.
An alternative to such semi-artificial price–quantity scenarios are fully artificial price–quantity scenarios. However, these scenarios should be sufficiently “realistic”; that is, they should capture those patterns of real- world data that can cause chain drift bias. To begin with, the price data should be generated by a transparent stochastic process that features ordinary price changes as well as sales. Furthermore, the transformation of the price scenario into a corresponding quantity scenario should mimic households that smooth consumption and benefit from stockpiling.
Once a price–quantity scenario is generated in this way, the index numbers of the various index methods can be computed and compared to the reference. As a result, some index methods may look superior to some other methods. However, this ranking may depend on the specific price–quantity scenario. Therefore, the complete process should be repeated many times and, for each index method, the deviations of the index numbers from the reference should be averaged over these repetitions.23
The ranking of the index methods may also depend on the parameter values of the function transforming the price scenarios into quantity scenarios. Therefore, alternative parameter values must be examined.
4 Simulation Framework
Simulation studies in the context of price index theory are not new. A prominent example is Diewert & Fox (2022).24 We elaborate their approach in various dimensions. Our simulation comprises periods (). In each period, the households can choose among the same items (). Each item receives a randomly drawn “base price” between 2.00 and 5.00. The simulation starts with a phase-in interval of 10 periods during which all items are sold at their base price. This interval is followed by a core interval of 100 periods in which some randomly drawn items exhibit price changes triggering quantity reactions. After the core interval, there is a phase-out interval of 10 periods in which all items are sold at their respective base prices. Therefore, not only the prices but also all quantities return to the levels that had prevailed at the start of the phase-in interval.
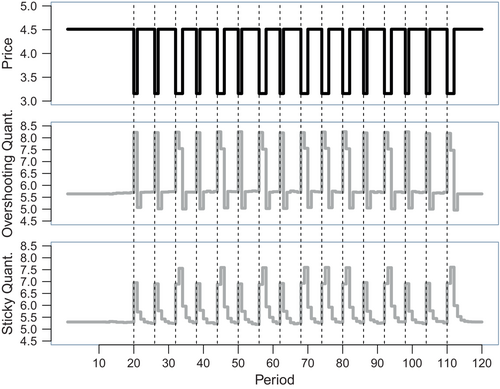
Of the 40 items, 10 keep their base price throughout the time horizon, while 10 other items exhibit cyclical sales patterns during the core interval. Every cycle starts with a price reduction that randomly lasts for one or two periods. Afterwards the price returns to its basic level and stays there until the next cycle starts. Each of the sales items has its own fixed price reduction (randomly drawn between 10 percent, 20 percent, 30 percent, and 40 percent) and its own fixed cycle length (randomly drawn from 6 to 12 periods). Also the period for the start of the first cycle differs between the items. It occurs within the first 12 periods of the core interval and is randomly drawn. As an illustration, the upper part of Figure 4 depicts the cyclical sales prices of item 10 of the simulation's first iteration (out of 5,000 iterations).
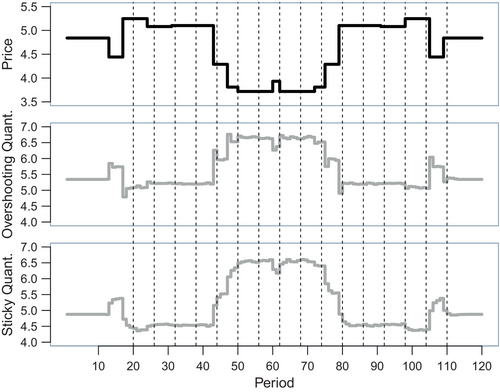
The remaining 20 items exhibit price changes that are not related to sales. On average, the price of such an item changes every fifth period. The periods of change are randomly drawn, and the new price can deviate from the previous price by a percentage drawn from a normal distribution (with mean 0 and standard deviation 0.2). This random process applies to periods 11–60, that is, to the first half of the core interval. For the second half of the core interval the order of the prices is simply reversed. Thus, even prices that have drifted a long way from their original levels return to these levels in a gradual manner.25 The upper panel of Figure 5 depicts the price evolution of item 9 of the simulation's first iteration.
All households are confronted with the same price tableau (40 items during 120 periods). Two different types of households exist: stockpiling households (they do not smooth consumption) and smoothing households (they do not stockpile). The stockpiling households generate overshooting quantities, while the smoothing households generate sticky quantities.
The upper panel of Figure 4 depicts the typical price pattern of regular sales. The middle panel shows the corresponding overshooting quantities purchased by stockpiling households. The sticky quantities purchased by smoothing households can be seen in the lower panel. The upper panel of Figure 5 shows price changes not attributable to sales. The corresponding overshooting quantities purchased by stockpiling households are depicted in the middle panel, while the bottom panel shows the sticky quantities of smoothing households. The details of the computations of the respective quantities are provided in the Online Appendix C as well as in von Auer (2024, pp. 24−29).
Three different scenarios are considered. In the overshooting quantities scenario, all households are stockpiling households, while in the sticky quantities scenario, only smoothing households exist. In the hybrid quantities scenario, every fourth household is a stockpiling household and all other households are smoothing households. For all three scenarios (overshooting, sticky, and hybrid), the index numbers of various chained bilateral indices and of many different R-GEKS, R-TPD, and R-GK variants are compiled.
The price level of period is set equal to 100. In period , all prices have returned to their initial values and stay there for all subsequent periods. Within a few periods, also the quantities return to their initial values. Therefore, in period the price index number generated by the various index methods should have returned to its initial level, that is, to 100.26 The extent of chain drift bias is the deviation of the price level in period from 100.
For each of the three scenarios and each index formula, this simulation exercise is repeated 5,000 times. For example, one receives 5,000 different numbers for the chain drift bias of a chained Törnqvist index in the overshooting quantities scenario (only stockpiling households exist). These 5,000 numbers are averaged. The result of this averaging is the top left number in Table 1. In the overshooting quantities scenario, the Törnqvist index reaches 8.51 percent downward chain drift. The other listed price indices exhibit a downward chain drift that varies between 7.96 percent and 8.68 percent. In the sticky quantities scenario (only smoothing households exist), the listed bilateral indices show an upward chain drift that varies between 9.13 percent and 9.63 percent. The results of the hybrid scenario (three quarters are smoothing households, one quarter are stockpiling households) lie between the other two scenarios.
| Overshooting | Sticky | Hybrid | |
|---|---|---|---|
| Törnqvist | 8.51 | 9.63 | 4.90 |
| Marshall–Edgeworth | 7.96 | 9.13 | 4.69 |
| Walsh | 8.68 | 9.46 | 4.86 |
| Theil | 8.60 | 9.48 | 4.86 |
| Sato–Vartia | 8.60 | 9.48 | 4.86 |
Table 2 documents the chain drift of the other chained bilateral price indices mentioned in the paper. Again, the overshooting quantities scenario generates a large downward chain drift that varies between the indices. Also the upward chain drift values arising from sticky quantities are similar to those listed in Table 1.
| Overshooting | Sticky | Hybrid | |
|---|---|---|---|
| Fisher | 7.95 | 9.12 | 4.68 |
| Banerjee | 8.60 | 9.48 | 4.86 |
| Davies | 7.96 | 9.13 | 4.69 |
| Lehr | 9.19 | 9.60 | 4.96 |
The tables show that chained bilateral indices generate the expected results. Overshooting quantities lead to considerable downward chain drift, while sticky quantities generate considerable upward chain drift. Overall, the bilateral price indices of Marshall–Edgeworth, Fisher, and Davies slightly outperform the other ones. This is true for overshooting quantities as well as for sticky quantities.
GEKS indices are transitive and, thus, immune to chain drift bias arising from overshooting quantities. Therefore, R-GEKS indices have been proposed as a remedy for chain drift bias. However, these indices involve some form of splicing which, in turn, can cause chain drift bias. The performance of the various R-GEKS indices may depend on the choice of the splicing method and the window length (e.g. Melser, 2018, p. 517). Therefore, Table 3 presents the results for various splicing methods and for window lengths of 4, 8, 12, and 24 periods. These results are derived from R-GEKS indices that use the Törnqvist index as their bilateral base index.
| Overshooting | Sticky | Hybrid | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Window length | 4 | 8 | 12 | 24 | 4 | 8 | 12 | 24 | 4 | 8 | 12 | 24 |
| R-GEKS | ||||||||||||
| Direct mean | 2.41 | 0.60 | 0.35 | 0.14 | 3.49 | 0.99 | 0.61 | 0.25 | 2.03 | 0.60 | 0.38 | 0.16 |
| Mean | 2.41 | 0.60 | 0.34 | 0.13 | 3.49 | 0.99 | 0.59 | 0.24 | 2.03 | 0.60 | 0.37 | 0.15 |
| Movement | 2.56 | 1.28 | 0.80 | 0.33 | 3.38 | 1.47 | 0.97 | 0.41 | 1.90 | 0.79 | 0.54 | 0.23 |
| Half | 2.11 | 0.23 | 0.01 | 0.15 | 3.72 | 0.59 | 0.20 | 0.28 | 2.27 | 0.39 | 0.15 | 0.18 |
| Window | 2.56 | 1.28 | 0.78 | 0.32 | 3.38 | 1.47 | 0.96 | 0.39 | 1.90 | 0.79 | 0.53 | 0.22 |
| R-TPD | ||||||||||||
| Direct mean | 1.65 | 0.21 | 0.01 | 0.22 | 3.14 | 0.65 | 0.33 | 0.03 | 2.00 | 0.44 | 0.25 | 0.03 |
| Mean | 2.44 | 0.60 | 0.33 | 0.12 | 3.33 | 0.98 | 0.58 | 0.23 | 1.96 | 0.60 | 0.36 | 0.14 |
| Movement | 0.16 | 0.09 | 0.46 | 0.68 | 2.70 | 0.60 | 0.17 | 0.29 | 1.97 | 0.47 | 0.24 | 0.06 |
| Half | 2.21 | 0.23 | 0.01 | 0.14 | 3.45 | 0.61 | 0.22 | 0.27 | 2.16 | 0.40 | 0.16 | 0.17 |
| Window | 4.91 | 2.62 | 2.01 | 1.29 | 3.86 | 2.30 | 1.71 | 1.04 | 1.76 | 1.10 | 0.81 | 0.47 |
| R-GK | ||||||||||||
| Direct mean | 4.03 | 1.34 | 1.24 | 1.22 | 1.23 | 0.45 | 0.91 | 1.46 | 0.04 | 0.67 | 0.99 | 1.41 |
| Mean | 2.67 | 0.64 | 0.35 | 0.13 | 3.63 | 1.03 | 0.60 | 0.23 | 2.13 | 0.62 | 0.37 | 0.14 |
| Movement | 6.88 | 4.18 | 4.00 | 3.35 | 3.48 | 3.58 | 4.17 | 4.23 | 4.34 | 3.74 | 4.13 | 4.02 |
| Half | 2.30 | 0.22 | 0.03 | 0.16 | 3.79 | 0.60 | 0.19 | 0.27 | 2.38 | 0.40 | 0.14 | 0.16 |
| Window | 1.36 | 1.46 | 2.35 | 2.75 | 11.12 | 6.96 | 6.46 | 5.26 | 8.77 | 5.62 | 5.46 | 4.65 |
The index numbers in the first two rows of Table 3 show that the direct mean splice and the mean splice produce virtually the same R-GEKS index numbers. Overall, the numbers reinforce the arguments of Diewert & Fox (2022, pp. 560-561) and de Haan (2015, pp. 25-26) in favor of a more “balanced” splicing approach than the movement splice or window splice. With a sufficiently large window, the R-GEKS approach in conjunction with the direct mean splice, mean splice, or half splice effectively curtails chain drift bias arising from overshooting quantities (upper left part of Table 3). The half splice with a window length of 12 months performs best. The upper middle part of Table 3 reveals that the previous findings carry over to the scenario of sticky quantities.
In the hybrid scenario, three quarters of the households are smoothing households. The resulting R-GEKS index numbers are listed in the upper right part of Table 3. The chain drift bias caused by the smoothing households seems to dominate the chain drift bias caused by the stockpiling households. However, this effect is driven by the parameters that determine the households' desire for stockpiling and smoothing as well as by the share of stockpiling households. When that share or the desire for stockpiling is sufficiently increased or the desire for smoothing is sufficiently reduced, the dominance would be reversed (not shown in the table). The other qualitative results are not affected by such changes. The direct mean splice, mean splice, and half splice remain the least biased options when applied with a sufficiently large window length.
R-GEKS indices are not the only approach to curb the chain drift problem. Among the alternatives are the R-TPD and the R-GK approaches. Therefore, the same stress test with the same splicing options and window lengths has been conducted for the R-TPD and the R-GK approaches. Table 3 also presents these results. For the R-GK approach, the choice of window length and splicing method causes more variation than for the R-GEKS and the R-TPD approaches.27 When the window splice is avoided, the R-TPD approach slightly outperforms the R-GEKS approach which, in turn, outperforms the R-GK approach. When the mean splice or the half splice is applied, the choice between R-GEKS, R-TPD, and R-GK is of minor relevance.28
It should be kept in mind that in the applied simulation no item attrition occurs. With item attrition, large windows may generate assignment or assortment bias (e.g. von Auer, 2017, pp. 83–84). In a context of item attrition, Melser & Webster (2021, pp. 777-783) identify in their own simulations life-cycle pricing and, in particular, run-out sales as an important driver of chain drift. The simulation framework developed in the present study could be modified and elaborated to gain further insights into the issue of item attrition and its effect on price measurement. To this end, it would be useful to identify the basic structure of product turnover in real- world scanner data and to transfer this structure to the simulations.
Such a simulation may also address another important issue. To mitigate chain drift bias, one may try to aggregate the weekly prices into monthly or even quarterly unit values (say, e.g. Diewert, 2007, p. 3). In the simulation one could systematically study the effects of such a strategy.
5 Concluding Remarks
Sales and the associated stockpiling give rise to “overshooting quantity” movements. It is well known that overshooting quantities create problems for sub-annual chaining of bilateral price indices because such quantities generate downward chain drift bias. The present study argues that overshooting quantities are only part of the chain drift problem. Other important causes of chain drift bias are search and adjustment costs as well as habits. They imply that price changes lead to delayed quantity changes. The resulting “sticky quantities” generate upward chain drift.
In the literature, R-GEKS, R-TPD, and R-GK approaches have been proposed as a remedy for chain drift bias. However, it is unclear whether these approaches merely reduce chain drift bias or even eliminate it. Furthermore, some approaches may be more effective than others. The present paper answers all these questions. To this end, it develops a novel simulation framework that is consistent with households that have a desire for stockpiling (overshooting quantities) and/or for smoothing quantity adjustments over time (sticky quantities).
Building on this framework, a stress test that examines the resilience of different price indices against chain drift is developed. This stress test is applied to various bilateral price indices and to several splicing variants and window lengths of R-GEKS, R-TPD, and R-GK indices. The bilateral price indices show the expected results. Overshooting quantities generate downward chain drift bias, while sticky quantities generate upward chain drift bias. R-GEKS, R-TPD, and R-GK indices reduce this bias, but do not eliminate it. Shorter window lengths tend to generate more chain drift bias than longer ones. The window splice is clearly outperformed by the half splice and mean splice. When the latter two splicing variants are used, the choice between R-GEKS, R-TPD, and R-GK indices is of minor relevance.
Acknowledgement
Open Access funding enabled and organized by Projekt DEAL.
References
- 1 Hill (2006, pp. 314-315) reaches a similar conclusion for the chained Laspeyres index and the chained Paasche index.
- 2 Hayashi (1985) identifies a similar effect for durables: “A higher level of expenditure means a larger stock of consumption, which will depress expenditure in the next period if households behave in a way to smooth out consumption (rather than expenditure) over time (p. 1092).”
- 3 Muellbauer (1988) emphasizes the relevance of habit formation for macroeconomic models. His empirical evidence appears to favor myopic habits, that is, consumers who are not aware of the impact of current consumption decisions on future consumption decisions.
- 4 A notable exception is Triplett (2003, p. 152) who points out that storage, search, and information cost may generate measurement problems for scanner data price indices.
- 5 For compact surveys, see, for example, Diewert & Fox (2022, pp. 357-359), Fox et al. (2022, pp. 9-12), Van Loon & Roels (2018, pp. 7-8), or Online Appendix B of the present paper.
- 6 For recent surveys of the various methods see, for example, Chessa et al. (2017), Chessa (2019), de Haan & Krsinich (2014), or Diewert & Fox (2022).
- 7 Walsh later calls condition (2) the circularity test (see Diewert, 1993, p. 40). In the current price index literature, this label is reserved for the condition . This condition is stricter than the alternative formalization of chain drift because it does not prescribe that the prices and quantities of periods 0 and 2 coincide. In the context of spatial price comparisons, circularity is usually denoted as transitivity. Diewert (1993, p. 40) coins the chain drift test as the “multiperiod identity test”. Note, however, that the chain drift (or multiperiod identity) test considers the case where the quantities reverse to their base period values, while in the identity test the evolution of the quantities is completely irrelevant. In fact, a chain drift test without the quantity reversal postulate is considered in de Haan (2008, p. 10). He calls it the “invariance to price bouncing test”.
- 8 An anonymous referee pointed out that for bilateral price indices that satisfy the time reversal test, one gets and condition (2) becomes . According to this alternative formalization, a bilateral price index suffers from chain drift when the ratio of the chained index and the corresponding bilateral index, , deviates from unity. Several writers use this alternative formalization of chain drift (e.g. Forsyth & Fowler, 1981, p. 234; Frisch, 1936, p. 8; Hill, 2006, pp. 14-15; Lent, 2000, p. 314; Persons, 1921, p. 109; Persons, 1928, p. 101).
- 9 The Fisher index and the generalized unit value (GUV) indices of Banerjee, Davies, and Lehr (von Auer, 2014, pp. 848–852) exhibit a similar type of “intertemporal symmetry”. A more complete classification of “symmetric bilateral price indices” is provided by von Auer & Shumskikh (2024, sect. 2).
- 10 Chain drift arises, however, for the Laspeyres and Paasche index. This issue is addressed in various studies including Forsyth & Fowler (1981, pp. 234-235), Szulc (1983, pp. 540-541), and Hill (2006, pp. 314-315).
- 11 This type of scenario is described, for example, in Ivancic et al. (2009, p. 4), de Haan & van der Grient (2011, p. 39), and Ribe (2012, p. 3).
- 12 A survey of this literature is Fisher Ellison (2016).
- 13 Stockpiling and consumption smoothing do not themselves create chain drift bias. They become relevant when not all prices and quantities move exactly the same and/or when some items are less suitable for stockpiling (e.g. hair cut) than others or some items are less suitable for consumption smoothing (e.g. medical service) than others.
- 14 A Cobb–Douglas index with weights that remain fixed over the complete time horizon would avoid such asymmetries.
- 15 This is also noted by Ribe (2012, p. 4).
- 16 In ILO (2004, p. 293), it is reported that the identity test is somewhat controversial. A more elaborate critique of the identity test can be found in von Auer (2008, pp. 2-7).
- 17 Adapting an artificial scenario analyzed in Persons (1928, p. 102), Diewert (2022) discusses a situation that combines sales with somewhat delayed quantity responses. This scenario resembles the pattern that Feenstra & Shapiro (2003) identify in their scanner dataset.
- 18 In footnote 7, Hill (2006, p. 315) states two sufficient conditions for the Fisher index to exhibit downward chain drift bias. Put simply, the first condition says that the quantities of period and the prices of period are negatively correlated. This condition corresponds to the case of antedated quantity reactions briefly mentioned in the present paper's exposition. The second condition says that the prices of period and the quantities of period are positively correlated. This correlation corresponds to the stockpiling behavior depicted in Figure 2 of the present study. Reversing the sign of the correlations yields two sufficient conditions for the Fisher index to exhibit upward chain drift bias. The second of these conditions corresponds to consumption smoothing depicted in Figure 3 of the present study.
- 19 The acronym GEKS honors the publications of Gini (1924), Éltető & Köves (1964), and Szulc (1964) who introduced this approach for interregional price comparisons. Balk (1981, pp. 73-74) adopts this approach to the intertemporal price measurement of seasonal products. That multilateral price indices can curtail chain drift bias is pointed out also in Kokoski et al. (1999, p. 141).
- 20 Diewert & Fox (2022, p. 561) advocate another splicing strategy that is not considered in the present study. Melser & Webster (2021, p. 765) point out that for theoretical purposes the linking stage could be replaced by a second round of GEKS aggregation.
- 21 An exposition of these methods can be found in various studies (e.g. Diewert & Fox, 2022, p. 561).
- 22 Estimating from real- world data the parameters driving the households' intertemporal consumption paths is a difficult task because the observable date of a product's acquisition often deviates from its unobservable date of consumption and stockpiling. Various sophisticated stockpiling models attempt to solve this problem. For example, Osborne (2018) considers stockpiling households and estimates a dynamic structural utility model from real- world household-level scanner data. The author also relates his approach to alternative stockpiling models, including those of Feenstra & Shapiro (2003) as well as Hendel & Nevo (2006). There is a separate but similarly sophisticated literature on empirical models of smoothing of consumption. For example, Hong & Shum (2006) show how the equilibrium conditions of standard search models can be exploited to estimate search cost distributions solely from observed prices. Honka et al. (2019) survey the econometric literature on consumer behavior in the presence of search cost.
- 23 Real- world data can be interpreted as an experiment with only one sample. Repeated samples could generate results that differ from the observed one. This possibility weakens the reliability of the results obtained from the actually observed sample.
- 24 Their simulation considers one price scenario covering 4 items and 12 periods. They allow for sales and derive the corresponding quantities from consumers with ordinary CES preferences. Because these CES preferences do not account for stockpiling, the quantities are manually adjusted afterwards.
- 25 This symmetric design was a suggestion of one of the anonymous referees. The design avoids unrealistic situations where prices and quantities that are far from their original values suddenly revert to these original values.
- 26 This is a weaker condition than the condition of the chain drift test (Definition 2) of bilateral price indices. The latter postulates that already in period the price index number must be 100.
- 27 This is in line with findings in Fox et al. (2022, pp. 17-22), Lamboray (2021, pp. 13-17) and Van Loon & Roels (2018, pp. 9-13). Note that the former study uses household-level scanner data, while the latter two studies use point-of-sales scanner data. None of these studies differentiates between stockpiling and consumption smoothing.
- 28 The comparable performance of the R-GEKS and R-GK approaches is also reported in Fox et al. (2022).




