Deciding with Thresholds: Importance Measures and Value of Information
Abstract
Risk-informed decision making is often accompanied by the specification of an acceptable level of risk. Such target level is compared against the value of a risk metric, usually computed through a probabilistic safety assessment model, to decide about the acceptability of a given design, the launch of a space mission, etc. Importance measures complement the decision process with information about the risk/safety significance of events. However, importance measures do not tell us whether the occurrence of an event can change the overarching decision. By linking value of information and importance measures for probabilistic risk assessment models, this work obtains a value-of-information-based importance measure that brings together the risk metric, risk importance measures, and the risk threshold in one expression. The new importance measure does not impose additional computational burden because it can be calculated from our knowledge of the risk achievement and risk reduction worth, and complements the insights delivered by these importance measures. Several properties are discussed, including the joint decision worth of basic event groups. The application to the large loss of coolant accident sequence of the Advanced Test Reactor helps us in illustrating the risk analysis insights.
1. INTRODUCTION
Risk analysis has become a dominant public-policy tool for informing risk managers and the public about the different policy options for protecting public health and the environment (Ref. 1, p. iv). The construction of probabilistic models that quantify the risk metric of interest has then become a central paradigm in risk-informed decision making (see Refs. 2 and 3 for a critical discussion of the advantages and limitations of quantitative risk assessment). Applications range from the selection of the site for a national nuclear waste repository,4 to the selection of maintenance policies for a chemical facility,5 to the planning of space missions,6, 7 to the analysis of precursor events.8
Probabilistic safety assessment (PSA) models are built on an underlying Boolean logics for characterizing the states of the systems, structures, and components (SSCs) involved in the analysis.9 This Boolean function can then be implemented either through event-trees/fault-trees or through binary decision diagrams10 that permit the identification of scenarios leading to the events of interest, typically system failure or success in performing a predetermined mission. The assessment of probabilities then leads to the quantification of the risk metrics of interest.
In this context, the decisions are sometimes accompanied by the use of thresholds of acceptable risk. For example, one in a million is the well-known threshold set by U.S. legislation for the increased lifetime chance of developing cancer due to lifetime exposure to a substance. This value then informs environmental and toxicological legislation.11 The astronaut office requires a probability of loss of crew lower than 1/1,000 (one in a thousand) as an acceptable risk for space missions.12 According to the well-known 1986 Nuclear Regulatory Commission policy statement, the risk of cancer fatalities to the population near a nuclear power plant should not exceed 0.1% of the sum of cancer fatality risks from all other causes.1 While the determination of precise threshold values is often subject to scientific controversy, it has been ascertained that setting targets facilitates decision and policy making in the presence of cognitively complex tasks.
Once a PSA model is implemented, a key insight for decisionmakers is to understand the relative importance of SSCs in the decision-making process.13, 14 Authorities demand a thorough investigation of the critical events whose occurrence could cause the risk metric to deviate from expectations.15 This information provides guidance in operational decisions such as the establishment of maintenance plans and the categorization of SSCs for their safety significance.16
Risk management strategies are subject to tight resource constraints. The allocation of scarce resources to minimize the risks of project failure is a major challenge for decisionmakers.6 In current practice, analysts use risk importance measures for this task. Importance measures, such as the risk achievement worth (RAW) and the risk reduction worth (RRW), are probabilistic expressions that communicate to a manager the increase (decrease) in the risk metric following the occurrence (nonoccurrence) of an event. However, limitations emerge in the use of importance measures in the design phase. In introducing the top event prevention methodology, Youngblood17, 18 observes that the set of components identified as important by risk importance measures may not necessarily include a complete path set, i.e., may not include a complete set of components/events whose functioning prevents the top event from occurring. But it is also well known that importance measures do not link the importance of an event to the overall level of risk of the system/mission/program under consideration, nor to the threshold value (acceptable risk). Thus, they allow only relative comparisons. Moreover, importance measures do not allow a risk manager to appreciate decision sensitivity. In fact, through importance measures, we gain insights on the overall change in the level of risk, but we do not gain a direct understanding of whether the occurrence (nonoccurrence) of an event causes the preferred alternative to change from (say) license to do not license.
We argue that a value of information approach may contribute in addressing these limitations of importance measures. Indeed, value of information is one of the most powerful sensitivity measures in decision analysis.19 Yet, its use in risk assessment problems supported by the creation of probabilistic safety assessment models is still scarce, if not absent, despite having been strongly suggested (see, for instance, Ref. 20). A possible reason is that value of information requires establishing the utility function of the decisionmaker. This task is problematic in the risk assessment of complex technological systems such as nuclear power plants or chemical facilities. In fact, in some applications, the decisionmaker might be not known (see Ref. 3, p. 221), or we might register the presence of multiple decisionmakers, with the problem of guaranteeing the coherence of the probability assignments and preferences of a single decisionmaker (Ref. 2, p. 1359).
To overcome these deadlocks, we propose a value of information approach to importance measures that exploits the Boolean nature of PSA models. This leads to the possibility of computing value of information for all applications without requiring the precise elicitation of the decisionmaker's utility function, and overcomes the problem of multiple decisionmakers. It is then possible to obtain the expression of a new value-of-information-based importance measure (decision worth, henceforth). The decision worth is an importance measure of decision sensitivity, whose expression brings together the risk metric, the RAW, and the RRW of the basic event of interest. In this way, RAW and RRW, which are measures of value sensitivity become active in a decision setting in which risk management alternatives are compared. Finally, no additional cost or burden for the analyst is imposed to find the decision worth of an event/component because the calculation of the new importance measure just requires the values of RAW and RRW, which are produced by standard PSA software. We then focus on decisions that involve thresholds values, and study the behavior of the decision worth of a component as a function of the acceptable risk and of the probability of occurrence. We show that decision worth is well posed also for groups of basic events and study its properties. A realistic case study and numerous examples illustrate the risk management insights that can be obtained by the use of decision worth in association with RAW and RRW.
The remainder of the article is organized as follows. Section 2., after providing a general literature review on value of information, offers an overview of the major importance measures in risk analysis, and highlights their drawbacks in a predecision setting. Section 3. introduces the decision worth, a new importance measure. Section 4. discusses the new importance measure in the context of risk-informed decisions based on the specification of an acceptable risk. Section 5. develops an application. Section 6. discusses the findings, while Section 7. concludes with suggestions for further research.
2. VALUE OF INFORMATION AND RISK IMPORTANCE MEASURES: A CONCISE REVIEW
This section offers a literature review. It concisely reviews value of information in the first part and then risk importance measures in the second part.
2.1. A Synthetic Review of Value of Information
 , and let (
, and let ( ) denote the associated probability space, with
) denote the associated probability space, with  denoting the probability measure that reflects the decisionmaker's degree of belief about
denoting the probability measure that reflects the decisionmaker's degree of belief about  . Depending on the decisionmaker's choice and on the realization of
. Depending on the decisionmaker's choice and on the realization of  (denoted with τ), the decisionmaker will incur a utility,
(denoted with τ), the decisionmaker will incur a utility, 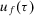 , where f denotes a generic strategy. The decisionmaker will select the strategy f that maximizes her expected utility:
, where f denotes a generic strategy. The decisionmaker will select the strategy f that maximizes her expected utility:
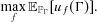 (1)
(1) , and uncertainty in
, and uncertainty in  is completely resolved. The expected value of perfect information is then defined as the difference between the expected profit that we shall obtain as a result of the clairvoyance and the expected profit that we would obtain without the clairvoyance (Ref. 19, p. 24). Then, ε is defined as:
is completely resolved. The expected value of perfect information is then defined as the difference between the expected profit that we shall obtain as a result of the clairvoyance and the expected profit that we would obtain without the clairvoyance (Ref. 19, p. 24). Then, ε is defined as:
 (2)
(2) is resolved. When
is resolved. When  is a random vector, resolving uncertainty in one of its components leads to the partial expected value of perfect information (value of information, henceforth):
is a random vector, resolving uncertainty in one of its components leads to the partial expected value of perfect information (value of information, henceforth):
 (3)
(3)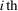 component of
component of  .
.Value of information has been extensively studied over the years. From a theoretical viewpoint, Hilton24 discusses the relationship between information value and its determinants: decision flexibility, risk aversion, initial uncertainty, and information system. There is a nonmonotonic relationship between value of information and its determinants, with the exception of the information system: it is possible, for this determinant, to state general conclusions for the monotonicity of value of information. Hazen and Sounderpandian25 compare the semantics of five alternative definitions of information value proposed in the literature. In particular, one can define value of information in terms of (expected) utility increase as in Equation 3, or as certainty equivalent increase, selling price, probability price, and buying price. The first four definitions are ordinally equivalent, while buying price is equivalent only under the assumption of linear or exponential utility functions. Hazen and Sounderpandian25 discuss that each definition has advantages and drawbacks and that, in particular, utility increase is widely used due to its tractability, especially in statistical decision theory—this is, in fact, the definition of value of information in classical statistical decision-making works such as Refs. 26 and 23. As noted in Ref. 22, the computation of the buying price requires the solution of an implicit equation and makes this choice less tractable than utility increase (see also Ref. 25).
As a sensitivity measure value of information is defined as per Equation 3, following Ref. 27 and applied in several works (see also Refs. 28-32). Bratvold et al.33 provide an overview of the application and use of value of information in the oil and gas industry. In a financial context, Pflug34 studies the link between value of information in Equation 3 and risk measures, showing that value of information satisfies the axioms of coherent risk measures.35 Keisler et al.20 perform a bibliometric analysis on the range of applications of value of information from 1990 to 2011. Nineteen trends were found to be at least weakly significant, with an overall increase in published papers using value of information. They note the large growth in the medical field, as well as suggest future research areas, such as loss avoidance and multiattribute value models. Value of information is increasingly used also in association with environmental risk assessment studies. Linkov et al.36 and Bates et al.37 apply value of information in the assessment of risks coming from nanomaterials and nanotechnologies. Bates et al.38 use value of information in a contaminated-sediment management study.
However, the notion of value of information has received little attention in risk analyses supported by probabilistic safety assessment studies for complex technological systems. To the authors' recollection, two works are relevant. Howard39 uses value of information to discuss the presence of epistemic uncertainty. Poern40 presents a discussion about the expected value of sample information in reliability analysis. Our work differs from Refs. 39 and 40 in several respects. First, there are different technical aspects: we consider decision making under risk and value of perfect information rather than sample information. Second, our approach is conceptually new: we aim to make explicit the connection between risk, importance, and value of information, in an all-around investigation.
2.2. Risk Importance Measures
Risk (or reliability) importance measures were introduced in seminal works of well-known statisticians and mathematicians in the late 1960s and early 1970s, the founding years of risk and reliability theory.41-43 Intuitively, importance measures are probabilistic expressions that assess the change in the baseline risk due to the occurrence of events of interest. Risk metrics are calculated through quantitative risk assessment models that help risk managers to identify scenarios (accident sequences) and their consequences and to assess their likelihoods.3, 44 These models are typically based on Boolean logic45 and consider success or failure. The end consequence is called the top event. To illustrate, loss of crew and core damage are typical top events in space7 and nuclear probabilistic safety assessments.2 We denote by Ψ the indicator variable of the top event.  denotes occurrence of the top event. The probability of the top event,
denotes occurrence of the top event. The probability of the top event, 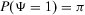 , is then the risk metric. Occurrence of the top event is, in turn, determined by the occurrence of a sequence of events of interest, called basic events. We let
, is then the risk metric. Occurrence of the top event is, in turn, determined by the occurrence of a sequence of events of interest, called basic events. We let 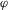 denote the vector of the basic event indicator variables. The expression that binds Ψ to
denote the vector of the basic event indicator variables. The expression that binds Ψ to 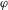 is called the structure function and is denoted by
is called the structure function and is denoted by 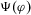 .
.
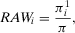 (4)
(4)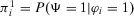 is the conditional value of the risk metric given that basic event i has occurred. From a risk management viewpoint, the events having the highest RAW are the most important for guaranteeing the present risk level.46
is the conditional value of the risk metric given that basic event i has occurred. From a risk management viewpoint, the events having the highest RAW are the most important for guaranteeing the present risk level.46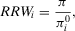 (5)
(5) is the conditional risk metric given that basic event i is not realized in the mission time of interest. RRW can be used to prioritize activities aimed at reducing the present level of risk.46 RRW and RAW provide alternative insights to the risk analyst.
is the conditional risk metric given that basic event i is not realized in the mission time of interest. RRW can be used to prioritize activities aimed at reducing the present level of risk.46 RRW and RAW provide alternative insights to the risk analyst. 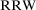 can be used to identify SSCs that have a large risk reduction potential. RAW provides the complementary information, indicating SSCs whose failure increases risk the most.
can be used to identify SSCs that have a large risk reduction potential. RAW provides the complementary information, indicating SSCs whose failure increases risk the most.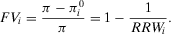 (6)
(6)In several applications, Fussell-Vesely importance and RAW are used jointly as measures of, respectively, risk and safety significance (see Refs. 48 and 13 for further details).
Example 1.A decisionmaker is evaluating two strategies, I and II, for a potential space mission. The events of interest are A and B, which represent the failures of components A and B. The failure probabilities are 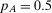 and
and 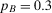 , respectively. The states of the world and the corresponding utilities used are given in Table 1. Table 2 reads as follows. If strategy I is selected, then 1) if both A and B occur, the utility is 0; 2) if A fails and not B, then the utility is 0.25; 3) if B fails but not A, then the utility is 0.27 (the different utility can be due to different costs of the two components or to different levels of environmental damage implied by their failure); 4) if none of them fails, the utility is 0.8. Similarly, Table 2 provides the utilities if strategy II is implemented.
, respectively. The states of the world and the corresponding utilities used are given in Table 1. Table 2 reads as follows. If strategy I is selected, then 1) if both A and B occur, the utility is 0; 2) if A fails and not B, then the utility is 0.25; 3) if B fails but not A, then the utility is 0.27 (the different utility can be due to different costs of the two components or to different levels of environmental damage implied by their failure); 4) if none of them fails, the utility is 0.8. Similarly, Table 2 provides the utilities if strategy II is implemented.
If the decisionmaker is interested in the component whose failure causes the highest risk increase, s(he) evaluates 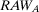 and
and 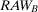 . As Table 2 shows, if the two components are in parallel,
. As Table 2 shows, if the two components are in parallel,  is equal to 2, and
is equal to 2, and 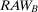 to 3.33. Hence, component B is more important than component A. If the two components are in series, they are equally important because
to 3.33. Hence, component B is more important than component A. If the two components are in series, they are equally important because 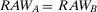 . If the risk manager wishes to understand which component has the greatest risk reduction potential, by looking at
. If the risk manager wishes to understand which component has the greatest risk reduction potential, by looking at 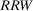 , s(he) would rank A as more important than B if the components are in series, while s(he) would consider them equally important if they are in parallel. The Fussell-Vesely importance would provide the same ranking as RRW.
, s(he) would rank A as more important than B if the components are in series, while s(he) would consider them equally important if they are in parallel. The Fussell-Vesely importance would provide the same ranking as RRW.
 |
Utility I | Utility II |
|---|---|---|
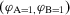 |
0 | 0 |
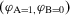 |
0.25 | 0.3 |
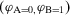 |
0.27 | 0.2 |
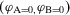 |
0.8 | 0.7 |
| Config | RAW | RRW | FV |
|---|---|---|---|
| Parallel | 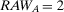 |
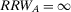 |
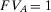 |
| Parallel | 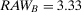 |
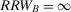 |
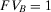 |
| Series | 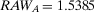 |
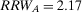 |
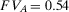 |
| Series | 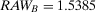 |
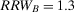 |
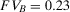 |
Note that, in Example 1, the ranking depends on the system configuration but not on the strategy to be selected. In fact, when considered from a decision analysis perspective, RAW, RRW, Fussell-Vesely, as well as all other risk importance measures, are measures of value sensitivity. A sensitivity measure is a measure of value sensitivity if it communicates to the decisionmaker information about the numerical change in risk metric given the occurrence of an event. As Felli and Hazen27 underline, a sensitivity measure is a measure of decision sensitivity if it can also communicate information about weather the failure (success) of an SSC causes the preferred alternative to change.
These measures, though, are not measures of decision sensitivity. Value of information is a measure of decision sensitivity.
Example 2.. (Example 1 Continued)Consider now that the decisionmaker is interested in knowing whether the decision problem is sensitive to the failure of component A or B. S(he) needs to compute value of information. By the data in Table 2, strategy I is the preferred one, with an expected utility of 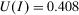 , while strategy II has an expected utility
, while strategy II has an expected utility 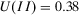 . Computing value of information according to the standard definition, the risk manager finds that
. Computing value of information according to the standard definition, the risk manager finds that 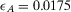 and
and  . Thus, component A is decision significant. Note that this result is independent of the system configuration.
. Thus, component A is decision significant. Note that this result is independent of the system configuration.
Nonetheless, computing value of information using Equation 3 requires the specification of utility values. Utility elicitation is a long process that might yield different results according to the procedure used.49 Such systematic discrepancies between different utility elicitation methods are mainly due to the fact that people deviate from expected utility.50 In realistic applications, moreover, the elicitation might not even be allowed because we do not know who the decisionmaker is or will be (Ref. 3, p. 222). Then, the challenge emerges of linking value of information and importance measures, with the goal of formulating an indicator that possibly combines the key risk insights offered by RAW and RRW in a decision-sensitivity measure. Such an importance measure would be relevant in all those applications in which the decisionmaker is making explicit the comparison between alternative risk management strategies.20, 37 In the next sections, we address such challenge.
3. A VALUE-OF-INFORMATION-BASED IMPORTANCE MEASURE
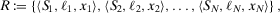 (7)
(7)- 1.
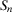 (
(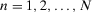 ) is a generic scenario and answers the question “What can happen?”
) is a generic scenario and answers the question “What can happen?” - 2.
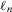 is the likelihood of such scenario, and answers the question “How likely is it that
is the likelihood of such scenario, and answers the question “How likely is it that 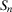 will happen?”3
will happen?”3 - 3.
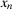 is the consequence of scenario
is the consequence of scenario 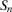 , answering the question “If
, answering the question “If 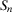 does happen, what is the consequence?”
does happen, what is the consequence?”
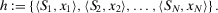 (8)
(8)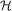 denote the set of all possible hazards. Informally, in Ref. 52, hazard is described as a potential source of danger. In the Savage theoretical setup, we have:
denote the set of all possible hazards. Informally, in Ref. 52, hazard is described as a potential source of danger. In the Savage theoretical setup, we have:
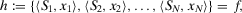 (9)
(9)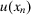 the utility of consequence
the utility of consequence 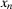 , and with
, and with 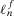 its probability, the expected utility of risk management strategy f is written as:
its probability, the expected utility of risk management strategy f is written as:
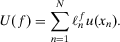 (10)
(10)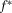 that maximizes her expected utility,
that maximizes her expected utility, 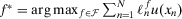 .
. 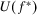 denotes the corresponding expected utility.
denotes the corresponding expected utility.Suppose now that the decisionmaker is interested in receiving information about an event E. If she is informed that E has occurred, then her degree of belief is represented by the conditional probability 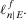 Correspondingly, she selects strategy
Correspondingly, she selects strategy  that maximizes her expected utility under the new degree of belief. The corresponding (maximal) expected utility is
that maximizes her expected utility under the new degree of belief. The corresponding (maximal) expected utility is 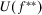 . If the clairvoyant communicates that E has not occurred, the decisionmaker's degree of belief is represented by
. If the clairvoyant communicates that E has not occurred, the decisionmaker's degree of belief is represented by 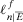 . She would then select strategy
. She would then select strategy 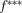 such that
such that 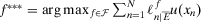 , with corresponding expected utility
, with corresponding expected utility 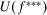 .
.
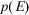 and
and 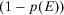 , respectively, we obtain the following expression for the value of information in a generic risk assessment problem:
, respectively, we obtain the following expression for the value of information in a generic risk assessment problem:
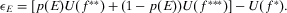 (11)
(11)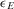 , a risk manager would be, in principle, capable of prioritizing information collection. However, Equation 11 would require us to assess the utilities of the decisionmaker for each consequence. Nonetheless, when the risk metric is computed through a quantitative risk assessment model, the following holds:
, a risk manager would be, in principle, capable of prioritizing information collection. However, Equation 11 would require us to assess the utilities of the decisionmaker for each consequence. Nonetheless, when the risk metric is computed through a quantitative risk assessment model, the following holds:
- 1. Reference 52's scenarios are all possible basic event configurations (all possible
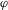 's);
's); - 2.
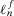 ,
, 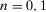 is the probability of the top event under risk management strategy f, that is,
is the probability of the top event under risk management strategy f, that is, 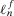 is the risk metric under strategy f. We can then write
is the risk metric under strategy f. We can then write 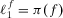 and
and 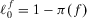 .
. - 3. Given the binary nature of the consequences,
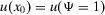 and
and 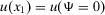 are the utilities for the occurrence/nonoccurrence of the top event. Then, a simple argument (actually, the same intuition is at the basis of Table 1 in Ref. 40, although not detailed in that work) allows us to simplify utility elicitation significantly. Specifically, consider a risk management strategy f. Then, the expected utility of the decisionmaker under such risk management strategy is:
Then, if the decisionmaker prefers
are the utilities for the occurrence/nonoccurrence of the top event. Then, a simple argument (actually, the same intuition is at the basis of Table 1 in Ref. 40, although not detailed in that work) allows us to simplify utility elicitation significantly. Specifically, consider a risk management strategy f. Then, the expected utility of the decisionmaker under such risk management strategy is:
Then, if the decisionmaker prefers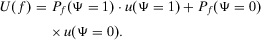
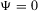 to
to  (as it is the case in a failure logic), we can assign
(as it is the case in a failure logic), we can assign 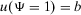 and
and 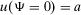 , with
, with 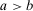 , and both a and b are real numbers. Then, we have:
Then, because utility functions are equivalent under monotonic transformations,57 we can assign
, and both a and b are real numbers. Then, we have:
Then, because utility functions are equivalent under monotonic transformations,57 we can assign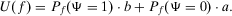
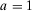 and
and 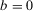 , without loss of generality. Then, we obtain:
This indicates that the alternative that maximizes utility is the alternative that maximizes the probability of success. This is true for all decisionmakers that prefer success
, without loss of generality. Then, we obtain:
This indicates that the alternative that maximizes utility is the alternative that maximizes the probability of success. This is true for all decisionmakers that prefer success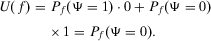
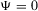 to failure
to failure  .
.
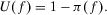 (12)
(12)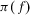 ). The relationship between utility and probability and the interpretation of a utility function as the probability of outperforming a given benchmark is discussed in more general settings by Ref. 58.
). The relationship between utility and probability and the interpretation of a utility function as the probability of outperforming a given benchmark is discussed in more general settings by Ref. 58.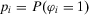 be the probability that basic event i occurs. Then, the expression of the value of information in Equation 11 becomes:
be the probability that basic event i occurs. Then, the expression of the value of information in Equation 11 becomes:
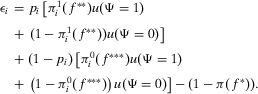 (13)
(13)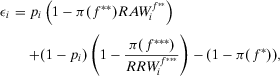 (14)
(14)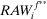 and
and 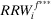 are the risk achievement and RRW of basic event i given that risk management strategies
are the risk achievement and RRW of basic event i given that risk management strategies 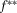 and
and 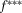 are selected, respectively. Let us call the importance measure in Equation 14 decision worth.
are selected, respectively. Let us call the importance measure in Equation 14 decision worth.Equation 14 shows that the decision worth brings together the risk importance measures of basic event i (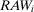 and
and 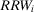 ), the conditional risk metric under the preferred strategy, and the probability of occurrence (and nonoccurrence) of the basic event itself. In fact, decision worth considers the status quo and the scenarios in which the basic event occurs and does not occur simultaneously. Note that RAW and RRW address these aspects separately. Also, the decision worth applies in a predecision setting (design or licensing phase) without requiring an assessment of the utility of a decisionmaker. We discuss these aspects further in the reminder.
), the conditional risk metric under the preferred strategy, and the probability of occurrence (and nonoccurrence) of the basic event itself. In fact, decision worth considers the status quo and the scenarios in which the basic event occurs and does not occur simultaneously. Note that RAW and RRW address these aspects separately. Also, the decision worth applies in a predecision setting (design or licensing phase) without requiring an assessment of the utility of a decisionmaker. We discuss these aspects further in the reminder.
We conclude this section with an observation. Recently, Ebrahimi et al.59 define a new importance measure of components and basic events based on the Kullback–Leibler divergence between the conditional and unconditional system failure probability functions. The importance measure possesses interesting properties, and compares well with importance measures such as the Birnbaum41 and Barlow-Proschan42 importance measures. The entropy-based importance of Ref. 59 or the Birnbaum and Barlow–Proshan importance measures, as well as other importance measures, such as the differential,60 criticality,13 and Fussell-Vesely,61 are measures of value sensitivity, insofar as they account for the change in (or contribution to) the value of the risk metric without explicit reference to changes in the preferred alternative. The decision worth differs from the above-mentioned importance measures because it explicitly compares different alternatives and is therefore a decision-sensitivity measure. We refer to Ref. 27 for further discussion on the distinction between value and decision sensitivity.
4. DECIDING WITH THRESHOLDS
In many risk assessment problems, risk analysts “may suggest some courses of action based on ... defined thresholds of acceptable risks” (Ref. 3, p. 221) or thresholds may be set by regulatory agencies. This section, after discussing the occurrence and nonoccurrence contributions to value of information, provides analytical results for the behavior of decision worth as a function of two of its determinants, namely, the acceptable risk and the probability of the basic event, as well as results for specific configurations and an extension to basic events/component groups.
4.1. Decision Worth: Occurrence and Nonoccurrence Contributions
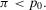 (15)
(15)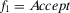 and
and 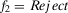 denote the license (authorize) and do not license (do not authorize) alternatives, respectively. We accept the system if the expected utility of accept (
denote the license (authorize) and do not license (do not authorize) alternatives, respectively. We accept the system if the expected utility of accept (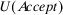 ) is greater than the expected utility of reject (
) is greater than the expected utility of reject (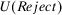 ). Then, it is easy to see4 that a risk manager confronted with a threshold decision is consistent with expected utility theory, provided that she sets
). Then, it is easy to see4 that a risk manager confronted with a threshold decision is consistent with expected utility theory, provided that she sets 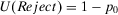 . Then, for threshold-based problems, the decision worth of basic event i becomes:
. Then, for threshold-based problems, the decision worth of basic event i becomes:
 (16)
(16)The decision worth in Equation 16 relates the risk metric, π, to the threshold probability p0 and to the relative risk increase (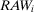 ) and decrease (
) and decrease (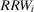 ) associated with the occurrence (nonoccurrence) of basic event i. Note that Equation 16 does not call for any new computation with respect to current practice because the calculation of the risk metric of
) associated with the occurrence (nonoccurrence) of basic event i. Note that Equation 16 does not call for any new computation with respect to current practice because the calculation of the risk metric of 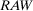 and
and 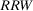 is already standard, being required by regulatory authorities, and corresponding subroutines are available in industry-used software.
is already standard, being required by regulatory authorities, and corresponding subroutines are available in industry-used software.
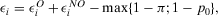 (17)
(17)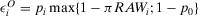 (18)
(18)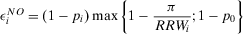 (19)
(19)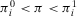 . The expected payoff without information is
. The expected payoff without information is 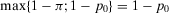 —the third term in Equation 17. The occurrence contribution to value of information of a generic basic event is given by:
—the third term in Equation 17. The occurrence contribution to value of information of a generic basic event is given by:
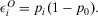 (20)
(20)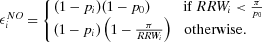 (21)
(21)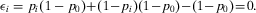 (22)
(22)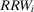 is smaller than the ratio between π and p0, is equivalent to stating that
is smaller than the ratio between π and p0, is equivalent to stating that 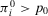 , that is, the conditional value of the risk metric remains higher than the acceptable level of risk even if we were capable of preventing the basic event in question. Then, the preferred alternative remains to reject. Conversely, if
, that is, the conditional value of the risk metric remains higher than the acceptable level of risk even if we were capable of preventing the basic event in question. Then, the preferred alternative remains to reject. Conversely, if 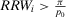 , we have a nonnull decision worth:
, we have a nonnull decision worth:
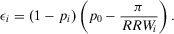 (23)
(23)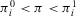 and the preferred alternative is Reject, an event can have a nonnull decision worth only if its nonoccurrence leads to a conditional value of the risk metric lower than the acceptable risk.
and the preferred alternative is Reject, an event can have a nonnull decision worth only if its nonoccurrence leads to a conditional value of the risk metric lower than the acceptable risk.The managerial implications are as follows. Risk management strategies typically foresee the substitution of current components for more efficient ones, the performance of specialized maintenance plans, or dedicated operator training. Marginal risk reductions are achieved with costs that are exponentially increasing and managers need to carefully prioritize resources. If no event has a decision worth greater than zero, no risk management strategy has the possibility of reverting the decision from Reject to Accept; no matter how resources are allocated, the system needs to be redesigned. Conversely, if some events have a nonnull decision worth, then these are the events to prioritize. Concentrating resources to make marginal improvements on these components/events within the current design can be successful in reverting the decision from Reject to Accept.
4.2. Decision Worth as Function of the Acceptable Risk
The next proposition addresses the behavior of decision worth as a function of the acceptable risk. We need to distinguish two cases that appear in practice: the case in which the occurrence of a basic event leads to an increase in the risk metrics and the case in which it leads to a decrease in the risk metrics. We observe that the first behavior is typical of coherent systems, while the second of noncoherent systems. The next proposition addresses the first case (see the Appendix for all proofs).
Proposition 1.Consider an Accept–Reject decision problem, with acceptable risk p0. If 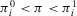 , then the decision worth of a basic event depends on the acceptable risk as follows:
, then the decision worth of a basic event depends on the acceptable risk as follows:
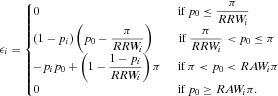 (24)
(24)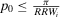 . Then, as the acceptable risk increases, the decision worth increases linearly. The marginal rate of increase is
. Then, as the acceptable risk increases, the decision worth increases linearly. The marginal rate of increase is 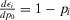 and depends only on the basic event probability of nonoccurrence. The peak is reached at
and depends only on the basic event probability of nonoccurrence. The peak is reached at  , where the peak value equals:
, where the peak value equals:
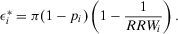 (25)
(25)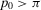 ,
,  starts decreasing until p0 equals
starts decreasing until p0 equals 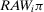 . The marginal rate of decrease is now
. The marginal rate of decrease is now  , with a slope equal to the probability of basic event occurrence. For
, with a slope equal to the probability of basic event occurrence. For  , the decision worth is null. Proposition 1 reassures us that this pattern repeats for any basic event.
, the decision worth is null. Proposition 1 reassures us that this pattern repeats for any basic event.
Remark 1.When the acceptable risk is equal to the risk metric  , the decision worth of a basic event is either maximal or null. If, even at
, the decision worth of a basic event is either maximal or null. If, even at  , a basic event has a null value of information, then a decisionmaker is reassured that such event cannot be decision significant for any value of the acceptable risk and can be screened out from further analysis.
, a basic event has a null value of information, then a decisionmaker is reassured that such event cannot be decision significant for any value of the acceptable risk and can be screened out from further analysis.
The next example illustrates Proposition 1.
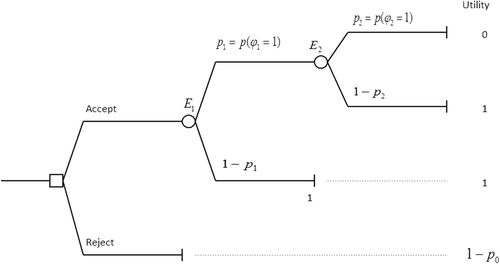
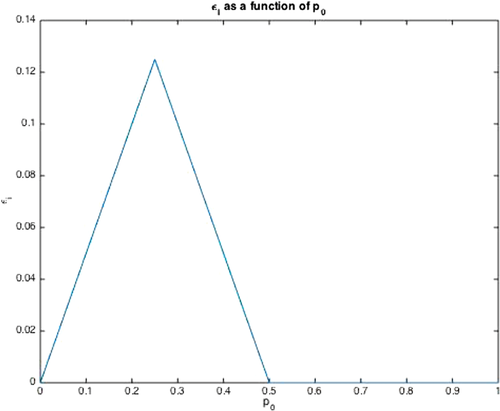
Example 3.We are evaluating whether to accept or reject a given design. Acceptance implies that the system failure probability is lower than p0. Failure requires two basic events to occur, E1 and E2. The corresponding probabilities are p1 and p2, and basic events are probabilistically independent. Then, the decision tree corresponding to this problem is represented in Fig. 1, where the upper branch corresponds to the alternative Accept. The lower branch is a degenerate tree with a sure alternative (Reject).
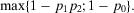 (26)
(26) (
( ), we can exploit Equation 16 and our knowledge of the risk importance measures. In particular, we know that RRW is infinite for both basic events, and
), we can exploit Equation 16 and our knowledge of the risk importance measures. In particular, we know that RRW is infinite for both basic events, and 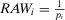 . Substituting into Equation 16 and simplifying, we obtain:
. Substituting into Equation 16 and simplifying, we obtain:
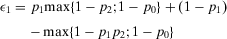 (27)
(27)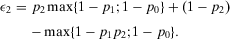 (28)
(28) (29)
(29)Equation 29 illustrates Equation 24. Assigning 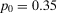 and
and 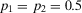 , we find
, we find 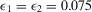 . Fig. 2 shows that the decision worth of any given component is zero when the threshold probability is higher than the failure probability of the other component,
. Fig. 2 shows that the decision worth of any given component is zero when the threshold probability is higher than the failure probability of the other component, 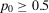 . Also,
. Also,  starts increasing for
starts increasing for 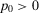 , reaches the peak at
, reaches the peak at 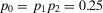 , and then starts decreasing for
, and then starts decreasing for 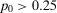 .
.
Note that if components are characterized by different failure probabilities, then the higher 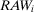 is, the higher the peak decision worth. Moreover, if
is, the higher the peak decision worth. Moreover, if 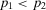 , we have
, we have 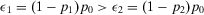 , because
, because 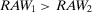 .
.
We now consider the case in which the occurrence of the basic event decreases the risk metric, which may occur in noncoherent systems.
Proposition 2.Consider an Accept–Reject decision problem with acceptable risk p0. If 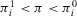 , then
, then  depends on the acceptable risk as follows:
depends on the acceptable risk as follows:
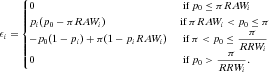 (30)
(30)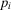 , while the decrease rate is
, while the decrease rate is 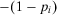 . The peak is reached again when the acceptable risk equals the risk metric (
. The peak is reached again when the acceptable risk equals the risk metric ( ). At the peak,
). At the peak,  assumes the value:
assumes the value:
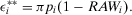 (31)
(31)In this respect, we need to recall an important distinction that comes from system modeling. If the assumption 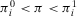 holds for all basic events, then the system, and consequently the decision problem, is coherent. In the risk assessment of a coherent system, the occurrence of an event always increases the probability of success. Conversely, if for some basic event
holds for all basic events, then the system, and consequently the decision problem, is coherent. In the risk assessment of a coherent system, the occurrence of an event always increases the probability of success. Conversely, if for some basic event 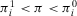 , the system and the corresponding decision problem are noncoherent. Then, in the risk assessment of a noncoherent system, we might even be in the counterintuitive position in which the occurrence of a basic event, such as the failure of a component, causes the preferred alternative to shift from Reject to Accept. Noncoherent problems appear frequently in the study of digital systems and are of growing importance in computer science. The analytical results of Proposition 1 and Proposition 2 then imply the following.
, the system and the corresponding decision problem are noncoherent. Then, in the risk assessment of a noncoherent system, we might even be in the counterintuitive position in which the occurrence of a basic event, such as the failure of a component, causes the preferred alternative to shift from Reject to Accept. Noncoherent problems appear frequently in the study of digital systems and are of growing importance in computer science. The analytical results of Proposition 1 and Proposition 2 then imply the following.
Remark 2.
- (i)
If the decision problem is about a coherent system, then Proposition 1 applies to all basic events.
- (ii)
If the decision problem is about a noncoherent system, then for a specific basic event i:
(ii.1) if
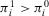 , then results in Proposition 1 hold, while
, then results in Proposition 1 hold, while(ii.2) if
 , then results in Proposition 2 hold.
, then results in Proposition 2 hold.
From a more general viewpoint, Propositions 1 and 2 overcome a well-known limitation of risk importance measures linking the importance of a basic event to level of risk that the decisionmaker is willing to bear.
4.3. Decision Worth as a Function of Basic Event Probabilities
This section discusses the relationship between the decision worth of a basic event and its probability of occurrence.
Lemma 1.Consider an Accept–Reject decision problem with acceptable risk p0. Then, if 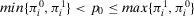 , there exists a unique indifference probability
, there exists a unique indifference probability
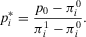 (32)
(32)In Equation 32, the numerator is the difference between the acceptable risk and the conditional risk metric given that the basic event does not occur. The denominator is the difference between the conditional risk metric given that the basic event occurs and given that it does not occur. Note that if a basic event is such that 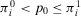 , as in a coherent system, then both the numerator and the denominator are positive. If the converse holds, as in a noncoherent system, then both the numerator and the denominator are negative, but Equation 32 still formally holds. Thus, the indifference probability in Equation 32 holds for decisions on both coherent and noncoherent systems.
, as in a coherent system, then both the numerator and the denominator are positive. If the converse holds, as in a noncoherent system, then both the numerator and the denominator are negative, but Equation 32 still formally holds. Thus, the indifference probability in Equation 32 holds for decisions on both coherent and noncoherent systems.
We also observe that for 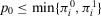 , there is no value of
, there is no value of 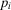 such that the preferred alternative is to accept. For
such that the preferred alternative is to accept. For 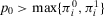 , the preferred alternative is to accept for any value of
, the preferred alternative is to accept for any value of 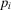 . Thus, we shall consider the nontrivial case
. Thus, we shall consider the nontrivial case 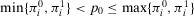 in the remainder. We have the following result.
in the remainder. We have the following result.
Proposition 3.Consider an Accept–Reject decision problem with acceptable risk p0. The decision worth of basic event i as a function of the probability of basic event i, 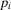 , has the following form:
, has the following form:
(A) If 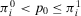 , then
, then
 (33)
(33)(B) If 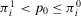 , then
, then
 (34)
(34)where 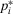 is the indifference probability in Equation 32.
is the indifference probability in Equation 32.
 behaves piecewise linearly as a function of the probability of occurrence of basic event i. It is increasing if
behaves piecewise linearly as a function of the probability of occurrence of basic event i. It is increasing if 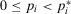 and decreasing if
and decreasing if 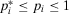 . The slope is dependent on whether
. The slope is dependent on whether 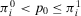 , or
, or 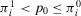 . The peak values are reached at indifference and given by:
. The peak values are reached at indifference and given by:
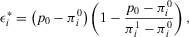 (35)
(35)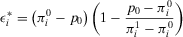 (36)
(36)To illustrate, let us reconsider Example 3. We have 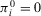 ,
, 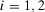 ,
, 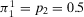 , and
, and 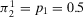 . Whence,
. Whence, 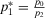 and
and 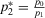 . Thus, we have that ε1 (ε2) is increasing with slope equal to
. Thus, we have that ε1 (ε2) is increasing with slope equal to 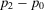 (
( ), for
), for 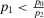 (
( ) and decreasing with slope
) and decreasing with slope 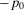 for
for 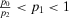 (
(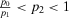 ).
).
Lemma 1 has several managerial implications. Suppose that basic event i concerns the execution of a certain task by an operator. By Equation 32, the risk manager knows the value of the failure probability that shifts the decision from Accept to Reject (or the converse). By comparing this value against her belief, the decisionmaker understands how sensitive the preferred strategy is to an error in 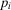 . In particular, we can look at the ratio between the basic event probability and the indifference probability,
. In particular, we can look at the ratio between the basic event probability and the indifference probability, 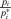 , as a measure of how far a basic event is from the critical threshold. If
, as a measure of how far a basic event is from the critical threshold. If 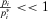 , then a small deterioration in the operator's ability to perform the required action will not cause the preferred strategy to change. Conversely, if the decisionmaker's belief is such that
, then a small deterioration in the operator's ability to perform the required action will not cause the preferred strategy to change. Conversely, if the decisionmaker's belief is such that 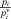 is close to 1, then interventions are needed to reduce the execution error.
is close to 1, then interventions are needed to reduce the execution error.
4.4. Parallel and Series Configurations
The previous results hold independently of the system configuration and of whether independent failures are assumed. Now, following the tradition in importance measure analysis, we study additional properties for more specific configurations. In particular, we consider the case in which a component is in parallel (series) with the rest of the system. As in the classical works of Refs. 42 and 62, we assume independent failures for simplicity.
We start with two components/basic events i and j that are both in parallel with the rest of the system. Here, we observe that we would not be able to distinguish them using RRW because all components/basic events in parallel with the top event have the same RRW.
Proposition 4.Consider an Accept–Reject decision problem with acceptable risk p0. If basic event i is in parallel with the rest of the system, then:
(1)
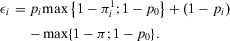 (37)
(37)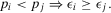 (38)
(38)Thus, for components/basic events i and j both in parallel with the rest of the system (the rest of the system does not need to be a parallel system itself), basic event i has a higher decision worth than basic event j if it is associated with a smaller failure probability. The next result shows that symmetric considerations hold when basic events i and j are in series with the rest of the system.
Proposition 5.Consider an Accept–Reject decision problem with acceptable risk p0. If basic events i and j are in series with the rest of the system, and failures are independent, then:
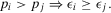 (39)
(39)Thus, if basic events i and j are in series with the rest of the system, the basic event with the higher probability of occurrence is associated with the higher decision worth. This result hints that among those basic events whose occurrence causes the top event, the ones with a higher failure probability are more important in a design phase. Note that these basic events are characterized by the same RAW and we would not be able to distinguish the most important using RAW.
4.5. Joint Decision Worth
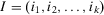 be the subscripts of the group of k basic events of interest. Then, let
be the subscripts of the group of k basic events of interest. Then, let 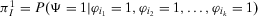 be the conditional risk metric given that the basic events in I occur and
be the conditional risk metric given that the basic events in I occur and 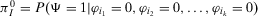 the conditional risk metric given that they do not occur. The decision worth of group I is then:
the conditional risk metric given that they do not occur. The decision worth of group I is then:
 (40)
(40)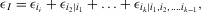 (41)
(41)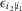 is the residual decision worth of basic event i2, given that we have received perfect information about basic event i1, etc. We can say that decision worth is conditionally additive. To illustrate, consider evaluating the joint decision worth of two basic events in an accept/reject decision problem. Letting
is the residual decision worth of basic event i2, given that we have received perfect information about basic event i1, etc. We can say that decision worth is conditionally additive. To illustrate, consider evaluating the joint decision worth of two basic events in an accept/reject decision problem. Letting 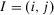 , we have:
, we have:
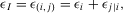 (42)
(42)Example 4.Consider a two component parallel system. Let 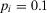 and
and 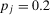 . Assume that failures are probabilistically independent and that
. Assume that failures are probabilistically independent and that 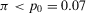 . Observing that
. Observing that 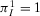 and
and 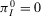 , because the components are in parallel with the rest of the system, and that
, because the components are in parallel with the rest of the system, and that 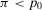 , by Equation 40, we obtain:
, by Equation 40, we obtain:
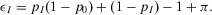 (43)
(43)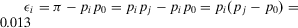 . Hence, by Equation 42, the residual decision worth of j given i is
. Hence, by Equation 42, the residual decision worth of j given i is 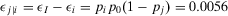 . Now, consider that information is received sequentially and we can choose on which basic event to be informed before. It is best to receive information first on i and then on j. Indeed, suppose we receive information about component j first. We register
. Now, consider that information is received sequentially and we can choose on which basic event to be informed before. It is best to receive information first on i and then on j. Indeed, suppose we receive information about component j first. We register 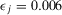 , with a residual decision worth of
, with a residual decision worth of 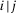 equal to 0.0126.
equal to 0.0126.To further illustrate the meaning of the residual decision worth 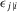 , we consider its direct calculation. The residual decision worth of j incorporates the fact that we know whether i fails or does not fail. Hence, conditioning Equation 37 on whether event i occurs or not, we obtain:
, we consider its direct calculation. The residual decision worth of j incorporates the fact that we know whether i fails or does not fail. Hence, conditioning Equation 37 on whether event i occurs or not, we obtain:
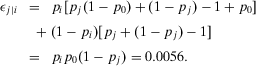 (44)
(44)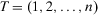 denote the collection of indices of all basic events and write
denote the collection of indices of all basic events and write 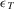 to denote the corresponding decision worth. The quantity
to denote the corresponding decision worth. The quantity 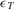 is the maximum value that the decision worth can assume and is called total decision worth. Now, letting
is the maximum value that the decision worth can assume and is called total decision worth. Now, letting 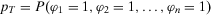 the probability that all basic events occur, by Equation 40, we find the following simple expression for the total decision worth (proof in Appendix, Equation (A.18)):
the probability that all basic events occur, by Equation 40, we find the following simple expression for the total decision worth (proof in Appendix, Equation (A.18)):
 (45)
(45)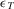 , which holds for any system and any configuration. To illustrate Equation 45, let us refer back to Example 4. Because π is lower than p0, the first of the two expressions in Equation 45 holds. Then, we have
, which holds for any system and any configuration. To illustrate Equation 45, let us refer back to Example 4. Because π is lower than p0, the first of the two expressions in Equation 45 holds. Then, we have 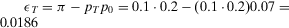 . Indeed,
. Indeed,  in this case.
in this case.We conclude this section considering two special groups, namely, minimal path sets (MPSs) and minimal cut sets (MCSs). Let us start with MPSs. Let I and J denote the collections of indices of basic events contained in MPS I and J, respectively, and let 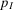 and
and 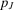 denote the corresponding probabilities. A MPS as a whole is, by definition, in parallel with the rest of the system. In fact, the nonoccurrence of the events in I (or J) prevents system failure. Then, by Proposition 4,
denote the corresponding probabilities. A MPS as a whole is, by definition, in parallel with the rest of the system. In fact, the nonoccurrence of the events in I (or J) prevents system failure. Then, by Proposition 4, 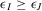 , if
, if 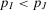 . Symmetric considerations hold for MCSs. An MCS is in series with the rest of the system. Then, if
. Symmetric considerations hold for MCSs. An MCS is in series with the rest of the system. Then, if 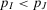 , we expect MCS J to have a higher decision worth than MCS I by Proposition 5. Thus, the higher the probability of an MCS, the greater the associated decision worth.
, we expect MCS J to have a higher decision worth than MCS I by Proposition 5. Thus, the higher the probability of an MCS, the greater the associated decision worth.
5. AN APPLICATION
The risk analysis of the large loss of coolant accident (LOCA) of the Advanced Test Reactor (ATR) is a well-known risk assessment case study.5 Moreover, for this case study, previous literature makes available the values of the RAW and RRW of all basic events as well as their failure probabilities.64 Thus, we can transparently compute decision worth exploiting the available values.
The large LOCA probabilistic risk analysis describes a sequence of events that can lead to reactor failure and core damage. The scenarios involve two major safety systems, namely, the SCRAM system and the firewater injection system. Failure to scram leads to core damage. Conversely, given successful scram, the firewater injection system must intervene to ensure that no core damage is achieved. Water is injected into the core by four injection lines. The LOCA originates with the failure of one of these lines. For the system to fail, the failure of the other three lines is necessary. The accident sequence foresees 48 basic events and 289 prime implicants.
Consider a risk manager performing a traditional PSA analysis. Fig. 3 displays the basic events RAW, RRW, and Fussell-Vesely. By Equation 6, a higher value of RRW implies a higher value for the Fussell-Vesely importance. Thus, Fussell-Vesely and RRW rank basic events in the same way. Conversely, the fact that RAW and RRW produce different rankings is expected and is related to the different scope of use, as we discussed. However, basic event 24 is an exception: this basic event has the highest RRW and the highest RAW. It is reasonable to assume that an event with a high RAW and high RRW is not only risk/safety, but also decision, significant.
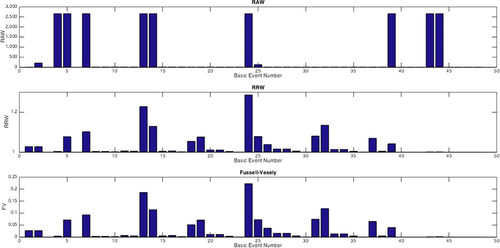
To illustrate, let us start considering that the authority sets the acceptable risk equal to the risk metric  . By this choice, the authority is indifferent between accepting and rejecting the system. By our knowledge of the RAW and RRW of the basic events, we can determine the decision worth of all basic events combining them through Equation 16. The resulting decision worths are reported in the second graph of Fig. 4. Let us compare the ranking of the decision worth with the ranking of RAW and RRW, respectively. Let
. By this choice, the authority is indifferent between accepting and rejecting the system. By our knowledge of the RAW and RRW of the basic events, we can determine the decision worth of all basic events combining them through Equation 16. The resulting decision worths are reported in the second graph of Fig. 4. Let us compare the ranking of the decision worth with the ranking of RAW and RRW, respectively. Let 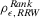 and
and 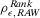 denote the rank correlation between the ranking induced by RRW and the decision worth, and by RAW and the decision worth, respectively.6 We register
denote the rank correlation between the ranking induced by RRW and the decision worth, and by RAW and the decision worth, respectively.6 We register 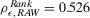 and
and 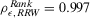 . These values show a rather low ranking agreement between
. These values show a rather low ranking agreement between 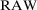 and the decision worth. In contrast, the rank correlation between the decision worth and
and the decision worth. In contrast, the rank correlation between the decision worth and  is quite high. As for specific basic events, basic event 24 ranks first, confirming the relevance of this event for the overall decision-making process. However, even basic events with a modest value of RAW and RRW, as, for example, basic event 2, turn out to be decision significant.
is quite high. As for specific basic events, basic event 24 ranks first, confirming the relevance of this event for the overall decision-making process. However, even basic events with a modest value of RAW and RRW, as, for example, basic event 2, turn out to be decision significant.
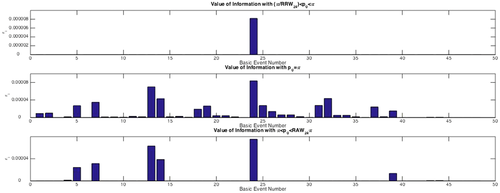
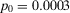 in the first graph,
in the first graph,  in the second, and
in the second, and 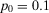 in the third).
in the third).Let us consider the managerial implications of these findings. From the perspective of a risk manager, in the case the authority sets a threshold equal to the risk metric, she/he knows that decision-significant basic events tend to be the ones characterized by a very high RRW. Thus, within the present design, resources for improvements must be concentrated toward increasing the probability of the nonoccurrence of these basic events. This result provides a message to the authority as well. The design would become acceptable only if actions are taken to significantly improve the performance of those components that have a nonnull decision worth. Then, recommendations to the applicant can be issued in this respect. In fact, a degraded performance in these crucial events would make Reject the preferred alternative. From a general risk management viewpoint, these results would also indicate that improving performance is more important for an accept decision than preventing failure. This result is, in spirit, consistent with the top event prevention methodology of Ref. 17.
Consider now the situation in which the design is unacceptable (the regulatory threshold is smaller than the risk metric). The preferred alternative is now to reject the design. Through our discussion in Section 4. we know that no contribution to value of information comes from the occurrence of a basic event. Thus, only basic events characterized by a high RRW are expected to be decision significant. In our application (we set an indicative value of 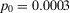 ), the only event with a nonnull decision worth is basic event 24. Thus, we obtain a strong disagreement with the rankings produced by importance measures, which also deem other events significant. The correlation between the ranks induced by
), the only event with a nonnull decision worth is basic event 24. Thus, we obtain a strong disagreement with the rankings produced by importance measures, which also deem other events significant. The correlation between the ranks induced by  and by decision worth now falls down to
and by decision worth now falls down to 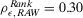 .
.
To the risk manager, this result suggests that the only improvement that can be made to revert the decision from Reject to Accept is an amelioration of the third pump (whose failure is basic event 24). The amelioration, however, should be such that it makes this component perfectly reliable. If this improvement is not at reach (and realistically, this is probably the case), then the design will never be acceptable. To the authority, this result suggests that there is little room for improvement within the present design.
Finally, let us consider the situation in which the design is acceptable. The third graph of Fig. 4 shows the basic event decision worths for the threshold at 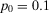 . In this case, a basic event can now make us change our mind also by its occurrence. In that case, we may shift the decision from Accept to Reject. Thus, we register a nonnull occurrence contribution to decision worth. Indeed, the correlation between the ranks induced by RAW and decision worth increases to
. In this case, a basic event can now make us change our mind also by its occurrence. In that case, we may shift the decision from Accept to Reject. Thus, we register a nonnull occurrence contribution to decision worth. Indeed, the correlation between the ranks induced by RAW and decision worth increases to 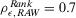 , significantly higher than in the previous cases. The correlation with RRW remains high, although lower than in the previous case, with
, significantly higher than in the previous cases. The correlation with RRW remains high, although lower than in the previous case, with 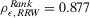 .
.
From a managerial perspective, we have the following. The design is acceptable. Hence, the risk manager can (ought to) also focus resources on avoiding the occurrence of basic events with high RAW (to remain in the acceptance area), in addition to basic events with high RRW. For the authority, unlike in the previous two cases, these results imply that care should also be devoted to basic events that have a high RAW because their occurrence can cause the preferred strategy to change from Accept to Reject.
6. DISCUSSION
Before presenting our conclusions, we would like to review some aspects that emerge from our previous analysis. A first observation is that the calculation of the decision worth of a basic event is straightforward. Because RAW and RRW are a standard output in most PSA software, the decision worth of a basic event is computed through Equation 16 directly, without additional runs of the PSA code.
A second observation concerns the scope of application of decision worth. PSA models are used in a variety of situations that go from the assignment of components to graded quality assurance programs, to the selection of maintenance and inspection strategies. The decision worth is not informative in all these applications. For instance, if we are considering an existing facility and are interested in knowing which component has the largest potential for improving system reliability (reducing risk), then the importance measure to employ is RRW. The decision worth is applicable in all those situations in which a PSA model is used in a yes/no decision where the risk metric is (1) computed through a PSA or reliability model and (2) compared against a given threshold. More generally, the decision worth is appropriate in the vast class of reliability decision problems sketched in Ref. 40, in which we have to decide whether the component should be accepted for use, if its reliability fulfils existing requirements, or rejected (Ref. 40, p. 19).
A third observation concerns results interpretation. Consider a system with n active components. All active components have a nonnull value of RAW, RRW, and Fussell-Vesely. However, only some of them may have a nonnull decision worth. In a realistic application, we may even expect that only a few basic events have a nonnull decision worth. The interpretation of this result is that those basic events are singled out by decision worth as the only decision-significant ones.
A fourth observation is linked to the third. Consider the case in which all basic events have a null decision worth. Such a result has a two-fold interpretation. On the one hand, we are reassured that the preferred alternative is stable to the success/failure of the individual basic events in the PSA model. If the decision is to reject, then no improvement (no matter how costly) on any individual basic event can lead to a decision reversal within the present design. The plant must be redesigned. Alternatively, we might wish to understand whether, instead of individual events, a group of basic events (likely a group of basic events referring to a given system) can become decision significant. If this further investigation is deemed relevant, we need to compute the joint decision worth of the basic events that correspond to the system. Such quantity is well defined, as we have seen in Section 4.5.. A computation that strictly follows the definition asks for two evaluations of the PSA model. In the first evaluation, we set the indicator variables of the basic events to unity and compute the risk metric; in the second evaluation, we set them equal to zero and compute the risk metric. We then obtain the values of the conditional probabilities 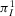 and
and 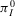 required from Equation 40.
required from Equation 40.
To illustrate, we perform additional numerical experiments on the ATR large LOCA sequence. We consider the following setup. The preferred alternative is to reject and the threshold is set at one order of magnitude lower than the risk metric (in numbers, 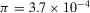 and
and 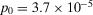 ). The decision worth of any individual basic event is now null. We then ask the question of whether there are groups of basic events that have the potential to reverse our decision. It turns out that
). The decision worth of any individual basic event is now null. We then ask the question of whether there are groups of basic events that have the potential to reverse our decision. It turns out that 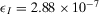 for
for 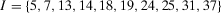 , but also
, but also 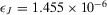 for
for 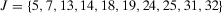 . Thus, improvements in at least 10 basic events are necessary in order to make the preferred alternative change from reject to accept. Of these basic events, basic event 5 corresponds to “no flow from the firewater injection system,” basic events 7, 13, and 14 to valve failures, basic events 18, 19, 24, 25, 31, and 32 to failures of the three deepwell pumps either to run or to start. This information would indicate to the risk manager that a thorough improvement in the reliability of the hydraulic system is necessary to reverse the decision. Whether this is doable with reasonable resources then becomes a management call.
. Thus, improvements in at least 10 basic events are necessary in order to make the preferred alternative change from reject to accept. Of these basic events, basic event 5 corresponds to “no flow from the firewater injection system,” basic events 7, 13, and 14 to valve failures, basic events 18, 19, 24, 25, 31, and 32 to failures of the three deepwell pumps either to run or to start. This information would indicate to the risk manager that a thorough improvement in the reliability of the hydraulic system is necessary to reverse the decision. Whether this is doable with reasonable resources then becomes a management call.
More in general, in several situations, we would like to recover the importance of a system from the importance of the corresponding basic events. The issue has been highlighted in works such as Refs. 13 and 63. Recently, Dutuit and Rauzy66 propose a way to extend importance measures from basic events to what they call complex components, i.e., parts of PSA models that are represented by gates rather than basic events. The recent findings in Ref. 66 are likely to provide a shortcut for the estimation of the system decision worth. This investigation is the subject of future research by the authors.
7. CONCLUSIONS
Risk-informed decision problems are frequently solved by target-oriented approaches combined with the development of probabilistic risk assessment models. Importance measures help risk managers and regulatory authorities to prioritize risk management efforts. However, risk importance measures provide limited insights in a predecision context. To overcome this impasse, this work explores the use of a value of information approach to risk-informed decision making. Applying the definition of value of information in a probabilistic risk assessment context, we obtain a new importance measure, called decision worth, which brings together the risk metric and the acceptable level of risk in one expression. The new importance measure does not require the precise specification of the decisionmaker's utility function, and does not impose additional computational burden.
The workable analytical expression allows us to characterize several properties of this sensitivity measure for individual components/basic events. Also, the importance measure is well posed for both individual basic event and groups. The risk analysis insights delivered by decision worth have been examined in detail and show that the new importance measure can help a risk manager in several ways.
ACKNOWLEDGMENTS
The authors wish to thank the Area Editor Prof. Seth Guikema and the Editor-in-Chief Prof. Tony Cox, as well as two anonymous reviewers for the perspective comments and constructive observations.
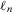 can be interpreted in alternative ways depending on the state of knowledge of the decisionmaker. Because reliability importance measures address aleatory uncertainty, our focus is on
can be interpreted in alternative ways depending on the state of knowledge of the decisionmaker. Because reliability importance measures address aleatory uncertainty, our focus is on 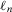 as a probability distribution expressing the credibility of the event of interest in probabilistic terms. Generalizations of risk triples have been introduced that also allow for nonprobabilistic representations of uncertainty. We refer to Refs. 53–55, as a thorough discussion is outside the scope of the present work.
as a probability distribution expressing the credibility of the event of interest in probabilistic terms. Generalizations of risk triples have been introduced that also allow for nonprobabilistic representations of uncertainty. We refer to Refs. 53–55, as a thorough discussion is outside the scope of the present work.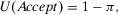 (16)
(16)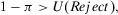 (17)
(17)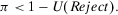 (18)
(18)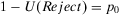 .
.Appendix A: PROOFS
Proof.Proof of Proposition 1. Because 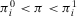 , it follows that
, it follows that  . Hence, we obtain the following:
. Hence, we obtain the following:
(1) By construction 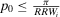 . Using
. Using 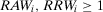 , we obtain
, we obtain 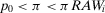 . Hence, Equation 16 results in the first line of Equation 24.
. Hence, Equation 16 results in the first line of Equation 24.
(2) Because 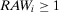 , and by construction
, and by construction 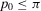 , we obtain
, we obtain 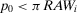 . Hence, Equation 16 results in the second line of Equation 24.
. Hence, Equation 16 results in the second line of Equation 24.
(3) Because 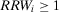 , we obtain
, we obtain 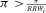 . By construction
. By construction 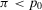 , hence it follows that
, hence it follows that  . Equation 16 results in the third line of Equation 24.
. Equation 16 results in the third line of Equation 24.
(4) Because by construction 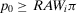 , using the fact that
, using the fact that 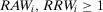 , it follows that
, it follows that 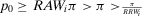 . Hence, Equation 16 results in the last line of Equation 24, since
. Hence, Equation 16 results in the last line of Equation 24, since 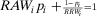 .
.
Proof.Proof of Proposition 2. Because 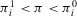 , it follows that
, it follows that 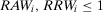 . Hence, we find that the following must hold:
. Hence, we find that the following must hold:
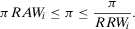 (A.1)
(A.1)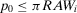 , and using the inequality A.1, we obtain that Equation 16 results in the first line of Equation 30.
, and using the inequality A.1, we obtain that Equation 16 results in the first line of Equation 30.(2) Because by construction 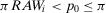 , and using the inequality A.1, we obtain that Equation 16 results in the second line of Equation 30.
, and using the inequality A.1, we obtain that Equation 16 results in the second line of Equation 30.
(3) By construction 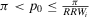 . As before, using the inequality A.1, we obtain that Equation 16 results in the third line of Equation 30.
. As before, using the inequality A.1, we obtain that Equation 16 results in the third line of Equation 30.
(4) By construction 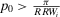 . Using the inequality A.1, and because
. Using the inequality A.1, and because 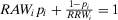 , we have that Equation 16 results in the last line of Equation 30.
, we have that Equation 16 results in the last line of Equation 30.
Proof.Proof of Lemma 1. By the total probability theorem, we can write:
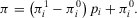 (A.2)
(A.2)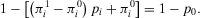 (A.3)
(A.3)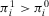 , then we have that from
, then we have that from 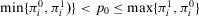 follows
follows 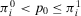 . Hence, we obtain:
. Hence, we obtain:
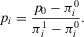 (A.4)
(A.4)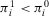 , then
, then 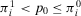 ; hence, the ratio is still positive and equal to Equation A.4.
; hence, the ratio is still positive and equal to Equation A.4.
Proof.Proof of Proposition 3. By combining Equation 16 and Equation A.3, we obtain:
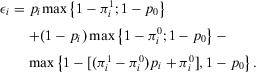 (A.5)
(A.5)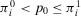 , we obtain
, we obtain 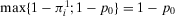 and
and 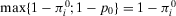 . If
. If 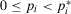 , that is, we accept the plant (by Lemma 1), the
, that is, we accept the plant (by Lemma 1), the 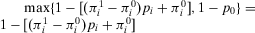 . Hence, we can rewrite Equation A.5 as follows:
. Hence, we can rewrite Equation A.5 as follows:
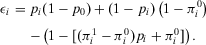 (A.6)
(A.6)With simple algebraic manipulations, we obtain 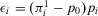 . This proves the first line of Equation 33.
. This proves the first line of Equation 33.
When 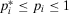 , that is, when we reject the plant (by Lemma 1), we obtain that the
, that is, when we reject the plant (by Lemma 1), we obtain that the 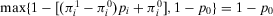 . Hence, we can rewrite Equation A.5 as follows:
. Hence, we can rewrite Equation A.5 as follows:
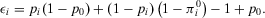 (A.7)
(A.7)Rearranging, we obtain 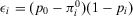 , which is what we wanted to prove (second line of Equation 33).
, which is what we wanted to prove (second line of Equation 33).
(B) Because by assumption 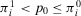 , we obtain that
, we obtain that 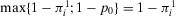 and
and 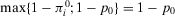 .
.
If  , that is, we reject the plant (by Lemma 1), we get that
, that is, we reject the plant (by Lemma 1), we get that 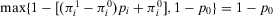 . Hence, we can rewrite Equation A.5 as follows:
. Hence, we can rewrite Equation A.5 as follows:
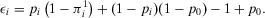 (A.8)
(A.8)With simple algebraic manipulations, we obtain 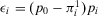 , which is what we wanted to prove (first line of Equation 34).
, which is what we wanted to prove (first line of Equation 34).
When 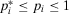 , that is, we accept the plant (by Lemma 1), we get that
, that is, we accept the plant (by Lemma 1), we get that 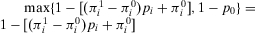 . Hence, we can rewrite Equation A.5 as follows:
. Hence, we can rewrite Equation A.5 as follows:
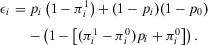 (A.9)
(A.9)Rearranging, we obtain 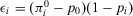 , which is what we want to prove (second line of Equation 34).
, which is what we want to prove (second line of Equation 34).
Proof.Proof of Proposition 4. If component i is in parallel with the rest of the system, we have:
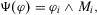 (A.10)
(A.10)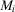 represents the rest of the system. Thus:
represents the rest of the system. Thus:
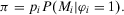 (A.11)
(A.11)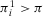 . Since
. Since 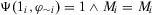 , we get
, we get  , hence:
, hence:
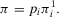 (A.12)
(A.12)We have to show that if 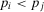 , then
, then 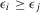 . If
. If 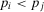 , then it follows, using Equation A.12, that
, then it follows, using Equation A.12, that 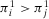 . Hence, there are three possible cases:
. Hence, there are three possible cases: 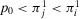 ,
, 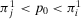 , and
, and 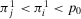 .
.
Case 1. If 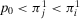 , then by Equation 37, we obtain:
, then by Equation 37, we obtain:
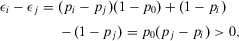 (A.13)
(A.13)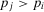 by assumption.
by assumption.Case 2. If 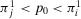 , then by Equation 37, we obtain:
, then by Equation 37, we obtain:
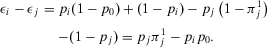 (A.14)
(A.14)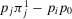 as
as 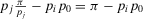 . Since
. Since 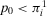 by construction, it results
by construction, it results 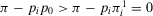 ; hence, it follows that
; hence, it follows that  .
.Case 3. If 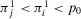 , then by Equation 37, we obtain:
, then by Equation 37, we obtain:
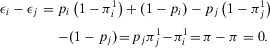 (A.15)
(A.15)
Proof.Proof of Proposition 5. If a component i is in series with the rest of the system, we get that:
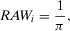 (A.16)
(A.16)Substituting Equation A.16 into Equation 16, we get:
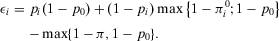 (A.17)
(A.17)Consider now a second component j in series with the rest of the system. Then, the risk metric is of the form:
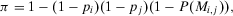 (A.18)
(A.18)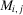 is the structure function of the rest of the system. Then, assuming independent failures, we have:
is the structure function of the rest of the system. Then, assuming independent failures, we have:
 (A.19)
(A.19)From Equation A.19, it follows that:
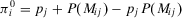 (A.20)
(A.20)and
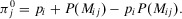 (A.21)
(A.21)If i and j are in series with the rest of the system, we want to prove that if 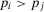 , then
, then 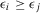 . By subtracting Equation A.20 from Equation A.21, we obtain:
. By subtracting Equation A.20 from Equation A.21, we obtain:
 (A.22)
(A.22)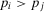 by assumption. Hence, if
by assumption. Hence, if 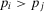 , it follows that
, it follows that 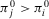 . We are going to see three cases:
. We are going to see three cases: 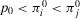 ,
, 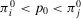 , and
, and 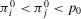 . We show that in all these three scenarios,
. We show that in all these three scenarios, 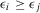 .
.Case 1. If 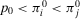 , by Equation A.17, we obtain:
, by Equation A.17, we obtain:
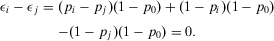 (A.23)
(A.23)Case 2. If 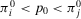 , by Equation A.17, we obtain:
, by Equation A.17, we obtain:
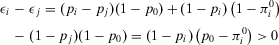 (A.24)
(A.24)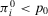 .
.Case 3. If 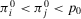 , by Equation A.17, we obtain:
, by Equation A.17, we obtain:
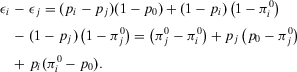 (A.25)
(A.25)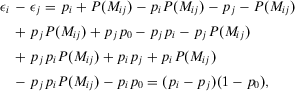 (A.26)
(A.26)which is greater than zero since  by assumption. This ends the proof.
by assumption. This ends the proof.



 and
and 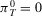 , we obtain:
, we obtain: