Production and Operations Management
Volume 31, Issue 5 pp. 2306-2323
ORIGINAL ARTICLE
Open Access

Queuing safely for elevator systems amidst a pandemic

Sai Mali Ananthanarayanan, 

Corresponding Author

Sai Mali Ananthanarayanan

Department of Industrial Engineering and Operations Research and Data Science Institute, Columbia University, New York, New York, USA

Correspondence

Sai Mali Ananthanarayanan, Department of Industrial Engineering and Operations Research and Data Science Institute, Columbia University, New York, NY 10027, USA.

Email: [email protected], [email protected]

Search for more papers by this author
Charles C. Branas, 

Charles C. Branas

Department of Epidemiology, Columbia University, New York, New York, USA

Search for more papers by this author
Adam N. Elmachtoub, 

Adam N. Elmachtoub

Department of Industrial Engineering and Operations Research and Data Science Institute, Columbia University, New York, New York, USA

Search for more papers by this author
Clifford S. Stein, 

Clifford S. Stein

Department of Industrial Engineering and Operations Research and Data Science Institute, Columbia University, New York, New York, USA

Search for more papers by this author
Yeqing Zhou, 

Yeqing Zhou

Department of Industrial Engineering and Innovation Sciences, Eindhoven University of Technology (TU/e), Eindhoven, The Netherlands

Search for more papers by this author
First published: 04 February 2022
https://doi.org/10.1111/poms.13686

Handling editor: Michael Pinedo

Accepted by Michael Pinedo, after two revisions.

Abstract

The requirement of social distancing during the COVID-19 pandemic has presented significant challenges for high-rise buildings, which heavily rely on elevators for vertical transportation. In particular, the need for social distancing has reduced elevator capacity typically by at least two-thirds or as much as over 90 % $90\%$ of the normal amount. This reduction is a serious concern, as reduced elevator capacities cause large queues to build up in lobbies, which makes social distancing difficult and results in large wait times. The objective of this study is to safely manage the elevator queues by proposing simple, technology-free interventions that drastically reduce the waiting time and length of lobby queues. We use mathematical modeling, epidemiological expertise, and simulation to design and evaluate our interventions. The key idea is to explicitly or implicitly group passengers that are going to the same floor into the same elevator as much as possible. In the Cohorting intervention, we attempt to find passengers going to the same floor as the first person in the queue. In the Queue Splitting intervention, we create a different queue for different groups of floors. Based on simulation and analytical findings, Cohorting and Queue Splitting can significantly reduce queue length and wait time, while also maintaining safety from viral transmission in otherwise crowded elevators, building lobbies, and entrances. These interventions are generally accessible for many buildings since they do not require programming the elevators, and rely on only using signage and/or a queue manager to guide passengers.

1 INTRODUCTION

The COVID-19 pandemic has made it imperative to design interventions for people to stay safe in potentially crowded areas. For high-rise buildings, social distancing reduces the capacity of elevators, cutting the number of passengers per elevator by two-thirds or as much as over 90 % $90\%$ of the normal amount (Swinarski, 2020, 2021; Weber, 2020). Reduced elevator capacity can cause large lobby queues and long wait times, resulting in crowding and reduced social distancing (Smith, 2020; van Rijn et al., 2020; Weber, 2020; Wilson, 2020). With no interventions and reduced capacity on elevators, the increased waiting times and queue lengths in the lobby could pose significant safety risks. Thus, an intervention to the public health problem of safely managing queues for elevator systems amidst a pandemic is needed (our team is composed of operations researchers and an epidemiologist). In fact, this project was directly in collaboration with the NYC Mayor's Office of the Chief Technology Officer and the Department of Citywide Administrative Services. These offices had continuous input into our work throughout the process and allowed us to conduct several on-site visits with building managers, where we talked to frontline staff and gathered input. We also presented our findings multiple times to a variety of agency staff, developed an instructional video, and provided open source code that can be tailored to the needs of different types of buildings.

One can broadly consider two major forms of interventions based on (i) changing passenger behavior and (ii) elevator artificial intelligence. A variety of technological innovations from elevator companies and building management have been considered during the pandemic (Wilson, 2020). In many elevator systems, especially in older ones, changing the algorithms and technology of how the elevators navigate through the building is challenging or infeasible, and would require long-term planning and expensive modifications. Thus, in order to safely manage how passengers use and board elevators, we focus on technology-free interventions, which should be more accessible and practical for an overwhelming majority of buildings with elevators. We specifically provide a detailed simulation study in addition to theoretical results of queuing systems to model and assess the efficacy of our various interventions.

Currently, many elevator systems take a hands-off approach to managing the flow of people to elevators, resulting in something that resembles first-come first-serve (FCFS) (Fujino et al., 1997). Our simulations, using data calibrated from a large New York City government building, show that such a hands-off approach will lead to large and unsafe queues if building occupancy returns to prepandemic levels while elevator capacities are still reduced due to social distancing. Thus, it is imperative that we design interventions that use the elevators more efficiently—getting passengers to their destination at a faster aggregate rate (higher throughput)—by more carefully managing who uses which elevator when. For instance, we shall consider interventions where we try to get passengers going to the same or nearby floor to ride an elevator together as well as interventions where passengers are encouraged to walk up or down a floor after riding the elevator.

1.1 Contributions

The social distancing requirement during a pandemic may lead to unsafe queues in the lobby with no interventions. Using mathematical modeling, epidemiological expertise, and simulation, we design and evaluate simple interventions to load passengers in elevators that can drastically reduce the length of lobby queues amidst a pandemic. The proposed interventions increase efficiency of the elevator system, and are effective beyond the constraints imposed by a pandemic, making them useful even after the pandemic to manage lobby queues. Our interventions do not require programming the elevators, and rely on using only signage and/or a queue manager (QM) to guide passengers. Our interventions are effective in reducing both the number of stops per trip and the travel distance per trip. Next, we outline our contributions in detail.
  • 1. We develop a general, open-sourced simulation model that captures many of the details of elevator systems and allows us to study the impact of various interventions and queuing behavior. Our simulation model allows us to specify the number of elevators, capacity, elevator speed, and boarding times, and to measure and visualize the queue length and wait time of elevator systems for the various interventions we consider. We primarily focus on a case study calibrated by data from a large government building in New York City that is in need of managing elevator traffic amidst the COVID-19 pandemic.
  • 2. We propose an intervention we call Cohorting, in which we attempt to find any and all passengers going to the same floor as the first person in the queue. Simulations show Cohorting reduces waiting time for passengers and the number of people in the lobby (queue length) significantly. In limited lobby spaces, we recommend the Cohorting with Pairing intervention, where we pair passengers going to the same floors. Pairing is practically easier to implement as it only requires matching two people at a time (rather than four, for instance). We also explore the impact of some passengers' willingness to walk up or down one floor from their destination. The queue length can be further reduced if just a small fraction of passengers are willing to walk.
  • 3. We also propose the Queue Splitting intervention where we create a different queue for different groups of floors and load the elevators from queues in a round-robin fashion. The travel time of elevators is naturally reduced since passengers are likely to be going to the same or nearby floors. Queue Splitting requires less management efforts comparing to Cohorting, and splitting into just two groups achieves comparable performance to Cohorting in our case study.
  • 4. We analytically investigate the reason behind the strong performance of Cohorting and Queue Splitting using a technique from queuing theory known as stability analysis. Specifically, we characterize the system parameters required for each intervention to ensure that the queues do not increase in length over time, that is, the queues are stable. Our theoretical analysis reveals that these interventions can effectively reduce the average distance traveled and the number of stops per elevator trip.

1.2 Related literature

Although researchers have studied algorithms for managing elevator systems (Al-Sharif et al., 2012; Barney & Al-Sharif, 2015; Barney & Dos Santos, 1975; Fujino et al., 1997; Lee et al., 2009; Pepyne & Cassandras, 1997), to the best of our knowledge, there is not much literature on designing elevator systems with pandemic safety considerations.

Our simulation model is based on queuing theory. A discrete event simulation (Ross, 2013) models the operation of a system as a sequence of events in time, thus we utilize a detailed simulation to estimate mean wait times and queue lengths. Previous works that utilize queuing theory in elevator systems (Alexandris, 1977; Barney & Al-Sharif, 2015; Finschi, 2010), and papers that use simulation for elevator traffic studies (Al Sukkar et al., 2017; Hakonen & Siikonen, 2008) do not consider the impact of reducing capacities while maintaining service quality. A recent paper in the context of the COVID-19 pandemic (Swinarski, 2021) models and predicts elevator traffic in a university classroom building when passengers mainly travel in the predetermined short time periods between two classes, with known class schedules and traffic patterns. The authors discuss an intervention that directs passengers to sort themselves into pairs of passengers with a shared destination floor, which can improve the performance, but is not as effective as moving classes to lower floors or staggering course start times. In this paper, we consider general building types with random arrival and destination patterns. In Mulvany and Randhawa (2021), the authors consider breaking FCFS rules in exchange for fairness considerations, whereas we break FCFS in exchange for safety reasons and improved performance.

The stability analysis in this paper is built upon literature in queuing and stochastic processing networks (Dai & Harrison, 2020; Dai & Li, 2003). The interventions in the paper are designed specifically for an elevator system, while they share similarities to some well-studied dispatch policies in multiclass queuing networks. The Cohorting intervention resembles the first-in-first-out dispatch policy (Bramson, 1996) if we consider passengers going to the same floor as a class and an empty server always picks a class whose head-of-line job arrived first. The Queue Splitting intervention is essentially a round-robin dispatch policy in the multiclass queuing literature, which is related to fair queuing policies widely studied in the computer network literature; see, for example, Demers et al. (1989) or Parekh and Gallager (1994).

1.3 Organization

We introduce the simulation model of the elevator system in Section 2 and present the simulation results in Section 3. Section 4 analyzes the stability condition for each intervention we propose and compares the results to FCFS. In Section 5, we discuss some practical issues and solutions for the Cohorting intervention. Finally, we conclude and discuss ideas for future work in Section 6.

2 SIMULATION MODEL

In this section, we describe our modeling framework. In particular, the model considers moving passengers upwards through a building from a lobby, which presents the biggest challenge for social distancing in a high-rise building. We study low-tech solutions (requiring no programming of elevators and no knowledge of internal elevator algorithms) and describe interventions to manage the queue of passengers in the lobby. We focus on analyzing solutions that work for high volume periods, for example, morning rush hour, lunchtime, and so forth, where social distancing is a challenge. These busy periods are referred to as uppeak (Barney & Dos Santos, 1975) and typically an elevator system working efficiently during the morning uppeak can handle interfloor traffic and downpeaks without any issues (Barney & Al-Sharif, 2015). Below we describe the model we use in the simulation. We will simplify some of the assumptions when deriving the analytical results in Section 4.

We model a building as having a lobby on floor 1, m $m$ destination floors denoted 2 , … , m + 1 $2,\ldots , m+1$ , and N $N$ elevators denoted 1 , … , N $1,\ldots , N$ . We assume passengers wanting to go to floor j $j$ at time t $t$ arrive at the lobby according to a non-stationary Poisson process with arrival rate λ j ( t ) $\lambda _j(t)$ . The Poisson assumption for individual arrivals is considered a good approximation to the arrival process (Alexandris, 1977; Barney & Al-Sharif, 2015). Each of the N $N$ elevators has a capacity of C $C$ , the number of people that the elevator can safely transport while ensuring social distancing.

Remark 1. (SAFE CAPACITIES)The capacity C $C$ of the elevators should be set based on the physical dimensions of each elevator. Social distancing needs to be taken into account to put floor markers for passengers to stand inside an elevator, for example, opposite corners of a diagonal for loading two people, or all corners for loading four people. In general, there is a fundamental trade-off between setting a lower elevator capacity and increased queues in the lobby.

In many high-rise buildings, elevators are constrained to certain floors so we let S ( n ) $S(n)$ denote the set of destination floors that elevator n $n$ can serve. If there is no restriction on the service range of the elevator n $n$ , then S ( n ) = { 2 , … , m + 1 } $S(n) = \lbrace 2 ,\ldots , m+1\rbrace$ . We assume the elevator travel time per floor ν $\nu$ is constant and the (de)boarding times of the elevator are a function of the number of people k $k$ that are (de)boarding, denoted by B o a r d i n g T i m e ( k ) $BoardingTime(k)$ . The (de)boarding time B o a r d i n g T i m e ( k ) $BoardingTime(k)$ is a constant time ω $\omega$ to open and close the elevator door, and additional time depending on the number of passengers k $k$ entering (exiting). For our theoretical results in Section 4, we assume that the service time only depends on ν $\nu$ and ω $\omega$ . But for the purpose of creating a realistic simulation tool we describe the elevator dynamics in greater detail.

The travel time to start at floor j 1 $j_1$ and stop at floor j 2 $j_2$ is T ( j 1 ; j 2 ) = ν ( j 2 − j 1 ) $T(j_1; j_2) = \nu (j_2- j_1)$ . If k $k$ (at most C $C$ ) passengers with destinations d 1 ≤ d 2 ≤ ⋯ ≤ d k ${d}_{1}\le {d}_{2}\le \cdots \le {d}_{k}$ board an elevator n $n$ at the lobby, we can create a count F ⃗ = { F 2 , … , F m + 1 } $\vec{F} = \lbrace F_2,\ldots ,F_{m+1}\rbrace $ of the number of passengers deboarding at each floor. Note that ∑ j = 2 m + 1 F j = k $\sum _{j=2}^{m+1} F_j = k$ , the number of passengers boarding at the lobby. The floor H : = d k $H := d_k$ is typically referred to as the highest reversal floor in the literature (Lee et al., 2009), and is useful in calculating the round trip time. We also need to approximate inter-floor traffic (including down traffic), which we do by using an estimated multiplier β $\beta$ (e.g., β = 1.3 $\beta = 1.3$ , which means it takes 30 % $30\%$ longer down) from the time the elevator takes to drop off the last passenger. Then the ascent time A s c e n t T i m e ( F ⃗ ) $AscentTime(\vec{F})$ without accounting for stops, is given by A s c e n t T i m e ( F ⃗ ) = T ( 1 ; d k ) $AscentTime(\vec{F}) = T(1;d_k)$ , the time spent making stops is S t o p T i m e ( F ⃗ ) = ∑ j = 2 m + 1 B o a r d i n g T i m e ( F j ) $StopTime(\vec{F}) = \sum _{j=2}^{m+1} BoardingTime(F_j)$ , and the descent time from when the last passenger has deboarded is D e s c e n t T i m e ( F ⃗ ) = β × A s c e n t T i m e ( F ⃗ ) = β T ( 1 ; d k ) $DescentTime(\vec{F}) = \beta \times AscentTime(\vec{F}) = \beta T(1;d_k)$ . The time to board at the lobby is B o a r d i n g T i m e ( F ⃗ ) = B o a r d i n g T i m e ( ∑ j = 2 m + 1 F j ) $BoardingTime(\vec{F})=BoardingTime(\sum _{j=2}^{m+1} F_j)$ . Thus the total round trip time R o u n d T r i p T i m e ( F ⃗ ) $RoundTripTime(\vec{F})$ of an elevator is
RoundTripTime ( F ⃗ ) = BoardingTime ( F ⃗ ) + AscentTime ( F ⃗ ) + StopTime ( F ⃗ ) + DescentTime ( F ⃗ ) . \begin{eqnarray} &&\hbox{\it RoundTripTime}\,(\vec{F}) = \hbox{\it BoardingTime}\,(\vec{F}) + \hbox{\it AscentTime}\,(\vec{F})\nonumber\\ &&\qquad\qquad\qquad\quad +\ \hbox{\it StopTime}\,(\vec{F}) + \hbox{\it DescentTime}\,(\vec{F}). \end{eqnarray} (1)

To measure the performance of different interventions in the simulation, we consider the following metrics: average waiting time of a passenger at the lobby (measured at every time unit), average number of passengers at the lobby (queue length, measured at every time unit), and the average round trip time of elevators. We also explore qualitative considerations like human and material resources needed, ease of understanding for managers and passengers, and perceived inequity (Berry et al., 2002; Larson, 1987) (e.g., when an intervention lets some passengers skip ahead of others).

We want to mathematically characterize the performance of the system. Let W i $W_i$ denote the wait time for passenger i $i$ . Let N ( t ) $N(t)$ denote the number of people waiting in the lobby at time t $t$ . In a classic service system, the traditional goal is to minimize the total (average) expected wait time, that is, E [ ∑ i W i ] $\mathbb {E}[\sum _i W_i]$ . However, the primary objective in the context of a pandemic is to maximize safety, which corresponds to minimizing the number of people in the lobby that are waiting for an elevator. Metrics of interest are the expected number of passengers in the lobby over a time horizon of T $T$ periods, 1 T ∫ 0 T E [ N ( t ) ] d t $\frac{1}{T} \int _{0}^T \mathbb {E}[N(t)] d t$ , and the maximum queue length, max t N ( t ) $\max _t N(t)$ .

Finally, we describe our system dynamics in the simulation. Passengers arrive at the (first floor) lobby according to the Poisson process λ j ( t ) $\lambda _j(t)$ defined above and queue in a line or multiple lines, depending on the intervention being implemented. When an elevator is available at the lobby (either there is a free elevator already or passengers wait for an elevator to arrive), it is loaded according to the rules of the intervention, up to the capacity limit C $C$ of the elevator. The logic of each intervention can be found in Section 2.1. At constant intervals ( Δ t ${\Delta}\hspace*{0.05em}\hspace*{0.05em}t$ seconds), we update the system by loading available elevators in the lobby with passengers already in line(s) using the rules of the intervention. Once loaded, the elevators make stops corresponding to destinations of the passengers, and finally come back to the lobby to be loaded again.

We shall refer to an instance as the sequence of random passenger arrival times and destinations generated during one simulated rush hour morning. We record all quantitative metrics listed above. We simulate 100 independent random instances for every set of parameters and report the average performance for each metric. The code for the simulations is publicly available online.

2.1 Interventions

The standard way most elevator systems operate is akin to first-come first-serve (FCFS). However, moving toward safe interventions requires moving away from FCFS, which means that some people may be allowed to “cut in line” in order to decrease queue lengths and waiting times, while serving as many passengers as possible. Our interventions may rely on a queue manager (QM) for implementation, where the QM can be thought of as a personnel or a device with a screen.

First, we discuss the status quo - FCFS - where the passengers who arrive at the lobby first will enter an elevator first. FCFS for elevator loading follows the standard social norm of queuing. There are obvious advantages for using the status quo, as it ensures fairness and requires no management of the queue. However, even pre-COVID especially during rush hours such as morning and lunchtime- the lobby may be crowded with passengers, elevators are fully loaded, and they may make many stops during a trip. With a social distancing rule during a pandemic such as COVID-19, the dramatically reduced elevator capacity could cause a severe increase in congestion in the lobby and thus increase the risk of disease spread.

Next, we propose the intervention, which we call Cohorting, which seeks to group together passengers going to the same floor. In this intervention, passengers line up in a queue in order of arrival. When an elevator arrives, the first passenger boards. Then, the QM asks if anyone in the queue is going to the same floor as the first passenger and then they board as well (according to their arrival order). This creates a cohort going to the same floor (such passengers are allowed to “cut in line”). If there is still capacity in the elevator, then the passenger at the front of the queue enters and the QM again allows passengers going to the same floor to board the elevator. This process is repeated until the elevator is full or the queue is empty. See Algorithm 1 in Supporting Information Section EC.4 for a detailed simulation pseudocode. Cohorting is the best-performing intervention to improve efficiency (as seen in Section 4), but requires a QM to interact effectively with the queue to learn where passengers are going. It may be difficult for the QM to know the destinations of passengers that are far back in the queue. Thus, in Section 5 we consider easier-to-implement variants where we can only communicate with the first few people in the queue and where we only try to cohort in pairs.

The next intervention we propose is Queue Splitting, where we form a separate queue for disjoint groups of floors. In Queue Splitting, floors are assigned to different groups, where each group consists of consecutive floors, for example, 2–8 and 9–16. We create a queue corresponding to each floor group. Arriving passengers join a queue corresponding to their floor group, and elevators are boarded from the queues in a round-robin fashion (possibly with the help of a QM). For instance, there can be four queues, each corresponding to six floors. When any elevator arrives, one of the queues sends the first C $C$ passengers in line to it. If there are less than C $C$ in the queue, then the next queue sends passengers and so on. The queues are chosen in a round-robin fashion (or in a way to dynamically balance the length of each queue). See Algorithm 2 in Supporting Information Section EC.4 for a detailed simulation pseudocode. By creating queues for every floor group, the travel time of elevators is naturally reduced since passengers are likely to be going to the same or nearby floors, which achieves an effect similar to Cohorting. The number of stops is also reduced compared to FCFS by grouping passengers in a limited floor range. This intervention does not require any programming of the elevator system, only requiring organizing the lobby space. A schematic showing the implementation of Cohorting and Queue Splitting is shown in Figure 1.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Illustrating the Cohorting and Queue Splitting interventions. Note: Passengers enter from the left and are guided by the queue manager (QM) to the elevators. Those exiting the elevator leave the building on the right, to ensure social distancing from entering passengers. In this example, the QM is loading an elevator in the lobby. We indicate the passengers who will board the next elevator using dark green circles. Under the Cohorting intervention in (a), the first elevator will stop at two floors, which are the destinations of the first and second passenger. Under the Queue Splitting intervention in (b), the QM is first loading from the queue for floors 2–5, and thus the elevator will stop at three floors

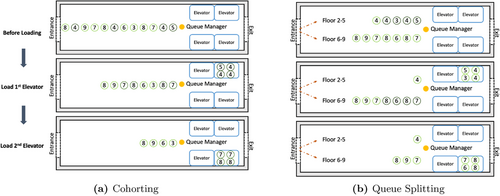
Finally, we discuss the Allocation intervention, where each elevator is assigned to only go to predetermined floors. This intervention can be accomplished by changing the elevator control system, or simply by adding signs on each elevator door. We propose several floor allocation interventions, including partitioning into ranges of floors, or splitting into odd and even floors. For instance, one building in our case study has 14 elevators and 24 destination floors to serve. We can split the 14 elevators into 2 groups of 7, where each group goes to 12 floors. Another possibility is to split into odd and even floors, which may encourage people to use one level of stairs to reach their final destination. The key intuition behind the allocation intervention is that each elevator, or each set of elevators is only serving a small range of floors. By doing so, the chances of two people in the same group going to the same or nearby floor increases, compared to FCFS. Thus, Allocation has an effect that resembles Cohorting and Queue Splitting, leading to a reduction in travel and deboarding time. It is also perhaps the easiest intervention to implement. In fact, many buildings are using Allocation to create a separation of high floors and low floors in practice, where some of the elevators only serve high floors and the others serve low floors. In this case, Cohorting and Queue Splitting can also be applied in addition to the Allocation intervention (we provide simulation results in Supporting Information, Section EC.3.2). We also note that Queue Splitting and Allocation are less likely to be perceived as unfair, as no one visibly cuts the line although it is possible that passengers do not board in FCFS order.

In this paper, we focus on the performance of Cohorting and Queue Splitting because Allocation does not perform well compared to the other two interventions. We only discuss the performance of the allocation intervention in Supporting Information Section EC.3.

3 SIMULATION RESULTS

In this section, we describe our findings via simulation from three examples corresponding to a small, medium, and large building. The discussions in this section are centered around the large building, while the small and medium buildings are discussed in Supporting Information, Section EC.2. The large building is calibrated using data from a large government building in New York City that is planning for reopening and urgently needs to manage elevator traffic amidst the COVID-19 pandemic. It is a historical building with a legacy elevator system, so only technology-free solutions can be implemented. Moreover, this building is heavily used and had more than 5500 people (staff and visitors) accessing it on a prepandemic day during the rush hour. The building has 25 floors and the 28 elevators are split into two elevator banks (North and South). Without loss of generality, we consider the South bank, where 14 elevators serve about 2750 visitors during the morning rush hour from 8 a.m. to 10 a.m. ( N = 14 , m = 24 $N = 14, m = 24$ ). In the two-hour period, we assume the arrival process is a stationary Poisson process with an arrival rate 2750 / 7200 ${2750/7200}$ passengers per second. Arriving passengers are equally likely to go to any of floors 2 through 25. Based on the physical dimensions of the elevators, the capacity is C = 4 $C=4$ . Every elevator n $n$ serves all floors, that is, S ( n ) = { 2 , … , 25 } $S(n) = \lbrace 2,\ldots ,25\rbrace$ . It takes 15 s for one passenger to (de)board, and an additional 2 s per extra passenger. Thus, B o a r d i n g T i m e ( k ) = 15 + 2 ( k − 1 ) $BoardingTime(k) = 15 + 2(k-1)$ s for k $k$ passengers in an elevator. The elevators have a constant travel time per floor of 1.4 s/floor, hence the time to travel from floor j 1 $j_1$ to floor j 2 $j_2$ is T ( j 1 ; j 2 ) = 1.4 ( j 2 − j 1 ) $T(j_1;j_2) =1.4(j_2-j_1)$ s. The speed multiplier β $\beta$ to account for interfloor traffic is β = 1.3 $\beta =1.3$ . All parameters used for our simulations can be found in Supporting Information, Section EC.1. Note that the queues will all eventually diminish after the end of rush hour because the passenger traffic goes down, but we do not simulate this. In the figures below, we simulate only until the end of rush hour (peak) and hence the queue decline after this time is not shown.

The results for FCFS, Cohorting, and Queue Splitting (two queues with floor ranges 2–13 and 14–25) on the large building are presented in Figure 2. One can observe that for FCFS, the number of people in the lobby grows linearly during the rush hour period we simulate. In fact, by the end of the rush hour, there can be up to 100 people in the queue and wait times can reach almost 5 min. Thus, an intervention is absolutely necessary to avoid this unsafe buildup of passengers. We see that Cohorting has a much lower range of queue lengths and waiting times compared to FCFS. Cohorting has a maximum queue length of around 12, which is over a factor of eight times smaller than the maximum queue length of FCFS. In other words, a passenger arriving at any point in the rush hour is likely to experience a queue of at most 12 people with the Cohorting intervention.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Comparison of interventions for our large building case study. Note: We run 100 independent random instances and report the average performance. (a) Plot of percentage of passengers experiencing different waiting times in the lobby across interventions. (b) Plot of percentage of time different queue lengths in the lobby occur (measured every 1 s) across interventions. (c) Plot of queue length in the lobby from beginning to end of the busy period across interventions

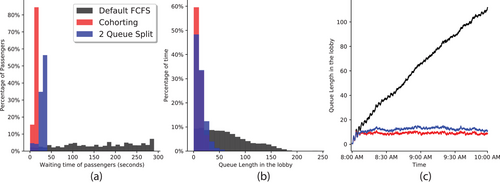
In the Queue Splitting intervention, we do not allocate any elevators but rather form a queue for every group of floors. In Figure 2, we see that Queue Splitting (into two queues) has a much lower range of queue lengths and waiting times compared to FCFS. Similar to Cohorting, the maximum queue length is around 15. In other words, a passenger arriving at any point in the rush hour is likely to experience a queue of less than 15 people in the 2 Queue Split intervention, which is over a factor of five times smaller than the maximum queue length of FCFS. One can see in Figure 2 that the maximum wait times and total queue length are relatively stable over time for this intervention, and with average reductions of over 80 % $80\%$ compared to the default FCFS. Thus, a 2 Queue Split achieves comparable performance to Cohorting, the best intervention.

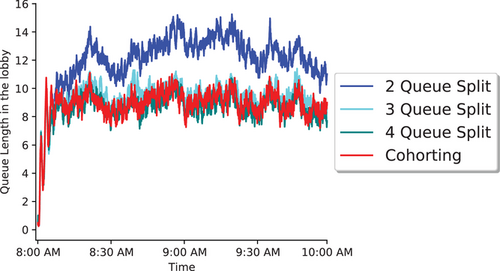
We also consider the effect of the number of queues used in Queue Splitting, with the results displayed in Figure 3 for the large building. The floor ranges for each queue are split evenly: { ( 2 − 13 ) , ( 14 − 25 ) } $\lbrace (2-13),(14-25)\rbrace$ in the 2 Queue Split, { ( 2 − 9 ) , ( 10 − 17 ) , ( 18 − 25 ) } $\lbrace (2-9),(10-17),(18-25)\rbrace$ in the 3 Queue Split, and { ( 2 − 7 ) , ( 8 − 13 ) , ( 14 − 19 ) , ( 20 − 25 ) } $\lbrace (2-7),(8-13),(14-19),(20-25)\rbrace$ in the 4 Queue Split. In this building, 4 Queue Split works better than 2 and 3 Queue Splits (higher number of queue splits achieves an effect similar to Cohorting). There is a marked improvement (Figure 3) from 2 to 3 Queue Split and only a marginal return on 4 Queue Split (which has almost the same queue length performance as Cohorting) instead of 3 Queue Split. In fact, the more queues we create, the more efficient the system becomes. However, the trade-off is that more queues require a more complex operation and more space in the lobby, especially for horizontal separation between the queues. We find that simply splitting into two to four queues already recovers most of the benefit in comparison to the Cohorting intervention.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Impact of Cohorting and Queue Splitting intervention into 2 , 3 $2,3$ , and 4 $\hskip.001pt 4$ queues for our large building case study. Note: We plot the queue length in the lobby (measured every 1 s) throughout rush hour. We run 100 independent random instances and report the average performance

3.1 Difference in round trip time

The round trip time of an elevator trip (service time) determines the efficiency of the elevator system. The shorter the round trip time is, the faster the elevator can come back and serve more people. We record the service time profile for FCFS, Cohorting, and 2 Queue Split in the simulation in Figure 4.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Comparison of interventions using round trip for our large building case study. Note: We run 100 independent random instances and report the average performance. (a) Plot of percentage of elevator trips with different round trip times (service times) across interventions. (b) Reporting average service time and average number of passengers per elevator trip for all interventions

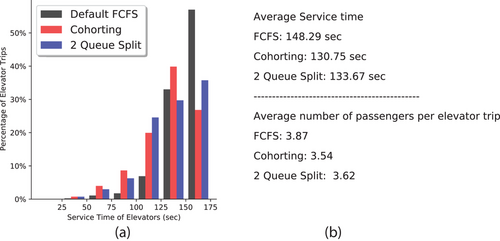
In Figure 4, Cohorting and Queue Splitting have a lower average round trip time (131 and 134 s, respectively) than FCFS (148 s). In terms of number of trips they can complete in the given time period, Cohorting and 2 Queue Split are much better than FCFS, indicating that our proposed interventions indeed make the elevator trips more efficient. Our main indicator of system performance, queue length, is typically inversely related to average service time in classic queuing models (Ross et al., 1996), and a seemingly small improvement in the round trip time as in Figure 4 has a big impact on system performance.

In Figure 4b, we also report the average number of passengers per elevator trip across interventions. With capacity 4, elevators under FCFS carry 3.87 passengers per trip on average, so most trips are at full capacity. Elevators under Cohorting carry only 3.54 passengers per trip on average and similarly under the 2 Queue Split intervention, elevators carry 3.62 passengers per trip on average. Our proposed interventions make the elevators more efficient compared to FCFS, using less of the elevator capacity on average per trip.

The round trip time of an elevator, as seen in (1) and discussed in detail in Section 4 is primarily determined by the number of stops S $S$ made and the highest reversal floor H $H$ of the trip. Therefore, we analyze the performance of different interventions by comparing the quantities S $S$ and H $H$ in Figure 5.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Comparison of interventions using number of stops and highest reversal floor of elevator trips for our large building case study. Note: We run 100 independent random instances and report the average performance. (a) The percentage of elevator trips with different number of stops made (or equivalently the number of buttons pressed in each trip by the passengers) across interventions. (b) The percentage of elevator trips with different highest reversal floor H $H$ across interventions. (c) Reporting average over 100 instances of the number of stops and highest reversal floor for all interventions. (d) Reporting standard deviation of the estimated mean (over 100 instances) of number of stops S $S$ and highest reversal floor H $H$ for all interventions

In Figure 5a, we plot the distribution of S $S$ , that is, the percentage of elevator trips with different number of stops made (or equivalently the number of buttons pressed in each trip by the passengers) across interventions. In FCFS, about 75 % $75\%$ of the trips make four stops. In Cohorting only about 25 % $25\%$ of the trips make four stops and about 70 % $70\%$ elevator trips make only two or three stops, which leads to shorter round trip times. 2 Queue Splitting does not perform as well as Cohorting, although it is better than FCFS, with more than 50 % $50\%$ of the trips making four stops and 40 % $40\%$ rides making only two or three stops.

In Figure 5b, we plot the distribution of H $H$ , that is, the percentage of elevator trips with different highest reversal floors across interventions. In the distribution of H $H$ for FCFS, more percentage of elevator trips reverse at the topmost floors than other interventions. For instance, about 50 % $50\%$ of FCFS trips reverse in the last four floors ( H ≥ 23 $H\ge 23$ ), while only 40 % $40\%$ of trips under Cohorting do so, suggesting that elevators come back to the lobby faster in Cohorting. 2 Queue split has similar distributions of H $H$ among the destination ranges of the two mini-queues and hence, 40 % $40\%$ of the trips have H $H$ at most 13, which is much better than Cohorting (less than 20 % $20\%$ of trips) and FCFS (less than 10 % $10\%$ of trips) for the same range.

In Figure 5, we report the average of the number of stops and highest reversal floors for all interventions, to supplement the distribution plots. In Figure 5d, we also report the standard deviation of the estimated mean of S $S$ and H $H$ over 100 instances (i.e., we estimate the mean value of S $S$ and H $H$ for each instance, and show the standard deviation over 100 independent random instances). Elevators under FCFS make an average of 3.64 ± 0.05 $3.64 \pm 0.05$ stops, whereas under Cohorting, they make on average only 2.78 ± 0.04 $2.78 \pm 0.04$ stops, a key driver of lower round trip time. 2 Queue split does not perform as well as Cohorting, making an average 3.27 ± 0.07 $3.27 \pm 0.07$ trips, which is comparable to FCFS. Similarly, FCFS has the highest average H $H$ of 20.3 ± 0.17 $20.3 \pm 0.17$ , whereas Cohorting has an average H $H$ of 18.7 ± 0.19 $18.7 \pm 0.19$ , 2 Queue Split has the lowest H $H$ at 17.6 ± 0.17 $17.6 \pm 0.17$ , due to the two similar distributions among the mini-queues.

Though 2 Queue Split makes a comparable average number of stops to FCFS, having the lowest highest reversal floor among all interventions explains why it performs closer to Cohorting in service time in Figure 4. Ultimately, the impact of S $S$ is higher than that of H $H$ in service time due to simulation parameters (each stop adds 15 s to service time, but each additional floor only adds 1.4 s one way).

3.2 Sensitivity analysis

In this subsection, we study how the performance of the interventions may change when parameters change. We investigate the sensitivity of average queue lengths to the two parameters that determine round trip time—travel time per floor ν $\nu$ and (de)boarding time ω $\omega$ .

In Figure 6a, we vary travel time per floor ν $\nu$ with a scaling in the interval [0.7,1.3] of the baseline ν 0 = 1.4 $\nu _0 = 1.4$ s/floor and observe the average queue lengths for FCFS and our interventions. The average queue length in FCFS is very sensitive to the parameter ν $\nu$ , since FCFS has the largest average highest reversal floor. 2 Queue Split performs comparably to Cohorting until the baseline, with an average queue length of less than 20 but rises to 50 when ν $\nu$ becomes 30 % $30\%$ more than the baseline. Cohorting is the least sensitive, maintaining an average queue length of less than 20 throughout.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Sensitivity of average queue lengths to ν $\nu$ and ω $\omega$ for our large building case study. Note: We run 100 independent random instances and report the average performance. Between 8 and 10 a.m., 2750 passengers with destinations ranging from floors 2 to 25 are served by 14 elevators (each with capacity 4). (a, b) Plots of average queue length from beginning to end of the busy period across interventions. In (a) we change the travel time per floor parameter ν $\nu$ . In (b) we change the (de)boarding time parameter ω $\omega$

In Figure 6b, we vary (de)boarding time ω $\omega$ with a scaling in the interval [0.7,1.3] of the baseline ω 0 = 15 $\omega _0 = 15$ s and observe the average queue lengths for FCFS and our interventions. The average queue length in FCFS is very sensitive to the parameter ω $\omega$ , since FCFS has the largest number of stops. 2 Queue Split performs comparably to Cohorting until the baseline, with an average queue length of less than 20 but rises to 100 when ν $\nu$ becomes 30 % $30\%$ more than the baseline. The parameter ω $\omega$ has a bigger sensitivity impact on 2 Queue Split than ν $\nu$ , showing the importance of number of stops to the round trip time. Cohorting is the least sensitive to ω $\omega$ , maintaining an average queue length of less than 20 throughout.

Other parameters also affect the performance of Cohorting and Queue Splitting. When the elevator capacity C $C$ becomes larger, the round trip time will become longer for all the interventions. Queue Splitting can keep the average highest reversal floor at a relatively low level because it separates the trips for high floors from low floors. However, it may be difficult to keep the number of stops low. On the other hand, Cohorting can still keep the number of stops S $S$ at a relatively low value. However, it becomes harder to keep the highest reversal floor H $H$ low, because we do not have the separation of high floors to low floors, and it is more likely to mix high floor trips with low floor trips when the capacity becomes larger. Also when capacity increases, it takes more time and effort to find a cohort of people going to the same floor. This practical issue may cause the Cohorting intervention to be less attractive, while the management effort for Queue Splitting does not scale up when capacity increases.

To conclude this section, we showed via simulation that Cohorting and Queue Splitting reduce the round trip time for the elevator trips and serve more passengers in a given time period. These numerical results provide motivation to understand why these two interventions perform similarly well while managing the queue completely differently. In the next section, we offer theoretical support for our proposed interventions and focus on the distribution of the number of stops and highest reversal floor.

4 STABILITY ANALYSIS

In this section, we investigate the theory behind the good performance of the proposed Cohorting and Queue Splitting interventions. As observed in Figure 2, the queue length does not grow over time under the Cohorting and Queue Splitting intervention, while under FCFS it keeps increasing. In other words, by using the Cohorting and Queue Splitting intervention, we manage to transfer an unstable queuing system into a stable one under the simulation setting in Section 3. In this section, we aim to establish stability conditions for each intervention and explain why the proposed interventions work. We find that our proposed interventions can be stable under higher arrival rates than FCFS for two reasons. First, the interventions reduce the number of stops in comparison to FCFS, and second, the interventions reduce the average total distance traveled by the elevators. In particular, the second reason is supported by a stochastic dominance result for the highest reversal floor distribution of the different policies. In Section 4.1 we provide a background on queuing stability and in Section 4.2 we explain assumptions needed to prove our results. In Section 4.3 we calculate the stability condition for a special case with two floors and one elevator and in Section 4.4 we extend our analysis to general settings.

4.1 Stability condition for a queuing network

In this section, we describe results in the literature on stability of multiclass queuing networks with different operations rules. The model we focus on has I $I$ buffers (or arrival classes) and K $K$ types of resources to serve the arrivals. Each arrival class is served by a specific resource type. The arrival process for each buffer i $i$ is a Poisson process with rate λ i $\lambda _i$ , and the service for type i $i$ requires a random time with mean t i $t_i$ . Each resource k $k$ is a pool of b k $b_k$ identical servers, where b ⃗ : = ( b 1 , … , b K ) $\vec{b} := (b_1, \ldots , b_K)$ . Each arrival class is processed by servers from a single specified pool, and each such service is accomplished by a single server from the pool. The set of buffers that resource k $k$ can serve is defined as I ( k ) $ \mathcal {I}(k)$ . The load vector ρ ⃗ : = ( ρ 1 , … , ρ K ) $\vec{\rho }:= (\rho _1, \ldots , \rho _K)$ is defined as ρ k = ∑ i ∈ I ( k ) λ i t i $\rho _k = \sum _{i\in \mathcal {I}(k)} \lambda _i t_i$ .

In Lemma 1 below, we see that the stability condition, also known as the standard load condition,
ρ ⃗ < b ⃗ \begin{equation} \vec{\rho } &lt; \vec{b} \end{equation} (2)
is a sufficient and necessary condition for the stability of the queuing network we study in this paper. For some queuing systems, such as M / M / 1 $M/M/1$ queue, it is well known that the system is stable if and only if the load vector ρ $\rho$ is less than 1. However, it is not always true that Equation (2) is a sufficient condition for a general queuing network (Bramson, 1996). In Lemma 1 below, we establish the stability condition for a feedforward queuing network under a non-idling control policy. Fortunately, the queuing models corresponding to the elevator interventions all fall within the category of a feedforward queuing network, which is defined as a queuing network in which the resources can be numbered in such a way that the arrival jobs never move from higher numbered servers to lower numbered ones (all passengers/jobs see one elevator/server). Also, the interventions we propose are non-idling dynamic control policies, which is defined as a control policy where no server remains idle while there is a job waiting in any of the buffers that are processed by the server.

Lemma 1.Under any non-idling policy, a feedforward queuing network is stable if and only if the stability condition ρ ⃗ < b ⃗ $\vec{\rho }&lt;\vec{b}$  holds.

Proof.The proof is supported by multiple results from Dai and Harrison (2020), which we list in Lemmas 2 and 3 below.

Lemma 2. (Proposition 5.1 and Theorem 5.2 in Dai & Harrison, [2020])If a unitary network is stable, then it satisfies the standard load condition ρ < b $\rho &lt;b$ .

Lemma 3. (Theorem 8.14 in Dai & Harrison, [2020])In a feedforward queuing network, if the standard load condition ρ ⃗ < b ⃗ $\vec{\rho }&lt;\vec{b}$ holds, then the queuing network is stable under any non-idling policy.

A unitary network is a general type of stochastic processing network. In simple words, it requires a one-to-one relationship between the service activity and the buffers, and there is only one way to process jobs of any given class. We note that the feedforward queuing network, which is how our interventions can be described, is a special case of a unitary network. Thus, by Lemma 2 we can conclude that if a feedforward queuing network is stable, then the standard load condition ρ ⃗ < b ⃗ $\vec{\rho }&lt;\vec{b}$ must hold. Finally, combining with Lemma 3, we can conclude that the condition ρ ⃗ < b ⃗ $\vec{\rho }&lt;\vec{b}$ is indeed a sufficient and necessary condition for the queuing network we are interested in. □ $\Box$

In the following subsections, we will specify the structure of the queuing network for each intervention, and derive the stability condition by using Lemma 1.

4.2 Assumptions and justification

We first simplify the simulation model from Section 2 for the sake of analysis. We formulate the elevator system as a queuing network, in which the N $N$ elevators are the servers and the round trip time of an elevator trip is the service time. As discussed in Section 2, the round trip time is composed of the boarding time, stop time, ascent time, and descent time. We simplify the calculation of round trip time by omitting the boarding time at the lobby, which is the same for all interventions. We let ν $\nu$ be the time it takes an elevator to travel one floor and we simplify the stop time of an elevator for one stop to be ω $\omega$ . We also simplify the ascent time and descent time to be identical. We assume the destination of passengers is uniformly at random across all the floors, and the aggregate arrival rate is λ $\lambda$ . Recall that F ⃗ $\vec{F}$ is the number of passengers going to each floor in a particular elevator trip. We let S $S$ be the random variable denoting the number of stops in an elevator trip, that is, S : = ∑ j = 2 m + 1 1 { F j > 0 } $S:= \sum _{j=2}^{m+1} \mathbb {1}\lbrace F_j&gt;0\rbrace$ . We let H $H$ be the random variable denoting the highest reversal floor in an elevator trip, that is, H : = max j j 1 { F j > 0 } $H{:}\; ={\max}_{j}\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em}j\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em}\hspace*{0.05em} \mathbb {1} \{{F}_{j}&gt;0\}$ .

We use τ ( H , S ) $\tau \hspace*{0.05em}\hspace*{0.05em}(H,S)$ to denote the round trip time for an elevator trip, which is a random variable with finite support, and its mean value depends on the random variables H $H$ and S $S$ . The conditional expected round trip time is defined as
E [ τ ( H , S ) | H , S ] : = 2 ν ( H − 1 ) + ω S , \begin{equation} \mathbb {E}[\tau (H,S)| H, S]{:}\; = 2\nu (H-1)+ \omega S, \end{equation} (3)
where 2 ν ( H − 1 ) $2\nu (H-1)$ is the ascent and descent time, and ω S $\omega S$ is the stop time. The distributions of H $H$ and S $S$ are determined by the random arrival process and the intervention, and are used to determine the expected round trip time. We do not make any further assumptions on the distribution of the round trip time.

For the Queue Splitting intervention, we assume that the m $m$ floors are divided into l $l$ groups, where each group is a separate buffer and consists of k $k$ consecutive floors, that is, m = l k $m = lk$ and l , k ≥ 2 $l,k\ge 2$ are integers. The j $j$ th floor in the i $i$ th group can be written as x : = ( i − 1 ) k + j + 1 $x:=(i-1)k+j+1$ , for i = 1 , … , l $i=1,\ldots ,l$ ; j = 1 , … , k $j = 1,\ldots ,k$ . For example, floor 2 is the first floor in the first group.

Next, we describe the queuing networks that represent our elevator system under different interventions. Our goal is to derive the stability conditions, under which the queue does not grow over time under, for each intervention. Thus, we only consider such a condition in a system with extremely long (infinite) queues. We assume that from now on, we treat a set of C $C$ passengers as one arrival job to the system, which is without loss of generality in this regime. The assumption of treating C $C$ passengers as one job allows us to utilize tools from the literature and have a sufficient and necessary condition for stability (Lemma 1). We note that Dai and Li (2003) provide stability analysis for batch service systems, and ρ ⃗ < b ⃗ $\vec{\rho }&lt;\vec{b}$ is a sufficient condition for stability for the queue under the operation rule corresponding to the Cohorting and Queue Splitting intervention.

We now connect the interventions to the setup described in Section 4.1. In FCFS, there is only one buffer and an arrival job will be C $C$ random passengers with independent and uniformly distributed destinations among all floors. In the Queue Splitting intervention, each floor group corresponds to one buffer. An arrival job will be C $C$ random passengers who are going to the same group of floors. In Cohorting, each destination floor corresponds to one buffer, and an arrival job is C $C$ passengers who are going to the same floor. Note that for FCFS, Cohorting, and Queue Splitting, there is only one resource type, that is, all elevators can serve all floors. In the Allocation intervention where elevators are assigned to floor groups, the elevators are divided into groups, which represents different types of resources. Each floor group forms a separate FCFS queue that can only be served by one resource type. This distinction makes the Allocation less effective than the other proposed interventions, as we show in Supporting Information, Section EC.3. In the following subsections, we focus on the analysis of the stability condition (2) for FCFS, Cohorting, and Queue Splitting. The stability analysis for Allocation is provided in Supporting Information, Section EC.3.1.

4.3 One elevator and two destination floors

We first focus on the simplest setting where the building only has two destination floors 2 and 3 and one elevator with capacity C = 2 $C = 2$ . The passengers arrive at the building according to a Poisson process with rate λ $\lambda$ , and go to floor 2 or 3 with equal probability. Equivalently, the arrival process for passengers who go to floor 2 (similarly for floor 3) is a Poisson process with rate λ 2 $\frac{\lambda }{2}$ .

The elevator system under FCFS is an M / G / 1 $M/G/1$ queue, where the new jobs arrive according to a Poisson process with rate λ / 2 $\lambda /2$ , and the elevator is the server with the round trip time being the service time. In an M / G / 1 $M/G/1$ queue, the stability condition Equation (2) is well-known and can be found in the literature and the textbooks (e.g., Ross et al., 1996, Example 4.3(a)). It can also be derived from Lemma 1 since an M / G / 1 $M/G/1$ queue is a special case of a feedforward queuing network, and FCFS is a non-idling policy.

For the Cohorting and 2 Queue Splitting intervention, we can think of the following multiclass queuing network with two queuing buffers and one server. The passengers who go to floor 2 form a queue in buffer 1, and the passengers who go to floor 3 form a separate queue in buffer 2. The passengers are also assigned into pairs, and a pair of passengers is considered as a job that is waiting to be served. This network with two buffers and one server satisfies the condition of a feedforward queuing network. In the Queue Splitting intervention, the server will choose a buffer to serve in a round-robin fashion once it finishes the previous job. In the Cohorting intervention, the elevator serves the first passenger in the queue and we let the second passenger whose destination is the same as the first passenger board the same elevator. We can represent the dynamic as a multiclass queue where each floor destination forms a buffer, and the server decides which job to take by choosing the buffer whose head of queue arrives the earliest to the system. In the literature, this is called an FCFS control policy (Bramson, 1994) since the way a server chooses between buffers is in the FCFS fashion. Both the Queue Splitting and Cohorting interventions are non-idling policies. Therefore, we can again use Lemma 1 to derive the stability condition.

Proposition 1.

  • (a) The elevator system is stable under FCFS if and only if the arrival rate
    λ < 4 7 ν + 3 ω : = η FCFS . \begin{equation*} \lambda &lt;\frac{4}{7\nu +3\hspace*{0.05em}\hspace*{0.05em}\omega}:={\eta}_{\textit{FCFS}}. \end{equation*}
  • (b) The elevator system is stable under the Cohorting and 2 Queue Splitting if and only if
    λ < 4 6 ν + 2 ω : = η C o h o r t = η Q S . \begin{equation*} \lambda &lt;\frac{4}{6\nu +2\omega }:=\eta _{Cohort} = \eta _{QS}. \end{equation*}

Proof.

  • (a) The queuing system corresponding to FCFS consists of only one buffer with λ / 2 $\lambda /2$ being the arrival rate of each pair of passengers. The service time distribution is a mixture of three distributions. With probability 0.25, the highest reversal floor H $H$ is 2 and the number of floors and the total number of stops S $S$ is 1. Similarly, with probability 0.25, the elevator only stops once and H $H$ is 2. With probability 0.5, H $H$ is 3 and S $S$ is 2. Therefore, the expected service time is
    E [ τ ( 2 , 1 ) ] + 2 E [ τ ( 3 , 2 ) ] + E [ τ ( 3 , 1 ) ] 4 = 2 ν ( 2 − 1 ) + ω + 2 ( 2 ν ( 3 − 1 ) + 2 ω ) + 2 ν ( 3 − 1 ) + ω 4 = 7 ν + 3 ω 2 . \begin{eqnarray*} &&\frac{ \mathbb {E}[\tau (2,1)]+2 \mathbb {E}[\tau (3,2)] + \mathbb {E}[\tau (3,1)]}{4}\nonumber\\ &&\quad = \frac{2\nu (\hspace*{-.5pt}2\hspace*{-.5pt}-\hspace*{-.5pt}1\hspace*{-.5pt})\hspace*{-.5pt}+\hspace*{-.5pt}\omega \hspace*{-.5pt}+\hspace*{-.5pt} 2\hspace*{-.5pt}(\hspace*{-.5pt}2\nu (\hspace*{-.5pt}3\hspace*{-.5pt}-\hspace*{-.5pt}1\hspace*{-.5pt})\hspace*{-.5pt}+\hspace*{-.5pt}2\omega \hspace*{-.5pt})\hspace*{-.5pt}+\hspace*{-.5pt} 2\nu (\hspace*{-.5pt}3\hspace*{-.5pt}-\hspace*{-.5pt}1\hspace*{-.5pt})\hspace*{-.5pt}+\hspace*{-.5pt}\omega }{4}\nonumber\\[2pt] &&\quad =\frac{7\nu +3\omega }{2}. \end{eqnarray*}
    By Lemma 1, the system is stable if and only if λ 2 · 7 ν + 3 ω 2 < 1 $\frac{\lambda }{2} \cdot \frac{7\nu +3\omega }{2}&lt;1$ , which is equivalent to λ < 4 7 ν + 3 ω $ \lambda &lt;\frac{4}{7\nu +3\omega }$ .
  • (b) The queuing system for Queue Splitting and Cohorting intervention has two buffers, each with arrival rate λ 4 $\frac{\lambda }{4}$ for a pair of passengers. For buffer 1, all passengers are going to floor 2, so the expected service time is E [ τ ( 2 , 1 ) ] = 2 ν ( 2 − 1 ) + ω $\mathbb {E}[\tau (2,1)]=2\nu (2-1) + \omega$ . Similarly, for buffer 2, all passengers are going to floor 3, so the expected service time is E [ τ ( 3 , 1 ) ] = 2 ν ( 3 − 1 ) + ω $\mathbb {E}[\tau (3,1)]=2\nu (3-1) + \omega$ . By Lemma 1, the system is stable if and only if λ 4 · E [ τ ( 2 , 1 ) ] + λ 4 · E [ τ ( 3 , 1 ) ] < 1 $ \frac{ \lambda }{4} \cdot \mathbb {E}[\tau (2,1)]+ \frac{\lambda }{4}\cdot \mathbb {E}[\tau (3,1)]&lt;1$ , which is equivalent to λ < 4 6 ν + 2 ω $\lambda &lt; \frac{4}{6\nu +2\omega }$ . □ $\Box$

Since the stability thresholds above provide an upper bound on the total arrival rate of passengers, the higher the threshold is, the better the system can deal with rush hour traffic. In the following proposition, we establish by how much the proposed interventions can improve the stability threshold.

Proposition 2.Consider a building with one elevator, two destination floors, and elevator capacity of two. The Cohorting and Queue Splitting intervention can increase the stability threshold by at least 16.67 % $16.67\%$ , and at most 50 % $50\%$ .

Proof.In this proof, we want to bound the ratio η Q S η F C F S $\frac{\eta _{QS}}{\eta _{FCFS}}$ . Plugging in the threshold we get from Proposition 1, we have η Q S η F C F S = 7 ν + 3 ω 6 ν + 2 ω $\frac{\eta _{QS}}{\eta _{FCFS}} = \frac{7\nu +3\omega }{6\nu +2\omega }$ . Since ν $\nu$ and ω $\omega$ are positive real numbers, 7 6 < 7 ν + 3 ω 6 ν + 2 ω < 3 2 $\frac{7}{6}&lt; \frac{7\nu +3\omega }{6\nu +2\omega }&lt;\frac{3}{2}$ , which yields the final result. □ $\Box$

Proposition 2 provides a clean explanation to the phenomenon we observe from the simulation: When facing the same passenger arrival pattern, the stability condition for FCFS is violated while the arrival rate is still below the threshold for Queue Splitting and Cohorting. Thus, the key driver for the good performance of the proposed interventions is that the expected service time is much shorter, thanks to the fact that both the highest reversal floor and the number of stops have smaller values. When we use FCFS, H = 3 $H = 3$ with probability 0.75, despite the fact that only half of the passengers go to floor 3. Using Cohorting and Queue Splitting intervention, we can make sure that only 50 % $50\%$ of the time the elevator will go to the higher floor. For the number of stops per elevator trip, using Cohorting and Queue Splitting intervention, we can ensure that the elevator only makes one stop in each elevator trip, while in FCFS, 50 % $50\%$ of the time the elevator will make two stops. Our proposed interventions can simultaneously reduce the stop time and the travel time of the elevator, and make the elevator trips more efficient. The analysis for the two-destination system can be extended to multiple floors. In the 2 Queue Split intervention, we have two destination ranges, the high floors and the low floors. When using FCFS, 75 % $75\%$ of the trips will end up in the high floor range, while using 2 Queue Split, we can reduce the fraction of trips going to the high floors to 50 % $50\%$ . In the next subsection, we provide detailed analysis of a building with multiple elevators and floors.

4.4 General case

In this subsection, we focus on a general building with m $m$ destination floors 2 , … , m + 1 $2, \ldots , m+1$ and N $N$ identical elevators that can serve all the floors. Though the expected service time is complicated to compute exactly in the general setting, we can focus on the distribution of H $H$ and S $S$ and show that the stability threshold for Queue Splitting and Cohorting is much higher than the one for FCFS. In this subsection, we again assume that we group C $C$ passengers together and let them enter the lobby as a new job to the queuing system. Lemma 3 below shows that the stability threshold η $\eta$ for each intervention is a simple function of the E [ H ] $\mathbb {E}[H]$ and E [ S ] $\mathbb {E}[S]$ .

Proposition 3.For intervention π ∈ { F C F S $\pi \in \lbrace FCFS$ , C o h o r t i n g , Q S } $Cohorting, QS\rbrace$ , the queue is stable if and only if the arrival rate λ < η π : = NC 2 ν ( E [ H π ] − 1 ) + ω E [ S π ] $\lambda &lt;{\eta}_{\pi}{:}\; =\frac{\textit{NC}}{2\hspace*{0.05em}\hspace*{0.05em}\nu \hspace*{0.05em}\hspace*{0.05em}(\mathbb{E}\hspace*{0.05em}\hspace*{0.05em}[{H}_{\pi}]-1)+\omega \mathbb{E}\hspace*{0.05em}\hspace*{0.05em}[{S}_{\pi}]}$ .

Proof.We start with FCFS. By Equation (2), the stability condition is λ C E [ τ ( H F C F S , S F C F S ) ] < N $\frac{\lambda }{C} \mathbb {E}[\tau (H_{FCFS},S_{FCFS})]&lt;N$ , which is equivalent to

λ C 2 ν ( E [ H F C F S ] − 1 ) + ω E [ S F C F S ] < N . \begin{align} \frac{\lambda }{C} {\left(2\nu (\mathbb {E}[H_{FCFS}]-1) + \omega \mathbb {E}[ S_{FCFS}] \right)}&lt;N. \end{align} (4)

Under the Cohorting intervention, the queuing network consists of m $m$ independent buffers for m $m$ floors, and an idle server will choose to serve the buffer with the earliest arrival time. By Equation (2), we need to specify the average round trip time for each buffer. The highest reversal floor for buffer i $i$ is simply i $i$ , and every trip only has one stop so E [ S C o h o r t ] = 1 $\mathbb {E}[S_{Cohort}]=1$ . Therefore, the stability condition (2) becomes ∑ i = 1 m λ i E [ τ ( H , 1 ) | H = i ] < N $\sum _{i = 1}^m \lambda _i \mathbb {E}[\tau (H,1)|H=i]&lt;N$ , where λ i = λ C m $\lambda _i = \frac{\lambda }{Cm}$ . Note that the highest reversal floor H C o h o r t $H_{Cohort}$ follows a uniform distribution, we can rewrite the left-hand side of the stability condition into

∑ i = 1 m λ i E [ τ ( H , 1 ) | H = i ] = λ C ∑ i = 1 m 1 m E [ τ ( H , 1 ) | H = i ] = λ C 2 ν ( E [ H C o h o r t ] − 1 ) + ω . \begin{eqnarray} \sum _{i = 1}^m \lambda _i \mathbb {E}[\tau (H,1)|H=i] &=& \frac{\lambda }{C}\sum _{i = 1}^m\frac{1}{m}\mathbb {E}[\tau (H,1)|H=i]\nonumber\\ & =&\frac{\lambda }{C} {\left(2\nu (\mathbb {E}[H_{Cohort}] -1)+ \omega \right)}. \qquad \end{eqnarray} (5)

Under the Queue Splitting intervention, recall that we assume that the m $m$ floors are divided into l $l$ groups, where each group is a separate buffer and consists of k $k$ consecutive floors. Note that m = l k $m=lk$ and l , k ≥ 2 $l,k\ge 2$ are integers. The stability condition becomes ∑ i = 1 l λ i E [ τ ( H , S ) | H ∈ group i ] < N ${\sum}_{i=1}^{l}{\lambda}_{i}\mathbb{E}[\tau (H,S)|H\in \hspace*{0.2424242424242424em}\text{group}\hspace*{0.2424242424242424em}i]&lt;N$ , where λ i = λ C l $\lambda _i =\frac{\lambda }{Cl}$ in this case. Since the jobs are processed in a round-robin fashion, the probability for a new job to be in group i $i$ is 1 l $\frac{1}{l}$ . Then we can rewrite the left-hand side of the stability condition as

∑ i = 1 l λ i E [ τ ( H , S ) | H ∈ group i ] = λ C l ∑ i = 1 l 2 ν ( E [ H Q S | H ∈ group i ] − 1 ) + ω E [ S Q S | H ∈ group i ] = λ C 2 ν ( E [ H Q S ] − 1 ) + ω E [ S Q S ] . \begin{eqnarray} &&\sum _{i = 1}^l \lambda _i \mathbb {E}[\tau (H,S)|H\in \text{group } i]\nonumber \\[-4pt] &&\quad = \frac{\lambda }{Cl} \sum _{i=1}^l\left(2\nu (\mathbb {E}[H_{QS}|H \in \text{group } i]-1)\right.\nonumber\\[-4pt] &&\qquad\left. +\ \omega \mathbb {E}[S_{QS}|H\in \text{group } i] \right)\nonumber\\[-4pt] &&\quad = \frac{\lambda }{C} {\left(2\nu (\mathbb {E}[H_{QS}]-1) + \omega \mathbb {E}[S_{QS}] \right)}. \end{eqnarray} (6)
Therefore, following the result in Lemma 1, for FCFS, Cohorting, and Queue Splitting intervention, the queue is stable if and only if λ < N C 2 ν ( E [ H π ] − 1 ) + ω E [ S π ] $\lambda &lt; \frac{NC}{2\nu (\mathbb {E}[H_{\pi }]-1)+ \omega \mathbb {E}[S_\pi ]}$ . □ $\Box$

From Lemma 3, we know that the key to compare the stability conditions for different interventions is to compare the expectation of the highest reversal floor and number of stops. The analysis for FCFS can be found in the literature of elevator analytics (Barney & Al-Sharif, 2015), whereas the Cohorting and Queue Splitting intervention require new analysis. Next, we compute the distribution and expectation of the highest reversal floor (Lemma 4) and number of stops (Lemma 5) and provide a comparison.

Lemma 4.

  • (a) For x = 2 , … , m + 1 $x =2,\ldots ,m+1$ , the cumulative density function of the highest reversal floors is
    P [ H F C F S ≤ x ] = x − 1 m C , P [ H Q S ≤ x ] = x − 1 k l + 1 l x − 1 − k x − 1 k k C , P [ H C o h o r t ≤ x ] = x − 1 m . \begin{eqnarray*} \mathbb {P}[H_{FCFS}\le x] &=& {\left(\frac{x-1}{m}\right)}^C,\nonumber\\[-2pt] \mathbb {P}[H_{QS}\le x]&=& \frac{\left\lfloor \frac{x-1}{k} \right\rfloor }{l}+\frac{1}{l} {\left(\frac{x-1-k\left\lfloor \frac{x-1}{k} \right\rfloor }{k}\right)}^C,\nonumber\\[-2pt] \mathbb {P}[H_{Cohort}\le x] &=& \frac{x-1}{m}. \end{eqnarray*}
  • (b) The expectation of the highest reversal floors is
    E [ H F C F S ] = m + 1 − 1 m C ∑ x = 1 m − 1 x C , E [ H Q S ] = k ( l + 1 ) 2 + 1 − ∑ j = 1 k − 1 j k C , E [ H C o h o r t ] = m + 1 2 + 1 . \begin{align*} \begin{split} \mathbb {E}[H_{FCFS}] &= m +1 - \frac{1}{m^C}\sum _{x=1}^{m-1}x^C,\\ \mathbb {E}[H_{QS}] &= \frac{k(l+1)}{2}+1-\sum _{j = 1}^{k-1} {\left(\frac{j}{k}\right)}^C,\\ \mathbb {E}[H_{Cohort}] &= \frac{m+1}{2}+1. \end{split}\end{align*}
  • (c) H F C F S $H_{FCFS}$ stochastically dominates H Q S $H_{QS}$ , and H Q S $H_{QS}$ stochastically dominates H C o h o r t $H_{Cohort}$ , that is, H F C F S ⪰ H Q S ⪰ H C o h o r t $H_{FCFS}\succeq H_{QS} \succeq H_{Cohort}$ . Therefore, E [ H F C F S ] ≥ E [ H Q S ] ≥ E [ H C o h o r t i n g ] $\mathbb {E}[H_{FCFS}]\ge \mathbb {E}[H_{QS}]\ge \mathbb {E}[H_{Cohorting}]$ .

Proof.

  • (a)

    In FCFS, the random event that the highest reversal floor to be no larger than x $x$ is equivalent to the event that the destination of each passenger is randomly chosen from 2 to x $x$ , which directly gives us the result.

    For the Queue Splitting intervention, we can rewrite floor x $x$ as ( i − 1 ) k + j + 1 $(i-1)k+j+1$ , so that floor x $x$ is the j $j$ th floor in the i $i$ th group. Therefore, i − 1 = ⌊ x − 1 k ⌋ $i-1= \lfloor \frac{x-1}{k} \rfloor$ , and j = x − 1 − ( i − 1 ) k $j = x-1-(i-1)k$ . Conditioning on the fact that the current service group is the i $i$ th group, the probability of the highest reversal floor is no larger than x = ( i − 1 ) k + j + 1 $x =(i-1)k+j+1$ is equal to j k C $\left(\frac{j}{k}\right)^C$ , following the same argument for FCFS. Note that if x $x$ is in floor group i $i$ , all the trips in group 1 , … , i − 1 $1,\ldots , i-1$ satisfy the condition H Q S ≤ x $H_{QS}\le x$ .

    P [ H QS ≤ x ] = ∑ y = 1 i − 1 P [ H QS in group y ] + P [ H QS ≤ ( i − 1 ) k + j + 1 | H QS in group i ] = i − 1 l + 1 l j k C . \begin{eqnarray*} \mathbb{P}[{H}_{\textit{QS}}\le x]& =& \sum _{y=1}^{i-1}\mathbb{P}[{H}_{\textit{QS}}\; \text{in}\; \text{group}\; y]\nonumber\\[2pt] &&+\, \mathbb{P}[{H}_{\textit{QS}}\; \def\eqcellsep{&}\begin{array}{cc}\le & (i\,{-}\,1)k\,{+}\,j\,{+}\,1|{H}_{\textit{QS}}\; \text{in}\; \text{group}\; i]\end{array} \nonumber\\[2pt] & =& \frac{i-1}{l}+\frac{1}{l}{\left(\frac{j}{k}\right)}^{C}. \end{eqnarray*}

    The distribution of the highest reversal floor for Cohorting directly follows from the definition of a uniform distribution on value 2 , … , m + 1 $2,\ldots , m+1$ .

  • (b) A straightforward calculation shows E [ H C o h o r t ] = m + 1 2 + 1 $\mathbb {E}[H_{Cohort}] = \frac{m+1}{2}+1$ . We next use the tail formula to derive the expectation for FCFS and Queue Splitting intervention:
    E [ H FCFS ] = ∑ x = 1 ∞ P [ H FCFS ≥ x ] = 1 + ∑ x = 2 m + 1 ( 1 − P [ H FCFS ≤ x − 1 ] ) = m + 1 − ∑ i = 2 m + 1 x − 2 m C = m + 1 − 1 m C ∑ x = 1 m − 1 x C . \begin{eqnarray*} \mathbb{E}[{H}_{\textit{FCFS}}]& =& \sum _{x=1}^{\infty}\mathbb{P}[{H}_{\textit{FCFS}}\ge x]=1+\sum _{x=2}^{m+1}(1-\mathbb{P}[{H}_{\textit{FCFS}} \def\eqcellsep{&}\begin{array}{cc}\;\le & x-1])\end{array} \\[2pt] &=& m+1-\sum _{i=2}^{m+1}{\left(\frac{x-2}{m}\right)}^{C}\\[2pt] & =& m+1-\frac{1}{{m}^{C}}\sum _{x=1}^{m-1}{x}^{C}. \end{eqnarray*}
    E [ H QS ] = ∑ x = 1 ∞ P [ H QS ≥ x ] = 1 + ∑ x = 2 m + 1 P [ H QS ≥ x ] = m + 1 − ∑ x = 2 m + 1 P [ H QS ≤ x − 1 ] = m + 1 − ∑ x = 2 m P [ H QS ≤ x ] = m + 1 − ∑ i = 1 l ∑ j = 1 k P [ H QS ≤ ( i − 1 ) k + j + 1 ] − 1 = m + 1 − ∑ i = 1 l i − 1 l k + ∑ j = 1 k j k C − 1 = k ( l + 1 ) 2 + 1 − ∑ j = 1 k − 1 j k C . \begin{eqnarray*} \mathbb{E}[{H}_{\textit{QS}}]& =& \sum _{x=1}^{\infty}\mathbb{P}[{H}_{\textit{QS}}\ge x]\nonumber\\[2pt] & =& 1+\sum _{x=2}^{m+1}\mathbb{P}[{H}_{\textit{QS}}\ge x]\nonumber\\[2pt] & =& m+1-\sum _{x=2}^{m+1}\mathbb{P}[{H}_{\textit{QS}}\le x-1]\nonumber\\ & =& m+1-\sum _{x=2}^{m}\mathbb{P}[{H}_{\textit{QS}}\le x]\nonumber\\ & =& m+1 - \left(\sum _{i=1}^{l}\sum _{j=1}^{k}\mathbb{P}[{H}_{\textit{QS}}\le (i-1)k+j+1]-1\right)\nonumber\\ & =& m+1-\left(\sum _{i=1}^{l}\frac{i-1}{l}k+\sum _{j=1}^{k}{\left(\frac{j}{k}\right)}^{C}-1\right)\nonumber\\ & =& \frac{k(l+1)}{2}+1-\sum _{j=1}^{k-1}{\left(\frac{j}{k}\right)}^{C}. \end{eqnarray*}
  • (c) We first prove that the random variables preserve stochastic dominance, that is, H C o h o r t ⪯ H Q S ⪯ H F C F S $H_{Cohort}\preceq H_{QS} \preceq H_{FCFS}$ . By definition, we only need to verify that P [ H C o h o r t ≤ x ] ≥ P [ H Q S ≤ x ] ≥ P [ H F C F S ≤ x ] $\mathbb {P}[H_{Cohort}\le x] \ge \mathbb {P}[H_{QS}\le x]\ge \mathbb {P}[H_{FCFS}\le x]$ is true for all x $x$ . The first inequality is easy to verify since
    P [ H C o h o r t ≤ x ] = ( i − 1 ) k + j k l = i − 1 l + 1 l j k ≥ i − 1 l + 1 l j k C = P [ H Q S ≤ x ] . \begin{eqnarray*} \hspace*{-22pt} \mathbb {P}[H_{Cohort}\le x] &=&\frac{(i-1)k+j}{kl} = \frac{i-1}{l} +\frac{1}{l} \frac{j}{k}\nonumber\\ &\ge& \frac{i-1}{l} +\frac{1}{l} {\left(\frac{j}{k} \right)}^C = \mathbb {P}[H_{QS}\le x]. \end{eqnarray*}
    Next we verify the second inequality:
    P [ H F C F S ≤ x ] = ( i − 1 ) k + j m C = i − 1 l + 1 l j k C = ( l − 1 ) l i − 1 ( l − 1 ) + 1 l j k C ≤ ( l − 1 ) l i − 1 l − 1 C + 1 l j k C = i − 1 l i − 1 l − 1 C − 1 + 1 l j k C ≤ i − 1 l + 1 l j k C = P [ H Q S ≤ x ] . \begin{eqnarray*} \mathbb {P}[H_{FCFS}\le x] &=& {\left(\frac{(i-1)k+j}{m}\right)}^C = {\left(\frac{i-1}{l} + \frac{1}{l} \frac{j}{k}\right)}^C\nonumber\\[2pt] &=& {\left(\frac{(l-1)}{l}\frac{i-1}{(l-1)} + \frac{1}{l} \frac{j}{k}\right)}^C \nonumber\\[2pt] &\le& \frac{(l-1)}{l} {\left(\frac{i-1}{l-1}\right)}^C + \frac{1}{l} {\left(\frac{j}{k}\right)}^C\nonumber\\ &=& \frac{i-1}{l} {\left(\frac{i-1}{l-1}\right)}^{C-1} + \frac{1}{l} {\left(\frac{j}{k}\right)}^C\nonumber\\ &\le& \frac{i-1}{l} +\frac{1}{l} {\left(\frac{j}{k} \right)}^C = \mathbb {P}[H_{QS}\le x]. \end{eqnarray*}
    The first inequality follows from Jensen's inequality, and the second inequality follows from the fact that i − 1 ≤ l − 1 $i-1\le l-1$ . Following the stochastic dominance result, we obtain the desired ordering in expectation. □ $\Box$

Since our simulation results in Section 3 are for a 25-story building, the highest reversal floor plays an essential role in the performance of the elevator system. Lemma 4 strongly supports the good performance of Cohorting and Queue Splitting in the simulation, as the distribution of the highest reversal floor preserves stochastic dominance across the three interventions we study. Note that the expected ascent time and descent time is equal to 2 ν ( E [ H ] − 1 ) $2\nu (\mathbb {E}[H]-1)$ . With the formula of E [ H ] $\mathbb {E}[H]$ from Lemma 4, in Proposition 4 we provide guarantees on the potential improvement by deriving the ratio of the expected ascent time and descent time between interventions.

Proposition 4.

  • (a) The ratio of the expected ascent time and descent time between FCFS and Cohorting is at least 2 C m ( C + 1 ) ( m + 1 ) $\frac{2Cm}{(C+1)(m+1)}$ .
  • (b) For the special case of C = 2 $C = 2$ and m ≥ 3 $m\ge 3$ , the ratio of the expected ascent time and descent time between FCFS and Cohorting is equal to 4 m − 1 3 m $\frac{4m-1}{3m}$ , which at least 11 9 $\frac{11}{9}$ . The ratio reaches the lower bound when there are only three floors and reaches the upper bound when the number of floors grows to infinity.
  • (c) For the special case of C = 2 $C = 2$ , the ratio of the expected ascent time and descent time between FCFS and Queue Splitting is equal to 4 m 2 + 3 m − 1 3 m 2 + 3 m + m k − l > 1 $\frac{4m^2+3m-1}{3m^2 + 3m +mk-l}&gt;1$ .

Proof.We first bound E [ H F C F S ] − 1 $\mathbb {E}[H_{FCFS}]-1$ and E [ H Q S ] − 1 $\mathbb {E}[H_{QS}]-1$ by replacing summation with integral.

E [ H F C F S ] − 1 = m − 1 m C ∑ i = 1 m − 1 i C ≥ m − ∫ x = 0 m x C d x = m − m C + 1 , E [ H Q S ] − 1 = k ( l + 1 ) 2 − ∑ j = 1 k − 1 j k C ≤ k ( l + 1 ) 2 − ∫ x = 0 k − 1 x k C d x = k ( l + 1 ) 2 − ( k − 1 ) C + 1 ( C + 1 ) k C . \begin{eqnarray*} \mathbb {E}[H_{FCFS}] -1 & =& m - \frac{1}{m^C}\sum _{i=1}^{m-1}i^C \nonumber\\[4pt] &\ge& m - \int _{x=0}^m x^C dx = m-\frac{m}{C+1},\nonumber\\[4pt] \mathbb {E}[H_{QS}] -1 & =& \frac{k(l+1)}{2}-\sum _{j = 1}^{k-1} {\left(\frac{j}{k}\right)}^C\nonumber\\[4pt] &\le& \frac{k(l+1)}{2}- \int _{x=0}^{k-1} {\left(\frac{x}{k}\right)}^Cdx\nonumber\\[5pt] & =& \frac{k(l+1)}{2}-\frac{(k-1)^{C+1}}{(C+1)k^C}. \end{eqnarray*}
  • (a) We compare the expected ascent time and descent time between FCFS and Cohorting by considering the ratio
    2 ν ( E [ H F C F S ] − 1 ) 2 ν ( E [ H C o h o r t ] − 1 ) ≥ m − m / ( C + 1 ) ( m + 1 ) / 2 = 2 C m ( C + 1 ) ( m + 1 ) . \begin{eqnarray*} \frac{2\nu (\mathbb {E}[H_{FCFS}]-1)}{2\nu (\mathbb {E}[H_{Cohort}]-1)} &\ge& \frac{m-m/(C+1)}{(m+1)/2}\nonumber\\[5pt] &=& \frac{2Cm}{(C+1)(m+1)}. \end{eqnarray*}
  • (b) When C = 2 $C = 2$ , we can compute E [ H F C F S ] $\mathbb {E}[H_{FCFS}]$ explicitly. Therefore, the ratio becomes
    2 ν ( E [ H F C F S ] − 1 ) 2 ν ( E [ H C o h o r t ] − 1 ) = m − 1 m 2 ∑ i = 1 m − 1 i 2 ( m + 1 ) / 2 = m − 1 m 2 ( m − 1 ) ( m − 1 + 1 ) ( 2 ( m − 1 ) + 1 ) 6 ( m + 1 ) / 2 = 4 m − 1 3 m . \begin{eqnarray} \frac{2\nu (\mathbb {E}[H_{FCFS}]-1)}{2\nu (\mathbb {E}[H_{Cohort}]-1)}&=& \frac{m-\frac{1}{m^2}\sum _{i=1}^{m-1}i^2}{(m+1)/2}\nonumber\\ &=& \frac{m-\frac{1}{m^2}\frac{(m-1)(m-1+1)(2(m-1)+1)}{6}}{(m+1)/2}\nonumber\\ &=& \frac{4m-1}{3m}. \end{eqnarray} (7)
    Note that since Equation (7) is increasing in m $m$ , we can plug in m = 3 $m = 3$ and yield the lower bound on the ratio and send m $m$ to infinity to get the upper bound.
  • (c) In the special case of C = 2 $C=2$ , we can also explicitly compute the expectation of H Q S $H_{QS}$ . Note that since m = k l $m = kl$ , we can simplify the ratio and get
    2 ν ( E [ H F C F S ] − 1 ) 2 ν ( E [ H Q S ] − 1 ) = m − 1 m 2 ( m − 1 ) ( m − 1 + 1 ) ( 2 ( m − 1 ) + 1 ) 6 k ( l + 1 ) 2 − ( k − 1 ) ( 2 k − 1 ) 6 k = 4 m 2 + 3 m − 1 3 m 2 + 3 m + m k − l . \begin{eqnarray*} \frac{2\nu (\mathbb {E}[H_{FCFS}]-1)}{2\nu (\mathbb {E}[H_{QS}]-1)} &=& \frac{m-\frac{1}{m^2}\frac{(m-1)(m-1+1)(2(m-1)+1)}{6}}{\frac{k(l+1)}{2} - \frac{(k-1)(2k-1)}{6k}}\nonumber\\ & =& \frac{4m^2+3m-1}{3m^2 +3m + mk-l}. \end{eqnarray*}
    Note that 4 m 2 + 3 m − 1 3 m 2 + 3 m + m k − l $\frac{4m^2+3m-1}{3m^2 +3m + mk-l}$ is always greater than 1 since l < m $l&lt;m$ . □ $\Box$

From Proposition 4, we can observe that the value of the ascent and descent time can be shifted to lower values through the Cohorting and Queue Splitting interventions. The more groups it splits into, the greater the reduction can be. Next, we consider the distribution of the number of stops. The distribution and expected value of the number of stops can be found in a book (Barney & Al-Sharif, 2015). We summarize the results in Lemma 5 below.

Lemma 5.

  • (a) For each intervention, the distribution of the number of stops is as follows
    S C o h o r t = 1 with probability 1 , P [ S F C F S = x ] = x ! m C m x C x , x = 1 , … , min { C , m } , P [ S Q S = x ] = x ! k C k x C x , x = 1 , … , min { C , k } , \begin{eqnarray*} S_{Cohort}&=& 1 \text{ with probability } 1,\nonumber\\ \mathbb {P}[S_{FCFS} = x] &=& \frac{x!}{m^C} {\binom{m}{x}} {C\atopwithdelims \lbrace \rbrace x}, x = 1, \ldots , \min \lbrace C,m\rbrace ,\nonumber\\ \mathbb {P}[S_{QS} = x] &=& \frac{x!}{k^C} {\binom{k}{x}} {C\atopwithdelims \lbrace \rbrace x}, x = 1, \ldots , \min \lbrace C,k\rbrace , \end{eqnarray*}
    where C x ${C\atopwithdelims \lbrace \rbrace x}$ is the Stirling number of the second kind, the number of ways to partition a set of C objects into x $x$ nonempty subsets.
  • (b) The expected number of stops for FCFS and Queue Splitting is
    E [ S F C F S ] = m 1 − m − 1 m C , E [ S Q S ] = k 1 − k − 1 k C . \begin{eqnarray*} \mathbb {E}[S_{FCFS}] &=& m{\left[ 1-{\left(\frac{m-1}{m}\right)}^C\right]}, \nonumber\\ \mathbb {E}[S_{QS}] &=& k{\left[ 1-{\left(\frac{k-1}{k}\right)}^C\right]}. \end{eqnarray*}

With the distribution of H $H$ and S $S$ being derived in Lemmas 4 and 5, we plot the expected values in Figure 7 for various parameter settings. When the number of destination floors m $m$ becomes large, the expected number of stops will approach the capacity C $C$ in both FCFS and Queue Splitting intervention. However, Queue Splitting is increasing much slower, and the more groups we split into, the lower the value is. Similar behavior can be observed in the expected highest reversal floor graphs.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Expected highest reversal floor and number of stops in Lemmas 4 and 5

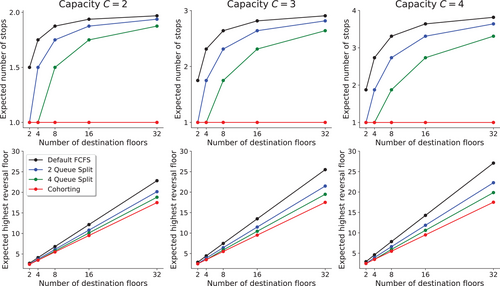
When the elevator capacity C $C$ increases, the reduction in the expected values of S $S$ and H $H$ becomes more significant for both the Queue Splitting and Cohorting intervention when compared with FCFS. Using a building with 32 floors as an example, 2 Queue Split can reduce the average number of stops by 4.6 % $4.6\%$ when C = 4 $C = 4$ , but only by 1.6 % $1.6\%$ when C = 2 $C = 2$ . For the average highest reversal floor, 2 Queue Split reduces it by 17.8 % $17.8\%$ when C = 4 $C = 4$ , but only by 11.8 % $11.8\%$ when C = 2 $C = 2$ . In general, the higher the capacity C $C$ is, and the larger the number of floors m $m$ is, the more difference we can observe from Figure 7. Therefore, it is indeed more critical for higher buildings with larger elevators to apply the proposed interventions to reduce the round trip time and make the queuing system more efficient.

5 PRACTICAL ISSUES IN COHORTING

Cohorting as discussed in Section 4 is focused on the situation where there is a large queue and we can create a cohort of passengers perfectly. Under this setup, we proved Cohorting is always the best in terms of highest reversal floor and number of stops (Lemmas 4 and 5). Of course, in our simulations it may not be always possible to cohort perfectly if the queue length is under control, and we see in the numerical results that Cohorting has inferior performance in highest reversal floor compared to 2 Queue Split in Figure 5. Cohorting has a slightly higher average H $H$ value (18.8) than 2 Queue Splitting (17.6). However, the number of stops in Cohorting (2.78) is lower than 2 Queue Split (3.27). Therefore, the overall round trip time, impacted by both number of stops and highest reversal floor is lower in Cohorting in the simulations, since each stop takes 15 s whereas traveling one floor takes only 1.4 s.

In the remainder of this section, we discuss three practice-related issues about our interventions that may improve or hurt their performance. For concreteness, we focus on Cohorting, but similar modifications can be made to other interventions.

5.1 The impact of willingness-to-walk

First, when the queue length is not large, we may not find enough people who go to the same floor. One way to increase the chance of people going to the same floor is by asking them to take the stairs. We model this behavior using the Willingness-to-Walk ( W t W $WtW$ ) parameter indicating the probability that a given passenger would walk one floor up or down from their intended destination instead of preferring to only go to their destination floor. For example, if W t W = 20 % $WtW=20\%$ , then 20 % $20\%$ of all passengers whose intended destination is floor d $d$ would consider the option of taking an elevator to any of the floors d − 1 , d $d-1,d$ or d + 1 $d+1$ . Our consideration of W t W $WtW$ is inspired by literature showing that leveraging demand-side flexibility can be effective in managing operations (Elmachtoub et al., 2019; Tao et al., 2020).

When some passengers have the willingness of walking one floor up or down to their intended destination, the system may benefit from the potential reduction in the number of stops each elevator trip needs to make. Using simulation, we can see how much value it provides for different levels of W t W $WtW$ on the Cohorting and Queue Splitting interventions. In the Cohorting intervention, passengers line up in a single queue and the QM asks along the line whether the passengers are going to the target floor, which is the first passenger's destination. If a passenger is going to an adjacent floor of the target floor and is willing to walk, then they would say yes and join the cohort with the first passenger. In the Queue Splitting intervention, we assume that a passenger who is willing to walk will choose the shortest queue to join upon arrival, which can either go to the final destination directly, or stop at one floor lower or higher. Note that this option is only available to passengers whose destination floor is at the boundary of a floor group. We summarize the results in Figure 8.

Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Plot of average queue length in the lobby vs. willingness-to-walk. Note: We run 100 independent random instances and report the average performance. Between 8 and 10 a.m., 2750 passengers with destinations ranging from floors 2 to 25 are served by 14 elevators (each with capacity 4). In the 4 Queue Split intervention, we divide the floor ranges equally among all the queues. The queue length under the default FCFS is on average 62 passengers across the 100 random instances

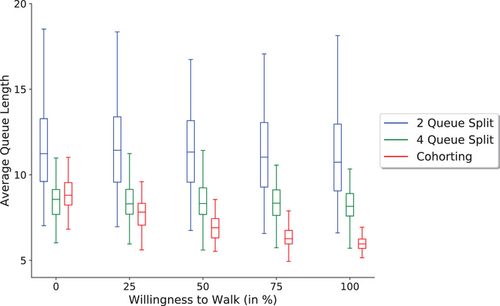
In Figure 8, we report the boxplot of the average queue length for three interventions with W t W $WtW$ level from 0 % $0\%$ to 100 % $100\%$ . When W t W = 0.25 $WtW=0.25$ , then Cohorting can be improved an additional 10%–20%, while if W t W = 100 % $WtW=100\%$ (which is idealistic), Cohorting can be improved by up to 30%–40%. There is barely any change in the queue length when increasing W t W $WtW$ from 0 % $0\%$ to 100 % $100\%$ for Queue Splitting, though the performance varies slightly due to randomness in the 100 simulated instances, because the distribution of the highest reversal floor and the number of stops do not change much when we allow passengers whose destination is at the boundary of the queue ranges to switch to another queue. Overall, the willingness of passengers to walk one flight can improve the performance if Cohorting is implemented, but the benefit is marginal (comparing to the queue length decrease one can observe by solely using Cohorting, which is approximately 62 in FCFS to 9 in Cohorting). Furthermore, the effect may be overestimated since passengers may not comply with their willingness to walk a flight of stairs once they board, since they can easily push the floor button they desire, and it may take extra time for communication when walking is included in the operations.

5.2 Limited space and communication time

The second practical issue relates to the number of passengers the QM can reach. In a particular building, the QM may not be able to communicate with everyone in the line. The QM cannot reach out to people beyond a point, perhaps due to a turn in the hallway or the small size of the lobby. We reevaluate the Cohorting intervention with an extra constraint, which is that the QM can only consider a certain number of passengers from the front of the queue. In Figure 9, we study Cohorting with a limited number of people within reach of the QM for the large building case study.

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Performance of the Cohorting intervention with practical considerations. Note: We run 100 independent random instances and report the average performance. Between 8 and 10 a.m., 2750 passengers with destinations ranging from floors 2 to 25 are served by 14 elevators (each with capacity 4). We consider two practical issues: (1) limited number of passengers within reach of the QM, and (2) only finding another passenger to be paired with the first passenger. The black, red, and pink dots in the graph are performance benchmarks without the limit on the number of passengers the QM can talk to

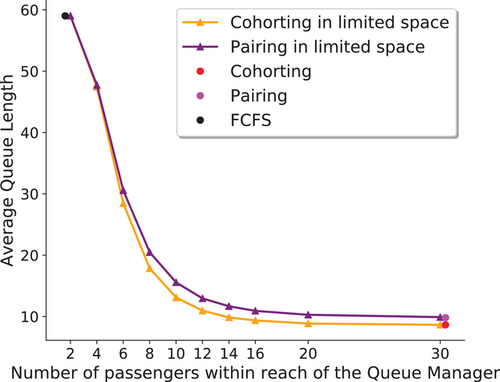
The final practical issue is the extra time Cohorting may take due to the communication time it takes for the QM to learn about the passengers' destination. To simplify the Cohorting implementation in this simulation, we propose the Cohorting with Pairing intervention, which only requires the QM to find one other passenger with the same destination as the first person and create a “pair” to board the same elevator. In the original Cohorting intervention, the QM tries to match up to C − 1 $C-1$ people with the first person in line. Loading an elevator of capacity 4 with one pair leads to at most three stops, and two pairs leads to two stops being made by the elevator. A pseudocode implementation of the Cohorting with Pairing intervention is available in Supporting Information, Section EC.4 as Algorithm 3.

Figure 9 shows the performance of Cohorting and Cohorting with Pairing interventions when the number of people within reach of the QM is limited. As comparison benchmarks, we also plot the performance of the FCFS, Cohorting, and Cohorting with Pairing intervention without the constraint on the number of passengers that can be considered by the QM. The first observation is that Cohorting with Pairing is an effective and easy-to-implement intervention, as it performs almost as good as the Cohorting intervention when the QM can reach the same number of passengers. Moreover, as the QM can approach passengers further in the queue, the average queue length shrinks rapidly. When the QM can reach out to about 10 people, the queue length is already less than 20 and being able to reach more than 10 passengers adds marginal value. Therefore, it is critical to design a safe queuing plan with physical distancing such that 10 people can hear the QM, which is a practical and reasonable target. Moreover, the QM can simply implement the Cohorting with Pairing intervention in the limited lobby space. The figures may vary across different buildings and our code implementation can easily be changed to analyze different settings.

6 CONCLUSIONS AND FUTURE WORK

This project was done with the guidance of New York City Mayor's Office of the Chief Technology Officer and the Department of Citywide Administrative Services, which had continuous input into our work throughout the process. Through this work, we combine mathematical modeling and epidemiological expertise to design interventions for safely managing elevator systems amidst a pandemic. The social distancing requirement during a pandemic may lead to large buildup of queues in the lobby during busy periods when using FCFS. We propose various interventions with a QM to help load passengers in the lobby. The fundamental idea behind these interventions is to try to reduce queue buildup by maximizing the number of people in an elevator trip going to the same floor (or nearby floors), which in turn reduces boarding/deboarding times as well as travel times. The interventions we study apply to generic buildings, and we have provided open-source code so other building settings can be studied. The intervention chosen by a building may depend on its particular simulation results, physical layout, personnel, and epidemiological considerations. For example, in the large NYC building case study, the maximum queue length in Cohorting and 2 Queue Split are, respectively, over a factor of eight and five times smaller than that of FCFS. Cohorting is even effective when the QM can only talk to the first few people in the queue, or when we cohort in pairs only. We also provide customizable open-source code and an instructional video explaining our interventions.

A comparison of the two proposed interventions is provided in Table 1. Our simulations show that the Cohorting intervention leads to lower waiting time for passengers in the lobby and reduces the number of people in the lobby (queue length) significantly. If the QM cannot talk to many people in the line, we suggest the Cohorting with Pairing intervention in limited space, which is easier to implement and provides similar benefits as Cohorting, as long as the QM's announcement can reach a suitable number of people in the line. We also propose the Queue Splitting intervention which implicitly groups similar passengers together to improve efficiency while needing less communication from the QM. Queue Splitting with even a small number of queues achieves comparable performance to Cohorting. The proposed interventions are effective beyond the constraints imposed by a pandemic, and thus are still useful after the pandemic to manage lobby queues.

TABLE 1. Cohorting versus Queue Splitting
Cohorting Queue splitting
Pros

  • Shortest service time in theory
  • Shorter queue length across buildings

  • Less communication needed, QM not necessary
  • Ease of understanding for users and managers
Cons

  • Need a QM for good implementation
  • Communication may be difficult

  • Worse than Cohorting under heavy traffic
  • Need space for horizontal separation of queues

In this paper, we have only considered the problem of moving people upwards in a building from the lobby. Without any elevator AI, it is near-impossible to do any interventions for downward and interfloor movement. Using sensors, it would be possible to know how many people are in each elevator, where they are going, which floors have a request, and how many people are waiting on each floor. We could then intervene, allowing us to design algorithms that balance efficiency of the system with fair waiting times, while maintaining the safety standards necessary (Pepyne & Cassandras, 1997). For instance, due to the reduced elevator capacities, a passenger on a middle floor may have difficulty leaving the building during lunchtime. Every time an elevator arrives, it may be filled with passengers from higher floors. In future work, one can design algorithms that mitigate such a situation, which is likely (and known) to occur.

There are many other considerations to be investigated. Due to perceived inequity in interventions like Cohorting, which let passengers jump the queue maybe for the greater good, there could be individual frustrations (Berry et al., 2002; Larson, 1987). One can also only implement an intervention when the queue length exceeds a threshold and otherwise rely on FCFS, which reduces the overall need of a QM. In our study, the passenger arrival patterns and destinations were generally stationary and uniform, and different effects may occur otherwise. However, we note that if some floors are more popular than others, then it may actually be easier to implement Cohorting. Finally, given more data and knowledge of the internal elevator algorithms, our models could simulate interfloor traffic more accurately.

ACKNOWLEDGMENTS

The authors are grateful to the senior editor and the two anonymous referees for their suggestions that helped improve this paper. The authors thank the New York City Department of Citywide Administrative Services and Neal Parikh, Director of Artificial Intelligence in the Mayor's Office of the Chief Technology Officer, New York City, for data used in this work. YZ did most of this work while at Columbia University. The study was supported by an award under Columbia Engineering's “Urban Living Tech Innovations” initiative to develop technology innovations for urban living in the face of COVID-19. AE and YZ were supported by NSF CMMI-1944428. CS and SMA were supported by NSF CCF-1714818.

    ENDNOTES

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.