Evolution of a biochemical model of steady-state photosynthesis
Abstract
On the occasion of the 40th anniversary of the publication of the landmark model by Farquhar, von Caemmerer & Berry on steady-state C3 photosynthesis (known as the “FvCB model”), we review three major further developments of the model. These include: (1) limitation by triose phosphate utilization, (2) alternative electron transport pathways, and (3) photorespiration-associated nitrogen and C1 metabolisms. We discussed the relation of the third extension with the two other extensions, and some equivalent extensions to model C4 photosynthesis. In addition, the FvCB model has been coupled with CO2-diffusion models. We review how these extensions and integration have broadened the use of the FvCB model in understanding photosynthesis, especially with regard to bioenergetic stoichiometries associated with photosynthetic quantum yields. Based on the new insights, we present caveats in applying the FvCB model. Further research needs are highlighted.
1 INTRODUCTION
The year of writing this paper marks the 40th anniversary of the widely used biochemical model of Farquhar, von Caemmerer, and Berry (1980) on C3 photosynthesis, known as the “FvCB model” (see Table 1 for all acronyms). The model is a mathematical representation of the biochemical processes in the chloroplast related to photosynthetic CO2 uptake of plants. The application of this model has gone far beyond the developers' expectations even 20 years ago (see the reflections by Farquhar, von Caemmerer, & Berry, 2001) and continues to rapidly rise today. It has become one of the most widely used models in plant science and beyond. For understanding leaf physiology, the model has been used to analyse gas exchange (sometimes combined with chlorophyll fluorescence) data (e.g., Long & Bernacchi, 2003; Sharkey, Bernacchi, Farquhar, & Singsaas, 2007; von Caemmerer & Farquhar, 1981; Yin et al., 2009), to understand photosynthetic control of electron transport (e.g., Foyer, Neukermans, Queval, Noctor, & Harbinson, 2012), and to quantify photosynthetic limitations (e.g., Busch & Sage, 2017; Deans, Farquhar, & Busch, 2019). When coupled to models of stomatal control, it contributes to understanding how water is traded for CO2 (Farquhar & Wong, 1984; Leuning, 1990) and how photosynthetic gas-exchange and water-relation traits are coordinated (Deans, Brodribb, Busch, & Farquhar, 2020). The FvCB model forms the basis of our understanding of photosynthetic isotope discrimination (Busch, Holloway-Phillips, Stuart-Williams, & Farquhar, 2020; Farquhar, 1983; Farquhar, O'Leary, & Berry, 1982; Ubierna et al., 2019). It has also been used to scale photosynthetic processes from the chloroplast and leaf level to higher levels (Bagley et al., 2015; Yin & Struik, 2008), and for assessing the impact of genetic engineering for identified photosynthetic targets on canopy productivity (e.g., Zhu, Portis Jr., & Long, 2004) and crop yield (Wu, Hammer, Doherty, von Caemmerer, & Farquhar, 2019; Yin & Struik, 2017a). The model is even used to inform climate models (Pitman, 2003) and describe plant carbon uptake on the global level as a component of Earth System Models (Rogers, Medlyn, & Dukes, 2014; Sellers et al., 1996). Here, we take a historical view of the original FvCB model and subsequently go into details of how this model has been extended since then.
| Acronym | Definition |
|---|---|
| BS | Bundle sheath |
| CCM | CO2-concentrating mechanism |
| CET | Cyclic electron transport around Photosystem I |
| CH2-THF | 5,10-methylene-tetrahydrofolate |
| FvCB model | The model of Farquhar, von Caemmerer, & Berry (1980) |
| GDC | Glycine decarboxylase |
| H+ | Proton |
| IAS | Intercellular air spaces |
| LET | Linear electron transport (i.e., the noncyclic electron transport for supporting the Calvin–Benson cycle and the photorespiratory cycle) |
| M | Mesophyll |
| NAD-ME | Nicotinamide adenine dinucleotide-malic enzyme |
| NADP-ME | Nicotinamide adenine dinucleotide phosphate-malic enzyme |
| NDH | NAD(P)H dehydrogenase |
| PEP | Phosphoenolpyruvate |
| PEPc | Phosphoenolpyruvate carboxylase |
| PEP-CK | Phosphoenolpyruvate-carboxykinase |
| 3-PGA | 3-phosphoglycerate |
| Pi | Phosphate |
| PPDK | Pyruvate phosphate dikinase |
| PSI | Photosystem I |
| PSII | Photosystem II |
| RuBP | Ribulose 1,5-bisphosphate |
| THF | Tetrahydrofolate |
| TP | Triose phosphate |
| TPU | Triose phosphate utilization |
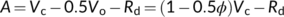 (1)
(1)| Symbol | Definition | Unit |
|---|---|---|
| a | Fraction of oxaloacetate that is reduced in mesophyll cells to malate moving to drive bundle sheath mitochondrial electron transport to produce ATP | — |
| A | Rate of CO2 assimilation | μmol m−2 s−1 |
| Ac | Rate of CO2 assimilation limited by Rubisco activity | μmol m−2 s−1 |
| Aj | Rate of CO2 assimilation limited by electron transport | μmol m−2 s−1 |
| Ap | Rate of CO2 assimilation limited by triose phosphate utilization | μmol m−2 s−1 |
| Cc | CO2 partial pressure at the carboxylating sites of Rubisco | μbar |
| Ci | CO2 partial pressure at intercellular-air spaces | μbar |
| Cm | CO2 partial pressure at mesophyll cytosol | μbar |
| f | Fraction of irradiance absorbed by photosynthetic pigments but unavailable for Calvin–Benson and photorespiratory cycles | — |
| F | Rate of photorespiratory CO2 release | μmol m−2 s−1 |
| fcyc | Fraction of Photosystem I electrons that follow cyclic electron transport | — |
| fNDH | Fraction of cyclic electron transport that follow the NAD(P)H dehydrogenase-dependent pathway | — |
| fpseudo | Fraction of the Photosystem I electrons that follow the pseudocyclic electron transport | — |
| frefix | Fraction of respired and photorespired CO2 that is refixed | — |
| frefix,cell | Fraction of respired and photorespired CO2 that is refixed within mesophyll cells | — |
| frefix,ias | Fraction of respired and photorespired CO2 that is refixed via the intercellular air spaces | — |
| fQ | Fraction of electrons at plastoquinone that follow the Q cycle | — |
| gbs | Bundle-sheath conductance | mol m−2 s−1 bar−1 |
| gm | Mesophyll conductance (inverse of mesophyll resistance), =1/rm | mol m−2 s−1 bar−1 |
| gmo | Mesophyll conductance constant, applied to the constant mesophyll conductance mode | mol m−2 s−1 bar−1 |
| h | Protons required per ATP synthesis (i.e., the H+:ATP ratio) | mol mol−1 |
| Iabs | Irradiance absorbed by photosynthetic pigments | μmol m−2 s−1 |
| J | Potential electron transport rate | μmol m−2 s−1 |
| J1 | Potential electron transport rate through Photosystem I | μmol m−2 s−1 |
| J2 | Potential electron transport rate through Photosystem II | μmol m−2 s−1 |
| Jatp | Potential rate of chloroplastic ATP production | μmol m−2 s−1 |
| Jmax | Light-saturated potential electron transport rate | μmol m−2 s−1 |
| J2max | Light-saturated potential electron transport rate through Photosystem II | μmol m−2 s−1 |
| k | Factor allowing for the effect of chloroplast gaps and the cytosol resistance such that the term kλ defines as the fraction of (photo)respiratory CO2 in the inner cytosol (0 ≤ kλ ≤ 1) | — |
| KmC | Michaelis–Menten constant of Rubisco for CO2 | μbar |
| KmO | Michaelis–Menten constant of Rubisco for O2 | mbar |
| Kp | Michaelis–Menten constant of PEPc for CO2 | μbar |
| L | Rate of CO2 leakage from bundle-sheath to mesophyll cells | μmol m−2 s−1 |
| m | Parameter lumping several mesophyll properties, = (1 − λk)rch/rm with 0 ≤ m ≤ 1 | — |
| n | ATP produced per NADH oxidation | mol mol−1 |
| Oc | O2 partial pressure at the active sites of Rubisco | mbar |
| Om | O2 partial pressure at mesophyll cytosol | mbar |
| rch | Chloroplast envelope and stroma resistance | mol−1 m2 s bar |
| rcx | Carboxylation resistance | mol−1 m2 s bar |
| rm | Mesophyll resistance, =rwp + rch | mol−1 m2 s bar |
| rsc | Stomatal resistance to CO2 transfer | mol−1 m2 s bar |
| rwp | Cell-wall and plasma-membrane resistance | mol−1 m2 s bar |
| Sc/o | Relative CO2/O2 specificity of Rubisco | mbar μbar−1 |
| Tp | Rate of triose phosphate utilization | μmol m−2 s−1 |
| uoc | Coefficient that lumps diffusivities of O2 and CO2 in water and their respective Henry constants, = 0.047 at 25°C | μmol μbar (μmol μbar)−1 |
| Vc | RuBP carboxylation rate | μmol m−2 s−1 |
| Vcmax | CO2-saturated maximum carboxylation rate of Rubisco | μmol m−2 s−1 |
| Vo | RuBP oxygenation rate | μmol m−2 s−1 |
| Vp | PEP carboxylation rate | μmol m−2 s−1 |
| Vpmax | Maximum carboxylation rate of PEPc | μmol m−2 s−1 |
| Rd | Day respiration (CO2 release in the light by processes other than photorespiration) | μmol m−2 s−1 |
| Rm | Day respiration in the mesophyll cells | μmol m−2 s−1 |
| Wc | RuBP carboxylation rate limited by Rubisco activity | μmol m−2 s−1 |
| Wj | RuBP carboxylation rate limited by electron transport | μmol m−2 s−1 |
| Wp | RuBP carboxylation rate limited by triose phosphate utilization | μmol m−2 s−1 |
| x | Fraction of the chloroplastic ATP that is used for the C4 cycle | — |
| z | Factor for ATP production per Photosystem II electron when the cyclic electron transport runs simultaneously | mol mol−1 |
| α | Fraction of glycolate carbon not returned to chloroplast | — |
| α2(LL) | Quantum yield of Photosystem II electron transport (under limiting light) on the basis of light absorbed by both photosystems | mol mol−1 |
| αbs | Fraction of Photosystem II that is in the bundle-sheath cells | — |
| αG | Fraction of glycolate carbon taken out from the photorespiratory pathway as glycine | — |
| αS | Fraction of glycolate carbon taken out from the photorespiratory pathway as serine | — |
| αT | Fraction of glycolate carbon taken out from the photorespiratory pathway as CH2-THF | — |
| δ | Factor defining a variable mesophyll conductance mode | — |
| ϕ | RuBP oxygenation : RuBP carboxylation ratio, =Vo:Vc | — |
| ϕL | Leakiness, =L/Vp | — |
| Φ1(LL) | Quantum yield of Photosystem I electron transport (under limiting light) | mol mol−1 |
| Φ2(LL) | Quantum yield of Photosystem II electron transport (under limiting light) | mol mol−1 |
| ΦCO2(LL) | Quantum yield of CO2 uptake (under limiting light) | mol mol−1 |
| ΦO2(LL) | Quantum yield of O2 evolution (under limiting light) | mol mol−1 |
| φ | Chloroplastic ATP required per C4 cycle, = 2 for the NADP-ME and NAD-ME subtypes and = 2 − (n + 1)a for the PEP-CK subtype | mol ATP (mol CO2)−1 |
| γ* | Half the inverse of Rubisco specificity, =0.5/Sc/o | μbar mbar−1 |
| Γ* | CO2-compensation point in the absence of day respiration, =0.5Oc/Sc/o | μbar |
| Γ*GT | Modified Γ* as a result of glycolate carbon exit in the form of glycine and CH2-THF from the photorespiratory pathway, =(1 − αG + 2αT)Γ* | μbar |
| λ | Fraction of mitochondria that locate closely behind chloroplasts in the inner cytosol | — |
| θ | Curvature factor of light response of electron transport | — |
| ρ2 | Factor for excitation partitioning to Photosystem II, =α2(LL)/Φ2(LL) | — |
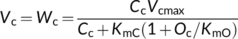 (2a)
(2a)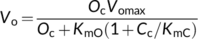 (2b)
(2b)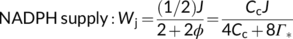 (3a)
(3a)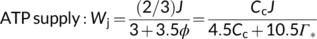 (3b)
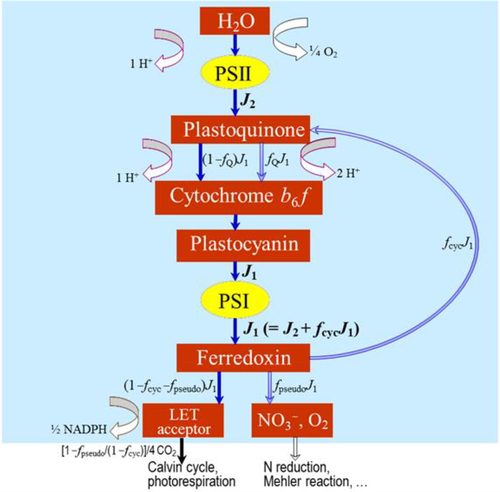
(3b)Equation (3a) is based on the stoichiometry of NADPH or electron requirement by the Calvin–Benson cycle and the photorespiratory cycle. First, carboxylation of one mol RuBP results in two mol 3-PGA, reduction of each 3-PGA to triose phosphate (TP) requires one mol NADPH (Figure 1a), and production of one mol NADPH requires two mol electrons; so, four electrons are required per carboxylation. The whole term in the numerator, (1/2)J, represents the rate of NADPH production from LET. Secondly, although oxygenation of one mol RuBP initially results in only one mol 3-PGA, it also results in one mol of the two-carbon molecule, 2-phosphoglycolate, which is dephosphorylated to glycolate in the chloroplast (Figure 1a,b). The glycolate is transported from the chloroplast into the peroxisome, where it is converted to glyoxylate and further to glycine (two carbons). The glycine is exported to the mitochondrion, where 0.5 mol glycine and tetrahydrofolate (THF) are converted by glycine decarboxylase (GDC) to 5,10-methylene-tetrahydrofolate (CH2-THF), releasing 0.5 mol ammonia and 0.5 mol CO2 in the process. CH2-THF reacts with the remaining 0.5 mol glycine to form 0.5 mol serine (three carbons). Serine moves to the peroxisome and is transformed to glycerate. The glycerate flows to the chloroplast and is converted to 0.5 mol 3-PGA. Its reduction before incorporation into the Calvin-Benson cycle consumes 0.5 mol NADPH. The 0.5 mol ammonia released by GDC is re-assimilated into glutamate requiring one mol reduced ferredoxin (equivalent to 0.5 mol NADPH). In sum, the photorespiratory cycle involving three organelles (chloroplast, peroxisome, and mitochondrion, Figure 1b) requires four electrons per oxygenation.
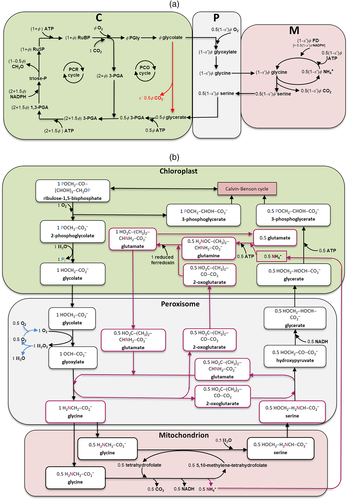
In Equation (3b), the coefficient 2/3 stems from understandings of that time (in 1980) about the stoichiometry that each mol electron in LET translocates two mol protons (H+) across the thylakoid membrane into the lumen, and synthesis of one mol ATP requires three mol H+; so, the whole term in the numerator, (2/3)J, represents the rate of ATP production from LET. The coefficient 3 in the denominator refers to the requirement of three mol ATP per mol RuBP carboxylated by the Calvin–Benson cycle, consisting of two mol ATP for the phosphorylation of two mol 3-PGA to two mol 1,3-bisphosphoglycerate (before the reduction step consuming NADPH) and one mol ATP for the subsequent phosphorylation of one mol ribulose 5-phosphate to one mol RuBP (Figure 1a). The coefficient 3.5 refers to the ATP requirement per oxygenation by the photorespiratory cycle. This consists of: (1) one mol ATP for the phosphorylation of one mol 3-PGA to one mol 1,3-bisphosphoglycerate before its reduction, (2) one mol ATP for the phosphorylation of ribulose 5-phosphate to RuBP, (3) 0.5 mol ATP for the phosphorylation of glycerate to 3-PGA plus 0.5 mol ATP for the subsequent phosphorylation of this 0.5 mol 3-PGA, and (4) 0.5 mol ATP for the re-assimilation of 0.5 mol ammonia (Figure 1a).
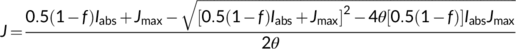 (4)
(4)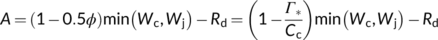 (5)
(5)Since its first publication, the model has been developed further several times for C3 photosynthesis (Busch, 2020; Busch, Sage, & Farquhar, 2018; Harley & Sharkey, 1991; Sharkey, 1985a, 1985b; Yin, van Oijen, & Schapendonk, 2004) and extended for C4 photosynthesis (von Caemmerer & Furbank, 1999). Also, this model has been integrated with models for mesophyll CO2-diffusion for various applications. In this paper, we outline the major extensions and review how these extensions and integration have broadened the use of the model in exploring the underlying physiology of photosynthesis.
2 EXTENSION 1: INTRODUCING THE THIRD LIMITATION SET BY TRIOSE PHOSPHATE UTILIZATION
2.1 Accommodating photosynthetic insensitivity to CO2 and O2
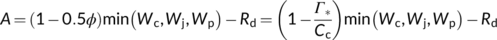 (6a)
(6a)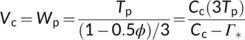 (6b)
(6b)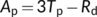 (6c)
(6c)2.2 Accommodating the reversed sensitivity to CO2 and O2
It has been frequently observed that A even declines with increasing CO2 partial pressure within the high CO2 range, particularly under low O2 conditions (e.g., von Caemmerer & Farquhar, 1981). Similarly, increasing O2 has been observed to stimulate CO2 assimilation under high CO2 conditions (Harley and Sharkey (1991). These reversed sensitivities to CO2 and O2 cannot be explained by the simple model, Equation (6c).
Sharkey and Vassey (1989) proposed that the reverse sensitivity was caused by inhibition of starch synthesis capacity, and in turn caused reduced stromal phosphoglucoisomerase activity resulting from metabolites interfering with its activity. An alternative explanation was proposed by Harley and Sharkey (1991) that a fraction of the glycolate carbon, which leaves the chloroplast and is recycled to glycerate in the photorespiratory cycle, does not return to the chloroplast, but after converting to glycine, is diverted from the photorespiratory cycle and used elsewhere for amino acid synthesis. Thus, the Pi normally used in converting glycerate to 3-PGA is made available for phosphorylation instead, thereby, stimulating RuBP regeneration. Based on this hypothesis, Harley and Sharkey (1991) used three values for the fraction (0.0, 0.5, and 1.0) to fit data and showed how the curvature of photosynthetic CO2-response curves (A–Ci curves) had varying extents of the reversed CO2 and O2 sensitivity.
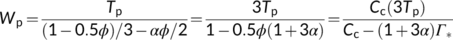 (7a)
(7a)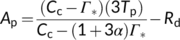 (7b)
(7b)2.3 Implications of TPU limitation in modelling leaf photosynthesis
Ellsworth, Crous, Lambers, and Cooke (2015) showed that TPU limitations to photosynthetic capacity are common in woody species grown in the field. However, TPU might not be the most important limitation under current climatic growth conditions, as evidenced by Kumarathunge, Medlyn, Drake, Rogers, and Tjoelker (2019), who reported that only ca 30% of A–Ci curves showed an obvious TPU limitation in a global data representing 141 species. Irrespective of its uncertain importance under field conditions, the inclusion of TPU limitation in models is important for elucidating the basic principles of photosynthetic mechanisms. In cases where TPU is actually limiting, the canonical, two-limitation FvCB model would underestimate Jmax (when fitting to A–Ci curves) and Vcmax or Jmax (when fitting to light response curves) because the maximum photosynthetic rate would be wrongly attributed to being limited by electron transport or by Rubisco activity.
It is important to note that TPU limitation is a form of very short-term sink–source disequilibrium (McClain and Sharkey (2019). It concerns the ability to remove TP quickly from the Calvin–Benson cycle. The half-life time of the cycle intermediates can be shorter than 1 s, while some larger pools still have a half-life time of <1 min. This means that TPU limitation can build up and disappear quickly. As discussed by Sharkey (2019), when plants are put into TPU limited conditions for hours or days, the TPU limitation is observable at first; but then other components like electron transport are regulated to a level that TPU is no longer “apparently” limiting (e.g., Pammenter, Loreto, & Sharkey, 1993). Furthermore, over a longer time, a larger sink can remove short-term TPU limitation. Kaschuk et al. (2012) showed that nodulated soybean plants had 14%–31% higher rates of photosynthesis and accumulated less starch in the leaves than nitrogen-fertilized plants, supporting that rhizobial symbiosis could stimulate photosynthesis due to the removal of carbon sink limitation by nodule activities.
Conversely, a small sink, especially when combined with a large source, can cause TPU limitation. Fabre et al. (2019) reported the occurrence of TPU limitation in panicle-pruned rice plants, especially those grown under 800 μmol mol−1 CO2. This reduction was associated with sucrose accumulation in the flag leaf resulting from the sink limitation. The photosynthetic stimulation by the elevated-CO2 was lower in pruned plants compared with control plants, and this response to CO2 in relation to sink size was also found when comparing various rice genotypes having contrasting leaf:panicle size ratios or source:sink ratios (Fabre et al., 2020). A recent review by Dingkuhn et al. (2020) even found the evidence from broader ranges of genotypes that stronger elevated-CO2 responsiveness in wild relatives and old cultivars of crops is related to sink strength as a result of adaptive plasticity involving branching. Perhaps, the most important result in recent work of Fabre et al. is that TPU, thus net CO2 assimilation rate, declines increasingly with time after the midday in a diurnal cycle. These findings suggest that not only TPU limitation in regulating photosynthesis should be considered, but also a shorter time-step would be needed to account for diurnal variations in sink feedback limitation to photosynthesis, in dynamic crop models for projecting the CO2-fertilization effect on crop production.
3 EXTENSION 2: INTRODUCING ALTERNATIVE ELECTRON TRANSPORT PATHWAYS
3.1 Accommodating a balanced ATP:NADPH ratio
In the canonical FvCB model, there are two different equations, Equations (3a) and (3b), for the same electron transport-limited carboxylation rate, Wj. By comparison of the two equations, one can immediately recognize that the value of Wj determined by the ATP supply is more limiting than that determined by the NADPH supply. The two equations were used largely in a random manner in the literature before 2000. To eliminate the “random” application of the FvCB model, Yin et al. (2004) developed a generalized model that covers, among others, the two forms of the FvCB model for the electron transport-limited rate.
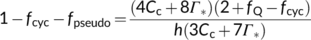 (8)
(8)
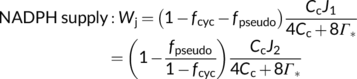 (9a)
(9a)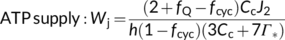 (9b)
(9b)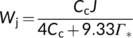 (9c)
(9c)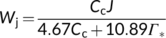 (9d)
(9d)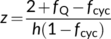 (9e)
(9e)3.2 Quantum efficiency of electron transport when cyclic and noncyclic pathways co-occur
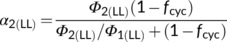 (10a)
(10a)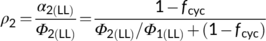 (10b)
(10b) (11)
(11)3.3 Quantum yield of CO2 uptake and of O2 evolution
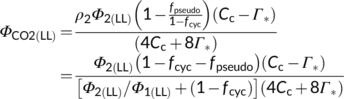 (12a)
(12a)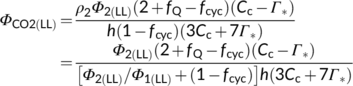 (12b)
(12b)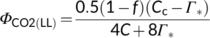 (12c)
(12c)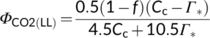 (12d)
(12d)Photosynthetic quantum yield can also be expressed in terms of O2 evolution (ΦO2(LL)). The electron requirement in support of both Calvin–Benson and photorespiratory cycles leads to O2 evolution at PSII from the splitting of H2O; so, the total O2 evolved can be expressed as (1 + 2Γ*/Cc)Vc. The O2 uptake by photorespiration consists of (i) one mol O2 consumed per mol RuBP oxygenation, and (ii) a further one mol O2 consumed in the conversion of one mol glycolate to one mol glyoxylate by glycolate oxidase in the peroxisome, producing one mol hydrogen peroxide (H2O2) which is immediately destroyed by the action of catalase into one mol H2O and 0.5 mol O2 (Figure 1b). So the total O2 uptake associated with the photorespiratory pathway is 1.5 mol O2 per mol RuBP oxygenated, which can be expressed as 1.5Vo = (3Γ*/Cc)Vc. Taking these together, the Rubisco-linked net O2 evolution is (1 − Γ*/Cc)Vc, which is the same as for CO2 uptake (von Caemmerer, 2000).
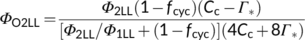 (12e)
(12e)3.4 Using the quantum yield model to infer hard-to-measure parameters
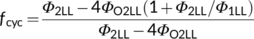 (13a)
(13a)Once fcyc is known, one can calculate another hard-to-measure light-partitioning parameter ρ2 from Equation (10b). The obtained ρ2 is ca 0.53, close to the assumed value 0.5 in the canonical FvCB model. This indicates that the requirement for a higher partitioning to the less efficient PSII is to some extent balanced by the requirement for a higher partitioning to PSI to run CET. Equation (10b) suggests that ρ2 equals exactly 0.5 only if the fraction for the noncyclic electron flow, 1 − fcyc, is equal to the Φ2LL:Φ1LL ratio.
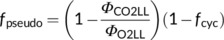 (13b)
(13b)Once fcyc and fpseudo are known, likely combinations of fQ and h can be solved from Equation (8) for C3 photosynthesis. Using the above estimates of fcyc and fpseudo for the nonphotorespiratory conditions, the solved h is ca 3.1 if fQ = 0 and is ca 4.67 if fQ = 1. The latter combination is very close to the contemporary belief that the operation of the Q cycle is obligatory (Sacksteder et al., 2000) and the structural data that chloroplast ATP synthase requires 4.67 c subunits or protons to produce one ATP (Seelert et al., 2000; Hahn et al., 2018). However, like the canonical FvCB model, Equation (8) does not account for small amounts of ATP required for starch synthesis and nitrogen assimilation. As ATP for these processes most likely come from chloroplasts (Noctor & Foyer, 1998), then the calculated h would approach 4. Energy requirements for nitrogen assimilation will further be discussed next.
4 EXTENSION 3: INTRODUCING PHOTORESPIRATION-ASSOCIATED NITROGEN AND C1 METABOLISMS
Nitrogen (N) assimilation can be intrinsically linked to the photorespiratory pathway (Bloom, 2015). While the electron and ATP requirement associated with re-cycling of the ammonia released by photorespiration is already accounted for (see Section 1), the energy requirement for reduction and assimilation of new nitrogen that enters the leaf is not accounted for in the canonical FvCB model. De novo assimilation of nitrogen in leaves of C3 plants can arise via the photorespiratory pathway because, as discussed earlier, the photorespiratory intermediate glycine can be diverted from the photorespiratory pathway and used elsewhere for amino acid synthesis, which explains the reversed photosynthetic sensitivity to CO2 and O2 (Harley & Sharkey, 1991). In addition, serine, a product of glycine decarboxylation in the photorespiratory pathway, can act as a precursor of several other amino acids (Ros, Muñoz-Bertomeu, & Krueger, 2014). The nitrogen molecules of both glycine and serine, if exported from the photorespiratory pathway for other uses or accumulated temporarily, have to be replenished by de novo assimilation of nitrogen; otherwise the pathway cannot be continued. Busch et al. (2018) extended both Wp- and Wj-limited rates of the FvCB model, by following the stoichiometry of energy requirement by both carbon and nitrogen assimilation as well as the stoichiometry for the amino-group balance. More recently, Busch (2020) further extended the model to account for the additional export of glycolate carbon as the photorespiratory pathway is also the main supply of the activated one-carbon units to the so-called C1 metabolism. This is because, as stated in Section 1, the glycine decarboxylation step can catalyse the conversion of the cofactor tetrahydrofolate (THF) to CH2-THF that acts as the leaf's currency for activated C1 units. Here, we collectively describe the extension involving both de novo nitrogen assimilation and C1 metabolisms (Figure 3).
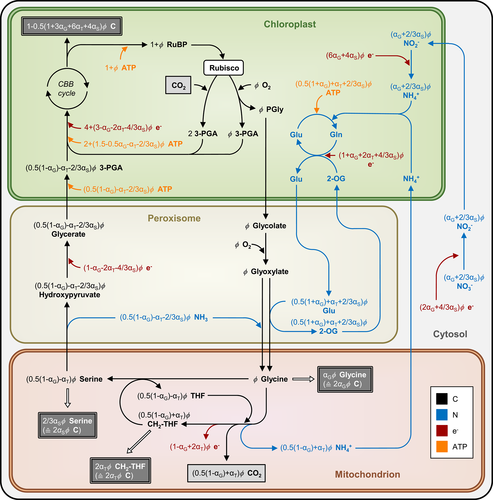
4.1 The general model of extension 3 integrating nitrogen and C1 metabolisms
 αS ≤
αS ≤  (1 − αG) − αT, where
(1 − αG) − αT, where  refers to the glycolate: serine carbon ratio (Figure 1b), and
refers to the glycolate: serine carbon ratio (Figure 1b), and  refers to half of glycine carbon lost during its decarboxylation. This relation can be converted into αG + 2αT +
refers to half of glycine carbon lost during its decarboxylation. This relation can be converted into αG + 2αT +  αS ≤ 1, thereby reflecting that the total proportion of glycolate carbon exports cannot exceed 1. Of course, none of αG, αT and αS can be lower than 0. In analogy to the derivation of Equation (7a) by Harley and Sharkey (1991), the rate of Pi consumption, which usually is (1 − 0.5ϕ)Vc/3, should be decreased by (αG + 2αT +
αS ≤ 1, thereby reflecting that the total proportion of glycolate carbon exports cannot exceed 1. Of course, none of αG, αT and αS can be lower than 0. In analogy to the derivation of Equation (7a) by Harley and Sharkey (1991), the rate of Pi consumption, which usually is (1 − 0.5ϕ)Vc/3, should be decreased by (αG + 2αT +  αS)ϕVc/2, and the net Pi consumption would be [(1 − 0.5ϕ)/3 − (αG + 2αT +
αS)ϕVc/2, and the net Pi consumption would be [(1 − 0.5ϕ)/3 − (αG + 2αT +  αS)ϕ/2]Vc. Thus, Wp as the rate of carboxylation set by TPU limitation in this case becomes:
αS)ϕ/2]Vc. Thus, Wp as the rate of carboxylation set by TPU limitation in this case becomes:
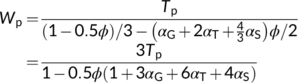 (14)
(14)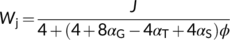 (15a)
(15a)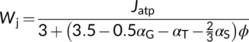 (15b)
(15b)Traditionally, the proportion of glycolate carbon that does not return to chloroplasts (α) is relevant only for the TPU-limited carboxylation rate Wp (see Equations (7a) and (7b)). Equations (15a) and (15b) suggest that the proportion parameters (αG, αT and αS) affect not only Wp but also Wj. The export of carbon as CH2-THF always increases Wj. Glycine and serine export associated with de novo N assimilation decreases Wj in terms of NADPH requirement whereas it increases Wj in terms of ATP requirement. This suggests that photorespiration-associated N assimilation can help alleviate the deficit of ATP relative to NADPH (see earlier discussions).
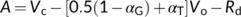 (16a)
(16a) (16b)
(16b)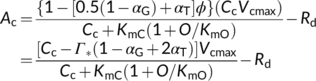 (16c)
(16c)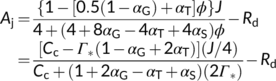 (16d)
(16d)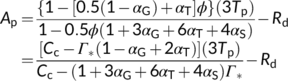 (16e)
(16e)In addition to exploring the ratio of O2 fixation by Rubisco to CO2 production by GDC to estimate αG, Busch et al. (2018) showed that αG and αS could be roughly estimated from model fitting to A–Ci curves. There is currently no information available about the possible value for the fraction of glycolate carbon diverted via the C1 metabolism (Busch, 2020). Therefore, hereafter we mainly discuss the relations with regard to the amino-acid exports.
4.2 Relationships with the previous two extensions
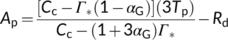 (17a)
(17a)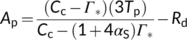 (17b)
(17b)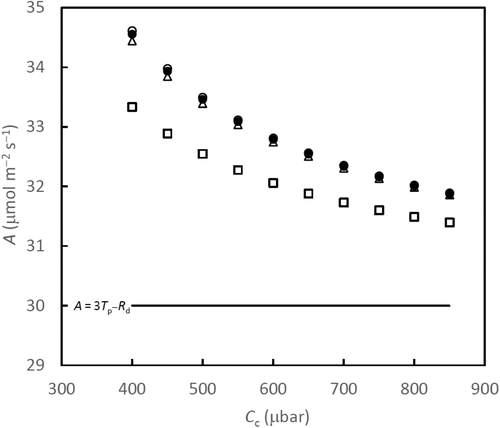
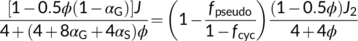 (18a)
(18a)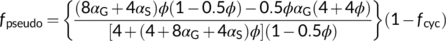 (18b)
(18b)Equation (18b) also reveals that surprisingly fpseudo does not increase monotonically with increasing ϕ if ϕ goes to a very high value (Figure 5a). The decline of fpseudo beyond a threshold ϕ occurs only in the presence of αG; and the higher is αG, the lower is the threshold ϕ. However, fpseudo always increases monotonically with increasing ϕ in the absence of αG, regardless of values of αS. All these responses are because αG, not αS, causes a decrease in CO2-compensation point, and this positive impact on A becomes increasingly important under high photorespiratory states (high ϕ values) that mathematically require a low fpseudo to enable the left and right sides of Equation (18a) in balance. For the same reason, although fpseudo generally increases with increasing αG or αS, its response to αG is stronger than to αS at a low ϕ (Figure 5b), is comparable at an intermediate ϕ corresponding to ambient-air conditions (Figure 5c), and is weaker than to αS at a high ϕ (Figure 5d).
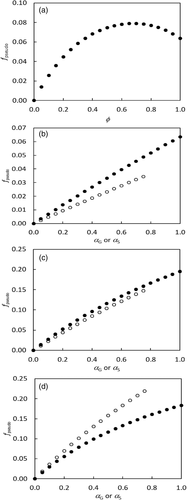
It is noteworthy that fpseudo calculated from Equation (18b) refers to the electron fraction responsible for supporting N assimilation only as result of amino acid export from the photorespiratory pathway. Therefore, the calculated fpseudo depends on the amount of photorespiration as shown in Figure 5. In contrast, fpseudo as one parameter in the model of Yin et al. (2004) for electron-transport-limited conditions lumps electron requirements for: (i) N assimilation of both via the photorespiratory pathway and not via this pathway and (ii) metabolic processes other than N assimilation that utilize chloroplastic electrons. As stated earlier, fpseudo of ca 0.10 was estimated from the assimilatory quotient for nonphotorespiratory conditions. The higher fpseudo estimated from the assimilatory quotient suggests that either not all nitrogen is assimilated via the photorespiratory pathway or/and processes other than N assimilation consumes chloroplastic electrons. Furthermore, the model of Busch et al. (2018) only applies to the case where it is NO3−-N that enters the leaf. However, it cannot be ruled out that nitrogen enters the leaf in the form of NH4+-N (Eichelmann, Oja, Peterson, & Laisk, 2011), and for such a case the stoichiometric coefficients of Equation (15a) has to be re-formulated whereas the model of Yin et al. (2004) remains the same but with a lower value of fpseudo.
5 COUPLING WITH THE MESOPHYLL CO2-DIFFUSION MODEL
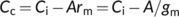 (19a)
(19a)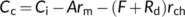 (19b)
(19b)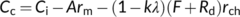 (19c)
(19c)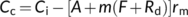 (19d)
(19d)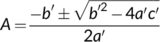 (20)
(20)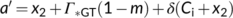
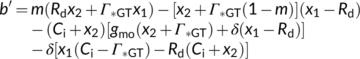
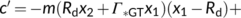

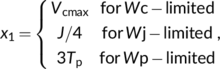
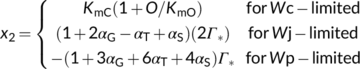
The solution to Equation (20) in case of Wc or Wj limitations is straightforward (the  term always taking the − sign). Gu, Pallardy, Tu, Law, and Wullschleger (2010) highlighted the mathematical complication arisen from a negative x2 in the case that Wp limits if the fraction of glycolate carbon not returned to chloroplasts is >0 and suggested a solution to that.
term always taking the − sign). Gu, Pallardy, Tu, Law, and Wullschleger (2010) highlighted the mathematical complication arisen from a negative x2 in the case that Wp limits if the fraction of glycolate carbon not returned to chloroplasts is >0 and suggested a solution to that.
The coupled gm-FvCB model offers a method to estimate gm (and other parameters) by fitting to gas exchange data only from exploring the curvature of A–Ci curves (Ethier & Livingston, 2004). When the coupled model is fitted to combined gas exchange and chlorophyll fluorescence data (Yin & Struik, 2009), it can improve the reliability of the estimates compared with the value of gm calculated from the conventional variable J method of Harley, Loreto, Di Marco, and Sharkey (1992). An alternative is using the stable 13C-isotope discrimination method (Farquhar et al., 1982), which was applied by Evans, Sharkey, Berry, and Farquhar (1986); Evans, von Caemmerer, Setchell, and Hudson (1994) to estimate gm (see review by Pons et al., 2009, and the most current model by Busch et al., 2020). But the chlorophyll fluorescence-based methods are more widely used because of the wider availability of the required device, despite the limitations (Evans, 2021). To minimize the influence of these limitations and of basal alternative transport pathways on estimating gm, van der Putten, Yin, and Struik (2018) demonstrated the importance of calibration using the measurements under nonphotorespiratory conditions. Any calibration method assumes that the fractions for alternative electron pathways are constant between photorespiratory and nonphotorespiratory conditions. However, recent reports by Abadie et al. (2016, 2018), Abadie and Tcherkez (2019) and Tcherkez and Limami (2019) suggest that the values of αG and αS, as well as the percentage of phosphoenolpyruvate (PEP) carboxylation and malate production (if any), and N-assimilation relative to CO2-assimilation may not be constant across various CO2/O2 gas mixtures. Chlorophyll-fluorescence-based methods to estimate gm require data that include the measurements under photorespiratory conditions such as at ambient CO2/O2 levels (Yin et al., 2020), whereas the 13C isotopic method has no such a requirement. On the other hand, estimates of gm by the 13C isotopic method are affected by assumptions made regarding the values of the fractionation factors (Busch et al., 2020; Gu & Sun, 2014; Pons et al., 2009). Thus, chlorophyll-fluorescence and 13C isotopic methods should be compared, whenever possible, for estimating gm.
 (21a)
(21a)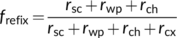 (21b)
(21b)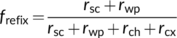 (21c)
(21c)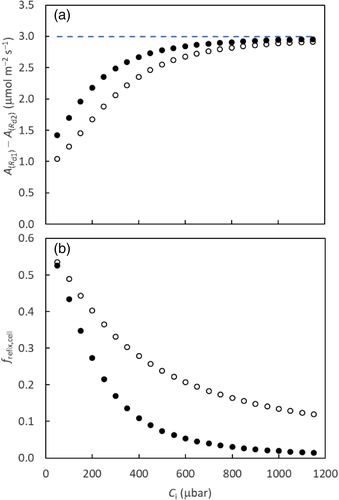
Refixation can occur both within the mesophyll cell (frefix,cell) and via the IAS (frefix,ias), which together constitute the total refixation (frefix = frefix,cell + frefix,ias) (Busch et al., 2013). In fact, the refixation of Rd illustrated in the above example using the coupled model with Ci as input (Figure 6a) actually refers to frefix,cell. frefix,cell and frefix,ias can also be directly calculated from resistance components and Yin et al. (2020) showed that if the term rsc is removed, Equations (21a)–(21c) become equivalent equations to calculate frefix,cell. They showed that frefix,cell generally dominates and leaves having the anatomical structure that Equation (19a) describes have a higher frefix,cell and thus a higher frefix than leaves having the structure that Equation (19b) describes despite the latter leaves having a higher frefix,ias. They quantitatively showed that for rice leaves where λk = 1, the estimated frefix was often high (≥0.5). These ideas of refixation have been exploited by synthetic biology approaches that engineer photorespiratory bypasses to relocate the photorespiratory CO2 release from mitochondria to chloroplasts (Kebeish et al., 2007; Shen et al., 2019; South, Cavanagh, Liu, & Ort, 2019; Figure 1a). The bypasses may be effective in increasing CO2 assimilation for leaves described by Equation (19b) under low CO2 conditions. However, values calculated based on resistance components represent the gross refixation of (photo)respired CO2, which is higher than the refixation reflected by results of the coupled model (Figure 6b). This suggests (photo)respired CO2 or bypassed CO2 decrease the chance of CO2 coming from IAS being assimilated; so, the net benefit of refixation must be smaller than what Equations (21a)–(21c) predict. But the bypass-associated saving of electrons and ATP that otherwise are consumed by the ammonia recycling (Figure 1a) provides more advantages (von Caemmerer, 2013).
6 THE C4 FORM OF THE MODEL
CO2 diffusion is also important for C4 photosynthesis because its CO2-concentrating mechanism (CCM) relies on the effective coordination of a series of diffusional processes and biochemical reactions. In the vast majority of terrestrial C4 species, this mechanism is achieved through the coordinated functioning via the Kranz structure involving mesophyll (M) and bundle-sheath (BS) cells (Hatch, 1987). CO2 initially diffuses to the M cytosol and is converted to HCO3−, which is fixed by PEP carboxylase (PEPc) into C4 acids. The C4 acids travel to the BS cells, where they are decarboxylated and the released CO2 is re-fixed by Rubisco exclusively localized in BS chloroplasts. The Km of PEPc is lower, and its maximum carboxylation rate is generally higher, than that of Rubisco. This will elevate the CO2 partial pressure in the BS compartment, despite some leakage of CO2 from BS back to M cells, which effectively suppresses photorespiration. Because Rubisco is operated in high-CO2 compartments, kinetic constants of C4 Rubisco differ from those of C3 Rubisco (Boyd, Gandin, & Cousins, 2015; Cousins, Ghannoum, von Caemmerer, & Badger, 2010; Sharwood, Ghannoum, Kapralov, Gunn, & Whitney, 2016), which together with the CCM per se, underlies the high photosynthetic nitrogen use efficiency of C4 plants (Ghannoum et al., 2005). C4 species are traditionally classified into three subtypes according to the decarboxylation enzymes, thus also decarboxylation sites: NADP-malic enzyme (ME) in chloroplasts, NAD-ME in mitochondria, and PEP-carboxykinase (CK) in the cytosol (Hatch, 1987). However, more recent opinions (e.g., Furbank, 2011; Wang, Brautigam, Weber, & Zhu, 2014; Yin & Struik, 2018) suggest that C4 species often have a mixed decarboxylation pathway, where one enzyme acts as the main decarboxylating enzyme alongside the others.
6.1 The standard model for C4 photosynthesis
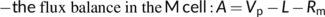 (22a)
(22a)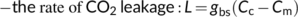 (22b)
(22b)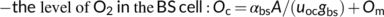 (22c)
(22c) (22d)
(22d)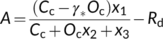 (22e)
(22e)Unlike in C3 leaves, the initial carbon fixation in C4 leaves is catalysed by PEPc in the cytosol and therefore gm does not involve CO2 diffusion from the cytosol to the chloroplast. Accordingly, estimates of gm in C4 leaves are somewhat higher than those in C3 leaves (e.g. Barbour, Evans, Simonin, & von Caemmerer, 2016), meaning gm appears to be less limiting to C4 photosynthesis as it is to C3 photosynthesis. However, gbs, which determines the amount of CO2 leakage (see Equation (22b)), is fundamentally important for the CCM, and thus, for determining C4 photosynthesis. So far there is no method that can directly estimate gbs. Its indirect estimate, mostly based on model fitting to gas exchange data (He & Edwards, 1996) and sometimes combined with chlorophyll fluorescence or 13C discrimination measurements, suggests a value between 1.0 and 10.0 mmol m−2 s−1 bar-1 (Yin et al., 2011), ca two- or three-order of magnitude smaller than gm. Like gm, gbs varies with leaf age or N content (Yin et al., 2011), temperature (Alonso-Cantabrana et al., 2018; Kiirats, Lea, Franceschi, & Edwards, 2002; Yin, van der Putten, Driever, & Struik, 2016), and growth light conditions (Bellasio & Griffiths, 2014; Kromdijk, Griffiths, & Schepers, 2010; Ubierna, Sun, Kramer, & Cousins, 2013). Danila et al. (2021) showed that suberization of the BS lamellae is required for a low gbs to minimize leakage. As gbs is a lumped model parameter, its value may also depend on other anatomical characteristics (like BS cell wall thickness, plasmodesmata density, bundle sheath surface area-to-leaf area ratio, intervein spacing, sheath layers) as well as biochemical characteristics (like the location of decarboxylation). Further research is needed to clarify how these characteristics influence gbs.
6.2 Energetic aspects of C4 photosynthesis
Although energy production or consumption can be cell-type specific (Yin & Struik, 2018, 2021), the model of von Caemmerer and Furbank (1999) for C4 photosynthesis assumed that energy is shared between M and BS cells, and used x to allocate Jatp to the CCM cycle (see Equation (22d)) and thus, 1 − x to the Calvin–Benson cycle (see Equation (22e)). The default value for x is 0.4, arising from φ/(φ + 3), where φ and 3 are ATP required for the CCM cycle and the Calvin–Benson cycle, respectively. For most C4 species, φ = 2; so x = 0.4 (von Caemmerer & Furbank, 1999; but see discussion later). Thus, the RuBP regeneration-limited form of Equation (22e) is expressed in terms of ATP supply. As with the C3 model, it is metabolically important to keep ATP and NADPH in balance (Foyer et al., 2012; Kramer & Evans, 2011); so, one may argue that ATP and NADPH co-determine the RuBP regeneration. For Equation (22e) if NADPH supply is limiting, one can write, according to Equation (9a), that x1 = [1 − fpseudo/(1 − fcyc)]J2/4, x2 = 2γ*, and x3 = 0. Based on this NADPH-determined model, Yin and Struik (2012) stated that the photosynthetic quantum yield models for C4 photosynthesis are the same as for C3 photosynthesis, that is, Equation (12a) or Equation (12e), reflecting that there is no net NADPH requirement for the C4 cycle (but again, see discussion later). Similarly, Equations (13a), (13b) and (10b) for calculating fcyc, fpseudo and ρ2, respectively, also suit for C4 photosynthesis.
As discussed earlier for C3 photosynthesis, one can rely on the unique feature of the NADPH-dependent equation for quantum yield to infer possible values of fcyc from measurements on quantum yields. ΦO2LL of C4 photosynthesis (virtually without photorespiration) is ca 0.069 (Björkman & Demmig1987), considerably lower than its counterpart value of C3 photosynthesis in the absence of photorespiration. Using Equation (13a), Yin and Struik (2012) solved fcyc, which was ca 0.45, considerably higher than the fcyc of C3 photosynthesis. This suggests that CET is essential for C4 photosynthesis, required for generating ATP required for the operation of the CCM cycle.
Once fcyc is known, ρ2 can be calculated from Equation (10b). The obtained ρ2 is ca 0.4 (Yin & Struik, 2012). This differs from Equation (4), where the energy partitioning factor of 0.5 is also used for C4 photosynthesis (von Caemmerer, 2000, 2013; von Caemmerer & Furbank, 1999). When fcyc is known, fpseudo can also be estimated from the assimilatory quotient (see Equation (13b)) and is ca 0.07 (Yin & Struik, 2012).
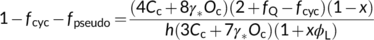 (23a)
(23a)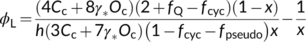 (23b)
(23b)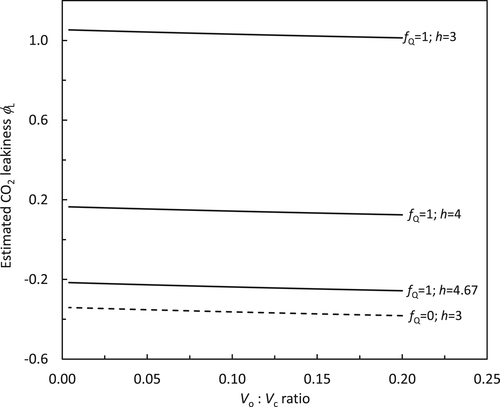
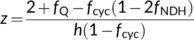 (24a)
(24a)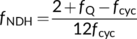 (24b)
(24b)Combining h = 4 and fNDH = 0 or h = 4.67 and fNDH = 0.47 suggests that the ATP production factor per PSII electron transport (z) is ca 1.16. This differs from the standard C4 model of von Caemmerer and Furbank (1999), in which Jatp is set to equal PSII electron transport rate. The standard model assumes: (i) the absence of CET and (ii) and h = 3. Equation (9e) suggests that these assumptions combined with an obligatory Q cycle make z = 1.
6.3 Accommodating the C4 species mixed with PEP-CK
It is important to point out that the above results of energetics are valid only for NADP-ME or NAD-ME subtypes of C4 photosynthesis, although the standard model has been wrongly applied in some reports to the PEP-CK subtype. As stated earlier, the value of 0.4 for x stems from that the parameter φ in Equation (22d) is 2, referring to two mol ATP required per CCM cycle for regenerating PEP by pyruvate phosphate dikinase (PPDK) in the M cell (Hatch, 1987; Kanai & Edwards, 1999). This high ATP requirement is reflected in measured quantum yields in species of the malic-enzyme subtypes, from which the model derived fcyc was high (ca 0.45). In the PEP-CK subtype, however, part of the oxaloacetates produced by the initial PEP carboxylation step move to and are decarboxylated in the BS cytosol by PEP-CK (Hatch, 1987). This decarboxylation reaction also generates PEP (requiring only one molecule of ATP per reaction), thereby partly bypassing the expensive step of PEP regeneration by PPDK. The remaining oxaloacetates are reduced to malate in the M cells, which move to and are decarboxylated in BS mitochondria. This decarboxylation also releases NADH, which drives mitochondrial electron transport to provide ATP for fuelling PEP-CK possibly (Kanai & Edwards, 1999), thereby further decreasing the chloroplastic ATP requirement. Given that the pure PEP-CK type hardly exists in nature and species having PEP-CK are often mixed with other decarboxylation types (Furbank, 2011; Wang et al., 2014), Yin and Struik (2021) presented a model for the electron transport-limited rate in all C4 subtypes including their mixed types.
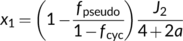 (25a)
(25a)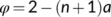 (25b)
(25b)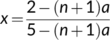 (25c)
(25c)7 CONCLUSIONS AND REMARKS
- Relative to the ATP-determined form, the extended NADPH-determined form for electron transport-limited rate has fewer uncertain parameters and is yet related to the fraction for CET (fcyc). This singular feature of the model allows fcyc to be first estimated from easily measured quantum yield for photosynthesis and quantum yield for photosystem electron transport. The estimated fcyc is negligible (ca 0.06) for C3 photosynthesis vs ca 0.45–0.50 for malic-enzyme subtypes of C4 photosynthesis. The NADPH-determined form also has an advantage in modelling C4 photosynthesis involving decarboxylation by PEP-CK, which requires additional NADPH, a lower ATP:NADPH ratio and probably a lower fcyc, than the malic-enzyme subtypes.
- Because of such a difference in fcyc, the factor for excitation partitioning to PSII (ρ2) was ca 0.5 or slightly higher for C3 photosynthesis, but ca 0.4 for malic-enzyme subtypes of C4 photosynthesis. This differs from the canonical FvCB model, where 0.5 is always set for both C3 and C4 photosynthesis models.
- If fcyc is known, one can also estimate fpseuso based on the assimilatory quotient (see Equation (13b)), and further infer values for uncertain parameters fQ and h in view of the ATP:NADPH ratio as required by metabolism. The most likely values are: fQ = 1 combined with h = 4 for C4 plants, and with h = 4.00 or 4.67 for C3 plants. If h is 4.67 for C4 plants, then ca 50% of CET must follow the NDH-dependent pathway in the malic-enzyme subtypes of C4 plants. The stoichiometric coefficients (fQ = 0 and h = 3) assumed in the ATP-limited form of the canonical C3 model (Equation (3b)) and of the standard C4 model are obsolete.
- The TPU limitation is commonly ignored in modelling C4 photosynthesis probably because it is hard to identify this limitation from its A–Ci curves. While the extension of the canonical FvCB model to account for this limitation to C3 photosynthesis in relation to the glycine export from the photorespiratory pathway has long been made, it appears now that assuming serine (rather than glycine) to exit from the pathway is more likely and internally consistent with regard to the CO2 compensation point. However, this notion may change as we find out more about the nature of carbon export as CH2-THF.
- Under TPU limited conditions plants can increase CO2 uptake, by serine, glycine, or CH2-THF exit from the photorespiratory pathway and associated de novo nitrogen assimilation or C1 metabolism in leaves of C3 plants. However, there exists nitrogen assimilation not associated with the photorespiratory pathway, especially for low-photorespiration situations as occurring in C4 plants or in C3 plants under high CO2/low O2 conditions.
- Loss as a result of photorespiration in C3 plants is lower than the commonly suggested value, owing to: (i) glycine, serine and CH2-THF exports, and (ii) significant refixation of (photo)respired CO2 both within mesophyll cells and via IAS. On the other hand, (photo)respired CO2 release decreases the chance of CO2 coming from IAS being assimilated. It is this net refixation of the (photo)respired CO2 that is taken into account by the coupled CO2-diffusion and FvCB model.
This review did not discuss the C3–C4 intermediate photosynthesis, for which von Caemmerer (2000) outlined a modelling framework. We also hardly discussed modelling photosynthetic temperature response (see Bernacchi et al., 2013), but focused on photosynthetic CO2- and light-responses. One may be surprised to notice that Equations (4) and (11) for modelling the light-response of electron transport are still empirical. However, Farquhar and von Caemmerer (1981) presented some mechanistic basis for using these simple equations. Harbinson and Yin (2017) reported a mechanistic but more complex equation for the irradiance response of PSI electron transport rate. The essence of the FvCB model is its simplicity while capturing the most important contributing mechanisms of photosynthesis (Farquhar et al., 2001). This feature is maintained in the extended models as all the equations we reviewed are analytical, and users can easily implement them for thought experiments to explore changes of photosynthetic pathways. The simplicity means that the models are for steady-state photosynthesis. Excellent, more detailed models for photosynthesis under either steady-state or fluctuating conditions and for the photosynthetic acclimation to growth environment are all omitted in this review, despite their high relevance for photosynthesis in field environments.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing is not applicable as no datasets were generated during writing this review article.




