Firm Recruitment Behaviour: Sequential or Non-sequential Search?†
We would like to thank Knut Roed for helpful comments and Marcel Hoogzaad for excellent assistance. Jos van Ommeren is affiliated with the Tinbergen Institute, Amsterdam. He would like to thank Netherlands Organisation for Scientific Research (NWO) for funding and the Frisch Centre, Oslo, Norway, for its hospitality. The authors are indebted to Lou Schreurs of Intomart b.v., in Hilversum (NL), for the use of the data. The authors would like to thank the Editor and one anonymous reviewer for their valuable comments and suggestions that improved the quality of the article. The views expressed in this article are solely those of the authors and do not necessarily reflect the positions or policies of Cedefop. The usual disclaimer applies.
Abstract
In the extensive job search literature, studies assume either sequential or non-sequential search. This article introduces a novel method to test the hypothesis that firms search sequentially based on the relationship between the number of rejected job applicants and the number of filled vacancies. We distinguish between ten different search methods. For most search methods, including methods that rely on social networks and temporary help agencies, we find that sequential search cannot be rejected. However, when firms use advertising or public/private employment agencies, sequential search is rejected. Hence, we find that both forms of search are relevant for our understanding of the labour market. Further, the form of search is closely related to the search method used.
I. Introduction
In the last few decades, search theory has become one of the main theoretical contributions to understanding the functioning of the labour market (see Devine and Kiefer, 1993; Mortensen and Pissarides, 1999).1 In this literature, the distinction between sequential and non-sequential search, which we label as two different strategies, is fundamental (Rogerson, Shimer and Wright, 2005). Most of the literature assumes that firms search sequentially (see, e.g. Mortensen, 1987, 2003). When searching sequentially, a firm screens each applicant immediately upon arrival, offers a job to the applicant when the productivity of the job applicant exceeds a certain threshold (the reservation productivity) and discontinues the search process if the job offer is accepted (Burdett and Cunningham, 1998). The first characterization of non-sequential search was offered by Stigler (1961): firms pool a number of applicants, screen them and offer the job to the best one. Refinements of the non-sequential search strategy that allowed for variable sample size over time were characterized in Burdett and Judd (1983) and Morgan and Manning (1985).
The main aim of the present article is to test whether firms search sequentially or non-sequentially. The main insight of our article is to consider the relationship between the number of (rejected) applicants and the number of vacancies per job as being indicative of the search strategy adopted by firms: sequential or non-sequential. When firms search sequentially, the number of (rejected) applicants must be proportional to the number of filled vacancies. Our analysis tests this basic statistical property of the sequential search process. Our data set of filled vacancies distinguishes between different search methods (e.g. the use of advertising, employment agencies, etc.), and this enables us to classify each search method as sequential or non-sequential. Conditional on the choice of the search method, we are then able to determine the type of search strategy (sequential or non-sequential) used by the firm. Our results, using microdata on number of vacancies per job, imply that for most search methods, the number of (rejected) applicants is proportional to the number of vacancies per job, implying that we are not able to reject sequential search. However, for advertisements and public and private employment agencies, proportionality does not hold so the hypothesis of sequential search is rejected. Our results are obtained for the Netherlands, where advertising and employment agencies cover 45% of vacancies, but in many other countries this proportion is much lower. This implies that sequential search is a fairly good approximation of firms' recruitment behaviour, particularly in countries where the use of informal search methods is common (such as in the US, e.g. De Varo, 2005), but that non-sequential search is likely too important to be completely ignored for policy purposes.2
The choice of the search strategy may have repercussions at the aggregate level. In fact, knowledge about the search behaviour of firms has been argued to be useful because it informs government policies regarding unemployment and vacancies (Gautier, 2002; Albrecht, Gautier and Vroman, 2003, 2006). When firms and job-seekers search sequentially, the labour market is characterized by search frictions arising from a coordination failure: some vacancies that could be productively filled are left vacant and, at the same time, some workers are unemployed. Posting a new vacancy has the usual congestion and thick market effects: it makes it harder for vacancies to find workers but easier for workers to find a vacancy. Although vacancy creation affects the wage in such a way that the two aforementioned effects may be balanced, search models often have the property that inefficiency is generic (Hosios, 1990), i.e. the decentralized solution does not coincide with the solution of the social planner who is facing the same labour market frictions.
When firms search non-sequentially, we believe that it is fair to say that the literature has not yet reached a general conclusion. Until the publication by Kircher (2009), it was generally believed that the outcome is inefficient. When firms search non-sequentially, the application period, the time between application and acceptance/rejection, does depend on the number of other applicants to be screened and selected. From the applicant's point of view, this is equivalent to waiting in a queue, so each application creates a negative externality. Hence, job-seekers will apply to more vacancies (at the same time) than would be optimal without this externality.
Job applicants can then use multiple job offers to make firms compete against one another, so that the applicants receive higher wages (Rynes, Bretz and Gerhart, 1991). Multiple applications imply that job-seekers search non-sequentially, so multiple applications can be interpreted as the job-seekers equivalent of firm non-sequential search.3 This makes it plausible that job-seekers respond to firms' non-sequential search procedures by adopting a non-sequential search strategy (Morgan and Manning, 1985; Black and Loewenstein, 2002; Gautier, 2002). So, job-seekers will apply to several vacancies for which they will be the preferred candidate and impose then an externality on firms (Albrecht et al., 2003). This behaviour has been argued to induce constrained inefficiency, because an increase in the number of vacancies will not generate an equal increase in the number of matches in the economy (Albrecht et al., 2006). However, recently, Kircher (2009) introduces a directed search model in which workers can simultaneously apply to multiple firms to increase their search intensity while observing firms' wages before choosing where to apply. The equilibrium is shown to be constrained efficient. Gautier and Holzner (2011) showed that the latter result may not hold generally when networks are introduced.
Another complication is that non-sequential search on the part of firms may induce a new form of wage variation because firms, when bargaining over wages with the preferred applicant, will take the productivity level of the second-best applicant in the pool into account. Hence, non-sequential strategies generate macroeconomic implications that differ from the sequential search model ( Villena-Roldán, 2009, 2010). It has been suggested that, given firm non-sequential search and multiple applications by job-seekers, the hiring probability increases in the number of applications, but the overall hiring rate is decreasing because selection times increase. This congestion externality can be reduced, and the efficiency of the labour market increased, by labour market intermediaries such as public employment agencies (e.g. Gautier, 2002).
The article proceeds as follows: the next section offers a literature review. Section III. introduces a theoretical model, to derive the relationship between the number of (rejected) applicants and the number of vacancies. Section IV. describes the data, and provides the results from the empirical analysis. Section V. concludes.
II. Search strategies and recruitment methods
Sequential search is a useful assumption that makes it possible to characterize labour market equilibrium from theoretical models of the labour market in a tractable way. However, knowledge of firms' search strategy is important for structural equilibrium search models, because the firms' sequential search assumption is one of the key assumptions through which these models are identified (Van den Berg and Ridder, 1998; Mortensen, 2003; Cahuc, Postel-Vinay and Robin, 2006). In addition, non-sequential search behaviour by firms is closely related to the stock-flow matching literature (Coles and Muthoo, 1998; Coles and Smith, 1998; Coles, 1999).
We are familiar with only a small number of studies that aim to test which of the two strategies is actually used by firms. Van Ours and Ridder (1992, 1993) and Abbring and Van Ours (1994) conclude, and Coles and Petrongolo (2008) suggest, that firms search non-sequentially. In contrast, Burdett and Cunningham (1998) argue that short vacancy durations suggest that the majority of firms use sequential search, and Andrews et al. (2008) offer a more nuanced interpretation of this fact. These studies, however, do not quantify the proportions of job matches in the economy filled by sequential and non-sequential search respectively.
In the above-mentioned studies, the choice of the specific search method, such as advertising, public agency, temporary agency, etc., is not made explicit, because the search method is not observed (e.g. Van Ours and Ridder, 1992, 1993; Burdett and Cunningham, 1998), or the data analyzed are based on observations from one search method (e.g. Abbring and Van Ours, 1994; Andrews et al., 2008). Hence, these studies are not able to relate their results to the recruitment literature, which focuses on differences between search methods and which suggests a strong relationship between search method and search behaviour; see Roper (1988), Russo et al. (2000), DeVaro (2005) and Andrews et al. (2008).
Since Rees (1966), it has become common to distinguish between formal and informal employer search methods. Informal search networks, which use embedded social networks to provide additional information on applicants, include walk-ins, asking current personnel and business relations for referrals, and searching internally within the firm. Formal search methods include advertisements and the use of employment agencies (temporary, public or private).
Informal search methods imply sequential search, as these methods do not involve large sunk costs, and imply a rather low applicants' arrival rate (Montgomery, 1992). In contrast, job advertising (a formal search method), implies non-sequential search, as the costs of advertising are sunk (Morgan, 1983; McKenna, 1985). Theory does not make sharp predictions about the search strategy when an employment agency is used. For example, in the case that employment agencies charge a fee per applicant, sequential search is more likely to occur, whereas if they charge a fee per vacancy filled, then non-sequential search may be the preferred strategy.
III. The test of sequential and non-sequential search
General setting
Consider a firm with v identical unfilled vacancies in a stationary environment (v≥1).4 The firm aims to maximize the value of these unfilled vacancies and needs workers to fill these vacancies. Workers are hired for ever. The firm's discount rate is denoted by ρ. Workers are heterogeneous in terms of their (net) productivity levels (so we ignore labour costs). The value of the vacancies depends on the costs of screening applicants and the benefits of filling the vacancies.
It is assumed that the firm's production function has constant returns to scale in filled vacancies. This implies that the benefit of each filled vacancy is fully determined by the productivity of the hired workers X (and does not depend on the productivity level of any other hired applicant). The applicants' productivity level is unknown to the firm, but the firm knows its probability density function f(X) and its corresponding cumulative function F(X). By screening of applicants, firms discover the productivity level of an applicant. Screening of applicants is costly, and screening costs per applicant, denoted by c, are fixed. Applicants who receive a job offer will accept the job offer (this assumption can be relaxed by assuming that the probability that the job offer will be accepted is independent of the number of vacancies). To attract job applicants, the firm must choose between two search methods (which may differ with respect to the production function as will the screening costs in line with Montgomery, 1992), which imply two different search strategies: sequential search or non-sequential search.5
Sequential search strategy
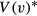 be the value of an unfilled vacancy when the firm has v−1 other (identical) vacancies. Applicants arrive at a given meeting rate q(v). The firm screens applicants one by one and offers the job to any applicant with a productivity level that exceeds the level of the reservation productivity,
be the value of an unfilled vacancy when the firm has v−1 other (identical) vacancies. Applicants arrive at a given meeting rate q(v). The firm screens applicants one by one and offers the job to any applicant with a productivity level that exceeds the level of the reservation productivity, 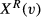 . The matching function at the level of the vth vacancy is
. The matching function at the level of the vth vacancy is 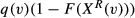 . The value of the vacancy is:
. The value of the vacancy is:
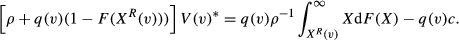
The reservation productivity level 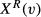 is (optimally) set by the firm while taking into account that a higher level increases the productivity level of the hired worker but also increases the expected number of applicants to be screened and therefore the screening costs.
is (optimally) set by the firm while taking into account that a higher level increases the productivity level of the hired worker but also increases the expected number of applicants to be screened and therefore the screening costs.
Now suppose that q(v)=q, which implies a linear meeting function. Given this assumption, the reservation productivity 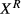 , as well as
, as well as 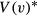 , must be independent of the number of vacancies, so a firm that aims to fill v vacancies in sequential order behaves as if it is attempting to fill a single vacancy v times (Mortensen, 1987). It immediately follows that V(v) equals
, must be independent of the number of vacancies, so a firm that aims to fill v vacancies in sequential order behaves as if it is attempting to fill a single vacancy v times (Mortensen, 1987). It immediately follows that V(v) equals 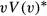 . The combination of the linear meeting function assumption and the constant returns filled vacancies assumption imply the (reservation) productivity independence assumption. Given this assumption, the expected number of applicants to be screened before the firm finds one applicant with a productivity level that exceeds
. The combination of the linear meeting function assumption and the constant returns filled vacancies assumption imply the (reservation) productivity independence assumption. Given this assumption, the expected number of applicants to be screened before the firm finds one applicant with a productivity level that exceeds 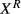 is then equal to
is then equal to 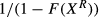 of which
of which 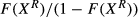 applicants are rejected.
applicants are rejected.
The reservation productivity independence assumption is only valid given the linear meeting function assumption. To understand the adequacy of this assumption, it is important to note that an increase in the number of vacancies v may result in a less-than-proportional increase in number of applicants, so a decrease in 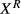 , which increases the likelihood of a match. We emphasize that the decrease in
, which increases the likelihood of a match. We emphasize that the decrease in 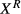 may not fully offset the increase in the number of applicants (see Van den Berg, 1994), so the number of rejected applicants will not increase proportionally as v increases when the meeting technology is concave. Later on, in the subsection ‘The productivity independence assumption', we will relax the productivity independence assumption and interpret our empirical results allowing for a concave meeting technology. Note however that the (reservation) productivity independence assumption has been argued to be reasonable (Akerlof, 1981), because firms are reluctant to create multiple identical vacancies if this reduces productivity (it is then usually more economical to spread vacancies over time).
may not fully offset the increase in the number of applicants (see Van den Berg, 1994), so the number of rejected applicants will not increase proportionally as v increases when the meeting technology is concave. Later on, in the subsection ‘The productivity independence assumption', we will relax the productivity independence assumption and interpret our empirical results allowing for a concave meeting technology. Note however that the (reservation) productivity independence assumption has been argued to be reasonable (Akerlof, 1981), because firms are reluctant to create multiple identical vacancies if this reduces productivity (it is then usually more economical to spread vacancies over time).
Given the productivity independence assumption, it follows that the number of applicants, denoted as n, as well as the number of rejected applicants, denoted as 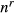 , is proportional to the number of vacancies posted. So, the expected number of rejected applicants in order to fill v vacancies equals
, is proportional to the number of vacancies posted. So, the expected number of rejected applicants in order to fill v vacancies equals 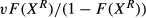 . We are interested in γ, which measures whether the number of (rejected) applicants is proportional to the number of vacancies. Given sequential search (and a linear meeting technology), the rejection vacancy ‘elasticity’, γ, defined here as the elasticity of the number of (rejected) applicants with respect to the number of vacancies, is equal to one (the number of vacancies is usually less than five, so the number of observations is discrete, and γ is strictly speaking not an elasticity). Consequently, the hypothesis that firms recruit sequentially can be tested by testing whether γ is equal to one. If γ is not equal to one, then firms do not search sequentially. Clearly, the number of applicants is a count variable. It is well known that given a fixed probability of a certain occurrence, the number of draws before this occurrence follows a negative binomial distribution. So, given sequential search, it also follows that the number of rejected applicants follows a negative binomial distribution (see, e.g. Mood, Graybill and Boes, 1974; Winkelmann, 2003). For this reason, in the empirical analysis, where we will test whether γ is equal to one, we will focus on the number of rejected (rather than the total) applicants as the main dependent variable of interest and use the negative binomial model to determine γ.
. We are interested in γ, which measures whether the number of (rejected) applicants is proportional to the number of vacancies. Given sequential search (and a linear meeting technology), the rejection vacancy ‘elasticity’, γ, defined here as the elasticity of the number of (rejected) applicants with respect to the number of vacancies, is equal to one (the number of vacancies is usually less than five, so the number of observations is discrete, and γ is strictly speaking not an elasticity). Consequently, the hypothesis that firms recruit sequentially can be tested by testing whether γ is equal to one. If γ is not equal to one, then firms do not search sequentially. Clearly, the number of applicants is a count variable. It is well known that given a fixed probability of a certain occurrence, the number of draws before this occurrence follows a negative binomial distribution. So, given sequential search, it also follows that the number of rejected applicants follows a negative binomial distribution (see, e.g. Mood, Graybill and Boes, 1974; Winkelmann, 2003). For this reason, in the empirical analysis, where we will test whether γ is equal to one, we will focus on the number of rejected (rather than the total) applicants as the main dependent variable of interest and use the negative binomial model to determine γ.
A necessary condition for sequential search is that the rejection vacancy elasticity is equal to one. The key assumption of sequential search is that firms screen applicants one by one. For example, the result that γ equals one does not hold in the case where firms screen more than one applicant per period and the likelihood of observing in the same period two applicants who both have a productivity level that exceeds the level of the reservation productivity is non-negligible (see Morgan, 1983). However, it is not necessarily a sufficient condition. Therefore, in the next section, we will follow the non-sequential search literature and assume a specific non-sequential search model. It will then be shown that in general the rejection vacancy elasticity will not be equal to one but will depend on the form of the production function as well as the cost of screening.
Non-sequential search strategy
In the non-sequential search case, firms pool an optimally-chosen number of applicants before the screening process begins (e.g. Morgan, 1983). We focus on the standard non-sequential search model, where the time aspect of recruitment is completely ignored. So, applicants in the pool are screened (within an infinitesimally small period) and the v most-productive workers are hired for ever. More formally, firms are assumed to fill v vacancies and screen n applicants (n≥v), order the applicants in terms of productivity, and hire the v applicants with the highest productivity level. As in the sequential case, firms incur costs c for screening an applicant and the firm's production function is assumed to be linear in filled vacancies, so the productivity of one hired applicant is independent of the productivity of any other applicant.
 (1)
(1) is the productivity of the hired applicant, i, and E is the expectation operator. The size of the pool of applicants is chosen by maximizing v with respect to n. The evaluation of the expectation is not standard and requires the use of order statistics (e.g. Mood et al., 1974). It is useful to note that the expected productivity of the best v candidates can be written as:
is the productivity of the hired applicant, i, and E is the expectation operator. The size of the pool of applicants is chosen by maximizing v with respect to n. The evaluation of the expectation is not standard and requires the use of order statistics (e.g. Mood et al., 1974). It is useful to note that the expected productivity of the best v candidates can be written as:
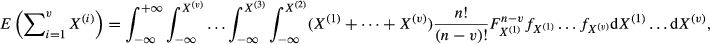 (2)
(2)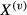 denotes the productivity level of the best applicant,
denotes the productivity level of the best applicant, 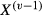 denotes the productivity level of the second-best applicant, etc. The relationship between the optimally-chosen n and v is now more complicated than in the sequential search case, so the rejection vacancy elasticity will depend on the functional form of the production function and on the cost of screening.
denotes the productivity level of the second-best applicant, etc. The relationship between the optimally-chosen n and v is now more complicated than in the sequential search case, so the rejection vacancy elasticity will depend on the functional form of the production function and on the cost of screening.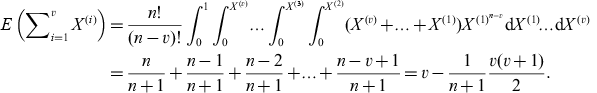 (3)
(3)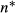 , can be written as:
, can be written as:
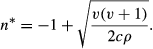 (4)
(4)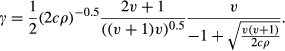 (5)
(5)Rather obviously, γ is not a constant equal to one. For reasonable (low) values for cρ, it can be shown that γ<1. In fact, the latter is true under the condition that cρ≤v/(8(v+1))≤0.0625, so when cρ is less than 6.25% of productivity. This condition is true for vacancies in the real world (see Russo, Hassink and Gorter, 2005). When cρ approaches zero, then γ=(2v+1)/(2v+2)<1. So, if the productivity distribution is uniform, then γ<1, which implies a less than proportional relationship between the number of vacancies and the number of applicants.6 We find the latter result intuitive, because, given non-sequential search, the number of applicants is a concave function of the number of job openings (Burrows, 1972). This implies that given the uniform distribution, non-sequential search implies γ<1, whereas sequential search implies γ=1.7 One may argue however that the assumption that n is continuous is strictly speaking incorrect. Our result that usually γ<1 is however also numerically obtained for discrete values of n. For example, for cρ=0.01 and v=1, it appears that 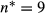 , whereas for the same value of cρ and v=2, it appears that
, whereas for the same value of cρ and v=2, it appears that 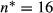 , so
, so 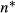 increases less than proportionally when the number of vacancies doubles.
increases less than proportionally when the number of vacancies doubles.
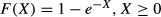 . Then, it can be shown that:
. Then, it can be shown that:
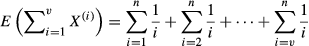 (6)
(6) numerically then it appears that for small values of v,
numerically then it appears that for small values of v, 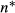 increases (almost always) proportionally. For example, we impose extremely large recruitment costs, so
increases (almost always) proportionally. For example, we impose extremely large recruitment costs, so 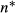 is rather small and hence best seen as discrete: for cρ=0.5, it appears that for v=1,
is rather small and hence best seen as discrete: for cρ=0.5, it appears that for v=1, 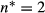 , and for v=2,
, and for v=2, 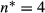 .
.The condition that γ equals one is not sufficient to characterize sequential search in the special case that the productivity distribution follows the exponential distribution. We do not want to overemphasize this result as unobserved productivity characteristics are unlikely to follow a monotonically downward sloping distribution (for example, wages that are frequently used as indicators of productivity are not monotonically downward distributed). Hence, in most circumstances, an empirical finding that γ is close or equal to unity – and precisely estimated – suggests that search is sequential. In the remainder of the article, we will test whether the vacancy elasticity is equal to one. The proposed test will be applied conditional on the chosen search method.8
IV. Data and results
The data and descriptive analysis
The data used in the empirical analysis were derived from a survey on the search behaviour of Dutch establishments entitled, ‘How do firms recruit?’ (HDFR, 1998). Here, establishments will be called firms, in line with the terminology of the theoretical model. The (cross-section) survey was carried out by telephone (every two months) between 1991 and 1998.
The survey records all recruitment actions concluded by the firm in the two months prior to the interview. A recruitment action refers to the recruitment activities of one type of job (e.g. secretary). An action may involve the filling of multiple identical vacancies (see, similarly, Barron and Bishop, 1985; Andrews et al., 2008). For all actions, information was gathered regarding occupational codes, job descriptions, and functions.
One of these recruitment actions was then randomly selected, using a pseudo-random generator procedure, as the focus of an in-depth interview. So, the interview focused only on one action that took place during the two months prior to the interview. During the interview, additional detailed information was gathered about this particular recruitment action. This article analyzes information obtained from this interview.
For the (randomly-selected) recruitment action, the survey provides information on many elements of the search process, such as the number of applications received, the search methods used and the number of (identical) vacancies. The question used in the survey about the number of (identical) vacancies reads as follows: ‘How many vacancies (of the selected type) have been filled during the (selected) recruitment action?’ By construction, identical vacancies share the same four-digit occupational code, job description and function. Moreover, detailed background information on both firm and vacancy characteristics (such as the educational level or work experience requirements, the presence of maximum age limits, whether it concerned a part-time position, and whether it concerned a permanent contract) is also provided (for summary statistics, see Appendix 1).
In the theoretical and empirical analysis, we focus on filled vacancies, which potentially differ from the vacancies to be filled (Andrews et al., 2008). The analysis may then generate biased estimates of the coefficients of interest, if the reported number of applicants relates not only to the vacancies that are filled but also to vacancies that are cancelled. The proportion of vacancies cancelled was found to be only 4% in the Dutch data studied by Van Ours and Ridder (1992), so any bias in the estimates will likely be negligible.
Firms may use multiple search methods during the hiring procedure (Roper, 1988). Our analysis distinguishes search activities by the first-employed search method, which is predominantly the only search method used. Most firms usually limit themselves to a single search method: in 82% of the cases (of randomly-selected hiring activities) only one search method was used. Such a high percentage is consistent with studies for Belgium and the UK (Roper, 1988), but not for the US, where multiple search methods are common with an average of about three to four (DeVaro, 2005). The frequency distribution of search methods is given in the first column of Table 1 (the second column repeats the result when only one search method is used). The third and fourth columns represent the frequency distribution of search methods, weighting the observations by the number of vacancies filled and by the number of applications received.
| Recruitment | Recruitment | |||
|---|---|---|---|---|
| action | action | Vacancies | Applications | |
| (1) | (2) | (3) | (4) | |
| Informal search methods | ||||
| Internal search | 9.38 | 8.29 | 7.65 | 3.11 |
| Via own personnel | 6.95 | 6.92 | 6.49 | 1.97 |
| Business relations | 6.27 | 6.97 | 4.55 | 1.54 |
| Walk-ins | 13.63 | 15.03 | 18.61 | 7.68 |
| Formal search methods | ||||
| Advertisements | 28.00 | 29.44 | 31.93 | 68.49 |
| Temporary help agency | 10.57 | 10.53 | 9.92 | 4.1 |
| Public employment agency | 14.31 | 12.59 | 11.47 | 6.81 |
| School search | 2.93 | 3.15 | 2.65 | 0.95 |
| Private employment agency | 2.69 | 3.00 | 2.07 | 3.16 |
| Other search method | 5.27 | 4.08 | 4.66 | 2.19 |
| Total | 100 | 100 | 100 | 100 |
| Number of observations | 39,814 | 32,546 | 70,730 | 450,858 |
- Note: The first column is based on all recruitment actions which may cover the filling of several vacancies. The last three columns are based on hiring activities that use only one search method.
Our original data cover 39,814 recruitment actions, involving 100,043 vacancies and 609,263 applications. To avoid the confounding effect of mixed recruitment strategies (those using more than one search method), in this section, we focus on the selected sample of 32,546 recruitment actions that used one search method exclusively (the multivariate analysis is conducted on the selected, as well as the whole, sample). These firms filled 70,730 vacancies and received 450,858 applications (see the bottom line of Table 1). Table 1 further shows, for example, that, in the whole sample, 28% of the recruitment actions relied on advertising. In the restricted sample (restricted to those recruitment actions that made use of one search method only), 29% of the recruitment actions and 32% of all vacancies used advertisements. Because advertisements tend to provide a large flow of applicants, 68% of all job applications are related to a recruitment action that used advertisements only.
In Table 1, the top four search methods are labelled ‘informal search methods’, whereas the remaining methods are referred to as ‘formal search methods’ (Rees, 1966). The residual category, ‘Other search methods’, includes a combination of less common methods such as Internet recruiting. Note that our sample refers to a period, prior to 1998, when Internet recruitment was still very rare.
Under the hypothesis of sequential search, the average number of applicants is proportional to the number of vacancies. The average number of applicants per filled vacancy should then remain constant, regardless of the number of vacancies filled. In about 90% of the cases, fewer than five vacancies were filled. The average number of applicants per vacancy by search method, when one, two, three and four vacancies are filled, is shown in Table 2; the last column contains the average number of applicants per filled vacancy (across search methods). On average, about nine applications per vacancy are received, in line with the literature (for example, Barron and Bishop (1985), report exactly the same number for the US). There is substantial variation in the average number of applicants per vacancy, across search methods. The use of advertising results in a significantly higher number of applicants per vacancy (about 21, on average). The use of business relations and school search implies a particularly low number of applicants per vacancy (about two, on average).
| Number of vacancies filled | |||||
|---|---|---|---|---|---|
| Whole | |||||
| 1 | 2 | 3 | 4 | sample | |
| Informal Search Methods | |||||
| Internal search | 6.77 | 4.98 | 4.14 | 3.37 | 5.80 |
| Via own personnel | 3.21 | 2.88 | 2.82 | 2.17 | 3.02 |
| Business relations | 2.75 | 2.44 | 1.94 | 1.82 | 2.65 |
| Walk-ins | 3.05 | 2.93 | 3.52 | 3.18 | 3.03 |
| Formal search methods | |||||
| Advertisements | 26.99 | 14.89 | 10.89 | 10.28 | 20.73 |
| Temporary help agency | 4.66 | 3.99 | 3.13 | 2.61 | 4.14 |
| Public employment agency | 7.25 | 4.52 | 4.07 | 3.77 | 5.94 |
| School search | 2.68 | 2.45 | 3.11 | 3.51 | 2.71 |
| Private employment agency | 12.87 | 8.71 | 5.31 | 5.29 | 11.46 |
| Other search method | 4.29 | 3.81 | 3.82 | 2.27 | 4.00 |
| All search methods | 11.11 | 7.07 | 5.63 | 5.06 | 9.02 |
| Number of observations | 24,157 | 7,199 | 2,860 | 1,523 | 39,814 |
- Note: Based on whole sample (see column (1) in Table 1).
Table 2 offers prima facie evidence that contradicts the hypothesis of sequential hiring for advertising and employment agencies, because for these methods the average number of applicants falls strongly when the number of filled vacancies increases. For other search methods this fall is absent (e.g. walk-ins) or rather small (e.g. business referrals).
Main empirical results
We aim to classify different search methods as being sequential or non-sequential. According to theory, the type of search strategy is closely related to the type of search method used, justifying our choice to estimate the vacancy elasticity for each search method separately. As a limited number of vacancies employ more than one search method, we distinguish between subgroups based on the first search method employed. However, an analysis of vacancies that use only one search method generates almost identical results. The dependent variable, the number of rejected applicants, will be treated as a count variable. In line with theory, we use a (generalized version of the) negative binomial regression model. The model corresponds to the negative binomial model NB2 (Cameron and Trivedi, 1998).
One disadvantage of the count model approach compared to a regression approach is the implicit assumption that the dependent variable is observed without measurement error. When the count variable is observed with measurement error, the estimates will be biased (in an unknown direction, see Winkelmann, 2003). The frequency distribution of the number of rejected applicants indicates that if the number of applicants exceeds about 15, then the number of rejected applicants is rounded to multiples of 5, 10 and 50 (e.g. 25 occurs much more frequently than does 24 or 26). To account for this peculiarity, we have right-censored all observations that received more than 20 applicants per vacancy. This affects only 2.45% of the sample, so losses in efficiency are small. By right-censoring, we also avoid the risk that a small number of outliers (observations with hundreds of applicants) drive the results. We have also experimented with other threshold points to right-censor the data (e.g. more than ten applicants, which refers to 11% of the sample), and the results remain robust.
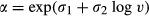 , where
, where 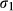 and
and 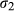 are parameters to be estimated, see e.g. Cameron and Trivedi (1998). Following Hilbe (2007) we write the (log) likelihood as:
are parameters to be estimated, see e.g. Cameron and Trivedi (1998). Following Hilbe (2007) we write the (log) likelihood as:
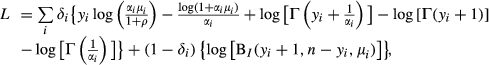 (7)
(7)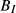 is the cumulative function of the incomplete (three parameters) Beta distribution, and δ is a dummy indicator which denotes that the observation is not censored. The incomplete Beta distribution is essentially the cumulative function of a negative binomial distribution, which is obtained by generalizing the interval of integration of the Beta function from the unit interval (0,1) to (0,y+1) (Gupta and Nadarajah, 2004). We emphasize that for this model, the parameter γ captures the overall effect of vacancies on the mean number of rejected applicants (so we are not specifically interested in
is the cumulative function of the incomplete (three parameters) Beta distribution, and δ is a dummy indicator which denotes that the observation is not censored. The incomplete Beta distribution is essentially the cumulative function of a negative binomial distribution, which is obtained by generalizing the interval of integration of the Beta function from the unit interval (0,1) to (0,y+1) (Gupta and Nadarajah, 2004). We emphasize that for this model, the parameter γ captures the overall effect of vacancies on the mean number of rejected applicants (so we are not specifically interested in 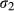 ).
).The results are presented in Tables 3(a, b). The first row in these tables contains the estimates of the main coefficient of interest, 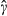 , the rejection vacancy elasticity. The test of sequential search amounts to testing whether this elasticity is different from one. Our main result is that sequential search is rejected when advertising, or employment agencies (but not temporary help agencies) are used.9 Note that these methods are formal methods. The estimated rejection vacancy elasticities for these methods are not only statistically different from one, but much less than one and are around 0.60. So, for these methods, firms are able to economize on recruitment costs through non-sequential search. We can only speculate about the underlying causes as to why these methods imply non-sequential search, but the low elasticity obtained for advertisements is consistent with the well-known observation that it involves substantial fixed costs. For the other search methods (except internal recruitment), sequential search is not rejected. Importantly, the estimated standard errors of the estimated rejection vacancies elasticities are rather small. Therefore, this result cannot be attributed to the lack of a sufficient number of observations. Only for internal recruitment is the test unclear: statistically, sequential search is rejected, but the size of the coefficient, 0.88, is so close to one that it suggests that the sequential search assumption may be a reasonable approximation.10 Later analyses will confirm this interpretation.
, the rejection vacancy elasticity. The test of sequential search amounts to testing whether this elasticity is different from one. Our main result is that sequential search is rejected when advertising, or employment agencies (but not temporary help agencies) are used.9 Note that these methods are formal methods. The estimated rejection vacancy elasticities for these methods are not only statistically different from one, but much less than one and are around 0.60. So, for these methods, firms are able to economize on recruitment costs through non-sequential search. We can only speculate about the underlying causes as to why these methods imply non-sequential search, but the low elasticity obtained for advertisements is consistent with the well-known observation that it involves substantial fixed costs. For the other search methods (except internal recruitment), sequential search is not rejected. Importantly, the estimated standard errors of the estimated rejection vacancies elasticities are rather small. Therefore, this result cannot be attributed to the lack of a sufficient number of observations. Only for internal recruitment is the test unclear: statistically, sequential search is rejected, but the size of the coefficient, 0.88, is so close to one that it suggests that the sequential search assumption may be a reasonable approximation.10 Later analyses will confirm this interpretation.
| Internal | Via own personnel | Via business relations | Walk-ins | Advertisements. | |
|---|---|---|---|---|---|
| Log number of vacancies | 0.884 | 1.048 | 0.922 | 0.950 | 0.603 |
| (0.044)* | (0.063) | (0.088) | (0.041) | (0.016)* | |
| Educational requirements | |||||
| University | 0.585 | 0.506 | 0.933 | 0.288 | 0.412 |
| (0.260)* | (0.300) | (0.309)* | (0.221) | (0.055)* | |
| Upper vocational | 0.486 | 0.701 | 0.858 | 0.229 | 0.407 |
| (0.184)* | (0.206)* | (0.234)* | (0.145) | (0.043)* | |
| Upper secondary general | 0.585 | 0.255 | 0.224 | 0.245 | 0.422 |
| (0.205)* | (0.232) | (0.325) | (0.164) | (0.048)* | |
| Secondary vocational | 0.611 | 0.669 | 0.516 | −0.012 | 0.292 |
| (0.172)* | (0.169)* | (0.212)* | (0.111) | (0.040)* | |
| Secondary general | 0.201 | 0.481 | 0.588 | 0.424 | 0.257 |
| (0.197) | (0.194)* | (0.263)* | (0.119)* | (0.048)* | |
| Primary vocational | 0.289 | 0.090 | 0.414 | 0.005 | −0.017 |
| (0.171) | (0.146) | (0.213) | (0.097) | (0.042) | |
| Vacancy characteristics | |||||
| Part time | −0.422 | −0.172 | −0.335 | −0.185 | −0.111 |
| (0.091)* | (0.112) | (0.159)* | (0.078)* | (0.027)* | |
| Permanent | 0.257 | 0.306 | 0.247 | 0.101 | 0.091 |
| (0.073)* | (0.101)* | (0.129) | (0.066) | (0.026)* | |
| Experience required | −0.146 | 0.150 | 0.093 | 0.126 | 0.041 |
| (0.080) | (0.097) | (0.142) | (0.065) | (0.020)* | |
| Age limits | 0.396 | 0.685 | 0.404 | 0.443 | 0.109 |
| (0.102)* | (0.122)* | (0.135)* | (0.073)* | (0.019)* | |
| Log number of employees | 0.231 | 0.253 | 0.165 | 0.182 | 0.053 |
| (0.025)* | (0.033)* | (0.037)* | (0.024)* | (0.006)* | |
| Business Cycle | |||||
| Log vacancies/employment | 0.020 | −0.257 | 0.037 | 0.004 | −0.080 |
| (0.109) | (0.155) | (0.175) | (0.110) | (0.030)* | |
| Log unemployment rate | 0.040 | −0.230 | 0.062 | 0.102 | 0.211 |
| (0.292) | (0.388) | (0.475) | (0.286) | (0.078)* | |
| Yearly dummies (7)* | Yes | Yes | Yes | Yes | Yes |
| Occupational dummies (8)* | Yes | Yes | Yes | Yes | Yes |
| Industry dummies (8)* | Yes | Yes | Yes | Yes | Yes |
| Constant | −1.162 | 1.527 | −1.422 | −1.511 | −0.399 |
| (0.630) | (0.797)* | (0.978) | (0.045)* | (0.022)* | |
| Dispersion parameter (α) | |||||
| Log number of vacancies | −0.072 | 0.035 | 0.272 | 0.166 | −0.436 |
| (0.042) | (0.053) | (0.091)* | (0.036)* | (0.021)* | |
| Constant | 0.984 | −1.790 | 1.842 | 1.536 | 1.125 |
| (0.046)* | (0.062)* | (0.065)* | (0.586)* | (0.162)* | |
| Goodness-of-fit | 0.43 | 0.50 | 0.37 | 0.43 | 0.41 |
| 3,734 | 2,766 | 2,496 | 5,426 | 11,147 | |
- Notes: Reference group of the variables is in parentheses: educational requirements (primary general), part-time (full-time), permanent (temporary), experience required (no experience required), age limits (no age limits). Standard errors in parentheses (*statistically significant at the 5% significance level). Goodness-of-fit is the correlation between predicted and observed number of applicants.
The search methods that imply non-sequential search cover 45% of the vacancies and 78% of the job applications (see Table 1). As job-seekers vary in the number of applications, the number of job applications cannot be interpreted as equivalent to the number of job-seekers, but it suggests that many job-seekers are somehow involved in a non-sequential selection process before finding a job.
| Temporary help agency | Public employment agency | School recruitment | Private employment agency | other recruitment methods | |
|---|---|---|---|---|---|
| Log number of vacancies | 0.968 | 0.677 | 0.867 | 0.568 | 0.961 |
| (0.049) | (0.031)* | (0.091) | (0.088)* | (0.074) | |
| Educational requirements | |||||
| University | 0.649 | 0.027 | 0.393 | 0.193 | 0.510 |
| (0.277)* | (0.217) | (0.593) | (0.333) | (0.273) | |
| Upper vocational | 0.815 | 0.064 | 0.130 | 0.300 | 0.444 |
| (0.165)* | (0.095) | (0.436) | (0.294) | (0.230) | |
| Secondary general | 0.756 | 0.030 | 0.185 | 0.582 | 0.378 |
| (0.167)* | (0.095) | (0.532) | (0.351) | (0.285) | |
| Secondary vocational | 0.694 | 0.181 | −0.071 | 0.429 | 0.312 |
| (0.147)* | (0.069)* | (0.414) | (0.294) | (0.207) | |
| Lower secondary general | 0.456 | 0.133 | −0.206 | 0.157 | 0.245 |
| (0.161)* | (0.076) | (0.444) | (0.338) | (0.210) | |
| Primary vocational | 0.232 | −0.049 | −0.019 | 0.162 | 0.050 |
| (0.139) | (0.062) | (0.413) | (0.350) | (0.183) | |
| Vacancy characteristics | |||||
| Part time | −0.295 | −0.127 | −0.083 | −0.388 | 0.120 |
| (0.105)* | (0.051)* | (0.191) | (0.158)* | (0.121) | |
| Permanent | 0.431 | 0.271 | 0.041 | 0.826 | 0.320 |
| (0.069)* | (0.042)* | (0.146) | (0.153)* | (0.114)* | |
| Experience required | 0.082 | 0.074 | 0.227 | −0.122 | −0.159 |
| (0.059) | (0.037)* | (0.138) | (0.142) | (0.109) | |
| Age limits | 0.332 | 0.162 | 0.573 | 0.429 | 0.508 |
| (0.059)* | (0.041)* | (0.143)* | (0.083)* | (0.123)* | |
| Log number of employees | 0.015 | 0.054 | 0.180 | 0.109 | 0.130 |
| (0.022) | (0.014)* | (0.049)* | (0.033)* | (0.037)* | |
| Business cycle | |||||
| Log vacancies/employment | 0.090 | 0.152 | 0.136 | −0.243 | −0.072 |
| (0.099) | (0.063)* | (0.253) | (0.137) | (0.179) | |
| Log unemployment rate | −0.010 | 0.059 | −0.263 | 0.229 | −0.661 |
| (0.258) | (0.175) | (0.648) | (0.345) | (0.441) | |
| Yearly dummies (7)* | Yes | Yes | Yes | Yes | Yes |
| Occupational dummies (8)* | Yes | Yes | Yes | Yes | Yes |
| Industry dummies (8)* | Yes | Yes | Yes | Yes | Yes |
| Constant | −0.663 | 0.108 | −1.523 | −0.342 | 0.741 |
| (0.044)* | (0.035)* | (0.100)* | (0.807) | (0.916) | |
| Dispersion Parameter (α) | |||||
| Log number of vacancies | −0.452 | −0.272 | 0.180 | −0.314 | 0.021 |
| (0.047)* | (0.036)* | (0.104) | (0.118)* | (0.055) | |
| Constant | 0.725 | 0.411 | 1.376 | 0.167 | 1.424 |
| (0.545) | (0.362) | (1.365) | (0.060)* | (0.067)* | |
| Goodness-of-fit | 0.35 | 0.55 | 0.73 | 0.34 | 0.29 |
| Number of Observations | 4,208 | 5,699 | 1,167 | 1,071 | 2,100 |
- Note: See Table 3(a).
We have also investigated whether the above results hold for subgroups. For example, it is plausible that the type of educational requirement affects the screening costs or the arrival rate of candidates and therefore the choice between sequential or non-sequential methods. We have therefore repeated the analysis for the ten different search methods distinguishing now between subgroups defined by educational requirements. In one analysis, we split the sample in two subgroups based on the level of educational requirement (low vs. high education); in another analysis, we split the sample in two groups using the type of educational requirement (vocational vs. general education). In essence, the results do not change and the rejection vacancy elasticity is about the same for each subgroup. Only firms using temporary help agencies display different search behaviour across educational levels: firms using temporary help agencies to fill vacancies with high educational requirements search non-sequentially whereas the opposite is true for firms filling vacancies with low educational requirements.11
The proposed test of sequential search tests whether the rejection vacancy elasticity is equal to one. One may argue that it may be useful to apply an alternative test that also tests whether the rejection vacancy elasticity is independent from the number of vacancies to be filled. To increase the statistical power of this test, we have pooled all observations that refer to the search methods identified above as being sequential (so we include all search methods except advertising and public/private employment agencies). As the number of observations with more than four filled vacancies is limited, we have selected only observations with a maximum of four filled vacancies. To apply the test, we have included the number of vacancies by means of dummy variables that capture whether the number of vacancies to be filled is either two, three or four (where one vacancy is the reference category). To ease interpretation of the results, the three vacancy dummies do not take the usual values, zero or one, but instead take the values zero or the logarithm of 2, 3 or 4, respectively. It appears that the rejection vacancy elasticities for two, three and four vacancies are equal to 1.017 (0.059), 0.990 (0.052) and 0.931 (0.053), respectively, where the standard errors are given in parentheses, so the estimates are essentially not different from one. A likelihood-ratio test does not reject the hypothesis that the elasticities are equal to each other and equal to one. Consequently, sequential search is not rejected using this alternative test.
Sensitivity analyses
The first row in Table 4 shows that the nature of the results does not change if controls are excluded, except when temporary help agencies or internal search method are used. In addition, local labour market conditions are almost never significant (and excluding them from the analysis does not alter any of the results) and this suggests that the prevailing search strategy characterizing the different search methods is robust to variation in the tightness of the local labour market.
Recent recruitment experience
We have also re-estimated the same models on a sample of firms that had filled at least one other vacancy during the previous year. These estimates are useful because firms with recent recruitment experience are most likely well informed about the state of the labour market, in line with the assumptions of the theoretical model, which requires that the productivity distribution of applicants is known to firms. For firms that did not recruit recently, this assumption may be less valid. The restricted sample contains 25,481 observations. Table 4 shows that given the selection, the parameter estimates (third row in Table 4) remain very close to those obtained when the whole sample was utilized (second row in Table 4). The only difference is that sequential search is not rejected when firms recruit internally (we find now a coefficient of 0.932 and a standard error of 0.053). This is consistent with our previous interpretation of internal recruitment.
| Internal | Via own personal | Via business relations | Walk-ins | Advertisements | |
|---|---|---|---|---|---|
| Number of vacancies (no controls) | 0.957 | 1.043 | 0.991 | 1.091 | 0.545 |
| (0.039) | (0.057) | (0.087) | (0.033) | (0.014)* | |
| Full model (controls) | 0.884 | 1.048 | 0.922 | 0.950 | 0.603 |
| (0.044)* | (0.063) | (0.088) | (0.041) | (0.016)* | |
| Firms that hired during the | 0.932 | 1.060 | 0.839 | 0.971 | 0.638 |
| previous year (restricted sample) | (0.053) | (0.080) | (0.118) | (0.049) | (0.020)* |
| Inclusion of firms' intention to Hire | 0.871 | 1.062 | 0.925 | 0.953 | 0.605 |
| (0.044)* | (0.063) | (0.088) | (0.042) | (0.016)* |
| Temporary help agency | Public employment | School recruitment | Private employment agency | Other recruitment methods | |
|---|---|---|---|---|---|
| Number of vacancies (no controls) | 0.763 | 0.664 | 1.135 | 0.561 | 1.016 |
| (0.042)* | (0.029)* | (0.086) | (0.094)* | (0.061) | |
| Full model | 0.968 | 0.677 | 0.867 | 0.568 | 0.961 |
| (0.049) | (0.031)* | (0.091) | (0.088)* | (0.074) | |
| Firms that hired during the | 0.977 | 0.682 | 0.936 | 0.652 | 0.947 |
| previous year (restricted sample) | (0.057) | (0.038)* | (0.133) | (0.108)* | (0.082) |
| Inclusion of firms' intention to Hire | 0.955 | 0.682 | 0.872 | 0.557 | 0.964 |
| (0.049) | (0.031)* | (0.092) | (0.089)* | (0.074) |
- Note: Robust standard errors in parentheses, *statistically different (smaller) from one (one-sided test).
Additional explanatory variables
One may argue that, despite the large number of explanatory variables, the omission of some variables, correlated with the number of filled vacancies, may potentially bias the estimated coefficients. In particular, unobserved skill level requirements may still be positively correlated with the number of vacancies (a large number of vacancies may reflect low job skill requirements), so the estimated elasticities are downward biased, suggesting we reject sequential search too often.
One way to capture unobserved job requirements is to note that unobserved skill requirements are usually correlated with job turnover. So, firms offering jobs with unobserved low skill requirements will be more likely to hire new personnel in the near future. Following this line of reasoning, we have controlled for firms' job skill content by using the firms' intention to hire new personnel in the next two months.12 As is shown in the fourth row of Table 4, the inclusion of this additional variable does not materially alter any of the rejection vacancy elasticities.
Alternative estimation methods
We have shown that sequential search implies that the expected number of (rejected) applicants is proportional to the number of vacancies. Hence, it is also possible to test for this relationship using a regression analysis. Particularly, in the case of advertising, when, on average, 21 applicants apply, and where usually the number of applicants exceeds the number of vacancies, a regression analysis based on a specification in logarithms offers some advantages compared to a count model, because it tends to be more robust than count model analysis, for example, with respect to underlying assumptions of measurement error in the dependent variable (see Winkelmann, 2003). Results using ordinary least squares (OLS) generate almost identical results as for the count model reported. Improving these estimates by taking into account that the number of applicants must exceed or be equal to the number of vacancies (Tobit models) does not affect this conclusion. We refer to Appendix 2 for more details.
The productivity independence assumption
Using arguments going back to Akerlof (1981) and consistent with Van Ours and Ridder (1991), we have argued above that it is plausible that the reservation productivity does not depend on the number of vacancies (conditional on observed characteristics). This implicitly assumes a proportional relationship between the applicants' arrival rate and the number of vacancies. Hence, if the number of vacancies doubles so does the number of applicants, such that the reservation productivity remains unchanged. This linear meeting technology is in line with studies such as Van Ours and Ridder (1991) which show that the reservation productivity does not fall over time.
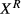 falls and, as discussed before, the acceptance probability,
falls and, as discussed before, the acceptance probability, 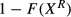 , becomes a positive function of the number of vacancies posted. To see the consequences for our empirical tests, assume that
, becomes a positive function of the number of vacancies posted. To see the consequences for our empirical tests, assume that 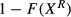 is related to the number of vacancies posted, in the following way:
is related to the number of vacancies posted, in the following way:
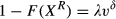 (8)
(8) , as shown in Tables 3 and 4, conflate the true γ and δ. In fact:
, as shown in Tables 3 and 4, conflate the true γ and δ. In fact: 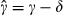 , hence
, hence 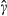 is downward biased if δ is strictly positive.
is downward biased if δ is strictly positive.Our theoretical analysis indicates that given sequential search, γ=1, and given non-sequential search, γ<1. Hence, if 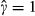 , then it is plausible that γ=1 and δ=0. Therefore, when
, then it is plausible that γ=1 and δ=0. Therefore, when 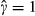 , the above conclusion – that we cannot reject the hypothesis of sequential search – is not affected. When
, the above conclusion – that we cannot reject the hypothesis of sequential search – is not affected. When 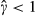 , however, there is the possibility that γ=1 and δ>0. This would imply sequential search combined with a concave meeting technology. This possibility is relevant for the search methods previously identified as being non-sequential. While one cannot rule out this possibility completely, the assumption of a linear meeting technology appears to be reasonable for other search methods, so it is generally likely to be a valid one.
, however, there is the possibility that γ=1 and δ>0. This would imply sequential search combined with a concave meeting technology. This possibility is relevant for the search methods previously identified as being non-sequential. While one cannot rule out this possibility completely, the assumption of a linear meeting technology appears to be reasonable for other search methods, so it is generally likely to be a valid one.
To examine the effect of the number of vacancies on the (reservation) productivity level, we apply a productivity-independence test. The test is based on the idea that the educational level of the applicant is a strong indicator of productivity (in line with the large human capital literature). If it is true that the reservation productivity depends negatively on the number of vacancies, which may have biased the above results, then the average productivity level of the accepted applicants must negatively depend on the number of vacancies. We have therefore estimated regression models where the dependent variable is the difference between the average educational level of the accepted applicants and the minimum educational level required in the vacancy (to calculate the average level, we assume that educational level required is a ordinal number). We do not find any evidence of a positive effect of number of vacancies on this measure of productivity. In fact, we find even a slight negative effect, suggesting that our test is slightly conservative. Furthermore, we have applied the same test on a subsample containing the non-sequential search methods and a subsample containing the sequential search methods and we have distinguished by level of education. Again, there is no evidence that the number of vacancies positively affects this measure of productivity.
Suppose, nevertheless, that the number of vacancies affects productivity in other (unobservable) ways, so one may argue that the above tests have their limitations as they assume a narrow definition of productivity. Further, suppose that the rejection of sequential search for three search methods is solely driven by changes in the reservation productivity. The implied fall in the reservation productivity, given sequential search, is then implausibly large. Our results for 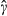 (about 0.6) would imply δ=0.4, and the probability of accepting an applicant increases by about 32% when the number of vacancies increases from one to two. This implies that the average productivity of the accepted applicants when two vacancies are filled is much lower than the productivity level of the accepted applicant in the case of one vacancy. This seems implausible. So, although it is theoretically possible that we reject sequential search too often if the assumption of linear meeting technology does not hold, all the evidence supports the assumption of a linear meeting technology, so the consequences for our tests are likely to be minor.
(about 0.6) would imply δ=0.4, and the probability of accepting an applicant increases by about 32% when the number of vacancies increases from one to two. This implies that the average productivity of the accepted applicants when two vacancies are filled is much lower than the productivity level of the accepted applicant in the case of one vacancy. This seems implausible. So, although it is theoretically possible that we reject sequential search too often if the assumption of linear meeting technology does not hold, all the evidence supports the assumption of a linear meeting technology, so the consequences for our tests are likely to be minor.
Instrumental variables approach
One may argue that that the above analysis measures the number of filled vacancies, whereas some vacancies may not have been filled, which creates a potential bias in the estimates. For this reason, we instrumented the number of filled vacancies using the average number of hired persons per function filled in the whole firm during the previous year as an instrument. This measure is obtained as the ratio of the number of persons hired to the number of functions – job titles – in which workers were hired.13 Information about this instrument is available only for firms that had at least one vacancy filled during the previous year (other than the recruitment action analyzed here), so the number of observations is reduced to 25,481 observations. Instrumenting the number of vacancies with the average number of persons hired per job title during the previous year does not alter the conclusions. The only slight difference is that sequential search is not rejected when firms recruit internally. This finding is consistent with our earlier result that the rejection vacancy elasticity for internal recruitment was close to one.
V. Conclusion
In the present article, we test whether firms search sequentially or non-sequentially for job applicants. This test is based on the relationship between the number of (rejected) applicants and the number of filled vacancies per job across search methods. We do not reject the hypothesis of sequential search when firms use informal search methods, such as the use of social networks, but we also do not reject this assumption for school recruitment or temporary help agencies.
All in all, the sequential search assumption holds pretty well for most search methods. However, we reject the null hypothesis of sequential search when firms use advertisements or public and private employment agencies. Hence, our main conclusion is that both forms of search are relevant for our understanding of the labour market.
The incidence of methods labelled as non-sequential is rather high in the Netherlands, as they cover about 45% of the filled vacancies. As non-sequential search methods such as advertising attract an above-average number of applicants it seems that the number of job-seekers who are confronted with non-sequential search by firms is even higher. This makes it plausible, indeed, that some job-seekers would respond to firms' non-sequential search procedures by adopting a non-sequential search strategy themselves, as argued by Morgan and Manning (1985), Black and Loewenstein (2002) and Gautier (2002). Our findings are also consistent with the stock-flow literature which suggests that job queues are an important element of the matching process.
Our interpretation of the results squares well with other studies that used more indirect evidence based on vacancy durations. Van Ours and Ridder (1992, 1993) suggest that the predominant use of advertising in the Dutch labour market may explain their conclusion that Dutch employers search non-sequentially. Abbring and Van Ours (1994) also conclude that employers search non-sequentially when public employment agencies are used (but, see Andrews et al.2008, for the UK). Our results indicate, therefore, that non-sequential search is an important feature of firm recruitment procedures, at least in the Netherlands. Nevertheless, it also suggests that in countries where the use of advertising is less common (e.g. the US and Italy), non-sequential search by firms might be relatively rare.
Our data predate the era of extensive use of Internet recruitment, which has largely replaced newspaper advertising. Newspaper advertising implies rather high fixed costs of recruitment and attracts applicants during a short period only. In contrast, Internet recruitment implies low fixed costs of advertising and, in principle, may attract applicants over an infinite period. So, Internet recruitment exhibits characteristics that are common for sequential search methods.
Appendix A: : Summary statistics
| Mean | SD | Min | Max | |
|---|---|---|---|---|
| Variable | ||||
| Log Number of applicants | 1.61 | 1.37 | 0.00 | 6.91 |
| Log Number of filled vacancies | 0.48 | 0.74 | 0.00 | 5.97 |
| Educational requirements | ||||
| University | 0.03 | 0.16 | 0.00 | 1.00 |
| Upper vocational | 0.18 | 0.39 | 0.00 | 1.00 |
| Secondary general | 0.05 | 0.21 | 0.00 | 1.00 |
| Secondary vocational | 0.28 | 0.45 | 0.00 | 1.00 |
| Lower Secondary general | 0.08 | 0.27 | 0.00 | 1.00 |
| Primary vocational | 0.27 | 0.44 | 0.00 | 1.00 |
| Primary general | 0.11 | 0.32 | 0.00 | 1.00 |
| Vacancy and firm characteristics | ||||
| Part time | 0.18 | 0.37 | 0.00 | 1.00 |
| Permanent | 0.76 | 0.43 | 0.00 | 1.00 |
| Experience required | 0.64 | 0.48 | 0.00 | 1.00 |
| Age limits | 0.19 | 0.40 | 0.00 | 1.00 |
| Log number of employees | 3.89 | 1.51 | 0.69 | 9.10 |
| Business cycle | ||||
| Log vacancies/employment (regional) | −0.13 | 0.48 | −1.23 | 0.99 |
| Log unemployment rate (regional) | 1.94 | 0.20 | 1.36 | 2.48 |
| 1991 | 0.09 | 0.28 | 0.00 | 1.00 |
| 1992 | 0.17 | 0.38 | 0.00 | 1.00 |
| 1993 | 0.15 | 0.36 | 0.00 | 1.00 |
| 1994 | 0.14 | 0.34 | 0.00 | 1.00 |
| 1995 | 0.13 | 0.33 | 0.00 | 1.00 |
| 1996 | 0.09 | 0.28 | 0.00 | 1.00 |
| 1997 | 0.14 | 0.35 | 0.00 | 1.00 |
| 1998 | 0.09 | 0.29 | 0.00 | 1.00 |
| Occupation | ||||
| Scientific personnel | 0.10 | 0.30 | 0.00 | 1.00 |
| Consultants | 0.09 | 0.29 | 0.00 | 1.00 |
| Managers | 0.03 | 0.17 | 0.00 | 1.00 |
| Administrative personnel | 0.19 | 0.39 | 0.00 | 1.00 |
| Commercial personnel | 0.11 | 0.31 | 0.00 | 1.00 |
| Service personnel | 0.12 | 0.32 | 0.00 | 1.00 |
| Agricultural workers | 0.02 | 0.14 | 0.00 | 1.00 |
| Supervisory and production personnel | 0.03 | 0.17 | 0.00 | 1.00 |
| Craftsmen | 0.11 | 0.32 | 0.00 | 1.00 |
| Industry | ||||
| Agriculture ISBN 1 | 0.03 | 0.16 | 0.00 | 1.00 |
| Mining ISBN 2 | 0.09 | 0.29 | 0.00 | 1.00 |
| Manufacturing ISBN 3 | 0.10 | 0.31 | 0.00 | 1.00 |
| Utilities ISBN 4 | 0.00 | 0.06 | 0.00 | 1.00 |
| Construction ISBN 5 | 0.13 | 0.34 | 0.00 | 1.00 |
| Trade and restaurants/hotels ISBN 6 | 0.20 | 0.40 | 0.00 | 1.00 |
| Transport and communications ISBN 7 | 0.07 | 0.25 | 0.00 | 1.00 |
| Financial and business services ISBN 8 | 0.11 | 0.31 | 0.00 | 1.00 |
| Personal Services ISBN 9 | 0.25 | 0.43 | 0.00 | 1.00 |
| Number of observations | 39,814 | |||
Appendix B: : Robustness of the results alternative estimation methods
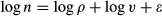 (B1)
(B1)| (Log) number of filled vacancies | Internal | Via own personnel | Via business relations | Walk-ins | Advertisements |
|---|---|---|---|---|---|
| Full sample (OLS) | 0.871 | 1.015 | 1.011 | 1.005 | 0.556 |
| (0.025)* | (0.022) | (0.032) | (0.016) | (0.017)* | |
| Restricted sample (OLS) | 0.889 | 1.002 | 0.982 | 0.999 | 0.584 |
| (0.030)* | (0.027) | (0.040) | (0.019) | (0.022)* |
| Temporary help agency | Public employment agency | School search | Private employment agency | Other search Methods | |
|---|---|---|---|---|---|
| Full sample (OLS) | 0.972 | 0.806 | 1.006 | 0.697 | 0.972 |
| (0.022) | (0.020)* | (0.038) | (0.076)* | (0.030) | |
| Restricted sample (OLS) | 0.963 | 0.800 | 1.051 | 0.664 | 0.957 |
| (0.027) | (0.025)* | (0.047) | (0.095)* | (0.035) |
- Note: Robust standard error in parentheses (*different from one at the 5% significance level).




