The role of gene flow in rapid and repeated evolution of cave-related traits in Mexican tetra, Astyanax mexicanus
Abstract
Understanding the molecular basis of repeatedly evolved phenotypes can yield key insights into the evolutionary process. Quantifying gene flow between populations is especially important in interpreting mechanisms of repeated phenotypic evolution, and genomic analyses have revealed that admixture occurs more frequently between diverging lineages than previously thought. In this study, we resequenced 47 whole genomes of the Mexican tetra from three cave populations, two surface populations and outgroup samples. We confirmed that cave populations are polyphyletic and two Astyanax mexicanus lineages are present in our data set. The two lineages likely diverged much more recently than previous mitochondrial estimates of 5–7 mya. Divergence of cave populations from their phylogenetically closest surface population likely occurred between ~161 and 191 k generations ago. The favoured demographic model for most population pairs accounts for divergence with secondary contact and heterogeneous gene flow across the genome, and we rigorously identified gene flow among all lineages sampled. Therefore, the evolution of cave-related traits occurred more rapidly than previously thought, and trogolomorphic traits are maintained despite gene flow with surface populations. The recency of these estimated divergence events suggests that selection may drive the evolution of cave-derived traits, as opposed to disuse and drift. Finally, we show that a key trogolomorphic phenotype QTL is enriched for genomic regions with low divergence between caves, suggesting that regions important for cave phenotypes may be transferred between caves via gene flow. Our study shows that gene flow must be considered in studies of independent, repeated trait evolution.
1 INTRODUCTION
Repeated adaptation to similar environments offers insight into the evolutionary process (Agrawal, 2017; Gompel & Prud'homme, 2009; Losos, 2011; Rosenblum, Parent, & Brandt, 2014; Stern, 2013; Stern & Orgogozo, 2009). Predictable phenotypes are likely when repeated evolution occurs through standing genetic variation and/or gene flow, such that the alleles are identical by descent, and when populations experience shared, strong selection regimes (Rosenblum et al., 2014). Understanding repeated evolution, however, requires an understanding of the basic parameters of the evolutionary process, including how long populations have diverged, how many independent phenotypic origins have occurred, the extent of gene flow between populations and the strength of selection needed to shape phenotypes (Roesti, Gavrilets, Hendry, Salzburger, & Berner, 2014; Rosenblum et al., 2014; Rougemont et al., 2017; Stern, 2013; Welch & Jiggins, 2014).
The predictable phenotypic changes observed in cave animals offer one of the most exciting opportunities in which to study repeated evolution (Elmer & Meyer, 2011). Cave animals also offer advantages over many systems in that the direction of phenotypic change is known (surface → cave) and coarse selection pressures are defined (e.g., darkness and low-nutrient availability). The cavefish (Astyanax mexicanus) in northeastern Mexico have become a central model for understanding the evolution of diverse developmental, physiological and behavioural traits (Keene, Yoshizawa, & McGaugh, 2015). Many populations of Astyanax mexicanus exhibit a suite of traits common to other cave animals including reduced eyes and pigmentation (Borowsky, 2015; Protas & Jeffery, 2012). In addition, many populations possess behavioural and metabolic traits important for survival in dark, low-nutrient environments (Aspiras, Rohner, Martineau, Borowsky, & Tabin, 2015; Bibliowicz et al., 2013; Duboué, Keene, & Borowsky, 2011; Jaggard et al., 2017, 2018; Jeffery, 2001, 2009; Protas et al., 2008; Riddle et al., 2018; Salin, Voituron, Mourin, & Hervant, 2010; Varatharasan, Croll, & Franz-Odendaal, 2009; Yamamoto, Byerly, Jackman, & Jeffery, 2009; Yoshizawa, Gorički, Soares, & Jeffery, 2010). Over 30 populations of cavefish are documented (Espinasa, Rivas-Manzano, & Pérez, 2001; Mitchell, Russell, & Elliott, 1977), and conspecific surface populations are a proxy for the ancestral conditions to understand repeated adaptation to the cave environment. Thus, A. mexicanus offers an excellent opportunity to evaluate the roles of history, migration, drift, selection and mutation to the repeated evolution of a convergent suite of phenotypes.
Despite evidence for the repeated evolutionary origin of cave-associated traits in A. mexicanus, the timing of cave invasions by surface lineages is uncertain, and the extent of genetic exchange between cavefish and surface fish is under debate (Bradic, Beerli, León, Esquivel-Bobadilla, & Borowsky, 2012; Bradic, Teotónio, & Borowsky, 2013; Coghill, Hulsey, Chaves-Campos, García de Leon, & Johnson, 2014; Fumey et al., 2018; Gross, 2012; Hausdorf, Wilkens, & Strecker, 2011; Ornelas-García, Domínguez-Domínguez, & Doadrio, 2008; Porter, Dittmar, & Pérez-Losada, 2007; Strecker, Bernatchez, & Wilkens, 2003; Strecker, Faúndez, & Wilkens, 2004; Strecker, Hausdorf, & Wilkens, 2012). High amounts of gene flow between cave and surface populations and among cave populations may complicate conclusions regarding repeated evolution (Mallet, Besansky, & Hahn, 2016; Ornelas-García & Pedraza-Lara, 2015). For instance, cavefish populations are polyphyletic (Bradic et al., 2012, 2013; Coghill et al., 2014; Gross, 2012; Ornelas-García et al., 2008; Strecker et al., 2003, 2012) which is consistent with repeated evolution. Yet, this pattern has been previously hypothesized as being consistent with a single invasion of the cave system, subterranean spread of fish and substantial gene flow of individual caves with their geographically closest surface population (suggested by Coghill et al., 2014; Espinasa & Borowsky, 2001). Alternatively, gene exchange among caves could result in a shared adaptive history even if cave populations were founded independently. Thus, additional work is needed to understand the demographic history of these populations and implications for the evolutionary process.
Here, we conduct an extensive examination of the gene flow between cave populations and between cave and surface populations of A. mexicanus to understand repeated evolutionary origins of cave-derived phenotypes and the potential for gene flow to enhance or impede adaptation to caves. Since we employ whole-genome resequencing as opposed to reduced representation methods, we were able to calculate genomewide absolute measures of divergence (dXY), compare to relative measures (pairwise FST) (reviewed in Cruickshank & Hahn, 2014; Ellegren, 2014; Lowry et al., 2016), and demonstrate that pairwise FST is predominantly driven by heterogeneous diversity across populations which obscured accurate inferences of divergence and gene flow among populations in past studies (Charlesworth, 1998). Our analyses reveal gene flow between cave populations is more extensive than previously appreciated, cave and surface populations exchange alleles (Wilkens & Strecker, 2003), and surface and cave populations have diverged recently. We show that given these demographic parameters, repeated evolution of cave phenotypes may reflect the action, rather than the relaxation of natural section. Additionally, we present evidence that at least one region of the genome important for cave-derived phenotypes may be transferred between caves, suggesting that gene flow among caves may play a role in the maintenance and/or origin of cave phenotypes.
2 METHODS
2.1 Sampling, DNA extractions, and sequencing
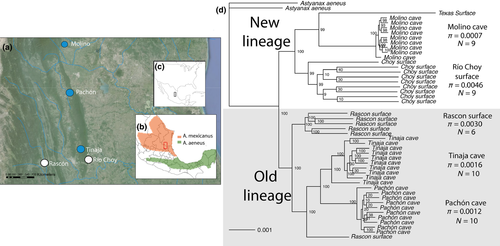
We sampled five populations of Astyanax mexicanus cave and surface fish from the Sierra de Guatemala, Tamaulipas, and Sierra de El Abra region, San Luis Potosí, Mexico: Molino, Pachón, and Tinaja caves and the Rascón and Río Choy surface populations (Figure 1). Two main lineages of cave and surface populations are often referred to as “new” and “old” in reference to when the lineages presumably reached northern Mexico, each with independently evolved cave populations. Populations in Molino cave and Río Choy are considered “new” lineage fish, and the populations of Pachón cave and Tinaja cave are typically classified as “old” lineage populations (Bradic et al., 2012; Coghill et al., 2014; Dowling, Martasian, & Jeffery, 2002; Ornelas-García et al., 2008). These cave populations were the focus of our study because they are the most commonly used cave populations for laboratory studies.
Rascón was selected because cytochrome b sequences are most similar to old lineage cave populations (Ornelas-García et al., 2008). Rascón is part of the river system of Rio Gallinas, which ends at the 105 m vertical waterfall of Tamul into Rio Santa Maria/Tampaon. It is hypothesized that new lineage surface fish could not overcome the 105 m waterfall and could not colonize the Gallinas river (e.g., Rascón population). Thus, Rascón likely has remained cut-off from nearby surface streams inhabited by new lineage populations, and it, thus, was an important surface locality to include. Most other surface populations are thought to be of “new” origin, exhibit low divergence between each other, and be panmictic (Bradic et al., 2012); thus, sampling Río Choy is an initial proxy for sampling surface populations range-wide.
Fin clips were collected from fish in Spring 2013 from Pachón cave, Río Choy (surface), and a drainage ditch near the town of Rascón in San Luis Potosí, Mexico. Samples from Molino cave were collected by W. Jeffery, B. Hutchins and M. Porter in 2005, and Pecos drainage in Texas in 1994 by W. Jeffery and C. Hubbs. Samples from Tinaja cave were collected in 2002 and 2009 by R. Borowsky.
We complemented our sequencing of these populations with four additional individuals. First, we sequenced an A. mexicanus sample from a Texas surface population. While this population is not of direct interest to this study, it has been the focus of many Quantitative Trait Loci (QTL) studies (e.g., O'Quin et al., 2015), and therefore, it is evolutionary relationship to our populations is of interest. Second, we aimed to sequence an outgroup to polarize mutations in A. mexicanus. To do so, we first sequenced two samples of a close congener Astyanax aeneus (Mitchell et al., 1977; Ornelas-García & Pedraza-Lara, 2015) from Guerrero, Mexico. However, despite being separated from the sampled Astyanax mexicanus populations by the Trans-Mexican Volcanic Belt (Mitchell et al., 1977; Ornelas-García & Pedraza-Lara, 2015), we found a history of gene flow between Astyanax aeneus and Astyanax mexicanus. We therefore sequenced a more distant outgroup, the white skirt tetra (long-finned) Gymnocorymbus ternetzi. Gymnocorymbus ternetzi was used only for polarizing 2D site frequency spectra.
DNA was extracted using the Genomic-Tip Tissue Midi kits and DNEasy Blood and Tissue kit (Qiagen). We performed whole-genome resequencing with 100 bp paired-end reads on an Illumina HiSeq2000 at The University of Minnesota Genomics Center. Samples were prepared for Illumina sequencing by individually barcoding each sample and processing with the Illumina TruSeq Nano DNA Sample Prep Kit using v3 reagents. Five barcoded samples were pooled and sequenced in two lanes. In total, 45 samples were sequenced across 18 lanes. We resequenced nine Pachón cavefish, ten Tinaja cavefish, nine Molino cavefish, six Rascón surface fish, nine Río Choy surface fish and two Astyanax aeneus samples. We also made use of the Astyanax genome project to add another sample from the Pachón population, and obtain genotype information for the reference sequence. For this reference sample, we used the first read (R1) from all of the 100 bp paired-end reads that were sequenced using an Illumina HiSeq2000 and aligned to the reference genome (McGaugh et al., 2014). The Texas population and the white skirt tetra were barcoded, pooled and sequenced across two lanes of 125 bp paired-end reads from a HiSeq2500 in High-Output run mode using v3 reagents.
For all raw sequences, we trimmed and cleaned sequence data with trimmomatic v0.30 (Lohse et al., 2012) and cutadapt v1.2.1 (Martin, 2011) using the adapters specific to the barcoded individual, allowing a quality score of 30 across a 6 bp sliding window, and removing all reads <30 nucleotides in length after processing. When one read of a pair failed QC, its mate was retained as a single-end read for alignment. Post-processing coverage statistics were generated by the fastx toolkit v0.0.13 ( http://hannonlab.cshl.edu/fastx_toolkit/) and ranged from 6.8- to 11.9-fold coverage (mean = 8.87-fold coverage; median = 8.65-fold coverage Table 1, Supporting Information Tables S1 and S2), assuming a genome size estimate of 1.19 Gb (McGaugh et al., 2014) for the Illumina Hi-Seq 2000 samples. For the Pachón reference genome sequence, which was excluded from the measures above, the coverage was 16.68-fold. All new Illumina sequence reads were submitted to NCBI's Sequence Read Archive (Supporting Information Table S3). We expect some heterozygosity dropout with this relatively low level of coverage, but we sought to balance number of samples and depth of coverage in a cost-effective manner. Heterozygosity dropout would lower our diversity estimates, and if directional (e.g., due to reference sequence bias) could increase divergence between populations and lower estimates of gene flow. As detailed below, our data estimate more recent divergence times and higher estimates of gene flow than past studies.
| Population | N | Aligned coverage mean (range) |
|---|---|---|
| Pachón – cave | 9 + reference | 9.94 (7.65, 17.74) |
| Tinaja – cave | 10 | 10.05 (7.27, 12.35) |
| Rascón – surface | 6 | 10.90 (8.63, 13.15) |
| Molino – cave | 9 | 9.39 (7.47, 12.32) |
| Río Choy – surface | 9 | 9.27 (8.38, 10.26) |
2.2 Alignment to reference and variant calling
The Astyanax mexicanusgenome v1.0.2 (McGaugh et al., 2014) was downloaded through NCBI genomes FTP. Alignments of Illumina data to the reference genome were generated with the BWA-mem algorithm (Li, 2013) in bwa-0.7.1 (Li & Durbin, 2009, 2010). Both genome analysis toolkit v3.3.0 (GATK) and picard v1.83 ( http://broadinstitute.github.io/picard/) were used for downstream manipulation of alignments, according to GATK Best Practices and forum discussions (Auwera et al. 2013; DePristo et al., 2011; McKenna et al., 2010). Alignments of paired-end and orphaned reads for each individual were sorted and merged using Picard. Duplicate reads that may have arisen during PCR were marked using Picard's MarkDuplicates tool and filtered out of downstream analyses. GATK's IndelRealigner and RealignerTargetCreator tools were then used to realign reads that may have been errantly mapped around indels (insertions/deletions). Additional details are in Supporting Information Methods.
The haplotypecaller tool in gatk v3.3.0 was used to generate GVCFs of genotype likelihoods for each individual. The genotypegvcfs tool was used to generate a multi-sample variant call format (VCF) of raw variant calls for all samples. Hard filters were applied separately to SNPs and indels/mixed sites using the variantfiltration and selectvariants tools (Supporting Information Table S4). Filtering variants was performed to remove low confidence calls from the data set. The filters removed calls that did not pass thresholds for base quality, depth of coverage and other metrics of variant quality (Supporting Information Table S4).
Alleles with 0.5 frequency appeared to be overrepresented in the site frequency spectra, and the depth of coverage for alleles with 0.5 frequency was greater than the coverage at other frequencies. Upon examination, every individual was heterozygous and these alleles occurred in small tracts throughout the genome. We concluded these were likely paralogous regions (teleost fish have an ancient genome duplication, Hoegg, Brinkmann, Taylor, & Meyer, 2004; Meyer & Van de Peer, 2005). Molino was the most severely impacted population, likely due to Molino's low diversity allowing for collapsing of paralogs (see below). To be conservative, we identified sites where 100% of individuals in any population were heterozygotes and excluded these sites in all analyses. We still observed slight inflation at 0.5 frequency even after our heterozygosity filtering, and these are probably instances of collapsed paralogs where our criterion of heterozygosity in every genotyped individual is not met.
We generated a VCF file with variant and invariant sites, and subset it to include biallelic only SNPs where applicable. We excluded sites that were defined as repetitive regions from a Repeat Modeler analysis in McGaugh et al. (2014). Next, we removed sites that had less than six individuals genotyped in all populations. We also scanned for indels in the VCF file and removed the indel as well as 3 bp ± around the indel. In total, 171,841,976 bp were masked from downstream analyses. Lastly, all sites that were tri- or tetra-allelic were removed. Thus, sites were either invariant or biallelic. To reduce issues of non-independence induced by linkage disequilibrium, we analysed a thinned set of biallelic SNPs by retaining a single SNP in each non-overlapping window of 150 SNPs for the ADMIXTURE, TreeMix, and F3 and F4 analyses, resulting in approximately 119,000 SNPs for those analyses.
2.3 Population phylogeny and divergence
We generated a phylogenetic reconstruction to understand population relationships using 47 sampled individuals (excluding white skirt tetra, but including A. aeneus and Texas A. mexicanus). The population phylogeny estimation was implemented in raxml v8.2.8 with the two A. aeneus specified as the outgroups. We converted the VCF to fasta format alignments by passing through the mvf format using mvftools v3 (Pease & Rosenzweig, 2015). This was done to preserve ambiguity codes at sites polymorphic in individuals. Sites with greater than 40% missing data were removed using trimal v1.2 (Capella-Gutiérrez, Silla-Martínez, & Gabaldón, 2009). We performed 100 rapid bootstrapping replicates followed by an ML search from two separate parsimony trees. For computational efficiency, we implemented the GTRCAT model, though we note that inferences using a smaller subset of the genome and the GTRGAMMA model recover the same topology as presented in Figure 1. The ML tree with bootstrap support was drawn using the ape package v3.5 (Paradis, Claude, & Strimmer, 2004) in r v3.2.1 (R Core Team, 2018) using the A. aeneus samples as the outgroup; however, our results are consistent even if the outgroup is left unspecified and this decision is justified by the observation that A. aeneus is more distant from all A. mexicanus populations than any are to one another, as measured by the mean number of pairwise sequence differences.
2.3.1 Intra- and interpopulation average pairwise nucleotide differences
Average pairwise nucleotide diversity values (π) reflect the history of coalescence events within and among populations (Hudson, 1990; Nei, 1987) and are directly informative about the history and relationships of a sample. Here, we use the following notation for inter- and intrapopulation average pairwise nucleotide diversity values: Intrapopulation values are designated with π, while interpopulation values are designated with dXY where X and Y are different populations (e.g., dRascón-Pachón). Pairwise nucleotide diversity estimates for fourfold degenerate sites were calculated for 46 individuals (excluding Texas A. mexicanus and white skirt tetra) from phased genomic data using the VCF file with invariant and variant sites unless otherwise noted. Additional details for each analysis (e.g., window size, site class used) are given Supporting Information Methods. We also performed windowed estimates along the entire genome to understand the fine-scale apportionment of ancestry.
We use these levels of diversity and divergence to estimate the difference in coalescent times between and within populations. In the absence of gene flow, this excess between populations can be translated into an estimate of divergence time (dXY − πanc = 2μT (Brandvain, Kenney, Flagel, Coop, & Sweigart, 2014; Hudson, Kreitman, & Aguadé, 1987), where T is the population split time, and using a diversity in surface population as a stand in for πanc). After removing recent hybrids identified by ADMIXTURE, we use this approach to estimate this excess coalescent time between pairs of populations. However, given extensive evidence for gene exchange (below), this estimate will be more recent than the true divergence time (Mallet et al., 2016), which we estimate with model-based approaches below.
In this and all other estimates of divergence time, below, we assume a neutral mutation rate of 3.5 × 10−9/bp/generation which is estimated using parent–offspring trios in cichlids (Malinsky et al., 2017). We know little about the age-specific reproductive outputs for Astyanax in the wild. However, in the laboratory, Astyanax is sexually mature as early as 6 months under optimal conditions, though this varies across laboratories (Borowsky, 2008a; Jeffery, 2001). Since conditions in the wild are rarely as optimal as in the laboratory, we assume generation interval (Fenner, 2005) is 1 year, though, our general conclusions are consistent if the generation interval is longer.
2.4 Genomewide tests for gene flow
2.4.1 ADMIXTURE
We estimated admixture (cluster membership) proportions for the individuals comprising the five populations studied, as well as A. aeneus samples, using admixture v1.3.0 (Alexander & Lange, 2011; Alexander, Novembre, & Lange, 2009). We conducted 10 independent runs for each value of K (the number of ancestral population clusters) from K = 2 to K = 6 and present results for the run with the K = 6 (i.e., the number of sampled biological populations).
2.4.2 F3 and F4 statistics
After removing recent hybrids, we used F3 and F4-statistics (as implemented in the threepop and fourpop programs packaged with treemix v1.12 (Pickrell & Pritchard, 2012)) to test for historical gene flow. For computational feasibility, we calculated a standard error for each statistic using a block jackknife with blocks of 500 SNPs, assessing significance by a Z-score from the ratio of F4 to its standard error.
The F3 statistic (Peter, 2016; Reich, Thangaraj, Patterson, Price, & Singh, 2009), represented as F3 (X;A,B), is calculated as E[(pX − pA)(pX − pB)], where X is the population being tested for admixture, A and B are treated as the source populations, and pX, pA, pB are the allele frequencies. Without introgression, F3, is positive, and a negative value occurs when this expectation is overwhelmed by a non-tree-like history of three populations. Importantly, complex histories of mixture in populations A and/or B do not result in significantly negative F3 values (Patterson et al., 2012; Reich et al., 2009).
F4 tests assess “treeness” among a quartet of populations (Reich et al., 2009). F4(P1,P2;P3,P4) is calculated as E[(p1 − p2)(p3 − p4)], and serves as a powerful test of introgression when P1, P2 and P3, P4 are sisters on an unrooted tree. A significantly positive F4 value means that P1 and P3 are more similar to one another than expected under a non-reticulate tree—a result consistent with introgression between P1 and P3, or between P2 and P4. Alternatively, a significantly negative F4 value is consistent with introgression between P1 and P4 or between P2 and P3. Regardless of the sign of this test, F4 values may reflect introgression events involving sampled, unsampled, or even extinct populations.
2.4.3 TreeMix
We used the treemix program v1.12 (Pickrell & Pritchard, 2012) to visualize all migration events after removing recent hybrids. Rather than representing population relationships as a bifurcating tree, treemix models population relationships as a graph in which lineages can be connected by migration edges. We used the same thinned biallelic SNPs as above. As with F3 and F4, we removed recent hybrids from this analysis. We first inferred the maximum-likelihood tree and then successively added single migration events until the proportion of variance explained by the model plateaued (Pickrell & Pritchard, 2012).
2.5 Demographic modelling
We modelled the demographic history of pairs of populations to further elucidate their relationships and migration rates. To conduct demographic modelling, we generated unfolded joint site frequency spectra (2D SFS) from the invariant sites VCF using a custom Python script. Detailed explanation of parameters and a user-friendly guide is available here: https://github.com/TomJKono/CaveFish_Demography/wiki.
White skirt tetra (Gymnocorymbus ternetzi) was used as the estimated ancestral state for all 10 pairwise combinations of Río Choy surface, Molino cave, Pachón cave, Rascón surface and Tinaja cave. Recently admixed individuals were excluded from the comparisons. To reduce the effect of paralogous alignment from the ancient teleost genome duplication, sites at 50% frequency in both populations were masked from the demographic modelling analysis. Sites were excluded if they were heterozygous in the representative outgroup sample or had any missing information in either of the populations being analysed. In addition, sites were excluded due to indels or repetitive regions as described above. Aside from these exclusions, all other sites, including invariant sites were included in all 2D SFS and the length of these sites make up locus length.
A total of seven demographic models were fit to each 2D SFS to infer the timing of population divergence, effective migration rates and effective population sizes using ∂a∂i 1.7.0 (Gutenkunst, Hernandez, Williamson, & Bustamante, 2009). The seven models were derived from previously published demographic modelling analysis (Tine et al., 2014). Briefly, the seven models are as follows: SI—strict isolation, SC—secondary contact, IM—isolation with migration, AM—ancestral migration, SC2M—secondary contact with two migration rates, IM2M—isolation with migration with two migration rates and AM2M—ancestral migration with two migration rates (see figure S9 of Tine et al., 2014). Two migration rates within the genome appeared to fit the data better in previous work (Tine et al., 2014), as this approach allows for heterogeneous genomic divergence (M which is most often the largest migration rate within the genome, Mi which is usually the lowest migration rate within the genome). Descriptions of the parameters and parameter starting values are given in Supporting Information Table S5 and Supporting Information Methods. For each replicate, Akaike information criterion (AIC) values for each model were converted into Akaike weights. The model with the highest mean Akaike weight across all 50 replicates was chosen as the best-fitting model (Rougeux, Bernatchez, & Gagnaire, 2017; Supporting Information Table S6; similar to Wagenmakers & Farrell, 2004).
The best-fitting demographic model for each 2D SFS comparison was used to generate estimates of the population parameters. Scaling from estimated parameters to real-value parameters was done assuming a mutation rate (μ) of 3.5 × 10−9 per bp per generation (Malinsky et al., 2017) and a locus length (L) of the number of sites used to generate the 2D SFS. For effective population size estimates, we estimated the reference population size, Nref, as the mean “theta” value from all 50 replicates of the best-fitting model multiplied by 1/(4 μL). The effective population sizes of the study populations were then estimated as a scaling of Nref. To estimate the per-generation proportion of migrants, we scaled the mean total migration rates from ∂a∂i by 1/(2Nref). Total times since divergence for pairs of populations were estimated as the sum of the split time (“Ts”) and time since secondary contact commenced (“Tsc”) estimates for each population pair.
2.6 Modelling of selection needed for cave alleles to reach high frequency
With demographic estimates provided by our whole-genome sequencing and ∂a∂i, we estimated the selection coefficients needed to bring alleles associated with the cave phenotype to high frequency. We implemented the 12-locus additive alleles model by Cartwright, Schwartz, Merry, and Howell (2017) with the parameters estimated for Molino cave, as this is the population where selection would need to be strongest to overcome the effects of drift. We estimated the one-way mutation rate of loci (μ) to be on the order of 1 × 10−6 (c.f. 3.5 × 10−9/bp/generation * 1170 bp, which is the median gene length across the genome). Other parameters were N = 7,335 (Molino Ne), h = 0.5 (additive alleles), k = 12 (number of loci) and Q = 0.1 (surface allele frequency of cave-favoured alleles). The simulation model was adapted from Cartwright et al. (2017) with the addition that the cave population was isolated for a period of time before becoming connected again with the surface. Consistent with our demographic models for Molino and Río Choy, migration rates spanned between 10−6 and 10−5 with 91,000 generations of isolation followed by 71,000 generations of connection. We also conducted simulations with the parameters from Tinaja cave as this is the cave population where selection would need to be weakest to overcome the effects of drift. All parameters were the same as above except N = 30,522 (Tinaja Ne), and 170,000 generations of isolation were followed by 20,000 generations of connection.
2.7 Candidate regions introgressed between caves
To identify regions of the genome that were likely transferred between cave populations or between cave and surface populations and were linked to cave-associated phenotypes, we implemented an outlier approach incorporating pairwise sequence differences and FST. To determine potential candidate regions, we utilized 5 kb dXY windows using all biallelic sites, not just fourfold degenerate, since so few sites would be available. We first phased the biallelic variant sites for all samples using beagle (version 4.1; Browning & Browning, 2007). We then determined the number of invariant sites (from the full genome VCF) and variant sites in each 5 kb window to calculate average pairwise diversity. We then identified 5 kb regions in which dXY was in the lower 5% tail of the genomic distribution of dXY for all three pairwise combinations of cave populations, but substantial divergence with either surface population as measured by FST or dXY. For FST outliers, we required that π per gene for both surface fish populations must be greater than the lowest 500 π values for genes across the genome. This requirement protects, in part, against including regions that are low diversity across all populations due to a feature of the genome.
To put the results in context of phenotypes mapped to the genome, we created a database of prior QTL from several key studies (Kowalko, Rohner, Linden et al., 2013; Kowalko, Rohner, Rompani et al., 2013; O'Quin, Yoshizawa, Doshi, & Jeffery, 2013; Protas, Conrad, Gross, Tabin, & Borowsky, 2007; Protas et al., 2008; Yoshizawa, Yamamoto, O'Quin, & Jeffery, 2012; Yoshizawa et al., 2015) and used overlapping markers between studies to position QTL relative to the linkage map in O'Quin et al. (2013). For markers in (Kowalko, Rohner, Rompani et al., 2013), we used blastn to place the marker on a genomic scaffold and placed the QTL from (Kowalko, Rohner, Rompani et al., 2013) in our database as locating to the entire scaffold. Our qtl database is given in Supporting Information Table S7.
3 RESULTS
3.1 Population phylogenetic reconstruction
We inferred the population phylogeny using half the nuclear genome (invariant and variant sites, but no mitochondrial sites) in the program raxml. Our phylogenetic tree clearly demarcates two lineages and indicates that the Rascón surface population and the Tinaja and Pachón cave populations form a monophyletic clade (Figure 1; often referred to as “old lineage”). Similarly, the Río Choy surface and Molino cave populations form a monophyletic clade (referred to as “new lineage”). Thus, this phylogeny indicates that many cavefish traits may be polyphyletic (i.e., evolved through repeated evolution).
In agreement with a previous study showing that Molino cave population has the lowest diversity of cave populations sampled, the Molino cave population exhibits shorter branches than other populations tested (Bradic et al., 2013), while the surface populations exhibit longer branch lengths. While all populations and the two lineages have high bootstrap support (≥99), bootstrap support with genomic-scale data provides little information about the evolutionary processes or the distribution of alternative topologies across the genome (Yang & Rannala, 2012); thus, we use a series of tests below to explore this further.
3.2 Diversity and divergence
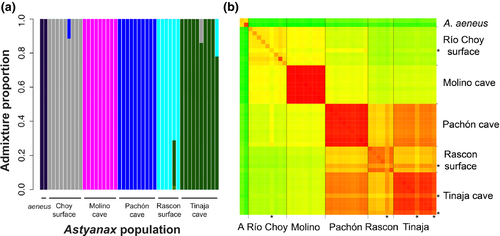
Patterns of diversity within populations, π, and interpopulation divergence, dXY, provide a broad summary of the coalescent history within and between populations. We present pairwise sequence differences at fourfold degenerate sites between all pairs of individuals (Figure 2). The “striped” individuals in Figure 2b correspond to recent hybrids as inferred by ADMIXTURE (Figure 2a). We removed these putative recent hybrids from our summary of diversity within and divergence between populations presented in Table 2.
| A. aeneus | Río Choy | Molino | Pachón | Rascón | Tinaja | |
|---|---|---|---|---|---|---|
| A. aeneus | 0.0035 | 398,239 | 372,641 | 276,735 | 281,219 | 264,154 |
| Río Choy | 0.00637 | 0.00387 | 113,913 | 96,569 | 156,597 | 118,333 |
| Molino | 0.00619 | 0.00438 | 0.00033 | 50,338 | 101,781 | 67,029 |
| Pachón | 0.00552 | 0.00426 | 0.00393 | 0.00080 | 139,541 | N/A |
| Rascón | 0.00555 | 0.00468 | 0.00429 | 0.00335 | 0.00237 | 113,321 |
| Tinaja | 0.00543 | 0.00441 | 0.00405 | 0.00218 | 0.00316 | 0.0092 |
Genomewide average diversity within cave populations (π4fold degen: Molino = 0.00074, Tinaja = 0.00129, Pachón = 0.00100; Table 2) is substantially lower than diversity within surface populations (π4fold degen: Río Choy = 0.00300, Rascón = 0.00207), reflecting a decrease in effective population size in caves (sensu Avise & Selander, 1972). Molino cave is the most homogenous. These results are consistent with the short branches in cave populations observed in the phylogenetic tree produced by RAxML (Figure 1). In contrast, the surface population Río Choy is the most diverse in our sample—so much so that two Río Choy fish may be more divergent than fish compared between any of the old lineage populations (e.g., Tinaja cave and Rascón sruface).
Genomewide average divergence between the new and old lineages (dXY 4fold degen = 0.00340 − 0.00374, Table 2) exceeds divergence between cave and surface populations within lineages (dXY 4fold degen Molino-Río Choy = 0.00332; Tinaja-Rascón = 0.00285; Pachón-Rascón = 0.00298; Table 2). Thus, old and new lineages diverged prior to (or have experienced less genetic exchange than) any of the cave–surface population pairs within lineages. The two old lineage caves are the least diverged populations in our sample (dXY 4fold degen: Pachón-Tinaja = 0.00225). These results are consistent with both the observation of monophyly of old and new lineages and the observation that old lineage cave populations are sister taxa in the raxml tree (Figure 1).
Divergence between populations suggests that a simple bifurcating tree does not fully capture the history of these populations. For example, divergence between the new lineage cave population (Molino) and the geographically closer old lineage cave population (Pachón) is less than divergence between Molino and the geographically further old lineage populations (Tinaja and Rascón; Table 2). Likewise, all old lineage populations are closer to Molino cave than they are to Río Choy. These results suggest gene flow between Molino cave and the old lineage populations, which is supported by additional analyses.
3.3 Genomewide tests suggest substantial historical and contemporary gene flow
3.3.1 ADMIXTURE
We focus our discussion on K = 6, the case where the number of clusters matches our presumed number of populations (Figure 2a), and additional cluster sizes are presented in (Supporting Information Figure S1). While, individuals largely cluster exclusively with others from their sampled population, we also observe contemporary gene flow between cave and surface populations, as well between new and old lineage taxa (Figure 2a, Supporting Information Figure S1).
Specifically, there appears to be reciprocal gene exchange between the Tinaja cave and the old lineage surface population (a Tinaja individual shares 22% cluster membership with Rascón surface and a Rascón individual shares 29% membership with Tinaja; Figure 2a, Supporting Information Figure S1 and S2). Another Tinaja sample appears to be a recent hybrid with the new lineage surface population (a Tinaja individual with 14% membership with Río Choy). One new lineage surface sample appears to have recent shared ancestry with samples from Pachón (i.e., Río Choy individual with 12% cluster membership with Pachón).
Although unsupervised clustering algorithms may show signs of admixture even when none has occurred (Falush, van Dorp, & Lawson, 2018), corroboration of ADMIXTURE results with supporting patterns of pairwise sequence divergence (Figure 2, Supporting Information Figure S1 and S2) in putatively admixed samples (Rascón 6, Tinaja 6, Choy 14, Tinaja E) strongly suggests that recent hybrids between cave and surface populations and old and new lineages are present in current-day populations.
While the existence of recent hybrids is consistent with long-term genetic exchange, such hybrids do not provide evidence for historical introgression. We, therefore, rigorously characterize the history of gene flow in this group, while removing putative recent hybrids identified from ADMIXTURE and pairwise sequence divergence to ensure that our historical claims are not driven by a few recent events.
3.3.2 F3 and F4 statistics
To test for historic genetic exchange, we calculated F3 and F4 “tree imbalance tests,” after removing recent hybrids identified by ADMIXTURE. Throughout the section below, gene flow is supported by F4 statistics between the two underlined taxa and/or the two non-underlined taxa in the four-taxa tree. Further, we interpret the F4 statistics in relation to the ranking of the F4 scores. Extreme F4 scores may be the result of both pairs (e.g., A–C and B–D) exchanging genes, amplifying the F4 score beyond what the score would be if gene flow occurred only between a single pair within the quartet.
F3 and F4 tests convincingly show that Rascón, the old lineage surface population, has experienced gene flow with a lineage more closely related to A. aeneus than to the other individuals in our sample (Table 3). This claim is supported by numerous observations including the observations that, while all F3 tests including Rascón are significantly negative (i.e., supporting admixture), the most extreme F3 statistic is from a test with Rascón as the target population and A. aeneus and Tinaja as admixture sources, reflecting that both A. aeneus and Tinaja have likely hybridized extensively with Rascón. Additionally, all F4 tests of the form (A. aeneus, new lineage; old lineage cave, Rascón) are significantly negative, meaning that Rascón is genetically closer to A. aeneus than expected given a simple tree (Supporting Information Figure S3). Therefore, A. aeneus is an imperfect outgroup to A. mexicanus. Our interpretation is that A. aeneus and Rascón hybridized too deep in the past to be detected by ADMIXTURE analysis, but sufficiently recently to be detected by F3 and F4 tests. This is further supported by an analysis included in the supplemental materials that did not find long blocks of sequence similarity to A. aeneus in the Rascón genome.
| (X; A, B) | F3-statistic | SE | z-score |
|---|---|---|---|
| Rascón; A. aeneus, Tinaja | −9.25e-04 | 5.63e-05 | −16.42 |
| Rascón; Río Choy, Tinaja | −7.34e-04 | 4.97e-05 | −14.78 |
| Rascón; Molino, Tinaja | −7.21e-04 | 5.17e-05 | −13.94 |
| Rascón; A. aeneus, Pachón | −5.52e-04 | 6.05e-05 | −9.13 |
| Rascón; A. aeneus, Molino | −3.73e-04 | 6.53e-05 | −5.71 |
| Rascón; Río Choy, Pachón | −2.04e-04 | 6.03e-05 | −3.38 |
| Rascón; Molino, Pachón | −1.46e-04 | 6.18e-05 | −2.36 |
| Río Choy; A. aeneus, Molino | −1.02e-04 | 5.51e-05 | −1.84 |
Our results also show that the new lineage surface population, Río Choy, experienced gene flow with an unsampled outgroup. A significantly negative F3 value demonstrates Río Choy (the new lineage surface population) is an admixture target with Molino (new lineage cave) and A. aeneus as admixture sources (Table 3). This claim is bolstered by significantly positive F4 values in all comparisons of the form (A. aeneus, old lineage; Río Choy, Molino) in Supporting Information Figure S3. However, because dXY between A. aeneus and both new lineage populations are nearly equivalent, we suggest this is an example of “the outgroup case” for F3 (Patterson et al., 2012) in which admixture is attributed to an uninvolved outgroup (in this case, A. aeneus) rather than the unsampled admixture source.
We uncover evidence for admixture between the old lineage cave population, Pachón, and both new lineage populations (Molino cave and Río Choy surface), as observed in recent hybrids in ADMIXTURE. Specifically, the significantly negative F4 values for (A. aeneus, new lineage; Pachón, Tinaja) (Supporting Information Figure S3) are consistent with gene flow between both new lineage populations and the old lineage Pachón cave, and/or gene flow between Tinaja and A. aeneus. Because no other evidence suggests gene flow between Tinaja and A. aeneus, we argue that this result reflects gene flow between Pachón and the new lineage populations. This claim is further supported by the observation that dXY between new lineage populations and Pachón is consistently lower than dXY between new lineage populations and the other old lineage populations (Table 2).
Additionally, our analyses are consistent with gene flow between the old lineage Tinaja cave and the old lineage surface population, Rascón. Again, this result complements the discovery of two recent hybrids between these populations in our ADMIXTURE analysis. This claim is supported by the significantly positive F4 value for (A. aeneus, Rascón; Pachón, Tinaja). Since we lack evidence of Pachón – A. aeneus admixture, this significant F4 statistic is likely driven by Rascón – Tinaja admixture.
Despite gene flow among most population pairs, there is one case in which tree imbalance tests failed to reject the null hypothesis of a bifurcating tree: F4 tests of the form (new lineage, new lineage; old lineage, old lineage) (Supporting Information Figure S3). This result is counter to both our observation of recent hybrids (between the new and old lineages observed in ADMIXTURE), and the gene flow observed in other F4 – statistics, as well as treemix (Figures 3, Supporting Information Figure S4), dXY nearest neighbour proportions (Supporting Information Figures S5–S7) and phylonet (Supporting Information Figure S8). In these cases, it is also plausible that F4 scores that do not differ from zero may reflect opposing admixture events that cancel out a genomewide signal, rather than an absence of introgression (see Reich et al., 2009).
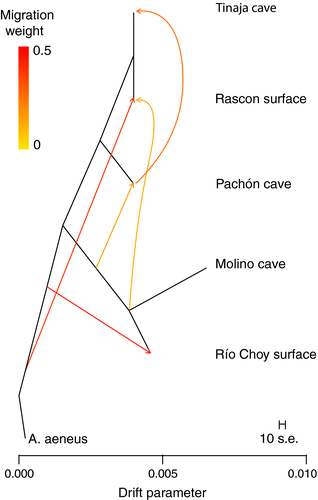
3.3.3 TreeMix
treemix allows us to visualize population relationships as a graph depicting directional admixture given a number of migration events, and uses the covariance structure of allele frequencies among populations rather than allele frequency difference correlations (e.g., F3 and F4). By examining multiple runs with different levels of migration, the treemix run with five migration events best explains the sample covariance (Supporting Information Figure S4).
treemix illustrates gene flow from the ancestral new lineage into both Rascón surface and Pachón cave (Figure 3; also suggested by F3 and F4 statistics), while providing evidence for gene flow from the lineage leading to A. aeneus samples to the Río Choy and Rascón lineages (also suggested by F3 and F4 statistics). Migration from Pachón cave into Tinaja cave is indicated (also supported by ∂a∂i modeling). However, the topology recovered by TreeMix places Pachón as the outgroup to (Rascón, Tinaja); thus, Pachón to Tinaja gene flow likely (partially) reflects this incorrect tree structure.
Care should be taken in interpreting the migration arrows drawn on the treemix result. First, we limited the number of migration edges to five, so further (possibly real) migration events are not represented. Second, any particular inferred admixture event is necessarily unidirectional and the source population is designated as the population with a migration weight ≤50%. Thus, while directionality is hard to pin down with these analyses, we can confidently report admixture among and between lineages and habitat types.
3.4 Divergence times are younger than expected without accounting for migration
The levels of diversity and divergence allow us to calculate a simple estimate of population split times. This approach results in remarkably recent divergence time estimates. For example, we estimate the oldest split between old and new lineages of approximately 156,597 generations (Table 2; using πA. aeneus as a proxy for ancestral diversity, and representing the old-new lineage split by dXY Choy,Rascón, ((4.68 − 3.58) × 10−3)/ (7 × 10−9). Assuming the generation interval of 1 year, the oldest estimate for the old and new split is more than an order of magnitude less than that estimated from the cytochrome b which places the divergence time between lineages between 5.7 and 7.5 mya (Ornelas-García et al., 2008). Similarly, we estimate that the split between new lineage cave (Molino) and new lineage surface (Río Choy) populations was approximately 113,913 generations ago ((4.38 − 3.58) × 10−3)/(7 × 10−9) similar to a recent analyses (Fumey et al., 2018). However, other estimates using this method were unstable, suggesting that A. aeneus is not a good proxy for ancestral diversity in the old lineage and/or introgression obscures any realistic estimate of divergence time. Our results that suggest gene flow (even with the exclusion of recently admixed individuals) indicate that true divergence times exceed those estimated from comparisons of dXY and π. We, therefore, pursue a model-based estimate of population divergence time while accounting for introgression.
3.5 Demographic modelling indicates cave populations are younger than expected when accounting for migration
Demographic modelling using ∂a∂i revealed extensive interdependence and contact for all populations studied. In all cases, models with multiple migration rates fit the population comparisons best, suggesting that some genomic regions are more recalcitrant to gene flow than others. For most pairwise population comparisons, the best-fitting models supported a period of isolation followed by a period of secondary contact (SC2M; Supporting Information Table S6). The only exceptions were the comparisons between Molino-Rascón and Pachón-Rascón that supported divergence with isolation (IM2M) slightly more than SC2M (Supporting Information Table S6). The distributions of divergence times for IM2M were multimodal (Molino-Rascón) or nearly flat (Pachón-Rascón) (Supporting Information Figure S9); thus, we present results from SC2M models that exhibit much tighter distributions for divergence estimates (Table 4; Supporting Information Figure S9).
| Pop1 | Pop2 | Model | MedianTs | MinTs | MaxTs | MedianTsc | MinTsc | MaxTsc | MedianTS+TSC |
|---|---|---|---|---|---|---|---|---|---|
| Choy | Molino | SC2M | 91,270 | 0 | 1,031,510 | 71,268 | 0 | 2,061,383 | 162,537 |
| Choy | Pachón | SC2M | 174,483 | 0 | 5,894,387 | 6,690 | 0 | 1,944,141 | 181,173 |
| Choy | Rascón | SC2M | 241,747 | 7,018 | 263,584 | 14,928 | 0 | 274,878 | 256,675 |
| Choy | Tinaja | SC2M | 182,107 | 0 | 497,367 | 24,859 | 0 | 519,170 | 206,966 |
| Molino | Pachón | SC2M | 195,724 | 60 | 641,127 | 30,431 | 0 | 603,939 | 226,155 |
| Molino | Rascón | IM2M | 1,242,575 | 228,667 | 1,799,441 | NA | NA | NA | NA |
| Molino | Rascón | SC2M | 210,396 | 0 | 1,593,512 | 27,023 | 0 | 1,044,418 | 237,418 |
| Molino | Tinaja | SC2M | 119,177 | 0 | 563,918 | 34,819 | 0 | 290,502 | 153,996 |
| Pachón | Rascón | IM2M | 1,239,971 | 140,387 | 11,358,780 | NA | NA | NA | NA |
| Pachón | Rascón | SC2M | 148,702 | 27,575 | 655,675 | 12,560 | 0 | 644,435 | 161,262 |
| Pachón | Tinaja | SC2M | 102,245 | 0 | 261,637 | 13,277 | 4,358 | 137,507 | 115,522 |
| Rascón | Tinaja | SC2M | 170,279 | 0 | 405,939 | 20,370 | 0 | 399,350 | 190,650 |
Effective population sizes for the surface populations were an order of magnitude higher than for the cave populations, and Molino exhibited the lowest effective population size of all five populations (Supporting Information Table S8). Notably, even for cave populations, estimates of effective population size were an order of magnitude larger than previous estimates (Avise & Selander, 1972; Bradic et al., 2012) and on par with mark-recapture census estimates (~8,500 fish in Pachon cave with wide 95% confidence interval of 1,279–18,283; Mitchell et al., 1977).
∂a∂i demographic modelling estimated deeper split times for populations than the divergence estimates calculated as T = (dXY − πancestral)/2μ (above) because they account for introgression that can artificially deflate these divergence estimates. The oldest divergence time between old and new lineages was estimated at 256,675 generations before present (Río Choy-Rascón), (Table 4, Supporting Information Tables S9 and S10; Figure S9; using SC2M models for all comparisons). Importantly, both the model-independent method and the demographic estimates presented here reveal relatively similar divergence times between the old and new lineages (~157 vs. ~257 k generations ago), and these estimates differ substantially from the several million year divergence time obtained through mtDNA (Ornelas-García et al., 2008), unless we have dramatically underestimated generation interval in the wild.
Cave–surface splits for both the new and old lineage comparisons were remarkably similar (Pachón – Rascón: 161,262 generations; Tinaja – Rascón: 190,650 generations; Molino – Río Choy: 162,537 generations). While the two old lineage cave populations (Pachón – Tinaja) are estimated to have split slightly more recently (115,522 generations before present), suggesting that colonization of one of the two old lineage caves was potentially from subterranean gene flow (as suggested by Espinasa & Espinasa, 2015). Distributions and estimates across 50 replicates are given in Supporting Information Figure S9, Tables S9 and S10.
Subterranean gene flow may be higher than surface to cave or between-lineage surface gene flow. The highest rates of gene flow are estimated between caves, and surprisingly, Molino cavefish exhibited a migration rate into Tinaja cave that is higher than Tinaja gene flow into Pachón cave. Surface fish gene flow rates into cave populations are also among the highest rates (especially Río Choy into all sampled caves). Notably, several caves also have relatively high rates of gene flow into surface populations (Molino into Río Choy and Tinaja into Rascón).
Heterogeneity in gene flow across the genome is also different across population pairs. Generally, more of the genome of cave–surface pairs (48%) seems to follow the lower migration rate than in cave–cave pairs (40%) and surface–surface pair (18%), suggesting the possibility that strong selection for habitat-specific phenotypes slows gene flow across the genome.
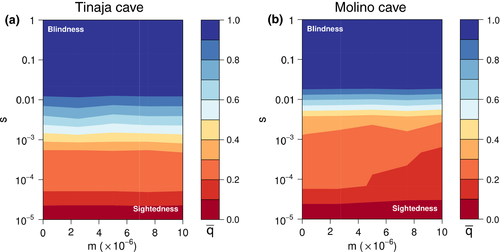
3.6 Modelling of selection needed for cave alleles to reach high frequency
Similarly to that estimated by (Cartwright et al. 2017), selection coefficients of ~0.01 are needed for cave phenotype alleles to reach high frequencies in either Molino or Tinaja cave populations with a 12-locus additive model (Figure 4). Animations of allele frequencies at different levels of selection across the historical demography are provided in Supplementary materials. There is an increase in noise at the secondary contact period because the influx of new alleles. This has little effect overall because the migration rate is of the same magnitude as the mutation rate and may be because prior to secondary contact, the loci are typically fixed for either the cave or surface allele and after contact, the loci may become more polymorphic. The average selection coefficients appear to approximately match the pre-secondary contact average.
In sum, our data support that cavefish population sizes are sufficiently large for selection to play a role shaping traits, gene flow is sufficiently common to impact repeated evolution, and cave–surface divergence is more recent than expected from mitochondrial gene trees.
3.7 Candidate gene regions introgressed between caves
In light of the suspected gene flow among populations, we identified genomic regions that showed molecular evolution signatures consistent with gene flow between caves and genomic regions that are likely affected by cave–surface gene flow. There were 997 5 kb regions (out of 208,354 total) that exhibited the lowest 5% of dXY windows of the genome for each of the cave–cave comparisons (Pachón-Molino, Pachón-Tinaja, Molino-Tinaja). These windows were spread across 471 scaffolds and overlapped 500 genes. We highlight some of these 500 genes in the context of Ensembl phenotype data in Supplementary text (see also Supporting Information Table S11).
Several of these regions cluster with known QTLs (O'Quin & McGaugh, 2015). We examined co-occurring QTLs for many traits on Linkage Group 2 and Linkage Group 17 (LG2, LG17, Supporting Information Table S12), which were two main regions highlighted in recent work on cave phenotypes (Yoshizawa, Yamamoto et al., 2012). We found that the co-occurring QTL on Linkage Group 2 harboured about 1.5-fold (odds ratio = 1.54, 95% CI = 1.139–2.089) the number of regions with low divergence among all three cave populations (44 windows with all three caves in lowest 5% of dXY/6070 total windows that had data across these same scaffolds) relative to the total across the entire genome (997/208354). This suggests that this region with many co-occurring QTL was potentially transferred among caves. Notably, we did not find a similar pattern for linkage group 17 (proportion of windows across all three caves in 5% lowest dXY = 0.00482 for LG17 and 0.00479 across the entire genome). The region on Linkage Group 2 is not simply an area of high sequence conservation (which could account for low divergence among all three cave populations) because the mean divergence between surface-surface comparisons for this region is very similar to the genomewide average (genomewide dXY = 0.00481, LG2 QTL region dXY = 0.00482).
We find genes that look to be affected by gene flow between caves. We found 1004 genes that exhibited dXY = 0 and another 370 genes with dXY in the lowest 5% across the genome for the three pairwise comparisons of the caves, many with substantial divergence to at least one surface population (Supporting Information Table S13). We associated these genes with previously known QTL with linkage groups that follow (O'Quin et al., 2013) and a qtl database is provided (Supporting Information Table S7). One example is fam136a (family with sequence similarity 136, member A), which is under a QTL for body condition on Linkage Group 10. This gene is expressed in the hair cells of the crista ampullaris, an organ important for detecting rotation and acceleration, in the semicircular canals of the inner ear in the rat (Requena et al., 2014). All caves are identical except for a SNP that may have come from the Rascon population in one of the admixed Tinaja individuals. fam136a is in the top 10% most divergent genes by dXY for Rascón surface—Pachón cave and Rascón surface—Tinaja cave populations (Molino-Rascón surface comparisons fall in the top 13% most divergent genes via dXY). Notably, Rascon and A. aeneus exhibit an E (glutamic acid) at 15aa (suggesting this is the ancestral state), whereas Río Choy and all caves exhibit a G (glycine). This amino acid switch is between a polar and a hydrophobic, thus not very functionally conserved. Such pattern could be produced by gene flow among caves or by gene flow of Río Choy with the cave populations.
4 DISCUSSION
The role of admixture between diverging populations is increasingly apparent as the application of genomic analyses has become standard, and such gene flow shapes the study of repeated evolution (Colosimo et al., 2005; Cresko et al., 2004; Roesti et al., 2014; Van Belleghem et al., 2018; Welch & Jiggins, 2014). Further, gene flow may create a signature that resembles parallel genetic divergence as effective migration is reduced in the same genomic regions for multiple ecotypic pairs upon secondary contact (Bierne, Gagnaire, & David, 2013; Rougemont et al., 2017). Thus, to understand the repeated origins of traits, an accurate understanding of the demography is required (Dasmahapatra et al. 2012; Rosenblum et al., 2014).
Astyanax mexicanus have been increasingly studied as a model of repeated evolution of wide-ranging traits (Elmer & Meyer, 2011; Krishnan & Rohner, 2017). Our data provide insight into some of the most pressing demographic questions needed to understand repeated evolution: (a) whether there are independent origins of Astyanax cavefish, (b) the age of cave invasions, (c) the amount of gene flow between populations, and (d) the strength of selection needed to shape traits. Genomic resequencing allowed an understanding not afforded by mitochondrial or reduced representation nuclear sequencing, and we were able to identify genes and a region of the genome potentially affected by gene flow between populations. Together, these findings provide a framework for understanding the repeated evolution of many complex, cave-derived traits.
4.1 Cave populations are younger than previously estimated
Our estimates fit in well with previous suggestions that the caves were colonized in the late Pleistocene (Avise & Selander, 1972; Fumey et al., 2018; Porter et al., 2007; Strecker et al., 2004) with both our dXY-based divergence estimation and demographic modelling. As our work documents extensive gene flow, we favour the divergence time estimates provided by demographic models that incorporated estimates of migration. Demographic models estimate split time between the two lineages at approximately 257 k generations ago, and estimates of cave–surface population splits are ~161–191 k generations ago. Notably, Astyanax is a species of fish with a limited distribution in northern latitudes, with its current most northern locality in the Edwards Plateau in Texas (Page & Burr, 2011). These split times are consistent with cooler temperatures in Northern Mexico associated with glaciation playing some role in the colonization of the caves by Astyanax mexicanus, potentially as thermally stable refugia (Cussac, Fernández, Gómez, & López, 2009). Our nuclear genomic data suggest that the “old” and “new” lineage split is more recent than the main volcanic activity of the Trans-Mexican Volcanic Belt (3–12 Mya) which was thought to have separated these two lineages, as well as other lineages in other vertebrates (Ornelas-García et al., 2008). This geographic barrier likely has been breached by Astyanax multiple times and likely led to cave invasions with each migration (Gross, 2012; Hausdorf et al., 2011; Strecker et al., 2012).
4.2 Historic and contemporary gene flow between most populations
Several cave populations exhibit intermediate phenotypes and experience flooding during the rainy season (Espinasa, unpublished, Strecker et al., 2012), suggesting that intermediate phenotypes are the result of admixture between cavefish and surface fish swept into caves during flooding (Avise & Selander, 1972; Bradic et al., 2012). However, it has been suggested that surface fish and hybrids are too maladapted to survive and spawn in caves (Coghill et al., 2014; Hausdorf et al., 2011; Strecker et al., 2012), and that cavefish populations with intermediate troglomorphic phenotypes represent more recent cave invasions, rather than hybrids (Hausdorf et al., 2011; Strecker et al., 2012). Despite evidence from microsatellites (Bradic et al., 2012; Panaram & Borowsky, 2005), mitochondrial capture (Dowling et al., 2002; Ornelas-García & Pedraza-Lara, 2015; Yoshizawa, Ashida, & Jeffery, 2012), and haplotype sharing of candidate loci (but see Espinasa, Centone, & Gross, 2014; Gross & Wilkens, 2013), there was still uncertainty in the literature regarding the frequency of gene flow between Astyanax cavefish and surface fish and the role gene flow may play in adaptation to the cave environment (Coghill et al., 2014; Espinasa & Borowsky, 2001; Hausdorf et al., 2011; Strecker et al., 2012).
Our work demonstrates recent and historical gene flow between cave and surface populations both within and between lineages (Figures 2 and 3). This result is also suggested by past work which showed most genetic variance is within individuals (Table 2 in (Bradic et al., 2012)) and very few private alleles (i.e., alleles specific to a population) were present among cave populations (Figure 3b in (Bradic et al., 2012)). Notably, many of the methods we employed take into account incomplete lineage sorting, are robust to nonequilibrium demographic scenarios, and detect recent admixture (<500 generations ago) (Patterson et al., 2012). In all our analyses the hybridization detected may not be between these sampled populations directly, but unsampled populations/lineages related to them (Patterson et al., 2012).
One of the most intensely studied cave populations is Pachón. Our data of Pachón cavefish hybridization with the new lineage are expected from past field observations and molecular data. Only extremely troglomorphic fish were found early (1940s–1970s; Avise & Selander, 1972; Mitchell et al., 1977) and late (1996–2000, (Dowling et al., 2002)) surveys, though, phenotypically intermediate fish were observed in 1986–1988, as well as in 2008 (Borowsky, unpublished). Thus, subterranean introgression from a nearby cave population may cause transient complementation of phenotypes or hybridization with surface fish (from flooding or human-introduction) may contribute to the presence of intermediate-phenotype fish in the cave (Langecker, Wilkens, & Junge, 1991; Wilkens & Strecker, 2017). Indeed, past studies suggested gene flow between Pachón and the new lineage populations, as Pachón mtDNA clusters with new lineage populations (Dowling et al., 2002; Ornelas-García & Pedraza-Lara, 2015; Ornelas-García et al., 2008; Strecker et al., 2003, 2012). Interestingly and divergent from past studies, Pachón mitochondria group with old lineage populations in the most recent analysis (Coghill et al., 2014). Continued intense scrutiny of other caves may reveal similar fluctuations in phenotypes and genotypes.
The most surprising signal of gene flow in our data is seen in the ∂a∂i analyses, in which the signal of Molino-Tinaja exchange is similar to that from Pachón-Tinaja, suggesting subterranean gene flow between all three caves, despite substantial geographic distances (the entrances are separated by >100 km; Mitchell et al., 1977). While our genomewide ancestry proportion data suggest some exchange of Molino with Tinaja (Supporting Information Figure S5–S7), we have no other evidence to corroborate this signal. Thus, the results from population demography could be picking up a signal of Molino with Tinaja that is actually driven by Pachón—new lineage hybridization and subsequent Tinaja—Pachón hybridization or Tinaja—Río Choy hybridization. Also, surprisingly, ∂a∂i analyses suggest that some of the highest migration occurs from Tinaja cave into Rascón surface and Molino cave into Río Choy surface.
Notably, many species of troglobites other than Astyanax inhabit caves spanning from southern El Abra to Sierra de Guatemala, and some were able to migrate among these areas within the last 12,000 years (Espinasa, Bartolo, & Newkirk, 2014). Due to the extensive connectivity and the span of geological changes throughout the hydrogeological history, it is likely that there have been ample opportunities for troglobites, including Astyanax, to migrate across much of the El Abra region (Espinasa & Espinasa, 2015).
Across many systems genomic data has revealed reticulate evolution is much more common than previously thought (Abbott, Barton, & Good, 2016; Arnold & Kunte, 2017; Brandvain et al., 2014; Dasmahapatra et al. 2012; Geneva, Muirhead, Kingan, & Garrigan, 2015; Malinsky et al., 2017; McGaugh & Noor, 2012; Rougemont et al., 2017), and the ability of populations to maintain phenotypic differences despite secondary contact and hybridization is increasingly appreciated (Arnold & Kunte, 2017; Fitzpatrick, Gerberich, Kronenberger, Angeloni, & Funk, 2015; Malinsky et al., 2017; Payseur & Rieseberg, 2016). Thus, despite gene flow from the surface into caves, it is entirely possible that cave-like phenotypes can be maintained. Indeed, gene flow may help to sustain cave populations from the effects of inbreeding (Åkesson et al., 2016; Ellstrand & Rieseberg, 2016; Fitzpatrick et al., 2016; Frankham, 2015; Kronenberger et al., 2017; Whiteley, Fitzpatrick, Funk, & Tallmon, 2015) or catalyze adaptation to the cave environment (sensu Clarkson et al., 2014; Meier et al., 2017; Richards & Martin, 2017). Though the rates of gene flow between Astyanax populations is considerably less than that documented in other contemporary diverging fish lineages (coastal and marine anchovies, Le Moan, Gagnaire, & Bonhomme, 2016; parasitic river and nonparasitic brook lampreys, Rougemont et al., 2017; benthic and dwarf limnetic lake whitefish, Rougeux et al., 2017; Atlantic and Mediterranean sea bass, Tine et al., 2014), they are similar to the historic gene flow between of polar bears into brown bears (Liu et al., 2014). Our data indicate hybridization between sampled lineages and suggest that cavefish are poised to be a strong contributor to understanding the role gene flow may play in repeated evolutionary adaptation.
4.3 Candidate genes shaped by gene flow
In some cases, we have evidence that particular alleles were transferred between caves, but are highly diverged from surface populations (Supporting Information Table S11 and S13). This suggests that gene flow between caves may hasten adaptation to the cave environment and suggests that repeated evolution in this system may, in part, rely on standing genetic variation. Notably, scaffolds under the co-localizing QTL on Linkage Group 2 for many traits exhibit 1.5-fold enrichment for 5 kb regions with lowest divergence across caves relative to genomewide, suggesting parts of this QTL have spread throughout caves.
For genes with high similarity among caves and substantial divergence between cave and surface populations, many appeared to be involved in classic cavefish traits such as pigmentation and eye development/morphology (mdkb, atp6v0ca, ube2d2 l, usp3 and cln8) and circadian functioning (usp2a) (Supporting Information Table S13). Additional common annotations suggest future areas of trait investigation, namely, cardiac-related phenotypes (mmd2, cyp26a1, tbx3a, tnfsf10, alx1 and ptgr1) as well as inner ear phenotypes (ncs1a, dlx6a, fam136a) (Supporting Information Table S13). Importantly, the sensory hair cells of the inner ear are homologous with sensory hair cells of the neuromasts of the lateral line (Fay & Popper, 2000); therefore, these genes may be impacting mechanoreception or sound reception.
4.4 Effective population sizes are much larger than expected and weak selection can drive cave phenotypes
Previous estimates of very small effective population sizes in cave populations of A. mexicanus suggested drift and relaxed selection shaped cave-derived phenotypes (e.g., Lahti et al. 2009). The estimates of nucleotide diversity and Ne provided here (Tables 1 and 2 and Supporting Information Table S8) indicated that positive selection coefficients need not be extreme to drive cave-derived traits (Akashi, Osada, & Ohta, 2012; Charlesworth 2009). To put these values in perspective, the cave populations have an average genetic diversity (which is proportional to Ne) somewhat similar to humans and the surface populations exhibit a similar genetic diversity to zebrafish (Leffler et al. 2012).
Our observations support theoretical and empirical results that selection likely shaped cavefish phenotypes (Borowsky, 2015; Cartwright et al. 2017; Moran, Softley, & Warrant, 2014). Simulations using demographic parameters from Molino and Tinaja cave populations suggest that selection coefficients across 12 additive loci (patterned after the number of eye-related QTL (O'Quin & McGaugh, 2015)) need to be above 0.01 to bring cave alleles to very high frequencies (Figure 4). Such selection coefficients are often found driving selective sweeps in natural systems (Nair et al., 2003; Rieseberg & Burke, 2001; Schlenke & Begun, 2004; Wootton et al., 2002).
4.5 Diverging lineages should be examined with reticulation methods and absolute divergence metrics
Our genomewide data allowed a unique perspective that was not available in past studies. First, our data represent an empirical demonstration of how well-supported phylogenetic reconstructions can be misleading. When using genome-scale data with maximum likelihood, bootstrap values are not a measure of the number of sites that support a particular phylogeny, though, this is often how they are interpreted (Yang & Rannala, 2012). Rather, if a genome-scale data set is slightly more supportive of a particular topology, maximum likelihood will find that topology consistently and exhibit high levels of bootstrap support (Yang & Rannala, 2012). With the cavefish, a previous RADseq study suggested relatively strongly supported branches (Coghill et al., 2014); however, a much more complex evolutionary history with reticulation among lineages was revealed here. Examination of recently diverged taxa with reticulation methods (e.g., Phylonet, F4, F3, TreeMix) may ensure a more comprehensive view of their evolutionary history than the successive bifurcations represented in a tree.
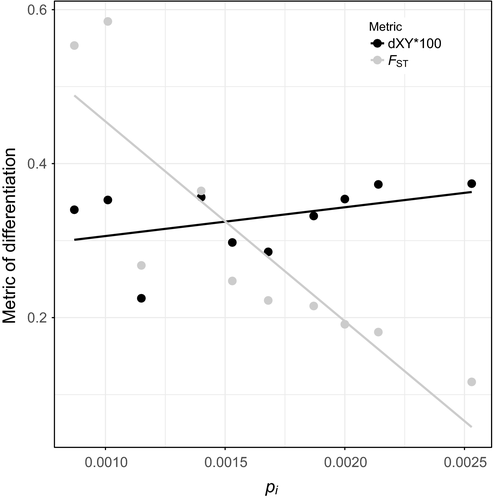
Second, our data set is yet another empirical demonstration of poor performance of pairwise FST in estimating population relationships when diversity is highly heterogeneous among populations (Figure 5, Table 2, Supporting Information Table S14; Fumey et al., 2018; Jakobsson, Edge, & Rosenberg, 2013). When diversity is highly heterogeneous, this can give the false impression that low-diversity populations are highly divergent, when in reality, the lower diversity drives greater pairwise FST, not higher absolute divergence (Charlesworth, 1998). These limitations of FST are especially important to appreciate in systems like the cavefish where diversity is highly heterogeneous across populations. Further, it is often suggested that high FST translates to low gene flow, but violations of the assumptions are common (Cruickshank & Hahn, 2014). In the case of Molino (a very low diversity population), high FST values were taken to indicate relative isolation from other populations with little gene flow (Bradic et al., 2012), and we show here that is not the case. Indeed, pairwise FST among surface fish populations is the lowest and pairwise FST among caves is the highest, yet absolute divergence between surface populations is slightly higher than absolute divergence among caves (Figure 5, Table 2 and Supporting Information Table S14). Future molecular ecology work should assay diversity and interpret pairwise FST accordingly or use absolute measures of divergence in conjunction with pairwise FST (Charlesworth, 1998; Cruickshank & Hahn, 2014; Noor & Bennett, 2009; Ritz & Noor, 2016).
5 CONCLUSION
In conclusion, our results suggest that investigations of repeated evolution of cave-derived traits should take into account hybridization between lineages, between cave and surface fish, and between caves. Due to gene flow, best practices to assign the putative ancestral character state of cave-derived traits include comparing cavefish phenotypes to multiple surface populations and a distantly related outgroup with no evidence of admixture (e.g., Astyanax bimaculatus, Ornelas-García et al., 2008). Complementation crosses and molecular studies remain essential for understanding evolutionary origins for each cave-derived trait (Borowsky, 2008b; Gross, Borowsky, & Tabin, 2009; O'Quin et al., 2015; Protas et al., 2006; Wilkens, 1971; Wilkens & Strecker, 2003).
We expect future work with greatly expanded sampling (Beerli, 2004; Hellenthal et al., 2014; Pease & Hahn, 2015; Slatkin, 2005) and ecological parameterization of the caves to provide a more comprehensive view of the ultimate drivers of demography of Astyanax mexicanus cavefish. Interestingly, many caves are nutrient-limited which is suggested to be one of the largest impediments to surface fish survival in the cave environment (Espinasa, Bibliowicz, Jeffery, & Rétaux, 2014; Moran et al., 2014). One of the emerging hypotheses is that high food availability allows surface-like fish to persist longer in the cave environment and enhances the probability for cave–surface hybridization (Mitchell et al., 1977; Strecker et al., 2012). Future studies evaluating hybridization levels in relation to food-availability or food-predictability are an important next step to examine drivers of cave phenotypes. We look forward to these future studies, and their potential to elucidate how demography and environmental factors impact repeated adaptive evolution (sensu Rosenblum et al., 2014).
ACKNOWLEDGEMENTS
Fish were collected under CONAPESCA permit PPF/DGOPA - 106 / 2013 to Claudia Patricia Ornelas García and SEMARNAT permit 02241 to Ernesto Maldonado. We thank the Mexican government for providing the collecting permit to R.B. in 2008 (DGOPA.00570.288108-0291). For 2002, the collection permit to R.B. was from fisheries department #01.01.02.613.03.1799 Molino samples were obtained under Mexican permit 040396-213-05. Animal care protocol numbers include #05-1235 by the New York University Animal Welfare Committee (UAWC) to R.B., UMD R-17-77 to WRJ, and UNAM animal care protocol to POG NOM-062-ZOO-1999. This work was supported by NIH grant 2R24OD011198-04A1 to WCW, The Genome Institute at Washington University School of Medicine, Cave Research Foundation Graduate Student Research Grant to BMC, a grant from the Eppley Foundation for Research to SEM, 5R01EY014619-08 to WRJ, and 1R01GM127872-01 to SEM and ACK. Raw sequence data were submitted to the SRA. Project Accession Number: SRP046999, Bioproject: PRJNA260715. We appreciate the resources provided by the Minnesota Supercomputing Institute, without which this work would not be possible.
DATA ACCESSIBILITY
All reads are available in NCBI short read archive under accession numbers given in Supporting Information Table S3. Supporting Information Methods, figures and tables are provided online. Within the supplementary tables are five separate spreadsheet tabs that detail genomic regions and genes that may be spread between caves, complete results from all demography replicates, and enrichment analyses of two QTL regions. Two simulations of selection, given our demography estimates, are included in online supplementary material. Scripts to perform demography analysis are available in a GitHub repository at https://github.com/TomJKono/CaveFish_Demography.
AUTHOR CONTRIBUTION
A.H. conducted portions of the analysis and helped write the paper. Y.B. conducted some analyses and edited the paper, J.W. processed DNA sequences. A.C.K. helped write the paper. T.J.Y. Kono conducted the Dadi analysis and helped write the paper. W.R.J., K.O., C.P.O-G., M.Y., B.C., E.M.J.B.G., R.H., H.B., R.B., L.E. helped with sampling and writing the paper. W.C.W. and S.E.M. planned the project. R.A.C. conducted demographic simulations and helped write the paper. S.E.M. carried out portions of the analyses and wrote the paper.




