Multicollinearity in spatial genetics: separating the wheat from the chaff using commonality analyses
Abstract
Direct gradient analyses in spatial genetics provide unique opportunities to describe the inherent complexity of genetic variation in wildlife species and are the object of many methodological developments. However, multicollinearity among explanatory variables is a systemic issue in multivariate regression analyses and is likely to cause serious difficulties in properly interpreting results of direct gradient analyses, with the risk of erroneous conclusions, misdirected research and inefficient or counterproductive conservation measures. Using simulated data sets along with linear and logistic regressions on distance matrices, we illustrate how commonality analysis (CA), a detailed variance-partitioning procedure that was recently introduced in the field of ecology, can be used to deal with nonindependence among spatial predictors. By decomposing model fit indices into unique and common (or shared) variance components, CA allows identifying the location and magnitude of multicollinearity, revealing spurious correlations and thus thoroughly improving the interpretation of multivariate regressions. Despite a few inherent limitations, especially in the case of resistance model optimization, this review highlights the great potential of CA to account for complex multicollinearity patterns in spatial genetics and identifies future applications and lines of research. We strongly urge spatial geneticists to systematically investigate commonalities when performing direct gradient analyses.
Direct gradient analyses in spatial genetics
Spatial genetics, including both landscape and seascape genetics, is an ebullient scientific field that aims at investigating the influence of spatial heterogeneity on the spatial distribution of genetic variation (Manel et al. 2003; Holderegger & Wagner 2008; Guillot et al. 2009; Storfer et al. 2010). In the context of accelerating landscape fragmentation worldwide, spatial genetics allows a thorough assessment of landscape functional connectivity (With 1997) and has now emerged as a valuable way of assisting both landscape management and wildlife conservation (Segelbacher et al. 2010).
Two main approaches can be used to investigate the influence of landscape (respectively, seascape) features on spatial genetic patterns (Balkenhol et al. 2009; Guillot et al. 2009): overlay methods and direct gradient analyses (sensu ter Braak & Prentice 1988). In overlay methods, genetic structures inferred from clustering algorithms (Pritchard et al. 2000; Chen et al. 2007; Jombart et al. 2008) or edge-detection methods (Monmonier 1973; Barbujani et al. 1989) are visually confronted to landscape patterns (e.g. Frantz et al. 2012; Prunier et al. 2014). In direct gradient analyses, regression procedures such as Mantel tests (Cushman et al. 2006; Shirk et al. 2010; Castillo et al. 2014), multiple regressions on distance matrices (MRDM; Legendre et al. 1994; Holzhauer et al. 2006; Lichstein 2007; Wang 2013; Balkenhol et al. 2014), mixed-effect models (Selkoe et al. 2010; Van Strien et al. 2012; Peterman et al. 2014) or constrained ordination techniques (e.g. distance-based redundancy analyses or canonical correspondence analyses, which imply multivariate regressions; Angers et al. 1999; Legendre & Anderson 1999; Balkenhol et al. 2009; Vangestel et al. 2012; Orsini et al. 2013 are used to investigate the relative contribution of various independent variables (predictors) to the variance of a dependent (response) variable. In spatial genetics, the dependent variable is most often expressed as genetic distances between pairwise sampled individuals and populations (Prunier et al. 2013; Luximon et al. 2014). In the specific case of constrained ordination techniques, it may also be expressed as the ordination solution of the pairwise distance matrix using principal coordinate analysis (PCoA; Legendre & Anderson 1999; Orsini et al. 2013). Explanatory variables are most often derived from categorical (e.g. land cover) or continuous spatial data. When focusing on the effects of landscape on gene flow, explanatory variables can be either expressed as relative proportions of categorical landscape features between pairwise sampled units (transect-based approaches; Angelone et al. 2011; Emaresi et al. 2011; Van Strien et al. 2012; Keller et al. 2013), as pairwise effective distances computed from parameterized resistance surfaces with least-cost or isolation-by-resistance modelling (Adriaensen et al. 2003; McRae 2006; Peterman et al. 2014) or, in constrained ordination techniques, as site-specific environmental measures (e.g. Pilot et al. 2006). When focusing on the effects of local environmental conditions on site-specific attraction or productivity, explanatory variables may also be expressed as environmental dissimilarities between sampled points (Wang 2013; Pfluger & Balkenhol 2014).
When the objective of the study is to maximize the predictive power of a regression model and eventually to compile several univariate resistance surfaces into a unique weighted multivariate one (Spear et al. 2010; Zeller et al. 2012), a model fit index, quantifying the proportion of variance in the dependent variable that is explained by a given model (e.g. zero-order correlation coefficients in univariate procedures, R2 in MRDM, 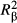 in mixed-effect models or AIC in constrained ordination techniques), is used as a criterion for stepwise regression (e.g. Legendre & Legendre 1998; Graves et al. 2012), hierarchical model selection (e.g. Selkoe et al. 2010; Emaresi et al. 2011; Dudaniec et al. 2012; Van Strien et al. 2012; Blair et al. 2013 or resistance model optimization (Shirk et al. 2010; Perez-Espona et al. 2012; Dudaniec et al. 2013; Castillo et al. 2014; Peterman et al. 2014). In an explanatory approach, that is, when the goal is simply to gain insight into the relative influence of explanatory variables on an observed biological response, model fit index is often only considered as a way to support the reliability of a unique (full) regression model (e.g. Wang 2013; Balkenhol et al. 2014; Guarnizo & Cannatella 2014; Nanninga et al. 2014). In both cases though, standardized regression weights (hereafter called beta weights β), or canonical coefficients in the case of constrained ordination techniques, are used to rank predictors according to their contributions in a multivariate regression equation. As pairwise genetic distances are nonindependent, significance levels of model fit and predictors are usually computed through matrix permutations (Legendre et al. 1994) or pseudobootstrap procedures (Worthington Wilmer et al. 2008).
in mixed-effect models or AIC in constrained ordination techniques), is used as a criterion for stepwise regression (e.g. Legendre & Legendre 1998; Graves et al. 2012), hierarchical model selection (e.g. Selkoe et al. 2010; Emaresi et al. 2011; Dudaniec et al. 2012; Van Strien et al. 2012; Blair et al. 2013 or resistance model optimization (Shirk et al. 2010; Perez-Espona et al. 2012; Dudaniec et al. 2013; Castillo et al. 2014; Peterman et al. 2014). In an explanatory approach, that is, when the goal is simply to gain insight into the relative influence of explanatory variables on an observed biological response, model fit index is often only considered as a way to support the reliability of a unique (full) regression model (e.g. Wang 2013; Balkenhol et al. 2014; Guarnizo & Cannatella 2014; Nanninga et al. 2014). In both cases though, standardized regression weights (hereafter called beta weights β), or canonical coefficients in the case of constrained ordination techniques, are used to rank predictors according to their contributions in a multivariate regression equation. As pairwise genetic distances are nonindependent, significance levels of model fit and predictors are usually computed through matrix permutations (Legendre et al. 1994) or pseudobootstrap procedures (Worthington Wilmer et al. 2008).
Multicollinearity issues
There is a growing but unresolved concern about the reliability of regression procedures in correctly identifying the spatial determinants of observed genetic patterns and ruling out noninformative spatial features (Balkenhol et al. 2009). Several simulation studies showed that partial Mantel tests may yield poor results in both ways (Cushman & Landguth 2010; Legendre & Fortin 2010; Cushman et al. 2013; Graves et al. 2013; Guillot & Rousset 2013), and researchers are rather encouraged to use multivariate approaches (Bolliger et al. 2014; Guarnizo & Cannatella 2014). Whatever the approach though, beta weights or canonical coefficients, their standard errors and thus marginal statistics used to test their significance as well as model fit indices may be heavily impacted by even weak levels of multicollinearity (nonindependence) among predictors (Angers et al. 1999; Graham 2003; Smith et al. 2009; Nimon & Reio 2011; Kraha et al. 2012). Multicollinearity is thus likely to cause serious difficulties in properly interpreting results of direct gradient analyses (Mac Nally 2000; Nimon et al. 2010; Dormann et al. 2013). For instance, it may be difficult to identify the likely causal variables among collinear predictors showing significant correlation with the response variable (Graham 2003; Spear et al. 2010; Dormann et al. 2013). Spurious correlations are also likely to occur in the presence of suppression, that is, when a variable confounds the variance explained by another (Courville & Thompson 2001; Nimon & Reio 2011; Beckstead 2012; Ray-Mukherjee et al. 2014). For instance, beta weights may be negative even when the predictor and the dependent variable are positively correlated. In case of multicollinearity, a thorough understanding of the correlation structure among predictors is thus primordial (Dormann et al. 2013).
Multicollinearity among explanatory variables is a regular feature in ecology (Graham 2003; Dormann et al. 2013) and is probably unavoidable in spatial genetic studies as predictors are derived from landscape characteristics that cannot be experimentally controlled (Graham 2003; King et al. 2005; Whittingham et al. 2006; Smith et al. 2009). Multicollinearity is multifaceted in origins. It is largely influenced by specific local landscape configuration patterns resulting from climate, geological events, past disturbances and anthropogenic pressures. Some trends can be observed though. Some spatial features usually come together (resulting in positive correlations among predictors), while others are mutually exclusive (resulting in negative correlations). Among features that usually come together: rivers and valleys or altitude and snow cover, obviously, but also rivers and urban areas, because of historical facilities offered by waterway transport, or motorways and agricultural surfaces, because of the regrouping of cultivated plots due to the increase in farmland value (Drescher et al. 2001; Prunier et al. 2014). On the contrary, categorical land-cover features are in essence mutually exclusive, as a pixel cannot be classified as ‘forest’ and as ‘bare land’ at the same time. As a consequence, when the landscape matrix is composed of a few predominant land-cover classes, negative correlations will often be observed between main predictors (King et al. 2005; Rioux Paquette et al. 2014). The same observation can be made in the context of transect-based approaches, when explanatory variables are expressed as relative quantities summing to 100% (e.g. habitat proportions in a delimited area; Angelone et al. 2011; Emaresi et al. 2011; Van Strien et al. 2012; Dormann et al. 2013).
Multicollinearity also typically arises in the specific case of resistance model optimization (Spear et al. 2010), when predictors are derived from a large set of alternative but closely related models (e.g. Cushman et al. 2013; Dudaniec et al. 2013). The use of various functions to reclassify or combine univariate resistance surfaces (Shirk et al. 2010; Spear et al. 2010; Peterman et al. 2014) may also influence patterns of nonindependence among predictors. To further complicate matters, multicollinearity patterns can vary depending on the spatial configuration of sampled points (Graves et al. 2013), change through time and differ across spatial scales (Dormann et al. 2013), making it an outstanding challenge in spatial genetics (Anderson et al. 2010).
Dealing with multicollinearity
There is a growing awareness of multicollinearity issues in spatial genetics (Garroway et al. 2011; Wedding et al. 2011; Dudaniec et al. 2012; Blair et al. 2013), and several approaches have been proposed to deal with multicollinearity issues. The simplest one is variable exclusion. The idea is to discard any variable showing correlations with other predictors higher than a certain threshold. A Pearson's correlation coefficient |r| > 0.7 is commonly used as a threshold (Dormann et al. 2013), although the exact value is left to the discretion of investigators (e.g. Angelone et al. 2011; Graves et al. 2012; Keller et al. 2013; Balkenhol et al. 2014). The estimation of variance inflation factors (VIF) can also be used as a way to identify nonindependence among predictors (Dyer et al. 2010; Blair et al. 2013). VIF is a positive value representing the overall correlation of each predictor with all others in a model. For a predictor Xi, VIFi is computed as the inverse of the coefficient of nondetermination  , where
, where 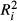 is the model fit of the multiple regression of Xi over all other predictors (Neter et al. 1990; Stine 1995). VIF values >10 are usually considered as evidence for substantial multicollinearity and often justify the removal of certain predictors (but see O'Brien 2007 for a discussion on this subject). Variable exclusion may also be based on the investigation of principal component analyses (PCA) to identify and select a few biologically relevant predictors among a set of collinear variables (Manel et al. 2010). Nevertheless, variable exclusion, ignoring the unique contribution of discarded predictors, may result in a loss of explanatory power (Graham 2003).
is the model fit of the multiple regression of Xi over all other predictors (Neter et al. 1990; Stine 1995). VIF values >10 are usually considered as evidence for substantial multicollinearity and often justify the removal of certain predictors (but see O'Brien 2007 for a discussion on this subject). Variable exclusion may also be based on the investigation of principal component analyses (PCA) to identify and select a few biologically relevant predictors among a set of collinear variables (Manel et al. 2010). Nevertheless, variable exclusion, ignoring the unique contribution of discarded predictors, may result in a loss of explanatory power (Graham 2003).
Multicollinearity may also be addressed through the computation of orthogonal predictors using unconstrained ordination techniques. For instance, linear combinations of collinear variables (principal components) can be used as synthetic independent predictors in principal component regressions (Vigneau et al. 1997). However, this kind of approach may show serious statistical pitfalls (Hadi & Ling 1998), while the new independent variables will often be difficult to interpret (see Dormann et al. 2013 for details and a review of other available methods).
In 2001, Courville & Thompson advocated the simultaneous interpretation of beta weights β and structure coefficients rs (or squared structure coefficients 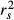 ) to improve the interpretation of multivariate regressions (Box 1). A structure coefficient is the bivariate (or zero-order) Pearson's correlation between a predictor X and predicted values
) to improve the interpretation of multivariate regressions (Box 1). A structure coefficient is the bivariate (or zero-order) Pearson's correlation between a predictor X and predicted values 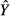 of the dependent variable Y (Pedhazur 1997; Nathans et al. 2012). A squared structure coefficient thus represents the amount of variance in model fit that is accounted for by a single predictor (Nimon et al. 2008). By construction, structure coefficients may also be considered as rescaled zero-order correlations (Box 1; Courville & Thompson 2001). Structure coefficients are thus independent of collinearity among explanatory variables and allow ranking independent variables based on their direct contribution to model fit (Kraha et al. 2012; Ray-Mukherjee et al. 2014). For instance, a situation where a predictor X shows low β but high
of the dependent variable Y (Pedhazur 1997; Nathans et al. 2012). A squared structure coefficient thus represents the amount of variance in model fit that is accounted for by a single predictor (Nimon et al. 2008). By construction, structure coefficients may also be considered as rescaled zero-order correlations (Box 1; Courville & Thompson 2001). Structure coefficients are thus independent of collinearity among explanatory variables and allow ranking independent variables based on their direct contribution to model fit (Kraha et al. 2012; Ray-Mukherjee et al. 2014). For instance, a situation where a predictor X shows low β but high 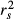 may indicate that, because of collinearity among predictors, a proportion of the variance in X was assigned to another predictor in the process of computing beta weights. However, structure coefficients are limited. They do not precisely indicate which predictors synergistically or antagonistically contribute to predicting the dependent variable nor do they allow quantifying the amount of shared variance between collinear predictors (Nathans et al. 2012). Other indices can be used to dissect the complexity of predictors’ relative contribution to model fit (Box 1). Among these indices, unique and common effects computed in commonality analysis are of great value (Box 2; Campbell & Tucker 1992; Nimon & Reio 2011).
may indicate that, because of collinearity among predictors, a proportion of the variance in X was assigned to another predictor in the process of computing beta weights. However, structure coefficients are limited. They do not precisely indicate which predictors synergistically or antagonistically contribute to predicting the dependent variable nor do they allow quantifying the amount of shared variance between collinear predictors (Nathans et al. 2012). Other indices can be used to dissect the complexity of predictors’ relative contribution to model fit (Box 1). Among these indices, unique and common effects computed in commonality analysis are of great value (Box 2; Campbell & Tucker 1992; Nimon & Reio 2011).
Box 1. Assessing variable importance in multivariate regression models
Here, we provide a brief description of the complementary indices that can be used to investigate the relative contribution of each predictor to the multivariate regression effect (see Kraha et al. 2012; Nathans et al. 2012 for details).
Beta weights
Beta weights correspond to classical regression weights when variables are z-transformed (by subtracting the mean and dividing by the standard deviation of the variable). Beta weights are thus comparable across various predictors. In logistic regressions, we speak about semi-standardized beta weights as the dichotomous dependent variable cannot be z-transformed. Beta weights quantify the change in the dependent variable (in standard deviation units) with a one standard deviation change in a predictor, all other predictors being held constant. They are thus measures of the total effect of a predictor on the dependent variable, accounting for the contribution of other predictors.
Zero-order (or bivariate) correlation coefficients
Zero-order correlation coefficients (also known as validity coefficients) range from −1 to 1 and represent the positive or negative linear (parametric Pearson's r) or monotonous (rank-based Spearman's ρ or Kendall's τ) relationship between two variables. In multivariate procedures, zero-order correlation coefficients are measures of the direct effect of a predictor on the dependent variable, without accounting for the contributions of other variables in the model; when z-transformed predictors are independent, they are equivalent to beta weights β. A discrepancy between zero-order correlation coefficients and beta weights is indicative of suppression.
Structure coefficients (see main text for details)
A structure coefficient rs is the zero-order Pearson's correlation between a predictor and predicted values 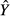 of the dependent variable Y (that is,
of the dependent variable Y (that is, 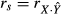 ). Structure coefficients are measures of the direct effect of a predictor on the dependent variable, irrespective of the influence of other predictors in the model. When squared, structure coefficients represent the amount of variance in model fit that is accounted for by a single predictor. Note that, in linear regressions, squared structure coefficients
). Structure coefficients are measures of the direct effect of a predictor on the dependent variable, irrespective of the influence of other predictors in the model. When squared, structure coefficients represent the amount of variance in model fit that is accounted for by a single predictor. Note that, in linear regressions, squared structure coefficients 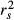 may also be computed by dividing the squared zero-order Pearson's correlation between a predictor and the dependent variable by the model fit index R2 (that is,
may also be computed by dividing the squared zero-order Pearson's correlation between a predictor and the dependent variable by the model fit index R2 (that is, 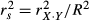 ). Structure coefficients may thus also be considered as rescaled validity coefficients (Courville & Thompson 2001). As previously, a discrepancy between structure coefficients and beta weights is indicative of suppression.
). Structure coefficients may thus also be considered as rescaled validity coefficients (Courville & Thompson 2001). As previously, a discrepancy between structure coefficients and beta weights is indicative of suppression.
Product measures (or Pratt measures; Pratt 1987)
For a given predictor, product measure is the zero-order correlation coefficient multiplied by the corresponding beta weight, thus reflecting in a single metric both direct and total effects of a predictor on the dependent variable. The computation of product measures is a variance-partitioning procedure, the sum of the k product measures (for k predictors) being equal to the model fit index. When compared to zero-order correlation coefficients and beta weights, negative product measures may help identify suppression situations.
Relative weights (or relative importance weights)
A relative weights analysis is another variance-partitioning technique, minimizing (but not fully addressing) the problem of multicollinearity among k predictors through the use of orthogonal principal components. Relative weights are the proportionate contribution of each predictor to the overall model fit after (partially) correcting for multicollinearity. Suppression situations may be suspected when the sum of the k relative weights is larger than model fit index.
General dominance weights
General dominance analysis uses the results from an all-possible-subsets regression (with 2k−1 subset models) to compute a set of k general dominance weights for a regression model containing k predictors. General dominance weights can be used to rank predictors according to a dominance hierarchy: they indicate the average difference in fit between all subset models of equal size that include a predictor and those that do not include it. As other variance-partitioning procedures, the sum of general dominance weights equals the model fit index. Other kinds of dominance indices exist (complete and conditional dominance weights) that can also be used to identify suppression situations (Azen & Budescu 2003; Nathans et al. 2012).
Commonalities (see main text for details)
As general dominance weights, commonalities result from an all-possible-subsets regression (with 2k−1 subset models; see Box 3), but there are 2k−1 commonality coefficients (rather than k), each one indicating the amount of variance that a predictor set uniquely shares with the dependent variable. By decomposing model fit indices into unique U and common (or shared) C variance components, CA helps identify the location and magnitude of multicollinearity as well as suppression situations. Note that CA encompasses several other indices, notably zero-order Pearson's correlation coefficients r and structure coefficients rs. Indeed, for a given predictor, T = U + C = r2 and 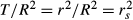 .
.
Box 2. Commonality coefficients in comparison with other regression-type metrics
Commonality analysis is similar to other variance-partitioning techniques in that it partitions the regression effect into orthogonal nonoverlapping parts. Unlike product measures, relative weights or general dominance weights that partition the regression effect into k parts (Box 1), commonality analysis partitions the regression effect into 2k−1 parts, where k equals the number of predictors in the regression equation (Box 3). Despite different analytical processes, general dominance weights and relative weights usually produce similar results. Some researchers therefore prefer to compute relative weights as they are less computationally burdensome than dominance analysis which demands an all-possible-subsets regression. Product measures are similarly easy to compute; however, they are criticized in the literature as they can produce negative coefficients, which some may find counterintuitive as a measure of variance. Among the variance-partitioning techniques reviewed, commonality analysis produces a more specific partitioning of the regression effect than product measures, relative weights or general dominance weights. Like product measures, commonality analysis may produce negative coefficients. While some researchers suggest these coefficients be interpreted as zero, Nimon & Oswald (2013) and others have suggested that negative commonality coefficients can be used to identify the loci and magnitude of suppression. This is a unique advantage of commonality analysis over other variance-partitioning techniques. For example, while a negative product measure signals a variable as a potential suppressor, product measures tell the researchers nothing about what variables are being suppressed. Similarly, by analysing the pattern of conditional dominance weights, researchers may be able to identify a variable as a suppressor. However, as documented by Beckstead (2012), dominance analysis may not always reveal complex suppression effects. Nor does dominance analysis provide information regarding the loci and magnitude of the suppression effect.
Note that commonality coefficients may also be used to derive squared validity and structure coefficients. Summing all the commonality coefficients that involve a predictor X1 (e.g. UX1, 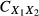 ,
,  ,
, 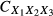 ) yields the per cent of variance that the predictor shares in common with the criterion (i.e. squared validity coefficient). Similarly, summing the commonality coefficients that have been divided by the magnitude of the regression effect (e.g. multiple R2) for a given predictor yields the amount of variance that the predictor has in common with
) yields the per cent of variance that the predictor shares in common with the criterion (i.e. squared validity coefficient). Similarly, summing the commonality coefficients that have been divided by the magnitude of the regression effect (e.g. multiple R2) for a given predictor yields the amount of variance that the predictor has in common with 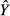 (i.e. squared structure coefficient). Like regression weights, commonality coefficients are considered measures of the total effect of an independent variable (see LeBreton et al. 2004), as they both take into account all independent variables in their computation. While regression weights indicate the amount of change in the criterion variable for each unit change in the independent variable holding all other independent variables constant, commonality coefficients indicate the amount of variance each variable set uniquely contributes to the regression effect. Note that in the case of perfect uncorrelated predictors, beta weights and commonality analysis will produce identical results; the unique effects from commonality analysis will be identical to the standardized regression weights, squared validity coefficients and squared structure coefficients.
(i.e. squared structure coefficient). Like regression weights, commonality coefficients are considered measures of the total effect of an independent variable (see LeBreton et al. 2004), as they both take into account all independent variables in their computation. While regression weights indicate the amount of change in the criterion variable for each unit change in the independent variable holding all other independent variables constant, commonality coefficients indicate the amount of variance each variable set uniquely contributes to the regression effect. Note that in the case of perfect uncorrelated predictors, beta weights and commonality analysis will produce identical results; the unique effects from commonality analysis will be identical to the standardized regression weights, squared validity coefficients and squared structure coefficients.
Commonality analysis
Commonality analysis (CA) is a detailed variance-partitioning procedure that was developed in the 1960s (Newton & Spurrel 1967). From the field of human sciences, it was very recently brought to the attention of ecologists (Ray-Mukherjee et al. 2014). CA can provide substantial guidance for the interpretation of generalized linear models, including linear and logistic regressions, hierarchical mixed-effect models and canonical correlation analyses (not to be confused with canonical correspondence analyses; Legendre & Anderson 1999), by decomposing the overall model fit into its unique and common effects (Campbell & Tucker 1992; Nimon & Oswald 2013; Nimon et al. 2013a). Unique and common effects are nonoverlapping components of variance that ensue from formulae involving the regression of the dependent variable over all possible subsets of predictors (Box 3; Nimon & Reio 2011; Nathans et al. 2012; Ray-Mukherjee et al. 2014). By predictor, we mean any additive term in a regression equation: interaction effects are thus considered as predictors (Ray-Mukherjee et al. 2014). For a number k of predictors, CA returns a table of (2k−1) commonality coefficients (or commonalities) including both unique and common effects. Unique effects U, or first-order effects, quantify the amount of variance in the dependent variable Y that is uniquely accounted for by a single explanatory variable. A negligible value of U indicates that the regression model only improves slightly with the addition of the predictor, when entered last in the model (Nathans et al. 2012; Roberts & Nimon 2012). Common effects represent the proportion of variance in the dependent variable that can be jointly explained by two or more predictors together, making CA particularly well suited in the case of multicollinearity (Campbell & Tucker 1992; Ray-Mukherjee et al. 2014). The common components of two or three (or k) variables are, respectively, called second- or third-order (or kth-order) commonalities. The sum C of all commonalities involving a specific predictor indicates the amount of variance explained by this predictor that is shared with other explanatory variables. When they are divided by model fit index, U and C, respectively, represent the unique and common contributions of a predictor to the explained variance (that is, unique and common contributions to model fit) rather than to the total variance in the dependent variable. The sum T = (U + C) represents the total contribution of a predictor to the dependent variable irrespective of collinearity with other variables, that is, in the case of linear regression, the squared zero-order (Pearson's) correlation r2 between the predictor and the dependent variable (Nimon & Reio 2011; Kraha et al. 2012). When T is divided by the model fit index, it is equivalent to the squared structure coefficient 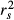 (Kraha et al. 2012; Nimon & Oswald 2013; Ray-Mukherjee et al. 2014) and indicates how much each predictor contributes to the explanation of the entire model (model fit index) irrespective of other predictors (Box 1).
(Kraha et al. 2012; Nimon & Oswald 2013; Ray-Mukherjee et al. 2014) and indicates how much each predictor contributes to the explanation of the entire model (model fit index) irrespective of other predictors (Box 1).
Box 3. Commonality coefficient formulae
For k predictors, there are 2k−1 commonality coefficients, each with a unique formula. In addition, the formulae for calculating commonality coefficients are based on the number of predictors. Therefore, the commonality coefficients formulae for two predictors will be different than the formulae, for example, for 3, 4, 5 or more predictors. While formulae for calculating commonality coefficients have been published for 2, 3 and 4 predictors (see for example Thompson 2006), Mood (1971) developed a general procedure that allows for developing commonality coefficient formulae for any number of predictors.
In Mood's procedure, (1−x) was used to represent variables in the common variance subset and (x) was used to represent variables not in the common variance subset. By negating the product of the variables in the subset and the variables not in the subset, deleting the −1 that may result from the expansion of the product and replacing x with R2, Mood noted that the formula for computing any commonality coefficient can be derived (Nimon et al. 2008).
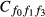 ) can be derived using Mood's procedure, expanding the results, and substituting x for R2 as follows:
) can be derived using Mood's procedure, expanding the results, and substituting x for R2 as follows:
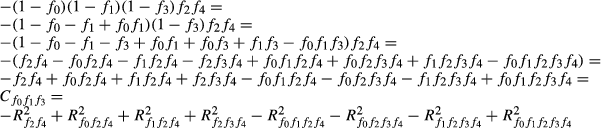
When predictors are independent, for instance in the case of principal component regressions (Dormann et al. 2013), common effects are null and the sum of unique effects equals the total variance of the dependent variable that is explained by the model (model fit index). However, when predictors show even low levels of multicollinearity, common effects are usually non-null and can show either positive or negative values. Positive common effects occur in the case of synergistic association among variables. Situations where C is substantially larger than U indicate that a predictor, showing significant contribution to the regression equation (high beta weight), only contributes indirectly to the dependent variable (or to model fit) because of its high positive correlation with other predictors. On the opposite, negative common effects are generally indicative of suppression (Capraro & Capraro 2001; Kraha et al. 2012).
The notion of suppression is an important contribution of CA over other variance-partitioning procedures (see Box 2): indeed, negative common effects are usually considered as embarrassing variation terms and thus interpreted as zero (Legendre & Legendre 1998; Peres-Neto et al. 2006). Suppression occurs in a variety of situations, depending on multicollinearity patterns among predictors (Lewis & Escobar 1986; Beckstead 2012). For instance, suppression may occur when correlations among predictors are of opposite sign. In all suppression situations, a predictor X1 (the suppressor), sharing no or little variance with the response Y, purifies the relationship between a predictor X2 and Y by removing (or suppressing) the irrelevant variance of X2 on Y. As a result, the contribution of X2 to the model fit is higher than would have been observed if X1 had not been considered in the regression, but at the cost of a spurious correlation between X1 and Y (Nimon & Reio 2011; Ray-Mukherjee et al. 2014). Suppression situations are sometimes so complex that no predictor can be identified as a specific suppressor variable (Lewis & Escobar 1986): in that case, predictors act as partial suppressors (Nimon 2010). Negative commonalities are the amount of predictive power that would be lost by other predictors if the (partial) suppressor variable was not considered in the regression model. Suppressor variables may also be detected by comparing beta weights β to structure coefficients rs. Situations where β is far larger than rs or where both indices are of opposite signs are indicative of suppression (Ray-Mukherjee et al. 2014).
The following section illustrates how CA can assist the interpretation of multivariate regressions and avoid spurious biological conclusions. We used three simulated genetic data sets so that there was no ambiguity as to the drivers of the observed genetic patterns (Cushman & Landguth 2010; Epperson et al. 2010). In each example, we investigated multicollinearity among predictors and performed multivariate regression along with CA. Output parameters (zero-order correlations, VIF, beta weights, structure and commonality coefficients) are reported and discussed in detail.
Interpreting commonality analyses
Simulated data
We first created two distinct artificial landscapes A and B (Fig. 1, panels a1 and b1) of 128 × 128 pixels each. The resolution (size of pixels) was arbitrarily set to 10 m. Both landscapes had distinct configurations but the same composition: a continuous feature f0 (e.g. topography; Fig. 1, panels a2 and b2), three categorical land-cover features f1 to f3 (e.g. woods, meadows and crops) and one categorical linear feature f4 (e.g. a road; panels a3 and b3). We then used cdpop 1.2.11 (Landguth & Cushman 2010) to simulate gene flow between 64 randomly located populations of 30 individuals each, according to the relative resistance of landscape features to be crossed. We did not consider all features as being resistant to dispersal: the true drivers of gene flow were feature f0 in landscape A and features f0 to f3 in landscape B (Fig. 1; Table 1). In landscape A, feature f0 was rescaled to range from 1 to 5 (Fig. 1, panel a2): the resulting resistance surface was used to compute pairwise effective distances based on least-cost paths. In cdpop, travelled distances were drawn from a probability distribution inversely proportional to a linear function, with the maximal dispersal cost distance that may be travelled onto this resistance surface (associated with a null probability) set to 1500 m in data set I and 500 m in data set II (Table 1). In landscape B, a first continuous resistance surface was created by rescaling feature f0 to range from 1 to 3 (Fig. 1, panel b2), while a second categorical layer representing the three features f1, f2 and f3 was created by assigning pixels with resistance values of 1, 2 or 3, respectively (Fig. 1, panel b3). Pixels associated with the ‘blank’ feature f4 were assigned a value of 1, as this linear feature was totally included within feature f1. Both continuous and categorical layers were then summed, and the resulting resistance surface rescaled to range from 1 to 5, as in landscape A. This final layer was finally used to compute pairwise effective distances based on least-cost paths, and simulations were performed with a maximal dispersal cost distance set to 1500 m (Table 1). In each case, cdpop was run for 100 generations with 20 neutral loci of 20 alleles each (see Appendix S1, Supporting information for details).
| Data set | Landscape | True drivers of gene flow | Maximal dispersal distance (m) | ||||
|---|---|---|---|---|---|---|---|
| f 0 | f 1 | f 2 | f 3 | f 4 | |||
| I | A | ✓ | 1500 | ||||
| II | A | ✓ | 500 | ||||
| III | B | ✓ | ✓ | ✓ | ✓ | 1500 | |
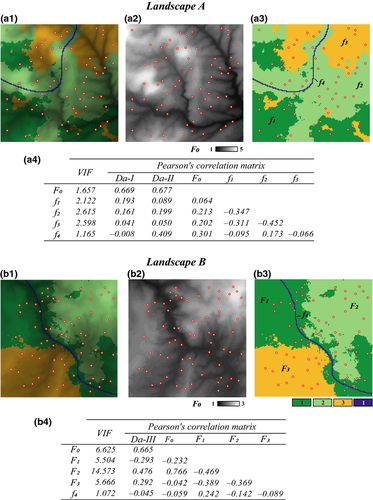
Genetic distances and spatial predictors
Pairwise genetic distances were computed between populations using the Nei's version of Cavalli-Sforza's chord distance Da (Nei et al. 1983), as it is not contingent on any theoretical assumption. To compute spatial predictors in landscapes A and B, a specific layer was created for each landscape feature. Layers associated with categorical features (f1 to f4) were binary, with pixels of value 1 for the considered feature and 0 otherwise. We then overlaid a 32 × 32 pixel grid on these layers and calculated the mean value of continuous feature f0 and the percentage of categorical features f1 to f4 per blocks of 4 × 4 pixels (Balkenhol et al. 2014). These layers were finally rescaled to range from 1 to 100 and used in circuitscape 3.5.8 (McRae & Shah 2009) to compute pairwise effective distances between populations. The reasoning for the systematic use of feature density (or mean feature value) per square surface as a proxy for matrix resistance was the following: areas with high densities of unsuitable feature are assumed to hinder dispersal because of higher physiological cost and predatory risk (positive relationship between feature density and genetic distances), while areas with high densities of neutral or suitable feature are not (null or negative relationship). Pairwise distances based on circuit theory being expressed in terms of random walk probabilities (McRae 2006; Spear et al. 2010), we did not include Euclidean distances as an additional explanatory variable (Garroway et al. 2011; Peterman et al. 2014). All variables were z-transformed (by subtracting the mean and dividing by the standard deviation) for output parameter estimates to be comparable (Schielzeth 2010).
MRDM and LRDM
When the maximal cost distance was set to 1500 m (data sets I and III), genetic distances were approximately normally distributed (Fig. 2a–c), allowing the use of linear regression such as MRDM (e.g. Braunisch et al. 2010; Blair et al. 2013; Nanninga et al. 2014). MRDM are similar to classical multiple ordinary least-square (OLS) regressions, except that the significance of model fit (multivariate R2) as well as the significance of beta weights β is assessed through permutations of the dependent matrix (Legendre et al. 1994). Linear MRDM and associated CA were, respectively, conducted using packages ecodist (Goslee & Urban 2007) and yhat (Nimon et al. 2013b) in r 3.1.0 (R Development Core Team 2014) with the following full model: Da = ∑(βi·fi). All significance levels were assessed with 10 000 permutations after sequential Bonferroni correction (Holm 1979). Ninety-five per cent confidence intervals around beta weights, structure coefficients and commonalities were computed using a bootstrap procedure, with 1000 replicates based on a random selection of 58 out of 64 populations without replacement (Peterman et al. 2014). This approach allows assessing the robustness of observed parameters to the random removal of a few sampling points: asymmetrical confidence intervals (e.g. Fig. 3) may result from multimodal distributions of metrics across bootstrap replicates, confirming that multicollinearity may vary with the spatial configuration of sampled points. This bootstrap procedure was also used to determine whether the observed differences between pairs of metrics (beta weights and structure coefficients) were robust to the removal of a few sampled points (Appendix S2, Supporting information).
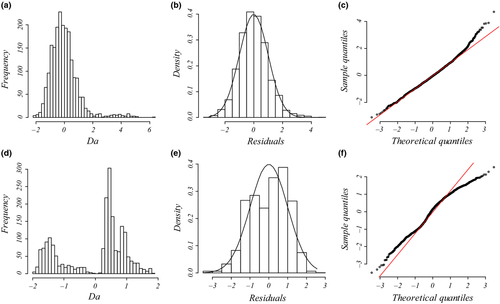
When the maximal cost distance was set to 500 m (data set II), genetic distances showed a multimodal distribution, thus violating the assumptions of normality of residuals in OLS regression (Fig. 2d–f). This kind of distribution usually requires the use of nonparametric, rank-based regression methods, assessing the monotonic rather than the linear relationships between the dependent variable and predictors (Van Strien et al. 2012; Dormann et al. 2013; Balkenhol et al. 2014). However, as variance-partitioning procedures such as CA cannot be applied in the case of nonparametric regressions, we transformed all genetic distances into binary variables and performed logistic regression on distance matrices (LRDM). Multivariate logistic regressions are used to predict the likelihood of a success (e.g. the probability 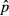 that Y = 1) given a set of predictors. When the dependent variable Y is expressed as the log odds of a success (logit transformation), the logistic regression equation is simply a linear combination of predictors where semi-standardized beta weights
that Y = 1) given a set of predictors. When the dependent variable Y is expressed as the log odds of a success (logit transformation), the logistic regression equation is simply a linear combination of predictors where semi-standardized beta weights 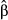 are estimated using maximum-likelihood procedures (Smith & McKenna 2013). Odd-ratios ψ, that is, semi-standardized beta weights raised to the exponent (
are estimated using maximum-likelihood procedures (Smith & McKenna 2013). Odd-ratios ψ, that is, semi-standardized beta weights raised to the exponent ( ), can then be used to evaluate the increase of the likelihood of a success with a one standard deviation change in X. Logistic regressions are uncommon in landscape genetics (but see for instance Weigel et al. 2013) but can be useful to handle nonlinear data. Using zero as a threshold, z-transformed genetic distances were thus recoded into binary data with 0 for pairs of individuals with negative z-scores and 1 for pairs of individuals with positive z-scores (‘success’ of being genetically dissimilar). Logistic regression was then performed using the glm function with a logit link in r 3.1.0, with all predictors being included in the model. Semi-standardized beta weights
), can then be used to evaluate the increase of the likelihood of a success with a one standard deviation change in X. Logistic regressions are uncommon in landscape genetics (but see for instance Weigel et al. 2013) but can be useful to handle nonlinear data. Using zero as a threshold, z-transformed genetic distances were thus recoded into binary data with 0 for pairs of individuals with negative z-scores and 1 for pairs of individuals with positive z-scores (‘success’ of being genetically dissimilar). Logistic regression was then performed using the glm function with a logit link in r 3.1.0, with all predictors being included in the model. Semi-standardized beta weights 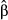 were computed following King (2007) with the mean predicted probabilities as a reference value. To evaluate overall model fit, we used the Nagelkerke's Index as a pseudo-R2, with a range (from 0 to 1) identical to the range of OLS multiple R2 (Roberts & Nimon 2012; Smith & McKenna 2013). Nagelkerke's Index was computed with the NagelkerkeR2 function in package fmsb, while logistic CA was performed with the cc4log function provided in Roberts & Nimon (2012). Structure coefficients were not computed here, as they are specific to linear regressions. Because binary data came from pairwise genetic distances and thus could not be considered as independent, significance levels of model fit and predictors were estimated using a randomization procedure similar to the one used in MRDM (Legendre et al. 1994). Rows and columns of the binary matrices were randomly permuted 10 000 times, and logistic regressions were performed on each permuted matrix to create a theoretical distribution of pseudo-R2 and beta weights
were computed following King (2007) with the mean predicted probabilities as a reference value. To evaluate overall model fit, we used the Nagelkerke's Index as a pseudo-R2, with a range (from 0 to 1) identical to the range of OLS multiple R2 (Roberts & Nimon 2012; Smith & McKenna 2013). Nagelkerke's Index was computed with the NagelkerkeR2 function in package fmsb, while logistic CA was performed with the cc4log function provided in Roberts & Nimon (2012). Structure coefficients were not computed here, as they are specific to linear regressions. Because binary data came from pairwise genetic distances and thus could not be considered as independent, significance levels of model fit and predictors were estimated using a randomization procedure similar to the one used in MRDM (Legendre et al. 1994). Rows and columns of the binary matrices were randomly permuted 10 000 times, and logistic regressions were performed on each permuted matrix to create a theoretical distribution of pseudo-R2 and beta weights 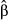 under the null hypothesis of random pairwise genetic distances. Observed pseudo-R2 and
under the null hypothesis of random pairwise genetic distances. Observed pseudo-R2 and 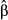 were then compared to theoretical distributions at a significance level of 0.05 with sequential Bonferroni correction (Holm 1979). As previously, 95% confidence intervals around commonalities were computed using a bootstrap procedure, with 1000 replicates based on a random selection of 58 out of 64 populations without replacement (Peterman et al. 2014).
were then compared to theoretical distributions at a significance level of 0.05 with sequential Bonferroni correction (Holm 1979). As previously, 95% confidence intervals around commonalities were computed using a bootstrap procedure, with 1000 replicates based on a random selection of 58 out of 64 populations without replacement (Peterman et al. 2014).
First illustration: data set I
Absolute zero-order Pearson's correlations among predictors in landscape A ranged from 0.064 to 0.452, while VIF ranged from 1.165 to 2.61 (Fig. 1, panel a4). As expected, predictors associated with the three predominant, and mutually exclusive, land-cover features (f1, f2 and f3) were negatively correlated and showed the highest VIF. Nonetheless, bivariate correlations and VIF were below traditional thresholds (|r| < 0.7 and VIF < 10, respectively), suggesting at first glance little multicollinearity in this data set.
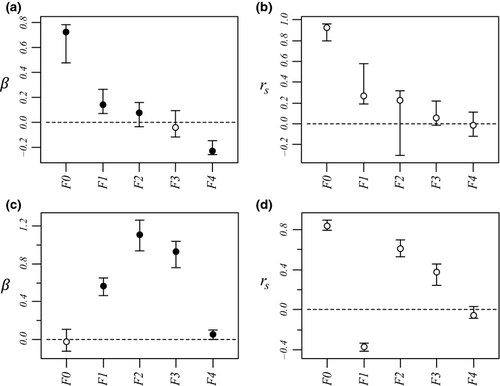
Multivariate regression model was significant and explained 52.10% of variance in the dependent variable (Table 2). Except f3, all predictors were significant after sequential Bonferroni correction. Comparing absolute values of β allowed ranking predictors from the most to the least influent in the following order: f0, f4, f1, f2 and f3 (Fig. 3a), although the difference between β2 and β3 was not robust to the random removal of a few sampling points (Appendix S2, Supporting information). For instance, the dependent variable increased by 0.721 standard deviation with a one standard deviation change in f0, all other predictors being hold constant. The linear feature f4 was the only significant predictor responsible for a decrease in genetic distances (β4 = −0.228). Most researchers would content themselves with such results, maybe looking for a rationale to explain how a linear feature such as roads (f4) could enhance gene flow. In our simulations though, the continuous feature f0 was the only driver of gene flow, and all other significant correlations were thus spurious ones.
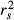 ), and finally, unique, common and total contributions of predictors to the variance in dependent variable (U, C and T)
), and finally, unique, common and total contributions of predictors to the variance in dependent variable (U, C and T)| Pred | Multiple R2 | β | P | r s |
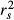
|
U | C | T |
|---|---|---|---|---|---|---|---|---|
| F 0 | 0.721 | <0.001 | 0.926 | 0.858 | 0.314 | 0.133 | 0.447 | |
| f 1 |
52.10% *** |
0.138 | <0.001 | 0.267 | 0.071 | 0.009 | 0.028 | 0.037 |
| f 2 | 0.075 | 0.008 | 0.223 | 0.050 | 0.002 | 0.024 | 0.026 | |
| f 3 | −0.044 | 0.103 | 0.056 | 0.003 | 0.001 | 0.001 | 0.002 | |
| f 4 | −0.228 | <0.001 | −0.011 | <0.001 | 0.045 | −0.045 | <0.001 |
- P-values in bold indicate significant predictors after sequential Bonferroni correction. Predictors in bold indicate main unique contributors to model fit according to CA (see text for details).
Examining structure (rs) and squared structure (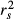 ) coefficients can help quantify the direct effect of predictors on the dependent variable (Nathans et al. 2012). The ranking of predictors based on absolute values of structure coefficients, that is, rescaled zero-order correlations (Box 1), diverged from the ranking based on beta weights (Fig. 3b), with f4 actually showing negligible rs value (Table 2). Furthermore, pairwise differences between rs2, rs3 and rs4 were not robust to the random removal of a few sampling points (Appendix S2, Supporting information). The actual direct contribution of f4 to model fit was null (
) coefficients can help quantify the direct effect of predictors on the dependent variable (Nathans et al. 2012). The ranking of predictors based on absolute values of structure coefficients, that is, rescaled zero-order correlations (Box 1), diverged from the ranking based on beta weights (Fig. 3b), with f4 actually showing negligible rs value (Table 2). Furthermore, pairwise differences between rs2, rs3 and rs4 were not robust to the random removal of a few sampling points (Appendix S2, Supporting information). The actual direct contribution of f4 to model fit was null (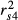 = 0), which in this case means that a substantial proportion of the variance in one or several other predictors was assigned to f4 in the process of computing beta weights, specifically designating it as a suppressor variable. Nevertheless, the spurious effects associated with f1 and f2 could not be explained. Structure coefficients indicate with no doubt that biological interpretations based only on β may be erroneous (Courville & Thompson 2001), despite low levels of collinearity (VIF < 3), but they cannot inform about which predictors jointly share variance in predicting the dependent variable or in what quantity.
= 0), which in this case means that a substantial proportion of the variance in one or several other predictors was assigned to f4 in the process of computing beta weights, specifically designating it as a suppressor variable. Nevertheless, the spurious effects associated with f1 and f2 could not be explained. Structure coefficients indicate with no doubt that biological interpretations based only on β may be erroneous (Courville & Thompson 2001), despite low levels of collinearity (VIF < 3), but they cannot inform about which predictors jointly share variance in predicting the dependent variable or in what quantity.
The actual synergistic or antagonistic processes operating among predictors can be assessed by CA. Figure 4 provides the 31 commonality coefficients, including both unique and common effects. Commonalities indicate the percentage of variance in the dependent variable that is uniquely explained by each predictor (unique effects) or set of predictors (common effects). With CA being a variance-partitioning procedure, the sum of commonalities equals the model fit index R2 (here, R2 = 0.521). %Total values are obtained by dividing commonalities by the fit index: they sum to 100 and represent the percentage of explained variance in model fit. CA indices reported in Table 2 can be derived from Fig. 4, by directly reading in the case of unique effects U or by summing all commonalities involving a given predictor in the case of common effects C. Total effects T are obtained by summing U and C. Note that T values may also be computed by squaring zero-order correlations r (Fig. 1, panel a4), indicating that CA actually encompasses several informative diagnostic indices (see Box 2).

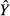 (that is, in model fit) by each set of predictors. In brackets: percentage of variance explained in the dependent variable (respectively, in model fit) that is due to suppression (sum of all negative commonalities).
(that is, in model fit) by each set of predictors. In brackets: percentage of variance explained in the dependent variable (respectively, in model fit) that is due to suppression (sum of all negative commonalities).The sum of all negative commonalities showed that 77.4% of the regression effect was caused by suppression. All predictors were associated with negative commonalities (Fig. 4), thus suggesting a complex suppression situation in this data set (Lewis & Escobar 1986). The importance of f0 was confirmed, as this predictor showed the highest unique contribution U0 to the variance in Da. Reported coefficients U0 are to be interpreted as follows: the continuous feature f0 uniquely contributed to 31.4% of the total variance in the dependent variable and to 60.27% of the 52.1% of variance explained by the regression model. Unique contributions of f1, f2 and f3 were actually negligible (U < 1%). Positive second- and fourth-order commonalities involving these predictors ([f0f1], [f0f2], [f0f3] and [f0f1f2f3]) were partially (or almost totally) counterbalanced by third-order negative commonalities ([f0f1f2], [f0f1f3] and [f0f2f3]; Fig. 4), resulting in positive sums C of commonalities if f1 (C1 = 0.028) and f2 (C2 = 0.024), and negligible one in f3 (C3 = 0.001; Table 2). All these commonalities involved f0: predictors f1 and f2 thus only contributed to the regression model because of their resultant synergistic association with f0. Negative commonalities involving f1, f2 and f3 were produced because correlations among land-cover predictors had opposite signs (Fig. 1, panel a4): these predictors acted as partial suppressors, suppressing irrelevant variance in f0, which thus showed a larger beta weight β0 than if the correlations had been in the same direction. Finally, the unique contribution of f4 to the dependent variable (U4 = 0.045) was almost totally counterbalanced by the negative second-order commonality [f0f4] (−0.044; Fig. 4), resulting in a null total contribution (T4 = 0; Table 2). The predictor f4 was actually unrelated to the dependent variable Da (r4 = −0.008) and acted as a suppressor variable: about 4.5% of irrelevant variance in f0 was assigned to f4 in the process of computing beta weights, increasing the overall model fit but also resulting in a significantly non-null value for β4.
To sum up, while the classical interpretation of beta weights would have yielded erroneous conclusions, CA correctly identified f0 as the true driver of gene flow. Other significant predictors either acted as suppressor (f4) or partial suppressors (f1 and f2), the latter indirectly contributing to model fit through their synergistic association with f0.
Second illustration: data set II
In the second data set, the exact same predictors were used, but the dependent variable was computed in the context of restricted dispersal (Table 1). The logistic model was significant and accounted for 51.56% of (pseudo-) variance in Da (Table 3). Three predictors were significant after sequential Bonferroni correction: f0, f3 and f4. Predictor f0 was identified as the main predictor (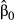 = 0.445), with an odd-ratio ψ0 = 1.56. This means that populations were 1.56 times more likely to show high pairwise genetic distances (Da > 0) with a one standard deviation change in f0 values. Predictor f4 was ranked second, with
= 0.445), with an odd-ratio ψ0 = 1.56. This means that populations were 1.56 times more likely to show high pairwise genetic distances (Da > 0) with a one standard deviation change in f0 values. Predictor f4 was ranked second, with 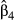 = 0.218 and ψ4 = 1.24, while predictor f3 showed a negative weight (
= 0.218 and ψ4 = 1.24, while predictor f3 showed a negative weight (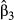 = −0.122). This means that populations were more likely to be genetically similar (ψ3 < 1) with a one standard deviation change in f3 values (Fig. 5). This last result was, however, inconsistent with the zero-order correlation r3 = 0.05 (Fig. 1, panel a4) that indicated a slightly positive relationship between f3 and untransformed values of Da. Furthermore, the continuous feature f0 was actually the only true driver of gene flow in landscape A.
= −0.122). This means that populations were more likely to be genetically similar (ψ3 < 1) with a one standard deviation change in f3 values (Fig. 5). This last result was, however, inconsistent with the zero-order correlation r3 = 0.05 (Fig. 1, panel a4) that indicated a slightly positive relationship between f3 and untransformed values of Da. Furthermore, the continuous feature f0 was actually the only true driver of gene flow in landscape A.
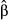 (computed using the mean predicted probability of 0.663 as a reference value), odd-ratios ψ and P-values P, and finally, unique, common and total contributions of predictors to the variance in dependent variable (U, C and T)
(computed using the mean predicted probability of 0.663 as a reference value), odd-ratios ψ and P-values P, and finally, unique, common and total contributions of predictors to the variance in dependent variable (U, C and T)| Pred | Pseudo-R2 |
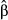
|
ψ | P | U | C | T |
|---|---|---|---|---|---|---|---|
| F 0 | 0.445 | 1.560 | <0.001 | 0.182 | 0.253 | 0.434 | |
| f 1 |
51.56% *** |
0.022 | 1.022 | 0.297 | <0.001 | 0.011 | 0.011 |
| f 2 | 0.037 | 1.038 | 0.187 | 0.001 | 0.036 | 0.037 | |
| f 3 | −0.122 | 0.886 | 0.001 | 0.013 | −0.012 | 0.001 | |
| f 4 | 0.218 | 1.244 | <0.001 | 0.021 | 0.280 | 0.301 |
- P-values in bold indicate significant predictors after sequential Bonferroni correction. Predictors in bold indicate main unique contributors to model fit according to CA (see text for details).
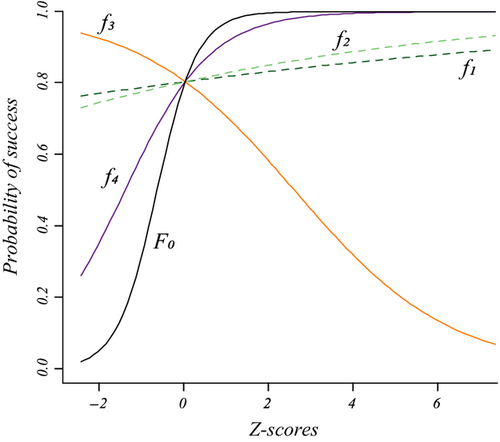
CA allowed clarifying these results. The sum of all negative commonalities showed that 42% of the regression effect was caused by suppression (Fig. 6). As previously, all predictors were associated with negative commonalities (Fig. 6), thus suggesting a complex suppression situation in this data set (Lewis & Escobar 1986). The importance of f0 was confirmed, as this predictor had the largest unique contribution to the variance in Da (U0 = 18.2%; Table 3) and accounted for 35.2% of the regression effect (Fig. 6). Predictor f3 was involved in second-, third-, fourth- and fifth-order non-null commonalities (Fig. 6) but was easily identified as a suppressor variable, as its unique contribution U3 was almost totally counterbalanced by the sum of its common contributions C3 (Table 3), thus providing a better understanding of the inconsistency between a slightly positive zero-order correlation r3 and a negative semi-standardized beta weight 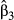 . While the unique contribution of f4 was low (U4 = 0.02), the sum of all commonalities involving f4 was high (C4 = 0.28), notably because of the second-order commonality [f0f4] that accounted for 39.25% of model fit (Fig. 6). Predictor f4 was positively correlated with predictor f0 (r = 0.301; Fig. 1, panel a4) and thus mainly contributed to the regression model because of its high common contribution with f0. Finally, and as expected, nonsignificant predictors f1 and f2 showed negligible unique contributions U and low common contributions C, the latter resulting from a trade-off between positive third-order commonalities ([f0f1f4] and [f0f2f4]) and negative third- and fourth-order commonalities (Fig. 6). Note that because it is involved in all the largest negative commonalities ([f0f1f2], [f0f1f3] and [f0f2f3]), predictor f0 may also be considered as a partial suppressor. As previously, while the classical interpretation of semi-standardized beta weights and odd-ratios would have yielded erroneous conclusions, CA correctly identified f0 as the true driver of gene flow. Other significant predictors either acted as suppressor (f3) or indirectly contributed to model fit through a synergistic association with f0 (f4).
. While the unique contribution of f4 was low (U4 = 0.02), the sum of all commonalities involving f4 was high (C4 = 0.28), notably because of the second-order commonality [f0f4] that accounted for 39.25% of model fit (Fig. 6). Predictor f4 was positively correlated with predictor f0 (r = 0.301; Fig. 1, panel a4) and thus mainly contributed to the regression model because of its high common contribution with f0. Finally, and as expected, nonsignificant predictors f1 and f2 showed negligible unique contributions U and low common contributions C, the latter resulting from a trade-off between positive third-order commonalities ([f0f1f4] and [f0f2f4]) and negative third- and fourth-order commonalities (Fig. 6). Note that because it is involved in all the largest negative commonalities ([f0f1f2], [f0f1f3] and [f0f2f3]), predictor f0 may also be considered as a partial suppressor. As previously, while the classical interpretation of semi-standardized beta weights and odd-ratios would have yielded erroneous conclusions, CA correctly identified f0 as the true driver of gene flow. Other significant predictors either acted as suppressor (f3) or indirectly contributed to model fit through a synergistic association with f0 (f4).

Third illustration: data set III
Absolute zero-order Pearson's correlations among predictors in landscape B ranged from 0.089 to 0.766, while VIF ranged from 1.072 to 14.573 (Fig. 1, panel b4), suggesting potential multicollinearity issues in this example. The most problematic predictor was f2 (VIF > 10), as it was highly correlated with f0 (r > 0.7; Fig. 1, panel b4). This predictor would usually be excluded from the model but was conserved here for illustration purpose. As in landscape A, predictors associated with the three predominant land-cover features (f1, f2 and f3) were negatively correlated.
The linear model was significant and accounted for 61.58% of variance in Da (Table 4). Except for f0, all predictors showed positive and significant beta weights after sequential Bonferroni correction. Comparing absolute values of beta weights allowed ranking predictors from the most to the least influent in the following order: f2, f3, f1, f4 and f0 (Fig. 3c), although the difference between β0 and β4 was not robust to the random removal of a few sampling points (Appendix S2, Supporting information). However, the ranking of predictors based on beta weights was inconsistent with the ranking based on structure coefficient rs (Fig. 3d). Indeed, predictor f0, though nonsignificant, showed the highest direct contribution to the dependent variable (rs0 = 0.834), while f1 actually appeared negatively correlated with Da (Table 4).
| Pred | Multiple R2 | β | P | r s |
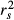
|
U | C | T |
|---|---|---|---|---|---|---|---|---|
| F 0 | −0.019 | 0.644 | 0.834 | 0.696 | <0.001 | 0.428 | 0.428 | |
| F 1 |
61.58% *** |
0.568 | <0.001 | −0.373 | 0.139 | 0.059 | 0.027 | 0.086 |
| F 2 | 1.107 | <0.001 | 0.607 | 0.368 | 0.084 | 0.143 | 0.227 | |
| F 3 | 0.926 | <0.001 | 0.372 | 0.138 | 0.151 | −0.066 | 0.085 | |
| f 4 | 0.056 | <0.001 | −0.057 | 0.003 | 0.003 | −0.001 | 0.002 |
- See legend in Table 2.
The sum of all negative commonalities indicated a really complex suppression situation here, as 92.8% of the regression effect was caused by suppression (Fig. 7). In particular, negative commonalities identified suppression involving predictors f0, f1, f2 and f3, through second-order ([f1f2], [f1f3], [f2f3]) and third-order commonalities ([f0f1f2], [f0f1f3], [f0f2f3]). These negative commonalities were partially counterbalanced by positive second-order ([f0f1], [f0f2], [f0f3]), third-order ([f1f2f3]) and fourth-order commonalities ([f0f1f2f3]), resulting in positive common contributions to the dependent variable in f0, f1 and f2 (C0 = 42.8%; C1 = 2.7%; C2 = 14.3%) and negative common contribution in f3 (C3 = −6.6%; Table 4). With such a negative common contribution but at the same time a non-null total contribution to model fit (T3 = 8.5%), predictor f3 was identified as a partial suppressor. This partial suppression effect notably ensued from the specific pattern of bivariate correlations in this data set, f3 being positively correlated with Da but negatively correlated with all other predictors (Fig. 1, panel b4). Predictor f1 may also be considered as a partial suppressor variable: there was a mismatch in the sign of beta weight β1 and structure coefficient rs1, but the sum C of all commonalities involving f1 was still positive (C1 = 0.027). The influence of these predictors was thus to be interpreted with much caution. Nevertheless, a few conclusions could still be drawn from this analysis. First, it is worth observing that unique contributions allowed ranking land-cover predictors f1, f2 and f3 in an order consistent with simulated process (that is, f3 >f2 >f1; Table 4), although neither the magnitude nor the sign of reported beta weights could be fully trusted. Second, the influence of predictor f4 on gene flow could be immediately ruled out: although characterized by a significant beta weight, f4 had both little unique and common contributions to the dependent variable (U4 = 0.003; C4 = −0.001; Table 4), resulting in a negligible total contribution to model fit (T4 = 0.2%), in accordance with simulated process. Finally, although nonsignificant, predictor f0 had actually the highest total contribution to model fit (T0 = 42.8%). This contribution was completely explained by common effects of f0 with other predictors (C0 = 42.8%), especially through the positive second-order commonality [f0f2] which accounted for 66.24% of model fit (Fig. 7). Because of high collinearity among these two predictors (r = 0.766; Fig. 1, panel b4), the variance in f0 was mainly assigned to f2 in the process of computing beta weights. Excluding f2 from the model made the percentage of suppression drop from 92.8% to <9% and allowed correctly identifying the main contributors to genetic distances while ruling out f4 (data not shown). But by doing so, f2 could obviously not be identified as one of the drivers to gene flow.

Advantages of commonality analyses
As a preliminary remark, note that because of multicollinearity among spatial features, zero-order correlations can be non-null despite no true causal relationship between the dependent variable and spatial predictors (e.g. f1 in data set I or f4 in data set II; Nathans et al. 2012), thus confirming the utility of multivariate procedures over univariate ones in resistance model optimization (Balkenhol et al. 2009; Spear et al. 2010; Graves et al. 2013). Whatever the model fit index used to identify the best resistance surface from a set of alternative surfaces (e.g. Perez-Espona et al. 2008; Shirk et al. 2010; Dudaniec et al. 2013; Peterman et al. 2014), multicollinearity among spatial features may indeed be responsible for the selection of suboptimal or even spurious univariate models (Spear et al. 2010). For instance, Perez-Espona et al. (2008) found that inland lochs and rivers might facilitate gene flow in Scottish red deers: this result may be biologically realistic, but may also ensue from artefactual correlations due to spatial multicollinearity among landscape features. However, the three provided illustrations also confirmed that the typical interpretation of multivariate regressions based on the ranking of significant beta weights is flawed by even weak levels of multicollinearity among predictors (Mac Nally 2002; Dormann et al. 2013), with the risk of erroneous conclusions, misdirected research and inefficient or counterproductive conservation measures. The investigation of commonalities can circumvent these flaws to some extent and provide insightful information about the relative influence of landscape predictors on the dependent variable in direct gradient analyses.
First, CA can be used to clarify the relative importance of predictors in the case of synergistic association among variables (Ray-Mukherjee et al. 2014). For instance, f4 in data set II showed little unique contribution U to model fit, especially when compared with the unique contribution of f0. The computation of the semi-standardized beta weight in f4 was actually dictated by collinearity between f4 and f0 so that 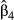 reflected the indirect rather than the real contribution of f4 to model fit. Similarly, f0 in data set III had negligible unique contribution to model fit: this predictor mostly explained variance in the dependent variable when in synergistic association with other predictors. In both cases, the classical interpretation of significant beta weights was flawed by positive collinearity among predictors. In an empirical situation, that is, in the absence of any information about potential drivers of gene flow, deciding whether a predictor with little unique contribution is or is not responsible for the observed biological response is left to the appreciation of investigators. Disentangling the relative contribution of such explanatory variables in a predictive perspective would actually require replications in different multicollinearity contexts (Anderson et al. 2010; Short Bull et al. 2011; Prunier et al. 2013). Nevertheless, this ability of CA to provide a clear quantification of unique contributions of predictors to model fit is valuable for interpreting results of multivariate regressions.
reflected the indirect rather than the real contribution of f4 to model fit. Similarly, f0 in data set III had negligible unique contribution to model fit: this predictor mostly explained variance in the dependent variable when in synergistic association with other predictors. In both cases, the classical interpretation of significant beta weights was flawed by positive collinearity among predictors. In an empirical situation, that is, in the absence of any information about potential drivers of gene flow, deciding whether a predictor with little unique contribution is or is not responsible for the observed biological response is left to the appreciation of investigators. Disentangling the relative contribution of such explanatory variables in a predictive perspective would actually require replications in different multicollinearity contexts (Anderson et al. 2010; Short Bull et al. 2011; Prunier et al. 2013). Nevertheless, this ability of CA to provide a clear quantification of unique contributions of predictors to model fit is valuable for interpreting results of multivariate regressions.
Second, CA can reveal spurious correlations that may have gone unnoticed in the framework of a typical interpretation of significant beta weights. The investigation of commonalities in data sets I and II confirmed that suppression may occur despite moderate levels of multicollinearity (Ray-Mukherjee et al. 2014). Researchers are thus probably often confronted to this kind of spurious effects although they may not be aware that they are dealing with a suppression situation (Lewis & Escobar 1986). This is especially true when the sign and the magnitude of beta weights make sense with regard to biological expectations. Should this not be the case, a convincing rationale is usually proposed to justify any unexpected outcome (Graves et al. 2013). By fully clarifying how variables contribute to prediction, CA provides a way to identify suppressors and to foil spurious correlations. Two predictors were identified as suppressors in data sets I (f4) and II (f3). When significant, these variables were thought to facilitate dispersal, although they were not part of the simulating process. However, the total contributions T of these two predictors, that is the amount of explained variance in the dependent variable irrespective of collinearity, were low, unique effects being counterbalanced by their negative commonalities. Suppression situations are to be identified for a proper interpretation of regression models, but they are not necessarily to be avoided (Lewis & Escobar 1986; Pandey & Elliott 2010). Once spurious correlations have been identified, suppression may eventually improve the detectability of influential predictors by removing the part of their variance that is irrelevant to predict the dependent variable (Nimon & Reio 2011; Ray-Mukherjee et al. 2014). It is yet essential to bear in mind that although some variables may act as explicit suppressors, suppression situations can also be particularly complex (data set III; Lewis & Escobar 1986): the interpretation of commonalities is thus always to be carried out with much caution (Ray-Mukherjee et al. 2014).
Finally, and contrary to procedures such as stepwise regression, CA is independent of variable order and thus replicable for a given model (Lewis 2007; Ray-Mukherjee et al. 2014). By allowing a thorough understanding of the relative contribution of spatial predictors to genetic variability, CA can help identify the most parsimonious set of predictors from a given full model (Kraha et al. 2012), thus making it a valuable complementary tool to model selection procedures.
Limitations and future applications
CA appears as a promising procedure in spatial genetics. However, this is not a panacea. First, although investigating commonalities allow identifying the location and magnitude of nonindependence among predictors (Nimon 2010), it cannot solve multicollinearity issues per se (Dormann et al. 2013). Indeed, CA does not provide any corrected or weighted parameter that may eventually be used in a predictive perspective. CA is also limited to parametric models: although it is hitherto available for use with linear regressions, logistic regressions, as well as mixed-effect models (Roberts & Nimon 2012; Ray-Mukherjee et al. 2014), commonalities cannot be interpreted in the context of nonlinear, rank-based regressions. LRDM may sometimes constitute an interesting alternative to nonparametric models (for instance in the case of multimodal distributions; see data set II), but may not properly represent all nonlinear relationships.
Furthermore, the interpretation of CA becomes more difficult as the number of predictors increases, because the number of commonalities expands exponentially with the number of predictors (Ray-Mukherjee et al. 2014; see Box 3). In our illustrations, we only considered a set of five predictors, a reasonable number when considering current spatial genetic studies (Zeller et al. 2012). Nevertheless, the number of commonalities would have increased from 31 to 63 with a single additional variable in full regression models. Although interpreting and reporting commonalities for a higher number of predictors may be highly informative (Nathans et al. 2012), the number of predictors may sometimes be too high or suppression situations too complex for all explanatory variables to be conserved in the regression model (e.g. data set III). CA thus does not resolve the problem of variable preselection (Dormann et al. 2013). Rather than using a predefined correlation threshold to avoid multicollinearity, investigators should investigate multicollinearity patterns and consider both the ecology of studied species and local landscape characteristics to select a set of nonredundant and biologically relevant predictors.
Finally, commonalities are specific to a given model, because of particular patterns of bivariate correlations. In a complex multicollinearity context, all predictors may, to some extent, remove irrelevant variance from some other variables (see Figs 4, 6 and 7; Lewis & Escobar 1986) so that adding or removing predictors is likely to modify commonalities, with the emergence of new suppression situations. This issue has no consequence on direct gradient analyses when they are performed in an explanatory perspective as a single full model is explored. In a predictive perspective though, regressions are often performed on a set of nested or alternative models and model fit indices are then compared to identify the model structure showing the best predictive power. As model fit indices are influenced by suppression situations (Paulhus et al. 2004), suppressors may be retained in the final best model, with the risk of erroneous conclusions. Ideally, commonalities should be systematically computed and thoroughly inspected to identify, in each model, both suppressors and main contributors to model fit (see Blair et al. 2013 for such a model selection procedure using VIF). This framework may though be unrealistic when the number of models is large, notably in resistance model optimization. As a consequence, CA cannot fully address the issues described by Graves et al. (2013) about the current low performance of predictive analyses in landscape genetics, although multicollinearity is in all likelihood part of the problem. In model selection or resistance model optimization, commonalities should at least be investigated in the final best-fitted multivariate model, to avoid any erroneous interpretation of multivariate regressions. When models are nested, CA may also be used as a preliminary tool to assess commonalities in the full model, providing initial indications as to the relative contributions of predictors to the dependent variable.
We illustrated the use of CA in spatial genetics and showed that an in-depth understanding of multivariate regression results could be achieved when local collinearity structure was taken into account. Providing information about the unique contribution of predictors to genetic variability while easily revealing spurious correlations, CA is a promising tool in spatial genetics, especially as commonalities are easily computed in linear and logistic regressions, with functions and scripts now available for use in various statistical softwares such as r, spss or sas (Nimon et al. 2008, 2010; Nimon 2010; Kraha et al. 2012; Roberts & Nimon 2012). CA may assume even greater value if used to assist the interpretation of regressions on data collected in different multicollinearity contexts, that is, coming from distinct spatial or temporal replicates (Anderson et al. 2010; Short Bull et al. 2011; Dormann et al. 2013), or on the contrary to assist the interpretation of regressions on data collected in distinct but co-occurring species (Storfer et al. 2010). CA may also facilitate the comparison of empirical and simulated data in the framework of landscape genetic model validation (Shirk et al. 2012). We thus strongly urge spatial geneticists to systematically investigate commonalities in explanatory full models or in best-fitted predictive models. Further methodological developments are now needed to determine how CA could be used to enhance the reliability of resistance model optimization procedures in spatial genetics. A particular attention should also be paid to the validity of regression CA in the specific framework of maximum-likelihood population-effects (MLPE) mixed models (Clarke et al. 2002), an increasingly used statistical tool in spatial genetics (Selkoe et al. 2010; Van Strien et al. 2012; Prunier et al. 2013). Finally, future studies should be conducted to assess how the location and magnitude of multicollinearity among predictors (including both synergistic associations and suppression situations) could be investigated using current variation-partitioning procedures in the framework of constrained ordination techniques (Borcard et al. 1992; Peres-Neto et al. 2006).
Acknowledgements
This work was supported by A. Bouron from the Fédération Régionale des Chasseurs du Centre, V. Giquel-Chanteloup from the Fédération Départementale des Chasseurs de L'Indre, as well as the Société de Vènerie and the Fondation François Sommer pour la Chasse et la Nature. We warmly thank two anonymous reviewers for insightful comments on a first draft of this manuscript.
References
J.G.P. designed the study, performed modelling and simulating the work and wrote the manuscript; J.G.P. and K.N. analysed output data; K.N., M.C., X.L. and M.C.F. provided edits to the study.
Data accessibility
Spatial data sets I, II and III, as well as corresponding R-scripts used to get provided results. Dryad Digital Repository: doi:10.5061/dryad.86gm0.




