Steep clines within a highly permeable genome across a hybrid zone between two subspecies of the European rabbit
Abstract
Maintenance of genetic distinction in the face of gene flow is an important aspect of the speciation process. Here, we provide a detailed spatial and genetic characterization of a hybrid zone between two subspecies of the European rabbit. We examined patterns of allele frequency change for 22 markers located on the autosomes, X-chromosome, Y-chromosome and mtDNA in 1078 individuals sampled across the hybrid zone. While some loci revealed extremely wide clines (w ≥ 300 km) relative to an estimated dispersal of 1.95–4.22 km/generation, others showed abrupt transitions (w ≈ 10 km), indicating localized genomic regions of strong selection against introgression. The subset of loci showing steep clines had largely coincident centers and stepped changes in allele frequency that did not co-localize with any physical barrier or ecotone, suggesting that the rabbit hybrid zone is a tension zone. The steepest clines were for X- and Y-chromosome markers. Our results are consistent with previous inference based on DNA sequence variation of individuals sampled in allopatry in suggesting that a large proportion of each genome has escaped the overall barrier to gene flow in the middle of the hybrid zone. These results imply an old history of hybridization and high effective gene flow and anticipate that isolation factors should often localize to small genomic regions.
Introduction
Studies of genetically distinct taxa that hybridize in nature allow exploration of long-term processes that are inaccessible with laboratory crosses, and yet central to our understanding of speciation (Abbott et al. 2013). Empirical evidence supports the view that introgression is a common and important evolutionary force (Phillips et al. 2004; Macholán et al. 2007; Putnam et al. 2007; Good et al. 2008; Kane et al. 2009; Melo-Ferreira et al. 2009; Storchová et al. 2010), with regions of the genomes of incipient species varying greatly in their permeability to foreign alleles. Hybridizing taxa are expected to exchange beneficial alleles easily (Barton 1979; Barton & Bengtsson 1986). In contrast, genomic regions underlying local adaptation or resulting in hybrid incompatibilities are not expected to move easily between hybridizing taxa.
Loci involved in reproductive isolation are typically embedded in divergent genomes containing many isolation factors, and this is expected to impact the dynamics of secondary contact through multilocus effects. Migration of individuals across species barriers creates strong genome-wide associations across loci (irrespective of whether they are physically linked or unlinked). Sorting and crossing over (summarized as recombination R) break down these associations, but if selection S against hybrids (due to incompatibilities or maladaptation) removes recombinants from the gene pool then S blocks this breakdown of associations. Barton (1983) showed a critical value of the coupling coefficient S/R above which the genome-wide associations (i.e. linkage disequilibria) due to migration will be maintained, reducing effective gene flow at large genomic scales, but below which the breakdown in associations will allow easier gene flow. This distinction may take many generations to become clear, but the coupling coefficient remains the best way to summarize the dynamics and equilibrium state for permeability of species barriers (Baird 1995). While these results are for selected loci evenly spread across a genome the implications if selected loci are clustered on a particular linkage group are clear. Because hybrid zones allow many generations of recombination to be explored, they provide an opportunity to study the extent to which genomes of recently separated taxa may diverge or be united by gene flow and how effective gene flow varies across the genome.
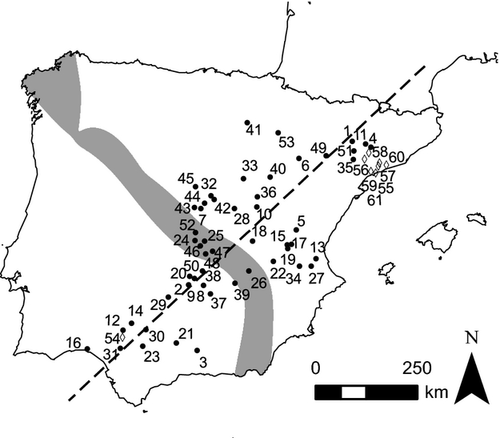
The two subspecies of the European rabbit (Oryctolagus cuniculus) provide a window into the early stages of speciation. The European rabbit traces its origins to the Iberian Peninsula over the last few million years and several studies note this region as an important refuge during the Quaternary glaciations (reviewed in Hewitt 2000). The long standing presence of rabbits in Iberia, together with the earlier amelioration of climatic conditions in this region when compared with higher latitudes, may have provided the opportunity for periods of isolation followed by periods of contact. Currently, the two rabbit subspecies are distributed parapatrically: O. c. algirus is localized in the southwest of Iberian Peninsula and O. c. cuniculus localized in the northeast of Iberian Peninsula and France (Fig. 1). The subspecies show slight phenotypic differences in size and cranial measurements (Sharples et al. 1996; Villafuerte 2002). Multiple genetic markers suggest a divergence time between the two subspecies that dates to ~1.8 Myr ago (Branco et al. 2000; Carneiro et al. 2009). DNA sequence data from rabbits sampled far away from the contact zone showed that the genomes of these two subspecies are characterized by highly heterogeneous patterns of differentiation (Geraldes et al. 2006, 2008; Carneiro et al. 2009, 2010). Some loci exhibit high levels of differentiation and these are preferentially located on the X-chromosome and near centromeres of several autosomes. The Y-chromosome also shows high levels of differentiation. These patterns of differentiation in rabbits are in agreement with theoretical and empirical predictions suggesting that low recombination regions (Faria & Navarro 2010; Nachman & Payseur 2012) and sex chromosomes (Coyne & Orr 2004) might facilitate species divergence in the face of gene flow. Notably, these regions stand out against a background genome practically devoid of fixed variation, and coalescent analysis based on isolation-with-migration models (IM, Hey & Nielsen 2004) suggest that rampant gene exchange has occurred (Carneiro et al. 2010). For example, DNA sequence variation in allopatric samples reveals two highly divergent haplotypes at several loci, but with both variants present in both subspecies, a pattern that likely reflects ancient vicariance and subsequent gene flow (e.g. HPRT1, Fig. 2).
Despite multiple studies of DNA sequence variation from allopatric sampling, there have been no studies of clinal variation in the region of contact and the presumed hybrid zone has remained uncharacterized genetically. Therefore, important questions remain about the abrupt or smooth nature of the contact, its location and how levels and patterns of introgression differ across loci. Here, we provide the first explicit spatial characterization of the rabbit hybrid zone. We sampled 1078 rabbits and carried out geographic and non-geographic clinal analyses of introgression for markers located in all four genomic compartments (autosomes, X-chromosome, Y-chromosome, and mtDNA). In addition, we compare our current findings with previous results based on DNA sequence variation from allopatric samples.
Materials and methods
DNA samples
Hybridization between O. c. algirus and O. c. cuniculus occurs along a Northwest–Southeast axis on the Iberian Peninsula (Fig. 1). Because the subspecies are morphologically similar and previous studies were based on limited sampling, very little was known about the geographic location and orientation of the rabbit hybrid zone. Transects with incorrect orientation relative to a contact zone will tend to lead to overestimates of cline width (Macholán et al. 2008), therefore, we chose localities to cover much of the geographic range of both rabbit subspecies in Iberia as well as the central overlap, allowing orientation of the zone to be estimated. We sampled a total of 1078 individuals from 61 localities (Fig. 1) between 2002 and 2005. Geographic coordinates and sample sizes for all localities are available in Table S1 (Supporting Information).
Single Nucleotide Polymorphisms choice and genotyping
We selected a total of 28 Single Nucleotide Polymorphisms (SNPs) from previous resequencing data (Branco et al. 2000; Geraldes et al. 2005, 2006, 2008; Carneiro et al. 2009, 2010), chosen to cover the four compartments of the genome (eight autosomal markers, 18 X-linked, 1 Y-linked and 1 mitochondrial; Table 1). Sequence data for XPO4 have not been reported in previous studies and are available on GenBank (Accession numbers: HM138911–HM138914). We selected three kinds of SNP markers from previous studies. First, we chose SNPs that were diagnostic between subspecies in individuals sampled away from the hybrid zone (AMOT, DGKK, F9, FMR1, G6PD, KLHL13, MSN, NRK, OGT, SHOX, STAG1, and XPO4). Second, we chose SNPs which were not diagnostic but showed marked allelic frequency differences between subspecies (>70%) at loci with few mismatched haplotypes in an otherwise well-sorted genealogy (ARGHF9, cytb-mtDNA, GLRA2, MGST3, PROC, SMCX, and SRY-Y-chromosome). Finally, we chose SNPs without significant frequency differences between subspecies but that were positioned on a genealogical branch uniting highly divergent haplogroups (ATP12A, DIAPH2, EDNRA, GK5, HPRT1, LUM, MAOA, PHKA2, and TNMD). These different categories of markers may be expected to show different patterns in clinal analyses (see 3).
| Gene | Chromosome | Chromosome locationb | References |
|---|---|---|---|
| LUMa | 4 | 70.32 | Carneiro et al. (2009) |
| PROCa | 7 | 59.22 | Geraldes et al. (2008) |
| XPO4 | 8 | 43.82 | This study |
| ATP12Aa | 8 | 45.29 | Carneiro et al. (2009) |
| MGST3a | 13 | 27.25 | Carneiro et al. (2009) |
| STAG1 | 14 | 30.26 | Carneiro et al. (2009) |
| GK5a | 14 | 35.61 | Carneiro et al. (2010) |
| EDNRA | 15 | 17.12 | Geraldes et al. (2008) |
| SHOX | X | Unknown | Carneiro et al. (2010) |
| GLRA2 | X | 0.61 | Carneiro et al. (2010) |
| PHKA2a | X | 4.72 | Geraldes et al. (2006) |
| MAOAa | X | 29.15 | Carneiro et al. (2010) |
| DGKK | X | Unknown | Carneiro et al. (2010) |
| SMCX | X | 34.72 | Geraldes et al. (2006) |
| ARHGEF9a | X | 42.30 | Carneiro et al. (2010) |
| MSN | X | 44.32 | Geraldes et al. (2006) |
| OGTa | X | 50.03 | Carneiro et al. (2010) |
| NRK | X | 54.60 | Carneiro et al. (2010) |
| AMOT | X | 61.38 | Carneiro et al. (2010) |
| KLHL13 | X | 66.54 | Carneiro et al. (2010) |
| TNMDa | X | 88.78 | Carneiro et al. (2010) |
| DIAPH2 | X | 92.70 | Carneiro et al. (2010) |
| HPRT1a | X | 108.78 | Geraldes et al. (2006) |
| F9 | X | Unknown | Carneiro et al. (2010) |
| FMR1 | X | Unknown | Carneiro et al. (2010) |
| G6PD | X | Unknown | Carneiro et al. (2010) |
| SRY | Y | Unknown | Geraldes et al. (2005) |
| Cytb | mtDNA | Unknown | Branco et al. (2000) |
- a Loci excluded from cline analysis either because the genotyping assay failed, levels of missing data were high or we could not attribute subspecific origin of alleles (see 3 section).
- b Chromosome and chromosome location in megabases were obtained at the Broad Institute website from the European rabbit 7X genome sequence assembly or from the rabbit physical map (Chantry-Darmon et al. 2005).
Multiplex SNP genotyping was carried out using Sequenom's (San Diego, USA) iPlex technology and detected in a Sequenom MassArray K2 platform following the manufacturer's protocol. Primers and multiplex conditions were designed using Sequenom's MassARRAY® Assay Design 3.0 software and are provided in Table S2 (Supporting Information). The resulting spectra and plots were manually inspected and software genotype calls were corrected whenever required. Y-chromosome and mtDNA genotypes were scored using previously described PCR-RFLP protocols (Branco et al. 2000; Geraldes et al. 2008). Individual genotypes have been deposited in the Dryad database under doi number http://10.5061/dryad.mj18p.
Data analysis
To control for potential non-independence of alleles due to relatedness and deviation from Hardy–Weinberg equilibrium, the effective number of alleles sampled at each locality was estimated following the procedures described in Macholán et al. (2007). The clinal analyses are therefore robust to the effects of deviations from random mating and local or familial relatedness within samples.
Orientation of the cline in two dimensions
Latitude and longitude georeferences were projected onto the plane around the centroid of the sampling localities using the Sundial implementation of gnomonic projection (Baird & Santos 2010). To avoid biases arising from drawing a transect oblique to the hybrid zone, the first step of analysis was to determine the orientation of the maximum gradient in allele frequency change. The orientation procedure was performed following Macholán et al. (2008) using the Pooled Adjacent Violators Algorithm (PAVA; Brunk 1955). For a given orientation, coordinates for each locality are orthogonally projected on a straight line and PAVA then calculates the maximum-likelihood (ML) monotonic cline through the locality allele counts at that orientation. The procedure is repeated to build up the likelihood profile for monotonic change over the interval of all possible orientations (0°–360°). Likelihood profiles for monotonic change were estimated for each locus independently, and orientation consistency among loci was checked by comparing the resultant profiles. These analyses were performed using functions implemented in Mathematica for Analyse v2.0beta (Baird SJE., and Barton NH in preparation).
Genotypic and allelic disequilibria
At each locality with more than five individuals sampled, log-likelihood profiles for FIS and scaled linkage disequilibrium (LD) were calculated as implemented in the computer package Analyse v1.3 by Barton and Baird (http://www.biology.ed.ac.uk/archive/software/Mac/Analyse/index.html). LD was also estimated using an alternative method based on the variance of the hybrid index (Barton & Gale 1993).
Cline fitting
Sampling localities were projected orthogonally onto a line following the most likely orientation of change. ML clines were fitted to effective counts of O. c. cuniculus versus O. c. algirus alleles along this line, as implemented in Analyse v1.3. Locality distances were measured relative to the orthogonal projection of the centroid of the sampling locality coordinates. ML estimation was performed separately for each locus and for three different models of cline shape (Szymura & Barton 1986). These models have been described in detail elsewhere (e.g. Phillips et al. 2004; Raufaste et al. 2005) so here we provide only a brief description. The first model, a sigmoid cline (Sig), has two parameters: c, the geographic location of the center of the cline, and w, the width of the cline, which is defined as the inverse of the maximum slope. The second model (stepped symmetric model; Sstep) is composed of three different sections: a central step and exponential tails with matching parameters of introgression. This model has two additional parameters compared to the first, θ and β, which describe the shape of the exponential tails relative to the central segment. θ is the rate of exponential decay and is proportional to the level of selection acting on a character outside the central step. β is the strength of the barrier to gene flow at the zone center and is interpreted as the physical distance that would result in an equivalent change in character state in the absence of a barrier to introgression. Finally, the third model (stepped asymmetric model; Astep) incorporates two additional θ and β parameters that allow the tails of introgression to differ, for a total of six parameters. Likelihood profiles were constructed following Phillips et al. (2004) using the multidimensional maximization algorithm FindMaximum from Mathematica (Wolfram 1992). Profile construction not only serves to check search convergence, but also allows rigorous exploration of the support for each parameter estimate. Given that the cline models are nested, likelihood ratio tests (LRT) were used to identify the model best describing the data for each locus, assuming that twice the difference in log likelihood is distributed as the chi-squared (χ2) distribution, with degrees of freedom equal to the difference in the number of parameters between models. If log-likelihood values between models were not significantly different, that with the fewest parameters (most parsimonious) was retained. Model choice was made at the 5% significance level.
Coincidence and concordance of cline estimates
To evaluate coincidence of cline center positions (c) among loci and concordance among cline widths (w), we used the likelihood profiles for these parameters to compare alternative hypotheses across loci: H1, all loci share some center/width parameter value; H2, each locus has its own independent center/width parameter value. A joint log-likelihood profile for the ML shared parameter was obtained by summing log-likelihood profiles for all loci and ML(H1) is the peak of this joint profile. ML(H2) is the sum of the peak values of the parameter profiles for each locus. Likelihood ratio tests as described earlier were used to compare ML(H1) to ML(H2).
Barton's concordance analysis
We further assessed heterogeneity in patterns of introgression by comparing clines at individual loci against the multilocus expectation (Szymura & Barton 1986; Macholán et al. 2011). If all loci show similar introgression patterns, then when plotting one locus versus the multilocus expectation we expect all points to lie on the diagonal (slope equals 1). We calculated hybrid indices over the set of 17 clinally changing diagnostic loci by summarizing the proportion of O. c. cuniculus alleles belonging to an individual. Barton's concordance analysis estimates two parameters: the first, α, describes a shift of the cline at a specific locus towards either O. c. algirus or O. c. cuniculus genomic background (i.e. directionality of introgression); the second, β, describes the abruptness in allele frequency transition for a given locus relative to the multilocus expectation. The significance of deviations from the average introgression expectation was obtained using likelihood ratio tests. Calculations were carried out in ANALYSE 2.0 beta.
Results
We successfully genotyped 1078 individuals for 22 markers out of the initial set of 28 loci. Three autosomal and two X-linked loci were excluded from subsequent analysis either because the genotyping assay failed (ATP12A, GK5, MGST3, OGT), or the percentage of missing calls was over 50% (ARGHF9). PROC was also excluded because we found a strong excess of heterozygotes in most O. c. algirus populations, which may result from the amplification of polymorphisms distinguishing paralogous sequences. Thus, our genotypic data set consisted of four loci located on the autosomes, 16 on the X-chromosome, one marker on the Y-chromosome, and one on the mitochondrial genome. AMOT and the mitochondrial cytb had the highest levels of missing data (17.0% and 12.6%, respectively), while for the remaining loci, the percentage of missing data was in all cases below 6%.
Patterns of variation
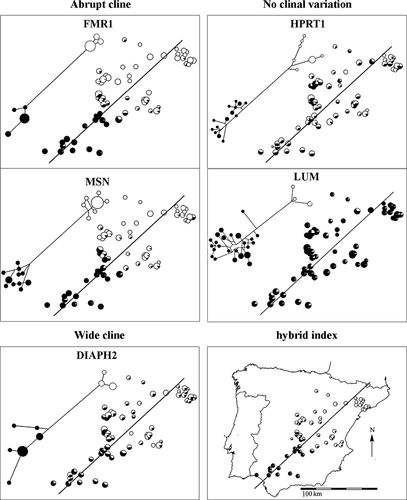
Allele frequencies across the sampling area for five representative loci are shown in Fig. 2. We observed substantial variation among loci in the spatial distribution of allelic frequencies among loci, as expected given the different strategies for choosing SNPs. Clines for FMR1 and MSN from O. c. algirus to O. c. cuniculus are abrupt but introgressed diagnostic alleles appeared at low frequencies in a few localities far from the hybrid zone. In contrast, the cline at DIAPH2 is much wider. For HPRT1 and LUM, there was no obvious pattern of clinal variation, and localities at the extremes of Iberia exhibited no strong differences in allele frequencies. Similar non-clinal patterns were observed for MAOA, PHKA2 and TNMD. The fact that the SNPs used for each of these loci fall on the branch uniting divergent haplogroups suggests that high levels of admixture may have eroded any clinal differentiation, and this is supported by very high estimates of gene flow for each of these loci using an isolation-with-migration model (Geraldes et al. 2006; Carneiro et al. 2010). Thus, these five loci were excluded from subsequent clinal analysis, leaving a remaining total of 17 loci that are listed in Table 2, and which were used in all subsequent analysis.
| Locus | Model | C | w | θ1 | θ2 | β1 | β2 |
|---|---|---|---|---|---|---|---|
| XPO4 | Sig | −20 | 450 | — | — | — | — |
| (−105, 55) | (180, 725) | — | — | — | — | ||
| STAG1 | Sig | −55 | 70 | — | — | — | — |
| (−120, 20) | (a, 665) | — | — | — | — | ||
| EDNRA | Sig | −95 | 175 | — | — | — | — |
| (a, a) | (a, a) | — | — | — | — | ||
| SHOX | Astep | −115 | 65 | 0.011 | 0.020 | 4 | 23 |
| (−150, −70) | (a, 385) | (0.000, 1.000) | (0.000, 1.000) | (0, 56) | (0, 431) | ||
| GLRA2 | Sig | −215 | 545 | — | — | — | — |
| (−390, −40) | (80, 1205) | — | — | — | — | ||
| DGKK | Astep | 15 | 365 | 0.000 | 0.174 | Inf | 31 |
| (−15, 105) | (35, 555) | (0.000, 1.000) | (0.141, 1.000) | (0, ?)a | (0, 32) | ||
| SMCX | Astep | −80 | 15 | 0.000 | 0.002 | 43 | 59 |
| (−90, −55) | (5, 175) | (0.000, 0.320) | (0.000, 0.704) | (0, 59) | (2, 59) | ||
| MSN | Astep | −85 | 10 | 0.002 | 0.002 | 10 | 53 |
| (−90, −55) | (5, 175) | (0.000, 1.000) | (0.002, 1.000) | (0, 363) | (0, 124) | ||
| DIAPH2 | Sig | −60 | 290 | — | — | — | — |
| (−135, 20) | (a, 880) | — | — | — | — | ||
| NRK | Astep | −85 | 10 | 0.000 | 0.001 | 71 | 57 |
| (−115, −75) | (5, 240) | (0.000, 0.433) | (0.001, 0.452) | (0, 71) | (0, 57) | ||
| AMOT | Astep | −85 | 10 | 0.0012 | 0.0015 | 12 | 61 |
| (−115, −60) | (5, 165) | (0.000, 0.105) | (0.002, 0.441) | (2, 67) | (7, 76) | ||
| KLHL13 | Sig | −75 | 390 | — | — | — | — |
| (−140, 0) | (210, 640) | — | — | — | — | ||
| F9 | Astep | −95 | 15 | 0.004 | 0.005 | 13 | 8 |
| (−150, −85) | (a, 215) | (0.000, 1.000) | (0.000, 0.293) | (0, 35) | (0, 83) | ||
| FMR1 | Astep | −90 | 20 | 0.008 | 0.005 | 9 | 64 |
| (−140, −80) | (a, 135) | (0.000, 1.000) | (0.000, 0.241) | (0, 763) | (0, 9973) | ||
| G6PD | Astep | −125 | 15 | 0.003 | 0.003 | 12 | 25 |
| (−130, −85) | (a, 180) | (0.000, 0.581) | (0.000, 0.237) | (1, 87) | (2, 224) | ||
| SRY | Astep | −85 | 25 | 1.000 | 0.008 | Inf | Inf |
| (−50, −90) | (10, 85) | (1.000, 1.000) | (0.000, 0,109) | (?, ?)a | (?,?)a | ||
| cytb | Astep | −85 | 60 | 0.000 | 0.000 | 118 | 90 |
| (−125, −75) | (a, 210) | (0.000, 0.240) | (0.000, 0.797) | (1, 123) | (0, 147) |
- Distance units are in kilometers.
- Sig, sigmoid model; Astep, asymmetric stepped model.
- a Two-unit support limits were not obtained within the interval of values surveyed.
Using the clinal nature of these 17 loci, we calculated hybrid indices for individual rabbits by averaging the overall proportion of alleles across loci derived from O. c. cuniculus. Numerous localities close to the central part of the hybrid zone showed intermediate hybrid indices, while those at the extremes are close to fixation (Fig. 2). This result highlights that our sampling was adequate relative to the width of the hybrid zone and indicates that the rabbit hybrid zone has many late generation hybrids. We did not find any pure O. c. algirus individuals in clear O. c. cuniculus territory (or vice versa) suggesting that long-distance migration or transport of pure subspecific individuals is not frequent. However, some localities at both extremities of the transect showed high frequencies of introgressed alleles at a subset of loci, especially on the O. c. cuniculus side (data not shown). These localities appear as clear outliers in our cline analyses and are likely explained by the practice of rabbit restocking in regions of low rabbit density for hunting purposes (Moreno et al. 2004). To avoid biasing our estimates, we removed these localities from subsequent analyses (Fig. 1).
Orientation of the zone
The best fit orientation of a linear zone center onto our two-dimensional sampling across Iberia was at a compass bearing of 43.1° estimated from the consensus orientation profile (Fig. 1). A visual inspection of the likelihood profiles suggested a similar orientation for all loci (Fig. S1, Supporting information). Maximum-likelihood estimates (MLE) for most loci varied between 43° and 60°, with the exception of EDNRA (13°), but even for this locus support intervals were wide and overlapped considerably with the other individual profiles and the consensus profile. A more formal test is to compare hypotheses, as previously described (see 2), using the locus specific profiles. We found no support for different orientations (LRTsame − diff. = 7.17, 16 df, P ≫ 0.05) versus a single orientation of change for all loci. Consensus profiles among genomic compartments also provided no evidence for differential orientations (P > 0.05 for all tests).
Geographic and non-geographic analyses of introgression
The orthogonal projection of localities onto the most likely orientation of change across the zone was used to analyse the shape of clines under three different models that describe patterns of allele frequency change along a transect (Table 2, Figs 3 and S2, Supporting information). The stepped asymmetric model resulted in a significantly superior fit for 11 loci; however six loci were most parsimoniously described by simpler sigmoid models. Maximum-likelihood estimates of cline center (c) were highly variable among loci, but often with overlapping support limits (Table 2 and Fig. S3, Supporting information). Although most clines had MLE estimates of c lying between −125 km and −55 km, three loci showed strongly shifted positions. GLRA2 showed a clear shift into algirus territory (c = −215 km), while DGKK (c = 15 km) and XPO4 (c = −20 km) showed shifts in the opposite direction. These non-coincident loci were also high-cline-width outliers. The ML of the consensus likelihood profile for cline centers across all loci was at −85 km (85 km southwest of the centroid of the sampling localities), and 15 loci out of 17 could be constrained to share this center without a significant drop in likelihood (LRTsame − diff. = 21.58, 14 df, P > 0.05; outliers: GLRA2 and XP04). We can thus conclude that the majority of loci showed no significant deviations from a common center. On the other hand, constraining all loci to share a common width causes a significant drop in likelihood (LRTsame − diff. = 38.53, 16 df, P < 0.01).
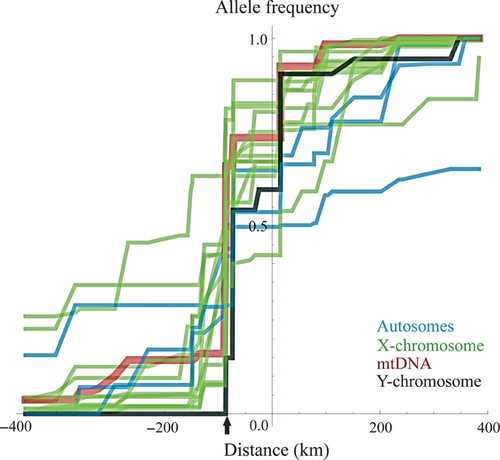
Next, we compared c and w estimates among the four genomic compartments. We formally compared likelihood profiles from a given compartment to the joint estimates obtained for another, asking whether a common c and w resulted in a significantly worse fit of the data to the model using LRTs. Joint estimates differ from the averages of point estimates in that they take into account the appropriate relative weights of evidence. We found that pairwise comparisons of c estimates of combined samples of autosomal and X-linked loci as well as the mitochondria and the Y-chromosome single markers are consistent with coincident clines centered at the same position for all compartments (LRTsame − diff. = 0–2.41, 1 df, P > 0.10 for all pairwise tests). For cline width, the consensus autosomal w was 430 km, which was significantly greater than that for X-linked loci (70 km), the mtDNA (60 km) and the Y-chromosome (25 km; LRTsame − diff. = 7.05–9.62, 1 df, P < 0.01 for all tests). All remaining pairwise comparisons were non-significant (LRTsame − diff. = 0.071–3.20, 1 df, P > 0.05 for all tests).
We were also interested in testing whether our cline estimates suggest overall asymmetrical introgression between O. c. algirus and O. c. cuniculus. The four tail parameters (θ1, θ2, β1 and β2) from the asymmetric stepped model retained for 11 loci suggest strong asymmetry in introgression at some loci, but not in a consistent direction (Table 2). As mentioned earlier, the model retained for GLRA2 and DGKK also resulted in strong shifts of center, but towards O. c. algirus and O. c. cuniculus territory respectively. We also evaluated the relationship between cline width and center as a positive correlation would tend to indicate that introgression is higher from O. c. algirus to O. c. cuniculus, while a negative correlation would indicate the opposite (Payseur et al. 2004). We found no significant correlation between the two variables (Spearman's r = 0.25; P = 0.33). In summary, the asymmetries in clines, while strong, are unlikely due to a systematic asymmetry in the rabbit hybrid zone.
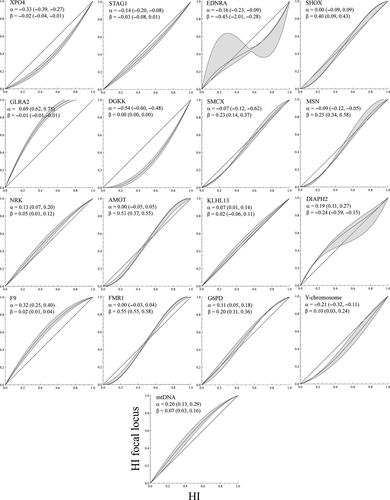
Geographic sampling heterogeneity can influence cline analyses. An alternative to geographic cline analyses is to replace the geographic distance axis with a hybrid index measure. Barton's non-geographic concordance ML estimates for directionality (α) and abruptness (β; see 2 for details) of introgression for each locus are provided along with support bounds in Fig. 4. With the exception of KLHL13, we found significant statistical evidence for non-concordant introgression patterns among loci when compared to the equal-introgression expectation (Table S3, Supporting Information). This highlights the complex pattern of admixture in the rabbit hybrid zone. A closer look at the two components of the model (α and β), and comparison with their geographic cline equivalents (c and w), sheds some light into the nature of these deviations. Regarding the abruptness parameter β, we found highly significant positive and negative deviations from the multilocus expectation, and these were roughly similar in pattern to the results obtained for widths in the geographic cline analysis. As in the geographic cline analysis, we inferred striking asymmetries across loci but no clear overall trend. Several loci showed positive values of α consistent with a shift into O. c. algirus genetic background (GLRA2, F9, mtDNA), while others showed negative values consistent with a shift into O. c. cuniculus (DGKK, XPO4, Y-chromosome).
Comparison of cline width and inferences of gene flow from allopatric populations
Next, we sought to compare estimates of cline width (w) with DNA sequence variation data. Because most previous studies based on allopatric localities were sampled in a slightly different manner, we focused on two studies with a similar sampling strategy based on localities situated at the extremes of the distribution of both subspecies (Carneiro et al. 2009, 2010). Our comparisons were therefore restricted to 11 data points. We found a weak negative correlation between the net nucleotide divergence (Da, Nei 1987) and w, although not significant (Spearman's r = −0.46; P > 0.05; Fig. S4, Supporting information). We were also interested in comparing locus-specific estimates of gene flow (2Nm) and w. Carneiro et al. (2009, 2010) obtained locus-specific estimates of 2Nm with DNA sequence data from allopatric samples using an IM model (Hey & Nielsen 2004). However, as a large proportion of the loci used here showed fixed differences between subspecies in the allopatric samples, most 2Nm values were estimated to be zero (Fig. S4, Supporting information). Nevertheless, it is clear from this Figure that some loci showing 2Nm estimates of zero showed large w estimates in this study. While we found general agreement between patterns of gene flow inferred from sequence variation in allopatric samples and clinal analyses with respect to reduced introgression of the X-chromosome and lack of an overall asymmetrical pattern of gene flow between rabbit subspecies, the clinal geographic analyses, as expected, provide a level of detailed comparative information inaccessible from analysis simply based on paired allopatric samples.
Estimates of dispersal and strength of selection
Using estimates of cline shape parameters and LD, we calculated biologically relevant quantities that help describe the process of contact between the rabbit subspecies, such as the scale of dispersal and selection against hybrids. The scale of dispersal (σ) was estimated from the relationship 
where r is the harmonic mean recombination rate among loci, w is the width of the zone, and R is the standardized LD value in the center of the zone (Szymura & Barton 1986). Recombination rate (r) was assumed to be 0.5 for unlinked markers, and for markers on the X-chromosome, we assumed 1 cM/1 Mb, giving an harmonic mean of 0.33. Estimation of the zone width parameter w was restricted to loci displaying stepped and concordant clines because sigmoid and non-coincident loci are likely to have escaped the central barrier, and thus are not informative about its current intensity. Cline width estimates over these loci (8 X-linked, 1 Y-linked, and 1 mitochondrial gene) cluster around 15 km, with two wider (≈60 km) outliers (SHOX, cytb). To take into account uncertainty associated with these outliers, we average both with and without them, giving us a width estimate in the range of 15–24.5 km. We estimated R for five locality samples (total 167 individuals) within 20 km of the estimated zone center (−85 km), and obtained an estimated value of 0.07 based on the maxi-mum-likelihood procedure implemented in the Analyse package and 0.10 based on the variance of the hybrid index (95% confidence interval 0.08, 0.12 using a F-distribution). Conservatively including all the sources of uncertainty described earlier, we estimated Σto lie in the range 1.95–4.22 km/generation. These values are consistent with individual movements of up to 2 km for animals released in rabbit-populated habitats in the Iberian Peninsula (Calvete & Estrada 2000). Using tension zone theory, and assuming that the rabbit hybrid zone is at migration-selection equilibrium, selection acting against hybrids can be calculated from the relationship s* = 8σ2/w2 (Bazykin 1969; Szymura & Barton 1986). Given σ = 1.95–4.22 km/generation, width w = 15–24.5 km, and the midpoint of these ranges as our point estimate, we estimated s* to be 20% (5–64%). Finally, we detected no significant heterozygote deficit across the contact zone (Fig. S5, Supporting information).
Discussion
The nature and dynamics of contact in the rabbit hybrid zone
We examined patterns of allele frequency change in a large number of individuals and provided the first detailed characterization of clinal change across the European rabbit hybrid zone. A model of stepped clines provided a good fit for 11 of the 17 loci. As expected, the majority of these 11 loci (8) were found to be diagnostic between subspecies in individuals sampled away from the center of the hybrid zone (see 2). The fact that we inferred stepped and largely coincident clines for several loci suggests that many independent genomic regions experience an overall barrier to gene flow in the middle of the hybrid zone. On the other hand, cline widths at some loci were exceptionally large and others showed center discordance, suggesting that for these, selection has not substantially restricted introgression. We note that some of the diagnostic markers (DGKK and KLHL13) also showed large cline widths (365 and 390 km) and center discordance (e.g. DGKK). Our results are therefore consistent with a central barrier to gene flow from which a large proportion of each genome has escaped and moved substantially into the other subspecies' territory, likely due to an old history of hybridization and/or high effective gene flow.
Cline shape alone does not allow alternative mechanisms maintaining steep clines to be distinguished (Kruuk et al. 1999). One potential cause of steep narrow coincident clines is a physical barrier to dispersal (Barton & Gale 1993); however, the center of the rabbit hybrid zone does not correspond to any obvious physical barrier such as mountain ridges or large rivers (Fig. S6, Supporting information). Further, the diagonal path (NW–SE) of the contact zone and the distribution ranges of both subspecies cut across the major climatic zones in the Iberian Peninsula (Mediterranean, Oceanic, and semi-arid) rather than aligning with any of them, and the broad ecological envelope of rabbits can be seen in their successful colonization across the world through man-mediated dispersal. In fact, the contact area is roughly equidistant from the putative refugial areas of the two subspecies during Quaternary glaciations (Branco et al. 2002), suggesting that, on the broad scale, the secondary contact location results from similar post-glacial range expansion rates. Another cause for steep narrow coincident clines is a recent contact; however, this explanation does not account for the variation we inferred in cline width among loci and the expected age of the zone. Taken together, our results suggest that the rabbit hybrid zone is a tension zone, as observed for numerous hybrid zones (Barton & Hewitt 1985), and likely to be primarily maintained by a balance between dispersal into the zone and endogenous selection against hybrid rabbits. We should not disregard, however, the possibility that isolating mechanisms resulting from exogenous factors may also be contributing to the subspecific barrier.
A pattern commonly characterizing secondary contact between taxa is that effective gene flow often occurs at different rates in each direction (Arnold 1997). Our results for rabbits provide no evidence for such an overall pattern, but rather, evidence for asymmetric introgression with heterogeneous directions across loci. Although higher gene flow was inferred from O. c. cuniculus to O. c. algirus using an IM model Carneiro et al. (2009, 2010), the difference was not statistically significant and could also reflect sampling differences between this and previous studies, which have only included sites far away from the hybrid zone. Thus, the asymmetric patterns of introgression in rabbits seems to be driven mainly by locus-specific effects and not by a general trend of biased introgression.
Loci characterized by high introgression can also be informative about the dynamics of the contact. Theory predicts that clines at neutral loci should gradually widen (Barton & Gale 1993), while loci where one taxon has advantageous alleles should quickly escape the tension zone and set up a travelling wave (Barton 1979; Piálek & Barton 1997). For the case of neutral mixing, the expected cline width t generations after two populations met in an abrupt step is w = 2.51σt 0.5, where σ is the scale of dispersal (Endler 1977; Barton & Gale 1993). Of the loci not closely associated with the tension zone center, four are wide and sigmoid (EDNRA, DIAPH2, KLH13, and STAG1) and centered around the 11 stepped loci, consistent with neutral expectations. If we assume there has been no barrier to gene flow at these four loci with wide clines and use our estimate of dispersal of 1.95–4.22 km/generation, it would take 1350–6350 generations for neutral diffusion to produce the widest of these clines (wKLHL13 = 390 km). Five other loci, which still maintain a haplotypic structure suggestive of ancient vicariance (HPRT1, LUM, MAOA, PHKA2, and TNDMD), show so little geographic association with either taxon that we cannot decide in which subspecies the alternate alleles originated (Fig. 2). The fact that we cannot detect clinal signal at these loci suggests their current pattern cannot be explained by neutral spread from refugia post last glacial maximum (18 000 ya). The argument is as follows: suppose that our sampling is only sufficient to detect allele frequency differences of greater than 10% between the extremes of the sampling area. Clines so wide that frequency differences cannot be detected between the extremes of the Iberian Peninsula must then have widths in excess of 8400 km. If we assume there has been no barrier to gene flow, then we can ask how many generations of neutral diffusion would be necessary to explain such width. For our estimate of dispersal (1.95–4.22 km/generation) and assuming a rate of dispersal constant through time, 0.6–3 million rabbit generations would be necessary to create neutral clines this wide—that is, at least two orders of magnitude more generations than years available since the onset of most recent contact after the last glacial maximum. Thus, the absence of detectable clinal variation at these markers may reflect a more ancient period of hybridization promoted by the glacial–interglacial oscillations of the Quaternary (Hewitt 1989), a suggestion which could be further explored from the perspective of asymmetry in gene trees (Slatkin & Pollack 2008).
Contrasting patterns of introgression among loci
Several studies report higher dispersal of male rabbits compared to females (Webb et al. 1995; Kunkele & Holst 1996; Richardson et al. 2002), as observed for numerous mammalian species (Lawson Handley & Perrin 2007). Therefore, gene flow between rabbit taxa should be preferentially driven by male dispersal. However, we found that the Y cline is narrower than that of the maternally transmitted mtDNA. We also found both abrupt and wide clines on the X, suggesting that differential patrilineal versus matrilineal dispersal scales are unlikely to be an important cause of the patterns we observe. The magnitude of genetic drift also differs between genomic compartments due to their differing ploidy, and stronger drift is expected to result in somewhat narrower width estimates (Polechova & Barton 2011). In the rabbit case, both uniparental markers (relative effective size when compared to autosomes of 1/4) have larger cline width estimates than many X-linked loci (relative effective size 3/4), suggesting that the patterns we observe are best explained by selection against hybrid genotypes acting differentially among loci.
The steep clines inferred for some loci on the X-chromosome are in agreement with previous inference based on an isolation-with-migration model that indicated lower levels of gene flow for X-linked loci when compared to autosomal loci (Carneiro et al. 2010). It should be noted that the sample of autosomal loci in this study is small when compared to the X-chromosome but it includes two of the three autosomal regions (near the centromeres of chromosomes 8 and 14) that showed the highest levels of differentiation and lowest estimates of gene flow in previous studies, where close to 40 autosomal markers were sampled (Geraldes et al. 2008; Carneiro et al. 2010). Thus, even when choosing autosomal loci most likely to show narrow clines, we find narrower X-linked loci. The narrow Y-chromosome cline is also consistent with high levels of Y differentiation found in a smaller data set (Geraldes et al. 2008). Notably, not a single Y from O. c. cuniculus was found in O. c. algirus territory, in contrast to other loci (Fig. 3). Our observations in rabbits are thus consistent with the notion that sex chromosomes play an important role in the maintenance of reproductive barriers between closely related species (Coyne & Orr 2004). However, a larger number of autosomal loci are needed to draw more definitive comparative conclusions.
In addition to variation in cline width, we detected strong asymmetries in the directionality of introgression among loci. Stochastic effects may underlie some of the observed variation but our dense 2D sampling and prior estimation of the direction of change across the hybrid zone should control at least for the stochasticity which arises from non-oriented sparse 1D sampling (Dufková et al. 2011; Macholán et al. 2011; Baird & Macholán 2012). At least two selective scenarios can also account for this locus-specific asymmetry. First, deterministic introgression could occur when alleles from one taxon have an advantage over alternative alleles from the other, and this selective regime has been commonly suggested to occur in hybrid zones (Arnold 1997; Rieseberg et al. 2003; Payseur et al. 2004). However, this seems unlikely for the loci showing strong asymmetrical introgression patterns in our study. For example, GLRA2 (c = −215 km) had a center displacement of 130 km. Assuming a model of weak selection (s = 0.025; Piálek & Barton 1997), dispersal of 1.95–4.22 km/generation, and a barrier strength (β) of 40 km (Table 2), the delay caused by the central barrier is expected to be tens of generations, and the time taken for the travelling wave to cover 130 km is in the low hundreds of generations. Given the likely much older contact between rabbit subspecies, loci under adaptive introgression would have travelled a much larger distance than 130 km. Second, the observed asymmetry could reflect Dobzhansky–Muller interactions (Dobzhansky 1936; Muller 1942) with asymmetric effects. Gavrilets (1997) simulated the behaviour of Dobzhansky–Muller interactions across a hybrid zone and concluded that asymmetric clines are likely to be formed. Several loci in our data set were characterized by such a pattern (see Figs 3 and 4) but two loci fit this model particularly well and are unlikely to result simply from stochastic variation (DGKK and GLRA2). Both show high levels of introgression in one direction but reduced introgression in the other direction.
Rabbit versus mouse hybrid zones
Greater insight into the genetics of speciation can be gained by comparing different model systems. Given that the choice of loci in our study was highly biased towards the X-chromosome, our results can be compared to results on the mouse hybrid zone (e.g. Macholán et al. 2011), which is one of the few systems for which comparable data exist (Nachman & Payseur 2012). The European house mouse hybrid zone is a contact between two synanthropic subspecies that meet along a front stretching between Scandanavia and the Black sea.
Among the key commonalities between the two systems are patterns of allele frequency change consistent with a tension zone (Payseur et al. 2004; Raufaste et al. 2005; Macholán et al. 2007) and the reduced introgression of sex chromosomes (e.g. Tucker et al. 1992; Macholán et al. 2007). A key difference relates to the patterns of asymmetrical introgression. In mice, asymmetric patterns of introgression throughout the genome and across independent transects often show higher introgression of M. m. domesticus alleles into the M. m. musculus background (Payseur et al. 2004; Raufaste et al. 2005; Macholán et al. 2007; but see Wang et al. 2011), suggesting that demographic processes play a substantial role, while in rabbits no such trend is observed. Perhaps the most striking difference between the two systems, however, is the level of introgression. In a previous related study, we noted that estimates of gene flow using an isolation-with-migration model were much higher in rabbits than in mice (Carneiro et al. 2010). Our cline analysis provides a similar picture indicating that the rabbit hybrid zone has been more permeated by gene flow than the mouse hybrid zone. On the X-chromosome, cline width estimates varied by a factor of 50 (10–545 km) while in mice estimates vary by a factor of 20 (0.37–7.53 km; Payseur et al. 2004) or 10 (1.40–13.62 km; Macholán et al. 2007), depending on the sampling design. These ratios across loci control for the difference in organism-specific scale of dispersal, allowing us to compare the underlying process. The higher apparent permeability in rabbits is particularly intriguing given that rabbit subspecies are thought to be older than the subspecies of house mice (1.8 vs. 0.5 Mya, respectively).
Several non-mutually explanations can account for this difference. First, we consider to what extent differences in ascertainment bias across studies could contribute to the apparent contrast between rabbits and mice. Studies of the house mouse hybrid zone have strictly focused on markers showing fixed differences between subspecies in individuals sampled away from the hybrid zone, whereas in this study, we considered loci with variable degrees of population differentiation between subspecies. If done blindly, this could potentially lead to the perception of higher permeability in rabbits than in mice. However, even when we focused on the subset of rabbit loci chosen in the same manner as mouse loci, cline width estimates in rabbits varied by a factor of ~40 (10–390 km). Thus, marker choice is unlikely to explain the observed discrepancy. The wider choice criteria for the remainder of the rabbit loci have the advantage of allowing us to measure extreme outliers for cline width and displacement (so extreme that, for example, no locality in Iberia can be expected to be fixed). Second, prezygotic isolating mechanisms may be stronger in mice than in rabbits. Both laboratory-based and semi-natural choice studies suggest no detectable mate preference between rabbit subspecies (Villafuerte et al. unpublished data), while mice subspecies show weak assortative preference in Y-maze studies (Bímová et al. 2005, 2011). However, such a weak effect is also unlikely to account for the magnitude of the differences we observe. Third, selection against hybrid phenotypes in mice may be stronger than in rabbits. In house mice, the great majority of hybrid males sampled in the contact zone display fertility defects (Albrechtová et al. 2012; Turner et al. 2012). Preliminary results in rabbits indicate a reduction of male fertility in early generation hybrids produced in the laboratory (Ferrand et al. unpublished data), although we have no information about hybrid fertility phenotypes in the contact zone, which is primarily populated by later generation crosses (see 3), nor do we have data about other hybrid phenotypes potentially contributing to reproductive barriers, leaving us with little information regarding relevant relative fitness of mouse versus rabbit hybrids. Finally, and perhaps most importantly, the rabbit hybrid zone is likely much older than the mouse hybrid zone. The fact that rabbits have a long historical presence on the Iberian Peninsula coupled with Iberia being one of the most important refugia during glaciations (see 1), suggests that the rabbit subspecies may have been in cyclical contact over previous climatic oscillations. In contrast, the house mouse hybrid zone is thought to be 6000 years old at its southern part (Sage et al. 1993) and perhaps as little as 250 years old at its northern part (Hunt & Selander 1973) associated with agriculture and the later amelioration of climatic conditions in northern Europe.
The patterns we have observed can be interpreted in the light of coupling theory (see introduction). Older and multiple contacts allow more generations of recombination between subspecies' genetic backgrounds, releasing regions of the genome from closely linked alleles involved in hybrid incompatibilities (Baird 1995) and/or unfavourable environment occurring in the center of the hybrid zone (Bierne et al. 2011). While the distinction between low and high coupling equilibrium outcomes is expected to develop slowly (Baird 1995), a long history of recombination will allow across-genome heterogeneity in the coupling coefficient (due to variation in the map density of selected loci) to be resolved into clearly distinguished areas of low and high barriers to gene flow. Thus, the highly permeated rabbit pattern is likely to be characteristic of taxa with a long history of hybridization (Phillips et al. 2004; Sequeira et al. 2005; Kane et al. 2009; but see Fijarczyk et al. 2011 and references therein) that also show comparatively few loci under selection spread unevenly across the genome, such that associations leading to large genomic regions of reduced effective gene flow cannot be maintained (Barton 1983, Baird 1995).
Acknowledgements
This work was partially supported by POPH-QREN funds from the European Social Fund and Portuguese MCTES [Ph.D. and postDoc grants to MC (SFRH/BD/23786/2005; SFRH/BPD/72343/2010)], by FEDER funds through the COMPETE program and Portuguese national funds through the FCT—Fundação para a Ciência e a Tecnologia—(PTDC/BIA-BDE/72304/2006; PTDC/BIA-EVF/111368/2009; PTDC/CVT/122943/2010; CGL2009-11665; POII09-0099-2557), and by National Science Foundation and National Institutes of Health grants to MWN. SJEB's contributions, and development of the inference tools used, were partially funded by a Fundação para a Ciência e a Tecnologia grant to SJEB (PTDC/BIA-BEC/103440/2008). We thank R. Pereira for valuable discussions and Chris Jiggins for valuable comments on an earlier version of the manuscript.
References
This work was part of M.C. PhD research under the supervision of M.W.N. and N.F., M.C., S.J.E.B., M.W.N. and N.F. designed the research; N.F. obtained funding; M.C., S.A. and H.T. collected the SNP data; M.C., S.J.E.B. and P.T. analysed the data; R.V. and E.R. collected the samples; M.C. and S.J.E.B. wrote the paper with comments from all authors. All authors read and approved the final manuscript.
Data accessibility
DNA sequences: GenBank accessions: HM138911–HM138914.
Sample locations: uploaded as online supporting information.
Genotype data: available in the Dryad database (doi: 10.5061/dryad.mj18p).
