Spatial scale affects landscape genetic analysis of a wetland grasshopper
Abstract
Most landscape genetic studies assess the impact of landscape elements on species' dispersal and gene flow. Many of these studies perform their analysis on all possible population pairs in a study area and do not explicitly consider the effects of spatial scale and population network topology on their results. Here, we examined the effects of spatial scale and population network topology on the outcome of a landscape genetic analysis. Additionally, we tested whether the relevant spatial scale of landscape genetic analysis could be defined by population network topology or by isolation-by-distance (IBD) patterns. A data set of the wetland grasshopper Stethophyma grossum, collected in a fragmented agricultural landscape, was used to analyse population network topology, IBD patterns and dispersal habitats, using least-cost transect analysis. Landscape genetic analyses neglecting spatial scale and population network topology resulted in models with low fits, with which a most likely dispersal habitat could not be identified. In contrast, analyses considering spatial scale and population network topology resulted in high model fits by restricting landscape genetic analysis to smaller scales (0–3 km) and neighbouring populations, as represented by a Gabriel graph. These models also successfully identified a likely dispersal habitat of S. grossum. The above results suggest that spatial scale and potentially population network topology should be more explicitly considered in future landscape genetic analyses.
Introduction
Habitat connectivity is an important issue in ecology and conservation (e.g. Crooks & Sanjayan 2006; Kindlmann & Burel 2008). Although connectivity is usually assessed by examining the spatial configuration of habitat patches (i.e. structural connectivity; Tischendorf & Fahrig 2000a,b), it has been recommended to focus on the ability of a species to disperse between habitat patches, which ensures functional connectivity (Goodwin 2003). To assess dispersal ability, information about species-specific behavioural responses to landscape elements is needed. For this purpose, the discipline of landscape genetics aims at assessing landscape effects on dispersal and gene flow (Segelbacher et al. 2010; Storfer et al. 2010).
Many of the currently available landscape genetic methods analyse landscape effects on gene flow between pairs of populations (Storfer et al. 2010). Least-cost path analysis (Adriaensen et al. 2003), for instance, uses lengths or costs of potential movement paths through assumed dispersal habitats to explain gene flow between population pairs. Most landscape genetic studies include all population pairs in a data set when assessing the effects of landscape elements on gene flow (e.g. Emaresi et al. 2011). However, from all population pairs, a subset could be selected, for instance, by a predetermined minimum or maximum distance between populations, representing a particular spatial scale. Subsets of population pairs could also be selected based on the presence or absence of intervening populations, as these are expected to have an influence on the amount of pairwise gene flow (McRae 2006). However, most studies do neither take spatial scale effects into account nor explicitly consider aspects of spatial population arrangement.
The effects of spatial scale on landscape genetic analyses have been considered in only a few landscape genetic studies (e.g. Wilmer et al. 2008; Mullen et al. 2010; Angelone et al. 2011; Galpern et al. 2012; Keller & Holderegger in press), although its evaluation has been recommended by several authors (Anderson et al. 2010; Cushman & Landguth 2010; Rasic & Keyghobadi 2012). Studies that conducted scale-specific analyses usually detected different results for different scales (e.g. Angelone et al. 2011). It is more probable that population pairs are within the maximum dispersal distance of a study species at smaller spatial scales, and dispersal between population pairs at larger spatial scales may be negligible due to physical limitations, regardless of any facilitating or inhibiting landscape effect on dispersing individuals. It has thus been suggested to restrict landscape genetic analyses to the spatial scale at which direct gene flow is likely to occur (Murphy et al. 2010; Angelone et al. 2011). For gene flow between population pairs located beyond a study species' maximum dispersal distance, various indirect dispersal routes via other populations might better represent the landscape encountered by dispersing individuals than direct dispersal routes between these populations (Van Strien unpublished data).
Indirect dispersal routes, determined by spatial population arrangement, can be assessed with population networks or graphs. While the introduction of network analysis to landscape ecology and conservation biology fostered various new approaches (Urban & Keitt 2001; Saura & Torne 2009; Urban et al. 2009), the use of network-based approaches has only started in landscape genetics (e.g. Garroway et al. 2008; Dyer et al. 2010; Murphy et al. 2010; Galpern et al. 2012). In such networks, habitats (e.g. Galpern et al. 2012) or populations (e.g. Brooks 2006) can be represented as nodes, which are connected by dispersal routes represented as edges (Galpern et al. 2011). In many ecological networks, edges are represented by simple geographic distance, and nodes are only connected if they lay within a specified threshold distance from each other. This threshold distance may be set at the maximum dispersal distance of a species, which is often difficult to determine (Moilanen 2011). However, isolation-by-distance (IBD) patterns could indicate a threshold for maximum dispersal distance. IBD, which is based on a stepping-stone model (Kimura & Weiss 1964), assumes more frequent dispersal among geographically close populations (Slatkin 1987). Under the stepping-stone model, a monotonically increasing relationship between genetic differentiation (FST) and Euclidian distance is expected (i.e. ‘case I’ scenario in Hutchison & Templeton 1999), if gene flow and drift are in equilibrium. Often, such a relationship is only found up to a certain distance between populations (i.e. ‘case IV’ scenario in Hutchison & Templeton 1999). This latter IBD pattern is observed when the relative importance of gene flow and drift varies across spatial scales under the ‘case IV’ scenario: gene flow being more important at smaller and drift at larger spatial scales. Although Keyghobadi et al. (2005) and Van Strien (unpublished data) showed that the distance at which a monotonically increasing relationship in IBD no longer exists is not always a reliable indicator of maximum dispersal distance, other studies found it to be a rather accurate estimate (e.g. Hanfling & Weetman 2006). However, landscape structure greatly affects IBD patterns, which reflect the balance between gene flow and drift.
Because gene flow can take place over several generations with several dispersal events, gene flow between two populations that are within a species' maximum dispersal distance may also be influenced by surrounding populations. High rates of gene flow between two populations could thus be caused by the existence of intermediate populations. To rule out this effect, only neighbouring populations without any intermediate populations can be considered. Indeed, a simulation study showed that landscape effects on gene flow are best detected when including only neighbouring populations in a regular lattice population network (Jaquiery et al. 2011). In landscape genetic analysis, population network topology can be used to restrict analyses to only neighbouring populations using Delaunay triangulation (Goldberg & Waits 2010) or Gabriel graphs (Gabriel & Sokal 1969; Arnaud 2003). In Gabriel graphs, circles are drawn in a way that two populations are on the edge of a circle, and the diameter of the circle equals the distance between the populations. An edge between two populations is only formed if no other population is present within this circle.
In the present study, we investigated the effects of population network topology and spatial scale (in terms of geographical distance thresholds) on the outcome of landscape genetic analyses. While spatial scale considers the geographic distances between population pairs, population network topology includes the spatial arrangement of populations. We expected that the consideration of scale positively influences the fit of landscape genetic models and that considering topology might even further increase this fit. In particular, we hypothesize that landscape effects on gene flow are more pronounced when landscape genetic analyses are restricted (i) to population pairs within a species' maximum dispersal distance and (ii) to neighbouring populations as defined by Gabriel graph-based population network topology. We further suggest that (iii) the relevant threshold of spatial scale for landscape genetic analysis can be identified by IBD patterns and population network topology. These hypotheses were tested in the following way. First, we visualized genetic patterns and connectivity across the study area by genetic clustering analysis and network operations (i.e. edge-thinning; Urban & Keitt 2001). Second, we assessed the most likely dispersal habitat of the study species without considering scale or population network topology. Third, we repeated this latter analysis by considering spatial scale; and fourth, we again repeated the analysis by considering both scale and population network topology. As a study data set, we use microsatellite genetic data of the large marsh grasshopper Stethophyma grossum in a fragmented agricultural landscape in Switzerland, where all present populations of this wetland grasshopper have been sampled.
Material and methods
Study species
Stethophyma grossum (Linnaeus, 1758; Acrididae) is distributed throughout Europe and Siberia. It is believed to be restricted to wetlands (Baur et al. 2006), as the development of eggs and larvae depends on high moisture of the top soil (Marzelli 1995; Koschuh 2004). Stethophyma grossum is thus found in fens, swamps, along lakes, streams and ditches, in moist meadows or extensively managed grasslands on valley bottoms (Koschuh 2004; Baur et al. 2006). In Switzerland, the species is red-listed as vulnerable, because its habitats are fragmented (Monnerat et al. 2007). However, in Southern Germany, the number of populations of S. grossum is increasing, and new colonizations have recently been recorded (Trautner & Hermann 2008). A similar trend is assumed to take place in Switzerland. While the habitat characteristics of S. grossum are well documented, knowledge on its dispersal habitat and potential is scarce. Compared with other grasshoppers, S. grossum is a good flier with observed flight distances of up to 41 m (Soerens 1996). Nevertheless, mark–recapture studies found only low dispersal with maximum distances of about 600 m (Marzelli 1995; Malkus et al. 1996; Bönsel & Sonneck 2011). However, Griffioen (1996) detected marsh grasshoppers 1500 m away from the nearest population. Similarly, larvae also show rather low mobility (Krause 1996). Concerning the species' dispersal habitat, Marzelli (1994) observed S. grossum crossing unsuitable dry grassland, but a 50 m wide highway acted as a barrier to dispersal. Furthermore, a 3 m wide stream was crossed by S. grossum (Malkus et al. 1996), but suitable habitat patches surrounded by trees were not readily colonized (Reinhardt et al. 2005), especially if trees were higher than 3 m (Soerens 1996).
Genetic sampling
Mapping and genetic sampling were carried out in July and August 2010 in the Oberaargau region of the Swiss lowlands. The study area was characterized by three valleys oriented from south to north. In an area of about 180 km2, all populations of S. grossum (at least 350 m apart from each other) were sampled (Fig. 1). As S. grossum is restricted to wetlands (Baur et al. 2006), we focused our search on areas along ponds, streams and rivers, and in swamps and valley bottoms. The distinct clicking sound of stridulating males facilitated the localization of S. grossum. At each sampling location, we recorded the coordinates of the centre point and sampled up to 30 individuals (males and females) within a radius of 20 m. Only individuals with all legs intact were sampled to avoid re-sampling of individuals. Tibia and tarsus of a mid-leg of each individual were removed and stored in 100% ethanol in the dark until DNA extraction. Additionally, we collected two populations in a neighbouring valley, 4 km away from the closest population in our study area. These two populations were only used for IBD analysis, but not considered for any further population network topology, genetic clustering or landscape genetic analysis, as their surrounding was not completely sampled. In total, we collected 936 individuals from 39 locations.

Genetic analysis
DNA extraction and genotyping were performed following the procedures described in Keller et al. (2012). Eight polymorphic microsatellite markers were used for PCR amplifications (Sgr10, Sgr13, Sgr14, Sgr15, Sgr19, Sgr38, Sgr40 and Sgr45; Keller et al. 2012). Fragments were analysed on an ABI 3730xl sequencer (Applied Biosystems) and scored with genemapper 3.7 (Applied Biosystems). To calculate genotyping error rates, we repeated PCR amplifications of about 6% of all samples. Tests for departures from Hardy–Weinberg equilibrium were calculated with genepop 4.0.10 (Raymond & Rousset 1995) using Fisher's exact test. As null alleles are often found in orthopteran species (e.g. Ustinova et al. 2006; Chapuis et al. 2008; Blanchet et al. 2010), we estimated null allele frequencies with freena (Chapuis & Estoup 2007) for all loci choosing the algorithm of Dempster et al. (1977). fstat 2.9.3.2 (Goudet 1995) was used to test for linkage disequilibrium and to estimate global genetic differentiation among populations (Weir & Cockerham 1984). As Sgr14 showed high genotyping error rate, abundant Hardy–Weinberg disequilibrium, high null allele frequencies and significant linkage with another locus, this marker was excluded from further analysis (see Results). Gene flow between all pairs of populations was indirectly estimated by pairwise FST values (Weir & Cockerham 1984) calculated with fstat 2.9.3.2 (Goudet 1995) and by pairwise FST values corrected for null alleles (corrFST) calculated with freena (Chapuis & Estoup 2007). Additionally, pairwise Dest, GST and G'ST values were calculated with smogd 1.2.5 (Crawford 2010).
As alternative measures of gene flow, we calculated the proportion of shared alleles (Dps) with msanalyzer 4.05 (Dieringer & Schlötterer 2003), genotype likelihood ratio distance (DLR; Paetkau et al. 1997) with DOH (http://www2.biology.ualberta.ca/jbrzusto/Doh.php) and pairwise mean assignment probabilities with geneclass 2.0.h (Piry et al. 2004). In geneclass, the assignment probability from a first population to a second (i.e. the average assignment probability of all individuals sampled in the first population) as well as the assignment probability from the second to the first population were estimated. Both values were then averaged, and the resulting pairwise mean assignment probabilities were used as an estimate of gene flow between the two populations. This was done using either all seven microsatellite markers (map7) or only the four markers (map4) with low null allele frequencies (<0.07; Sgr10, Sgr15, Sgr19, Sgr38; see Results). Tests for IBD were calculated with the ‘lmorigin’ function of the R-package (R Development Core Team 2011) ‘ape’ (Paradis et al. 2004) using untransformed FST values and Euclidian distances. For all further analyses, we excluded the two distant populations in the eastern valley of the study area (resulting data set: N = 37 populations).
Population network topology
We first created a complete population network, where all nodes were connected to each other, with spatially referenced nodes and distance-weighted edges. Every pair of nodes (i.e. populations) was connected by an edge, represented by a straight line (Euclidian distance). With edge-thinning (Urban & Keitt 2001), edges are iteratively removed from the complete population network (from longest to shortest edges) to identify the threshold distance at which the population network is no longer connected and breaks into isolated components (i.e. connected subnetworks). Edge-thinning can thus give an indication of how well populations are connected. We created a first population network by thinning edges till all nodes still formed one single component (by removing one more edge, the population network would have been broken into several components). A second population network was created by thinning edges till each node was still connected to at least two other nodes. From both population networks, the length of the longest connecting edge, that is, the threshold edge distance, was calculated (Urban & Keitt 2001). We then used the mean of the threshold edge distance from the two population networks described above to create a network including all edges that were not longer than the mean threshold edge distance (i.e. the ‘minimum connecting population network’). Subsequently, we identified edges whose removal disconnected this ‘minimum connecting population network’ (cut-edges; Urban & Keitt 2001) by visual inspection. Finally, the population network was transformed into an FST-weighted population network, where weights of edges represented pairwise FST values among nodes.
Genetic clustering
Spatial genetic clustering analysis was performed with tess v.2.3 (Chen et al. 2007). tess groups populations into clusters by maximizing Hardy–Weinberg equilibrium and minimizing linkage disequilibrium within clusters and also includes spatial information of sampling locations. We used the admixture model (CAR) and set the spatial interaction parameter to h = 0.6 (default) to calculate 10 runs for Kmax = 2–7 clusters, with a total of 500 000 sweeps of which 100 000 were burn-in. This was repeated for h = 0 (no spatial information taken into account) and h = 0.99 (high spatial dependence). The optimal number of clusters was estimated from a deviance information criterion plot (DIC; Chen et al. 2007). For the most likely number of clusters, mean cluster membership probabilities of the 10 runs were estimated with clumpp v.1.1.2 (Jakobsson & Rosenberg 2007). For each cluster, these mean cluster membership probabilities were interpolated over the entire study area by kriging (Ripley 1981), using a slightly modified version of the R-script provided with tess v.2.3 (Chen et al. 2007), which uses the ‘krig’ function of the R-package ‘fields’ (Furrer et al. 2010). Interpolated grids were then exported to arcgis 9.3.1 (ESRI) by showing for each grid cell the highest cluster membership value of any of the identified clusters. The resulting cluster maps were then overlaid with the FST-weighted ‘minimum connecting population network’ for comparison of cluster boundaries with cut-edges (Urban & Keitt 2001) or ‘weak’ edges in the population network, that is, edges whose removal would disconnect or weaken the population network. As assignment tests can be affected by null alleles (Carlsson 2008), we repeated the analysis for h = 0.6 based on only the four microsatellite markers with low null allele frequencies.
Dispersal habitat analysis
Landscape genetics offers various tools to identify likely dispersal habitat(s) of a study species. In one popular landscape genetic method, ‘least-cost paths’, paths with the lowest accumulative cost, are calculated from a landscape raster, in which each cell represents a cost or resistance to movement (Adriaensen et al. 2003; Storfer et al. 2010). The length or cost of the path is then used to explain genetic distances. Alternatively, the ‘transect approach’ assesses how gene flow is affected by the abundance of landscape elements along a straight line or within a linear transect between pairs of populations (e.g. Angelone et al. 2011; Emaresi et al. 2011). Disadvantages of these methods are that least-cost paths require a priori knowledge on the dispersal preferences of the study species (Spear et al. 2010) and that more or less straight-line dispersal is assumed in the transect approach. With least-cost transect analysis (LCTA), the advantages of least-cost path and transect analyses are combined (Van Strien et al. 2012). LCTA tests several land-cover types as potential dispersal habitats and simultaneously identifies landscape elements that facilitate or hinder gene flow. In brief, for each potential dispersal habitat, a binary landscape raster is built, and least-cost paths, which connect pairs of populations, are created. Least-cost paths are then buffered to form transects, and the proportion of landscape elements within transects is determined. These proportions together with the length of the transect are used as predictor variables in multiple regression on distance matrices (Lichstein 2007) with the response variable gene flow (e.g. FST values). Finally, the most likely dispersal habitat is determined by selecting the best fitting model (highest R2). From this best model, the effects of landscape elements on gene flow are also identified.
We applied LCTA to identify dispersal habitats of S. grossum. We chose five land-cover types from vectorized land-cover maps (vector25; based on 1:25 000 maps; resolution = 10 m; Swisstopo) as potential dispersal habitats: WATER (aboveground water bodies), ROADS (larger roads and highways), FOREST (patches of closed forests), SETTLEMENTS (residential areas) and HABITAT. Additionally, we considered straight-line transects, that is, no preferred land-cover type (NONE). All these landscape elements together with the length of the corresponding least-cost path (LENGTH) were also used as predictor variables. The specification of HABITAT was based on the knowledge of S. grossum's habitat preferences taken from the literature: habitats had to be close to open water (distance ≤500 m), they had to be located within areas of open agricultural land and within relatively flat areas where water accumulates. The latter was determined by selecting areas from a digital terrain model (resolution = 20 m; Swisstopo) that were not more than 20 m higher than the lowest point in a 500 m radius. The resulting habitat map covered the sites of 35 of the 37 larger populations in the study area (Fig. 1).
The landscape raster of each potential dispersal habitat type was composed of the respective habitat type and matrix (=binary landscape). We assigned to cells of habitat a value of 1, that is, a low resistance cost, and to cells of matrix high resistance costs of 8, 64, 512 and 4096. The corresponding least-cost paths were buffered with 8, 50, 100 or 200 m (transect width = 16, 100, 200 or 400 m), and regression models were built using the following formula: FST ~ ROADS + FOREST + SETTLEMENTS + WATER + HABITAT + LENGTH. Pairwise FST values, corrected FST values (corrFST), pairwise proportions of shared alleles (Dps), pairwise genotype likelihood ratio distances (DLR), pairwise mean assignment probabilities based on seven microsatellite markers (map7) or mean assignment probabilities based on four markers (map4) were used as response variables. As predictor variables, the proportion of each landscape element (ROADS, FOREST, SETTLEMENTS, WATER, HABITAT) within a transect was calculated by dividing the area of a given landscape element by the total transect area. Resulting values of predictor and response variables were rank-transformed, because it is not clear what kind of relationship can be expected between predictor and response variables.
For each of the potential dispersal habitats, an overall regression model was built across the whole data set as well as a separate regression model for each of four different distance classes (0–3 km, 3–6 km, 6–9 km, >9 km), in which only population pairs within the specified spatial scale were included. The smallest distance class represented the threshold distance of the ‘minimum connecting population network’ (see Results). As sample sizes were not equal for all distance classes and there is currently no generally accepted or appropriate way to calculate adjusted R2 in regression on distance matrices (Legendre & Fortin 2010), we randomly chose 97 pairs (smallest sample size) of each distance class and repeated the analysis 1000 times. From the 1000 R2 values obtained, the mean was calculated. For the best fitting model, that is, the most likely dispersal habitat, significance of regression coefficients and R2 value were calculated by permuting the response variable as vector, using the ‘lmorigin’ function of the R-package ‘ape’ (Paradis et al. 2004). To ascertain the independence of predictor variables, we checked for collinearity of predictor variables. As suggested by Tabachnick & Fidell (2007), we considered correlation coefficients larger than 0.7 to show overly correlated predictor variables.
For the model settings (i.e. matrix resistance value, corridor width, distance class and response variable) that resulted in the best fitting models (highest R2), we additionally performed LCTA considering population network topology including only neighbouring population pairs as represented by a Gabriel graph (N = 45; Fig. 4c; Gabriel & Sokal 1969). To compare the results of this analysis with the results obtained from analysis including all population pairs as well as the results from the distance class of the best fitting model, we repeated all analyses by randomly choosing 45 population pairs and repeating the analyses 1000 times. The mean R2 from the 1000 R2 values was then calculated.
Results
Genetic analysis
Genotyping error was maximally 6.9% across seven loci, except for locus Sgr14 where it was 39.6%. Mismatches were caused by allelic dropout or amplification failure, but not by misidentified alleles. Departure from Hardy–Weinberg equilibrium was significant for some loci in some populations, but there were no consistent patterns across populations (except for locus Sgr14). High null allele frequencies were found for locus Sgr14 (average 0.21; range = 0.00–0.42). Null allele frequencies for all other loci were lower, but marker Sgr40 still showed high null allele frequencies (0.15; 0.00–0.33), followed by Sgr45 (0.14; 0.00–0.42). Null allele frequencies of Sgr13 were slightly lower (0.10; 0.00–0.24) and substantially lower for markers Sgr10 (0.03; 0.00–0.20), Sgr15 (0.07; 0.00–0.24), Sgr19 (0.01; 0.00–0.08) and Sgr38 (0.02; 0.00–0.11). Significant linkage was found for some pairs of loci, but this no longer held true after Bonferroni correction, except for the combination of Sgr10 and Sgr14. Sgr14 was therefore excluded from all further analyses.
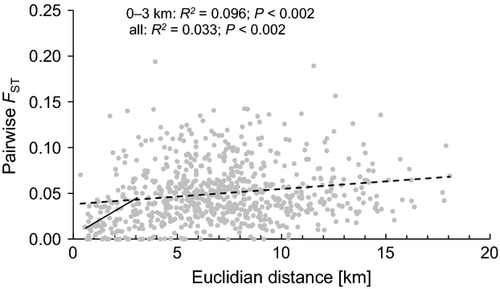
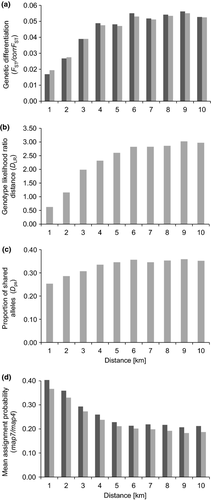
Global FST was 0.055 at the seven remaining loci. As the pairwise genetic distance measures Dest, GST and G'ST were highly correlated with FST and corrFST (r ≥ 0.91 in all cases; Table S1, Supporting information), we discarded these measures from further analysis. Thus, we used pairwise FST, corrFST, Dps, DLR, map7 and map4 as measures for gene flow. Global IBD was significant (P < 0.002), but the relationship was weak, except for those population pairs that were <3 km apart (Fig. 2). Accordingly, a clear trend of increasing average FST, corrFST, DLR, or Dps and decreasing map7 or map4 with increasing Euclidean distance was observed for distance classes up to 3–4 km (Fig. 3). For larger distance classes, there was no obvious trend in FST, corrFST, DLR, Dps, map7 or map4.
Population connectivity
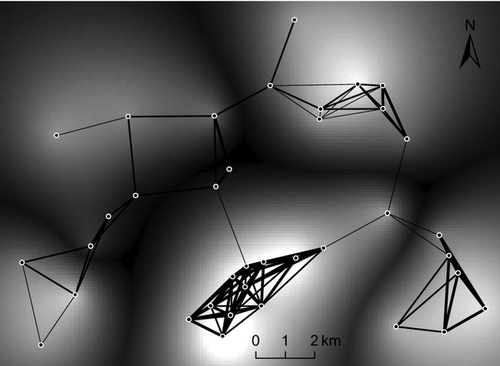
The threshold edge distance in the population network with all populations (nodes) still forming one single component before breaking into several smaller components was 2743 m. With a threshold edge distance of 3264 m, each population was connected with at least two other populations. We used the mean threshold edge distance of these two population networks (i.e. 3004 m) to build the ‘minimum connecting population network’ (Fig. 4a). This population network showed three main population communities (i.e. groups of populations that were highly connected; Garroway et al. 2008): one population community was located in the southern part of the study area, one in the northern and one in the southeastern part. A fourth population community, where populations generally had less connections than those in other communities, was found in the west of the study area. There was no cut-edge identified in the ‘minimum connecting population network’, that is, an edge whose removal would have disconnected the whole population network (Urban & Keitt 2001). Nevertheless, the removal of four central ‘weak’ edges (Fig. 4a; dashed lines) would have disconnected the population network and isolated the above four population communities. An FST-weighted population network, with weights representing pairwise FST values, showed that edges with little gene flow (Fig. 4b, thin edges) coincided with the ‘weak’ edges mentioned above (Fig. 4a).

Genetic clustering
With the statistical DIC plot, we chose the most likely number of clusters. The plot showed that populations in our study area were grouped into five clusters (Fig. S1; based on seven or four microsatellite markers, Supporting information). The five clusters were consistent across the three different spatial interaction factors (h) tested. All further analyses were therefore based on the default spatial interaction factor h = 0.6. The overlay of the five interpolated clusters with a land-cover map showed a good overlap of the three southern clusters with the three main valleys in the study area (data not shown). Cluster boundaries also spatially coincided with the ‘weak’ edges in the FST-weighted ‘minimum connecting population network’ (Fig. 4b), except for the edges between the north and northwestern population communities and the northwestern and southwestern population communities (Fig. 5).
Dispersal habitat
Generally, model fits were better when we used pairwise proportions of shared alleles (Dps) or genotype likelihood ratio distances (DLR) instead of pairwise FST values as response variables (Table 1). However, the best model fits were achieved when using pairwise mean assignment probabilities (map7). The use of genetic distance measures corrected for null alleles (map4, corrFST) did not change the outcome of LCTA. Neither different corridor widths nor different resistance cost values had a substantial impact on the best fitting models (Table 1), which were generally those calculated for distance class 0–3 km (Table 1). Note that a distance of approximately 3 km was also identified as threshold edge distance in the ‘minimum connecting population network’. This was especially the case when pairwise proportions of shared alleles (Dps), genotype likelihood ratio distances (DLR) or mean assignment probabilities (map7, map4) were used as response variable. The overall best fitting models (R2 = 0.56; distance class = 0–3 km) always assumed HABITAT as dispersal habitat, used map7 as response variable, had a corridor width of 100 m and matrix resistance cost values of either 64, 512 or 4096.
| Response variable | Transect width (m) | Resistance value | Best model | ||
|---|---|---|---|---|---|
| Distance class (km) | Dispersal habitat | Model fit (R2) | |||
| F ST | 16 | 8 | 0–3 | SETTLEMENTS | 0.335 |
| F ST | 16 | 64 | 0–3 | HABITAT | 0.352 |
| F ST | 16 | 512 | 0–3 | HABITAT | 0.347 |
| F ST | 16 | 4096 | 0–3 | HABITAT | 0.350 |
| F ST | 100 | 8 | 0–3 | HABITAT | 0.345 |
| F ST | 100 | 64 | 0–3 | HABITAT | 0.354 |
| F ST | 100 | 512 | 0–3 | HABITAT | 0.352 |
| F ST | 100 | 4096 | 0–3 | HABITAT | 0.353 |
| F ST | 200 | 8 | 0–3 | WATER | 0.394 |
| F ST | 200 | 64 | 0–3 | HABITAT | 0.385 |
| F ST | 200 | 512 | 0–3 | HABITAT | 0.376 |
| F ST | 200 | 4096 | 0–3 | HABITAT | 0.377 |
| F ST | 400 | 8 | 0–3 | WATER | 0.343 |
| F ST | 400 | 64 | 0–3 | WATER | 0.308 |
| F ST | 400 | 512 | >9 | HABITAT | 0.352 |
| F ST | 400 | 4096 | >9 | HABITAT | 0.360 |
| corrF ST | 16 | 8 | 0–3 | HABITAT | 0.320 |
| corrF ST | 16 | 64 | 0–3 | HABITAT | 0.335 |
| corrF ST | 16 | 512 | 0–3 | HABITAT | 0.329 |
| corrF ST | 16 | 4096 | 0–3 | HABITAT | 0.331 |
| corrF ST | 100 | 8 | 0–3 | HABITAT | 0.324 |
| corrF ST | 100 | 64 | 0–3 | HABITAT | 0.328 |
| corrF ST | 100 | 512 | 0–3 | HABITAT | 0.326 |
| corrF ST | 100 | 4096 | 0–3 | HABITAT | 0.326 |
| corrF ST | 200 | 8 | 0–3 | HABITAT | 0.344 |
| corrF ST | 200 | 64 | 0–3 | HABITAT | 0.361 |
| corrF ST | 200 | 512 | 0–3 | HABITAT | 0.350 |
| corrF ST | 200 | 4096 | 0–3 | HABITAT | 0.351 |
| corrF ST | 400 | 8 | >9 | HABITAT | 0.315 |
| corrF ST | 400 | 64 | 0–3 | WATER | 0.301 |
| corrF ST | 400 | 512 | >9 | HABITAT | 0.341 |
| corrF ST | 400 | 4096 | >9 | HABITAT | 0.348 |
| D ps | 16 | 8 | 0–3 | HABITAT | 0.402 |
| D ps | 16 | 64 | 0–3 | HABITAT | 0.393 |
| D ps | 16 | 512 | 0–3 | HABITAT | 0.388 |
| D ps | 16 | 4096 | 0–3 | HABITAT | 0.392 |
| D ps | 100 | 8 | 0–3 | HABITAT | 0.408 |
| D ps | 100 | 64 | 0–3 | HABITAT | 0.402 |
| D ps | 100 | 512 | 0–3 | HABITAT | 0.401 |
| D ps | 100 | 4096 | 0–3 | HABITAT | 0.403 |
| D ps | 200 | 8 | 0–3 | HABITAT | 0.459 |
| D ps | 200 | 64 | 0–3 | HABITAT | 0.450 |
| D ps | 200 | 512 | 0–3 | HABITAT | 0.450 |
| D ps | 200 | 4096 | 0–3 | HABITAT | 0.451 |
| D ps | 400 | 8 | 0–3 | HABITAT | 0.378 |
| D ps | 400 | 64 | 0–3 | HABITAT | 0.379 |
| D ps | 400 | 512 | 0–3 | HABITAT | 0.380 |
| D ps | 400 | 4096 | 0–3 | HABITAT | 0.380 |
| D LR | 16 | 8 | 0–3 | HABITAT | 0.465 |
| D LR | 16 | 64 | 0–3 | HABITAT | 0.484 |
| D LR | 16 | 512 | 0–3 | HABITAT | 0.489 |
| D LR | 16 | 4096 | 0–3 | HABITAT | 0.491 |
| D LR | 100 | 8 | 0–3 | HABITAT | 0.455 |
| D LR | 100 | 64 | 0–3 | HABITAT | 0.462 |
| D LR | 100 | 512 | 0–3 | HABITAT | 0.465 |
| D LR | 100 | 4096 | 0–3 | HABITAT | 0.465 |
| D LR | 200 | 8 | 0–3 | HABITAT | 0.448 |
| D LR | 200 | 64 | 0–3 | HABITAT | 0.447 |
| D LR | 200 | 512 | 0–3 | HABITAT | 0.455 |
| D LR | 200 | 4096 | 0–3 | HABITAT | 0.457 |
| D LR | 400 | 8 | 0–3 | HABITAT | 0.365 |
| D LR | 400 | 64 | 0–3 | HABITAT | 0.356 |
| D LR | 400 | 512 | 0–3 | HABITAT | 0.365 |
| D LR | 400 | 4096 | 0–3 | HABITAT | 0.366 |
| map7 | 16 | 8 | 0–3 | HABITAT | 0.540 |
| map7 | 16 | 64 | 0–3 | HABITAT | 0.541 |
| map7 | 16 | 512 | 0–3 | HABITAT | 0.543 |
| map7 | 16 | 4096 | 0–3 | HABITAT | 0.546 |
| map7 | 100 | 8 | 0–3 | HABITAT | 0.552 |
| map7 | 100 | 64 | 0–3 | HABITAT | 0.560 |
| map7 | 100 | 512 | 0–3 | HABITAT | 0.561 |
| map7 | 100 | 4096 | 0–3 | HABITAT | 0.561 |
| map7 | 200 | 8 | 0–3 | HABITAT | 0.538 |
| map7 | 200 | 64 | 0–3 | HABITAT | 0.555 |
| map7 | 200 | 512 | 0–3 | HABITAT | 0.554 |
| map7 | 200 | 4096 | 0–3 | HABITAT | 0.555 |
| map7 | 400 | 8 | 0–3 | HABITAT | 0.434 |
| map7 | 400 | 64 | 0–3 | HABITAT | 0.443 |
| map7 | 400 | 512 | 0–3 | HABITAT | 0.444 |
| map7 | 400 | 4096 | 0–3 | HABITAT | 0.445 |
| map4 | 16 | 8 | 0–3 | HABITAT | 0.465 |
| map4 | 16 | 64 | 0–3 | HABITAT | 0.457 |
| map4 | 16 | 512 | 0–3 | HABITAT | 0.459 |
| map4 | 16 | 4096 | 0–3 | HABITAT | 0.461 |
| map4 | 100 | 8 | 0–3 | HABITAT | 0.460 |
| map4 | 100 | 64 | 0–3 | HABITAT | 0.454 |
| map4 | 100 | 512 | 0–3 | HABITAT | 0.454 |
| map4 | 100 | 4096 | 0–3 | HABITAT | 0.454 |
| map4 | 200 | 8 | 0–3 | HABITAT | 0.455 |
| map4 | 200 | 64 | 0–3 | HABITAT | 0.455 |
| map4 | 200 | 512 | 0–3 | HABITAT | 0.454 |
| map4 | 200 | 4096 | 0–3 | HABITAT | 0.455 |
| map4 | 400 | 8 | 0–3 | HABITAT | 0.358 |
| map4 | 400 | 64 | 0–3 | HABITAT | 0.347 |
| map4 | 400 | 512 | 0–3 | HABITAT | 0.349 |
| map4 | 400 | 4096 | 0–3 | HABITAT | 0.350 |
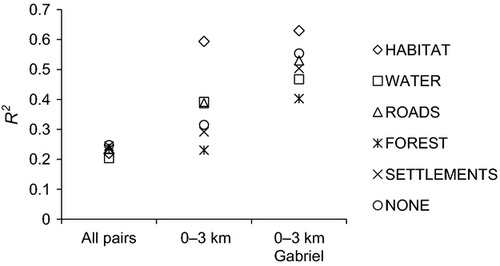
These settings (map7, corridor width = 100 m, resistance cost value = 64) were then used to compare models across all distance classes with models restricted to distance class 0–3 km (taking spatial scale into account) and models including distance class 0–3 km further restricted to neighbouring populations as represented by a Gabriel graph (considering scale and population topology; Fig. 4c). Results of the regression models across all distance classes showed an only low model fit (R2 ≤ 0.248), regardless of dispersal habitat (Fig. 6). For models only considering population pairs in distance class 0–3 km, R2 values were more variable (R2 = 0.230–0.593), and the model assuming HABITAT as dispersal habitat clearly outperformed all other models. Even better fitting models (R2 = 0.403–0.630) were found when only Gabriel population pairs in distance class 0–3 km were included in the analysis. Again, the best model was based on dispersal through HABITAT.
Influence of landscape elements
For the best fitting model (dispersal habitat = HABITAT, distance class = 0–3 km, response variable = map7; Table 2), we found a significant negative correlation of the length of the transect, proportion of forest and proportion of settlements with pairwise mean assignment probabilities, indicating less gene flow with increasing path lengths and increasing proportions of forest and settlements. In contrast, the proportion of water bodies and roads was positively correlated with map7. Pairwise correlations between predictor variables did not show collinearity (r ≤ 0.7). The results for models additionally restricted to neighbouring populations defined by a Gabriel graph were similar, but the predictor SETTLEMENTS was no longer significant (Table 2).
| Populations | 0–3 km | 0–3 km Gabriel |
|---|---|---|
| WATER | (+)** | (+)** |
| ROADS | (+)*** | (+)** |
| FOREST | (−)** | (−)* |
| SETTLEMENTS | (−)(*) | n.s. |
| HABITAT | n.s. | n.s. |
| LENGTH | (−)*** | (−)*** |
| R 2 | 0.560 | 0.630 |
- P-values: ***≤0.001, **≤0.01, *≤0.05, (*)≤0.1.
Discussion
The present study confirmed our expectations that the outcome of landscape genetic studies depends on spatial scale and, to some degree, on population network topology and that their disregard could lead to misinterpretations. Moreover, in our study system, the relevant distance threshold up to which landscape elements strongly influenced dispersal and gene flow was reflected by IBD patterns and population network topology.
Isolation-by-distance
In our study, a pronounced IBD pattern was only found at smaller spatial scales, that is, for distance classes up to about 3–4 km for all analysed measures of gene flow (Figs 2 and 3). This indicated that up to 3–4 km, gene flow between populations of S. grossum was more important than drift, but that for larger distances, drift was the driving factor. A similar IBD pattern (‘case IV’ scenario) was found by Hutchison & Templeton (1999), who studied populations of collared lizards in different landscapes with different colonization periods. Likewise, Mullen et al. (2010) detected a positive correlation of FST with stream distance within catchments, but not among catchments for the Idaho giant salamander. If populations and landscapes have not been stable for long enough time periods to reach gene flow–drift equilibrium and if gene flow is more important between close populations, such an IBD pattern is expected (Hutchison & Templeton 1999). Therefore, significant IBD can only be found up to a spatial scale threshold where gene flow is more important than drift. As conditions in European agricultural landscapes have strongly changed during the last decades (Stoate et al. 2001) and S. grossum might currently be expanding, it is not surprising to find a ‘case IV’ IBD pattern in our study system. Even though other studies did not consistently find a correlation between maximum dispersal distance and IBD patterns (i.e. the point at which an FST-distance plot flattens out; Keyghobadi et al. 2005; Van Strien unpublished data), in our study, IBD analysis gave a good estimate of the spatial scale at which a landscape effect on dispersal could be detected.
Population network topology
The distance threshold of about 3–4 km detected in IBD analysis was also evident from population network topology. Below a threshold edge distance of 2743 m, the population network changed from one large component into several smaller components, disconnecting the populations in the study area. Thus, all populations are functionally connected, if the dispersal capabilities of S. grossum equal or exceed this threshold distance. The threshold edge distance of a population network, where each population was linked with at least two other populations, was 3264 m. If S. grossum can cover this threshold distance, gene flow between all populations does not depend on one single edge. If the direct edge between a pair of populations was interrupted, for instance by anthropogenic intervention, a detour through other populations would still connect the populations. Nevertheless, there are three main general concerns about population network topology analyses. First, dispersal potential is often unknown or underestimated for many species (Van Dyck & Baguette 2005; Kamm et al. 2009), as it was the case for S. grossum (Marzelli 1995; Malkus et al. 1996; Bönsel & Sonneck 2011). Dispersal distances can be determined by first-generation migrant assignment tests of genetic data sets (Paetkau et al. 2004), if high enough global genetic differentiation (FST) is available. Alternatively, IBD patterns can denote those spatial scales with frequent gene flow (see above). The second concern deals with the potential underestimation of scale thresholds if real dispersal paths differ from straight-line paths. It has, therefore, been suggested to use least-cost paths as edges between pairs of populations in networks (Urban et al. 2009). However, the parameterization of resistance surfaces for creating least-cost paths requires previous knowledge on the dispersal preferences of the study species, which is often not available (Anderson et al. 2010). Third, the outcome of population network analysis is only meaningful if a complete sampling of populations in a study area is available. In our case, such a complete population sampling was available and enabled meaningful analyses of population network topology. In a similar analysis, Brooks (2006) studied coincidences between properties of a salamander population network and spatial autocorrelation of genetic patterns. In contrast to our study, the author found that the scale of genetic spatial autocorrelation (20 km) matched with a spatial scale at which the population network was still divided into several components (27.5 km). However, as discussed in Brooks (2006), the population network could well consist of less components at a scale of 27.5 km, if all existing populations in the study area had been sampled.
The fact that we found a distance threshold at 3–4 km for both IBD patterns (indicating frequent gene flow) and the ‘minimum connecting population network’ (based on spatial population arrangement) indicated functional connectivity of populations across our study area. However, population network topology identified not only highly connected population communities but also ‘weak’ edges within the networks. Network edges that linked highly connected population communities showed higher genetic differentiation than edges within the linked population communities in the FST-weighted network (Fig. 4b), indicating limited gene flow between the linked population communities. This suggests that not only spatial scale, but potentially also population network topology influenced genetic patterns in our study system. Within the linked population communities, there were several populations located within the species’ maximum dispersal distance, and thus, gene flow was secured because of the existence of multiple direct and indirect dispersal routes between population pairs. Nevertheless, we used a basic network analysis, which was mainly based on visual inspection, but there are various other methods available to describe community structure (e.g. Bodin & Norberg 2007).
Genetic clustering analysis generally supported the above findings. The genetic clusters found (tess analysis; Fig. 5) largely coincided with the topology of the ‘minimum connecting population network’. The population communities discussed above fell within one genetic cluster, except for the eastern population community, which was located in two clusters (Fig. 5). The cluster boundaries also spatially coincided with the ‘weak’ edges in the distance-weighted population network (Fig. 4a) and showed high genetic differentiation (i.e. little gene flow) in the FST-weighted population network (Fig. 5). Although clustering analysis is one of the most used methods in landscape genetics (Storfer et al. 2010), it is prone to overestimate the real number of clusters if there is IBD (Guillot et al. 2009), which was the case in our study. The spatial coincidence of cluster boundaries and ‘weak’ network edges should thus be further verified (e.g. with overlap statistics; Fortin & Dale 2005) as overlaps could just occur by chance (Anderson et al. 2010). However, in many studies, the overlay approach of landscape genetics has been used for the detection of major landscape barriers to gene flow (Holderegger et al. 2010). Whether the genetic clusters in our study are the result of reduced gene flow between valleys or whether they simply represent the currently established population communities in suitable habitat has yet to be determined.
Dispersal habitat
The successful detection of a most likely dispersal habitat of S. grossum with landscape genetic analysis (LCTA) proved to be highly dependent on spatial scale. In fact, when considering all population pairs, landscape genetic models only weakly explained patterns of gene flow, and no most likely dispersal habitat could be identified (Fig. 6). In contrast, the consideration of spatial scale by performing separate landscape genetic analyses for different distance classes greatly improved model fits. Best models were found for distance class 0–3 km, a spatial scale that most likely represents the maximum dispersal distance of S. grossum (see above). For these best models, a distinct dispersal habitat could be identified (Fig. S2, Supporting information): almost all models were based on dispersal routes through HABITAT. This indicated that S. grossum mainly uses its reproductive habitat as preferred dispersal habitat, at least at shorter distances of <3 km. Conservation management of S. grossum should therefore focus on maintaining and restoring the species' reproductive habitat, to preserve existing populations (network nodes) and to enhance or re-establish dispersal and gene flow (network edges).
Pairwise proportions of shared alleles (Dps), genotype likelihood ratio distance (DLR) and especially mean assignment probabilities explained landscape patterns better than pairwise FST values (Table 1; Dps: R2 = 0.38–0.46; DLR: R2 = 0.36–0.49; map7: R2 = 0.43–0.56; FST: R2 = 0.31–0.39). In contrast to FST, these measures might be useful to study fine-scaled population structure (as shown for DLR by Paetkau et al. 1997) and potentially more recent gene flow events (with assignment tests; Manel et al. 2005), which are relevant properties in changing environments.
For larger spatial scales (>3 km), model fits were generally low, and the most likely dispersal habitat could usually not be identified (Fig. S2, Supporting information). There might be several explanations for this result. First, it is possible that dispersal behaviour and dispersal habitats differ among different spatial scales (Van Dyck & Baguette 2005; Wilmer et al. 2008; Delattre et al. 2010). Long-distance dispersal in S. grossum might occur along various dispersal routes, being less dependent on the landscape elements encountered, except for major barriers, such as forests (Table 2; Reinhardt et al. 2005). Second, the rarity of long-distance dispersal might hamper the detection of a preferred dispersal habitat at larger spatial scales. Third, as direct dispersal can only occur between population pairs within the species' maximum dispersal distance (Murphy et al. 2010), least-cost path transects as used in LCTA between population pairs beyond the species' maximum dispersal distance might not assess the landscape actually encountered by dispersing individuals. At larger spatial scales, gene flow might happen in a stepping-stone way via other populations across several generations, which is, for instance, represented in a population network topology.
We represented population topology by a Gabriel graph (Gabriel & Sokal 1969), which connected neighbouring population pairs whose edges represented dispersal routes that were not surrounded by other nearby populations. With such graphs, we anticipated to represent the direct landscape effects on gene flow between population pairs, that is, without the effect of other populations enhancing or reducing gene flow. Our results showed slightly better fitting models when taking only Gabriel graph populations of the ‘minimum connecting population network’ into account (Table 2).
Landscape effects on gene flow at small spatial scales
Two models were considered to analyse the impact of landscape elements on gene flow (measured by map7). The first model considered HABITAT as dispersal habitat and was restricted to distance class 0–3 km (Table 2). The second model had the same settings but only considered neighbouring populations as defined by a Gabriel graph. As expected for the hygrophilous S. grossum, the proportion of water bodies, and probably the associated wet grasslands, had a positive effect on dispersal and gene flow. Surprisingly, the proportion of larger roads also enhanced gene flow between pairs of populations. However, we did not differentiate between roads in parallel to least-cost transects and roads intersecting these transects, as for instance suggested by Holzhauer et al. (2006). In a landscape genetic study on the bush cricket Metrioptera roeselii, these authors found a positive effect of parallel roads, but a negative effect of crossing roads on gene flow. Our results could nevertheless be explained by a positive effect of less intensively managed road verges (Holderegger & Di Giulio 2010), which were rather abundant in the study area.
Negative impacts on gene flow were found for forests, settlements (although only marginally; Table 2) and path length. Forests have previously been detected as barriers to dispersal in a mark–recapture study on S. grossum (Soerens 1996), and gene flow was expected to decrease with increasing path length at small spatial scales as exemplified by the detected IBD pattern (Fig. 3). We thus show that results derived from LCTA can directly and easily be interpreted, in contrast to other landscape genetic approaches, and can help enhancing our understanding of the dispersal ecology of particular study species.
Conclusions
Spatial scale (i.e. distance classes) proved to be an important factor in the present landscape genetic analysis and had a substantial impact on our results. Similarly, population network topology (i.e. the ‘minimum connecting population network’) seemed to affect the analysis to some degree. In particular, both IBD analysis and population network topology identified a spatial scale threshold of 3–4 km, which indicated the relevant spatial scale for landscape genetic analysis. Up to this threshold, landscape elements significantly influenced dispersal and gene flow in S. grossum. In fact, when analysing direct dispersal routes between all population pairs, weak IBD patterns and low model fits in LCTA were obtained. Meaningful results were only found when population pairs beyond the species’ potential maximum dispersal distance were excluded from analysis. Additionally, the consideration of population network topology (i.e. restricting the data set to neighbouring (Gabriel graph) populations) slightly improved our results. We therefore advise against conducting landscape genetic analyses across all possible population pairs if a species’ dispersal potential is limited. Moreover, we strongly support the suggestion of Anderson et al. (2010) and Van Strien (unpublished data) to consider spatial scale as well as population network topology in future landscape genetic studies in a more comprehensive way.
Acknowledgements
We thank Esther Jung for help in the laboratory, Ernst Grütter for information about the study species and its habitat, the Smaragd Oberaargau project for information about the study area, the Genetic Diversity Centre of ETH Zurich for laboratory facilities and the CCES-ENHANCE project of the ETH domain for financial support. Corine Schöbel, Lisette Waits and four anonymous reviewers gave helpful comments that greatly improved the manuscript. Sampling permissions were issued by the Swiss Cantons of Aargau, Berne, Lucerne and Solothurn.
References
This study is part of D.K.'s PhD thesis on insect dispersal in fragmented agricultural landscapes. R.H. is interested in landscape and ecological genetics and their application in conservation management. M.V.S. focuses on the development of landscape genetic methods.
Data accessibility
GenBank accession numbers for microsatellite markers: JQ026313 (Sgr10), JQ026314 (Sgr13), JQ026315 (Sgr14), JQ026316 (Sgr15), JQ026317 (Sgr19), JQ026319 (Sgr38), JQ026320 (Sgr40), JQ026321 (Sgr45).
Population coordinates, individual genotypes, measures of gene flow (pairwise FST, corrFST, DLR, Dps, map7, map4) and predictor variables of the best fitting model: Dryad Digital Repository. doi:10.5061/dryad.17cm4.




