Journal of Public Economic Theory
Volume 27, Issue 4 e70037
ORIGINAL ARTICLE
Open Access

Coalitions Improve the Coordination and Provision of Public Goods: Theory and Experimental Evidence

Sheryl Ball, 

Sheryl Ball

Department of Economics, Virginia Tech, Blacksburg, Virginia, USA

Search for more papers by this author
Sudipta Sarangi, 

Corresponding Author

Sudipta Sarangi

Department of Economics, Virginia Tech, Blacksburg, Virginia, USA

Correspondence: Sudipta Sarangi ([email protected])

Search for more papers by this author
Sakshi Upadhyay, 

Sakshi Upadhyay

Department of Economics, Skidmore College, Saratoga Springs, New York, USA

Search for more papers by this author
First published: 13 July 2025
https://doi.org/10.1111/jpet.70037

ABSTRACT

We study a public goods game with heterogeneous agents who care about their own payoff as well as that of the player who receives the lowest payoff. The weight of own payoff varies across players and is private information. We first develop a theoretical model and then test the predictions of our model in a laboratory setting under different parameter conditions. In both our model and experiments, introducing a coalition formation stage before making a contribution decision enables sorting of players according to their preferences, resulting in higher contributions to the public good. Additionally, we find that participants in our experiment take previous period outcomes into account while making current period decisions. These results help explain successful coalitions, like International Environmental Agreements, that are effective in creating real-world public goods like reductions in carbon emissions.

1 Introduction

We study ways to improve the provision of public goods by bringing together two stylized facts: (i) in practice, the provision of public goods is difficult because agents have heterogeneous preferences which are private information, and (ii) real-world solutions often involve the creation of a coalition, an alliance formed when two or more parties agree to work together to achieve a common goal. The landmark 2015 Paris Agreement, for example, was adopted by 196 countries whose ongoing goal is to limit global warming by implementing country-specific economic and social changes to reduce carbon emissions, with more developed countries providing financial support to developing countries. Taking these two-styled facts into account, we consider a two-stage public goods game with heterogeneous players who care about their own payoff as well as the payoff of the player with the lowest payoff. The weights on these two components of the payoff function are private information. In the first stage, players choose whether to join a coalition. In the second stage, coalition members vote on whether the coalition will contribute to the public good, where the outcome of the vote is binding on all members of the coalition. Also in the second stage, nonmembers make independent decisions about whether to contribute. We show that contributions to the public good increase with both the number of participants who satisfy a derived threshold condition based on their social preferences, and with the marginal per capital return (MPCR). In the Perfect Bayesian Equilibrium (PBE) of the game, players who satisfy the threshold condition will join the coalition, and anyone who joins the coalition in the first stage will vote to contribute to the public good in the second stage. We design and conduct experiments that support our model's predictions.

In our model, coalitions increase contributions by helping players to coordinate on an equilibrium. When coalitions are disallowed, multiple equilibria are possible, and players may reduce contributions to avoid coordination failures in situations where they are the sole contributor. In the version of the game with coalitions, players learn the number of coalition members before deciding whether to vote to contribute, with the outcome of the voting game determined by majority rule. Thus, it is impossible for a player to be the sole contributor unless they knowingly choose to be. At the same time, the coalition sorts players so that those who have stronger social preferences join the coalition while those with weaker social preferences do not. The conditions for joining the coalition are equivalent to the conditions for contributing, so players can reason ex ante that those who choose to join the coalition will vote to contribute. Our experimental results provide support for our model.

Our paper adds to a substantial literature on mechanisms for increasing voluntary contributions to public goods, some of which work by helping individuals coordinate their actions. First, note that while the experimental results on public good contributions stand in contrast to the standard free-riding prediction and suggest higher contribution rates at 40%–60% of the efficient level (Ledyard 1995), many strategies and mechanisms have been proposed to reach full efficiency. Making individual contributions observable, for example, increases contributions in both laboratory experiments (Savikhin Samek and Sheremeta 2014) and field experiments (Rogers et al. 2016). Other attempts include adding a preplay communication stage (Isaac and Walker 1988a; Ostrom et al. 1994; Reischmann and Oechssler 2018; Tavoni et al. 2011) and allowing punishment of free riders (Ostrom et al. 1994; Fehr and Gächter 2000; Ramalingam et al. 2019; Kosfeld et al. 2009) both of which facilitate higher contributions to the public good (Chaudhuri 2011).

We also add to the existing literature on the role of coalitions as a mechanism for coordination in public good games. Coalition formation helps in establishing conditions under which individuals will join a coalition and also contribute to the public good. Previous work has established a minimum participation threshold for forming a coalition and shows that when this threshold is satisfied, coalitions form and free-riding behavior is mitigated (Burger and Kolstad 2009; Kosfeld et al. 2009; McEvoy 2010; Kolstad 2014; Weikard et al. 2015). Another approach is to require coalition members to announce their planned contribution levels and set a binding rule that all coalition members must contribute to the minimum of these announced levels (Dannenberg et al. 2014; Schmidt and Ockenfels 2021). These approaches not only help in coordinating an individual's action but also result in higher contributions than expected under a Voluntary Contribution Mechanism (VCM).

Since we assume that players have social preferences, this study also contributes to the literature in behavioral economics that has often focused on how social preferences affect the outcomes of games. In our model, players' social preferences are such that players care about both their own earnings and those of the lowest-earning player. Models that incorporate social preferences provide a motivation for why individuals may contribute more to a public good than standard theory predicts (Chaudhuri 2011; Fehr and Fischbacher 2002). For example, cooperation can increase when individuals are motivated by reciprocity (Rabin 1993; Fehr and Fischbacher 2002; Gurerk et al. 2006), when players are altruistic (Andreoni et al. 2010), or when they prefer equitable resource distributions (Fehr and Schmidt 1999). Cooperation can also increase when individuals are inequality averse, for example, Kosfeld et al. (2009) allow players to sanction other players who do not contribute their full endowment, and find that inequality aversion can explain large coalitions. Similarly, Tavoni et al. (2011) create inequality in endowments and find that, over time, successful groups eliminate inequality. Status concerns and the desire to conform to your peers can also explain higher contributions in voluntary provision of public good games (Cabo et al. 2024).

Our work also adds to the growing literature on International Environment Agreements (IEAs), sometimes called climate clubs, which are coalitions of countries formed to address environmental issues. Here, theoretical models have been able to explain the existence of large coalitions. For example, adding ratification constraints to an IEA by adding a pivotal agent with veto power in the ratification decision of his/her country leads to increases in the number of coalition member countries and increases the welfare gains realized by IEA Köke and Lange (2017). When countries have inequality-averse preferences over differences in abatement levels, IEA coalitions become larger, resulting in increased cooperation rates (Lange 2006). In addition, stable coalitions with substantial abatement levels result when member countries have the ability to impose tariffs on nonmembers (Nordhaus 2015).

Finally, while in traditional models the MPCR does not affect the expected outcomes of VCM games, experimental work finds that higher MPCR significantly increases the probability of joining the coalition and contributing to the public good (Ledyard 1995; Chaudhuri 2011). While in our model, higher MPCR leads to more people joining the coalition and contributing to the public good, this is not always the case. Some existing models (Komisar 1969; Barrett 1994) suggest an inverse relationship between coalition size and MPCR. This relationship may also hold for IEAs, which means that IEAs may only be successful when the number of involved countries is small (Dixit and Olson 2000; Carraro et al. 2006). These theoretical predictions, however, stand in contrast to both our theory and experimental results, as well as to the existence of large-sized coalitions, such as International Environmental Agreements (2015 Paris Agreement, Kyoto Protocol, etc.). Large coalitions are also predicted by a dynamic model where countries invest in green technologies before the coalition formation stage (Battaglini and Harstad 2016). Here the hold-up problem results in reduces the benefit of participating in small coalitions more than large coalitions, resulting in a greater likelihood of observing coalitions that are large.

In spirit, our paper is closest to Burger and Kolstad (2009), where the authors assume binary contributions in a two-stage public good game. There are three key differences between our papers. First, in our paper, we allow for other-regarding preferences that have not been taken into account by Burger and Kolstad (2009). Second, in our paper, using heterogeneous other-regarding preferences, we show how coalitions work as a sorting mechanism. Third, the theoretical setup in Burger and Kolstad (2009) paper predicts an inverse relationship between coalition size and MPCR, which differs from their experimental predictions. On the other hand, both our theoretical model and experimental results establish a positive relationship between coalition size and MPCR.

Professor Myrna Wooders has made important contributions to the literature on public goods, and clubs and coalitions, topics closely related to our work. One line of her research is small group effectiveness (Wooders 2013; Winter and Wooders 2008), where she shows that gains to collective action can be achieved with a small group of players. Indeed, Wooders (2008) demonstrates that a relatively small group of players can realize all, or almost all, the benefits of collective action, making large groups inessential. Our paper contributes to this literature by adding prosocial preferences in a public good game as well as allowing for asymmetric information. We study the relationship between coalition size and MPCR and show that coalitions form. The size of the coalitions depends on a threshold condition that is determined by the MPCR and participants' social preferences. Participants join the coalition whenever the gain from being part of a coalition with prosocial preferences is larger than the weight the individual puts on their own earnings relative to others' earnings. Another significant line of Wooders's work is studying how individuals interact in a club providing club goods. Wooders (2012) provides an exhaustive review of endogenous club and coalition formation, another feature we exploit to show that such a possibility can help get around the asymmetric information regarding the weight on prosocial preferences. Finally, our work also uses a similar approach as Wooders (2020), where the coalition in an extensive form game becomes a single player and only players who have yet to make a decision can form coalitions to coordinate their decisions. Our mechanism also allows players desirous of resolving uncertainty and coordinating their actions to join a coalition which, in our case, helps solve the VCM coordination problem.

In Section 2, we develop the theoretical model, and in Section 3, we provide our experimental design and hypotheses. Section 4 describes our experimental results, and Section 5 concludes with a discussion.

2 Model

Let N = { 1 , 2 , … , n } $N=\{1,2,{\rm{\ldots }},n\}$ denote the set of players, each with a unit endowment ω i ${\omega }_{i}$ , that is, ω i = 1 ${\omega }_{i}=1$ to allocate in a two-stage public good game. Contributions are assumed to be binary, that is, individuals must either contribute their entire endowment or nothing. In Stage I of the game, each player decides whether or not to join a coalition, denoted by the set M $M$ . Players that choose not to join are called fringe members and belong to the set F $F$ . Thus N = M ∪ F $N=M\cup F$ , where ∣ M ∣ $| M| $ and ∣ F ∣ $| F| $ denote the respective set cardinalities. At the end of Stage I, all players learn the cardinality of each set. In Stage II, each fringe member independently decides whether to contribute, while members of the coalition vote on whether or not they will contribute to the public good, with the outcome determined by majority rule. In the case of a tie vote, we assume that the coalition will contribute to the public good, that is, if at least half of the coalition members vote to contribute, then the coalition contributes to the public good. Every i ∈ N $i\in N$ knows before the start of the game that the outcome of this vote is binding on all members of the coalition M $M$ . S i 1 = { 0 , 1 } ${S}_{i}^{1}=\{0,1\}$ is the strategy set of player i $i$ in Stage 1. To simplify the exposition regarding i $i$ 's strategies across the two stages, we will resort to some notation abuse regarding i $i$ 's strategies as described below.
j i ∈ S i 1 = 1 if i decides to join the coalition , 0 if i decides to not join the coalition . ${j}_{i}\in {S}_{i}^{1}=\left\{\begin{array}{cc}1 & \,\text{if}\,\,i\,\,\text{decides to join the coalition},\\ 0 & \,\text{if}\,\,i\,\,\text{decides to not join the coalition}.\end{array}\right.$
In Stage 2, i $i$ is either a part of coalition or fringe based on their respective decision in Stage 1—to join or not join the coalition. If j i = 1 ${j}_{i}=1$ , then i $i$ is part of the coalition. In this case, i $i$ 's strategy set is denoted by S i 2 C = { 0 , 1 } ${S}_{i}^{2C}=\{0,1\}$ . i $i$ 's strategy is denoted by v i ${v}_{i}$ as described below.
v i ∈ S i 2 C = 1 if i ∈ M votes yes to contribute , 0 if i ∈ M votes not to contribute . ${v}_{i}\in {S}_{i}^{2C}=\left\{\begin{array}{cc}1 & \,\text{if}\,\,i\in M\,\,\text{votes\unicode{x02007}yes\unicode{x02007}to\unicode{x02007}contribute},\\ 0 & \,\text{if}\,\,i\in M\,\,\text{votes\unicode{x02007}not\unicode{x02007}to\unicode{x02007}contribute}.\end{array}\right.$
Else if j i = 0 ${j}_{i}=0$ , then i $i$ is part of the fringe. In this case, i $i$ 's strategy set is denoted by S i 2 F = { 0 , 1 } ${S}_{i}^{2F}=\{0,1\}$ . As a fringe member, i $i$ chooses strategy e i ∈ S i 2 F ${e}_{i}\in {S}_{i}^{2F}$ described below.
e i ∈ S i 2 F = 1 if i ∈ F contributes , 0 if i ∈ F does not contribute . ${e}_{i}\in {S}_{i}^{2F}=\left\{\begin{array}{cc}1 & \,\text{if}\,\,i\in F\,\,\text{contributes},\\ 0 & \,\text{if}\,\,i\in F\,\,\text{does not contribute}.\end{array}\right.$

On the basis of the above description of strategies in Stage 2, i $i$ 's Stage 2 strategy set S i 2 = S i 2 C ∪ S i 2 F ${S}_{i}^{2}={S}_{i}^{2C}\cup {S}_{i}^{2F}$ . In addition, players have their own private types λ i ∈ [ 0 , 1 ] ${\lambda }_{i}\in [0,1]$ drawn from a common uniform distribution that is common knowledge. Thus player i $i$ has beliefs about the types of all the other players over the same support.

Before proceeding further, we define the remaining components of the game. Let F ′ ${F}^{^{\prime} }$ denote the set of fringe members who contribute to the public good, and let Q $Q$ denote the total number of individuals who contribute. If at least the majority of coalition members vote to contribute then Q = ∣ M ∣ + ∣ F ′ ∣ $Q=| M| +| {F}^{^{\prime} }| $ and Q = ∣ F ′ ∣ $Q=| {F}^{^{\prime} }| $ otherwise.

Recall that as a coalition member, i $i$ 's strategy v i ${v}_{i}$ consists of only voting yes or no on contributions. Player i $i$ does not choose to contribute as this decision is governed by majority rule. The majority rule in this setting states that if majority players in the coalition contribute or the tie-breaking rule is satisfied, then i $i$ has to contribute. Likewise, if the majority chooses not to contribute, then i $i$ does not contribute.

Player i $i$ 's individual rationality constraint for joining the coalition and voting for the public good is
γ ∣ M ∣ ≥ 1 ,     ∀ ∣ M ∣ ≥ 2 . $\gamma | M| \ge 1,\unicode{x02007}\unicode{x02007}\forall | M| \ge 2.$
This states that the payoff from joining a coalition of size ∣ M ∣ $| M| $ is at least greater than the individual's endowment of 1 unit. If ∣ M ∣ ≥ 2 $| M| \ge 2$ then the payoff of player i $i$ from joining coalition is γ ∣ M ∣ $\gamma | M| $ , whereas if they do not join they receive a payoff of 1 from their private endowment. Since the coalition size can be less than N $N$ , we need to check for all possible deviations and hence we need the incentive compatible condition in Stage 2 to also hold true. After being a part of the coalition, the incentive compatible condition or incentive compatibility (IC) ensures that i $i$ being a coalition member prefers to vote yes (act as a coalition member) over no (act as a fringe member) given i $i$ 's beliefs about the types of other players. In other words, the expected payoffs from voting yes must be at least equal to voting no:
∑ λ − i π i v i = 1 , S − i 2 λ i ≥ ∑ λ − i π i v i = 0 , S − i 2 λ i . $\sum _{{\lambda }_{-i}}{\pi }_{i}\left.\left.\left({v}_{i}=1,{S}_{-i}^{2}\right.{\lambda }_{i},)\right)\ge \sum _{{\lambda }_{-i}}{\pi }_{i}\left.\left.\left({v}_{i}=0,{S}_{-i}^{2}\right.{\lambda }_{i},)\right).$
It is easy to check that this is satisfied as long as
λ i ≤ γ M . ${\lambda }_{i}\le \gamma M.$

We arrive at this condition by comparing the expected payoff i $i$ receives by voting yes to contribute with the expected payoff i $i$ receives from voting no to contribute.

In Stage 2, the IC for fringe members ensures that if fringe member i $i$ chooses not to contribute instead of contributing as a coalition member given i $i$ 's beliefs about other players' types is
∑ λ − i π i e i = 0 , S − i 2 λ i ≥ ∑ λ − i π i e i = 1 , S − i 2 λ i . $\sum _{{\lambda }_{-i}}{\pi }_{i}\left.\left.\left({e}_{i}=0,{S}_{-i}^{2}\right.{\lambda }_{i},)\right)\ge \sum _{{\lambda }_{-i}}{\pi }_{i}\left.\left.\left({e}_{i}=1,{S}_{-i}^{2}\right.{\lambda }_{i},)\right).$
The IC of the fringe member will be satisfied as long as
λ i > γ . ${\lambda }_{i}\gt \gamma .$

We arrive at this condition by comparing the expected payoff i $i$ receives from contributing with the expected payoff i $i$ receives from not contributing.

We can now articulate the final payoff for players. The MPCR of player i ∈ N $i\in N$ is denoted by γ > 0 $\gamma \gt 0$ . Each individual's total payoff is a convex combination of their “own payoff” and a “social payoff” which captures their social preferences. As discussed earlier, each player has their own private type λ i ∈ [ 0 , 1 ] ${\lambda }_{i}\in [0,1]$ . λ i ${\lambda }_{i}$ is the weight on “own payoff” and 1 − λ i $1-{\lambda }_{i}$ is a player's weight on their “social payoff,” that is, the payoff of the least well-off person. With binary contributions, the “lowest own payoff” of γ Q $\gamma Q$ is received by contributors, making them the least well-off individuals. In contrast, a “higher own payoff” of 1 + γ Q $1+\gamma Q$ is earned by noncontributors.

Equation (1) represents the payoff of i $i$ from joining the coalition in Stage 1 given payoffs are governed by the majority rule. Equation (2) represents the Stage 2 payoff of i $i$ as a fringe member, which depends on whether i $i$ contributes or not.
π i ( j i = 1 ) = λ i ( γ Q ) + ( 1 − λ i ) γ Q = γ Q if majority votes yes , λ i ( 1 + γ Q ) + ( 1 − λ i ) γ Q = λ i + γ Q if majority votes no , ${\pi }_{i}({j}_{i}=1)\,=\left\{\begin{array}{cc}{\lambda }_{i}(\gamma Q)+(1-{\lambda }_{i})\gamma Q=\gamma Q & \,\text{if majority votes yes},\,\\ {\lambda }_{i}(1+\gamma Q)+(1-{\lambda }_{i})\gamma Q\,={\lambda }_{i}+\gamma Q & \,\text{if majority votes no},\end{array}\right.$ (1)
π i ( e i ) = λ i ( γ Q ) + ( 1 − λ i ) γ Q = γ Q if e i = 1 , λ i ( 1 + γ Q ) + ( 1 − λ i ) γ Q = λ i + γ Q if e i = 0 . ${\pi }_{i}({e}_{i})=\left\{\begin{array}{cc}{\lambda }_{i}(\gamma Q)+(1-{\lambda }_{i})\gamma Q=\gamma Q & \,\text{if}\,\,{e}_{i}=1,\\ {\lambda }_{i}(1+\gamma Q)+(1-{\lambda }_{i})\gamma Q={\lambda }_{i}+\gamma Q & \,\text{if}\,\,{e}_{i}=0.\end{array}\right.$ (2)

The primary difference between 1 and 2 lies in how we arrive at the payoffs. If i $i$ is a coalition member, their payoff in 1 depends on how the majority votes. Remember, however, that if i $i$ votes no to contributing, but the majority of the coalition members vote yes, i $i$ will earn the same amount as the rest of the coalition members. Fringe members' payoffs depend on whether they decide to contribute or not.

Like all public good games, our game also permits a trivial zero-contribution equilibrium. However, below we focus on the nontrivial equilibrium with positive contributions. Below we formally define the PBE of our game.

2.1 The Equilibrium

The equilibrium strategies are given by ( S i 1 , S i 2 C ) = ( 1 , 1 ) $({S}_{i}^{1},{S}_{i}^{2C})=(1,1)$ and ( S i 1 , S i 2 F ) = ( 0 , 0 ) $({S}_{i}^{1},{S}_{i}^{2F})=(0,0)$ . Moreover, for i ∈ M $i\in M$ , it must be true that player believes λ i ≤ γ ${\lambda }_{i}\le \gamma $ for all members of the coalition.

2.2 Explanation of the Equilibrium

In Stage 2, i $i$ perfectly observes the number of coalition members M $M$ and fringe members F $F$ . Given this, i $i$ forms a common uniform belief p j i ${p}_{j}^{i}$ of any other player j ≠ i $j\ne i$ contributing where j ∈ M $j\in M$ . If player i $i$ believes that all players joining the coalition have λ i ≤ γ ${\lambda }_{i}\le \gamma $ , then i $i$ 's IC is satisfied and they will contribute. Heterogeneity in preferences (or heterogeneous λ i ${\lambda }_{i}$ ) implies different probabilities of contributing to the public good for each j $j$ . In the proof, we use the expected payoffs over p = min { p j i }   ∀ j ∈ M $p=\min \{{p}_{j}^{i}\}\unicode{x02007}\forall j\in M$ to establish the strictest condition for contributing. In essence, if the condition guarantees contribution under p $p$ , then it should also guarantee contribution for any p j i > p ${p}_{j}^{i}\gt p$ , taking care of the heterogeneity in λ $\lambda $ . See the proof in the Appendix for details.

Now using backward induction, given Stage 2 beliefs, in Stage 1, i $i$ chooses to be a part of the coalition iff
∑ p * π i ( j i = 1 , j − i ∣ λ i ) ≥ ∑ p * π i ( j i = 0 , j − i ∣ λ i ) . $\sum _{p* }{\pi }_{i}({j}_{i}=1,{j}_{-i}| {\lambda }_{i})\ge \sum _{p* }{\pi }_{i}({j}_{i}=0,{j}_{-i}| {\lambda }_{i}).$

Under consistent beliefs, this condition is satisfied when λ i ≤ γ ${\lambda }_{i}\le \gamma $ . Note that this inequality can be obtained by comparing the expected payoff from joining versus not joining. Since the condition works for the lowest p $p$ , the condition will also hold true ∀ p j i > p $\forall {p}_{j}^{i}\gt p$ . Moreover, since λ i > γ ${\lambda }_{i}\gt \gamma $ for fringe members, they do not contribute.

Following the equilibrium and our explanation, we arrive at the following two propositions in our paper. Proposition 1 states the Stage II equilibrium and Proposition 1 states the Stage I equilibrium.

Proposition 1.In Stage 2 equilibrium, if λ i ≤ γ M ${\lambda }_{i}\le \gamma M$ , then all coalition members vote yes to contribute, v i * = 1 ${v}_{i}^{* }=1$ , and all fringe members choose not to contribute, e i * = 0 ${e}_{i}^{* }=0$ .

Proposition 2.Given λ i ≤ γ M ${\lambda }_{i}\le \gamma M$ , in Stage 1, i $i$ joins the coalition, j i * = 1 ${j}_{i}^{* }=1$ , iff λ i ≤ γ ${\lambda }_{i}\le \gamma $ . Else if λ i > γ , i ${\lambda }_{i}\gt \gamma ,i$ chooses not to join the coalition, j i * = 0 ${j}_{i}^{* }=0$ .

From Proposition 2, we see that only individuals with relatively lower weight on their own payoff in comparison to γ $\gamma $ ( λ i ≤ γ ${\lambda }_{i}\le \gamma $ ) will join the coalition. If λ i ≤ γ ${\lambda }_{i}\le \gamma $ is satisfied, so is the condition for contributing to the public good (Proposition 1). Hence if player has λ i ≤ γ ${\lambda }_{i}\le \gamma $ then i $i$ will both join the coalition and contribute.

We now use a three-player example to illustrate the role of heterogeneous weights and coalitions in determining the equilibrium public good outcome.

Example 1.Let N = { 1 , 2 , 3 } $N=\{1,2,3\}$ and λ 1 = 0.2 , λ 2 = 0.4 ${\lambda }_{1}=0.2,{\lambda }_{2}=0.4$ , and λ 3 = 0.6 ${\lambda }_{3}=0.6$ be the possible weights of the players on their own payoffs. We focus on positive contribution equilibrium. The equilibrium strategies are given by ( S i 1 , S i 2 C ) = ( 1 , 1 ) $({S}_{i}^{1},{S}_{i}^{2C})=(1,1)$ and ( S i 1 , S i 2 F ) = ( 0 , 0 ) $({S}_{i}^{1},{S}_{i}^{2F})=(0,0)$ . Moreover, for i ∈ M $i\in M$ , it must be true that player believes λ i ≤ γ ${\lambda }_{i}\le \gamma $ for all the members of the coalition.

Let us first examine the underlying behavior in this equilibrium. For simplicity, we will assume that only the players who join the coalition contribute. If only one individual contributes to the public good, the payoff of this individual will be: π i = λ i ( γ ) + ( 1 − λ i ) ( γ ) = γ ${\pi }_{i}={\lambda }_{i}(\gamma )+(1-{\lambda }_{i})(\gamma )=\gamma $ . Since γ < 1 $\gamma \lt 1$ , this entails that contributing is not profitable. If two people contribute, their payoff will be 2 γ $2\gamma $ . Both will choose to contribute iff γ > 1 ∕ 2 $\gamma \gt 1\unicode{x02215}2$ . Similarly, if γ > 1 ∕ 3 $\gamma \gt 1\unicode{x02215}3$ , then all three players contribute. Hence, if players are deciding individually whether or not to contribute, then γ ∣ M ∣ > 1 $\gamma | M| \gt 1$ satisfies the individual rationality condition ∀ M ≥ 2 $\forall M\ge 2$ under consistent beliefs. The coalition size can be less than N $N$ and we need to check the condition for no deviation by any representative player. If everyone contributes, the payoff is 3 γ $3\gamma $ and if one of the players deviates from contributing the payoff is π i = λ i ( 1 + 2 γ ) + ( 1 − λ i ) ( 2 γ ) = λ i + 2 γ ${\pi }_{i}={\lambda }_{i}(1+2\gamma )+(1-{\lambda }_{i})(2\gamma )={\lambda }_{i}+2\gamma $ . Everyone contributing will be an equilibrium iff λ i ≤ γ ${\lambda }_{i}\le \gamma $ .

Example 1 illustrates how the introduction of a coalition formation stage can potentially help achieve an equilibrium outcome by sorting individuals and facilitating coordination. As we saw in this example, if individuals simply decide on their own to contribute, there can be various possible outcomes. Every subject has a common belief that λ i ${\lambda }_{i}$ is uniformly distributed over [ 0 , 1 ] $[0,1]$ , and this common prior is common knowledge. If player i $i$ believes that all players joining the coalition have λ i ≤ γ ${\lambda }_{i}\le \gamma $ , then i $i$ 's IC is satisfied, and they will contribute. For instance, for MPCR γ = 0.5 $\gamma =0.5$ , individuals with λ i = 0.2 ${\lambda }_{i}=0.2$ and 0.4 will join the coalition and vote to contribute. Further, for γ > 0.6 $\gamma \gt 0.6$ , everyone will join the coalition and vote to contribute. Thus, although λ i ${\lambda }_{i}$ is private information, Stage I automatically sorts the players and thereby facilitates coordination.

3 Experiments and Hypotheses

3.1 Experimental Methods

The experiment was divided into two parts. In Part I, participants played an “all-or-nothing” (binary), eight-round, VCM public goods game to familiarize them with the public goods setting.

Following Part I, participants were given separate instructions for Part II and then played 12 rounds of the two-stage “coalition” version of the public goods game described in our model. Part II of the experiment added a first stage to the public goods game as well as including social preferences in participant utility functions. In both parts of the experiment, participants were randomly reassigned to groups consisting of 6 members at the start of each round.

At the conclusion of the experiment, participants were paid for one randomly chosen round each from Parts I and II. Instructions included a number of examples of how preferences were calculated, and participants maintained the same social preferences throughout Part II. This allowed us to more cleanly explore the effect of experience in previous rounds and to help avoid participant confusion. We conducted sessions with both heterogeneous and homogeneous weights on players' own utility, to examine if participants would be sensitive to these variations. In the homogeneous sessions, there was only one player type, although player types varied across these sessions. In the heterogeneous sessions, a participant's social preference weights were randomly assigned by the computer, while ensuring that all types were equally represented in each session.

We conducted a total of 9 sessions, 6 homogeneous sessions, and 3 heterogeneous, with 12 participants in each session for a total of 108 participants. Experimental protocols were approved by the Virginia Tech Institutional Review Board, and all participants provided informed consent at the start of their session. Experiments were computerized using z-Tree (Fischbacher 2007). Participants were primarily undergraduate students, recruited through the Virginia Tech Economic Research Lab's SONA system. Participants earned an average of $20, which included both a $10 show-up fee and their earnings from Parts I and II of the experiment, and which was paid to them in cash at the end of the experiment. Full instructions are available in Supporting Information Appendix C.

In each round, participants had 10 units ( ω i = 10 ${\omega }_{i}=10$ ), which could be entirely allocated to either their individual (private) account or the group project (public good). Following Isaac and Walker (1988b), we chose two values of MPCR ( γ $\gamma $ ) to explore the effect of low MPCR ( γ = 0.3 $\gamma =0.3$ ) versus high MPCR ( γ = 0.7 $\gamma =0.7$ ). These values occur randomly, with equal probability, throughout both stages of the experiment.

Payoffs for participants in Part I were calculated using Equations (1) and (2). Here γ $\gamma $ is either 0.3 or 0.7. Equation (3) is derived from Equations (1) and (4) is derived from Equation (2) with an endowment of 10 instead of 1.
π i ( j i = 1 ) = λ i ( 10 γ Q ) + ( 1 − λ i ) 10 γ Q = 10 γ Q if majority votes yes , λ i ( 1 + 10 γ Q ) + ( 1 − λ i ) 10 γ Q = λ i + 10 γ Q if majority votes no , ${\pi }_{i}({j}_{i}=1)\,=\left\{\begin{array}{cc}{\lambda }_{i}(10\gamma Q)+(1-{\lambda }_{i})10\gamma Q\,=10\gamma Q & \,\text{if majority votes yes},\\ {\lambda }_{i}(1+10\gamma Q)+(1-{\lambda }_{i})10\gamma Q\,={\lambda }_{i}+10\gamma Q & \,\text{if majority votes no},\end{array},\,\right.$ (3)
π i ( e i ) = λ i ( 10 γ Q ) + ( 1 − λ i ) 10 γ Q = 10 γ Q if e i = 1 , λ i ( 1 + 10 γ Q ) + ( 1 − λ i ) 10 γ Q = λ i + 10 γ Q if e i = 0 . ${\pi }_{i}({e}_{i})=\left\{\begin{array}{cc}{\lambda }_{i}(10\gamma Q)+(1-{\lambda }_{i})10\gamma Q=10\gamma Q & \,\text{if}\,\,{e}_{i}=1,\\ {\lambda }_{i}(1+10\gamma Q)+(1-{\lambda }_{i})10\gamma Q\,={\lambda }_{i}+10\gamma Q & \,\text{if}\,\,{e}_{i}=0.\end{array}\right.$ (4)

For Part II of the experiment, rather than participants making decisions based on their own innate social preferences, we assigned each participant one of three weights for their payoffs. The payoff to participants in Part II was also calculated using Equations (3) and (4). The payoff also depends on an individual's λ i ${\lambda }_{i}$ and γ $\gamma $ . These values of λ i ${\lambda }_{i}$ represent different levels of other-regarding preferences, for example, individuals with λ i = 0.8 ${\lambda }_{i}=0.8$ put a very low weight on others' payoff, meaning they are relatively selfish. This allows us to test whether behavior is consistent across different thresholds for joining and contributing λ i ≤ γ ${\lambda }_{i}\le \gamma $ (Proposition 2). Note that for γ = 0.3 $\gamma =0.3$ or 0.7 $0.7$ participants with λ i = 0.2 ${\lambda }_{i}=0.2$ will always satisfy the contribution threshold. Similarly, participants with λ i = 0.5 ${\lambda }_{i}=0.5$ only satisfies the threshold when γ = 0.7 $\gamma =0.7$ and participants with λ i = 0.8 ${\lambda }_{i}=0.8$ will never satisfy the threshold. Before deciding to contribute, all the participants learn both the weights on their own and the lowest earner's payoff, and how their payoffs are calculated. At the end of each round, participants learned their earnings from both their endowment and the public good. Participants also learned the number of contributors and the earnings of the lowest-earning group member.

At the conclusion of the experiment, participants were paid for one randomly chosen round each from Parts I and II. Instructions included a number of examples of how preferences were calculated, and participants maintained the same social preferences throughout Part II. This allowed us to more cleanly explore the effect of experience in previous rounds and to help avoid participant confusion. We conducted sessions with both heterogeneous and homogeneous weights on players' own utility, to examine if participants would be sensitive to these variations. In the homogeneous sessions, there was only one player type, although player types varied across these sessions. In the heterogeneous sessions, a participant's social preference weights were randomly assigned by the computer while ensuring that all types were equally represented in each session.

We conducted a total of 9 sessions, 6 homogeneous session, and 3 heterogeneous, with 12 participants in each session for a total 108 participants. Experimental protocols were approved by the Virginia Tech Institutional Review Board, and all participants provided informed consent at the start of their session. Experiments were computerized using z-Tree (Fischbacher 2007). Participants were primarily undergraduate students, recruited through the Virginia Tech Economic Research Lab's SONA system. Participants earned an average of $20, which included both a $10 show-up fee and their earnings from Parts I and II of the experiment, and which was paid to them in cash at the end of the experiment. Full instructions are available in Supporting Information Appendix C.

3.2 Design Choices

3.2.1 Inducing Social Preferences

Our primary goal was to provide a direct test of the theory, that is, if the option to form coalitions can solve the asymmetric information problem in the presence of prosocial preferences. Our primary motive in assigning extrinsic social preferences using payoff functions with exogenous lambda is to make certain that we have a distribution of prosocial preferences and that we can distinguish participants, even if imperfectly, that have different levels of prosocial preferences. This allows us to say something about whether the behavior is consistent with the model.

Since it is impossible to entirely eliminate prosocial motives, intrinsic prosocial preferences may still influence participants' choices. Instead, we use data from Part I of the experiment to measure and control for prosocial preferences in our Part II, and still find support for hypotheses based on extrinsic social preferences (see Supporting Information Appendix C).

3.2.2 Rawlsian Preferences

In our model, players' social preferences are Rawlsian in spirit, in the sense that players care about both their own earnings as well as those of the lowest-earning player. Preferences that care about the least well-off person are represented by maxmin preferences. Maximin preferences are aimed at maximizing the minimum payoff in a group. This is what payoffs of individuals in our model look like, where an individual's final payoff goes up when the payoff of the least well-off person (minimum payoff) goes up.

Research on social preferences has demonstrated that people are concerned about the welfare of low-payoff players (Charness and Rabin 2002; Engelmann and Strobel 2004). One can also derive motivation to understand these preferences from “Parable of the Good Samaritan, New Testament, Luke 10: 30–34,” which can be translated to “Who will help an unfortunate person when everybody believes that somebody else is likely to do the job?” Bergstrom (2017).

To see how our model would work with a different type of social preference, we also looked at our coalition game using the model by Charness and Rabin (2002) (hereafter C&R). Here, the authors assume individuals are concerned about the social surplus in the economy and the minimum payoff received in the group. The results are reported in Supporting Information Appendix D. The motivation to use this model of preferences comes from Engelmann and Strobel (2004) who compare two models of inequality aversion (Bolton and Ockenfels 2000; Fehr and Schmidt 1999) and find that a combination of maximin preferences, selfishness, and efficiency concerns (C&R model-Charness and Rabin 2002) can rationalize most of the data.

3.3 Binary Choice VCM Games

Although nonbinary contributions are popular for studying public goods/VCM games, there is a long history of using “all-or-nothing” choice restrictions to explain cooperation in VCM games (see, e.g., T. R. Palfrey and Rosenthal 1994, 1984; Cadsby and Maynes 1999; Burger and Kolstad 2009). Recently, the binary contribution mechanism was used in a paper by T. Palfrey et al. (2017) to study the efficiency of cheap talk in a threshold public good game. In fact, since nonbinary contributions allow a continuous distribution of free-riding behavior, they eliminate the effectiveness of coalitions as a sorting and coordinating mechanism. To see why, note that an important benefit of an “all-or-nothing” approach is that it simplifies the decision process for the coalition. When individuals can contribute a fraction of their endowment, the coalition must decide whether to contribute, and then how much to contribute. A binary choice environment, on the other hand, means that the coalition's action can be decided by a single vote. A binary choice also makes decisions about whether to join a coalition with binding votes easier for players, since they have fewer options to consider. Since our model and experiments have two stages with a decision in each, we chose to avoid further complications by using a binary contributions model. We also note that allowing only binary strategies helps simplify the dual decision-making process by clearly identifying the free riders.

Work on climate treaties shows that while a country's decision to reduce global emissions is a binary choice, deciding on how much each country should reduce emissions is more complex, and requires a more complicated mechanism (Oechssler et al. 2022). This paper tests the applicability of earlier work (Reischmann and Oechssler 2018) which uses a binary conditional contribution mechanism (BCCM) to study repeated public good games. The BCCM helps agents find an optimal threshold level for contribution that the individuals endogenously determine. In Oechssler et al. (2022), the authors extend the applicability of the BCCM mechanism and validate their results for nonbinary contributions as well. They show that contributions under the conditional cooperation mechanism, whether binary or nonbinary, are significantly higher than in the VCM games. In other work, Cadsby and Maynes (1999) show that a continuous contributions rule leads to higher contribution levels than a binary rule. Keeping in line with this finding, we believe that our results may provide a lower threshold for participants who will join the coalition and contribute. Since the coalition works as a self-selection mechanism in our paper, having a binary contribution ensures that cooperators who join the coalition will also contribute to the public good. Thus, we believe that notwithstanding the complexity of the game, if we had continuous contributions, we might have achieved higher levels of cooperation, in terms of larger coalition size and more contributors.

3.4 Hypotheses

Based upon our model in Section 2 we offer two hypotheses that organize our data analysis.

Hypothesis 1.Individuals with a threshold value that satisfies λ i ≤ γ ${\lambda }_{i}\le \gamma $ both join the coalition and contribute to the public good.

Proposition 2 requires that individuals who join the coalition ( λ ≤ γ $\lambda \le \gamma $ ) also satisfy the cutoff for contributing to the public good ( λ i ≤ γ M ${\lambda }_{i}\le \gamma M$ ) from Proposition 1.

Hypothesis 1 comes directly from our theory and tests whether players who satisfy the threshold λ i ≤ γ ${\lambda }_{i}\le \gamma $ will join the coalition and contribute.

Hypothesis 2.When MPCR ( γ $\gamma $ ) is high, we observe larger coalitions and more contributions to the public good.

Hypothesis 2 follows from Proposition 2, which says that as γ $\gamma $ increases, more individuals satisfy the cutoff for joining the coalition, and Proposition 1, which says that a high MPCR ( γ = 0.7 $\gamma =0.7$ ) leads to more individuals contributing to the public good.

Note that if we do not allow for coalitions, then for γ = 0.3 $\gamma =0.3$ and 0.7 $0.7$ , it is not IC for a single player to contribute since γ < 1 $\gamma \lt 1$ . When γ = 0.7 $\gamma =0.7$ , if two individuals contribute, they get a higher payoff than not contributing. If two participants contribute, the payoff from contribution 2 ( γ ) > 1 $2(\gamma )\gt 1$ holds when γ = 0.7 $\gamma =0.7$ , however, note that participants can earn even larger payoffs if everyone contributes. When MPCR is 0.3, we would need at least 4 group members to contribute so that everyone who contributes receives a payoff of 4 γ > 1 $4\gamma \gt 1$ . One can also generalize this result to say that if γ > 1 ∕ M $\gamma \gt 1\unicode{x02215}M$ , then a group of size M $M$ will join the coalition and contribute. Note that in this case, the coalition size and MPCR have an inverse relationship. Essentially, we need a larger M $M$ when MPCR is low and vice versa, a result that has been documented in the public goods literature (Komisar 1969; Barrett 1994, 2002; Finus and Maus 2008; Burger and Kolstad 2009). The models in these papers do not allow for heterogeneous private social preferences. However, Burger and Kolstad (2009) incorporate payoff uncertainty by making the eventual payoff of public good investments uncertain. The authors find that while contributions decrease when the public good returns are uncertain, they increase when individuals can form a coalition to provide the good.

In our model by incorporating prosocial preferences, we can establish a positive relationship between coalition size ( M $M$ ) and MPCR, as can be seen in Proposition 2: λ i ≤ γ ${\lambda }_{i}\le \gamma $ which gives the threshold for joining the coalition (and also contributing). We find that when γ $\gamma $ increases, more people are willing to join the coalition and contribute. Hence, high MPCR leads to more individuals contributing to the public good.

4 Results

The paper's results focus on player i $i$ 's decisions in any given period. The dependent variables, the decisions to join and contribute, are at the subject (individual) level. The testable hypothesis in the experiment is based on the propositions from the theory model, which specify the equilibrium condition for each i $i$ to join the coalition and contribute. Since the treatment is at the subject level (lambda), the analysis is at the subject level and standard errors are clustered at the subject level (Abadie et al. 2023). In our regression analysis, group-level variables, such as the number of contributors, payoff in the last period, and payoff of the least well-off person, are included as controls.

We begin our analysis with some summary statistics. Remember that Part I of the experiments was a binary choice VCM, with coalitions added in Part II. The pattern of contributions to the public good we observed in both parts of the experiment is found in Figure 1. First note that, as is typical in VCM experiments (Ledyard 1995), average contributions in Part I are high in the first period and then decline. In Part II of the experiment, when coalitions are possible, however, neither contributions by coalition members nor fringe members appear to decline. The percentage of players who contribute after joining a coalition is significantly higher in Part II than Part I (94% compared with 55%), whereas the percentage of fringe players who contribute in Part II is significantly lower than players who contribute in Part I (24% compared with 55%, Kruskal–Wallace, p = 0.0001). In summary, the possibility of joining a coalition seems to reduce the chance that the public goods contributions will decline over time, unlike VCM games with no coalitions. This also provides some indirect evidence that coalitions are absorbing.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Comparison of contributions between Parts 1 and 2.

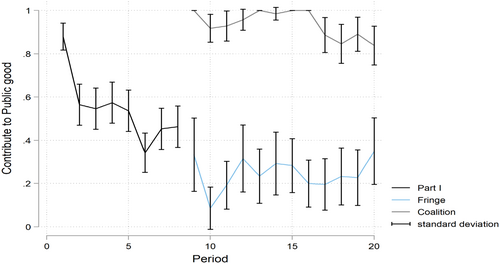
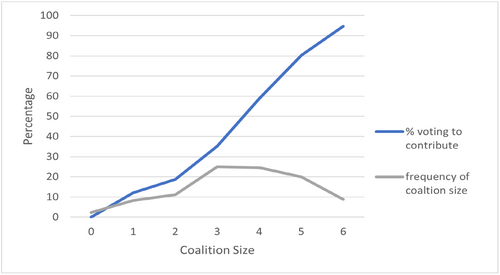
Note that since participants do not know how many others are likely to contribute in Part I because social preferences are private information, participants who prefer to contribute only when others also contribute choose to opt for the zero-contribution equilibrium. When coalitions are possible, however, participants have information on how much other participants likely plan to contribute before they vote on the coalition's contribution decision. Each participant who joins a coalition recognizes that participants who join the coalition likely satisfy the contribution threshold, which increases their confidence that they will not be the only contributor in their group. Figure 2 illustrates the relationship between coalition size and the frequency with which participants vote to contribute. In our model, the optimal coalition size varies based on the number of participants who satisfy the threshold. If everyone in a group meets the threshold then the optimal coalition size is six, whereas in a heterogeneous session where two players meet the threshold the optimal coalition size is two. Moreover, every participant who joins the coalition should vote for the public good. Interestingly, while 12% of participants voted to contribute when they were the only member of the coalition, this rate rises to 94.7% for coalitions with six members. These results are consistent with previous observations that many people care about equity in outcomes and thus conditionally cooperate in public goods games (Reischmann and Oechssler 2018; Oechssler et al. 2022).

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Percentage of votes conditional on coalition size.

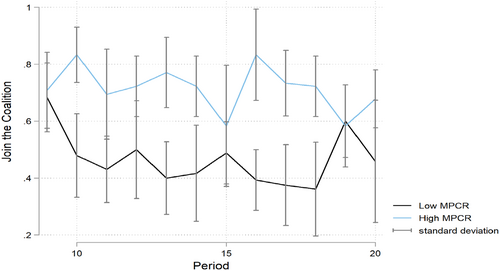
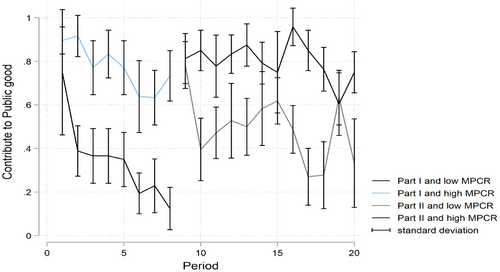
Another standard result in the public goods literature is that the MPCR affects contribution levels (Ledyard 1995). In Table 1, we report summary statistics on play in both the high and low MPCR conditions and show that in Part I, contributions ( p < 0.001 $p\lt 0.001$ ) and hence the payoffs ( p < 0.001 $p\lt 0.001$ ) increase under the high MPCR condition. In Part II, the likelihood of joining the coalition is higher when the MPCR is high ( p < 0.001 $p\lt 0.001$ , see Figure 3 as are both contributions by coalitions ( p < 0.001 $p\lt 0.001$ , see Figure 4) and fringe members ( p < 0.001 $p\lt 0.001$ ). It follows, therefore, that payoffs of coalition members, fringe members, and the least well-off person in each group are higher when MPCR is high ( p < 0.001 $p\lt 0.001$ for all three tests). These results are consistent with Hypothesis 2 as well as previous experimental results on the relationship between MPCR and coalition size (Burger and Kolstad 2009; Kosfeld et al. 2009).

Table 1. Descriptive statistics: Low and high MPCR.
High MPCR Low MPCR Difference
Part I
Player contributes to the public good 0.782 0.308 0.475
(0.0298)
Part II
Player joins the coalition 0.718 0.469 0.248
(0.0264)
Contribute to the public good by coalition members 0.974 0.878 0.0959
(0.0177)
Contribute to the public good by fringe members 0.344 0.189 0.155
(0.0387)
Coalition size 4.306 2.815 1.491
(0.0707)
  • Notes: Standard errors in parentheses. t Test for the difference of means.
  • Abbreviation: MPCR, marginal per capital return.
  • *** p < 0.0001 $p\lt 0.0001$
  • ** p < 0.05 $p\lt 0.05$
  • * p < 0.01 $p\lt 0.01$ .
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Effect of MPCR on decision to join the coalition in Part II. MPCR, marginal per capital return.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Effect of MPCR on decision to contribute. MPCR, marginal per capital return.

Before moving to the formal regression, we show the distribution of subjects across the various values of λ i ${\lambda }_{i}$ and MPCR in Table 2. Overall we see a trend with more subjects joining the coalition and contributing under high MPCR than low MPCR.

Table 2. Decision to join and contribute (by percentage): with λ i ${\lambda }_{i}$ and MPCR.
High MPCR (%) Low MPCR (%) Total (%)
Decision to join
Type 1 ( λ i = 0.2 ${\lambda }_{i}=0.2$ ) 74.04 45.37 59.7
Type 2 ( λ i = 0.5 ${\lambda }_{i}=0.5$ ) 80.5 57.8 69.2
Type 3 ( λ i = 0.8 ${\lambda }_{i}=0.8$ ) 60.6 37.5 49.07
  • Notes: The values reported here are the percentage of players joining over type and MPCR.
  • Abbreviation: MPCR, marginal per capital return.

We next conducted a more formal regression analysis to tease apart some of the factors that influence contributions. Since the decision to join and contribute is binary, we use Probit. To test Hypothesis 1, we need to use the threshold conditions under which players join the coalition and contribute. To achieve this, we divide our sample into two groups. The first group comprises subjects who always satisfy the threshold λ i ≤ γ ${\lambda }_{i}\le \gamma $ . Recall that we have three possible values of λ $\lambda $ , that is, λ i = 0.2 , 0.5 , 0.8 ${\lambda }_{i}=0.2,0.5,0.8$ . We have two possible values of γ $\gamma $ , that is, γ = 0.3 , 0.7 $\gamma =0.3,0.7$ . The first group includes all those who satisfy λ i ≤ γ ${\lambda }_{i}\le \gamma $ , that is, all subjects with λ i = 0.2 ${\lambda }_{i}=0.2$ and subjects who have λ i = 0.5 ${\lambda }_{i}=0.5$ and γ = 0.7 $\gamma =0.7$ . Subjects with the remaining parameters are in the second group as they never satisfy the threshold, so they should never join or contribute. The results from this analysis are reported in Table 3. We find that players who satisfy the threshold condition are both more likely to join the coalition ( p < 0.001 $p\lt 0.001$ ) and contribute to the public good ( p < 0.001 $p\lt 0.001$ ). Other factors also influence players' decisions. We find that, while our experiment consists of a series of one-shot games, players do respond to their previous game experience. The payoff of the least well-off player in the previous game is negatively associated with both the decision to both join the coalition ( p < 0.01 $p\lt 0.01$ ) and to contribute ( p < 0.01 $p\lt 0.01$ ). This is consistent with our Rawlsian style social preferences in the sense that players increase their contributions in response to seeing the earnings of the least well-off member of the group decline. In addition, coalition size in the previous period has a positive effect on both the decision to join the coalition ( p < 0.01 $p\lt 0.01$ ) and decision to contribute ( p < 0.01 $p\lt 0.01$ ). We also test our results by including the lag in the number of contributors and find similar results (Supporting Information Appendix B Table B.2).

Table 3. Probit estimates of average marginal effect on the decision to join and contribute to the coalition.
(1) (2)
Decision to join Decision to contribute
Threshold satisfied 0.202 0.214
(0.0422) (0.0362)
Lagged payoff of the least well-off person −0.00445 −0.00458
(0.00150) (0.00144)
Lagged coalition size 0.0398 0.0429
(0.0150) (0.0138)
Controls Yes Yes
Observations 1188 1188
  • Notes: Dependent variable is decision to join/contribute (1, yes; 0, no), margins reported here. Results on threshold satisfied are in comparison to the threshold not satisfied. Controls include gender dummy, political orientation, and number of economics classes taken. Full table available in Supporting Information Appendix B (Table B.1). Standard errors (clustered at the participant level) in parentheses.
  • * p < 0.05 $p\lt 0.05$
  • ** p < 0.01 $p\lt 0.01$
  • *** p < 0.001 $p\lt 0.001$ .

Hypothesis 2 proposes a positive relationship between MPCR and the likelihood of joining the coalition and contributing. To examine this, we include λ i ${\lambda }_{i}$ and MPCR as regressors in Table 4. In the table, results for λ i = 0.5 ${\lambda }_{i}=0.5$ and 0.8 $0.8$ are reported in comparison to λ i = 0.2 ${\lambda }_{i}=0.2$ . In support of Hypothesis 2, we find that High MPCR has a positive and significant marginal effect on joining the coalition ( p < 0.001 $p\lt 0.001$ ) and contributing to the public good ( p < 0.001 $p\lt 0.001$ ). This is to be expected, both based on prior experimental results and, specifically to our formulation of the problem, the fact that as MPCR increases, more players satisfy the threshold. We find that selfish preferences ( λ i = 0.8 ${\lambda }_{i}=0.8$ ) are associated with reduced likelihood of contributing to the public good ( p < 0.01 $p\lt 0.01$ ). Inclusion of participants with heterogeneous preferences had no significant effect on participants' behavior, a finding that is not surprising since our model says preference heterogeneity should not matter. We again find a negative effect of the payoff of the least well-off player in the previous period on both the decision to join the coalition ( p < 0.01 $p\lt 0.01$ ) and to contribute ( p < 0.001 $p\lt 0.001$ ). Finally, coalition size in the previous period has a significant positive effect on the decision to join the coalition ( p < 0.05 $p\lt 0.05$ ) and a significant effect on the decision to contribute ( p < 0.05 $p\lt 0.05$ ). We also test our results by including the lag of the number of contributors and find similar results (Supporting Information Appendix B Table B.4).

Table 4. Average marginal effect of key explanatory variables on the decision to join and contribute to coalition: Estimates from Probit regression (with coalition size).
(1) (2)
Decision to join Decision to contribute
Type 2 (0.5) 0.0857 0.0587
(0.0563) (0.0450)
Type 3 (0.8) −0.113 −0.139
(0.0623) (0.0520)
High MPCR 0.269 0.307
(0.0326) (0.0279)
Homogeneous 0.0574 0.0606
(0.0523) (0.0425)
Lag of the payoff of the least well-off person −0.00458 −0.00491
(0.00150) (0.00133)
Lag of coalition size 0.0312 0.0329
(0.0153) (0.0129)
Controls Yes Yes
Observations 1188 1188
  • Notes: Dependent variable is decision to join/contribute (1, yes; 0, no), margins reported here. Results on λ i = 0.8 ${\lambda }_{i}=0.8$ and 0.5 $0.5$ are in comparison to the base category of λ i = 0.2 ${\lambda }_{i}=0.2$ . Results on High MPCR are in comparison to low MPCR. Results in homogeneous session are in comparison to heterogeneous session. Controls include gender dummy, political orientation, and number of economics classes taken. Full table available in Supporting Information Appendix B (Table B.3). Standard errors in parentheses and clustered at participant level.
  • Abbreviation: MPCR, marginal per capital return.
  • * p < 0.05 $p\lt 0.05$
  • ** p < 0.01 $p\lt 0.01$
  • *** p < 0.001 $p\lt 0.001$ .

5 Discussion

In this paper, we explore a novel role of coalitions for public good provisioning, namely that in a society where social preferences are heterogeneous and private information, coalitions can act as a self-selection mechanism to sort agents according to the strength of their social preferences. In the absence of coalitions, multiple equilibria exist, meaning that coordination failure in the form of low contributions is the most likely result. We show that individuals with relatively lower weight on their own payoff opt to join the coalition and contribute to the public good. Even though the weight on an individual's own payoff is private information, the coalition stage sorts players and insures a unique equilibrium where players who satisfy a threshold condition join the coalition and contribute. Moreover, high MPCR increases the likelihood of joining a coalition and contributing to the public good. Unlike some previous theoretical findings (Komisar 1969; Barrett 1994; Kolstad 2012, 2014) our framework ensures the existence of large-sized coalitions even for high MPCR.

We also conducted lab experiments to test the predictions of our model and found that the data provided support for our model. First, we find that individuals who satisfy the threshold condition shown in our model are more likely to both join the coalition and contribute to the public good. As in our model, both coalition size and contributions to the public good increase with MPCR, a result consistent with previous experimental work (Burger and Kolstad 2009; Kosfeld et al. 2009). The role of coalitions as a signaling device is also supported since we find that if more people join the coalition the higher the percentage of coalition members vote to contribute to the public good.

Our experiment reveals that the probability of joining the coalition and contributing to the public good can be affected by two additional factors not captured by our one-shot public goods game—the previous period's payoff of the least well-off person, and the previous period's coalition size. These results are consistent with existing work showing that decision makers who care about justice, inequality, and those who are conditional cooperators (cooperate when others cooperate) and support the success of coalitions (Kosfeld et al. 2009; Lin 2018). These results are also consistent with research that shows that participants who observe that they are earning more or less than their peers may adjust their contributions in subsequent periods (see, e.g., Lin 2018).

Our model can be generalized in several ways. For example, we can show that a unanimous voting rule can serve as an alternative to majority rule. It is easy to see that an individual who contributes under majority rule will also contribute under a unanimous rule, because everyone who joins the coalition satisfies λ i ≤ γ ${\lambda }_{i}\le \gamma $ , thereby also satisfying λ i ≤ γ M ${\lambda }_{i}\le \gamma M$ , meaning they will vote to contribute. Thus, any public good provided under majority rule will also be provided under unanimous voting.

Future research should explore how the threshold for joining the coalition and voting to contribute changes when we allow for players to have other-regarding preferences that allow for benefits outside of the public good.

Acknowledgments

We are very grateful to the editor Myrna Wooders and two anonymous reviewers whose comments and suggestions have greatly improved the paper. The authors thank the undergraduate researchers at Virginia Tech Economics Laboratory who helped conduct the experiments. We also thank Shubhro Sarkar, Eric Bahel, Tim Cason, Abhinaba Nandy, and Michael Moehler, as well as participants from the SEA 89th Annual Meeting 2019, Midwest Economic Association Conference 2019, Stony Brook International Game Theory Conference 2019, and ESA World Meeting 2022, for their feedback and suggestions. This study was supported by the National Science Foundation (Grant number 480389). Laboratory experiments were reviewed by the Institutional Review Board at Virginia Tech (approval: IRB 19-865). Sudipta Sarangi would like to acknowledge the support of Collegium de Lyon and the French Institutes of Advanced Study where a part of this study was carried out.

    Endnotes

  1. 1 This setup relies on incomplete contracts and can explain the large number of countries in the Kyoto Protocol.
  2. 2 For simplicity, we assume M $M$ to be odd, though our results will hold true when M $M$ is even as well.
  3. 3 We thank an anonymous referee for suggesting that we incorporate this tie-breaking. This also makes our model more consistent with the lab experiment.
  4. 4 If no one contributes and everyone retains their endowment of 1, the public good is not provided, resulting in the lowest possible total payoff.
  5. 5 We are thankful to an anonymous reviewer and editor for helping us refine our proof and example.
  6. 6 Since the objective of Part I was to familiarize subjects with the public goods setting we did not switch the two parts in any session. Moreover, Ashley et al. (2010) find no differences in individual behavior between the two halves of an experiment consisting of two different 10-round VCM games. Hence we did not randomize the order of the parts of the experiment.
  7. 7 We used an endowment of 10 instead of 1 to reduce the number of decimal places when computing payoffs.
  8. 8 Testing the threshold condition in our experiment can additionally be viewed as a test of rationality.
  9. 9 Before starting the experiment participants needed to successfully pass a quiz, which, among other things, tested whether they understand the payoff functions.
  10. 10 Alternatively, we could also rely on induced value theory (Smith 1976), which suggests that inducing social preferences enhances experimental control, allowing for a more precise test of our model's predictions (see Section 3.2 for details). Since our experiment is intended to directly test our theoretical predictions, relying on individuals' homegrown preferences could introduce confounding factors for this purpose. Rather than assessing whether individuals exhibit these preferences, the focus is on how they behave in their presence. For a recent paper that argues in favor of this approach, see Agranov et al. (2024).
  11. 11 One can view social preferences in our setup as a social constraint on individuals, where individuals are constrained to think about the least well-off person. This interpretation should be viewed with caution, however, as our model also allows for individuals to be strictly selfish as well ( λ i = 1 ${\lambda }_{i}=1$ ). For 0 < λ i < 1 $0\lt {\lambda }_{i}\lt 1$ , individuals are concerned about their own payoff as well as the payoffs of others. We thank the editor for this important observation.
  12. 12 We are using the abbreviations for the papers to be consistent with their paper. ERC refers to the theory of equity, reciprocity, and competition by Bolton and Ockenfels (2000) and F&S refers to the theory of fairness, competition, and cooperation by Fehr and Schmidt (1999).
  13. 13 Players send conditional cooperation messages, the implemented outcome is the one which satisfies all individuals' conditions and also achieves the highest level of contribution. The message is of the form: “I am willing to contribute to the public good if at least k $k$ agents contribute in total will contribute.” See the paper for more details.
  14. 14 We thank the editor for making this observation and helping us refine Section 4.
  15. 15 We want to thank an anonymous reviewer for suggesting this observation.
  16. 16 The lag of the number of contributors and coalition size are highly correlated; hence, we use different regression models in Supporting Information Appendix B Tables B.2 and B.4.

    17. Data Availability Statement

    The data that support the findings of this study are available from the corresponding author upon reasonable request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.