Is There a Replication Crisis in Finance?
ABSTRACT
Several papers argue that financial economics faces a replication crisis because the majority of studies cannot be replicated or are the result of multiple testing of too many factors. We develop and estimate a Bayesian model of factor replication that leads to different conclusions. The majority of asset pricing factors (i) can be replicated; (ii) can be clustered into 13 themes, the majority of which are significant parts of the tangency portfolio; (iii) work out-of-sample in a new large data set covering 93 countries; and (iv) have evidence that is strengthened (not weakened) by the large number of observed factors.
- 1.
No internal validity. Most studies cannot be replicated with the same data (e.g., because of coding errors or faulty statistics) or are not robust in the sense that the main results cannot be replicated using slightly different methodologies and/or slightly different data.1 For example, Hou, Xue, and Zhang (2020) state that:
“Most anomalies fail to hold up to currently acceptable standards for empirical finance.”
- 2.
No external validity. Most studies may be robustly replicated, but are spurious and driven by “p-hacking,” that is, find significant results by testing multiple hypotheses without controlling the false discovery rate (FDR). Such spurious results are not expected to replicate in other samples or time periods, in part because the sheer number of factors is simply too large, and too fast growing, to be believable. For example, Cochrane (2011) asks for a consolidation of the “factor zoo,” and Harvey, Liu, and Zhu (2016) state that:
“most claimed research findings in financial economics are likely false.”2
In this paper, we examine these two challenges both theoretically and empirically. We conclude that neither criticism is tenable. The majority of factors do replicate, do survive joint modeling of all factors, do hold up out-of-sample, are strengthened (not weakened) by the large number of observed factors, are further strengthened by global evidence, and the number of factors can be understood as multiple versions of a smaller number of themes.
These conclusions rely on new theory and data. First, we show that factors must be understood in light of economic theory, and we develop a Bayesian model that offers a very different interpretation of the evidence on factor replication. Second, we construct a new global data set of 153 factors across 93 countries. To help advance replication in finance, we have made this data set easily accessible to researchers by making our code and data publically available.3
Replication results. Figure 1 illustrates our main results and how they relate to the literature in a sequence of steps. It presents the “replication rate,” that is, the percent of factors with a statistically significant average excess return. The starting point of Figure 1—the first bar on the left—is the 35% replication rate reported in the expansive factor replication study of Hou, Xue, and Zhang (2020). The second bar in Figure 1 shows a 55.6% baseline replication rate in our main sample of U.S. factors. It is based on significant ordinary least squares (OLS) t-statistics for average raw factor returns, in direct comparability to the 35% calculation from Hou, Xue, and Zhang (2020). This difference arises because our sample is longer, we add 15 factors to our sample that come from prior literature but are not studied by Hou, Xue, and Zhang (2020), and, we believe, minor conservative factor construction details that robustify factor behavior.4 We discuss this decomposition further in Section II, where we detail our factor construction choices and discuss why we prefer them.
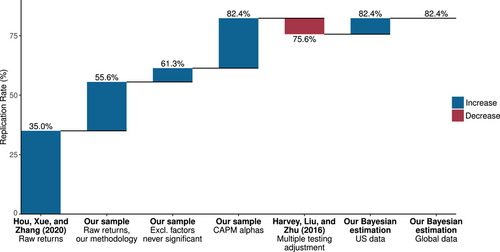
The Hou, Xue, and Zhang (2020) sample includes a number of factors that the original studies find to be insignificant.5 We exclude these when calculating the replication rate. After making this adjustment, the replication rate rises to 61.3%, as shown in the third bar in Figure 1.
Alpha, not raw return. Hou, Xue, and Zhang (2020) analyze and test factors' raw returns, but if we wish to learn about “anomalies,” economic theory dictates the use of risk-adjusted returns. The raw return can lead to incorrect inferences for a factor if this return differs from the alpha. When the raw return is significant but the alpha is not, this simply means that the factor is taking risk exposure and the risk premium is significant, which does not indicate anomalous factor returns. Likewise, when the raw return is insignificant but the alpha is significant, the factor's efficacy is masked by its risk exposure. An example of this is the low-beta anomaly, whereby theory predicts that the alpha of a dollar-neutral low-beta factor is positive but its raw return is negative or close to zero (Frazzini and Pedersen (2014)). In this case, the “failure to replicate” of Hou, Xue, and Zhang (2020) actually supports the betting-against-beta theory. We analyze the alpha to the capital asset pricing model (CAPM), which is the clearest theoretical benchmark model that is not mechanically linked to other so-called anomalies in the list of replicated factors. The fourth bar in Figure 1 shows that the replication rate rises to 82.4% based on tests of factors' CAPM alpha.
MT and our Bayesian model. The first four bars in Figure 1 are based on individual OLS t-statistics for each factor. But Harvey, Liu, and Zhu (2016) rightly point out that this type of analysis suffers from an MT problem. Harvey, Liu, and Zhu (2016) recommend MT adjustments that raise the threshold for a t-statistic to be considered statistically significant. We report one such MT correction using a leading method proposed by Benjamini and Yekutieli (2001). Accounting for MT in this manner, we find that the replication rate drops to 75.6% (the fifth bar of Figure 1). For comparison, Hou, Xue, and Zhang (2020) consider a similar adjustment and find that their replication rate drops from 35% with OLS to 18% after MT correction.
However, common frequentist MT corrections can be unnecessarily crude. Our handling of the MT problem is different. We propose a Bayesian framework for the joint behavior of all factors, resulting in an MT correction that sacrifices much less power than its frequentist counterpart, which we demonstrate via simulation.6 To understand the benefits of our approach, note first that we impose a prior that all alphas are expected to be zero. The role of the Bayesian prior is conceptually similar to that of frequentist MT corrections—it imposes conservatism on statistical inference and controls the FDR. Second, our joint factor model allows us to conduct inference for all factor alphas simultaneously. The joint structure among factors leverages dependence in the data to draw more informative statistical inferences (relative to conducting independent individual tests). Our zero-alpha prior shrinks alpha estimates of all factors, leading to fewer discoveries (i.e., a lower replication rate), with similar conservatism as a frequentist MT correction. At the same time, however, the model allows us to learn more about the alpha of any individual factor, borrowing estimation strength across all factors, and the improved precision of alpha estimates for all factors can increase the number of discoveries. Which effect dominates when we construct our final Bayesian model—the conservative shrinkage to the prior or the improved precision of alphas—is an empirical question.
In our sample, we find that the two effects exactly offset on average, which is why the Bayesian MT view delivers a replication rate identical to the OLS-based rate. Specifically, our estimated replication rate rises to 82.4% (the sixth bar of Figure 1) using our Bayesian approach to the MT problem.7 The intuition behind this surprising result is simply that having many factors (a “factor zoo”) can be a strength rather than a weakness when assessing the replicability of factor research. It is obvious that our posterior is tighter when a factor has performed better and has a longer time series. But the posterior is further tightened if similar factors have also performed well and if additional data show that these factors have performed well in many other countries.8
Benefits of our model beyond the replication rate. One of the key benefits of Bayesian statistics is that one recovers not just a point estimate but rather the entire posterior distribution of parameters. The posterior allows us to make any possible probability calculation about parameters. For example, in addition to the replication rate, we calculate the posterior probability of false discoveries (FDR) and the posterior expected fraction of true factors. Moreover, we calculate Bayesian confidence intervals (also called credibility intervals) for each of these estimates. We find that our 82.4% replication rate has a tight posterior standard error of 2.8%. The posterior Bayesian FDR is only 0.1% with a 95% confidence interval of , demonstrating the small risk of false discoveries. The expected fraction of true factors is 94.0% with a posterior standard error of 1.3%.
Global replication. Having found a high degree of internal validity of prior research, we next consider external validity across countries and over time. Regarding the former, we investigate how our conclusions are affected when we extend the data to include all factors in a large global panel of 93 countries. The last bar in Figure 1 shows that based on the global sample, the final replication rate is 82.4%. This estimate is based on the Bayesian model applied to a sample of global factors that weights country-specific factors in proportion to the country's total market capitalization. The model continues to account for MT. The global result shows that factor performance in the United States replicates well in an extensive cross section of countries. Serving as our final estimate, the global factor replication rate more than doubles that of Hou, Xue, and Zhang (2020) by grounding our tests in economic theory and modern Bayesian statistics. We conclude from the global analysis that factor research demonstrates external validity in the cross section of countries.
Postpublication performance. McLean and Pontiff (2016) find that U.S. factor returns “are 26% lower out-of-sample and 58% lower post-publication.”9 Our Bayesian framework shows that, given a prior belief of zero alpha but an OLS alpha () that is positive, our posterior belief about alpha lies somewhere between zero and . Hence, a positive but attenuated postpublication alpha is the expected outcome based on Bayesian learning, rather than a sign of nonreproducibility. Further, when comparing factors cross-sectionally, the prediction of the Bayesian framework is that higher prepublication alphas, if real, should be associated with higher postpublication alphas on average. This is what we find. We present new and significant cross-sectional evidence that factors with higher in-sample alpha generally have higher out-of-sample alpha. The attenuation in the data is somewhat stronger than predicted by our Bayesian model. We conclude that factor research demonstrates external validity in the time series, but there appears to be some decay of the strongest factors that could be due to arbitrage or data mining.10
Publication bias. We also address the issue that factors with strong in-sample performance are more likely to be published while poorly performing factors are more likely to be unobserved in the literature. Publication bias can influence our full-sample Bayesian evidence through the empirical Bayes (EB) estimation of prior hyperparameters. To account for this bias, we show how to pick a prior distribution that is unaffected by publication bias by using only out-of-sample data or estimates from Harvey, Liu, and Zhu (2016). Using such priors, the full-sample alphas are shrunk more heavily toward zero. The result is a slight drop in the U.S. replication rate to 81.5%. If we add an extra degree of conservatism to the prior, the replication rate drops to 79.8%. Further, our out-of-sample evidence over time and across countries is not subject to publication bias.
Multidimensional challenge: A Darwinian view of the factor zoo. Harvey, Liu, and Zhu (2016) challenge the sheer number of factors, which Cochrane (2011) refers to as “the multidimensional challenge.” We argue that the factor universe should not be viewed as hundreds of distinct factors. Instead, factors cluster into a relatively small number of highly correlated themes. This property features prominently in our Bayesian modeling approach. Specifically, we propose a factor taxonomy that algorithmically classifies factors into 13 themes possessing a high degree of within-theme return correlation and economic concept similarity, and low across-theme correlation. The emergence of themes in which factors are minor variations on a related idea is intuitive. For example, each value factor is defined by a specific valuation ratio, but there are many plausible ratios. Considering their variations is not spurious alpha-hacking, particularly when the “correct” value signal construction is debatable.
We estimate a replication rate greater than 50% in 11 of the 13 themes (based on the Bayesian model including MT adjustment), the exceptions being “low leverage” and “size” factor themes. We also analyze which themes matter when simultaneously controlling for all other themes. To do so, we estimate the ex post tangency portfolio of 13 theme-representative portfolios. We find that 10 of the 13 themes enter into the tangency portfolio with significantly positive weights, where the three displaced themes are “profitability,” “investment,” and “size.”
Why, the profession asks, have we arrived at a “factor zoo”?11 Evidently the answer is because the risk-return trade-off is complex and difficult to measure. The complexity manifests in our inability to isolate a single silver-bullet characteristic that pins down the risk-return trade-off. Classifying factors into themes, we trace the economic culprits to roughly a dozen concepts. This is already a multidimensional challenge, but it is compounded by the fact that within a theme there are many detailed choices for how to configure the economic concept, which results in highly correlated within-theme factors. Together, the themes (and the factors in them) each make slightly different contributions to our collective understanding of markets. A more positive take on the factor zoo is not as a collective exercise in data mining and false discovery, but rather as a natural outcome of a decentralized effort in which researchers make contributions that are correlated with, but incrementally improve on, the body of knowledge.
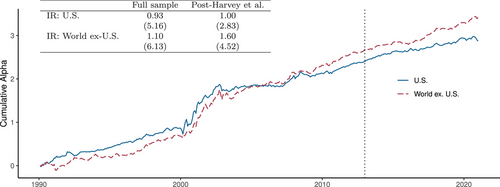
Economic implications. Our findings have broad implications for finance researchers and practitioners. We confirm that the body of finance research contains a multitude of replicable information about the determinants of expected returns. Further, we show that investors would have profited from factors deemed significant by our Bayesian method but insignificant by the frequentist MT method proposed by Harvey, Liu, and Zhu (2016). Figure 2 plots the out-of-sample returns of the subset of factors discovered by our method but discarded by the frequentist method. As can be seen, these factors produce an annualized information ratio (IR) of 0.93 in the Unites States and 1.10 globally (ex-U.S.) over the full sample, with t-statistics above five. If we restrict analysis to the sample after that of Harvey, Liu, and Zhu (2016), the performance differential remains large and significant.12 These findings show strong external validity (postoriginal publications, post–Harvey, Liu, and Zhu (2016), different countries) and significant economic benefits of exploiting the joint information in all factor returns rather than simply applying a high cutoff for t-statistics. We also show that the optimal risk-return profile has improved over time as factors have been discovered. In other words, the Sharpe ratio of the tangency portfolio has meaningfully increased over time as truly novel determinants of returns have been discovered. These findings can help inform asset pricing theory.
The paper proceeds as follows. Section I describes our Bayesian model of factor replication. Section II presents our new public data set of global factors. Section III contains our empirical assessment of factor replicability. Section IV concludes.
I. A Bayesian Model of Factor Replication
This section presents our Bayesian model for assessing factor replicability. We first draw out some basic implications of the Bayesian framework for interpreting evidence on individual factor alphas. We then present a hierarchical structure for simultaneously modeling factors in a variety themes and across many countries.
A. Learning about Alpha: The Bayes Case
A.1. Posterior Alpha
When evaluating out-of-sample evidence, a positive but lower alpha is sometimes interpreted as a sign of replication failure. But this is the expected outcome from the Bayesian perspective (i.e., based on the latest posterior) and can be fully consistent with a high degree of replicability. In fact, postpublication results (as also studied by McLean and Pontiff (2016)) have tended to confirm the Bayesian's beliefs and as a result the Bayesian posterior alpha estimate has been extraordinarily stable over time (see Section III.B.2).
A.2. Alpha-Hacking
Proposition 1. (Alpha-Hacking)The posterior alpha with alpha-hacking is given by
The Bayesian posterior alpha accounts for alpha-hacking in two ways. First, the estimated alpha is shrunk more heavily toward zero since the factor is now smaller. Second, the alpha is further discounted by the intercept term κ0 due to the bias in the error terms.
We examine alpha-hacking empirically in Section III.B in light of Proposition 1. We consider a cross-sectional regression of factors' out-of-sample (e.g., postpublication) alphas on their in-sample alphas, looking for the signatures of alpha-hacking in the form of a negative intercept term or a slope coefficient that is too small. In addition, Section III.C.2 shows how to estimate the Bayesian model in a way that is less susceptible to the effects of alpha-hacking. Appendix A presents additional theoretical results characterizing alpha-hacking.
B. Hierarchical Bayesian Model
B.1. Shared Alphas: The Case of Complete Pooling
To see the power of global evidence (or, more generally, the power of observing related strategies), we consider the posterior when observing both the domestic and global evidence.
Proposition 2. (The Power of Shared Evidence)The posterior alpha given the domestic estimate, , and the global estimate, , is normally distributed with mean
Naturally, the posterior depends on the average alpha observed domestically and globally. Furthermore, the combined alpha is shrunk toward the prior of zero. The shrinkage factor is smaller (heavier shrinkage) if the markets are more correlated because the global evidence provides less new information. With low correlation, the global evidence adds a lot of independent information, shrinkage is lighter, and the Bayesian becomes more confident in the data and less reliant on the prior. The proposition shows that if a factor has been found to work both domestically and globally, then the Bayesian expects stronger out-of-sample performance than a factor that has only worked domestically (or has only been analyzed domestically).
Two important effects are at play here, and both are important for understanding the empirical evidence presented below: The domestic and global alphas are shrunk both toward each other and toward zero. For example, suppose that a factor worked domestically but not globally, say, %. Then, the overall evidence points to an alpha of but shrinkage toward the prior results in a lower posterior, say, 2.5%. Hence, the Bayesian expects future factor returns in both regions of 2.5%. The fact that shared alphas are shrunk together is a key feature of a joint model, and it generally leads to different conclusions than when factors are evaluated independently. We next consider a perhaps more realistic model in which factors are only partially shrunk toward each other.
B.2. Hierarchical Alphas: The Case of Partial Pooling
This hierarchical model is a realistic compromise between assuming that all factor alphas are completely different (using equation (4) for each alpha separately) and assuming that they are all the same (using Proposition 2). Rather than assuming no pooling or complete pooling, the hierarchical model allows factors to have a common component and an idiosyncratic component.
Proposition 3. (Hierarchical Alphas)The posterior alpha of factor i given the evidence on all factors is normally distributed with mean
The main insight of this proposition is that having data on many factors is helpful for estimating the alpha of any of them. Intuitively, the posterior for any individual alpha depends on all of the other observed alphas because they are all informative about the common alpha component. Put differently, the other observed alphas tell us whether alpha exists in general, that is, whether the CAPM appears to be violated in general. Further, the factor's own observed alpha tells us whether this specific factor appears to be especially good or bad. Using all of the factors jointly reduces posterior variance for all alphas. In summary, the joint model with hierarchical alphas has the dual benefits of identifying the common component in alphas and tightening confidence intervals by sharing information among factors.
To understand the proposition in more detail, consider first the (unrealistic) case in which all factor returns have independent shocks (). In this case, we essentially know the overall alpha when we see many uncorrelated factors. Indeed, the average observed alpha becomes a precise estimator of the overall alpha with more and more observed factors, . Since we essentially know the overall alpha in this limit, the first term in (17) becomes when , meaning that we do not need any shrinkage here. The second term is the outperformance of factor i above the average alpha, and this outperformance is shrunk toward our prior of zero. Indeed, the outperformance is multiplied by a number less than one, and this multiplier naturally decreases in the return volatility σ and in our conviction in the prior (increases in ).
In the realistic case in which factor returns are correlated (), we see that both the average alpha and factor i's outperformance are shrunk toward the prior of zero. This is because we cannot precisely estimate the overall alpha even with an infinite number of correlated factors—the correlated part never vanishes. Nevertheless, we still shrink the confidence interval, , since more information is always better than less.
B.3. Multilevel Hierarchical Model
The model development to this point is simplified to draw out its intuition. Our empirical implementation is based on a more realistic (and slightly more complex) model that accounts for the fact that factors naturally belong to different economic themes and to different regions.
In our global analysis, we have N different characteristic signals (e.g., book-to-market) across K regions, for a total of factors (e.g., U.S., developed, and emerging markets versions of book-to-market). Each of the N signals belongs to a smaller number of J theme clusters, where one cluster consists of various value factors, another consists of various momentum factors, and so on. One level of our hierarchical model allows for partially shared alphas among factors in the same theme cluster. Another level allows for commonality across regions among factors associated with the same underlying characteristic, capturing, for example, the connections between the book-to-market factors in different markets.
In some cases, we analyze this model within a single region, (e.g., in our U.S.-only analysis). In this case, there is no difference between signal-specific alphas and idiosyncratic alphas, so we collapse one level of the model by setting and for . In any case, the following result shows how to compute the posterior distribution of all alphas based on the prior uncertainty, Ω, and a general variance-covariance matrix of return shocks, . This result is at the heart of our empirical analysis.
Proposition 4.In the multilevel hierarchical model, the posterior of the vector of true alphas is normally distributed with posterior mean
As noted above, we set the mean prior alpha to zero () in our empirical implementation. This prior is based on economic theory and leads to a conservative shrinkage toward zero as seen in (24). We note that, in the data, the observed alphas are mostly positive, not centered around zero. However, these positive alphas are related to the way that factors are signed, that is, according to the convention in the original paper, which almost always leads to a positive factor return in the original sample. If we view this signing convention as somewhat arbitrary, then a symmetry argument implies that a prior of zero is again natural. Put differently, factor means would be centered around zero if we changed signs arbitrarily, so our prior is agnostic about these signs.
C. Bayesian Multiple Testing and Empirical Bayes Estimation
Frequentist MT corrections embody a principle of conservatism that seeks to limit false discoveries by controlling the family-wise error rate (FWER) or the FDR. Leading frequentist methods do so by widening confidence intervals and raising p-values, but do not alter the underlying point estimate.
C.1. Bayesian Multiple Testing
A large statistics literature shows that Bayesian modeling is effective for making reliable inferences in the face of MT.20 Drawing on this literature, our hierarchical model is a prime example of how Bayesian methods accomplish their MT correction based on two key model features.
The first such feature is the model prior, which imposes statistical conservatism in analogy to frequentist MT methods. It anchors the researcher's beliefs to a sensible default (e.g., all alphas are zero) in case the data are insufficiently informative about the parameters of interest. Reduction of false discoveries is achieved first by shrinking estimates toward the prior. When there is no information in the data, the alpha point estimate is the prior mean and there are no false discoveries. As empirical evidence accumulates, posterior beliefs migrate away from the prior toward the OLS alpha estimate. In the process, discoveries begin to emerge, though they remain dampened relative to OLS. In the large-data limit, Bayesian beliefs converge on OLS with no MT correction, which is justified because in the limit there are no false discoveries. In other words, the prior embodies a particularly flexible form of conservatism—the Bayesian model decides how severe of an MT correction to make based on the informativeness of the data.
The second key model feature is the hierarchical structure that captures factors' joint behavior. Modeling factors jointly means that each alpha is shrunk toward its cluster mean (i.e., toward related factors), in addition to being shrunk toward the prior of zero. So, if we observe a cluster of factors in which most perform poorly, then this evidence reduces the posterior alpha even for the few factors with strong performance—another form of Bayesian MT correction. In addition to this Bayesian discovery control coming through shrinkage of the posterior mean alpha, the Bayesian confidence interval also plays an important role and changes as a function of the data. Indeed, having data on related factors leads to a contraction of the confidence intervals in our joint Bayesian model. So while alpha shrinkage often has the effect of reducing discoveries, the increased precision from joint estimation has the opposite effect of enhancing statistical power and thus increases discoveries.
In summary, a typical implementation of frequentist MT corrections estimates parameters independently for each factor and leaves these parameters unchanged, but inflates p-values to reduce the number of discoveries. In contrast, our hierarchical model leverages dependence in the data to efficiently learn about all alphas simultaneously. All data therefore help to determine the center and width of each alpha's confidence interval (Propositions 3 and 4). This leads to more precise estimates with “built-in” Bayesian MT correction.
C.2. Empirical Bayes Estimation
Given the central role of the prior, it might seem problematic that the severity of the Bayesian MT adjustment is at the discretion of the researcher. A powerful (and somewhat surprising) aspect of a hierarchical model is that the prior can be learned in part from the data. This idea is formalized in the idea of “empirical Bayes (EB)” estimation, which has emerged as a major toolkit for navigating MT in high-dimensional statistical settings (Efron (2012)).
The general approach to EB is to specify a multilevel hierarchical model and then use the dispersion in estimated effects within each level to learn about the prior parameters for that level. In our setting, the specific implementation of EB is dictated by Proposition 4. We first compute each factor's abnormal return, , as the intercept in a CAPM regression on the market excess return. We then set the overall alpha prior mean, , to zero to enforce conservatism in our inferences.
From here, the benefits of EB kick in. The realized dispersion in alphas across factors helps determine the appropriate prior beliefs (i.e., the appropriate values for , , and ). For example, if we compute the average alpha for each cluster, (e.g., the average value alpha, the average momentum alpha), the cross-sectional variation in suggests that . The same idea applies to . Likewise, variation in observed alphas after accounting for hierarchical connections is informative about , where .
The above variances illustrate that EB can help calibrate prior variances using the data itself. But those calculations are too crude, because they ignore sampling variation coming from the noise in returns, ε, which has covariance matrix Σ. EB estimates the prior variances by maximizing the prior likelihood function of the observed alphas, , where the notation emphasizes that Ω depends on , , and according to (23). The likelihood function accounts for sampling variation through a plug-in estimate of the covariance matrix of factor return shocks, .21 We collect the resulting hyperparameters in τ, that is, , , and .
C.3. Bayesian FDR and FWER
The following proposition is a novel characterization of the Bayesian FDR, and shows that it is the posterior probability of a false discovery, averaged across all discoveries:
Proposition 5. (Bayesian FDR)Conditional on the parameters of the prior distribution τ and data with at least one discovery, the Bayesian FDR can be computed as
This result shows explicitly how the Bayesian framework controls the FDR without the need for additional MT adjustments.23 The definition of a discovery ensures that at most 2.5% of the discoveries are false according to the Bayesian posterior, which is exactly the right distribution for assessing discoveries from the perspective of the Bayesian. Further, if many of the discovered factors are highly significant (as is the case in our data), then the Bayesian FDR is much lower than 2.5%.24
C.4. A Comparison of Frequentist and Bayesian False Discovery Control
We illustrate the benefits of Bayesian inference for our replication analysis via simulation. We assume a factor-generating process based on the hierarchical model above and, for simplicity, consider a single region (as in our empirical U.S.-only analysis), removing and from equations (21) and (23). We analyze discoveries as we vary the prior variances and . The remaining parameters are calibrated to our estimates for the U.S. region in our empirical analysis below.
We simulate an economy with 130 factors in 13 different clusters of 10 factors each, observed monthly over 70 years. We assume that the mean alpha, , is zero. We then draw a cluster alpha from and a factor-specific alpha as . Based on these alphas, we generate realized returns by adding Gaussian noise.25
We compute p-values separately using OLS with no adjustment or OLS adjusted using the Benjamini and Yekutieli (2001) (BY) method. We also use EB to estimate the posterior alpha distribution, treating and as known to simplify simulations and focus on the Bayesian updating. For OLS and BY, a discovery occurs when the alpha estimate is positive and the two-sided p-value is below 5%. For EB, we consider it a discovery when the posterior probability that alpha is negative is less than 2.5%. For each and pair, we draw 10,000 simulated samples and report average discovery rates over all simulations.
Figure 3 reports alpha discoveries based on the OLS, BY, and EB approaches. For each method, we report the true FDR in the top panels (we know the truth since this is a simulation) and the “true discovery rate”26 in the bottom panels.
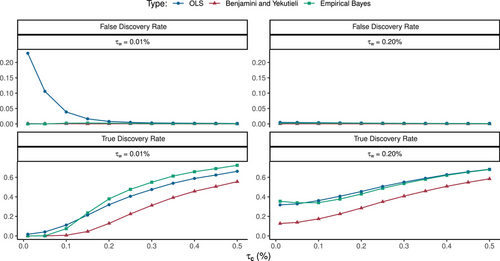
When idiosyncratic variation in true alphas is small (left panels with ) and the variation in cluster alphas is also small (values of near zero on the horizontal axis), alphas are very small and true discoveries are unlikely. In this case, the OLS FDR can be as high as 25% as seen in the upper left panel. However, both BY and EB successfully correct this problem and lower the FDR. The lower left panel shows that the BY correction pays a high price for its correction in terms of statistical power when is larger. In contrast, EB exhibits much better power to detect true positives while maintaining a similar false discovery control as BY. In fact, when there are more discoveries to be made in the data (as increases), EB becomes even more likely to identify true positives than OLS. This is due to the joint nature of the Bayesian model, whose estimates are especially precise compared to OLS due to EB's ability to learn more efficiently from dependent data. This result illustrates the observation by Greenland and Robins (1991) that “Unlike conventional multiple comparisons, empirical-Bayes and Bayes approaches will alter and can improve point estimates and can provide more powerful tests and more precise (narrower) interval estimators.” When the idiosyncratic variation is larger (), there are many more true discoveries to be made, so the FDR tends to be low even for OLS with no correction. Yet, in the lower right panel, we continue to see the costly loss of statistical power suffered by the BY correction.
In summary, EB accomplishes a flexible MT adjustment by adapting to the data-generating process. When discoveries are rare so that there is a comparatively high likelihood of false discovery, EB imposes heavy shrinkage and behaves similarly to the conservative BY correction. In this case, the benefit of conservatism costs little in terms of power exactly because true discoveries are rare. Yet, when discoveries are more likely, EB behaves more like uncorrected OLS, giving it high power to detect discoveries and suffering little in terms of false discoveries because true positives abound.
The limitations of frequentist MT corrections are well studied in the statistics literature. Berry and Hochberg (1999) note that “these procedures are very conservative (especially in large families) and have been subjected to criticism for paying too much in terms of power for achieving (conservative) control of selection effects.” The reason is that, while inflating confidence intervals and p-values reduces the discovery of false positives, it also reduces power to detect true positives.
Much of the discussion around MT adjustments in the finance literature fails to consider the loss of power associated with frequentist corrections. But as Greenland and Hofman (2019) point out, this trade-off should be a first-order consideration for a researcher navigating MT, and frequentist MT corrections tend to place an implicit cost on false positives that can be unreasonably large. Unlike some medical contexts for example, there is no obvious motivation for asymmetric treatment of false positives and missed positives in factor research. The finance researcher may be willing to accept the risk of a few false discoveries to avoid missing too many true discoveries. In statistics, this is sometimes discussed in terms of an (abstract) cost of Type I versus Type II errors,27 but in finance we can make this cost concrete: We can look at the profit of trading on the discovered factors, where the cost of false discoveries is then the resulting extra risk and money lost (Section III.C.1).
II. A New Public Data Set of Global Factors
We study a global data set with 153 factors in 93 countries. In this section, we provide a brief overview of our data construction. We have posted the data and code along with extensive documentation detailing each implementation choice that we make for each factor.28
A. Factors
The set of factors that we study is based on the exhaustive list compiled by Hou, Xue, and Zhang (2020). They study 202 different characteristic signals from which they build 452 factor portfolios. The proliferation is due to treating one-, six-, and 12-month holding periods for a given characteristic as different factors, and due to their inclusion of both annual and quarterly updates of some accounting-based factors. In contrast, we focus on a one-month holding period for all factors, and we only include the version that updates with the most recent accounting data—this could be either annual or quarterly. Finally, we exclude a small number of factors for which data are not available globally. This gives us a set of 180 feasible global factors. For this set, we exclude factors based on industry or analyst data because they have comparatively short samples.29 This leaves us with 138 factors. Finally, we add 15 factors studied in the literature that were not included in Hou, Xue, and Zhang (2020). For each characteristic, we build the one-month-holding-period factor return within each country as follows. First, in each country and month, we sort stocks into characteristic terciles (top/middle/bottom third) with breakpoints based on non-micro stocks in that country.30 For each tercile, we compute its “capped value weight” return, meaning that we weight stocks by their market equity winsorized at the NYSE 80 percentile. This construction ensures that tiny stocks have tiny weights and any one mega stock does not dominate a portfolio in an effort to create tradable, yet balanced, portfolios.31 The factor is then defined as the high-tercile return minus the low-tercile return, corresponding to the excess return of a long-short zero-net-investment strategy. The factor is long (short) the tercile identified by the original paper to have the highest (lowest) expected return.
We scale all factors such that their monthly idiosyncratic volatility is (i.e., 10% annualized), which ensures cross-sectional stationarity and a prior that factors are similar in terms of their information ratio. Finally, we compute each factor's via an OLS regression on a constant and the corresponding region's market portfolio.
For a factor return to be nonmissing, we require that it have at least five stocks in each of the long and short legs. We also require a minimum of 60 nonmissing monthly observations for each country-specific factor for inclusion in our sample. When grouping countries into regions (U.S., developed ex-U.S., and emerging), we use the Morgan Stanley Capital International (MSCI) development classification as of January 7, 2021. When aggregating factors across countries, we use capitalization-weighted averages of the country-specific factors. For the developed and emerging market factors, we require that at least three countries have nonmissing factor returns.
B. Clusters
We group factors into clusters using hierarchical agglomerative clustering (Murtagh and Legendre (2014)). We define the distance between factors as one minus their pairwise correlation and use the linkage criterion of Ward (1963). The correlation is computed based on CAPM-residual returns of U.S. factors signed as in the original paper. Figure IA.15 of the Internet Appendix shows the resulting dendrogram, which illustrates the hierarchical clusters identified by the algorithm. Based on the dendrogram, we choose 13 clusters that demonstrate a high degree of economic and statistical similarity. The cluster names indicate the types of characteristics that dominate each group: Accruals*, Debt Issuance*, Investment*, Leverage*, Low Risk, Momentum, Profit Growth, Profitability, Quality, Seasonality, Size*, Short-Term Reversal, and Value, where (*) indicates that these factors bet against the corresponding characteristic (e.g., accrual factors go long stocks with low accruals while shorting those with high accruals). Figure IA.16 shows that the average within-cluster pairwise correlation is above 0.5 for nine out of 13 clusters. Table IA.II provides details on the cluster assignment, sign convention, and original publication source for each factor.
C. Data and Characteristics
Return data are from CRSP for the United States (beginning in 1926) and from Compustat for all other countries (beginning in 1986 for most developed countries).32 All accounting data are from Compustat. For international data, all variables are measured in U.S. dollars (based on exchange rates from Compustat) and excess returns are relative to the U.S. Treasury bill rate. To alleviate the influence of data errors in the international data, we winsorize returns from Compustat at 0.1% and 99.9% each month.
We restrict our focus to common stocks that are identified by Compustat as the primary security of the underlying firm and assign stocks to countries based on the country of their exchange.33 In the United States, we include delisting returns from CRSP. If a delisting return is missing and the delisting is for a performance-based reason, we set the delisting return to −30% following Shumway (1997). In the global data, delisting returns are not available, so all performance-based delistings are assigned a return of −30%.
We build characteristics in a consistent way, that sometimes deviates from the exact implementation used in the original reference. For example, for characteristics that use book equity, we always follow the method in Fama and French (1993). Furthermore, we always use the most recent accounting data, whether annual or quarterly. Quarterly income and cash flow items are aggregated over the previous four quarters to avoid distortions from seasonal effects. We assume that accounting data are available four months after the fiscal period end. When creating valuation ratios, we always use the most recent price data following Asness and Frazzini (2013). Section IX in the Internet Appendix contains detailed documentation of our data set.
D. EB Estimation
We estimate the hyperparameters and the posterior alpha distributions of our Bayesian model via EB. Appendix B provides details on the EB methodology and the estimated parameters.
III. Empirical Assessment of Factor Replicability
We now report replication results for our global factor sample. We first present an internal validity analysis by studying U.S. factors over the full sample. We then analyze external validity in the global cross section and in the time series (postpublication factor returns).
A. Internal Validity
We plot the full-sample performance of U.S. factors in Figure 4. Each panel shows the CAPM alpha point estimate of each factor corresponding to the dot at the center of the vertical bars. Vertical bars represent the 95% confidence interval for each estimate. Bar colors and linetypes differentiate between three types of factors. Solid blue indicates factors that are significant in the original study and remain significant in our full sample. Dashed red indicates factors that are significant in the original study but insignificant in our test. Dotted green indicates factors that are not significant in the original study but are included in the sample of Hou, Xue, and Zhang (2020).
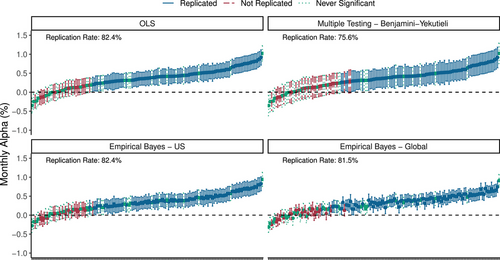
The four panels in Figure 4 differ in how the alphas and their confidence intervals are estimated. The upper left panel reports the simple OLS estimate of each alpha, , and the 95% confidence intervals based on unadjusted standard errors, .34 The factors are sorted by OLS estimate, and we use this ordering for the other three panels as well. We find that the OLS replication rate is 82.4%, computed as the number of solid blue factors (98) divided by the sum of solid blue and dashed red factors (119). Based on OLS tests, factors are highly replicable.
The upper right panel repeats this analysis using the MT adjustment of BY, which is advocated by Harvey, Liu, and Zhu (2016) and implemented by Hou, Xue, and Zhang (2020). This method leaves the OLS point estimate unchanged, but inflates the p-value. We illustrate this visually by widening the alpha confidence interval. Specifically, we find the BY-implied critical value35 in our sample to have a t-statistic of 2.7, and we compute the corresponding confidence interval as . We deem a factor as significant according to the BY method if this interval lies entirely above zero. Naturally, this widening of confidence intervals produces a lower replication rate of 75.6%. However, the BY correction does not materially change the OLS-based conclusion that factors appear to be highly replicable.
The lower left panel is based on our EB estimates using the full sample of U.S. factors. For each factor, we use Proposition 4 to compute its posterior mean, , shown as the dot at the center of the confidence interval. These dots change relative to the OLS estimates, in contrast to BY and other frequentist MT methods that only change the size of the confidence intervals. We also compute the posterior volatility to produce Bayesian confidence intervals, . The replication rate based on Bayesian model estimates is 82.4%, larger than BY and, coincidentally, the same as the OLS replication rate. This replication rate has a built-in conservatism from the zero-alpha prior, and it further accounts for the multiplicity of factors because each factor's posterior depends on all of the observed evidence in the United States (not just own-factor performance).
The lower right panel again reports EB estimates for U.S. factors, but now we allow the posterior to depend on data from all over the world, not just on U.S. data. That is, we compute the posterior mean and variance for each U.S. factor conditional on the alpha estimates for all factors in all regions. The resulting replication rate is 81.5%, which is slightly lower than the EB replication rate using only U.S. data. Some posterior means are reduced due to the fact that some factors have not performed as well outside the United States, which affects posterior means for the United States through the dependence among global alphas. For example, when the Bayesian model seeks to learn the true alpha of the “U.S. change in book equity” factor, the Bayesian's conviction regarding positive alpha is reduced by accounting for the fact that the international version of this factor has underperformed the U.S. version.36
To further assess internal validity, we investigate the replication rate for U.S. factors when those factors are constructed from subsamples based on stock size. One of the leading criticisms of factor research replicability is that results are driven by illiquid small stocks whose behavior largely reflects market frictions and microstructure as opposed to just economic fundamentals or investor preferences. In particular, Hou, Xue, and Zhang (2020) argue that they find a low replication rate because they limit the influence of micro-caps. We find that factors demonstrate a high replication rate throughout the size distribution. Panel A of Figure 5 summarizes replication rates for U.S. size categories shown in the five bars: mega stocks (largest 20% of stocks based on NYSE breakpoints), large stocks (market capitalization between the 80th and 50th percentile of NYSE stocks), small stocks (between the 50th and 20th percentile), micro stocks (between the 20th and 1st percentile), and nano stocks (market capitalization below the 1st percentile).
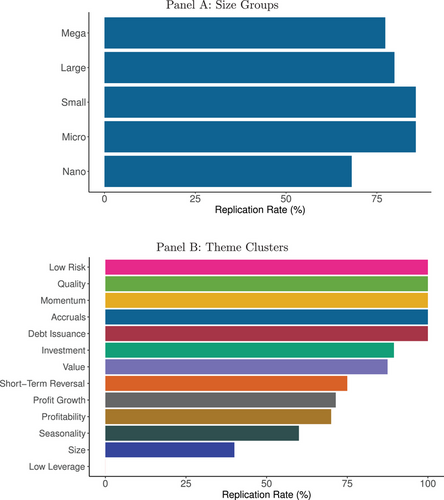
We see that the EB replication rates in mega- and large-stock samples are 77.3% and 79.8%, respectively. This is only marginally lower than the overall U.S. sample replication rate of 82.4%, indicating that criticisms of factor replicability based on arguments around stock size or liquidity are largely groundless. For comparison, small, micro, and nano stocks deliver replication rates of 85.7%, 85.7%, and 68.1%, respectively.
In Panel B of Figure 5, we provide U.S. factor replication rates by theme cluster. Eleven out of 13 themes are replicable with a rate of 50% or better, with the exceptions being the low leverage and size themes. To understand these exceptions, we note that size factors are stronger in emerging markets (bottom panel of Figure IA.7) and among micro and nano stocks (bottom panels of Figure IA.8). The theoretical foundation of the size effect is compensation for market illiquidity (Amihud and Mendelson (1986)) and market liquidity risk (Acharya and Pedersen (2005)). Theory predicts that the illiquidity (risk) premium should be the same order of magnitude as the differences in trading costs, and these differences are simply much larger in emerging markets and among micro stocks.
Another reason some factors and themes appear insignificant is that we do not account for other factors. Factors published after 1993 are routinely benchmarked to the Fama-French three-factor model (and, more recently, to the updated five-factor model). Some factors are insignificant in terms of raw return or CAPM alpha, but their alpha becomes significant after controlling for other factors. Indeed, this explanation accounts for the lack of replicability for the low-leverage theme. While CAPM alphas of low-leverage factors are insignificant, we find that it is one of the best-performing themes when we account for multiple factors (see Section III.D.2 below).
B. External Validity
We find a high replication rate in our full-sample analysis, indicating that the large majority of factors are reproducible at least in-sample. We next study the external validity of these results in international data and in postpublication U.S. data.
B.1. Global Replication
Figure 6 shows corresponding replication rates around the world. We report replication rates from four testing approaches: (i) OLS with no adjustment, (ii) OLS with MT adjustment of BY, (iii) the EB posterior conditioning only on factors within a region (“Empirical Bayes – Region”), and (iv) EB conditioning on factors in all regions (“Empirical Bayes – All”). Even when using all global data to update the posterior of all factors, the reported Bayesian replication rate applies only to the factors within the stated region.
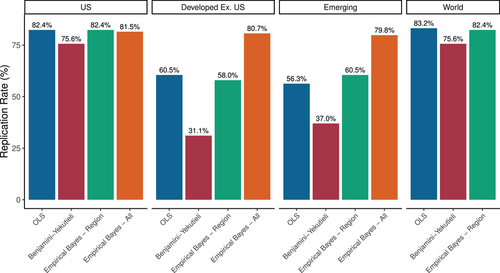
The first set of bars establishes a baseline by showing replication rates for the U.S. sample, summarizing the results from Figure 4. The next two sets of bars correspond to the developed ex.-U.S. sample and the emerging markets sample, respectively.37 Each region's factor is a capitalization-weighted average of that factor among countries within a given region, and the replication rate describes the fraction of significant CAPM alphas for these regional factors.
OLS replication rates in developed and emerging markets are generally lower than in the United States, and the frequentist BY correction has an especially large negative impact on replication rate. This is a case in which the Bayesian approach to MT is especially powerful. Even though the alphas of all regions are shrunk toward zero, the global information set helps EB achieve a high degree of precision, narrowing the posterior distribution around the shrunk point estimate. We can see this in increments. First, the EB replication rate using region-specific data (“Empirical Bayes – Region” in the figure) is just below the OLS replication rate but much higher than the BY rate. When the posterior leverages global data (“Empirical Bayes – All” in the figure), the replication rate is even higher, reflecting the benefits of sharing information across regions, as recommended by the dependence among alphas in the hierarchical model.
Finally, we use the global model to compute, for each factor, the capitalization-weighted average alpha across all countries in our sample (“World” in the figure). Using data from around the world, we find a Bayesian replication rate of 82.4%.
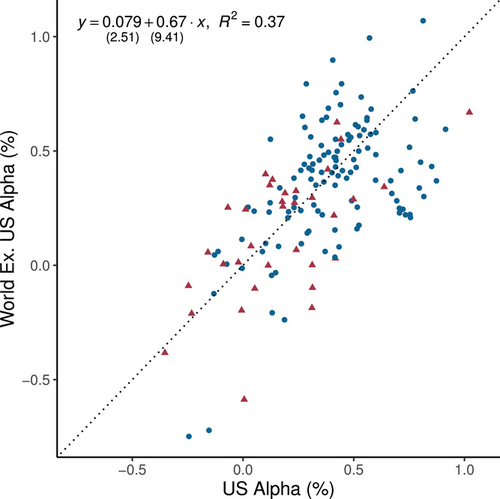
In summary, our EB-All method yields a high replication rate in all regions. That said, the OLS replication rates are lower outside the U.S. than in the U.S., which is primarily due to the fact that foreign markets have shorter time samples—the point estimates of alphas are similar in magnitude for the U.S. and international data. Figure 7 shows the alpha of each U.S. factor against the alpha of the corresponding factor for the world ex.-U.S. universe. The data cloud aligns closely with the 45 line, demonstrating the close similarity of alpha magnitudes in the two samples. But shorter international samples widen confidence intervals, and this is the primary reason for the drop in OLS replication rates outside the United States.
B.2. Time-Series Out-of-Sample Evidence
McLean and Pontiff (2016) document the intriguing fact that, following publication, factor performance tends to decay. They estimate an average postpublication decline of 58% in factor returns. In our data, the average in-sample alpha is 0.49% per month and the average out-of-sample alpha is 0.26% when looking postoriginal sample, implying a decline of 47%.
We gain further economic insight by looking at these findings cross-sectionally. Figure 8 provides a cross-sectional comparison of the in-sample and out-of-sample alphas of our U.S. factors. The in-sample period is the sample studied in the original reference. The out-of-sample period in Panel A is the period before the start of in-sample period, while in Panel B it is the period following the in-sample period. Panel C defines out-of-sample as the combined data from the periods before and after the originally studied sample. We find that 82.6% of the U.S. factors that were significant in the original publication also have positive returns in the preoriginal sample, 83.3% are positive in the postoriginal sample, and 87.4% are positive in the combined out-of-sample period. When we regress out-of-sample alphas on in-sample alphas using generalized least squares (GLS), we find a slope coefficient of 0.57, 0.26, and 0.35 in Panels A, B, and C, respectively. The slopes are highly significant (ranging from to ), indicating that in-sample alphas contain something “real” rather than being the outcome of pure data mining, as factors that performed better in-sample also tend to perform better out-of-sample.
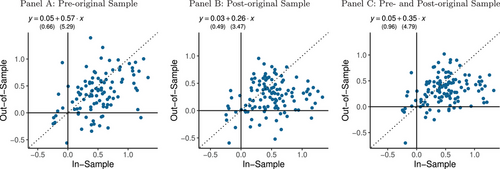
The significantly positive slope allows us to reject the hypothesis of “pure alpha-hacking,” which would imply a slope of zero, as seen in Proposition 1. Further, the regression intercept is positive, while alpha-hacking of the form studied in Proposition 1 would imply a negative intercept. That the slope coefficient is positive and less than one is consistent with the basic Bayesian logic of equation (4). As we emphasize in Section I, a Bayesian would expect at least some attenuation in out-of-sample performance. This is because the published studies report the OLS estimate, while Bayesian beliefs shrink the OLS estimate toward the zero-alpha prior. More specifically, with no alpha-hacking or arbitrage, the Bayesian expects a slope of approximately 0.9 using equation (5) and our EB hyperparameters (see Table I).38 Hence, the slope coefficients in Figure 8 are too low relative to this Bayesian benchmark. In addition to the moderate slope, there is evidence that the dots in Figure 8 have a concave shape (as seen more clearly in Figure IA.3). These results indicate that, while we can rule out pure alpha-hacking (or p-hacking), there is some evidence that the highest in-sample alphas may be data-mined or arbitraged down.
| This table presents as the estimated dispersion in cluster alphas (e.g., the dispersion in the alpha of the value cluster alpha, momentum cluster). When we estimate a single region, is the idiosyncratic dispersion of alphas within each cluster. When we jointly estimate several regions, then is the estimated dispersion in alphas across signals within each cluster, and is the estimated idiosyncratic dispersion in alphas for factors identified by their signal and region. | |||
|---|---|---|---|
| Sample | |||
| USA | 0.35% | 0.21% | |
| Developed | 0.24% | 0.18% | |
| Emerging | 0.32% | 0.24% | |
| USA, Developed & Emerging | 0.30% | 0.19% | 0.10% |
| World | 0.37% | 0.23% | |
| World ex.-US | 0.29% | 0.20% | |
| USA—Mega | 0.26% | 0.16% | |
| USA—Large | 0.31% | 0.18% | |
| USA—Small | 0.44% | 0.26% | |
| USA—Micro | 0.48% | 0.32% | |
| USA—Nano | 0.42% | 0.28% | |
From the Bayesian perspective, another interesting evaluation of time-series external validity is to ask whether the new information contained in out-of-sample data moves the posterior alpha toward zero. Imagine a Bayesian observing the arrival of factor data in real time. As new data arrive, she updates her beliefs for all factors based on the information in the full cross section of factor data. In the top panel of Figure 9, we show how the Bayesian's posterior of the average alpha would have evolved in real time.39 We focus on all the world factors that are available since at least 1955 and significant in the original paper. Starting in 1960, we reestimate the hierarchical model using the EB estimator in December of each year. The plot shows the CAPM alpha and corresponding 95% confidence interval of an equal-weighted portfolio of the available factors. The posterior mean alpha becomes relatively stable from the mid-1980s, around 0.4% per month. Further, as empirical evidence has accumulated over time, the confidence interval narrows by one-third, from about 0.16% in 1960 to 0.10% in 2020.
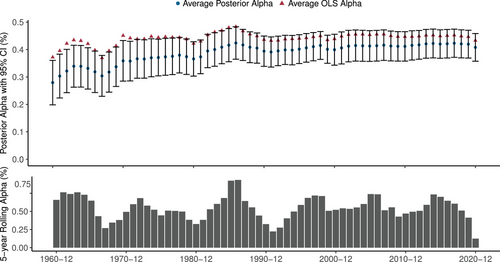
To understand the posterior alpha, Figure 9 also shows the average OLS alpha (red triangles) and the bottom panel in Figure 9 shows the rolling five-year average monthly alpha among all these factors. We see that the EB posterior is below the OLS estimate, especially in the beginning, which occurs because the Bayesian posterior is shrunk toward the zero prior. Naturally, periods of good performance increase the posterior mean as well as the OLS estimate, and vice versa for poor performance. Over time, the OLS estimate moves nearer to the Bayesian posterior mean.
To further understand why the posterior alpha is relatively stable with a tightening confidence interval, consider the following simple example. Suppose a researcher has years of data for factors with an OLS alpha estimate of with standard error . Further, assume that their zero-alpha prior is equally as informative as their 10-year sample (i.e., ). Then, the shrinkage factor is using equation (5). So, after observing the first 10 years with , the Bayesian expects a future alpha of (equation (4)). What happens if this Bayesian belief is confirmed by additional data, that is, the factor realizes an alpha of 5% over the next 10 years? In this case, the full-sample OLS alpha is , but now the shrinkage factor becomes because the sample length doubles, . This results in a posterior alpha of . Naturally, when beliefs are confirmed by additional data, the posterior mean does not change. Nevertheless, we learn something from the additional data, because our conviction increases as the posterior variance is reduced. If , the posterior volatility goes from 2.2% with 10 years of data to 1.8% with 20 years of data, and the confidence interval, , decreases from to .
C. Bayesian MT
A great advantage of Bayesian methods for tackling challenges in MT is that, from the posterior distribution, we can make explicit probability calculations for essentially any inferential question. We simulate from our EB posterior to investigate the FDRs and FWERs among the set of global factors that were significant in the original study. We define a false discovery as a factor where we claim that the alpha is positive, but the true alpha is negative.40
First, based on Proposition 5, we calculate the Bayesian FDR in our sample as the average posterior probability of a false discovery, p-null, among all discoveries. We find that , meaning that we expect roughly one discovery in 1,000 to be a false positive given our Bayesian hierarchical model estimates. The posterior standard error for is 0.3% with a confidence interval of [0,1%]. In other words, the model generates a highly conservative MT adjustment in the sense that once a factor is found to be significant, we can be relatively confident that the effect is genuine.
From the posterior, we can also compute the expected fraction of discovered factors that are “true,” which in general is different than the replication rate. The replication rate is the fraction of factors having , while the expected fraction of true factors is . The replication rate gives a conservative take on the number of true factors—the expected fraction of true factors is typically higher than the replication rate. To understand this conservatism, consider an example in which all factors have a 90% posterior probability of being true. These would all individually be counted as “not replicated,” but they would contribute to a high expected fraction of true factors. Indeed, we estimate that the expected fraction of factors with truly positive alphas is 94% (with a posterior standard error of 1.3%), which is notably higher than our estimated replication rate.
C.1. Economic Benefits of More Powerful Tests
MT adjustments should ultimately be evaluated by whether they lead to better decisions. It is important to balance the relative costs of false positives versus false negatives, and the appropriate trade-off depends on the context of the problem (Greenland and Hofman (2019)). We apply this general principle in our context by directly measuring costs in terms of investment performance. Specifically, we can compute the difference in out-of-sample investment performance from investing using factors chosen with different methods. We compare two alternatives. One is the BY decision rule advocated by Harvey, Liu, and Zhu (2016), which is a frequentist MT method that successfully controls false discoveries relative to OLS, but in doing so sacrifices power (the ability to detect true positives). The second alternative is our EB method, whose false discovery control typically lies somewhere between BY and unadjusted OLS. EB uses the data sample itself to decide whether its discoveries should behave more similarly to BY or to unadjusted OLS.
For investors, the optimal decision rule is the one that leads to the best performance out-of-sample. For the most part, the set of discovered factors for BY and EB coincide. It is only in marginal cases where they disagree, which occurs in our sample when EB makes a discovery that BY deems insignificant. Therefore, to evaluate MT approaches in economic terms, we track the out-of-sample performance of factors included by EB but excluded by BY. If the performance of these is negative on average, then the BY correction is warranted and preferred by the investor.
We find that the out-of-sample performance of factors discovered by EB but not BY is positive on average and highly significant. The alpha for these marginal cases is 0.35% per month among U.S. factors ().41 This estimate suggests that the BY decision rule is too conservative: An investor using the rule would fail to invest in factors that subsequently have a high out-of-sample return. Another way to see that the BY decision rule is too conservative comes from the connection between the Sharpe ratio and t-statistics: . If we have a factor with an annual Sharpe ratio of 0.5, an investor using the 1.96 cutoff would in expectation invest in the factor after 15 years, whereas an investor using the 2.78 cutoff would not start investing until observing the factor for 31 years.
C.2. Addressing Unobserved Factors, Publication Bias, and Other Biases
A potential concern with our replication rate is that the set of factors that make it into the literature is a selected sample. In particular, researchers may have tried many different factors, some of which are observed in the literature, while others are unobserved because they never got published. Unobserved factors may have worse average performance if poor performance makes publication more difficult or less desirable. Alternatively, unobserved factors could have strong performance if people chose to trade on them in secret rather than publish them. Either way, we next show how unobserved factors can be addressed in our framework.
The key insight is that the performance of factors across the universe of observed and unobserved factors is captured in our prior parameters . Indeed, large values of these priors correspond to a large dispersion of alphas (i.e., a lot of large alphas “out there”), while small values mean that most true alphas are close to zero. Therefore, a smaller τ leads to stronger shrinkage toward zero for our posterior alphas, leading to fewer factor “discoveries” and a lower replication rate. Figure 10 shows how our estimated replication rate depends on the most important prior parameter, , based on the that we estimate from the data.42
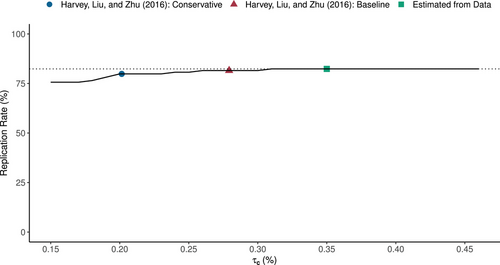
In Figure 10, we show how the replication rate varies with in precise quantitative terms. Note that while the replication rate does indeed rise with , the differences are small in magnitude across a large range of values, demonstrating robustness of our conclusions about replicability.
The stable replication rate in Figure 10 also suggests that the replication rate among the observed factors would be similar even if we had observed the unobserved factors. The figure highlights several key values of : both the value of that we estimated from the observed data (as explained in Appendix B) and values that adjust for unobserved data in different ways.
We adjust for unobserved factors as follows. We simulate a data set that proxies for the full set of factors in the population (including those that are unobserved), and then estimate the τ's that match this sample. One set of simulations is constructed to match the baseline scenario of Harvey, Liu, and Zhu (2016, table 5.A, row 1), which estimates that researchers have tried factors, of which 39.6% have zero alpha and the rest have a Sharpe ratio of 0.44. We also consider the more conservative scenario of Harvey, Liu, and Zhu (2016, table 5.B, row 1), which implies that researchers have tried factors, of which 68.3% have zero alpha. Section IV of the Internet Appendix provides more details on these simulations. The result, as seen in Figure 10, is that values of that correspond to these scenarios from Harvey, Liu, and Zhu (2016) still lead to a conclusion of a high replication rate in our factor universe. The replication rate is 81.5%, and 79.8% for the prior hyperparameters implied by the baseline and conservative scenario, respectively.
A closely related bias is that factors may suffer from alpha-hacking as discussed in Section I.A (Proposition 1), which makes realized in-sample factor returns too high. To account for this bias, we estimate the prior hyperparameters using only out-of-sample data. The estimated values are and . These hyperparameters are similar to those implied by the baseline scenario of Harvey, Liu, and Zhu (2016) as seen in Figure 10. With these hyperparameters, the replication rate is 81.5%.
D. Economic Significance of Factors
Which factors (and which themes) are the most impactful anomalies in economic terms? We shed light on this question by identifying which factors matter most from an investment performance standpoint.
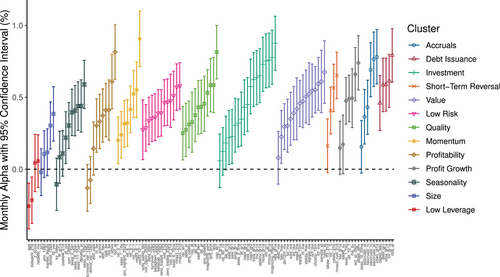
Figure 11 shows the alpha confidence intervals for all world factors, sorted by the median posterior alpha within clusters. This figure is similar to Figure 4, but now we focus on the world instead of the U.S. factors, and here we sort factors into clusters. We also focus on factors that the original studies conclude are significant. We see that world factor alphas tend to be economically large, often above 0.3% per month, and highly significant in most clusters. The exception is the low-leverage cluster, where we also see a low replication rate in preceding analyses.
D.1. By Region and By Size
We next consider which factors are most economically important across global regions and across stock size groups. In Panel A of Figure 12, we construct factors using only stocks in the five size subsamples presented earlier in Figure 5, namely, mega, large, small, micro, and nano stock samples. For each sample, we calculate cluster-level alphas as the equal-weighted average alpha of rank-weighted factors within the cluster.43 We see, perhaps surprisingly, that the ordering and magnitude of alphas is broadly similar across size groups. The Spearman rank correlation of alphas for mega caps versus micro caps is 73%. Only the nano stock sample, defined as stocks below the 1st percentile of the NYSE size distribution (which amounted to 458 out of 4,356 stocks in the United States at the end of 2020), exhibits notable deviation from the other groups. The Spearman rank correlation between alphas of mega caps and nano caps is 36%.
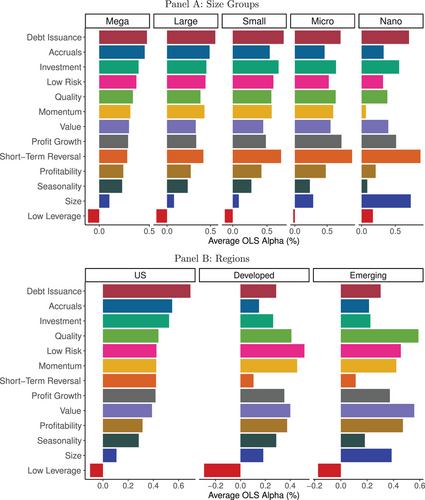
Panel B of Figure 12 shows cluster-level alphas across regions. Again, we find consistency in alphas across the globe, with the obvious standout being the size theme, which is much more important in emerging markets than in developed markets. U.S. factor alphas share a 62% Spearman correlation with the developed ex.-U.S. sample, and a 43% correlation with the emerging markets sample.
D.2. Controlling for Other Themes
We have focused so far on whether factors (or clusters) possess significant positive alpha relative to the market. The limitation of studying factors in terms of CAPM alpha is that it does not control for duplicate behavior other than through the market factor. Economically important factors are those that have large impact on an investor's overall portfolio, and this requires understanding which clusters contribute alpha while controlling for all others.
To this end, we estimate cluster weights in a tangency portfolio that invests jointly in all cluster-level portfolios. We test the significance of the estimated weights using the method of Britten-Jones (1999). In addition to our 13 cluster-level factors, we also include the market portfolio as a way to benchmark factors to the CAPM null. Lastly, we constrain all weights to be nonnegative (because we have signed the factors to have positive expected returns according to the findings of the original studies).
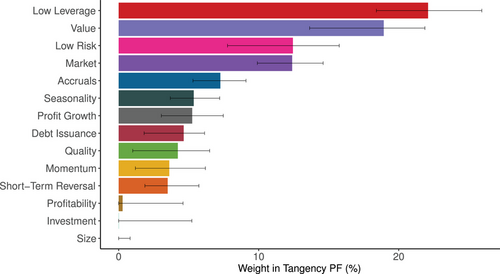
Figure 13 reports the estimated tangency portfolio weights and their 90% bootstrap confidence intervals. When a factor has a significant weight in the tangency portfolio, it means that it matters for an investor, even controlling for all the other factors. We see that all but three clusters are significant in this sense. We also see that conclusions about cluster importance change when clusters are studied jointly. For example, value factors become stronger when controlling for other effects because of their hedging benefits relative to momentum, quality, and low leverage. More surprisingly, the low-leverage cluster becomes one of the most heavily weighted clusters, in large part due to its ability to hedge value and low-risk factors. The hedging performance of value and low-leverage clusters is clearly discernible in Table IA.16, which shows the average pairwise correlations among factors within and across clusters.44 Section VI of the Internet Appendix provides further performance attribution of the tangency portfolio at the factor level.45
D.3. Evolution of Finance Factor Research
The number of published factors has increased over time as seen in the bottom panel of Figure 14. To what extent have these new factors continued to add new insights versus simply repackage existing information?
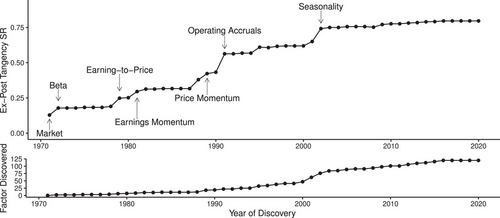
To address this question, we consider how the optimal risk-return tradeoff has evolved over time as factors have been discovered. Specifically, Figure 14 computes the monthly Sharpe ratio of the ex post tangency portfolio that only invests in factors discovered by a certain point in time.46 The starting point (on the left) of the analysis is the 0.13 Sharpe ratio of the market portfolio in the U.S. sample over 1972 to 2020 when all factors are available. The ending point (on the right) is the 0.80 Sharpe ratio of the tangency portfolio that invests the optimal weights across all factors over the same U.S. sample period.47 In between, we see how the Sharpe ratio of the tangency portfolio has evolved as factors have been discovered. The improvement is gradual over time, but we also see occasional large increases when researchers have discovered especially impactful factors (usually corresponding to new themes in our classification scheme). An example is the operating accruals factor proposed by Sloan (1996), which increased the tangency Sharpe ratio from 0.43 to 0.56. More recently, the seasonality factors of Heston and Sadka (2008) have increased the Sharpe ratio from 0.65 to 0.74.
IV. Conclusion: Finance Research Posterior
We introduce a hierarchical Bayesian model of alphas that emphasizes the joint behavior of factors and provides a more powerful MT adjustment than common frequentist methods. Based on this framework, we revisit the evidence on replicability in factor research and come to substantially different conclusions than prior literature. We find that U.S. equity factors have a high degree of internal validity in the sense that over 80% of factors remain significant after modifications in factor construction that make all factors consistent and more implementable while still capturing the original signal (Hamermesh (2007)) and after accounting for MT concerns (Harvey, Liu, and Zhu (2016), Harvey (2017)).
We also provide new evidence demonstrating a high degree of external validity in factor research. In particular, we find highly similar qualitative and quantitative behavior in a large sample of 153 factors across 93 countries as we find in the United States. We also show that, within the United States, factors exhibit a high degree of consistency between their published in-sample results and out-of-sample data not considered in the original studies. We show that some out-of-sample factor decay is to be expected in light of Bayesian posteriors based on publication evidence. Therefore, the new evidence from postpublication data largely confirms the Bayesian's beliefs, which has led to relatively stable Bayesian alpha estimates over time.
In addition to providing a powerful tool for replication, our Bayesian framework has several additional applications. For example, the model can be used to correctly interpret out-of-sample evidence, look for evidence of alpha-hacking, compute the expected number of false discoveries and other relevant statistics based on the posterior, analyze portfolio choice taking into account both estimation uncertainty and return volatility, and evaluate asset pricing models.
Finally, the code, data, and meticulous documentation for our analysis are available online. Our large global factor data set and the underlying stock-level characteristics are easily accessible to researchers by using our publicly available code and its direct link to WRDS. Our database will be updated regularly with new data releases and code improvements. We hope that our methodology and data will help promote credible finance research.
Editors: Stefan Nagel, Philip Bond, Amit Seru, and Wei Xiong
Appendix A: Additional Results and Proofs
A.1. Additional Results on Alpha-Hacking
We consider the situation where the researcher has in-sample data from time 1 to time T and an out-of-sample (oos) period from time to . The researcher may have used alpha-hacking during the in-sample period, but this does not affect the out-of-sample period. The researcher is interested in the posterior alpha based on the total evidence, in-sample and out-of-sample, which is useful for predicting factor performance in a future time period (i.e., a time period that is out-of-sample relative to the existing out-of-sample period).
Proposition A.1. (Out-of-sample alpha)The posterior alpha based on in-sample data from time 1 to T with alpha-hacking, and an out-of-sample period from to is given by
We see that the more alpha-hacking the researcher has done (higher ), the less weight we put on the in-sample period relative to the out-of-sample period. Further, the in-sample period has the nonproportional discounting due to alpha-hacking (), which we do not have for out-of-sample evidence.
This result formalizes the idea that an in-sample backtest plus live performance is not the same as a longer backtest. For example, 10 years of backtest plus 10 years of live performance is more meaningful that 20 years of backtest with no live performance. The difference is that the out-of-sample performance is free from alpha-hacking.
A.2. Proofs and Lemmas
The proofs also make use of the following two lemmas.
Lemma A.1.For random variables , and z, it holds that and, if the random variables are jointly normal, then .
Lemma A.2.Let A be an matrix for which all diagonal elements equal a and all off-diagonal elements equal b, where and . Then the inverse exists and is of the same form:
Proof of Lemma A.1.Using the definition of conditional variance, we have
Proof of Lemma A.2.The proof follows from inspection: The product of A and its proposed inverse clearly has the same form as A with diagonal elements
Proof of Equations (4) to (6).The posterior distribution of the true alpha given the observed factor return is computed using (A3). The conditional mean is
Proof of Proposition 1.The posterior alpha with alpha-hacking is given via (A3) as
Proof of Proposition 2.The posterior mean given and is computed via (A3) as
The result about the posterior variance follows from Lemma A.1.
Proof of Proposition 3.The prior joint distribution of the true and estimated alphas is given by the following expression, where we focus on factor 1 without loss of generality:
Proof of Proposition 4.We write the joint prior distribution of true and observed alphas in the multilevel hierarchical model as
Proof of Proposition 5.Based on the definition of the Bayesian FDR, we have:
Proof of Proposition A.1.The posterior mean alpha is
Appendix B: EB Estimation
This estimation approach is an example of the EB method. It approximates the fully Bayesian posterior calculation (which requires integrating over a hyperprior distribution of hyperparameters, usually an onerous calculation) by setting the hyperparameters to their most likely values based on the marginal likelihood. It is particularly well suited to hierarchical Bayesian models in which parameters for individual observations share some common structure, so that the realized heterogeneity across individual observations is informative about sensible values for the hyperparameters of the prior. Our model and estimation approach implementation is a minor variation on Bayesian hierarchical normal mean models that are common in Bayesian statistics (textbook treatments include Efron (2012), Gelman et al. (2013), and Maritz (2018)). We conduct sensitivity analysis to ensure that our results are robust to a wide range of hyperparameters (see Figure IA.6). Also, we note that our EB methodology is more easily replicable than a full-Bayesian setting with additional hyperpriors as EB relies on closed-form Bayesian updating rather than numerical integration.
To ensure cross-sectional stationarity, we scale each factor such that their monthly idiosyncratic volatility is 10% (i.e., 10% annualized). To construct a plug-in estimate of the factor residual return covariance matrix, denoted , we face two main empirical challenges. First, the sample covariance is poorly behaved due the relatively large number of factors compared to the number of time-series observations. Second, we have an unbalanced panel because different factors come online at different points in time. To address the first challenge, we impose a block equicorrelation structure on Σ based on factors' cluster membership.49 The correlation between factors in clusters i and j is estimated as the average correlation among all pairs such that one factor is in cluster i and the other is in j. In our global analyses, blocks correspond to region-cluster pairs. To address unbalancedness, we use the bootstrap. In particular, we generate 10,000 bootstrap samples that resample rows of the unbalanced factor return data set. Each bootstrap sample is, therefore, also unbalanced, and we use this to produce a distribution of alpha estimates. From this we calculate as the covariance of alphas across bootstrap samples (imposing the block equicorrelation structure).
Table I shows the estimated hyperparameters across different samples. While most of our analysis is based on these full-sample estimates, we also consider rolling estimates of the hyperparameters when considering out-of-sample evidence as seen in Figure IA.5.
REFERENCES
- 1 Hamermesh (2007) contrasts “pure replication” and “scientific replication.” Pure replication is “checking on others' published papers using their data,” also called “reproduction” by Welch (2019), while scientific replication uses a “different sample, different population and perhaps similar, but not identical model.” We focus on scientific replication. We propose a new modeling framework to jointly estimate factor alphas, we use robust factor construction methods that are applied uniformly to all factors, and we test both internal and external validity of prior factor research along several dimensions, including out-of-sample time-series replication and international sample replication. In complementary and contemporaneous work, Chen and Zimmermann (2022) consider pure replication, attempting to use the same data and methods as the original papers for a large number of factors. They are able to reproduce nearly 100% of factors, but Hou, Xue, and Zhang (2020) challenge the scientific replication and Harvey, Liu, and Zhu (2016) challenge validity due to multiple testing (MT).
- 2 Similarly, Linnainmaa and Roberts (2018) state that: “the majority of accounting-based return anomalies, including investment, are most likely an artifact of data snooping.”
- 3 The data are available at https://jkpfactors.com. The data will be updated over time and will also be available through Wharton Research Data Services (WRDS). The code is available at https://github.com/bkelly-lab/ReplicationCrisis.
- 4 In particular, we use tercile spreads while they use deciles, we use tercile breakpoints from all stocks above the NYSE 20th percentile (i.e., non-micro-caps) while they use straight NYSE breakpoints, we always lag accounting data four months while they use a mixture of updating schemes, we exclude factors based on IBES data due to its relatively short history, we use capped value-weighting while they use straight value-weights, and we look at returns over a one-month holding period while they use one, six, and 12 months. In Section I of the Internet Appendix, we detail how each change affects the replication rate. The Internet Appendix may be found in the online version of this article.
- 5 We identify 34 factors from Hou, Xue, and Zhang (2020) for which the original paper did not find a significant alpha or did not study factor returns (see Table IA.II of the Internet Appendix).
- 6 A large statistics literature (see Gelman et al. (2013) and references therein) explains how Bayesian estimation naturally addresses MT problems and Gelman, Hill, and Yajima (2012) conclude that “the problem of multiple comparisons can disappear entirely when viewed from a hierarchical Bayesian perspective.” Chinco, Neuhierl, and Weber (2021) use a Bayesian estimation framework similar to ours for a different (but conceptually related) problem. They infer the distribution of coefficients in a stock return prediction model to calculate what they refer to as the “anomaly base rate.”
- 7 Our Bayesian approach leads to an even larger increase in the replication rate when using pure value-weighted returns (see Figure IA.1 of the Internet Appendix) and when considering global evidence outside the United States (as we show later, in Figure 6).
- 8 Taking this intuition further, we can obtain additional information from studying whether factors work in other asset classes, as has been done for value and momentum (Asness, Moskowitz, and Pedersen (2013)), betting against beta (Frazzini and Pedersen (2014)), time-series momentum (Moskowitz, Ooi, and Pedersen (2012)), and carry (Koijen et al. (2018)).
- 9 Extending the evidence to global stock markets, Jacobs and Müller (2020) find that “the United States is the only country with a reliable post-publication decline in long-short returns.” Chen and Zimmermann (2020b) use Bayesian methods to estimate bias-corrected postpublication performance and find that average returns drop by only 12% after publication in U.S. data.
- 10 Data prior to the sample used in original studies also constitute out-of-sample evidence (Linnainmaa and Roberts (2018), Ilmanen et al. (2021)). Our external validity conclusions hold when we also include pre–original-study out-of-sample evidence.
- 11 See Bryzgalova, Huang, and Julliard (2023), Kelly, Pruitt, and Su (2019), Chordia, Goyal, and Saretto (2020), Kozak, Nagel, and Santosh (2020), Green, Hand, and Zhang (2017), and Feng, Giglio, and Xiu (2020) for other perspectives on high-dimensional asset pricing problems, and Chen (2021) for an argument regarding why p-hacking cannot explain the existence of so many significant factors.
- 12 The out-of-sample performance across all significant factors under EB is also highly significant as shown in Figure IA.2 of the Internet Appendix.
- 13 Here, we seek to derive some simple expressions that illustrate the economic implications of Bayesian logic. In the empirical implementation, we use a slightly richer model, as discussed further below. The empirical implementation normalizes factors so that σ is given at 10% for all factors, while β must be estimated, but this does not affect the economic points that we make in this section.
- 14 We note that this elevated variance cannot be detected by looking at the in-sample variance of residual returns since the alpha-hacking term u does not depend on time t.
- 15 The framework can be generalized to a situation in which the global shocks have a different volatility and sample length. In this case, the Bayesian posterior puts more weight on the sample with lower volatility and longer length.
- 16 Alternatively, we can write the error terms in a similar way as we write the alphas in (14), namely, , where are idiosyncratic shocks that are independent across factors and of the common shock , with . Note that we require (the empirically realistic case) that since we cannot have an arbitrarily large number of normal random variables with equal negative correlation (because the corresponding variance-covariance matrix would not be positive semidefinite for large enough N).
- 17 The general hierarchical model is used extensively in the statistics literature (see, e.g., Gelman et al. (2013)), but to our knowledge the results in Proposition 3 are not in the literature.
- 18 The notation 1N refers to an vector of ones and is the identity matrix.
- 19 Stated differently, each diagonal element of Ω is . Further, if , then the element of Ω is if i and k are constructed from the same signal in the same cluster in different regions, it is if i and k are constructed from different signals in the same cluster, and it is zero if i and k are in different clusters.
- 20 See Greenland and Robins (1991), Berry and Hochberg (1999), Efron and Tibshirani (2002), Gelman, Hill, and Yajima (2012), among others. See Gelman (2016) for an intuitive, informal discussion of the topic.
- 21 We provide details on our EB estimation procedure in Appendix B.
- 22 We use a critical value of 2.5% rather than 5% because the 1.96 cutoff corresponds to a two-sided test, while false discoveries are only on one side in the Bayesian framework.
- 23 Efron (2007) includes related analysis but, to our knowledge, this particular result is new.
- 24 Proposition 5 formalizes the argument of Greenland and Robins (1991) that “from the empirical-Bayes or Bayesian perspective, multiple comparisons are not really a ‘problem.’ Rather, the multiplicity of comparisons provides an opportunity to improve our estimates through judicious use of any prior information (in the form of model assumptions) about the ensemble of parameters being estimated.”
- 25 The noise covariance matrix has a block structure calibrated to our data, with a correlation of 0.58 among factors in the same cluster and a correlation of 0.02 across clusters. The residual volatility for each factor is 10% per annum.
- 26 We define the true discovery rate to be the number of significantly positive alphas according to, respectively, OLS, BY, and EB divided by the number of truly positive alphas. Given our simulation structure, half of the alphas are expected to be positive in any simulation. Some of these will be small (i.e., economically insignificant) positives, so a testing procedure would require a high degree of statistical power to detect them. This is why the true discovery rate is below one even for high values of .
- 27 As Greenland and Robins (1991) point out, “Decision analysis requires, in addition to the likelihood function, a loss function, which indicates the cost of each action under the various possible values for the unknown parameter (benefits would be expressed as negative costs). Construction of a loss function requires one to quantify costs in terms of dollars, lives lost, or some other common scale.”
- 28 The data and code are available at https://jkpfactors.com/ and https://github.com/bkelly-lab/ReplicationCrisis. The data will be updated over time and will also be available via WRDS.
- 29 Global industry codes (GICS) are only available from 2000. I/B/E/S data are available from the mid-1980s but coverage in early years is somewhat sparse.
- 30 Specifically, we start with all nonmicro stocks in a country (i.e., larger than NYSE 20 percentile) and sort them into three groups of equal numbers of stocks based on the characteristic, say book-to-market. We then distribute the micro-cap stocks into the three groups based on the same characteristic breakpoints. This process ensures that the nonmicro stocks are distributed equally across portfolios, creating more tradable portfolios.
- 31 For robustness, Figure IA.1 of the Internet Appendix reports our replication results when using standard, uncapped value weights to construct factors.
- 32 Table IA.IV shows start date and other information for all countries included in our data set.
- 33 Compustat identifies primary securities in the United States, Canada, and rest of the world. This means that some firms can have up to three securities in our data set. In practice, the vast majority of firms (97%) only have one security in our sample at a given point in time.
- 34 We define as the diagonal of the alpha covariance matrix , which we estimate according to Appendix B.
- 35 We compute the BY-implied critical value as the average of the t-statistic of the factor that is just significant based on BY (the factor with the highest BY-adjusted p-value below 5%) and the t-statistic of the factor that is just insignificant (the factor with the lowest BY-adjusted p-value above 5%).
- 36 To provide a few more details on this example, the U.S. factor based on annual change in book equity (be_gr1a) has a posterior volatility of 0.095% using U.S. data and 0.077% using global data, leading to a tighter confidence interval with the global data. However, the posterior mean is 0.22% using only U.S. data and 0.13% using global data.
- 37 The developed and emerging samples are defined by the MSCI development classification and include 23 and 27 countries, respectively. The remaining 43 countries in our sample that are classified as neither developed nor emerging by MSCI do not appear in our developed and emerging region portfolios, but they are included in the “world” versions of our factor portfolios.
- 38 The slope is , where , the average in-sample period length is months, and .
- 39 Here, we keep and fixed at their full-sample values of 0.37% and 0.23% to mimic the idea of a decision maker who starts with a given prior and updates this view based on new data, while keeping the prior fixed. Figure IA.4 shows that the figure is almost the same with rolling estimates of and , and Figure IA.5 shows that this consistency arises because the rolling estimates are relatively stable.
- 40 In particular, we define a discovery as a factor for which the posterior probability of the true alpha being negative is less than 2.5%. With this definition, we start with 153 world factors. We then focus on the 119 factors that were significant in the original studies. Of these 119 factors, 98 are considered discoveries.
- 41 For the developed ex.-U.S. sample, the monthly alpha for marginal cases is 0.24% per month (), and for the emerging sample it is 0.27% (), in favor of the EB decision rule. Table IA.I reports additional details for this analysis.
- 42 Figure IA.6 shows that the results are robust to alternative values of .
- 43 Rank-weighting is similar to equal-weighting and used here to illustrate the performance of typical stocks in each size group. See equation (1) in Asness, Moskowitz, and Pedersen (2013).
- 44 Tables IA.9 and IA.10 show how tangency portfolio weights vary by region and by size group.
- 45 Figure IA.11 shows the performance of each cluster together with the market portfolio, Figure IA.12 shows how the optimal portfolio changes when one cluster is excluded, and Figure IA.14 shows the importance of each factor for the optimal portfolio.
- 46 We estimate tangency portfolio weights following the method of Pedersen, Babu, and Levine (2021), which offers a sensible approach to mean-variance optimization for high-dimensional data. Estimation details are provided in Section VI of the Internet Appendix.
- 47 The high Sharpe ratio partly reflects the fact that we are conducting in-sample optimization. If we instead run a pseudo out-of-sample analysis via cross-validation, we find a monthly Sharpe ratio of 0.56.
- 48 We abstract from uncertainty in CAPM betas to emphasize the Bayesian updating of alphas. Our conclusions are qualitatively insensitive to accounting for beta uncertainty.
- 49 As advocated by Engle and Kelly (2012) and Elton, Gruber, and Spitzer (2006), block equicorrelation constrains all pairs of factors in the same block to share a single correlation parameter, and likewise for cross-block correlations. This stabilizes covariance matrix estimates by dramatically reducing the parameterization of the correlation matrix, while leaving the individual variance estimates unchanged.




